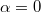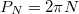Abstract
We analyze time crystal effects in a finite system of bosons which form a bright soliton clump on the Aharonov-Bohm ring. In the large particle number limit, N → ∞, this setup corresponds to the Wilczek model, where it is known that the time crystal behavior cannot be observed in the ground state of the system because a spontaneously formed soliton does not move. Here, we show that while the spontaneous formation of a moving soliton in the ground state can occur for 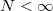 , the soliton decays before it makes a single revolution along the ring and the time crystal dynamics is impossible.
, the soliton decays before it makes a single revolution along the ring and the time crystal dynamics is impossible.
Export citation and abstract BibTeX RIS

Published by the EPLA under the terms of the Creative Commons Attribution 4.0 International License (CC-BY). Further distribution of this work must maintain attribution to the author(s) and the published article's title, journal citation, and DOI.
A genuine quantum time crystal would be a system revealing periodic evolution in its lowest-energy state. Quantum time crystals were proposed by Wilczek who considered attractively interacting bosons on a one-dimensional ring [1]. In the presence of a magnetic-like flux α penetrating the ring (the so-called Aharonov-Bohm ring), bosons were expected to form a bright soliton wave packet that would move periodically along the ring even if the energy of the system was minimal. It turned out that it was not possible because in the limit of the number of bosons N → ∞, the bright soliton that forms spontaneously in the lowest-energy solution was always stationary [2,3]. Generally, for many-body systems with two-body interactions a genuine quantum time crystals cannot be formed in the thermodynamic limit [4–6] (however, note that for multi-body interactions, a time crystal behavior in a system's ground state is possible [7]). For reviews see [8–11].
While it is clear that in the limit of N → ∞ a genuine time crystal in a soliton model proposed by Wilczek cannot exist, one may ask a question whether a glimpse of a time crystal, i.e., at least a single oscillation of a solitonic clump in the ground state, could be observed in a finite particle system (see ref. [12] and also a discussion in refs. [13–17]). In other words, is it possible that for large but finite N the lifetime of a spontaneously formed moving soliton could be at least longer than the period of its evolution along the ring? This question is addressed in the present paper.
We consider N bosons on a ring of the unit circumference which interact via contact potential in the presence of a magnetic-like flux α. The corresponding many-body Hamiltonian reads

where g0 < 0 determines the strength of the attractive interactions and we assume 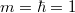 . For
. For 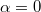 and
and  , it is known that in the mean-field description the ground state of the system breaks spontaneously the space translation symmetry and a bright soliton is formed [18]
1
. In the case of a single particle on the ring, the momentum is quantized, i.e.,
, it is known that in the mean-field description the ground state of the system breaks spontaneously the space translation symmetry and a bright soliton is formed [18]
1
. In the case of a single particle on the ring, the momentum is quantized, i.e., 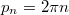 , and a proper choice of α leads to a non-vanishing probability flux along the ring. Indeed, if α is not an integer multiple of
, and a proper choice of α leads to a non-vanishing probability flux along the ring. Indeed, if α is not an integer multiple of 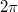 , then the particle velocity
, then the particle velocity 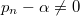 . Nevertheless, in such a case the corresponding particle density is spatially uniform due to translational invariance of the system. When we switch to the many-body case and a bright soliton forms spontaneously in the system ground state, the soliton velocity can be calculated by introducing the the center-of-mass position and the conjugate momentum which is the total momentum P of all particles. The center-of-mass energy reads
. Nevertheless, in such a case the corresponding particle density is spatially uniform due to translational invariance of the system. When we switch to the many-body case and a bright soliton forms spontaneously in the system ground state, the soliton velocity can be calculated by introducing the the center-of-mass position and the conjugate momentum which is the total momentum P of all particles. The center-of-mass energy reads

and consequently the corresponding center-of-mass velocity can be determined as follows:

where we have substituted a quantized value of the total momentum 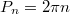 . It is clear from eq. (3) that in the limit of N → ∞ it is always possible to find such n that the velocity vanishes and the spontaneously formed bright soliton does not move in the ground state of the system. However, for
. It is clear from eq. (3) that in the limit of N → ∞ it is always possible to find such n that the velocity vanishes and the spontaneously formed bright soliton does not move in the ground state of the system. However, for 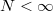 , one can always choose α which leads to a non-zero center-of-mass velocity and thus resulting in a motion of a soliton along the ring. If it is so, there is a question if the lifetime of the soliton is long enough to complete at least one full revolution along the ring before it decays due to quantum many-body effects.
, one can always choose α which leads to a non-zero center-of-mass velocity and thus resulting in a motion of a soliton along the ring. If it is so, there is a question if the lifetime of the soliton is long enough to complete at least one full revolution along the ring before it decays due to quantum many-body effects.
To address this question it is sufficient to consider 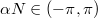 , for which the ground state corresponds to n = 0. Note that the soliton velocity is maximized when the magnetic-like flux
, for which the ground state corresponds to n = 0. Note that the soliton velocity is maximized when the magnetic-like flux 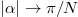 . Thus, following the idea presented in ref. [3], we analyze a density-density correlation function
. Thus, following the idea presented in ref. [3], we analyze a density-density correlation function

for 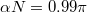 and the strength of the attractive interactions between particles given by
and the strength of the attractive interactions between particles given by 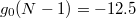 , where ψ is the bosonic field operator. Such a choice guarantees a formation of a bright soliton wave packet that propagates with 99% of the maximal velocity if we start with the ground state of the system consisting of
, where ψ is the bosonic field operator. Such a choice guarantees a formation of a bright soliton wave packet that propagates with 99% of the maximal velocity if we start with the ground state of the system consisting of 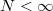 bosons. To break the space translation symmetry possessed by the ground state of the translationally invariant system we perform an initial measurement of a single boson at
bosons. To break the space translation symmetry possessed by the ground state of the translationally invariant system we perform an initial measurement of a single boson at 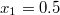 and at
and at 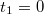 . Thanks to this, we can monitor a temporal behaviour of the single particle density after the initial measurement,
. Thanks to this, we can monitor a temporal behaviour of the single particle density after the initial measurement, 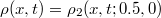 , which reveals a soliton-like wave packet propagating along the ring with the expected velocity
, which reveals a soliton-like wave packet propagating along the ring with the expected velocity  and decaying in time due to quantum many-body effects. The lifetime tc
of the soliton can be estimated basing on the contrast quantity
and decaying in time due to quantum many-body effects. The lifetime tc
of the soliton can be estimated basing on the contrast quantity

see ref. [3]. Here we define tc
as the minimal time for which 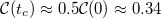 .
.
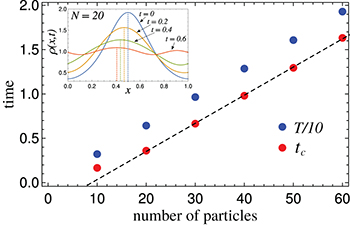
In fig. 1 we show that in the soliton model regardless of how small N one chooses, it is not possible to observe even a single revolution of a soliton before it spreads along the ring.
Fig. 1: Comparison between the lifetime tc
of the soliton and the period 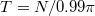 of the soliton's motion around the ring for different numbers of particles N. Note that tc
(red dots) increases linearly with N, where
of the soliton's motion around the ring for different numbers of particles N. Note that tc
(red dots) increases linearly with N, where 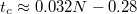 for
for 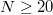 (dashed black line represents the linear fit) and is more than 10 times shorter than the period T (note that blue dots correspond to
(dashed black line represents the linear fit) and is more than 10 times shorter than the period T (note that blue dots correspond to 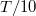 ). For illustration, in the inset we present how the soliton structure visible in
). For illustration, in the inset we present how the soliton structure visible in 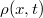 dies out in time for N = 20. Vertical dotted lines guide the eye and indicate the position of the soliton clump in four different time moments
dies out in time for N = 20. Vertical dotted lines guide the eye and indicate the position of the soliton clump in four different time moments 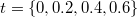 .
.
Download figure:
Standard imageOne could argue that after performing just a single particle position measurement on the ground state the symmetry broken many-body state is far from being the perfect condensate where all of the particles occupy the mean-field solution. Indeed, as shown in the inset of fig. 1, the symmetry broken state at t = 0 reveals a soliton-like clump of width larger than the width of the corresponding mean-field soliton density. The reason for this is that after the measurement of a single particle the center of mass of a resulting soliton is delocalized on a distance comparable to the width 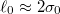 of the mean-field soliton density [8], where according to the sech approximation, the standard deviation of the mean-field soliton density is given by
of the mean-field soliton density [8], where according to the sech approximation, the standard deviation of the mean-field soliton density is given by ![$\sigma_0=\pi/[\sqrt{3}|g_0|(N-1)]$](https://content.cld.iop.org/journals/0295-5075/134/6/66001/revision1/epl20613ieqn29.gif) . As shown in ref. [3], the condensate fraction will only approach unity after the measurement of a significant fraction of particles or with increasing the initial number of particles N. The latter, however, decreases the maximal speed of revolution of the ground-state soliton and in the thermodynamic limit the soliton is stationary. On the other hand, increasing the number of measurements on the ground state at t = 0 will lead to the stronger localization of the center-of-mass position, and consequently to the smaller width of the solitonic clump. This, in turn, decreases the lifetime of the soliton, which can be understood through a very straightforward argument. Namely, a strong localization of the center of mass in the position space is equivalent to a wide distribution in the momentum space which leads to the faster spreading and to the faster decay of the soliton.
. As shown in ref. [3], the condensate fraction will only approach unity after the measurement of a significant fraction of particles or with increasing the initial number of particles N. The latter, however, decreases the maximal speed of revolution of the ground-state soliton and in the thermodynamic limit the soliton is stationary. On the other hand, increasing the number of measurements on the ground state at t = 0 will lead to the stronger localization of the center-of-mass position, and consequently to the smaller width of the solitonic clump. This, in turn, decreases the lifetime of the soliton, which can be understood through a very straightforward argument. Namely, a strong localization of the center of mass in the position space is equivalent to a wide distribution in the momentum space which leads to the faster spreading and to the faster decay of the soliton.
The above reasoning can be formulated more quantitatively. We can assume that the wave function of the center of mass after an initial measurement of a single particle is approximated by a Gaussian wave packet of width 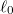 . Then, due to the time evolution by the Hamiltonian in eq. (2), its width expands as
. Then, due to the time evolution by the Hamiltonian in eq. (2), its width expands as 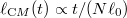 after the initial short time sublinear growth. Therefore, the decay time tc
scales as
after the initial short time sublinear growth. Therefore, the decay time tc
scales as 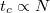 . We confirm this prediction in fig. 1. On the other hand, additional measurements of consecutive particles' positions drive the subsystem of the remaining particles the closer to the condensate product state, the more particles were measured. In the ideal situation, after the detection of a significant fraction of particles at t = 0, the symmetry-broken state describes particles occupying the same mean-field soliton solution. In such a case, according to the central limit theorem, the probability density of the center-of-mass position is given by a Gaussian with a standard deviation
. We confirm this prediction in fig. 1. On the other hand, additional measurements of consecutive particles' positions drive the subsystem of the remaining particles the closer to the condensate product state, the more particles were measured. In the ideal situation, after the detection of a significant fraction of particles at t = 0, the symmetry-broken state describes particles occupying the same mean-field soliton solution. In such a case, according to the central limit theorem, the probability density of the center-of-mass position is given by a Gaussian with a standard deviation 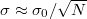 , which leads to
, which leads to 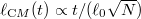 , with the decay time
, with the decay time 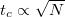 [8]. In conclusion, the measurement of many particles only deteriorates the decay time. Therefore, in this letter we consider only the best-case scenario where the symmetry of the ground state is broken by a single particle position measurement only. Note that the single particle measurement we perform is consistent with the standard symmetry-breaking definition in thermodynamic limit, where the symmetry breaking is equivalent to a periodic behavior of the second-order correlation function.
[8]. In conclusion, the measurement of many particles only deteriorates the decay time. Therefore, in this letter we consider only the best-case scenario where the symmetry of the ground state is broken by a single particle position measurement only. Note that the single particle measurement we perform is consistent with the standard symmetry-breaking definition in thermodynamic limit, where the symmetry breaking is equivalent to a periodic behavior of the second-order correlation function.
In this letter we have shown that a genuine time crystal behavior cannot be observed in a bright soliton model for a finite number of bosons N. Although the numerical simulations have been performed for a single choice of the interaction strength, 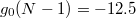 , it is a representative example of a general behavior. Since the speed of the soliton cannot be greater than
, it is a representative example of a general behavior. Since the speed of the soliton cannot be greater than 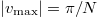 , its minimal period of the revolution around the unit ring would be equal to
, its minimal period of the revolution around the unit ring would be equal to 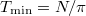 . Nevertheless, the following reasoning shows that the lifetime of the soliton tc
is also bounded from above, and cannot exceed
. Nevertheless, the following reasoning shows that the lifetime of the soliton tc
is also bounded from above, and cannot exceed 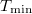 .
.
After a single position measurement at t = 0 the width of the particle distribution in the symmetry broken state 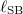 can be approximated as
can be approximated as

where 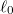 is the width of the corresponding mean-field soliton density and
is the width of the corresponding mean-field soliton density and 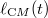 denotes a width (double standard deviation) of the Gaussian distribution describing the delocalization of the center-of-mass position. The latter quantity,
denotes a width (double standard deviation) of the Gaussian distribution describing the delocalization of the center-of-mass position. The latter quantity, 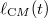 , increases in time according to the solution of the standard quantum mechanics textbook problem
, increases in time according to the solution of the standard quantum mechanics textbook problem

with the above-mentioned assumption 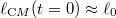 . Note that for
. Note that for 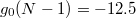 , in the sech approximation we have
, in the sech approximation we have 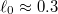 and
and 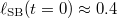 , which is consistent with our numerical results, cf. the inset of fig. 1. Let us for simplicity assume that the soliton can be recognized in the particle distribution if
, which is consistent with our numerical results, cf. the inset of fig. 1. Let us for simplicity assume that the soliton can be recognized in the particle distribution if 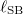 does not exceed the length of the ring, i.e., in our units, if
does not exceed the length of the ring, i.e., in our units, if 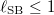 . Solving eq. (6) with respect to t, we get
. Solving eq. (6) with respect to t, we get

This simple analysis allows us to estimate the upper bound for the critical time tc , i.e.,

where the width of the mean-field soliton density corresponding to a symmetry-broken state satisfies 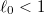 .
.
In result it is not possible to observe even a single revolution of the soliton before its decay for any choice of the system parameters. Note that the estimation was made assuming that the soliton structure becomes invisible when its width is equal to the system size. This is why the resulting upper bound for tc exceeds lifetimes presented in fig. 1. The latter were defined through the contrast quantity, eq. (5), which is a more restrictive definition of tc .
To conclude, by means of full many-body simulations we have shown that time crystal dynamics cannot be observed in a soliton model for a finite number of bosons. The reason for that is a quick decay of a spontaneously formed soliton which happens due to quantum many-body effects. We have considered a simple case where the continuous time translation symmetry of the many-body state is spontaneously broken by an initial measurement of a single particle. Although the initial measurement of many particles improves the center-of-mass localization, it simultaneously decreases the lifetime of the soliton. Our numerical simulations are consistent with a simple analytical picture for the temporal delocalization of the center of mass of the soliton. In particular, the numerical results presented here are supported by the estimation of the upper bound for the lifetime of the soliton. The latter is always smaller than the minimal period of the revolution of the soliton around the ring.
Acknowledgments
The work was supported by the National Science Centre, Poland via Projects No. 2018/28/T/ST2/00372 (AS) and No. 2018/31/B/ST2/00349 (AK and KS) and Olle Engkvists stiftelse (AS). AK acknowledges the support of Austrian Academy of Sciences' (ÖAW) ESQ-Discovery Grant.
Footnotes
- 1
On the other hand, within this model it is possible to observe time crystal behavior in an excited eigenstate of the system. Indeed, in ref. [3] it was shown that if for
 one restricts to the Hilbert subspace corresponding to
one restricts to the Hilbert subspace corresponding to  , the lowest-energy eigenstate in that subspace (which is not the ground state in the entire Hilbert space) does reveal time crystal behavior. This kind of behavior is called a symmetry protected time crystal (protected by the presence of the constant of motion PN
) but it is not the genuine time crystal [11].
, the lowest-energy eigenstate in that subspace (which is not the ground state in the entire Hilbert space) does reveal time crystal behavior. This kind of behavior is called a symmetry protected time crystal (protected by the presence of the constant of motion PN
) but it is not the genuine time crystal [11].