Abstract
We calculate the pion mass from Goldstone modes in the Higgs mechanism related to the neutron decay. The Goldstone pion modes acquire mass by a vacuum misalignment of the Higgs field. The size of the misalignment is controlled by the ratio between the electronic and the nucleonic energy scales. The nucleonic energy scale is involved in the neutron to proton transformation and the electronic scale is involved in the related creation of the electronic state in the course of the electroweak neutron decay. The respective scales influence the mapping of the intrinsic configuration spaces used in our description. The configuration spaces are the Lie groups U(3) for the nucleonic sector and U(2) for the electronic sector. These spaces are both compact and lead to periodic potentials in the Hamiltonians in coordinate space. The periodicity and strengths of these potentials control the vacuum misalignment and lead to a pion mass of 135.2(1.5) MeV with an uncertainty mainly from the fine structure coupling at pionic energies. The pion decay constant 92 MeV results from comparing the fourth-order self-coupling in an effective pion field theory with the corresponding fourth-order term in the Higgs potential. We suggest analogies with the Goldberger-Treiman relation.
Export citation and abstract BibTeX RIS

Published by the EPLA under the terms of the Creative Commons Attribution 4.0 International License (CC-BY). Further distribution of this work must maintain attribution to the author(s) and the published article's title, journal citation, and DOI.
Introduction
The dichotomous nature of the pion as both a Goldstone boson [1] and as an interaction quantum for baryons has been stressed as an enigma within the standard model [2]. We addressed this enigma in [3] and in the present work review and elaborate on the problem. We view the pion mass  as originating in a revived Goldstone mode in a slightly misaligned Higgs field vacuum where strong and electroweak degrees of freedom meet. We find the misalignment from considering the neutron to proton decay where also the leptonic sector is involved. In other words we see the massiveness of pions as following from the spontaneous breaking of the approximate isospin symmetry for the neutron and the proton. We also give a derivation of the pion decay constant
as originating in a revived Goldstone mode in a slightly misaligned Higgs field vacuum where strong and electroweak degrees of freedom meet. We find the misalignment from considering the neutron to proton decay where also the leptonic sector is involved. In other words we see the massiveness of pions as following from the spontaneous breaking of the approximate isospin symmetry for the neutron and the proton. We also give a derivation of the pion decay constant  from the fourth-order self-coupling interaction term in the Higgs potential and suggest analogies with the Goldberger-Treiman relation [1,4].
from the fourth-order self-coupling interaction term in the Higgs potential and suggest analogies with the Goldberger-Treiman relation [1,4].
Revival of Higgs field components
This section is revised from [3]. The Higgs field is a complex doublet

governed by a Higgs potential [7], see fig. 1

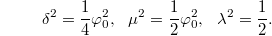
Fig. 1: A Higgs potential (cyan, eq. (2)) shaped and scaled to an intrinsic periodic potential (red "egg tray", eq. (20)) involved in the neutron to proton transition (23) [5,6]. Figure from [3].
Download figure:
Standard imageHere  are real-valued fields and
are real-valued fields and

We express the constants  in terms of the scale
in terms of the scale  given in (25) below [5,6]. Aitchison and Hey note that the simple structure in
given in (25) below [5,6]. Aitchison and Hey note that the simple structure in  —treating the
—treating the  's symmetrically— implies a global SU(2) symmetry [8]. They change notation
's symmetrically— implies a global SU(2) symmetry [8]. They change notation

to investigate this also in the generalized kinetic term of the Lagrangian and consider the covariant  derivative for zero U(1) coupling
derivative for zero U(1) coupling  ,
,

Here  contains the three SU(2) isospin generators
contains the three SU(2) isospin generators  in 2D representation. The term for the Lagrangian follows
in 2D representation. The term for the Lagrangian follows

The symmetry inferred [8] is a global isospin rotation common for the isospin vectors π and 

for an isospin rotation vector ε that leaves σ untouched.
The invariance is seen up to first order in  by direct calculation for instance in the
by direct calculation for instance in the  term where
term where  ,
,
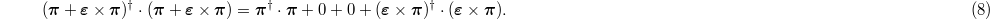
Since  (cf. p. 198 in [9]), where the (isospin) rotation generators in 3D representation are
(cf. p. 198 in [9]), where the (isospin) rotation generators in 3D representation are

one infers for finite rotations (cf. p. 200 in [9])

The finite rotation (10) immediately shows invariance,

What interests us especially here is the mass determinations. In the standard treatment  is chosen for the Higgs mechanism and the three
is chosen for the Higgs mechanism and the three  field degrees of freedom are "absorbed" in otherwise massless gauge bosons
field degrees of freedom are "absorbed" in otherwise massless gauge bosons  and Z0 which then acquire mass. Let us return to (4) to investigate the possibility of reviving the π-fields possibly with a different mass scale. First we rewrite the components of the Higgs field ϕ in a polar form [8],
and Z0 which then acquire mass. Let us return to (4) to investigate the possibility of reviving the π-fields possibly with a different mass scale. First we rewrite the components of the Higgs field ϕ in a polar form [8],

where  and
and  are dimensionless. Then we redefine the field variables to
are dimensionless. Then we redefine the field variables to

where  and
and  are dimensionful and identical to those in (4). The polar form (12) shows that the Higgs field components are open to different mass scales, one for ρ and another, common for the three π components.
are dimensionful and identical to those in (4). The polar form (12) shows that the Higgs field components are open to different mass scales, one for ρ and another, common for the three π components.
Charges from topological changes
The baryons are described as stationary states from a Hamiltonian structure [10]

on the U(3) Lie group configuration space with energy scale  and length scale a determined by the classical electron radius as
and length scale a determined by the classical electron radius as  [10,11]. This corresponds to
[10,11]. This corresponds to  at baryonic values of the fine structure coupling α inherent in re
. The Hamiltonian can be expressed via the three dynamical colour eigenangles
at baryonic values of the fine structure coupling α inherent in re
. The Hamiltonian can be expressed via the three dynamical colour eigenangles
 in the three eigenvalues
in the three eigenvalues  of the configuration variable
of the configuration variable  and six more dynamical variables spanned by the remaining six non-Abelian, off-diagonal generators of U(3). The space U(3) namely has nine degrees of freedom spanned by nine corresponding kinematical operators in laboratory space,
and six more dynamical variables spanned by the remaining six non-Abelian, off-diagonal generators of U(3). The space U(3) namely has nine degrees of freedom spanned by nine corresponding kinematical operators in laboratory space,

Here

and Sj and Mj correspond respectively to spin and the less well-known Laplace-Runge-Lenz vector (which is a constant of motion in Kepler orbits and in the hydrogen atom) [9,12]. All nine generators act as derivatives in the Laplacian [13]

where [14]

and the generators Sk and Mk take care of spin and flavour, respectively.
Equation (14) may look like the non-relativistic Schrödinger equation. But this is just a formal analogue. The configuration variable is intrinsic, i.e., it is dimensionless, just like the SU(2) space for spin. One may consider u as a generalized spin variable.
The trace potential is half the squared geodetic distance from the origo e to u, i.e.,  implies left-invariance which corresponds to gauge invariance in the laboratory space [10,15]. The potential folds out in periodic functions in eigenangle space [16]
implies left-invariance which corresponds to gauge invariance in the laboratory space [10,15]. The potential folds out in periodic functions in eigenangle space [16]

where (see fig. 1)

This opens for the introduction of Bloch phase factors in the wave function Ψ which can slightly lower the eigenvalue  [15], cf. fig. 3. The Bloch phase factors change the topology of the eigenstate and these changes are interpreted as the origin of the electrical charges. We used the Higgs field to open the Bloch degrees of freedom [5,6]. The lowered ground state is identified with the proton.
[15], cf. fig. 3. The Bloch phase factors change the topology of the eigenstate and these changes are interpreted as the origin of the electrical charges. We used the Higgs field to open the Bloch degrees of freedom [5,6]. The lowered ground state is identified with the proton.
It is possible to solve (14) accurately by a Rayleigh-Ritz method [17] for states with angular periodicity  [15]. With
[15]. With  this gives the ground state eigenvalue
this gives the ground state eigenvalue  —with 3078 base functions— at the limit of our computer programme [10,15]. Thus one gets [10,15]
—with 3078 base functions— at the limit of our computer programme [10,15]. Thus one gets [10,15]

The fine structure coupling  contained in
contained in  for
for  is obtained by sliding iteratively by radiative corrections [18] from
is obtained by sliding iteratively by radiative corrections [18] from  [11] and the result of eq. (21) is [15]
[11] and the result of eq. (21) is [15]

in agreement with the experimental value  [11].
[11].
Now consider the neutron beta decay

We already described in [5,6] the Higgs field as mediator in the topological transformation of the intrinsic nucleon state from the uncharged neutron n to the charged proton p.
From [5,6,18], we take as a fundamental relation between the strong and the electroweak regime the Ansatz among a colour angle θ and a Higgs field component φ

for the U(3) description (14) of the neutron to proton transition with strong coupling Λ and electroweak coupling α. From  shifts in the θ-values in the baryonic state we inferred from (24) the Higgs field vacuum expectation value v (see footnote
1
) determined by
shifts in the θ-values in the baryonic state we inferred from (24) the Higgs field vacuum expectation value v (see footnote
1
) determined by

This corresponds to one unit of space quantum of action hc exchanged between the electroweak and strong interaction sectors.
We are now ready to state a model for the related creation of the charge of the electron e.
The electron has spin but neither colour nor quark flavour. This leads to suggest that the electron should be accomodated into a U(2) intrinsic configuration variable where there is room for spin degrees of freedom but no room for colour nor strong flavour (as opposed to the U(3) configuration space of the baryons in (14)). A further argument for U(2) is that this is exactly the group singled out when applying the Higgs mechanism to allow the period doublings of the U(3) states in the transformation from the  -periodic neutronic ground state of (14) to the slightly lower
-periodic neutronic ground state of (14) to the slightly lower  -periodic protonic eigenstate [5,6,10]. Thus we accommodate the electron into the ground state of an intrinsic Hamiltonian on the Lie group U(2),
-periodic protonic eigenstate [5,6,10]. Thus we accommodate the electron into the ground state of an intrinsic Hamiltonian on the Lie group U(2),

with energy scale  (determined in (35)), eigenvalue
(determined in (35)), eigenvalue  and configuration variable
and configuration variable  . Note that with (26) we do not mean to imply that the electron comes in discretely excited editions. That would presumably have been discovered long ago. Rather we imply that (26) describes energy levels in the U(2) subspace into which the electron rest energy should match such that the neutron decay matches the scale of the electroweak degree of freedom set in the creation of me
c2.
. Note that with (26) we do not mean to imply that the electron comes in discretely excited editions. That would presumably have been discovered long ago. Rather we imply that (26) describes energy levels in the U(2) subspace into which the electron rest energy should match such that the neutron decay matches the scale of the electroweak degree of freedom set in the creation of me
c2.
Solving the intrinsic electron equation
The configuration variable  in (26) can be expressed as
in (26) can be expressed as

with two toroidal generators  and two off-toroidal Pauli generators
and two off-toroidal Pauli generators  . In a two-dimensional matrix representation the toroidal generators and the off-diagonal Pauli matrices read
. In a two-dimensional matrix representation the toroidal generators and the off-diagonal Pauli matrices read

The dynamical variables corresponding to the four degrees of freedom spanned by these four generators are  respectively. The above expression (27) of the configuration variable u suits the polar decomposition of the Laplacian [13]
respectively. The above expression (27) of the configuration variable u suits the polar decomposition of the Laplacian [13]

where  are dynamical toroidal eigenangles from the two eigenvalues
are dynamical toroidal eigenangles from the two eigenvalues  of the configuration variable u and [14]
of the configuration variable u and [14]

Differentiating the "sandwiched" J2 in the first term in (29) we rearrange to get

The trace potential is a sum of periodic eigenangle potentials [16]

Next we multiply (26) by J, introduce the measure-scaled wave function  and integrate over the two off-toroidal degrees of freedom,
and integrate over the two off-toroidal degrees of freedom,  to get eq. (33) with
to get eq. (33) with 
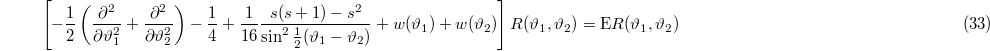
for the measure-scaled toroidal wave function  of states with intrinsic spin quantum number s. In the centrifugal potential nominator we have exploited the arbitrary labelling among
of states with intrinsic spin quantum number s. In the centrifugal potential nominator we have exploited the arbitrary labelling among  and
and  and used
and used  . Because of the arbitrary labelling of
. Because of the arbitrary labelling of  and
and  the toroidal part τ should be symmetric in these and since J is antisymmetric, so is R and we can construct R as a Slater determinant [19]. We thus expand R on
the toroidal part τ should be symmetric in these and since J is antisymmetric, so is R and we can construct R as a Slater determinant [19]. We thus expand R on

with  . We can solve (33) by a Rayleigh-Ritz method [15,17,20] to find a preliminary eigenvalue
. We can solve (33) by a Rayleigh-Ritz method [15,17,20] to find a preliminary eigenvalue  for spin
for spin  . The
. The  periodicity of the parametric potential, however, calls for the introduction of concepts from solid state physics, where Bloch phase factors are introduced into the wave function. In our case we can allow integer and half odd-integer values for p and q [15,20] while still keeping the square of the wave function single-valued on U(2).
periodicity of the parametric potential, however, calls for the introduction of concepts from solid state physics, where Bloch phase factors are introduced into the wave function. In our case we can allow integer and half odd-integer values for p and q [15,20] while still keeping the square of the wave function single-valued on U(2).
The dimensionless ground state eigenvalue  of (33) is calculated to be 2.2655(1) for 3368 base functions
of (33) is calculated to be 2.2655(1) for 3368 base functions  , which is at the limit of our computer programme. With the scale
, which is at the limit of our computer programme. With the scale  defined by
defined by

this gives  .
.
Higgs field misalignment
In the baryonic sector we introduced Bloch phase factors in the proton wave function [10,15]. Here we argue that similar phase factors, allowed by the Higgs mechanism, occur in the lepton sector during the neutron decay. For this we need to revive the massless pion modes as massive particles. The revival leads to reasonable pion masses from the resulting relation (43).
We expand the Higgs field around a misaligned vacuum with non-zero vacuum expectation values for all four degrees of freedom, thus

where  ,
,  . The fields σ and π have been shifted to live around the respective vacuum expectation values
. The fields σ and π have been shifted to live around the respective vacuum expectation values  and
and  . We may call
. We may call  the misalignment vector, see fig. 2.
the misalignment vector, see fig. 2.
Fig. 2: The Higgs potential (cyan) as a wine bottle bottom on a periodically rippled egg tray (orange). The egg tray structure is the periodic intrinsic potential scaled from the baryonic sector and the ripples are scaled from the leptonic sector. Both are active in the neutron decay where the neutron changes to a charged proton and a charge-compensating electron. The size of the ripples is grossly exaggerated for clarity (drawing for  as opposed the physical case
as opposed the physical case  in (46)). The size of the Higgs field vacuum expectation value
in (46)). The size of the Higgs field vacuum expectation value  in (25) is shown by the red line. A component of the misalignment vector
in (25) is shown by the red line. A component of the misalignment vector  introduced in (36) is shown as a rose arrow. The misalignment means that the toroidal coordinates
introduced in (36) is shown as a rose arrow. The misalignment means that the toroidal coordinates  in the leptonic sector are slightly rotated with respect to the toroidal coordinates
in the leptonic sector are slightly rotated with respect to the toroidal coordinates  in the baryonic sector, i.e., the ripples run slightly askew to the major structure. The misalignment even means a slight rotation into the third toroidal coordinate. This is not shown in the figure. The free movement of the Goldstone bosons in the Higgs potential ditch is prohibited by the periodic potentials and the pion field is caught in the ripples leading to physical pion particles with masses determined by the vacuum misalignment. Figure from [3].
in the baryonic sector, i.e., the ripples run slightly askew to the major structure. The misalignment even means a slight rotation into the third toroidal coordinate. This is not shown in the figure. The free movement of the Goldstone bosons in the Higgs potential ditch is prohibited by the periodic potentials and the pion field is caught in the ripples leading to physical pion particles with masses determined by the vacuum misalignment. Figure from [3].
Download figure:
Standard image
We collect terms of different types

The σ field mass coefficient with  and
and  from (2) becomes
from (2) becomes

Similarly, in the case of  we get
we get

Pion mass value
We are now able to determine  . There are two different intrinsic potentials at play and the U(2) potential from the leptonic sector can be thought of as ripples on the U(3) potential from the baryonic sector. We make a similar Ansatz to (24) in the leptonic sector for the U(2) description of the intrinsic electronic accommodation with torodial angles ϑ and a pionic field component
. There are two different intrinsic potentials at play and the U(2) potential from the leptonic sector can be thought of as ripples on the U(3) potential from the baryonic sector. We make a similar Ansatz to (24) in the leptonic sector for the U(2) description of the intrinsic electronic accommodation with torodial angles ϑ and a pionic field component  ,
,

Then the electron intrinsic toroidal angles are coupled to the pion fields by (41) and the free movement of the pion fields becomes prohibited by the geodetic, egg tray potential in (26) with the U(2) toroidal angles  and
and  . To get the scale of the mechanism we open a
. To get the scale of the mechanism we open a  shift of ϑ to lower the energy of the ground state by the introduction of Bloch phase factors in the intrinsic wave function in eq. (33). This corresponds to the exchange of one unit of space quantum of action hc between the pion and the lepton sector. Thus the
shift of ϑ to lower the energy of the ground state by the introduction of Bloch phase factors in the intrinsic wave function in eq. (33). This corresponds to the exchange of one unit of space quantum of action hc between the pion and the lepton sector. Thus the  shift corresponding to half odd-integer Bloch phase vectors gives the vacuum expectation value
shift corresponding to half odd-integer Bloch phase vectors gives the vacuum expectation value  of the pion field determined by
of the pion field determined by

The ratio between the σ and π field vacuum expectation values is determined by the value for  . Inserting
. Inserting  from (42) into (40) we have
from (42) into (40) we have

with  as the dimensionless ground state eigenvalue in (33). With
as the dimensionless ground state eigenvalue in (33). With  [11] this yields a pion mass
[11] this yields a pion mass  . We may condense higher-order corrections to this value by using sliding scale values of the fine structure coupling among two different scales
. We may condense higher-order corrections to this value by using sliding scale values of the fine structure coupling among two different scales  and
and  [5,6,18],
[5,6,18],

This second-order approximation is valid for small couplings and for scales not too far apart, i.e.,  and
and  . Sliding from
. Sliding from  we get
we get  . Sliding from
. Sliding from  [11] we get
[11] we get  . Taking a simple arithmetic mean between these two coarse estimates to insert for iteration in (43) we get
. Taking a simple arithmetic mean between these two coarse estimates to insert for iteration in (43) we get

Fermionic corrections to the fine structure coupling are not available at pion energies as this is outside the range of pertubative calculations. The 4–5 MeV extra mass for the charged pion partners is calculated since long as radiative corrections [1,21]. The experimental masses are  and
and  , respectively [11]. Note that
, respectively [11]. Note that  is not a free parameter. It is fixed in (42) by the electron mass in
is not a free parameter. It is fixed in (42) by the electron mass in  . The small value of
. The small value of 

corresponds to the quite different energy scales for the intrinsic electronic state and the intrinsic nucleonic state. If we interpret the scalar field σ as the Higgs particle we get a hardly distinguishable change in the predicted Higgs mass compared to that of (2),

The main uncertainty is from the fine structure coupling  which we get by sliding from
which we get by sliding from  [11]. The experimental value for the Higgs mass is
[11]. The experimental value for the Higgs mass is  [11].
[11].
Discussion and pion decay constant
The neutron decay in (23) involves changes both in the strong interaction sector and in the electroweak sector. In the strong sector the baryonic ground state undergoes a period doubling which we interpreted as a topological origin of the proton charge [10,15]. In the electroweak sector we see the creation of a corresponding opposite charge in a leptonic state. The pion field can be exploited as a degree of freedom to capture both sectors like in

where both level changes and changes in period doubling take place. We interpret the level changes in fig. 3 as the strong interaction component of the decay and the Bloch phase changes as the electroweak component giving the resulting charge reshuffling as envisaged by the dots in fig. 3.
Fig. 3: Reduced zone scheme [22] for the Delta to proton decay. The pion degrees of freedom play a double role. 1) They take up the strong interaction energy shift in the decay from level 4 to level 3. And 2) they serve as Goldstone bosons for the reshuffling of period doublings related to electroweak changes. The specific choice of Bloch phase vectors κ shown by black dots here relates to the specific decay  . Note the reshuffling in level 1 as related to the creation of the proton and emission of the pion. The band widths are exaggerated in the lower levels for clarity. Figure from [3].
. Note the reshuffling in level 1 as related to the creation of the proton and emission of the pion. The band widths are exaggerated in the lower levels for clarity. Figure from [3].
Download figure:
Standard imageThe dichotomous nature of the pion field may be expressed in a phenomenological pion model [23] with an adjusted Lagrangian like [3]

The pion fields  are incorporated in
are incorporated in

as an expansion on the isospin matrices  embedded in U(3) in the "upper left corner", with the three Pauli matrices
embedded in U(3) in the "upper left corner", with the three Pauli matrices  and where
and where  is the pion decay constant. A mass matrix
is the pion decay constant. A mass matrix  has been introduced inspired by standard phenomenological models [23] and we have introduced also an operator
has been introduced inspired by standard phenomenological models [23] and we have introduced also an operator  that projects out the upper left corner of q. The fractional mass elements in q may be interpreted as a distribution of the pion mass on three colour degrees of freedom. In total the sum of the two potential terms gives a canonical pion mass term as seen in (52)
2
. In (49) we interpret
that projects out the upper left corner of q. The fractional mass elements in q may be interpreted as a distribution of the pion mass on three colour degrees of freedom. In total the sum of the two potential terms gives a canonical pion mass term as seen in (52)
2
. In (49) we interpret  as the quark side of the dichotomy and we interpret
as the quark side of the dichotomy and we interpret  in (26) as the Goldstone side of the dichotomy with
in (26) as the Goldstone side of the dichotomy with  giving pion terms in VH
in (38). Expanding U in the first potential term of the model (49), we observe (with odd orders cancelling)
giving pion terms in VH
in (38). Expanding U in the first potential term of the model (49), we observe (with odd orders cancelling)

Taking the traces, we get the effective Lagrangian to fourth order with canonical mass term [3]

When compared with the fourth-order term  in (38) for
in (38) for  we have (2)
we have (2)

to get a satisfactory value for the pion decay constant  [3] with
[3] with  . Confer this with
. Confer this with  from sect. 71 in [11]. Combining (43) and (21) we get a more fundamental relation
from sect. 71 in [11]. Combining (43) and (21) we get a more fundamental relation

which may be considered an intrinsic edition of the Goldberger-Treiman relation [1,4]

that in subtle ways combine the pion-nucleon coupling constant  [1] from the strong interaction sector and the electroweak Gamov-Teller beta decay constant
[1] from the strong interaction sector and the electroweak Gamov-Teller beta decay constant  [1] into the semileptonic pion decay constant
[1] into the semileptonic pion decay constant  . Steven Weinberg writes on page 185 in [1] that: "... although the chiral symmetry of the strong interactions does not depend in any way on the existence of weak interactions, the (vector and axial vector) symmetry currents ... happen to be the currents entering into ... semileptonic weak interactions like nuclear beta decay." Equation (54) relates the strong and electroweak sectors because it is based on setting the electroweak energy scale (25) from the neutron beta decay to the proton (23) and shaping the Higgs potential (2) by the intrinsic potential (19) from the strong sector. The relation between strong and electroweak sectors is developed further by accommodating the electron into an intrinsic state (26) to yield a pion decay constant (54) to describe semileptonic pion decays. Weinberg's "happen to be" implying an accidental happenstance may be less of a haphazard after all.
. Steven Weinberg writes on page 185 in [1] that: "... although the chiral symmetry of the strong interactions does not depend in any way on the existence of weak interactions, the (vector and axial vector) symmetry currents ... happen to be the currents entering into ... semileptonic weak interactions like nuclear beta decay." Equation (54) relates the strong and electroweak sectors because it is based on setting the electroweak energy scale (25) from the neutron beta decay to the proton (23) and shaping the Higgs potential (2) by the intrinsic potential (19) from the strong sector. The relation between strong and electroweak sectors is developed further by accommodating the electron into an intrinsic state (26) to yield a pion decay constant (54) to describe semileptonic pion decays. Weinberg's "happen to be" implying an accidental happenstance may be less of a haphazard after all.
Conclusion
We have described the pion as a revived Goldstone boson acquiring mass from a slightly misaligned Higgs field vacuum. The misalignment is determined by energy scales from both the strong and the electroweak sectors. This yielded a pion (and Higgs) mass compatible with observation. Comparing the Higgs potential to fourth order with a hybrid pion model we derived an expression for the pion decay constant giving a reasonable value. We interpreted the expression as an intrinsic analogue of the Goldberger-Treiman relation.
Acknowledgments
We thank The Technical University of Denmark for an inspiring working environment.
Data availability statement: All data that support the findings of this study are included within the article (and any supplementary files).
Footnotes
- 1
Note that our value is related to the standard model value by the up-down quark mixing matrix element, i.e.,
 .
. - 2
The model in [23] is constructed in a similar way to yield the pion mass in a second-order expansion but with no independent way of determining the pion mass as opposed to our case where we get the pion mass from (43). The phenomenological model in [23] uses flavour quark masses together with a constant of proportionality B0 which is determined from pion and flavour quark mass ratios,
 . By enlarging the model with a strange quark to SU(3) one gets expressions also for kaon and eta masses in the lowest lying meson octet. The quark flavour masses can then be determined by fitting to experimental meson masses. From meson sum rules Donoghue, Golowich and Holstein [23] find quark mass relations
. By enlarging the model with a strange quark to SU(3) one gets expressions also for kaon and eta masses in the lowest lying meson octet. The quark flavour masses can then be determined by fitting to experimental meson masses. From meson sum rules Donoghue, Golowich and Holstein [23] find quark mass relations  and
and  which they comment by stating (p. 205) that "The u quark is seen to be lighter than the d quark with
which they comment by stating (p. 205) that "The u quark is seen to be lighter than the d quark with  . The reason why this large deviation from unity does not play a major role in the low-energy physics is that both mu
and md
are small compared to the confinement scale of QCD. This is, in fact the origin of isospin symmetry, which in terms of quark mass is simply the statement that neither mu
nor md
plays a major physical role, aside from the crucial fact that
. The reason why this large deviation from unity does not play a major role in the low-energy physics is that both mu
and md
are small compared to the confinement scale of QCD. This is, in fact the origin of isospin symmetry, which in terms of quark mass is simply the statement that neither mu
nor md
plays a major physical role, aside from the crucial fact that  . Why these two masses lie so close to zero is a question which the Standard Model does not answer." In [15] one of us (OLT) discusses flavour quark masses as a manifestation of curvatures
. Why these two masses lie so close to zero is a question which the Standard Model does not answer." In [15] one of us (OLT) discusses flavour quark masses as a manifestation of curvatures  in intrinsic orbits and finds
in intrinsic orbits and finds  which yields
which yields  and
and  at
at  from an approximate proton wave function, i.e.,
from an approximate proton wave function, i.e.,  to compare with
to compare with  [11].
[11].




















