Abstract
In this article, by using self-consistent phonon (SCP) theory, compressed sensing (CS) technology and Boltzmann transport equation (BTE), we studied the role of quartic anharmonicity in the lattice dynamics and thermal transport characteristics of Bi-based binary compounds A3Bi (A = K, Rb), with a particular focus on unraveling the impacts of quartic anharmonicity on lattice thermal conductivity 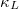 . By analyzing the phonon dispersion curve and the phonon density of states, we found that the strong quartic anharmonicity, which is mainly caused by the alkali metal atoms A1 in A3Bi (A = K, Rb), hardens the vibration frequency of the low-lying phonon branch and ensures the lattice dynamic stability. Through the relaxation time approximation of the Boltzmann transport equation, the calculated
. By analyzing the phonon dispersion curve and the phonon density of states, we found that the strong quartic anharmonicity, which is mainly caused by the alkali metal atoms A1 in A3Bi (A = K, Rb), hardens the vibration frequency of the low-lying phonon branch and ensures the lattice dynamic stability. Through the relaxation time approximation of the Boltzmann transport equation, the calculated 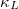 considering the three-phonon (3ph) and four-phonon (4ph) scattering process shows an ultra-low value. In addition, we also conducted a detailed analysis of the normalized lattice thermal conductivity, phonon group velocity, phonon scattering rate, and scattering phase space, revealing that the extremely low
considering the three-phonon (3ph) and four-phonon (4ph) scattering process shows an ultra-low value. In addition, we also conducted a detailed analysis of the normalized lattice thermal conductivity, phonon group velocity, phonon scattering rate, and scattering phase space, revealing that the extremely low 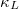 in A3Bi is mainly due to its relatively strong 4ph scattering process. Our research proves the existence of strong quartic anharmonicity in A3Bi, and we have studied in detail the influence of 3ph and 4ph scattering processes on the thermal transport properties of A3Bi, which has never been reported before.
in A3Bi is mainly due to its relatively strong 4ph scattering process. Our research proves the existence of strong quartic anharmonicity in A3Bi, and we have studied in detail the influence of 3ph and 4ph scattering processes on the thermal transport properties of A3Bi, which has never been reported before.
Export citation and abstract BibTeX RIS
Introduction
Thermal conductivity plays a vital role in the development of many modern sciences and technologies such as thermoelectric (TE) devices and transistors, and it can represent the heat conduction performance of materials under limited temperature gradients [1]. In the TE field, we need to minimize the thermal conductivity to get the best energy conversion efficiency, and high thermal conductivity is necessary for the heat dissipation of the devices in the reactor [2,3]. Therefore, semiconductors that exhibit extremely high or extremely low thermal conductivity, such as TE materials with low lattice thermal conductivity  , which have been widely studied in recent years [4–7], are worthy of our attention.
, which have been widely studied in recent years [4–7], are worthy of our attention.
The Bi-based binary compounds are very interesting compounds and have recently attracted much attention due to their unusual electronic properties [8–11]. Studies have shown that in the low-temperature hexagonal crystal structure, these compounds possess 3D Dirac states, which are protected by crystal symmetry [12], which makes them widely used in the study of various topological properties [13–15]. At present, most of the researches are on the Bi-based binary compounds in the hexagonal phase, while the research on the cubic-phase Bi-based binary compounds is very rare, this is because the traditional harmonic approximation (HA) based on density functional theory (DFT) fails in these severe anharmonic materials.
Ultra-low  and inelastic neutron scattering spectra have proved that lattice anharmonic effects are universal in thermoelectric materials [16]. In the past few decades, by including lattice anharmonic effects, people have developed a variety of methods to calculate finite temperature anharmonic phonons [17,18]. We chose the self-consistent phonon (SCP) theory from these methods [19,20]. Combined with compressed sensing (CS) lattice dynamics, the interatomic force constants (IFCs) can be quickly trained according to the required displacement and force data sets [21,22]. Phonon scattering caused by lattice anharmonicity is also a key factor that affects
and inelastic neutron scattering spectra have proved that lattice anharmonic effects are universal in thermoelectric materials [16]. In the past few decades, by including lattice anharmonic effects, people have developed a variety of methods to calculate finite temperature anharmonic phonons [17,18]. We chose the self-consistent phonon (SCP) theory from these methods [19,20]. Combined with compressed sensing (CS) lattice dynamics, the interatomic force constants (IFCs) can be quickly trained according to the required displacement and force data sets [21,22]. Phonon scattering caused by lattice anharmonicity is also a key factor that affects 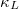 . The
. The 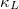 in the compound is obtained by the Boltzmann transport equation (BTE) solution with three-phonon (3ph) scattering (arising from cubic IFCs), which can successfully reveal the microscopic mechanism of high and low
in the compound is obtained by the Boltzmann transport equation (BTE) solution with three-phonon (3ph) scattering (arising from cubic IFCs), which can successfully reveal the microscopic mechanism of high and low 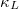 [23–25]. However, current research has found that sometimes only considering 3ph scattering can cause
[23–25]. However, current research has found that sometimes only considering 3ph scattering can cause 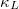 to be higher than the experimental value [26,27]. In this case, we further consider that four-phonon (4ph) scattering (arising from quartic IFCs) can reduce the obtained
to be higher than the experimental value [26,27]. In this case, we further consider that four-phonon (4ph) scattering (arising from quartic IFCs) can reduce the obtained 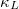 [28], which is equivalent to the experimental result, indicating the necessity of fourth-order anharmonicity.
[28], which is equivalent to the experimental result, indicating the necessity of fourth-order anharmonicity.
In summary, we use the first-principles calculation method combining SCP theory, CS lattice dynamics and BTE to calculate 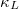 containing 3ph and 4ph scattering in the Bi-based binary compounds A3Bi (A = K, Rb), and the results show that the Bi-based binary compounds A3Bi (A = K, Rb) of the cubic phase have extremely low
containing 3ph and 4ph scattering in the Bi-based binary compounds A3Bi (A = K, Rb), and the results show that the Bi-based binary compounds A3Bi (A = K, Rb) of the cubic phase have extremely low 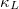 . According to previous studies, K3Bi and Rb3Bi are hexagonal phases at low temperatures, and transform to cubic phases at about 550 K and 500 K [29,30].
. According to previous studies, K3Bi and Rb3Bi are hexagonal phases at low temperatures, and transform to cubic phases at about 550 K and 500 K [29,30].
Methodology
All calculations are implemented through the density functional theory (DFT) software package Vienna Ab initio Simulation Package (VASP) [31, 32]. The projector augmented wave (PAW) [33] potentials and the exchange-correlation functional of Perdew-Burke-Ernzerhof revised for solids (PBEsol) [34] are used to emulate the ion cores and valence electrons with a cutoff energy of 600 eV. We set the criterion of the force acting on each atom to be less than 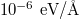 , and set the energy convergence criterion to
, and set the energy convergence criterion to 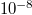 to fully optimize the primitive cell, where the k-point mesh is
to fully optimize the primitive cell, where the k-point mesh is 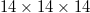 to sample the Brillouin zone.
to sample the Brillouin zone.
According to the density functional perturbation theory (DFPT) [35], we can calculate Born effective charge and dielectric tensor required by the non-analytic part of the dynamic matrix. By encoding in the ALAMODE software package, we obtained the harmonic IFCs in the 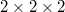 supercell using the finite displacement method, with a displacement of 0.01 Å [20,36,37], and further through the CS lattice dynamics approach to obtain cubic and quartic IFCs. To be more specific, we first simulated a 4000-step ab initio molecular dynamics (AIMD) at 300 K with a time step of 2 fs in a
supercell using the finite displacement method, with a displacement of 0.01 Å [20,36,37], and further through the CS lattice dynamics approach to obtain cubic and quartic IFCs. To be more specific, we first simulated a 4000-step ab initio molecular dynamics (AIMD) at 300 K with a time step of 2 fs in a 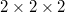 supercell to sample 80 snapshots. In order to obtain quasi-random configurations, each sample will move all atoms by 0.1 Å in a random direction. Then, we use static DFT in a
supercell to sample 80 snapshots. In order to obtain quasi-random configurations, each sample will move all atoms by 0.1 Å in a random direction. Then, we use static DFT in a 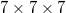 k-point mesh to calculate the Hellmann-Feynman force of each quasi-random configuration. Finally, the least absolute shrinkage and selection operator (LASSO) technique is used to estimate the anharmonic IFCs using a data set composed of displacements and forces of the 80 quasi-random configurations [38,39]. In the process of calculating harmonics and third-order IFCs, all interatomic interactions in the supercell are considered, and the quartic IFCs is considered to the fifth nearest neighbor interaction; since the fifth- and sixth-order IFCs will not change the results too much, the third and second nearest neighbor interactions are considered, respectively.
k-point mesh to calculate the Hellmann-Feynman force of each quasi-random configuration. Finally, the least absolute shrinkage and selection operator (LASSO) technique is used to estimate the anharmonic IFCs using a data set composed of displacements and forces of the 80 quasi-random configurations [38,39]. In the process of calculating harmonics and third-order IFCs, all interatomic interactions in the supercell are considered, and the quartic IFCs is considered to the fifth nearest neighbor interaction; since the fifth- and sixth-order IFCs will not change the results too much, the third and second nearest neighbor interactions are considered, respectively.
Based on the SCP theory, the anharmonic frequencies are obtained through the calculated harmonic and anharmonic IFCs. Since we used 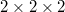 supercell when generating IFCs, a fixed
supercell when generating IFCs, a fixed 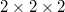 q-mesh is utilized in the reciprocal-to-real-space Fourier interpolation, and a
q-mesh is utilized in the reciprocal-to-real-space Fourier interpolation, and a 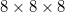 q1-mesh was further applied to the inner loop of the SCP equation [37], which is used to achieve the convergence of anharmonic phonon eigenvalues. The FourPhonon package is a revised version of the ShengBTE code [28,40,41], which is used to solve the phonon BTE. In the calculation process, a
q1-mesh was further applied to the inner loop of the SCP equation [37], which is used to achieve the convergence of anharmonic phonon eigenvalues. The FourPhonon package is a revised version of the ShengBTE code [28,40,41], which is used to solve the phonon BTE. In the calculation process, a 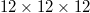 q-mesh was used to simulate the phonon wave vector. We use the iterative solution of 3ph scattering to solve the BTE, while the iterative solution of 4ph scattering is processed by single-mode relaxation time approximation (SMRTA) due to the huge computational cost.
q-mesh was used to simulate the phonon wave vector. We use the iterative solution of 3ph scattering to solve the BTE, while the iterative solution of 4ph scattering is processed by single-mode relaxation time approximation (SMRTA) due to the huge computational cost.
Results and discussion
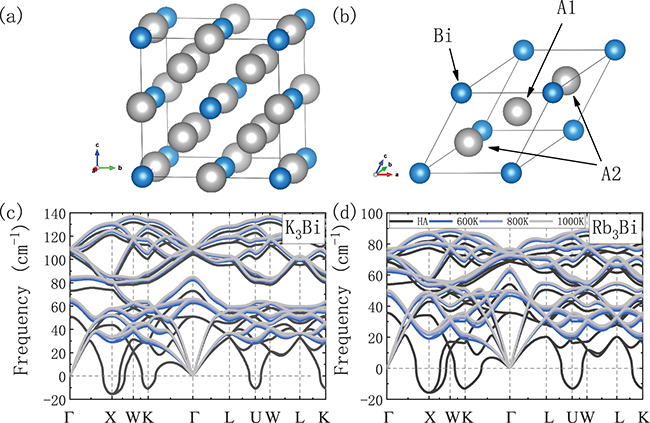
The Bi-based binary compounds A3Bi (A = K, Rb) in the cubic phase have the same lattice structure as shown in fig. 1(a) and (b), and their face-centered cubic unit cell belongs to the space group of 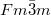 . The primitive cell of A3Bi (A = K, Rb) is composed of three A atoms (gray sphere) and one Bi atom (blue sphere) as shown in fig. 1(b), it is worth noting that only two of the three A atoms are equivalent, so we use A1 and A2 to distinguish them. The calculated lattice constants are 8.72 and 9.14 Å for K3Bi and Rb3Bi, respectively, as listed in table S1 of the Supplementary Material
Supplementarymaterial.pdf (SM) which are similar to the experimental values [29,42] and the result of Rusinov et al. [8]. In addition, we also calculated the dielectric tensor
. The primitive cell of A3Bi (A = K, Rb) is composed of three A atoms (gray sphere) and one Bi atom (blue sphere) as shown in fig. 1(b), it is worth noting that only two of the three A atoms are equivalent, so we use A1 and A2 to distinguish them. The calculated lattice constants are 8.72 and 9.14 Å for K3Bi and Rb3Bi, respectively, as listed in table S1 of the Supplementary Material
Supplementarymaterial.pdf (SM) which are similar to the experimental values [29,42] and the result of Rusinov et al. [8]. In addition, we also calculated the dielectric tensor 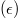 and Bonn effective charges
and Bonn effective charges 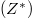 of A3Bi and listed them in table S1 of the SM.
of A3Bi and listed them in table S1 of the SM.
Fig. 1: (a) The unit cell and (b) the primitive unit cell for A3Bi (A = K, Rb), the gray and blue spheres represent the A (A = K, Rb) and Bi atom, respectively. HA and SCP phonon spectra for (c) K3Bi and (d) Rb3Bi, the black curve represents the HA result, and the blue, purple and gray curves represent the SCP results at 600, 800, and 1000 K, respectively.
Download figure:
Standard imageIn order to better study the vibration characteristics of the Bi-based binary compounds A3Bi (A = K, Rb), the phonon dispersion curves of finite temperature are calculated by solving the SCP equation [39],

Here, 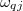 is the harmonic phonon frequency with the momentum q and the branch index j;
is the harmonic phonon frequency with the momentum q and the branch index j; 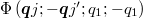 is the reciprocal representation of the fourth-order IFCs;
is the reciprocal representation of the fourth-order IFCs; 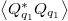 is the mean square displacement of the normal coordinate Qq
. The quartic anharmonic usually increases the frequency of low-lying rattling modes, which can be attributed to the dominant and positive contributions of the diagonal term of the quartic coefficients, for the low-lying optical modes j we have
is the mean square displacement of the normal coordinate Qq
. The quartic anharmonic usually increases the frequency of low-lying rattling modes, which can be attributed to the dominant and positive contributions of the diagonal term of the quartic coefficients, for the low-lying optical modes j we have 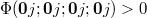 . We have drawn the phonon dispersion curves of K3Bi and Rb3Bi as shown in fig. 1(c) and (d), where black curve represents the harmonic phonon dispersion, and the anharmonic phonon dispersion at 600 K, 800 K and 1000 K are represented by blue, purple, and gray curves, respectively. Since we mentioned earlier that the temperatures at which K3Bi and Rb3Bi transform into cubic phases are 550 K and 500 K, respectively, we have only given the anharmonic phonon dispersion curves above 600 K, and we will use the calculation data at 600 K in the subsequent descriptions. The dynamic stability of materials can usually be judged by observing whether there are imaginary frequencies
. We have drawn the phonon dispersion curves of K3Bi and Rb3Bi as shown in fig. 1(c) and (d), where black curve represents the harmonic phonon dispersion, and the anharmonic phonon dispersion at 600 K, 800 K and 1000 K are represented by blue, purple, and gray curves, respectively. Since we mentioned earlier that the temperatures at which K3Bi and Rb3Bi transform into cubic phases are 550 K and 500 K, respectively, we have only given the anharmonic phonon dispersion curves above 600 K, and we will use the calculation data at 600 K in the subsequent descriptions. The dynamic stability of materials can usually be judged by observing whether there are imaginary frequencies 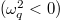 in the phonon spectrum, and through the harmonic phonon dispersion in fig. 1(c) and (d), it is obvious that there are multiple imaginary frequencies with the lowest value of
in the phonon spectrum, and through the harmonic phonon dispersion in fig. 1(c) and (d), it is obvious that there are multiple imaginary frequencies with the lowest value of 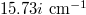 at
at 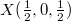 ,
, 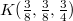 and
and 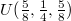 points. Comparing the results of HA phonon density of states (PDOS) in fig. 2(a) and (c), it can be found that the imaginary frequency is mainly caused by A1 (A = K, Rb). After considering quartic anharmonic renormalization based on the SCP theory, the imaginary frequency of the SCP phonon spectrum in A3Bi disappears at the considered temperature because the low-lying phonon mode frequency in the materials are significantly hardened, as shown in fig. 1(c) and (d), this is mainly due to the positive and dominant contribution of the diagonal term of the quartic coefficient to the eigenvalue of the phonon, which is usually manifested as the quartic anharmonic effect increasing the frequency of the low-lying phonon mode [27,37]. In addition, the SCP phonon dispersion curve did not change significantly as the temperature increased to 1000 K. By plotting the anharmonic PDOS at 600 K in fig. 2(b) and (d), it can be found that the vibration frequency of A1 is significantly increased and that A1 and the heavier Bi atoms contribute to the low-frequency PDOS, and the PDOS at intermediate and high frequencies is mainly contributed by the lighter A2 atoms. Through the stable structure and corresponding phonon properties, the lattice thermal conductivity
points. Comparing the results of HA phonon density of states (PDOS) in fig. 2(a) and (c), it can be found that the imaginary frequency is mainly caused by A1 (A = K, Rb). After considering quartic anharmonic renormalization based on the SCP theory, the imaginary frequency of the SCP phonon spectrum in A3Bi disappears at the considered temperature because the low-lying phonon mode frequency in the materials are significantly hardened, as shown in fig. 1(c) and (d), this is mainly due to the positive and dominant contribution of the diagonal term of the quartic coefficient to the eigenvalue of the phonon, which is usually manifested as the quartic anharmonic effect increasing the frequency of the low-lying phonon mode [27,37]. In addition, the SCP phonon dispersion curve did not change significantly as the temperature increased to 1000 K. By plotting the anharmonic PDOS at 600 K in fig. 2(b) and (d), it can be found that the vibration frequency of A1 is significantly increased and that A1 and the heavier Bi atoms contribute to the low-frequency PDOS, and the PDOS at intermediate and high frequencies is mainly contributed by the lighter A2 atoms. Through the stable structure and corresponding phonon properties, the lattice thermal conductivity 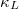 can then be calculated.
can then be calculated.
Fig. 2: The (a) harmonic phonon density of states (HPDOS) and (b) anharmonic phonon density of states (AHPDOS) at 600 K for K3Bi. (b) and (c) are same as (a) and (b) but for Rb3Bi. The embedded pictures in (a) and (b) are enlarged pictures of the imaginary frequency part.
Download figure:
Standard imageAccording to the solution of phonon BTE [43], the 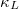 along the α-axis can be expressed as
along the α-axis can be expressed as

where ℏ and kB
are the reduced Planck constant and Boltzmann constant; T, Ω and Nq
are absolute temperature, volume of the unit cell and the number of wave vectors q, respectively; 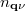 ,
, 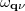 and
and 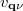 are the population, frequency and group velocity of the phonon mode
are the population, frequency and group velocity of the phonon mode 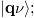 and
and 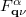 can be written as
can be written as

where 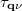 and
and 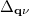 are the lifetime of phonon and correction term of the phonon mode
are the lifetime of phonon and correction term of the phonon mode  .
.
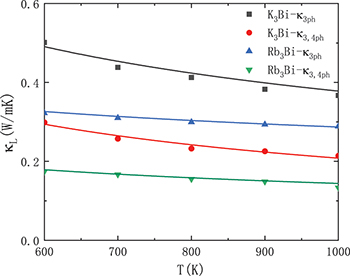
Since there is an imaginary frequency in the HA phonon dispersion curve, which indicates that it is dynamically unstable, we will not further study its related properties. The calculated SCP lattice thermal conductivity 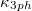 and
and 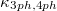 of the Bi-based binary compounds A3Bi (A = K, Rb) are plotted in fig. 3. As mentioned above, the transition temperatures of cubic phase K3Bi and Rb3Bi are 550 K and 500 K, respectively, so we only carry out calculation research on A3Bi above 600 K. It can be found from fig. 3 that A3Bi has extremely low
of the Bi-based binary compounds A3Bi (A = K, Rb) are plotted in fig. 3. As mentioned above, the transition temperatures of cubic phase K3Bi and Rb3Bi are 550 K and 500 K, respectively, so we only carry out calculation research on A3Bi above 600 K. It can be found from fig. 3 that A3Bi has extremely low 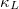 and the
and the 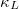 decreases with increasing temperature. For K3Bi,
decreases with increasing temperature. For K3Bi,  and
and 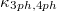 are 0.501 (0.367) and 0.299 (0.214) W/mK at 600 K (1000 K), and for Rb3Bi,
are 0.501 (0.367) and 0.299 (0.214) W/mK at 600 K (1000 K), and for Rb3Bi, 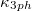 and
and  are 0.322 (0.289) and 0.174 (0.134) W/mK at 600 K (1000 K), which are much lower than classical TE materials PbTe [44] and PdTe [45], and can even be comparable to the recently discovered full-Heusler semiconductors [6] with extremely low
are 0.322 (0.289) and 0.174 (0.134) W/mK at 600 K (1000 K), which are much lower than classical TE materials PbTe [44] and PdTe [45], and can even be comparable to the recently discovered full-Heusler semiconductors [6] with extremely low 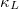 . In addition, compared to the
. In addition, compared to the 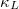 calculated by SCP + 3ph, SCP + 3,4ph can increase the total scattering rates (SRs) without changing the phonon group velocity (vph
), thereby reducing the phonon lifetime, resulting in a lower
calculated by SCP + 3ph, SCP + 3,4ph can increase the total scattering rates (SRs) without changing the phonon group velocity (vph
), thereby reducing the phonon lifetime, resulting in a lower 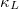 (a reduction of nearly 40% and 44% for K3Bi and Rb3Bi at 600 K). In general, a lower Debye temperature indicates a smaller
(a reduction of nearly 40% and 44% for K3Bi and Rb3Bi at 600 K). In general, a lower Debye temperature indicates a smaller  due to the enhanced phonon scattering at a given temperature. The Debye temperature of K3Bi and Rb3Bi is 125.1 K and 93.2 K, respectively, which can further confirm the extremely low
due to the enhanced phonon scattering at a given temperature. The Debye temperature of K3Bi and Rb3Bi is 125.1 K and 93.2 K, respectively, which can further confirm the extremely low 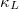 of K3Bi and Rb3Bi.
of K3Bi and Rb3Bi.
Fig. 3: The calculated lattice thermal conductivity 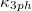 and
and 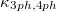 for A3Bi (A = K, Rb).
for A3Bi (A = K, Rb).
Download figure:
Standard imageGenerally, in the HA + BTE calculations, because of the changes in the Bose distribution function, the increase of temperature results in the enhanced 3ph scattering and reduces phonon lifetime [41]. There is a universal law of 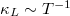 in ordinary semiconductors. However, in the present SCP + BTE calculations [37], since the effect of the changes in the Bose distribution function is offset by the frequency enhancement caused by the strong quartic anharmonic renormalization, the three-phonon scattering and phonon lifetimes of the soft modes are less sensitive to the increase of temperature. Therefore, considering that the three-phonon scattering of the soft modes plays a significant role in the final
in ordinary semiconductors. However, in the present SCP + BTE calculations [37], since the effect of the changes in the Bose distribution function is offset by the frequency enhancement caused by the strong quartic anharmonic renormalization, the three-phonon scattering and phonon lifetimes of the soft modes are less sensitive to the increase of temperature. Therefore, considering that the three-phonon scattering of the soft modes plays a significant role in the final 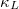 , the temperature dependence of
, the temperature dependence of 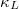 calculated from SCP + BTE is weaker than the power law of
calculated from SCP + BTE is weaker than the power law of 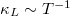 given by conventional HP + BTE method. As listed in table 1, the temperature dependences of the
given by conventional HP + BTE method. As listed in table 1, the temperature dependences of the 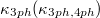 for K3Bi and Rb3Bi are
for K3Bi and Rb3Bi are 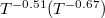 and
and 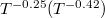 , it can be found that the temperature dependence of A3Bi has increased to a certain extent after considering 4ph scattering, making the result closer to the trend of
, it can be found that the temperature dependence of A3Bi has increased to a certain extent after considering 4ph scattering, making the result closer to the trend of  , which indicates that 4ph scattering occupies a larger proportion in the calculation of the
, which indicates that 4ph scattering occupies a larger proportion in the calculation of the 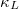 for A3Bi.
for A3Bi.
Table 1:. The contribution ratio of the three acoustic phonon branches (TA1, TA2 and LA) and the optical phonon branch to 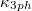 and
and 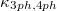 at 600 K. The temperature dependence of
at 600 K. The temperature dependence of 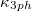 and
and 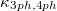 for A3Bi (A = K, Rb) is in the last column.
for A3Bi (A = K, Rb) is in the last column.
| Material | TA1 | TA2 | LA | Optic | Temperature dependence | |
|---|---|---|---|---|---|---|
| K3Bi |
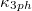
| 30.0% | 18.8% | 28.7% | 22.5% |
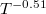
|
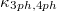
| 27.2% | 20.8% | 26.7% | 25.3% |
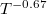
| |
| Rb3Bi |
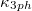
| 27.2% | 15.5% | 27.3% | 30.0% |
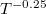
|
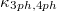
| 23.6% | 15.5% | 24.0% | 36.9% |
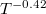
|
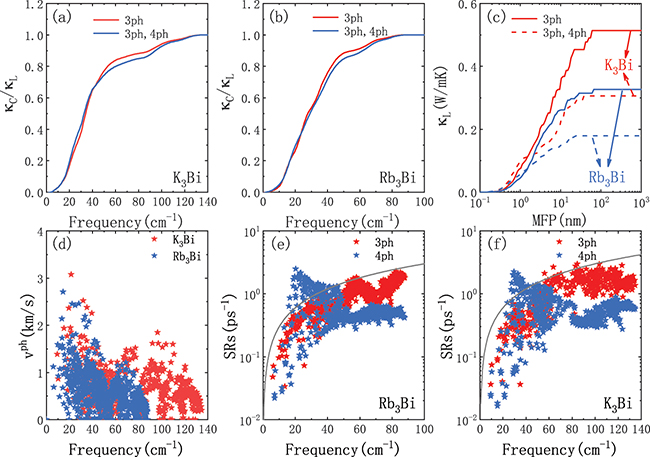
We analyzed the contribution ratio of different phonon branches to the 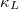 in table 1, and plotted the normalized lattice thermal conductivity
in table 1, and plotted the normalized lattice thermal conductivity 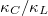 of K3Bi and Rb3Bi in fig. 4(a) and (b). The contribution of acoustic phonons to the
of K3Bi and Rb3Bi in fig. 4(a) and (b). The contribution of acoustic phonons to the  are 77.5% (74.7%) for K3Bi and 70% (63.1%) for Rb3Bi, which indicates that the
are 77.5% (74.7%) for K3Bi and 70% (63.1%) for Rb3Bi, which indicates that the  in A3Bi is mainly contributed by the low-frequency acoustic phonons. From the
in A3Bi is mainly contributed by the low-frequency acoustic phonons. From the 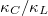 in fig. 4(a) and (b), we can also find that the slope of
in fig. 4(a) and (b), we can also find that the slope of 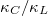 first increases and then decreases as the frequency increases, indicating that low-frequency phonons occupy the main component in the contribution of the
first increases and then decreases as the frequency increases, indicating that low-frequency phonons occupy the main component in the contribution of the 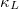 . It is worth noting that the acoustic branches of K3Bi are distinguished in fig. S5 in the SM. The results show that TA is not always the branch with the lowest frequency. However, the contribution of lattice thermal conductivity of each branch can be directly output by ShengBTE code, and the hybridization of LA and TA branches does not affect the final thermal conductivity results. In addition, in order to evaluate the influence of the size effect on the
. It is worth noting that the acoustic branches of K3Bi are distinguished in fig. S5 in the SM. The results show that TA is not always the branch with the lowest frequency. However, the contribution of lattice thermal conductivity of each branch can be directly output by ShengBTE code, and the hybridization of LA and TA branches does not affect the final thermal conductivity results. In addition, in order to evaluate the influence of the size effect on the 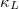 , we discussed the
, we discussed the 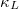 of phonon maximum mean-free path (MFP) allowed in the SCP + 3ph and SCP + 3,4ph models in fig. 4(c) to show the effect of the 3ph and 4ph processes on the size-dependent
of phonon maximum mean-free path (MFP) allowed in the SCP + 3ph and SCP + 3,4ph models in fig. 4(c) to show the effect of the 3ph and 4ph processes on the size-dependent 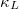 . We can see that 1) in the SCP + 3ph (SCP + 3,4ph) approximation, the total
. We can see that 1) in the SCP + 3ph (SCP + 3,4ph) approximation, the total 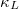 increases continuously with the increase of MFP, until
increases continuously with the increase of MFP, until 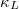 reaches the maximum value at MPF equal to 60 (38) nm for K3Bi, and 29 (22) nm for Rb3Bi; 2) in K3Bi (Rb3Bi), 4ph scattering significantly inhibits the heat conduction of carriers when the MFP is larger than 1.3 (1.6) nm; 3) the
reaches the maximum value at MPF equal to 60 (38) nm for K3Bi, and 29 (22) nm for Rb3Bi; 2) in K3Bi (Rb3Bi), 4ph scattering significantly inhibits the heat conduction of carriers when the MFP is larger than 1.3 (1.6) nm; 3) the 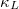 below 10 nm occupies 70% (80%) and 76% (84%) of the total
below 10 nm occupies 70% (80%) and 76% (84%) of the total  and
and 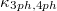 for K3Bi (Rb3Bi). Therefore, in order to significantly reduce the
for K3Bi (Rb3Bi). Therefore, in order to significantly reduce the  in A3Bi, we need to reduce the sample size below 10 nm.
in A3Bi, we need to reduce the sample size below 10 nm.
Fig. 4: The normalized lattice thermal conductivity 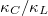 of (a) K3Bi and (b) Rb3Bi. (c)The MFP cumulative
of (a) K3Bi and (b) Rb3Bi. (c)The MFP cumulative 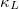 and (d) phonon group velocity vph
for A3Bi (A = K, Rb). The 3ph and 4ph SRs for (e) Rb3Bi and (f) K3Bi. All data are calculated at 600 K. The gray curves in (e) and (f) indicate that the SRs equal phonon frequency
and (d) phonon group velocity vph
for A3Bi (A = K, Rb). The 3ph and 4ph SRs for (e) Rb3Bi and (f) K3Bi. All data are calculated at 600 K. The gray curves in (e) and (f) indicate that the SRs equal phonon frequency 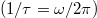 .
.
Download figure:
Standard imageThe vph
and phonon SRs are closely related to the 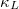 . In order to explore the difference in
. In order to explore the difference in  between K3Bi and Rb3Bi, we will conduct a detailed analysis for the vph
and phonon SRs of A3Bi (A = K, Rb). Figure 4(d) shows the vph
of A3Bi as a function of frequency. It can be found that low-frequency phonons have a larger vph
, which is consistent with our previous analysis of low-frequency phonons contributing more
between K3Bi and Rb3Bi, we will conduct a detailed analysis for the vph
and phonon SRs of A3Bi (A = K, Rb). Figure 4(d) shows the vph
of A3Bi as a function of frequency. It can be found that low-frequency phonons have a larger vph
, which is consistent with our previous analysis of low-frequency phonons contributing more 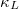 . In addition, the vph
of K3Bi is significantly higher than that of Rb3Bi, indicating that K3Bi may have a larger
. In addition, the vph
of K3Bi is significantly higher than that of Rb3Bi, indicating that K3Bi may have a larger 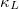 , which is consistent with the trend of
, which is consistent with the trend of 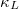 in fig. 3. Figures 4(e) and (f) show the 3ph and 4ph scattering process of A3Bi. Recent studies have shown that the acoustic mode is less affected by the 4ph scattering process compared to the optical mode [28,46], so it is surprising that the 4ph SRs of A3Bi is higher than the 3ph SRs at low frequencies. We have previously analyzed that the
in fig. 3. Figures 4(e) and (f) show the 3ph and 4ph scattering process of A3Bi. Recent studies have shown that the acoustic mode is less affected by the 4ph scattering process compared to the optical mode [28,46], so it is surprising that the 4ph SRs of A3Bi is higher than the 3ph SRs at low frequencies. We have previously analyzed that the 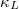 of A3Bi is mainly contributed by low-frequency phonons, while the 4ph SRs plays a major role in the low-frequency phonons, it is not surprising that
of A3Bi is mainly contributed by low-frequency phonons, while the 4ph SRs plays a major role in the low-frequency phonons, it is not surprising that 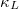 is severely suppressed when 4ph scattering process is considered. The gray solid line indicates that the SRs equal phonon frequency
is severely suppressed when 4ph scattering process is considered. The gray solid line indicates that the SRs equal phonon frequency 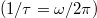 as shown in fig. 4(e) and (f), which means that the phonon lifetime is equivalent to the vibration period of the phonon quasiparticle. The 3ph and 4ph SRs are mainly distributed below the phonon quasiparticle picture curve, which supports the effectiveness of the BTE solution in this research. The only known limitation of the BTE approach is that the oscillation caused by the wave vector should have a long enough lifetime that its frequency is well defined
as shown in fig. 4(e) and (f), which means that the phonon lifetime is equivalent to the vibration period of the phonon quasiparticle. The 3ph and 4ph SRs are mainly distributed below the phonon quasiparticle picture curve, which supports the effectiveness of the BTE solution in this research. The only known limitation of the BTE approach is that the oscillation caused by the wave vector should have a long enough lifetime that its frequency is well defined 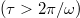 . However, the high temperature increases the scattering rate of phonons, so that phonons may not have a long enough phonon lifetime to complete an oscillation. In order to verify the effectiveness of BTE solution at high temperature, the SRs of A3Bi at 1000 K and phonon quasiparticle picture curve are presented in fig. S3 of the SM. Most of the scattering rates in fig. S3 are lower than the phonon quasiparticle picture curve, ensuring that A3Bi at 1000 K has sufficient phonon lifetime when the BTE method is used for calculation, which further verifies the accuracy of our calculation results. In addition, we show the Normal and Umklapp processes of the 4ph scatterings for A3Bi in fig. S1 of the SM. Both the Umklapp processes of K3Bi and Rb3Bi are higher than the Normal process, which shows the rationality of the SMRTA scheme used in the BTE solution to treat the 4ph scattering process.
. However, the high temperature increases the scattering rate of phonons, so that phonons may not have a long enough phonon lifetime to complete an oscillation. In order to verify the effectiveness of BTE solution at high temperature, the SRs of A3Bi at 1000 K and phonon quasiparticle picture curve are presented in fig. S3 of the SM. Most of the scattering rates in fig. S3 are lower than the phonon quasiparticle picture curve, ensuring that A3Bi at 1000 K has sufficient phonon lifetime when the BTE method is used for calculation, which further verifies the accuracy of our calculation results. In addition, we show the Normal and Umklapp processes of the 4ph scatterings for A3Bi in fig. S1 of the SM. Both the Umklapp processes of K3Bi and Rb3Bi are higher than the Normal process, which shows the rationality of the SMRTA scheme used in the BTE solution to treat the 4ph scattering process.
In order to further understand the 4ph scattering process, we show the 3ph and 4ph scattering phase spaces (P3 and P4) of A3Bi and the three independent processes that make up the P4 in fig. S2 the SM. Figures S2(a) and (b) of the SM show the variation of P3 and P4 with frequency for K3Bi and Rb3Bi, respectively. Both K3Bi and Rb3Bi have quite high P4 that can be comparable to P3, which can explain the high 4ph SRs in fig. 4(e) and (f). As shown in fig. S2(c) and (d) of the SM, the P4 can also be decomposed into three separate processes, namely, splitting 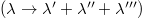 , redistribution
, redistribution  , and recombination
, and recombination 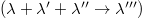 processes. Taking into account the constraints of phonon energy conservation in the scattering processes, we estimate that the splitting processes is mainly related to the high-frequency phonon modes, while the recombination processes mainly exist in the low-frequency phonon modes. The redistribution processes, which are more flexible in satisfying the energy conservation, are found to contribute many more 4ph scattering events, thus dominating the scattering phase space [47].
processes. Taking into account the constraints of phonon energy conservation in the scattering processes, we estimate that the splitting processes is mainly related to the high-frequency phonon modes, while the recombination processes mainly exist in the low-frequency phonon modes. The redistribution processes, which are more flexible in satisfying the energy conservation, are found to contribute many more 4ph scattering events, thus dominating the scattering phase space [47].
Conclusion
In summary, we calculated the A3Bi (A = K, Rb) phonon dispersion curve and the PDOS using the SCP theory considering the quartic anharmonicity, and found that the strong quartic anharmonicity, which is mainly caused by the alkali metal atoms A1 in A3Bi (A = K, Rb), hardens the vibration frequency of the low-lying phonon branch and ensures the lattice dynamic stability. Through the RTA of the BTE, the calculated 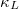 considering the 3ph and 4ph scattering process shows an ultra-low value, which is 0.299 (0.214) and 0.174 (0.134) W/mK for K3Bi and Rb3Bi at 600 K (1000 K). In addition, we also conducted a detailed analysis of the normalized lattice thermal conductivity,
considering the 3ph and 4ph scattering process shows an ultra-low value, which is 0.299 (0.214) and 0.174 (0.134) W/mK for K3Bi and Rb3Bi at 600 K (1000 K). In addition, we also conducted a detailed analysis of the normalized lattice thermal conductivity, 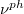 , phonon SRs, and scattering phase space, revealing that the extremely low
, phonon SRs, and scattering phase space, revealing that the extremely low 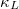 in A3Bi is mainly due to its relatively strong 4ph scattering process. In order to further study the method of reducing the
in A3Bi is mainly due to its relatively strong 4ph scattering process. In order to further study the method of reducing the 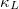 of A3Bi, we also studied the size-dependent cumulative lattice thermal conductivity of A3Bi. The results show that controlling the sample size below 10 nm can effectively reduce the
of A3Bi, we also studied the size-dependent cumulative lattice thermal conductivity of A3Bi. The results show that controlling the sample size below 10 nm can effectively reduce the 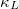 of A3Bi. Our research prove the existence of strong quartic anharmonicity in A3Bi, and we have studied in detail the influence of 3ph and 4ph scattering processes on the thermal transport properties of A3Bi, which has never been reported before.
of A3Bi. Our research prove the existence of strong quartic anharmonicity in A3Bi, and we have studied in detail the influence of 3ph and 4ph scattering processes on the thermal transport properties of A3Bi, which has never been reported before.
Acknowledgments
This research was supported by the National Natural Science Foundation of China under Grant No. 11974302, and No. 12174327.
Data availability statement: All data that support the findings of this study are included within the article (and any supplementary files).