Stick-slip contact line motion on Kelvin-Voigt model substrates

The capillary interaction of liquids with soft solids is a ubiquitous situation in natural or technological settings [1–4], ranging from droplets that interact with epithelia, for instance in the human eye [5], or epithelial cells governed by capillary physics [6], to ink-jet printing on flexible materials [7]. The capillary tractions, exerted by the liquid onto their soft support, cause strong deformations if the substrate is soft or the considered length scale is sufficiently small [8,9]. The typical scale below which capillarity deforms solids is given by the elastocapillary length, $\ell = \gamma/G_0$, the ratio of surface tension γ and static shear modulus G₀. At three-phase contact lines, the length scale of the exerted traction lies in the molecular domain, deforming the solid into a sharp-tipped wetting ridge [10]. As a liquid spreads over a soft surface, the traction moves relative to the material points of the substrate. The necessary rearrangement of the solid deformation leads to strong viscoelastic dissipation which counteracts the motion, a phenomenon called viscoelastic braking [11–19]. At small speeds, the motion remains steady [11,12], whereas, at large speeds, unsteady motion, frequently termed stick-slip, has been observed [13,20–24]. In this mode, the contact line velocity and the apparent contact angle undergo strong, periodic oscillations. On paraffin gels, Kajiya et al. observed stick-slip motion only in an intermediate velocity range, returning to continuous motion if the speed was increased even further [21].

The origin of this stick-slip motion remains debated in the literature. It is clear that the pinning and depinning is not associated with permanent surface features, but rather with the dynamics of the wetting ridge itself: the solid deformation cannot follow the fast contact line motion of the depinned (slip) phase of a stick-slip cycle [23,24]. Unclear, however, are the conditions upon which a contact line may escape from its ridge, thus eliminating the viscoelastic braking force. The depinning of a contact line from a sharp-tipped feature on a surface is governed by the Gibbs inequality [23,25]. Van Gorcum et al. [23] postulated a dynamical solid surface tension, which would alter the local force balance and thus allow the contact line to slide down the slope of the ridge. Still, the physico-chemical origin of such dynamic solid surface tension remains elusive. Roche et al. [15] postulated the existence of a point force due to bulk viscoelasticity, but the shear-thinning nature of typical soft polymeric materials would prevent such a singularity at the strain rates encountered in soft wetting [24,26]. Unclear as well is the role of the fluid phase during the cyclic motion, mainly because a comprehensive multi-physics model for the unsteady soft wetting problem is not available to date.

Here we present the first fully unsteady numerical simulations of dynamical soft wetting, fully accounting for liquid and solid mechanics, and for the capillarity of the interfaces, by which we reveal the life cycle of stick-slip motion. We derive phase diagrams of steady and unsteady contact line motion by tuning parameters over large ranges, recovering stick-slip behavior at intermediate speeds. At small and large speeds, we observe steady motion, in quantitative agreement with an analytical model.

Figure 1(a) shows the geometric setup of the numerical simulations. A hollow cylinder (undeformed inner radius R), made of a soft viscoelastic material (gray, thickness $h_s\ll R$), with a fixed (rigid) outer surface, is partially filled with a liquid (blue) and an ambient fluid phase (transparent). To keep physics conceivable, we use a minimal model and apply the Stokes limit and identical viscosities for fluid and ambient, and assume constant and equal surface tensions $\gamma=\gamma_s$ on all interfaces (liquid-ambient, solid-liquid, and solid-ambient). The inner surface of the soft viscoelastic cylinder wall is deformed into a wetting ridge due to the capillary action of the liquid meniscus (cf. panel (b)). We use an incompressible Kelvin-Voigt constitutive model, characterized by a frequency-dependent complex modulus $G^* = G_0 + i\,\eta_s\,\omega$, with static shear modulus G₀ and effective substrate viscosity $\eta_s$, obtaining an elastocapillary length $\ell = \gamma/G_0 \ll h_s$, a characteristic time scale $\tau = \eta_s/G_0$, and an elastocapillary velocity $v_{\ell} = \ell/\tau=\gamma/\eta_s$.

Zoom In Zoom Out Reset image size

Our numerical model is formulated with cylindrical symmetry, implementing the two-phase fluid by a phase field approach. Thus the liquid-ambient interface has a finite thickness $\epsilon \ll \ell \ll h_s$, and the capillary traction of the meniscus onto the solid is distributed over this characteristic width. The solid is modelled by a finite element approach, with a sharp interface toward the fluid. The grid size is about $5\%$ of the elastocapillary length at the liquid-ambient interface, and typically about $20\%$ outside of the interface region. All phases are fully coupled to each other by kinematic and stress boundary conditions. The material parameters are listed in table 1, details on the numerical model are given in [27] and the Supplementary Material Supplementarymaterial.pdf (SM). The liquid meniscus is forced to move by imposing the fluxes Φ on either end of the cylinder, but can freely change its shape (curvature) in response to the fluid flow. Thus the instantaneous contact line velocity v is not imposed, but rather its long-term mean $\overline{v} = \Phi/(\pi\,R^2)$. All simulations are started at t = 0 with a flat substrate, a flat meniscus, and a constant imposed flux at the boundaries, and run until a steady state or limit cycle has been reached.

Table 1:.  Material parameters.

Symbol	Value	Meaning
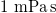
η	$1\ \text{mPa s}$	Liquid viscosity
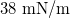
γ	$38\ \text{mN/m}$	Liquid surface tension
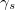
$\gamma_s$	$38\ \text{mN/m}$	Solid surface tension
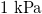
G0	$1\ \text{kPa}$	Static shear modulus
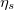
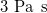
$\eta_s$	$3\ \text{Pa s}$	Substrate viscosity
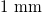
hs	$1\ \text{mm}$	Substrate thickness
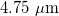
	$4.75\ \mu \text{m}$	Interface thickness
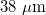
ℓ	$38\ \mu \text{m}$	Elastocapillary length
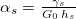
$\alpha_s = \frac{\gamma_s}{G_0\,h_s}$	0.038	Elastocapillary number
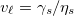
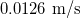
$v_{\ell}=\gamma_s/\eta_s$	$0.0126\ \text{m/s}$	Elastocapillary velocity

We compare our simulation results for the solid deformation to the analytical plane-strain model from [13], imposing a constant contact line velocity $v=\overline{v}$ and replacing the δ-shaped traction by

$$\begin{equation} T(x) = \frac{3 \gamma}{4 \sqrt{2}\, \epsilon } \left(1-\tanh^2\left(\frac{x - v t}{\sqrt{2}\,\epsilon }\right)\right)^2, \end{equation} \tag{ 1 }$$

which can be derived for the phase field model in equilibrium (see the SM for details). Since $h_s\ll R$, the substrate deformation is well approximated by plane-strain conditions. Importantly, since $\epsilon \ll \ell$, our analytical and numerical results do not significantly depend on the actual value of . Figure 1(b) shows the quasi-stationary substrate deformation for several imposed velocities, comparing simulation results (markers) to the analytical model (lines), in excellent agreement. Note that this comparison is only possible as steady ridge shapes are observed for the chosen velocities. We chose a static ridge $(\overline{v}=0)$ and very fast ridges $(\overline{v}/v_{\ell}>6)$, where shapes are significantly different from the static case. One important feature of fast ridges is the emergence of a dissipative "bump", well behind the contact line (see the SM for details about the ridge geometry). In an intermediate velocity range we find unsteady cyclic shape dynamics, as detailed below, which cannot be grasped by the analytical model.

The dynamics of the contact line motion are characterized by the time-dependent contact line velocity v(t) and rotation $\phi = \theta-\theta_{eq}$ of the liquid interface at the triple line (cf. fig. 1(a)). In the following, we focus on the three characteristic regimes that we find in our simulations, corresponding to small, intermediate, and large $\overline{v}$. Due to the large differences in $\overline{v}$, the dynamics are best compared by plotting ϕ as a function of contact line position (fig. 2; see the SM for plots of v(t) and $\phi(t)$.) At small speed ($v\lesssim v_{\ell}$, blue), after some initial transient the contact line moves steadily, with a constant speed and a constant dynamic contact angle. Here, the relation between v and ϕ is permanently dominated by viscoelastic braking [11–13]. Once the forcing velocity exceeds a critical value, the motion becomes unsteady, finding a limit cycle after an initial transient (red): the liquid interface rotation ϕ shows large oscillations, of peak-to-peak amplitude Δϕ on the order of the mean rotation $\overline{\phi}$, with a non-trivial waveform, as the contact line advances at an oscillatory speed v(t) (see fig. 3 and the SM). This behavior is not captured by the simple analytical model. For larger speeds (yellow), we observe again constant v and ϕ after an initial transient. We note here that the motion in this regime is very sensitive to discretization artifacts and requires rather fine grid resolutions to give consistent results. Supplementary movies Movie1_v0.27_(blue_curve).m4v, Movie2_v3.47_(red_curve).m4v, Movie3_v3.89_(yellow_curve).m4v illustrate contact line motion and substrate dynamics for the three modes in fig. 2.

Zoom In Zoom Out Reset image size

Figure 3 shows a phase portrait of the contact line motion, i.e., in terms of the physically relevant variables ϕ and v: $\phi=\theta-\theta_{eq}$ is a measure of the imbalance in Young's equation, and thus a measure of the total dissipative force (liquid and solid). Multiplying by the instantaneous velocity, one obtains the total dissipated power per unit length of contact line, since our equations of motion are overdamped. For slow forcing speeds (blue), we observe a continuous, steady contact line motion, up to the scale of grid artifacts (mind the logarithmic scales). For intermediate forcing speeds (red), we observe a limit-cycle: As the liquid rotation exceeds a well-defined maximum (${\unicode{9312}}$ in fig. 3), the contact line accelerates. In this phase, it surfs down its own wetting ridge, releasing energy stored in the meniscus curvature, rate-limited partly by liquid dissipation (${\unicode{9313}}$ in fig. 3). It thus decelerates, and a new wetting ridge starts to grow, opposing the contact line motion further (${\unicode{9314}}$ in fig. 3) until the next cycle starts. For larger forcing speeds, the region covered by the limit cycle decreases until it virtually vanishes (yellow), up to grid artifacts. This is caused by the growing importance of liquid dissipation, which effectively limits, and finally prevents, the large-speed excursions during the slip phases.

Zoom In Zoom Out Reset image size

We characterize the contact line motion by $\phi_{max}$ (${\unicode{9312}}$ in fig. 3), $\phi_{min}$ (${\unicode{9314}}$ in fig. 3), and $\overline{\phi}$, the maximum, minimum, and mean values of ϕ, respectively, in the stationary/limit cycle regime. Figure 4 shows these values as a function of the imposed (long-term mean) $\overline{v}$. For small speeds, $v=\overline{v}$, and the simulated ϕ (symbols) coincides with the result of the analytical model (black line), indicating the stability of steady contact line motion.

Zoom In Zoom Out Reset image size

The onset of stick-slip motion (gray region) aligns with the maximum of ϕ observed in the analytical model where v is imposed instead of $\overline{v}$. This was stipulated in [13] since the rotation ϕ is a measure for the dissipative (viscoelastic braking) force: A dissipative force that decreases with speed causes acceleration, and thus an unstable motion. The maximum braking force is observed at $\overline{v} \sim v_{\ell} = \gamma_s/(G_0\,\tau) = \gamma_s/\eta_s$, the elastocapillary velocity: The finite width of the traction distribution regularizes the dissipation singularity at the scale $\epsilon\ll\ell\ll h_s$. Thus the largest characteristic frequency $\omega \sim \overline{v}/\epsilon$ dominates the dissipation associated with the contact line motion. One may evaluate the complex modulus at the dominant frequency to define a dynamical elastocapillary length $\ell_{\overline{v}}\sim\gamma_s/|G^*(\overline{v}/\epsilon)|$ [23]. Near the maximum braking force, $G''(\overline{v}/\epsilon) = \eta_s\,\overline{v}/\epsilon \gg G_0$, and we approximate $|G^*|\sim \eta_s\, \overline{v}/\epsilon$ to obtain $\ell_{\overline{v}} = \gamma_s\,\epsilon/(\eta_s\,\overline{v})$. Resonance is expected at $\epsilon\sim\ell_{\overline{v}}$, i.e., $\overline{v}\sim\gamma_s/\eta_s$, independent of the choice of , which is confirmed in our analytical model (see the SM). $\phi_{max}$ remains approximately constant upon entering the stick-slip regime, indicating a well-defined upper limit of the viscoelastic braking force also in unsteady situations (cf. location ${\unicode{9312}}$ in fig. 3). However, this force periodically drops to much smaller values, as indicated by the much smaller values of $\phi_{min}$. In these surfing phases (${\unicode{9313}}$ in fig. 3), liquid dissipation and the finite capillary energy stored in the curved meniscus are the rate-limiting factors.

As the imposed $\overline{v}$ is increased further, the amplitude of the oscillation Δϕ shrinks, reaching virtually zero (indicated by the fading gray region). In this regime, the reduced viscoelastic braking force $(\phi_{max})$ limits the build-up of capillary energy in the meniscus, while liquid dissipation prevents its fast release. This balance between capillarity and liquid dissipation can be quantified by the capillary number $\mathrm{Ca} = \overline{v}\,\eta/\gamma = (\gamma_s/\gamma)(\eta/\eta_s)(\overline{v}/v_{\ell})$. If $\mathrm{Ca}$ exceeds a certain critical value $\mathrm{Ca}_{\mathrm{c}}$, the oscillatory motion is effectively damped out by liquid dissipation. $\mathrm{Ca}_{\mathrm{c}}$ depends on the solid parameters, most notably the ratio $\gamma/\gamma_s$ which sets the scale of ϕ. Further, decay and growth rates of abandoned and new ridges during the stick-slip cycle matter, and thus we expect also some dependence on $\eta_s$. For $\mathrm{Ca}\gtrsim\mathrm{Ca}_{\mathrm{c}}$, the overall motion is still governed by viscoelastic braking: $\overline{\phi}\sim \overline{v}^{-1}$ closely follows the result from the analytical model. The increased mean liquid rotation for the largest velocity ${\sim}28 v_{\ell}$, relative to the prediction of the analytical model, is another consequence of liquid dissipation. This can be rationalized by a comparison with the Cox-Voinov law for moving contact lines on rigid surfaces which predicts, for $\mathrm{Ca} \sim 10^{-2}$, rotations of this order of magnitude [28–30]. In this hydrodynamic regime, one returns to the classical wetting physics on rigid surfaces.

Zoom In Zoom Out Reset image size

In fig. 5, we summarize the dynamical wetting behavior in terms of these three modes, as a function of the imposed mean speed and the solid parameters. Steady small-speed, stick-slip, and steady high-speed modes are indicated by blue, red, and yellow discs, respectively. On panel (a), we vary on the vertical axis the solid and liquid surface tensions and thus the elastocapillary number $\alpha_s = \ell / h_s$, while keeping the Neumann angles of static wetting constant. Since G₀ and h_s merely enter $\alpha_s$, they are not varied separately but their effect can be extracted from fig. 5(a). The onset of stick-slip is located near $\overline{v}=v_{\ell}$, given by the maximum of ϕ vs. v. This maximum is independent of $\alpha_s$, up to a small correction due to the finite thickness of the fluid interface, as can be shown by the analytical model (see fig. 1 of the SM). In physical units, however, the onset of stick-slip is inversely proportional to $\gamma_s$ since $v_{\ell} \sim \gamma_s$. The transition to the fast continuous mode is, in scaled units, nearly independent of the surface tension. This can be rationalized again by a critical capillary number: since we tuned γ and $\gamma_s$ simultaneously, the scale of $\phi\sim\gamma/\gamma_s$ [13] remains constant, and neither $\mathrm{Ca}_{\mathrm{c}}$, nor $\mathrm{Ca}\sim (\gamma_s/\gamma)(\overline{v}/v_{\ell})$ changes along the vertical axis. The stick-slip mode disappears at very low $\gamma=\gamma_s$, where ℓ∼.

Similarly, the solid viscosity $\eta_s$ (panel (b)) has no measurable impact on the critical $v/v_{\ell}$ for the transition to stick slip since the maximum ϕ, which governs this transition, is independent of $\eta_s$. Still, the physical critical velocity is proportional to $\eta_s$ since $v_{\ell}\sim\eta_s^{-1}$. The transition to the fast continuous mode behaves differently. $\mathrm{Ca}\sim (\eta/\eta_s)(\overline{v}/v_{\ell})$ increases with decreasing $\eta_s$, and the damping effect of liquid dissipation becomes noticeable already at smaller $\overline{v}/v_{\ell}$. Thus the transition back to steady motion occurs earlier, such that the stick-slip region ultimately disappears at very low $\eta_s$. In any case, at very large speeds, liquid dissipation will take over, leading to wetting dynamics equivalent to those on rigid surfaces.

In this letter, we provide a comprehensive numerical analysis of dynamical soft wetting, including the physics of all relevant elements, the liquid, the solid, and the interfaces. For each element, we used the minimal required level of complexity, to keep physics intact and conceivable: The Stokes limit for the fluid, a Kelvin-Voigt constitutive relation for the soft solid, regularized at a constant scale $\epsilon \ll \ell$, and constant and equal solid surface tensions on all three interfaces. This simple model already requires a complex, strongly coupled multi-physics modelling approach, and exhibits rich behaviors.

Our numerical experiments cover a wide range of system parameters, and we reveal three regimes in which the dominant physical mechanisms differ: i) a slow regime, in which the contact line motion is entirely dominated by the dissipation in the solid. This regime is observed as long as the viscoelastic braking force increases with speed. ii) an intermediate regime, in which the dominant rate-limiting mechanism periodically switches from solid to liquid dissipation. This regime starts where the viscoelastic braking force exhibits a maximum with respect to the contact line velocity. This maximum is caused by a resonance effect, due to the regularization of a singular dissipation at some finite (constant) length scale. Other mechanisms, like dynamic solid surface tensions (surface constitutive relations [23,31–35]) or a constitutive relation that exhibits resonance (e.g., standard-linear solid [13]) would lead to the same phenomenology. iii) a ${\text{large}}-\overline{v}$ regime with continuous motion, yet governed by viscoelastic braking, in which liquid dissipation prevents strong oscillations of the meniscus. This regime, and especially the transition into it, is based on a strong coupling between solid and fluid physics, and has so far, to the best of our knowledge, been reported only in a single experimental work [21]. Since the viscoelastic braking force, in contrast to liquid dissipation, does not increase with velocity, we ultimately find again liquid dissipation dominating the contact line motion, and one recovers the wetting physics of rigid surfaces.

With this first comprehensive overview of soft wetting physics scenarios, we provide a strong basis for interpreting the different phenomenology observed in experiments, ranging from paraffins [21] over microelectronic sealants [8,23] to biology [5,6,36] and motivate experiments on the the so-far little explored transition to continuous motion beyond stick-slip.

SK and SA acknowledge funding by the German Research Foundation (DFG project No. KA4747/2-1 to SK and AL1705/5-1 to SA). Simulations were performed at the Center for Information Services and High Performance Computing (ZIH) at TU Dresden.

Data availability statement: The data that support the findings of this study are available upon reasonable request from the authors.