Abstract
We present an updated analysis of the total expression for the Aharonov-Bohm (AB) phase of a charged particle in an electromagnetic field, which we previously obtained through the superposition principle for quantum phases of charges and dipoles (Sci. Rep., 8 (2018) 11937), and here we re-derive it directly in the framework of the general approach, when the source, the electromagnetic field and the charged particle are quantized. The disclosure of the full set of quantum phase effects for a moving charged particle allows an important update of the wave-particle duality concept by generalizing the de Broglie relationship, where the wave vector associated with the particle is proportional to the vector sum of the mechanical and interactional electromagnetic momenta.
Export citation and abstract BibTeX RIS
Introduction
In our recent papers [1,2] devoted to the analysis of quantum phase effects for charges and dipoles, we predicted two new fundamental quantum phases for moving charged particles, which we have named as the complementary magnetic Aharonov-Bohm (AB) phase given by the equation

and complementary electric AB phase defined as

which should therefore be added to the well-known magnetic AB phase

and electric AB phase

Here
A
,  are the vector and scalar potentials, correspondingly,
v
is the velocity of charge,
are the vector and scalar potentials, correspondingly,
v
is the velocity of charge,  is the path element, and other designations are standard.
is the path element, and other designations are standard.
We remind that the prediction of complementary AB phases (1), (2) has been made through the analysis of the full set [3] of quantum phase effects for dipoles with application of the principle of superposition of quantum phases (SQP), where the phase of a dipole is presented as a superposition of quantum phases for all charges composing the dipole.
The validity of SQP follows from the linearity of the fundamental equations of quantum mechanics and, as we have shown in [1], the full set of quantum phases for moving dipoles disclosed in [3] consists of three fundamental phases (1)–(3) for moving point-like charges, which fulfils the requirements of the SQP principle (see the next section).
Despite the fact that the complementary AB phases (1), (2) are v/c times smaller than the corresponding AB phases (3) and (4), they play an important role in the clarification of the physical meaning of the AB effect, and lead to important implications for the entire quantum physics, as we discuss below.
This makes the problem of direct derivation of complementary AB phases (1) and (2) through some general principles of quantum physics applied to the system "source, charge and their electromagnetic (EM) field" topical, and at the moment, this problem remains still unsolved.
As we will show below, a first step towards solving this problem was made in ref. [4], where in the framework of a fully quantum model (where the source, the EM field and the charged particle are quantized), the authors of ref. [4] derived a new expression for the "point-by-point" quantum phase, aimed to elucidate the primary role of EM fields over EM potentials in the determination of the AB phase.
In the present contribution, we will show that further development of the approach of [4] allows us to derive directly a full set of quantum phase effects for point-like charges (1)–(4), including complementary magnetic (1) and complementary electric (2) AB phases.
We discuss the importance of this finding and conclude in the last section.
Quantum phase effects for charges and dipoles
We remind that, by the end of the 20th century, two quantum phase effects for moving dipoles had been predicted: the Aharonov-Casher (AC) effect for a magnetic dipole m in an electric field [5], and the He-McKellar-Wilkens (HMW) effect for an electric dipole p in a magnetic field [6,7], and both of them have later been confirmed by experiments [8,9].
At the same time, the derivation of the AC and HMW phases was carried out in [5–7] with particular expressions for the Lagrangian of a dipole in an EM field, which left unanswered the question of the possible existence of other quantum phases for dipoles.
Seeking an answer to this question, we proposed [3] to use the covariant expression for the Lagrangian density of a material medium in an EM field [10]
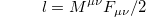
(where  is the magnetization-polarization tensor, and
is the magnetization-polarization tensor, and  is the tensor of EM field) to determine the corresponding Lagrangian L and the Hamilton function
is the tensor of EM field) to determine the corresponding Lagrangian L and the Hamilton function  for a compact dipole. Then, going to the quantum limit and defining the corresponding Hamiltonian, we discovered the quantum phase of the moving dipole as the sum of four components, which in the weak relativistic limit, up to the terms of order
for a compact dipole. Then, going to the quantum limit and defining the corresponding Hamiltonian, we discovered the quantum phase of the moving dipole as the sum of four components, which in the weak relativistic limit, up to the terms of order 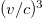 , reads [1,2]
, reads [1,2]

with all quantities evaluated in a labframe.
The first and second terms on the r.h.s. of (5) correspond to the AC and HMW phases, respectively, while the third and fourth terms thus stand for new quantum phases associated with the motion of an electric dipole in an electric field, and the motion of a magnetic dipole in a magnetic field.
The disclosure of four quantum phase effects for moving dipoles definitely makes the physical interpretation of each term of eq. (5) topical, which should be based on some unified and general physical principle, equally applicable to each component of phase (5). Such a general principle of SQP has been advanced in refs. [1,2], where we assumed that due to linearity of fundamental equations of quantum mechanics, the quantum phase for a dipole should be presented as a superposition of quantum phases for all charges composing the dipole.
Exploring this idea, it is convenient to introduce the scalar potential and the vector potentials for the EM field, as well as the charge density  and the current density
and the current density  for dipoles, where
u
is the flow velocity of carriers of current in the rest frame of the magnetic dipole. After some calculus, we have obtained [1,2]
for dipoles, where
u
is the flow velocity of carriers of current in the rest frame of the magnetic dipole. After some calculus, we have obtained [1,2]




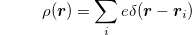
for an electrically neutral dipole (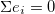 ), we found that the HMW phase
), we found that the HMW phase  (6b) represents the algebraic sum of the magnetic AB phases (3) over all charges of the electric dipole, while the phase
(6b) represents the algebraic sum of the magnetic AB phases (3) over all charges of the electric dipole, while the phase 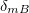 (6d) can be presented as the sum of the complementary magnetic phases (1) over all charges of the magnetic dipole [2]. Next, addressing to the AC phase
(6d) can be presented as the sum of the complementary magnetic phases (1) over all charges of the magnetic dipole [2]. Next, addressing to the AC phase 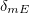 (6a) and the phase
(6a) and the phase  (6c) we revealed their common origin as the composition of the complementary electric AB phases (2) for all charges of the dipoles [2].
(6c) we revealed their common origin as the composition of the complementary electric AB phases (2) for all charges of the dipoles [2].
Therefore, experimental confirmation [8] of the AC phase (6a) concurrently serves as the validation of the complementary electric AB phase (2), which already leaves no doubts about the existence of the complementary magnetic AB phase (1), too, although direct measurement of the phase 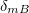 (6d) is still required.
(6d) is still required.
Note that the electric AB phase (4) cannot contribute to the total quantum phase (5) for a moving dipole, where its components explicitly depend on the velocity of dipole v . At the same time, it is well known that the electric AB phase does not explicitly depend on the velocity of the charge, and can exist already for a charge at rest.
Anyway, three velocity-dependent phases (1)–(3) are sufficient to explain the full set of quantum phases for a moving dipole (5) by applying the SQP principle [2].
In this situation, the direct derivation of complementary AB phases for a point-like charge in an EM field acquires a fundamental importance, which thus represents the principal new point of the present contribution.
As we mentioned in the introduction section, a first step towards the solution of this problem has been recently made in ref. [4] on the basis of a general model, where a charged particle, a source and its electromagnetic (EM) field are quantized. In the framework of this approach, the authors of [4] have derived a new expression for the "point-by-point" quantum phase

where

is the interactional EM energy between the charge and the solenoid. (Here we removed the incorrect factor 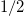 present in the corresponding equation of [4]). In this equation,
r
c
,
r
s
designate the radial coordinates of the charge and the solenoid, respectively, in the motional plane of the electron,
B
0,
E
0 stand for the magnetic and electric fields of the solenoid,
B
c
,
E
c
are the magnetic and electric fields of the charge, and other designations are standard.
present in the corresponding equation of [4]). In this equation,
r
c
,
r
s
designate the radial coordinates of the charge and the solenoid, respectively, in the motional plane of the electron,
B
0,
E
0 stand for the magnetic and electric fields of the solenoid,
B
c
,
E
c
are the magnetic and electric fields of the charge, and other designations are standard.
Equations (7) and (8) show an explicit dependence of the AB phase on EM fields, and the problem of the locality of the AB effect was solved in [4] through entanglement of the quantum charge and the quantized EM field.
We add that, based on eqs. (7) and (8), the authors of [4] predicted a gauge-independent phase difference at each point along the charge path, which definitely elucidates the primary role of EM fields over EM potentials in generating the AB phase. This can be seen from the known fact that the integral
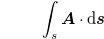
is gauge independent for a closed path only. By such a way, Marletto and Vedral [4] arrived at their principal claim that the AB phase is generated locally, like all other quantum phases, and proposed the idea of an experiment to measure the "partial" AB phase.
Now, we will show that the new presentation (7), (8) for the "point-by-point" phase of a charged particle does not lead to the customary expression for the total AB phase as the sum of the magnetic (3) and electric (4) components only, but the resulting new expression does contain two more terms, which exactly coincide with the complementary magnetic (1) and complementary electric (2) AB phases, correspondingly.
In order to prove the validity of this assertion, we consequently consider two typical configurations: the first one is aimed to observe the magnetic AB effect (an elongated solenoid as a source of magnetic field
B
0 with  ) and the second one is aimed to observe the electric AB effect (a parallel plate charged capacitor as a source of electric field
E
0 with
) and the second one is aimed to observe the electric AB effect (a parallel plate charged capacitor as a source of electric field
E
0 with 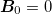 ).
).
In the first case (magnetic AB effect), eq. (8) takes the form (in CGS units used below)

Next, we define the AB phase of the electron, which is acquired between time moments 0 and t

Here 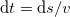 , where v is the velocity of the electron. For a non-radiating electron, we have [11]
, where v is the velocity of the electron. For a non-radiating electron, we have [11]
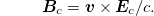
Substituting this equality into eq. (10), and using the identity 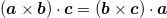 , we obtain
, we obtain

where

is the interactional EM field momentum of the system "solenoid and electron".
At this point, it is important to emphasize that, in general, the EM field momentum (12), being expressed through potentials, is not equal to 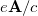 and contains an additional term, so that eq. (11) is not equivalent to the customary expression for the magnetic AB effect (3).
and contains an additional term, so that eq. (11) is not equivalent to the customary expression for the magnetic AB effect (3).
We can arrive at an explicit expression for the phase (11) through the vector potential
A
, using the expression of the interactional EM field momentum via
A
obtained in [12] at 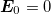 ,
,

Further on, combining eqs. (11) and (13), we obtain a new expression for the magnetic AB phase through the vector potential, resulting from eqs. (7), (8),

Thus, we see that the second term on the r.h.s. of eq. (14) corresponds to the complementary magnetic AB phase (1), which we have predicted earlier [1] by applying the SQP principle to the analysis of quantum phase effects for dipoles.
Next, we consider the electric AB effect, where at 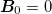 we have
we have

Evaluating phase (15), we assumed that an electron moves along the axis x outside a parallel plate charged capacitor oriented in the xy plane. In this case, the inner electric field of the capacitor
E
0 is collinear with the axis z, and, in general, the field and the corresponding scalar potential 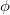 do not represent smooth functions. Therefore, the theorems of vector analysis become inapplicable to evaluate the volume integral in eq. (15). In this situation, we have to calculate directly the product
do not represent smooth functions. Therefore, the theorems of vector analysis become inapplicable to evaluate the volume integral in eq. (15). In this situation, we have to calculate directly the product 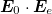 inside the capacitor, using in the relativistic case the Heaviside expression [11] for the electric field
inside the capacitor, using in the relativistic case the Heaviside expression [11] for the electric field 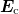 of a uniformly moving charge e. Then, for a small distance d between the plates, we obtain
of a uniformly moving charge e. Then, for a small distance d between the plates, we obtain

where
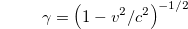
is the Lorentz factor of the charge, and we designated  . Integrating (16), we derive
. Integrating (16), we derive

Here 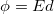 is the scalar potential at the location of the charge with an appropriate choice of its value at infinity. Using equalities
is the scalar potential at the location of the charge with an appropriate choice of its value at infinity. Using equalities

we transform eq. (17) to the form

Thus, a new expression for the electric AB phase (18), derived from the general equations (7) and (8) of ref. [4], is not equivalent to the customary expression for the electric AB effect (4), and contains an additional term of the complementary AB phase (2), which has already been derived in ref. [1] by applying the SQP principle to the analysis of quantum phase effects for dipoles.
Finally, considering the general case, where both the electric field E 0 and the magnetic field B 0 are not vanishing, we obtain the total quantum phase of a charged particle as the sum of eqs. (14) and (18),

Here, the first and second terms on the r.h.s. stand for the usual electric and magnetic components of the AB phase, while the third and fourth terms describe the complementary electric and complementary magnetic AB phases, correspondingly.
By such a way, the approach of SQP suggested in refs. [1,2] for the analysis of quantum phase effects for charges and dipoles, as well as the general quantum approach of ref. [4], leading to new expressions (7), (8) for the "point-by-point" quantum phase of a charged particle, do converge to each other with respect to the complete expression for the total AB phase (19), containing complementary magnetic (1) and complementary electric (2) phase components.
Further, we would like to elaborate on the clarification of the physical meaning of eq. (19) for the total quantum phase of charged particle, which can be presented in the form

where

stands for the velocity-dependent component of the quantum phase of the charge.
In order to analyze the physical meaning of eq. (20), it is convenient to express the interactional EM field momentum for the system "source, EM field, charged particle"

through the EM field potentials [12]

Combining eqs. (20) and (21b), we reveal the equality

Next, we notice that in the absence of EM fields, the phase of a quantum particle associated with its motion can be presented in the form

due to the de Broglie relation

between the wave vector k free and the mechanical momentum P M of the charge. By analogy with eq. (23), we can represent the AB phase (20) as

where the introduced wave vector is equal to

Hence, defining the total wave vector as the sum of k free and k AB , we obtain
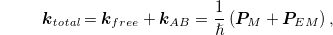
and the wavelength of a charged particle in an EM field becomes equal to

Therefore, at constant
P
M
(no force on the electron), 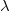 can still vary due to the variation of
P
EM
. In particular, for the magnetic AB effect,
P
EM
has opposite signs for two different electron passes around the solenoid, which leads to the corresponding phase shift.
can still vary due to the variation of
P
EM
. In particular, for the magnetic AB effect,
P
EM
has opposite signs for two different electron passes around the solenoid, which leads to the corresponding phase shift.
Thus, eq. (24), first obtained in [13,14] and named the "generalized de Broglie relationship", clearly clarifies the origin of the AB effect, where the observed phase difference over different paths of charge is explained by the corresponding difference in wavelengths over both paths, where the interactional EM field momentum P EM can be different. One can also see that eq. (24) predicts a measurable phase shift along any non-closed path; and hence, a physically meaningful presentation of P EM that ensures the gauge-invariance of eq. (24) should always be done through EM fields, see eq. (21a).
Discussion
Let us remind that eq. (19) for the total quantum phase of a charged particle has already been obtained in refs. [1,2,15] by applying the heuristical SQP principle to quantum phases for dipoles, and was discussed in our recent publications (see, e.g., [13,14]). Besides the evident advantage of being rigorous, present re-derivation through eqs. (7), (8) in the framework of the general quantum model [4] allows us to disclose more implications of eq. (19).
Gauge invariance of the total quantum phase
First of all, we remind that the known expression for the AB phase through the Hamiltonian or charged particle

(where  ,
,  stand for the Hamiltonian in the presence and absence of the EM field, correspondingly) yields only the known magnetic (3) and electric (4) AB phases, when the customary definition of the energy-momentum operator for an electrically charged particle in an EM field
stand for the Hamiltonian in the presence and absence of the EM field, correspondingly) yields only the known magnetic (3) and electric (4) AB phases, when the customary definition of the energy-momentum operator for an electrically charged particle in an EM field

is used. (Here 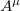 {
{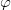 , A/c}is the four-potential, and
, A/c}is the four-potential, and 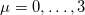 ).
).
Thus, the failure of eq. (25) with the momentum operator (26) to obtain the total quantum phase of a charged particle as the sum of four components in eq. (19), motivated us to re-define the energy-momentum operator in a more general form [2,15],

where 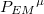 represents the interactional EM four-momentum of the system "charged particle in an EM field"; its zeroth component is defined through the interactional electric energy, while its spatial components are given by the interactional EM field momentum (21a) for the system "charged particle in EM field".
represents the interactional EM four-momentum of the system "charged particle in an EM field"; its zeroth component is defined through the interactional electric energy, while its spatial components are given by the interactional EM field momentum (21a) for the system "charged particle in EM field".
Next, comparing alternative definitions (26) and (27), we see that the transition from the customary definition of the momentum operator (26) to its new form (27) in the equations of quantum mechanics is formally equivalent to replacing the four-potential 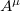 with the four-momentum
with the four-momentum 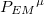 . Hence, the known old expression for AB phase
. Hence, the known old expression for AB phase

(which includes the electric (4) and magnetic (3) AB phases only) is modified to the form

which yields eq. (19) with application of eq. (21b).
Further on, one should emphasize that the customary expression for the AB phase (28) is gauge-invariant only for a closed path of a charged particle, whereas the AB phase (29) is manifestly gauge-invariant for an arbitrary closed or open path. The latter property of eq. (29) seems especially significant in connection with the principal possibility to measure the difference of AB phases along an open path revealed in [4].
Preliminary analysis of applications of the new momentum operator (27) to various physical problems was presented in ref. [2], and lies beyond the scope of the present paper.
Locality of AB effect
Next, we should comment on a typical situation in observing the AB effect, where the field momentum P EM for the considered system "source of EM field and charge" has a finite value, while both the electric field and the magnetic field vanish on the charge. In this situation, it is important to emphasize the revealed link between eqs. (7), (8) obtained in [4] and the generalized de Broglie relationship (24). Therefore, the problem of the locality of AB effect, as substantiated in [4], is solved through the quantum entanglement of the quantized EM field and quantum charge.
Generalized de Broglie relationship
One should emphasize that the derivation of the generalized de Broglie relationship (24) became possible only with the disclosure of complementary AB phases (1) and (2) and subsequent re-definition of the energy-momentum operator (27). Therefore, eq. (24) can be considered as a relativistic extension of the well-known de Broglie relationship

obtained in the framework of non-relativistic quantum mechanics.
Further perspectives
First, we emphasize that the problem of experimental confirmation of the complementary phases (1) and (2) is closely related to the experimental verification of the generalized de Broglie relationship (24). However, nowadays such experiments for non-relativistic charges, which are usually used in the observations of AB effect, look rather difficult.
It seems that a more realistic way to confirm the existence of complementary magnetic (1) and complementary electric (2) AB phases can be to measure the total AB phase of relativistic charged particles with 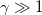 .
.
As can be seen from eq. (19), AB phase should go to zero at 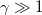 due to mutual cancellation of AB phase components (1)–(4). Therefore, observations of this effect could indicate the validity of eq. (19) for the total AB phase.
due to mutual cancellation of AB phase components (1)–(4). Therefore, observations of this effect could indicate the validity of eq. (19) for the total AB phase.
We also find interesting the application of the total expression for the AB phase (2) to bound states in relativistic quantum systems [16], where new physical implications and experimental schemes for verification of the phases (19) can be found.
In addition, there exists an indirect way to confirm the existence of complementary AB phases by measuring the full set of quantum phase effects for dipoles (5), especially its two new terms predicted in refs. [3] (third and fourth on the r.h.s. of eq. (5)). In the case of successful implementation of such experiments, the existence of complementary AB phases for electrically charged particles becomes plausible to the same extent as an adoption of the SQP principle, connecting quantum phases of charges and dipoles.
Finally, the achieved successes of the SQP principle make its application to the non-Abelian and non-dispersive phases for dipoles interesting, in particular, to the analogue of the HMW phase described in ref. [17], to the AC phase in the presence of a Lorentz-violating background coupled to a spinor and a gauge field (see, e.g., [18]).
Acknowledgments
The authors thank the referees for their helpful remarks and comments, which allowed us to improve the paper.
Data availability statement: No new data were created or analysed in this study.





