Export citation and abstract BibTeX RIS
In response to the Comment [1], we show here that the energy eigenvalues obtained in Cases A, B in the original paper [2] are correct while it is not so for the one obtained in Case C which is correctly presented here. We disagree with the energy eigenvalues presented in all cases in the Comment. It is worth mentioning here that there is a typo in the normalized radial wave function in the original paper [2]) which we correctly present here.
The Klein-Gordon equation under Lorentz symmetry violation defined by a fixed vector field 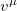 is described by (replacing coupling constant
is described by (replacing coupling constant  here)
here)

The KG-oscillator can be studied by replacing the operator 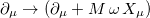 [2,3] in the above equation. Therefore, the KG-oscillator under Lorentz symmetry violation is described by the following wave equation:
[2,3] in the above equation. Therefore, the KG-oscillator under Lorentz symmetry violation is described by the following wave equation:

where we have defined in polar coordinates 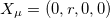 with g the determinant of the metric tensor and
with g the determinant of the metric tensor and 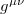 the inverse metric tensor. We imposed the condition that the fixed vector field satisfies
the inverse metric tensor. We imposed the condition that the fixed vector field satisfies  [2]. The Minkowski metric in polar coordinates is of the form
[2]. The Minkowski metric in polar coordinates is of the form 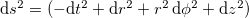 with
with

Therefore, the KG-oscillator equation in the background (3) becomes

where ![$\nabla^2=[\frac{1}{r}\,\frac{\partial}{\partial r}\,(r\,\frac{\partial}{\partial r})+\frac{1}{r^2}\,\frac{\partial^2}{\partial \phi^2}+\frac{\partial^2}{\partial z^2}]$](https://content.cld.iop.org/journals/0295-5075/141/6/60003/revision2/epl23100159ieqn8.gif) . The above equation is exactly similar to eq. (3) in the original paper [2] (please see γ in eq. (5) in ref. [3], where a term
. The above equation is exactly similar to eq. (3) in the original paper [2] (please see γ in eq. (5) in ref. [3], where a term 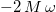 appears for the KG-oscillator equation). In ref. [4], we have shown how this term
appears for the KG-oscillator equation). In ref. [4], we have shown how this term 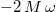 will appear in the KG-oscillator.
will appear in the KG-oscillator.
In Case A, the vector field is chosen by 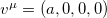 and solves the radial equation using the NU-method. The energy eigenvalue expression is given by (see eq. (10) in ref. [2])
and solves the radial equation using the NU-method. The energy eigenvalue expression is given by (see eq. (10) in ref. [2])

Now, we will check the correctness of this energy eigenvalue expression. Let 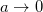 , that is, without Lorentz symmetry violation effect. Therefore, the energy eigenvalue (5) reduces to
, that is, without Lorentz symmetry violation effect. Therefore, the energy eigenvalue (5) reduces to

which is similar to the energy eigenvalue obtained in ref. [3] (see eq. (12) in ref. [3] by substituting 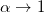 and
and 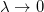 there), whereas the eigenvalue presented in the Comment never reduces to that result (6) for
there), whereas the eigenvalue presented in the Comment never reduces to that result (6) for  . There are no doubts that the energy eigenvalues obtained in ref. [3] are incorrect. Hence, the energy eigenvalue in Case A in the original paper [2] is correct while we disagree with the claim made in the Comment [1].
. There are no doubts that the energy eigenvalues obtained in ref. [3] are incorrect. Hence, the energy eigenvalue in Case A in the original paper [2] is correct while we disagree with the claim made in the Comment [1].
The normalized radial wave function is given by

In the original expression in ref. [2], the multiplicative term 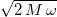 was missing, basically a typo there.
was missing, basically a typo there.
In terms of r, where 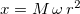 , one can write
, one can write

which satisfies the normalization condition 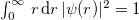 .
.
The total wave function will be

where En, l
is given in eq. (5). This total wave function is influenced by the Lorentz symmetry violation defined by the fixed vector field 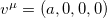 but not the radial function.
but not the radial function.
Similarly, one can show that the energy eigenvalue presented in Case B in the original paper [2] is correct. The normalized radial wave function is the same given by (7), whereas the total wave function will be

where En, l
is given in Case B in ref. [2]. The total wave function is influenced by the Lorentz symmetry violation defined by the fixed vector field 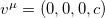 .
.
For the chosen vector field 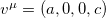 in Case C in the original paper [2], the correct energy eigenvalue expression is given by
in Case C in the original paper [2], the correct energy eigenvalue expression is given by

One can easily show that for 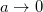 and
and 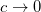 , this eigenvalue (11) reduces to the result (6). We therefore disagree with the energy expression presented in the Comment [1].
, this eigenvalue (11) reduces to the result (6). We therefore disagree with the energy expression presented in the Comment [1].
The normalized radial wave function will be the same given by (7), whereas the total wave function will be

where En, l
is given by eq. (11). The total wave function is influenced by the Lorentz symmetry violation defined by the fixed vector field 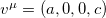 .
.
We have shown that the energy eigenvalue expression presented in Cases A, B in the original paper [2] agree with the known result obtained earlier without the Lorentz symmetry violation effects. While for Case C in the original paper [2], the correct energy expression is given by eq. (11) which is different from the result presented in the Comment. In addition, the normalized radial functions in all cases are the same as that given by eq. (7) but the total wave functions Ψ given by eqs. (9), (10) and (12) are different due to the influence of the Lorentz symmetry violation defined by the fixed vector field 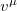 but not the radial function. It is better to mention here that the energy eigenvalues obtained in ref. [3] are absolutely correct, which confirms our results, too. Thus, we disagree with the results presented in the Comment [1].
but not the radial function. It is better to mention here that the energy eigenvalues obtained in ref. [3] are absolutely correct, which confirms our results, too. Thus, we disagree with the results presented in the Comment [1].
Acknowledgments
The author sincerely thanks the anonymous referee for valuable suggestions.





