Influence of laser-drive parameters on annular fast electron transport in silicon

The large currents of relativistic (fast) electrons generated in the interaction of an ultraintense laser pulse with a solid can be used to drive the formation of strong fields and for heating applications, often at significant distances (hundreds of micrometres) from the source. Understanding the transport physics of these electrons in solids is therefore important for applications such as the fast ignition approach to inertial confinement fusion [1] and for tailoring the properties of beams of sheath-accelerated ions [2].

In recent years, attention has focused on the role of target electrical resistivity in defining the properties of fast electron transport, both in terms of the different transport patterns in metals and insulators (see for example [3–5]), and in the possible use of self-generated resistive magnetic fields to control fast electron transport. As the fast electron population is accelerated into the target it draws a balancing cold return current, spatially overlapped with it and moving in the opposite direction, to satisfy the overall charge neutrality requirement [6]. If the fast electron current density is designated as j_f and the cold return current density as j_r then j_f + j_r ≈ 0 [7]. From Ohm's law, the self-generated electric field is E = −ηj_f, which when combined with Faradays law enables the self-generated magnetic field B to be written as ∂B/∂t = η ∇ × j_f + ∇η × j_f where η is the target resistivity and t is time. The first term on the right-hand side of this equation (η∇ × j_f) generates a magnetic field which pushes fast electrons into regions of higher current density, while the action of the second term (∇η × j_f) is to push fast electrons into regions of higher resistivity. The resulting magnetic field strength and growth rate can be significant. Growth rates of ∼10¹⁴ T s⁻¹ are produced in typical intense laser–solid interactions i.e. approximately 200 T in 1 ps. Fields of this magnitude have a strong effect on the propagation of multi-MeV electrons, and give rise to effects such as beam pinching or collimation [8], hollowing [9] and resistive instability-driven filamentation [10].

Schemes involving structured targets have been explored both experimentally [11, 12] and numerically [13] in an effort to use resistive gradients formed at the boundary between two different materials to induce magnetic field growth within solids, with the aim of collimating the fast electron beam. An extension of this layered target approach has been proposed to produce a 'magnetic switch-yard' scheme for controlling fast electron transport in advanced fusion targets [14]. In other work a technique for optically controlling the divergence of the electron beam by using double laser pulse drive has been demonstrated [15].

Recently we have shown that the resistivity of the solid at relatively low temperatures (eV to tens of eV regime) can have a defining influence on the properties of fast electron transport [16, 17]. Using different forms (allotropes) of carbon, the influence of lattice structure in defining the resistivity evolution of the target and the subsequent onset of resistive fast electron beam filamentation was demonstrated [16]. It was shown that the shape of the resistivity–temperature profile of the target material plays a key role in defining the beam transport pattern. An annular beam profile was demonstrated in silicon, arising due to a dip in resistivity at a few eV [17]. The ability to fundamentally change the beam transport pattern from a Gaussian-like to an annular fast electron beam profile by controlling the resistively generated magnetic fields could have important consequences for applications. Alfvén showed that compared to a uniform beam, a higher current can be transported in an annular beam [18]. The Alfvén limit increases by a factor of r/δr, where r is the radius of the beam and δr is the width of the annulus. Davies [19] developed the idea by proposing schemes directly applicable to fast ignition, and Hatchett et al [20] discuss the advantages of using annular beams to reduce the energy requirements of the ignition drive beam. Annular fast electron beam transport in a solid can also be used to produce an annular beam of sheath-accelerated ions [17]. Temporal et al [21] propose the use of an annular proton beam in combination with a second uniform proton beam to reduce the total energy required for ignition by a factor of almost two compared to a single uniform proton beam. Thus understanding and controlling the formation and subsequent evolution of annular fast electron beam transport is not only of fundamental interest, but may also have important implications for applications of intense laser–solid interactions.

In this paper, the sensitivity of annular fast electron beam transport to the parameters of the drive laser pulse is investigated numerically via 3D hybrid-particle-in-cell (PIC) simulations. Changes to the size of the ring and the density of the electrons forming it are quantified as a function of laser pulse energy, duration and focal spot radius, and explained in terms of the effects on the resistive magnetic fields.

The particle-based 3D-hybrid code ZEPHYROS [11, 14], in which the fast electrons are described using a PIC algorithm while the background plasma is treated as a fluid [22, 23], is used. A 200 µm × 400 µm × 400 µm simulation grid was used, with a cell resolution of ΔX = ΔY = ΔZ = 1 µm. As with many other hybrid-PIC codes, the fast electron source is not calculated self-consistently. The properties of the electron beam at the source are defined based on previous theory, experiment and PIC simulation studies of fast electron generation, and the electrons are introduced or injected into the computational grid in a 'laser-spot' profile region. The electron source is centred at [X, Y, Z] = [0, 0, 0], with a transverse intensity profile determined by $I = \alpha I_{\rm L} \exp(-\frac{r}{r_{\rm L}})$, where r and r_L are the radius and focal spot radius respectively, I_L is the peak laser intensity and α is the fraction of laser energy converted to fast electrons (set to 0.3). The electron pulse has a top-hat temporal profile. The fast electrons propagate in the X-direction with an exponential energy distribution (of the form $\exp(-\frac{E}{T_{\rm f}}))$, where E is the electron kinetic energy and the mean temperature T_f scales ponderomotively $(k_{\rm B}T_{\rm f} = 0.511[(1+0.73I_{18}\lambda_{\mu {\rm m}}^{2})^{1/2}-1]\,{\rm MeV}$, where I₁₈ is the peak laser intensity in units of 10¹⁸ W cm⁻² and λ_µm is the laser wavelength in micrometres [24]). The electrons are injected with a uniform angular distribution over a cone subtended by a half-angle of 50° [25] and in all cases the initial target temperature is set equal to 1 eV.

Although the fast electron source parameters, as defined by the percentage of the laser energy absorbed by the electrons and their injection angle and distribution, are expected to vary with the properties of the laser pulse, the precise nature of these dependencies are still not well understood and are the subject of ongoing work. Therefore, as this investigation focuses on the transport pattern of the fast electron beam within the target, the source parameters, α and the injection angle, are kept constant throughout.

The silicon resistivity–temperature profile used, presented in figure 1(a), is based on a quantum molecular dynamics (QMD) Kubo–Greenwood calculation [26, 27], as discussed in MacLellan et al [17]. In that work, it was shown that the dip in the resistivity at a few eV leads to a reversal in the resistivity gradient near the edges of the fast electron beam, where the target is heated to relatively low temperatures. An example 2D temperature map from the simulations (for I_L = 5 × 10²⁰ W cm⁻²; E_L = 192 J; τ_L = 1 ps and r_L = 3.5 µm) is shown in figure 1(b) and the corresponding 2D map of magnetic flux density is shown in figure 1(c), (both sampled after 1400 fs). This reversal in the resistivity gradient leads to a reversal in the direction of the self-generated resistive magnetic field, via the ∇η × j_f term. The combination of the collimating effect of the azimuthal magnetic field enveloping the beam (the collimating component) and the reversed magnetic field just inside the edge of the beam (the hollowing component) drive a localized increase in the fast electron beam current density in an annular profile. If the ring is of sufficient size and contains a large enough fraction of the total electron current, the transport pattern is maintained and even reinforced as the electrons propagate across the remainder of the target. The reinforcement occurs due to the local increase in resistive heating arising from the increase in j_f (resistive heating scales as 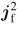${\bit j}_{\rm f}^{2}$ [22]) which drives a local increase in resistivity and thus larger resistivity gradients and azimuthal B-fields surrounding the annulus.

Zoom In Zoom Out Reset image size

We begin by defining two parameters to quantify annular transport in the simulation results. These are (1) the inner radius of the annulus at the end of the simulation box, i.e. at X = 200 µm (this is defined as the ratio at which the electron density increases by a factor of 5 with respect to the axial density); and (2) the ratio of the electron densities in the annulus to the axial position ([200,0,0]), again at the end of the simulation box. These quantities effectively measure the size of the ring and the annulus-to-axial contrast ratio.

To investigate the sensitivity of these parameters to the drive laser pulse parameters, three series of simulation scans were performed, as follows: (A) variation of laser pulse energy, E_L in the range 78–385 J, for fixed focal spot radius r_L = 3.5 µm and fixed laser pulse duration τ_L = 1 ps; (B) variation of r_L in the range 2.5–5.5 µm, for fixed E_L = 192 J and τ_L = 1 ps; and (C) variation of τ_L in the range 0.5–2.5 ps, for fixed E_L = 192 J and r_L = 3.5 µm. These parameter ranges were chosen such that the peak laser pulse intensity, I_L, was varied in the range 2 × 10²⁰–1 × 10²¹ W cm⁻² for all three scans.

Figure 2 presents the results from these simulations. The fast electron density in the [X, Y] mid-plane is shown, at an example time of τ_L + 0.4 ps—this time is chosen such that the full population of electrons has been initiated in the simulation and has propagated at least 100 µm across the target, the majority having reached the rear surface. We find that the stability of the annular transport pattern is maintained until significant refluxing of electrons, driven by reflection at the target rear side, occurs in the simulation (fast electron refluxing has been previously shown to perturb the resistive magnetic field structure within solids [28]). Scan A is presented in the top row (figures 2(a)–(e)), B in the middle row (figures 2(f)–(j)), and C in the bottom row (figures 2(k)–(o)). The corresponding simulation outputs for the [Y, Z] rear-plane snapshots are displayed in figure 3.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

In scan A, we find that increasing the energy from 78 to 385 J, which effectively increases the current of electrons, results in an increase in the overall divergence of the electron beam and thus an increase in the radius of the annular feature. By contrast, when increasing the intensity over the same range by decreasing the focal spot radius from r_L = 5.54 to 2.48 µm, scan B, the increase in both the overall beam divergence and the radius of the ring is smaller. Note that the fixed laser pulse energy in combination with the increasing laser intensity means that fewer electrons are injected as the focal spot radius is decreased, producing the beam density decrease observed in figures 2(f)–(j). This influences the target temperature and resistivity evolution, and subsequent electron transport properties, as will be explained later. In scan C, significant changes in the beam transport are found for variation of the pulse duration. As τ_L is increased over the range 1–2.5 ps, the overall beam divergence and radius of the annular structure are found to decrease, effectively leading to more uniform beam transport for the longer pulse durations (see figures 2(n)–(k). However, reducing τ_L to 0.5 ps also results in a loss of the annular structure and a significant increase in the overall fast electron beam divergence which, as will be discussed later, is a result of a reduction in the magnetic field strength.

To examine these trends more closely, the rear-surface simulation outputs from figure 3 are analysed to quantify the variation of the size of the annulus and the relative density of electrons contained within it, as a function of I_L for each of the three scans. The radius of the annular structure is defined as the distance from the centre of the rear-surface simulation grid (i.e. at [Y, Z] = [0, 0]) to the inner annulus of the ring structure, and the results are shown in figure 4(a). Note that the 10²¹ W cm⁻² point in scan C (τ_L = 0.5 ps) is excluded as a clear ring profile is not observed for this case. Figure 4(b) shows the ratio of the fast electron density in the annulus (peak density) to the density of the centre of the beam, [Y, Z] = [0, 0].

Zoom In Zoom Out Reset image size

3.1. Overall effect of laser intensity

3.2. Laser focal spot dependence

Although for all three parameter scans, the ring radius increases with I_L, it is clear from figure 4(a) that the scaling with intensity is different when varying the focal spot radius compared to variation of either E_L or τ_L. This difference is accounted for by the size of the electron beam at source. A decrease in r_L has two main effects: (1) j_f, and hence B, increases, decreasing the overall divergence of the beam; and (2) the radius at which hollowing is seeded decreases. Both effects influence the radius of the beam annulus downstream, and we consider each in turn:

• (1)  
  The magnetic field which defines the overall beam divergence scales inversely with r_f, as discussed above, and is strongest at the source, where j_f is highest and defined by the size of the laser focal spot. Let us consider the simulation result at 5 × 10²⁰ W cm⁻², which is common to all three scans, and for which r_L = 3.5 µm, as a reference. As r_L is decreased to 2.5 µm (1 × 10²¹ W cm⁻²), j_f at the source, and hence the peak magnetic field strength, is enhanced by approximately a factor of two. The simulation result shows a reduction in the annulus radius, corresponding to an overall beam divergence angle reduction of ∼36%, compared to the simulations at the same intensity in scans A and C for which r_L = 3.5 µm. Similarly, an increase in r_L from 3.5 to 4.3 µm (I_L = 3.3 × 10²⁰ W cm⁻²) results in a 50% decrease in j_f and B at the source, which contributes to the ∼35% increase in the ring divergence in the simulation results (again compared to the simulations at the same intensity in scans A and C).
• (2)  
  The effect of varying r_L on the radius at which the annular transport pattern is seeded is explored in figure 5. The transverse intensity profiles of the drive laser pulse are shown in figures 5(a) and (d) for the energy and focal spot scans (A and B), respectively. For brevity, scan C is not considered in detail because the results are very similar to A. For each scan, three example I_L are considered: 2 × 10²⁰ W cm⁻², 5 × 10²⁰ W cm⁻² and 1 × 10²¹ W cm⁻² (displayed as the black, red and blue plots, respectively) and the full-width at half-maximum (FWHM) for each is marked. The corresponding target temperature and resulting resistivity profiles (along the y-axis) at X = 50 µm (depth at which the annular transport evolves) are shown in figures 5(b) and (c) and figures 5(e) and (f) for scan A and B respectively. The red dotted line highlights the temperature at 3.5 eV and the corresponding reversal in the resistivity gradient at the edges of the beam which seeds annular transport [17]. From these plots we see that the radius at which seeding of the annular transport occurs increases with intensity for scan A (and C), but decreases slightly with intensity for scan B, due to the change in r_L. For I_L = 2 × 10²⁰ W cm⁻², for example, the radius at which annular transport is seeded is ∼35% larger in scan B than A, due to the larger r_L, which contributes to the larger annular profile at the rear of the simulation box.

Zoom In Zoom Out Reset image size

Note that the simulation profiles in figure 5 show spikes in target temperature which grow at the edge of the beam and arise due to the local increase in the beam density (and hence collisional return current) due to the deflection induced by the magnetic field. As discussed above and in MacLellan et al [17], this drives a localized increase in resistivity for temperatures above ∼3.5 eV and hence the region near the edge of the beam remains more resistive than the centre, which reinforces the annular transport pattern as the beam propagates over the remainder of the target.

With reference to figure 5(e), it is interesting to note that reducing r_L for fixed E_L and τ_L significantly reduces the overall heating of the target. This occurs because I_L and hence T_f increases, which for a fixed total fast electron energy (assuming a fixed energy conversion efficiency from laser to electrons), reduces the total number of fast electrons, and hence 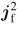${\bit j}_{\rm f}^{2}$ heating. Additionally, we note that there is a general trend of the onset of fast electron beam filamentation with increasing E_L, as manifested in the temperature oscillations across the beam observed in figure 5(b). This is a consequence of the increase in background temperature between ∼3.5 and ∼70 eV, which produces a high resistivity (figure 1), leading to a higher resistive instability growth rate [16].

3.3. Influence of laser pulse duration

To explore why the annular transport pattern is washed out for the τ_L = 0.5 ps simulation in scan C, the spatial profile of the resistively generated magnetic field is examined as a function of τ_L. Lineouts are extracted along the Y-direction (i.e. transverse, or radial, profile) of the simulation grid, at the x-axis position to which the magnetic field extends (which changes with τ_L). This is defined as the position at which the magnitude of the collimating magnetic field is reduced by 50%. For the cases shown in figure 6(a), this represents depths of 45 µm, 50 µm, 55 µm, 60 µm and 65 µm for τ_L = 0.5 ps, 1 ps, 1.5 ps, 2 ps and 2.5 ps, respectively. The resulting field profiles are shown in figure 6(a) for radius up to 80 µm (i.e. Y = 0 corresponds to the centre of the beam) for each of the five simulations. These plots demonstrate the complex interplay between pulse duration and the generation of the collimating magnetic field which envelopes the beam, forcing the electrons towards the axis (positive B_Z in figure 6(a)), and the hollowing reversed magnetic field which forms just inside the circumference of the beam, driving electrons outwards (negative B_Z in figure 6(a)). Achieving a balance between these opposing azimuthal components of the magnetic field is important for seeding the annular transport pattern.

Zoom In Zoom Out Reset image size

The magnitude and rate of the resistive magnetic field growth depend on both the fast electron current density and bunch duration (effectively the drive laser-pulse duration) [6]. Figure 6(a) shows example profiles of the magnetic field, exhibiting both the collimating component and the oppositely directed hollowing component, for given τ_L. We find that the amplitude of both magnetic field components increases with pulse duration, as a consequence of the longer duration over which the field grows [22], and generally that the differences between the magnitude of the components decreases. This is observed in figure 6(b) which shows the temporal evolution of both magnetic field components for three example τ_L, and figure 6(c) showing the magnitude of both components as a function of pulse duration. The greatest difference between the two components is observed for τ_L = 1 ps, which explains the resulting strong annular transport patterns. With increasing pulse duration the difference decreases, as the collimating field becomes more dominant. Eventually for τ_L above 2 ps, there is a switch over in the dominant field component. As a result, the annular transport pattern is no longer sustained and the rear-surface fast electron spatial profile becomes uniform, as seen in figure 3(k). Furthermore, for the shortest pulse duration explored (i.e. τ_L = 0.5 ps), the peak collimating magnetic field is approximately balanced by the peak hollowing magnetic field, and the magnitude of each is not large enough to seed significant annular transport. In general, we find that the best conditions for seeding a strong annular transport pattern occurs when the magnitude of the hollowing component is larger than the collimating component.

With reference to figure 6(a), we also find that with increasing pulse duration the position of the maximum of each field component in the Y-axis decreases (i.e. the radius of the ring decreases). This is a direct consequence of the increasing collimating field which acts to decrease the overall beam divergence.

In conclusion, the annular transport patterns of fast electron beams in silicon, arising from oppositely directed azimuthal components of the self-generated resistive magnetic field, have been investigated as a function of the parameters of the drive laser pulse, using a 3D hybrid-PIC code. The results demonstrate that there is an optimum laser peak intensity range for transporting fast electrons within an annular structure produced in this way. The size of the annulus is found to increase with peak intensity, due to a decrease in the magnitude of the collimating magnetic field which defines the overall beam divergence. We find that there is an optimum laser intensity for enhancing the annulus-to-axial electron density contrast ratio, which is determined by the relative strength of the resistive magnetic field components. The hollowing component should be high to deflect electrons into the annulus, but the collimating component should not be so high as to produce a strongly collimated beam. The resulting trade-off explains the observed optimum laser-drive intensity. We further find that the size of the annular profile is sensitive to the laser focal spot size, which enables some degree of tuning of the annular transport pattern for a fixed beam temperature or drive laser intensity.

We acknowledge computing resources provided by STFC's e-Science project. This work is financially supported by EPSRC (grant numbers EP/J003832/1, EP/L001357/1 and EP/K022415/1). The research leading to these results has also received funding from LASERLAB-EUROPE (grant agreement no 284464, EC's Seventh Framework Programme) and is sponsored by the Air Force Office of Scientific Research, Air Force Material Command, USAF, under grant number FA8655-13-1-3008. The US Government is authorized to reproduce and distribute reprints for Governmental purpose notwithstanding any copyright notation thereon.