Positive-entropy geodesic flows on nilmanifolds

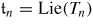Let T_n be the nilpotent group of real n × n upper-triangular matrices with 1s on the diagonal. The Hamiltonian flow of a left-invariant Hamiltonian on T^*T_n naturally reduces to the Euler flow on , the dual of . This paper shows that the Euler flows of the standard Riemannian and sub-Riemannian structures of T₄ have transverse homoclinic points on all regular coadjoint orbits. As a corollary, left-invariant Riemannian metrics with positive topological entropy are constructed on all quotients D \ T_n where D is a discrete subgroup of T_n and n ⩾ 4.