The non-local Fisher–KPP equation: travelling waves and steady states

We consider the Fisher–KPP equation with a non-local saturation effect defined through an interaction kernel ϕ(x) and investigate the possible differences with the standard Fisher–KPP equation. Our first concern is the existence of steady states. We prove that if the Fourier transform 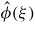is positive or if the length σ of the non-local interaction is short enough, then the only steady states are u ≡ 0 and u ≡ 1. Next, we study existence of the travelling waves. We prove that this equation admits travelling wave solutions that connect u = 0 to an unknown positive steady state u_∞(x), for all speeds c ⩾ c^*. The travelling wave connects to the standard state u_∞(x) ≡ 1 under the aforementioned conditions: 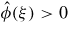or σ is sufficiently small. However, the wave is not monotonic for σ large.