Abstract
In the setting of intermittent Pomeau–Manneville maps with time dependent parameters, we show a functional correlation bound widely useful for the analysis of the statistical properties of the model. We give two applications of this result, by showing that in a suitable range of parameters the bound implies the conditions of the normal approximation methods of Stein and Rio. For a single Pomeau–Manneville map belonging to this parameter range, both methods then yield a multivariate central limit theorem with a rate of convergence.
Export citation and abstract BibTeX RIS
Recommended by Dr Sebastien Gouezel
Footnotes
- 1
Given a unit vector
 , we say that f is a coboundary in the direction v if there exists a function
, we say that f is a coboundary in the direction v if there exists a function ![$ \newcommand{\bR}{{{\mathbb R}}} g_v:[0, 1]\to\bR$](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAAEAAAABCAQAAAC1HAwCAAAAC0lEQVR42mNkYAAAAAYAAjCB0C8AAAAASUVORK5CYII=) in
in  such that
such that  .
. - 2
- 3
We denote by
![$ \newcommand{\round}[1]{\lfloor#1\rfloor} \round{x}$](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAAEAAAABCAQAAAC1HAwCAAAAC0lEQVR42mNkYAAAAAYAAjCB0C8AAAAASUVORK5CYII=) the greatest non-negative integer n with
the greatest non-negative integer n with  .
. - 4




![$ \newcommand{\bR}{{{\mathbb R}}} g_v:[0, 1]\to\bR$](https://content.cld.iop.org/journals/0951-7715/30/11/4239/revision1/nonaa85d0ieqn092.gif)


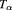
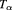
![$ \newcommand{\round}[1]{\lfloor#1\rfloor} \round{x}$](https://content.cld.iop.org/journals/0951-7715/30/11/4239/revision1/nonaa85d0ieqn256.gif)