Abstract
We consider a smooth one-parameter family  of diffeomorphisms with compact transitive Axiom A attractors
of diffeomorphisms with compact transitive Axiom A attractors  , denoting by
, denoting by  the SRB measure of
the SRB measure of 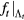 . Our first result is that for any function θ in the Sobolev space
. Our first result is that for any function θ in the Sobolev space  , with
, with  and 0 < r < 1/p, the map
and 0 < r < 1/p, the map  is α-Hölder continuous for all
is α-Hölder continuous for all  . This applies to
. This applies to 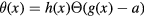 (for all
(for all 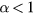 ) for h and g smooth and
) for h and g smooth and 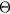 the Heaviside function, if a is not a critical value of g. Our second result says that for any such function
the Heaviside function, if a is not a critical value of g. Our second result says that for any such function 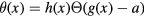 so that in addition the intersection of
so that in addition the intersection of  with the support of h is foliated by 'admissible stable leaves' of ft, the map
with the support of h is foliated by 'admissible stable leaves' of ft, the map  is differentiable. (We provide distributional linear response and fluctuation-dissipation formulas for the derivative.) Obtaining linear response or fractional response for such observables θ is motivated by extreme-value theory.
is differentiable. (We provide distributional linear response and fluctuation-dissipation formulas for the derivative.) Obtaining linear response or fractional response for such observables θ is motivated by extreme-value theory.
Export citation and abstract BibTeX RIS
Recommended by Professor Rafael de la Llave


