Abstract
We test the conjecture that non-Markovian dynamics may help to protect quantum entanglement. To this end, we address an open system whose environment behaves either as a quantal system or as an effective reservoir, depending on the regime chosen to rule the system–environment dynamics. This allows us to study entanglement dynamics within Markovian and non-Markovian regimes. We focus on the recently introduced definition of quantum non-Markovianity that is based on the trace distance between pairs of initial states. The corresponding quantum measure  for assessing the non-Markovianity of a quantum map Φ is submitted to test. We report cases for which
for assessing the non-Markovianity of a quantum map Φ is submitted to test. We report cases for which  signals non-Markovianity, even though Φ belongs to a purely dissipative regime. We argue that
signals non-Markovianity, even though Φ belongs to a purely dissipative regime. We argue that  is not generally applicable to assess the non-Markovianity of a quantum process, because information is not always encoded in a way that depends on the distinguishability between states. When entanglement is used as the carrier of information, non-Markovianity should be diagnosed in terms of an entanglement measure. We thus compare the dynamics of Wooters concurrence and of trace distance between states, showing that they may behave qualitatively alike but leading to conflicting diagnosis about the backflow of information from the environment to the system. In contrast to other studies, in our case entanglement is transferred only to potential carriers of information, thereby excluding paradoxical situations that involve entangled reservoirs.
is not generally applicable to assess the non-Markovianity of a quantum process, because information is not always encoded in a way that depends on the distinguishability between states. When entanglement is used as the carrier of information, non-Markovianity should be diagnosed in terms of an entanglement measure. We thus compare the dynamics of Wooters concurrence and of trace distance between states, showing that they may behave qualitatively alike but leading to conflicting diagnosis about the backflow of information from the environment to the system. In contrast to other studies, in our case entanglement is transferred only to potential carriers of information, thereby excluding paradoxical situations that involve entangled reservoirs.
Export citation and abstract BibTeX RIS
1. Introductory remarks
It is by now well known that entanglement can suddenly disappear, stay absent for some time and then reappear. These phenomena, respectively termed as 'entanglement sudden death' (ESD) [1] and 'entanglement sudden birth' (ESB) [2], appear under conditions that have been extensively studied. Recently, Yönaç et al [3] considered a four-qubit system and analysed entanglement for its six possible partitions. These authors found a series of interesting features in the not yet completely understood dynamics that rules entanglement transfer. By using Wooters concurrence [4] as an entanglement measure, they obtained results that pointed towards the possible existence of conservation laws ruling entanglement transfer, a possible way of achieving entanglement protection. Now if we understand entanglement's evolution of two unconnected parties as a pure information-exchange process, then memory effects become an issue. The system that Yönaç et al analysed was a pair of two-level atoms, each sitting in its own lossless cavity and interacting with a single mode. The dynamics was ruled by the Jaynes–Cummings Hamiltonian. The results presented in [3] suggested that memory effects might play a crucial role and that non-Markovianity could be essential for entanglement's rebirth. As a natural follow-up of these investigations, people addressed similar cases, thereby replacing non-Markovian features by Markovian ones [5–8]. For instance, López et al [5] considered two initially entangled but subsequently unconnected qubits, each of them being in contact with its own environment. The environments were assumed to be reservoirs coupling to the qubit within the Markov approximation. Specifically, the qubits in [5] were single-cavity modes and the reservoirs vacuum states at zero temperature. Under these circumstances, each cavity mode suffers an exponential decay that follows from the Weisskopf–Wigner approximation and the excitation of the cavity is eventually transferred to the environment. Hence, the environment has two possible collective states, one which is empty and a second one hosting a single excited mode within an infinity of other, unoccupied modes. Such a dichotomic situation calls out for a qubit-like description of a system that thereby comprises four qubits, as in [3]. Entanglement can thus be calculated among six possible pairings. López et al concluded that ESD in the two-qubit system was necessarily related to ESB between the respective, memoryless environments [5]. Thus, the conjecture raised in [3], that memory effects might be crucial for entanglement transfer, seemed to be ruled out in [5]. We believe that this conclusion is questionable. Memory effects, like those experimentally tested in [9], appear to be necessary for the recovery of entanglement and further investigation is still needed to settle the issue. Indeed, due to their very nature, reservoirs should be incapable of becoming entangled. To the best of our knowledge, neither a theoretical model nor any experimental observations have been reported about entangled reservoirs. An environment acting as a reservoir must be in a steady state, and it typically has a deleterious effect on quantum information. If results like those reported in [5] were correct, then entangled reservoirs could be used as carriers of quantum information, something that sounds physically meaningless. Now, within the Weisskopf–Wigner approach, the reservoir appears like a qubit only from the system's perspective. Treating the environment as a qubit amounts to its replacement by a so-called environment simulator, a commonly used tool when dealing with open quantum systems [10]. From the system's perspective, there is no difference between the environment and its simulator, as the predicted system's dynamics is the same in both cases. However, physically there is a great difference between a reservoir and a qubit simulating it. To begin with, the jumping from one qubit state to the other is irreconcilable with the defining feature of a reservoir: its being in a steady state. One can certainly implement arrangements behaving like the reservoir's simulators [11], but these arrangements markedly differ from physical reservoirs. For example, Salles et al [12] used dichotomic path modes in an interferometric array that would be suitable for testing entanglement swapping from a system to its environment simulator. However, we cannot take this as a test for predictions about the reservoir's behaviour. In [12], a single photon carries two qubits, one being the system and the other the environment simulator. The latter then constantly jumps between two states, conditioned on what happens to the first. This notoriously differs from the behaviour of a reservoir that—while being itself in steady state—may influence the dynamics of a small system. Clearly, we may not draw conclusions about the environment's behaviour from that of its simulator. The simulator's services finish once we have derived the system's dynamics.
In order to study information transfer, possibly translating into global conservation of quantities like concurrence, we must deal with systems that can be entangled. One such open system, being analytically solvable [10, 13], is a two-level atom in a lossy cavity at zero temperature. It allows us to study the transfer of concurrence among quantal parties, and the irreversible loss of information into a reservoir. By tuning the cavity's quality factor  , we can go from the underdamped regime (signalled by damped Rabi oscillations) to the overdamped regime (without Rabi oscillations). Qualitatively, the former regime is non-Markovian, while the latter is Markovian. Quantitatively, we can assess the non-Markovianity of quantum processes Φ(t) that connect an initial state—given by the density matrix ρ(0)—with an evolved state ρ(t) = Φ(t)ρ(0) by using a recently introduced measure [14] that depends on the trace distance between two states: D(ρ1, ρ2) = tr|ρ1 − ρ2|/2, with
, we can go from the underdamped regime (signalled by damped Rabi oscillations) to the overdamped regime (without Rabi oscillations). Qualitatively, the former regime is non-Markovian, while the latter is Markovian. Quantitatively, we can assess the non-Markovianity of quantum processes Φ(t) that connect an initial state—given by the density matrix ρ(0)—with an evolved state ρ(t) = Φ(t)ρ(0) by using a recently introduced measure [14] that depends on the trace distance between two states: D(ρ1, ρ2) = tr|ρ1 − ρ2|/2, with  . Using the rate of change σ(t, ρ1, 2(0)) = dD(ρ1(t), ρ2(t))/dt for any two initial states ρ1, 2(0), one defines a measure
. Using the rate of change σ(t, ρ1, 2(0)) = dD(ρ1(t), ρ2(t))/dt for any two initial states ρ1, 2(0), one defines a measure  for the non-Markovianity of the process Φ as
for the non-Markovianity of the process Φ as

As explained below, a slightly modified version of this measure proves useful for analysing the connection between non-Markovianity and the dynamics of concurrence. Recent investigations [15, 16] have addressed similar issues and found that in the non-Markovian regime, as expected, a limited amount of information returns to the system. An alternative definition [17] of non-Markovianity is based on the divisibility of the quantum map. The corresponding measure  is given in terms of the Choi matrix associated with Φ. The condition
is given in terms of the Choi matrix associated with Φ. The condition  signals that the divisibility of a completely positive (CP) map is broken. It has been shown [18] that in some cases
signals that the divisibility of a completely positive (CP) map is broken. It has been shown [18] that in some cases  while
while  , the two measures leading thus to conflicting quantifications of the same process, although it holds true [19] that whenever
, the two measures leading thus to conflicting quantifications of the same process, although it holds true [19] that whenever 
 . That is, any process that is diagnosed as non-Markovian according to
. That is, any process that is diagnosed as non-Markovian according to  , is also non-Markovian according to
, is also non-Markovian according to  , while the converse might not be true. This happens because
, while the converse might not be true. This happens because  quantifies the backflow of information from the environment to the system, whereas
quantifies the backflow of information from the environment to the system, whereas  is based on a different—though related—feature: the divisibility of the quantum map. Chruściński et al have proposed a way to reconcile the two aforementioned measures [19]. Now, even having the two defining features—divisibility and backflow of information—already captured in a single measure, the question about the connection between non-Markovianity and the dynamics of concurrence would remain still open. We can thus focus on the widely accepted measure
is based on a different—though related—feature: the divisibility of the quantum map. Chruściński et al have proposed a way to reconcile the two aforementioned measures [19]. Now, even having the two defining features—divisibility and backflow of information—already captured in a single measure, the question about the connection between non-Markovianity and the dynamics of concurrence would remain still open. We can thus focus on the widely accepted measure  , for the sake of analysing the relationship between non-Markovianity and entanglement protection (nonetheless, in appendix C, we briefly discuss divisibility). We will thus henceforth refer to non-Markovian processes whenever
, for the sake of analysing the relationship between non-Markovianity and entanglement protection (nonetheless, in appendix C, we briefly discuss divisibility). We will thus henceforth refer to non-Markovian processes whenever  .
.
As we shall see, the non-Markovianity of a process does not necessarily preclude a definite loss of information. Indeed, there are processes that are non-Markovian, but in these processes, information could be carried by entanglement and ESD might occur without revival. This raises questions about the meaning of  . Let us recall that the current interpretation of
. Let us recall that the current interpretation of  is as follows. Because there are times during which the distinguishability between two states grows (σ(t, ρ1, 2(0)) > 0), then for these times information is returning to the system. However, we should be careful and not generally ascribe to processes with
is as follows. Because there are times during which the distinguishability between two states grows (σ(t, ρ1, 2(0)) > 0), then for these times information is returning to the system. However, we should be careful and not generally ascribe to processes with  the property of being good keepers of information. If we have encoded information using entanglement, then it is its dynamics that matters, not the dynamics of trace distance. We have found σ(t, ρ1, 2(0)) > 0 in cases for which no revival of concurrence takes place. Even more striking, we have found
the property of being good keepers of information. If we have encoded information using entanglement, then it is its dynamics that matters, not the dynamics of trace distance. We have found σ(t, ρ1, 2(0)) > 0 in cases for which no revival of concurrence takes place. Even more striking, we have found  in purely dissipative, overdamped regimes, which are intuitively taken as Markovian. Thus, an overall diagnosis of Φ as being non-Markovian according to
in purely dissipative, overdamped regimes, which are intuitively taken as Markovian. Thus, an overall diagnosis of Φ as being non-Markovian according to  not always conveys a useful characterization of the process. This is an important issue, in view of current efforts to counteract information corrupting effects in quantum-information processing.
not always conveys a useful characterization of the process. This is an important issue, in view of current efforts to counteract information corrupting effects in quantum-information processing.
By addressing the simple, yet not trivial case of a system that consists of two atom–cavity units with losses, we can illustrate the limits of  as a tool for diagnosing non-Markovianity. The system we address is a realizable one and serves also the purpose of highlighting the difference between a reservoir and its simulator. In the following sections, we present our main results and conclusions. For the sake of clarity, we have relegated the details of some calculations to a series of appendices.
as a tool for diagnosing non-Markovianity. The system we address is a realizable one and serves also the purpose of highlighting the difference between a reservoir and its simulator. In the following sections, we present our main results and conclusions. For the sake of clarity, we have relegated the details of some calculations to a series of appendices.
2. Markovian and non-Markovian features in the system
Our basic building block is the density matrix ρ that describes the atom–cavity unit. It evolves in time as ruled by the following equation [10]:
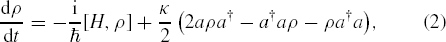
where H = ℏωegσz/2 + ℏωca†a − iℏΩ(aσ+ − a†σ−)/2. We neglect the atomic spontaneous emission rate Γat and assume a cavity's finesse  . By varying κ and Ω, we can go from the underdamped to the overdamped regime. The atom–photon correlation time is comparable to the atom's evolution time in the underdamped regime, but it becomes negligible in the overdamped case, when the atom is effectively coupled to the reservoir, keeping no memory from past influences. If the initial state has no photons, then the relevant Hilbert space is spanned by |1〉 = |e, 0〉, |2〉 = |g, 1〉, |3〉 = |g, 0〉. Equation (2) can be readily solved, the analytical expressions being simpler for the resonant case, ωeg = ωc, that we assume henceforth. As shown in appendix A, the components ρ11, ρ22 and ρ12 + ρ21 are coupled among themselves only, and similarly ρ13, ρ23, which evolve separately from the others (hence also ρ31, ρ32). As for ρ33, it evolves according to dρ33/dt = κρ22 and is thus fixed by ρ22.
. By varying κ and Ω, we can go from the underdamped to the overdamped regime. The atom–photon correlation time is comparable to the atom's evolution time in the underdamped regime, but it becomes negligible in the overdamped case, when the atom is effectively coupled to the reservoir, keeping no memory from past influences. If the initial state has no photons, then the relevant Hilbert space is spanned by |1〉 = |e, 0〉, |2〉 = |g, 1〉, |3〉 = |g, 0〉. Equation (2) can be readily solved, the analytical expressions being simpler for the resonant case, ωeg = ωc, that we assume henceforth. As shown in appendix A, the components ρ11, ρ22 and ρ12 + ρ21 are coupled among themselves only, and similarly ρ13, ρ23, which evolve separately from the others (hence also ρ31, ρ32). As for ρ33, it evolves according to dρ33/dt = κρ22 and is thus fixed by ρ22.
We consider now a system comprising two independent atom–cavity units (A, B), and study entanglement between different parties. Taking as the initial state |ΨAB(0)〉 = (cos θ|gA〉|gB〉 + sin θ|eA〉|eB〉)⊗|0A〉|0B〉, the corresponding initial density matrix ρAB(0) = |ΨAB(0)〉〈ΨAB(0)| reads
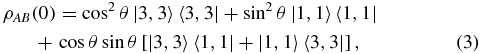
with |3, 3〉〈1, 1| = |3A〉〈1A|⊗|3B〉〈1B|, etc. The general solution of equation (2) yields the evolution of each atom–cavity subsystem: ρi = A, B(t), thereby defining the map ρi(0) → ρi(t) = ∑μK(i)μ(t)ρi(0)K†(i)μ(t), with the Kraus operators K(i)μ. The evolution of ρAB is given by ρAB(0) → ρAB(t) = ∑μνK(A)μ(t)⊗K(B)ν(t)ρAB(0)K†(B)ν(t)⊗K†(A)μ(t). Thus, by applying this last map to each state in equation (3), we obtain ρAB(t) from ρAB(0). Using the general solution of equation (2), one obtains |3〉〈3| → |3〉〈3|; |3〉〈1| → ρ31(t)|3〉〈1| + ρ32(t)|3〉〈2|; |1〉〈1| → ρ11(t)|1〉〈1| + ρ12(t)|1〉〈2| + ρ21(t)|2〉〈1| + ρ22(t)|2〉〈2| + ρ33(t)|3〉〈3|, from which ρAB(t) follows, as shown in appendix B. Once we have ρAB(t), we can study different partitions of our system. A key parameter is α2 ≡ κ2 − 4Ω2. Depending on whether α2≶0, we are in the underdamped or in the purely dissipative regime, as further explained in appendix A.1. As we shall see, for positive values of α2, entanglement asymptotically decays. This would be consistent with a concomitant Markovian evolution. To see whether this is the case, we evaluate  for the quantum maps that correspond to different partitions of our system. Now, the evaluation of
for the quantum maps that correspond to different partitions of our system. Now, the evaluation of  , as defined in equation (1), requires that we perform a maximization over all initial states. For our present purposes, however, we may restrict the maximization to a subset of initial states. We will comment on this point later on but let us now stress that, in practice, when performing a quantum computational task, one is generally restricted to deal with a subset of initial states.
, as defined in equation (1), requires that we perform a maximization over all initial states. For our present purposes, however, we may restrict the maximization to a subset of initial states. We will comment on this point later on but let us now stress that, in practice, when performing a quantum computational task, one is generally restricted to deal with a subset of initial states.
We thus define a restricted non-Markovianity measure  similarly to
similarly to  in equation (1), but with the maximization restricted to the initial values ρaa(θ, 0) of a given form, e.g., equation (3) traced over the cavities. This is a valid definition, with the proviso that it does not characterize the whole map Φaa, only its restriction to a well-defined domain
in equation (1), but with the maximization restricted to the initial values ρaa(θ, 0) of a given form, e.g., equation (3) traced over the cavities. This is a valid definition, with the proviso that it does not characterize the whole map Φaa, only its restriction to a well-defined domain  . Note that if there are two initial states in
. Note that if there are two initial states in  (labelled θ1, θ2) and a time t for which σaa(t, θ1, θ2) > 0, then Φaa is non-Markovian according to the standard definition. On the other hand, according to this definition, the vanishing of
(labelled θ1, θ2) and a time t for which σaa(t, θ1, θ2) > 0, then Φaa is non-Markovian according to the standard definition. On the other hand, according to this definition, the vanishing of  for all initial states in
for all initial states in  is not sufficient for Φaa to be Markovian (it should be
is not sufficient for Φaa to be Markovian (it should be  ). It is nonetheless useful to term Φaa a (restricted) Markovian map, whenever
). It is nonetheless useful to term Φaa a (restricted) Markovian map, whenever  .
.
In the following, we will assess the non-Markovianity of different partitions and compare them with the corresponding concurrences. Generally, calculating  requires evaluation of ρd ≡ ρ1 − ρ2, which is Hermitian, so that
requires evaluation of ρd ≡ ρ1 − ρ2, which is Hermitian, so that  and
and  , where the rk are the eigenvalues of ρd. We thus obtain for the rate of change σ(t, ρ1, 2(0)) = dD(ρ1, ρ2)/dt the expression
, where the rk are the eigenvalues of ρd. We thus obtain for the rate of change σ(t, ρ1, 2(0)) = dD(ρ1, ρ2)/dt the expression  , which yields analytical results.
, which yields analytical results.
2.1. The atom–atom partition
Let us first address the atom–atom partition. Tracing ρAB(t) over the cavities gives the atom–atom density matrix
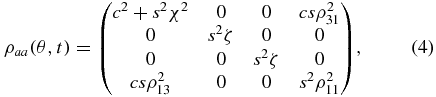
with c = cos θ, s = sin θ, χ = ρ22 + ρ33, ζ = ρ11χ. The process Φaa: ρaa(0) → ρaa(t) that is defined through equation (4) gives ρdifaa(t) = ρaa(θ2, t) − ρaa(θ1, t) as
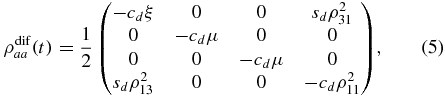
with cd = cos 2θ2 − cos 2θ1, sd = sin 2θ2 − sin 2θ1, ξ = ρ11(ρ11 − 2), μ = ρ11(1 − ρ11). In order to obtain  we need the eigenvalues of ρdifaa(t). These are
we need the eigenvalues of ρdifaa(t). These are
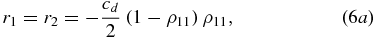

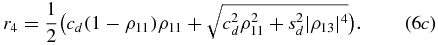
Since c2d(2 − ρ11)ρ311 + sd2|ρ13|4 ⩾ 0, it follows that c2d(1 − ρ11)2ρ211 = cd2ρ211 − cd2(2 − ρ11)ρ311 ⩽ c2dρ112 + s2d|ρ13|4, so that
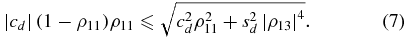
We can see that r3 ⩽ 0. Indeed, for cd < 0 it is obvious, and for cd > 0 the inequality (7) implies r3 ⩽ 0. Similarly, one obtains r4 ⩾ 0. From the explicit results of appendix A, we can check that |ρ13|2 = ρ11, so that we have
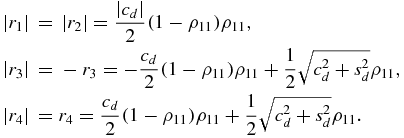
We can now calculate the trace distance as  and its rate of change is thus given by
and its rate of change is thus given by
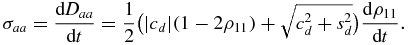
Because  , it follows that
, it follows that  , so that dDaa/dt > 0⇔dρ11/dt > 0 . The explicit expression of dρ11(t)/dt reads
, so that dDaa/dt > 0⇔dρ11/dt > 0 . The explicit expression of dρ11(t)/dt reads

One sees that for α2 > 0, it holds dρ11/dt < 0, so that the evolution of ρaa(θ, t) is indeed Markovian in this regime.
For α2 < 0, there are time intervals for which σaa > 0, as illustrated in figure 1, and the process is thus non-Markovian. From the given expression of dρ11/dt, we can obtain the times tm for which σaa = 0. The time intervals for which σaa > 0 are [t1, t2], [t3, t4], ..., so that we can write
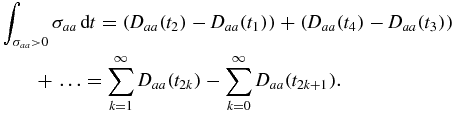
After some algebra, we obtain
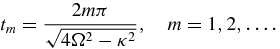
Now, because
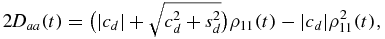
in order to calculate  we need to evaluate only the quantities I1 = ∑∞k = 1ρ11(t2k) − ∑∞k = 0ρ11(t2k + 1) and I2 = ∑∞k = 1ρ211(t2k) − ∑∞k = 0ρ112(t2k + 1). We obtain the following closed expressions:
we need to evaluate only the quantities I1 = ∑∞k = 1ρ11(t2k) − ∑∞k = 0ρ11(t2k + 1) and I2 = ∑∞k = 1ρ211(t2k) − ∑∞k = 0ρ112(t2k + 1). We obtain the following closed expressions:

where Ωr = 2Ω/κ. Note that the positiveness of the above expressions requires Ωr to be constrained by Ωr ⩾ 2.3325, which follows from  . In any case, it is clear that
. In any case, it is clear that  is a quantity that scales as
is a quantity that scales as  .
.
Figure 1. Rate of change σ'aa = σaa(t, θ, −θ)/100 of trace distance for the atom–atom partition. The parameters are κ = 1, Ω = 22, θ = 2π/5 (underdamped regime: α2 < 0). The times at which σaa = 0 are given by tm = 2mπ(4Ω2 − κ2)−1/2, m = 1, 2, ....
Download figure:
Standard imageThe behaviour of σaa(t), as shown in figure 1 for the underdamped case, is similar to that of concurrence in the same regime. We could thus also talk of sudden death and rebirth in terms of σaa(t). We will return to this point and compare concurrence and σaa(t) in a regime in which both behave similarly.
2.2. The cavity–cavity partition
By applying a similar procedure, we obtain for the cavity–cavity subsystem a matrix ρcc which follows from ρaa by the replacements  , ρ31 → ρ32, ρ13 → ρ23. From the so-obtained ρcc, it follows that ρdifcc(t) = ρcc(θ2, t) − ρcc(θ1, t) is given by
, ρ31 → ρ32, ρ13 → ρ23. From the so-obtained ρcc, it follows that ρdifcc(t) = ρcc(θ2, t) − ρcc(θ1, t) is given by
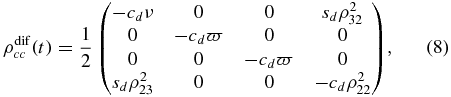
with cd = cos 2θ2 − cos 2θ1, sd = sin 2θ2 − sin 2θ1, ν = ρ22(ρ22 − 2) and ϖ = ρ22(1 − ρ22). As in the case of the atom–atom subsystem, for calculating  we need the eigenvalues of ρdifcc(t), which are
we need the eigenvalues of ρdifcc(t), which are
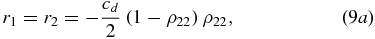
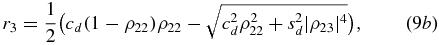
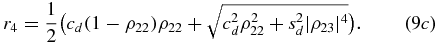
From the explicit solution given in appendix A, we observe that |ρ23|2 = ρ22, and by a similar reasoning as in the previous section, one obtains r3 ⩽ 0 and r4 ⩾ 0, so that the trace distance results in
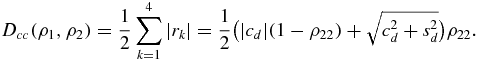
Its rate of change is then given by
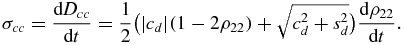
As with the atom–atom evolution, also in this case we easily conclude that  , so that in order to see whether dDcc/dt > 0 we need to analyse only the sign of
, so that in order to see whether dDcc/dt > 0 we need to analyse only the sign of
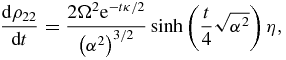
where  . This expression can be written in the form
. This expression can be written in the form
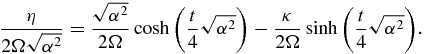
By setting cosh u = κ/2Ω and  the above equation reads
the above equation reads
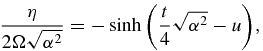
with
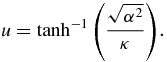
For α2 > 0, we see that η > 0 and thus σcc > 0 provided that t is such that  . In this case, the evolution is non-Markovian, even though we are in a purely dissipative regime. We see also that there is a single time t0 for which σcc = 0, which is given by
. In this case, the evolution is non-Markovian, even though we are in a purely dissipative regime. We see also that there is a single time t0 for which σcc = 0, which is given by
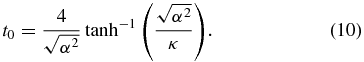
The behaviour of t0(κ, Ω) is shown in figure 2. We will come back to discuss the behaviour of t0(κ, Ω), after we have dealt with concurrences.
Figure 2. The time  for which the map giving
for which the map giving  begins to be Markovian.
begins to be Markovian.
Download figure:
Standard imageFor α2 < 0, the evolution is also non-Markovian, as expected, but now the times tm for which σcc = 0 are given by
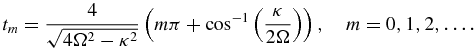
By proceeding similarly to the atom–atom case, one can calculate  , if needed.
, if needed.
3. Entanglement evolution
In the present case, for all the two-qubit partitions of ρAB, we obtain matrices of the X form [3]. Concurrences are then given by  , with j, k ∈ {a, c} (we append a subindex if necessary, to avoid ambiguity: aAcB means atom of unit A and cavity of unit B, etc). In the present case, we obtain Cjk = 2max {0, Qjk}, with
, with j, k ∈ {a, c} (we append a subindex if necessary, to avoid ambiguity: aAcB means atom of unit A and cavity of unit B, etc). In the present case, we obtain Cjk = 2max {0, Qjk}, with

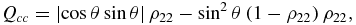
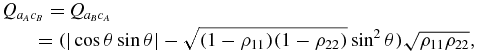
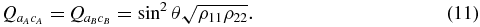
Concurrences of all partitions are thus ruled by just two quantities, ρ11 and ρ22, the populations of |e, 0〉 and |g, 1〉. Based on equations (11), we can address questions like those raised by Yönaç et al [3]. Consider, e.g., Caa and Ccc. We see from equations (11) that the conditions Caa > 0 and Ccc > 0 are equivalent to f(ρ11, θ) > 0 and f(ρ22, θ) > 0, respectively, with

Thus, by analysing f(x, θ) we can predict ESD, ESB and entanglement transfer. An example is shown in figure 3, in which we observe entanglement transfer as well as entanglement rebirth in the underdamped regime (α2 < 0), signalled by the atom–atom and cavity–cavity concurrences. On the other hand, as illustrated in figure 4, in the purely dissipative regime (α2 > 0), neither ESD nor ESB shows up. Both atom–atom and cavity–cavity concurrences asymptotically decay. However, a non-vanishing Ccc, signalling entanglement transfer, is somewhat unexpected for cavities that behave as reservoirs for the atoms. Clearly, the collective behaviour does not reflect the behaviour of the constituent parties. In any case, we should expect that under these circumstances, the evolution of the corresponding partition of the system is Markovian. To confirm this, we look at  for the respective maps.
for the respective maps.
Figure 3. Atom–atom (Caa) and cavity–cavity (Ccc) concurrences in the underdamped regime ( KHz,
KHz,  , with ω/2π = 51 GHz and Q = 3 × 108). The initial atom–atom state is
, with ω/2π = 51 GHz and Q = 3 × 108). The initial atom–atom state is  with
with  . We observe entanglement transfer and rebirth. Caa > 0 and Ccc > 0 whenever f1 = f(ρ11, θ) > 0 and f2 = f(ρ22, θ) > 0, respectively, with
. We observe entanglement transfer and rebirth. Caa > 0 and Ccc > 0 whenever f1 = f(ρ11, θ) > 0 and f2 = f(ρ22, θ) > 0, respectively, with  .
.
Download figure:
Standard imageFigure 4. Atom–atom (Caa) and cavity–cavity (Ccc) concurrences in the overdamped regime (α2 = 23, κ = 12, Ω = 5.5). Initial atom–atom states are as follows: |ψAB(0)〉 = cos θ|gAgB〉 + sin θ|eAeB〉 with θ = π/18. In this regime, the atoms see their cavities as reservoirs causing excited atomic states to exponentially decay with Γ = 2.52. A non-vanishing Ccc is unexpected for cavities behaving as reservoirs.
Download figure:
Standard image3.1. Interplay between entanglement and non-Markovianity
As already shown, for the atom–atom partition we have σaa(t, θ1, θ2) > 0⇔dρ11/dt > 0, while for the cavity–cavity partition σcc(t, θ1, θ2) > 0⇔dρ22/dt > 0. Within the purely dissipative regime (α2 > 0), it holds dρ11/dt < 0, so that in the atom–atom case  , as expected. However, there are cases (see figure 5, left panel) in which σcc(t, θ1, θ2) > 0 for 0 < t < t0. This implies that for the cavity–cavity partition, the process Φcc can be diagnosed as non-Markovian (
, as expected. However, there are cases (see figure 5, left panel) in which σcc(t, θ1, θ2) > 0 for 0 < t < t0. This implies that for the cavity–cavity partition, the process Φcc can be diagnosed as non-Markovian ( ), even within a purely dissipative regime (α2 > 0).
), even within a purely dissipative regime (α2 > 0).
Figure 5. Left panel: a case with σcc(t, 2π/5, −2π/5) > 0 for κ = 6.1, Ω = 3 (purely dissipative regime: α2 > 0), leading to  . Right panel: concurrence Caa(t, θ) and rate of change σ'aa = σaa(t, θ, −θ)/20 of trace distance for κ = 1, Ω = 22, θ = 2π/5 (underdamped regime: α2 < 0). For times t ≳ 0.6, non-Markovianity, signalled by σ'aa > 0, does not reflect that entanglement has ceased to be a resource.
. Right panel: concurrence Caa(t, θ) and rate of change σ'aa = σaa(t, θ, −θ)/20 of trace distance for κ = 1, Ω = 22, θ = 2π/5 (underdamped regime: α2 < 0). For times t ≳ 0.6, non-Markovianity, signalled by σ'aa > 0, does not reflect that entanglement has ceased to be a resource.
Download figure:
Standard imageFurthermore, ρdifaa yields results like that of figure 5, right panel. We observe sudden death and rebirth in both Caa(t, θ1) and σaa(t, θ1, θ2) > 0, the latter being required for having  . As we see, sudden death and rebirth in one and the other case obey different dynamics. Even when Caa(t, θ) is definitely gone, σaa(t, θ, −θ) keeps reappearing during time windows, each window lasting a time Taa = 2π(4Ω2 − κ2)−1/2. The rate of change σaa(t, θ, −θ) corresponds to the distance between two entangled states having the same concurrence. If we employ atom–atom entangled states as a resource, and if at a given time this resource becomes unavailable, it is immaterial whether two such evolved states remain distinguishable. Hence, figure 5 illustrates how a diagnosis about the return of 'information' back to the system (σaa > 0) fails to capture that our chosen carrier of information, namely entanglement, is not available any longer (Caa = 0). The non-Markovianity of this map can be calculated, giving
. As we see, sudden death and rebirth in one and the other case obey different dynamics. Even when Caa(t, θ) is definitely gone, σaa(t, θ, −θ) keeps reappearing during time windows, each window lasting a time Taa = 2π(4Ω2 − κ2)−1/2. The rate of change σaa(t, θ, −θ) corresponds to the distance between two entangled states having the same concurrence. If we employ atom–atom entangled states as a resource, and if at a given time this resource becomes unavailable, it is immaterial whether two such evolved states remain distinguishable. Hence, figure 5 illustrates how a diagnosis about the return of 'information' back to the system (σaa > 0) fails to capture that our chosen carrier of information, namely entanglement, is not available any longer (Caa = 0). The non-Markovianity of this map can be calculated, giving  and is therefore somewhat misleading for assessing the action of Φaa. Similar remarks can be made for the map Φcc.
and is therefore somewhat misleading for assessing the action of Φaa. Similar remarks can be made for the map Φcc.
3.2. Additional entanglement features in the system
Besides α, also Γ = Ω2/κ is a physically meaningful parameter. For large enough α, the excitation of each atom–cavity unit exponentially decays ruled by Γ alone, as shown in appendix A.1. Thus, Γ serves us to make sure that we are definitely in a regime in which each atom sees its cavity as a reservoir. In such a case, we should expect that the cavities are unable to entangle. However, for appropriate choices of Ω and κ, we find non-vanishing cavity–cavity concurrences which initially grow, reach a maximum and finally decay approaching zero asymptotically. This was, for instance, the case shown in figure 4. It illustrates a rather counterintuitive feature, because it signals entanglement transfer from qubits to entities which from the qubit's perspective look like reservoirs.
On the other hand, as we saw before, for α2 > 0 there is a single time t0, given by equation (10), for which σcc = 0. We can study how t0(κ, Ω) changes when we vary Ω and κ, keeping Γ = Ω2/κ fixed. We can further choose κ ≫ Ω, so as to be in the overdamped regime, in which the atomic dynamics is ruled by Γ alone. The cavities are then practically all the time in their vacuum states and behave as reservoirs for the atoms. We should thus expect that within this regime, no quantum features related to the cavities show up. But this is not the case. As shown in figure 6, t0 is not a function of Γ alone. It depends separately on κ and Ω, so that for a given Γ we can obtain quite different values of t0. We can thus identify here a feature that is related to the entanglement of two cavities, even though we should expect these cavities to be incapable of becoming entangled, as they behave like reservoirs for the individual atoms. This is reminiscent of ESD: the collective dynamics of the entangled system markedly departs from the dynamics of its constituents. Furthermore, such a collective dynamics is established in the absence of any physical connection between the constituents. In contrast to other studies that address (quantum) simulators, the effects reported here involve quantal environments that can effectively behave like reservoirs for some other entities, while keeping their entanglement's capability.
Figure 6. The time  at which the map ruling
at which the map ruling  begins to be Markovian. As shown in the inset,
begins to be Markovian. As shown in the inset,  increases linearly with Γ. For each value of Γ, the parameters Ω and
increases linearly with Γ. For each value of Γ, the parameters Ω and  are chosen such that
are chosen such that  . The values of
. The values of  cover a range in which the atomic overdamped regime definitely holds, from
cover a range in which the atomic overdamped regime definitely holds, from  to
to  . As can be seen, t0 is not a function of Γ alone, even though the cavities behave like reservoirs and the atomic dynamics is ruled by Γ. Only for very large values of
. As can be seen, t0 is not a function of Γ alone, even though the cavities behave like reservoirs and the atomic dynamics is ruled by Γ. Only for very large values of  does
does  behave as expected, i.e., as a function of Γ alone.
behave as expected, i.e., as a function of Γ alone.
Download figure:
Standard image3.3. Experimental feasibility
Because our main goal was to study the interplay between entanglement and non-Markovianity, we have generally chosen parameter values that were appropriate to such a goal, without regard to experimental feasibility. However, figure 3 is an exception, as it corresponds to parameter values that are within the reach of present technological capabilities [20]. Indeed, the chosen parameter values ( KHz, κ = ω/Q, with ω/2π = 51 GHz and Q = 3 × 108) correspond to those attainable in cavity quantum electrodynamics experiments performed by Haroche's group at ENS in Paris. As a matter of fact, the assumed cavity quality factor Q = 3 × 108 is a rather modest one, as values as high as Q = 4.2 × 1010 have recently been reported [21]. As shown in figure 3, entanglement transfer occurs within some tens of microseconds. The photon storage time Tc of the open cavity for the assumed value of κ is about 1 ms. Standard experiments in which several Rabi oscillations were observed [20] required a time window of some 100 μs. Now, in our case the photon storage time is not the only limitation we have to consider. An additional one comes from our assumption of zero temperature, which means that there are no thermal photons in the cavity. At thermal equilibrium, the open cavity contains about 0.7 thermal photons on the average. This mean photon number can be reduced down to 0.1 by sending atoms in the lower level through the cavity, in order to absorb as much thermal photons as possible. After this 'cleaning' process, the proper run of the experiment begins. As a result, there is a time window of 0.3 Tc available for an experimental run [20]. In our case, the time window amounts 280 μs, so that it would be wide enough for observing entanglement transfer from the atoms to the cavities. As for the preparation of the initial state, entangled atomic states like the EPR pair |ψ〉 ∼ |e1, g2〉 − |g1, e2〉 have since long been demonstrated using open cavities [22], and more recently by exploiting the so-called Rydberg blockade [23, 24]. Now, even though the capabilities of laboratories like the ENS in Paris appear to support the experimental feasibility of our results, there is still a long way to go before being able to efficiently work with two (or three) open cavities in conjunction.
KHz, κ = ω/Q, with ω/2π = 51 GHz and Q = 3 × 108) correspond to those attainable in cavity quantum electrodynamics experiments performed by Haroche's group at ENS in Paris. As a matter of fact, the assumed cavity quality factor Q = 3 × 108 is a rather modest one, as values as high as Q = 4.2 × 1010 have recently been reported [21]. As shown in figure 3, entanglement transfer occurs within some tens of microseconds. The photon storage time Tc of the open cavity for the assumed value of κ is about 1 ms. Standard experiments in which several Rabi oscillations were observed [20] required a time window of some 100 μs. Now, in our case the photon storage time is not the only limitation we have to consider. An additional one comes from our assumption of zero temperature, which means that there are no thermal photons in the cavity. At thermal equilibrium, the open cavity contains about 0.7 thermal photons on the average. This mean photon number can be reduced down to 0.1 by sending atoms in the lower level through the cavity, in order to absorb as much thermal photons as possible. After this 'cleaning' process, the proper run of the experiment begins. As a result, there is a time window of 0.3 Tc available for an experimental run [20]. In our case, the time window amounts 280 μs, so that it would be wide enough for observing entanglement transfer from the atoms to the cavities. As for the preparation of the initial state, entangled atomic states like the EPR pair |ψ〉 ∼ |e1, g2〉 − |g1, e2〉 have since long been demonstrated using open cavities [22], and more recently by exploiting the so-called Rydberg blockade [23, 24]. Now, even though the capabilities of laboratories like the ENS in Paris appear to support the experimental feasibility of our results, there is still a long way to go before being able to efficiently work with two (or three) open cavities in conjunction.
4. Summary and conclusions
In this paper, we have dealt with one of the few open systems that can be exactly solved and that is capable of showing Markovian and non-Markovian regimes: a two-level atom in a lossy cavity. By taking two such atom–cavity units to conform a larger system, it was possible to analytically study its evolution when only the atoms are initially entangled. We could observe entanglement transfer under Markovian and non-Markovian regimes. The lossy cavities may behave either as quantum objects or as reservoirs, depending on the chosen regime. It is possible to observe entanglement transfer from the atoms to the cavities. The latter represent actual physical systems. Our findings refer to these actual systems, not to their simulators. In particular, we have predicted entanglement transfer when the cavities appear to the atoms as reservoirs. This phenomenon could in principle be submitted to experimental test and contrasted against recently studied cases in which actual reservoirs were substituted by (quantum) simulators [12]. Our results confirm also a recent claim [25], namely that the generation of bright and dark periods in the entanglement dynamics can occur for a wide variety of environments.
In order to quantitatively assess the degree of non-Markovianity, we applied a recently introduced measure  that is based on the trace distance between states. We have submitted this measure to critical scrutiny. The current interpretation of a growing distance between states is that 'information' is flowing from the environment back to the system. We argue that it is necessary to tighten this interpretation by being more specific about the chosen carriers of information. It might be that a quantum process is classified as non-Markovian, but information could have been encoded using a feature not directly related to the distinguishability between states. In order to illustrate the possible shortcomings of
that is based on the trace distance between states. We have submitted this measure to critical scrutiny. The current interpretation of a growing distance between states is that 'information' is flowing from the environment back to the system. We argue that it is necessary to tighten this interpretation by being more specific about the chosen carriers of information. It might be that a quantum process is classified as non-Markovian, but information could have been encoded using a feature not directly related to the distinguishability between states. In order to illustrate the possible shortcomings of  we compared it with the degree of entanglement, as measured by Wooters concurrence. We have presented a quantum map for which σaa(t) > 0 when concurrence—a possible carrier of information—is no longer available (Caa(t) = 0). Moreover, we have found (figure 5, left panel) that
we compared it with the degree of entanglement, as measured by Wooters concurrence. We have presented a quantum map for which σaa(t) > 0 when concurrence—a possible carrier of information—is no longer available (Caa(t) = 0). Moreover, we have found (figure 5, left panel) that  in purely dissipative, overdamped regimes, which are intuitively taken as Markovian.
in purely dissipative, overdamped regimes, which are intuitively taken as Markovian.
Finally, we stress that by having restricted our analysis to a specific family of entangled states, we followed an approach that is representative of most quantum informational tasks. Any source of entanglement defines a set of available initial states, thereby fixing an effective and restricted quantum channel. Our analysis could be extended to different families of initial states. Future work might show interesting features connected to the chosen family, but the general picture should prevail: generally, we should expect that entanglement can be transferred from a system only when its environment is capable of carrying quantum information. In our model, entanglement occurs between quantal environments, not between reservoirs. Our treatment thus avoids paradoxical situations involving entangled reservoirs, something reminiscent of Schrödinger's cat. We emphasize the inadequacy of using environment simulators as substitutes of true environments when the dynamics of the latter matters. Also, that proper non-Markovianity measures should be tailored to the actually employed carriers of information. To find such measures is thus a challenge issued by our results.
Acknowledgments
We thank B Mejía for critical reading of our manuscript, and DGI-PUCP for partial financial support.
Appendix A.: Quantum map of the atom–cavity unit
The Lindblad equation for the atom–cavity unit yields the following differential equations for the components of ρ:
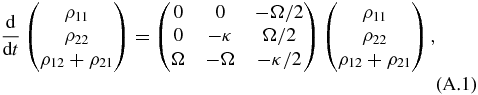
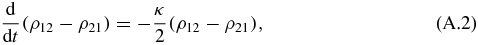

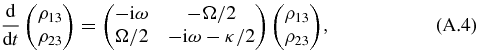
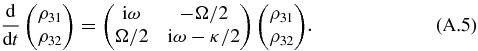
The system of equations (A.1)–(A.5) can be explicitly solved, thereby defining a map
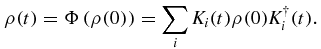
For an initial state ρ(0) = ∑k, lαkl|k〉〈l|, we obtain ρ(t) from the action of Ki(t) on each element |k〉〈l|, i.e.
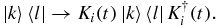
The action of the map on |k〉〈l| can be obtained case by case. First, from equations (A.1)–(A.5), the evolution of |3〉〈3| follows from setting ρ33(0) = 1 and all other ρij(0) = 0. This gives (see equations (A.1) and (A.3)) ρ33(t) = ρ33(0) = 1, so that
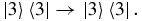
The evolution of |1〉〈3| and |3〉〈1| follows from setting ρ13(0) = 1 = ρ31(0) and all other ρij(0) = 0. We obtain

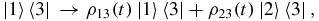
where
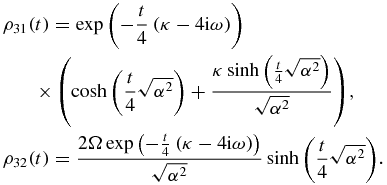
For the evolution of |1〉〈1|, we set ρ11(0) = 1, all other ρij = 0, and obtain
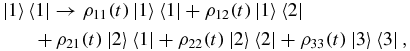
with
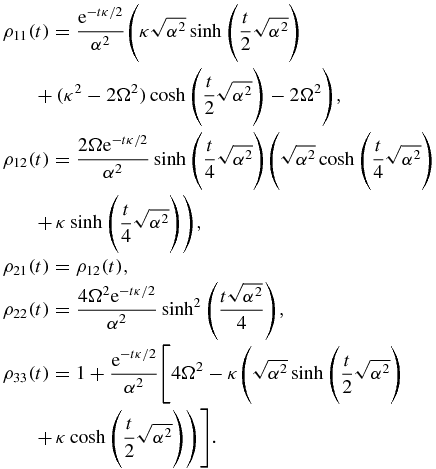
For the evolution of |1〉〈2| and |2〉〈1|, we use equations (A.1)–(A.3) with ρ12(0) = ρ21(0) = 1 and all other ρij = 0. Having obtained ρ22(t), ρ33(t) follows from equation (A.3). For the evolution of |2〉〈2|, we use equations (A.1)–(A.3) with ρ22(0) = 1 and all other ρij = 0. We thus obtain maps of the form
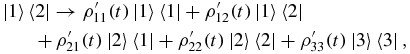
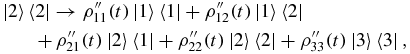
with ρ'ij and ρ''ij determined as already explained.
A.1. Evolution regimes and adiabatic approximation
We can distinguish two markedly different regimes for the evolution of our system. On the one hand, we identify the underdamped regime, in which the cavity sustains a photon long enough for the excitation to come back to the atom. This regime is defined by α2 ≡ κ2 − 4Ω2 < 0. The results of appendix A show that this condition leads to an oscillatory decay of the atom's higher level population. On the other hand, we recognize the purely dissipative regime, in which α2 > 0, so that the atom cannot perform Rabi oscillations.
Moreover, and as a subset of the purely dissipative regime, we establish the overdamped regime, characterized by κ ≫ Ω (i.e. α2 ≫ 0). In this regime, the probability ρ22 for a photon to be in the cavity decays very rapidly, and so also the coherences ρ12 and ρ21. The cavity remains thus practically all the time in its vacuum state, acting as a fully dissipative environment for the atom. Under these circumstances, we may apply the adiabatic approximation to the evolution of ρ12 + ρ21 (see equation (A.1)), which results in

Inserting this expression into the equation for dρ11/dt gives
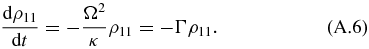
Hence, in the overdamped regime, ρ11 decays asymptotically with an effective decay constant Γ ≡ Ω2/κ. From the atom's perspective, the cavity behaves as a vacuum-like reservoir.
Appendix B.: Quantum map for the complete system
Taking as the initial state |ΨAB(0)〉 = (cos θ|gA〉|gB〉 + sin θ|eA〉|eB〉)⊗|0A〉|0B〉, the initial density matrix is given by
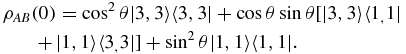
To obtain ρ(t), we apply Kij(t) = K(A)i(t)⊗K(B)j(t) to each |kAkB〉〈lAlB|, that is,
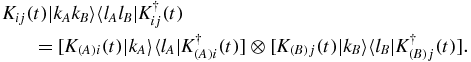
The actions of K(A)i and K(B)i are formally the same. Hence, it suffices to obtain the map for a single atom–cavity unit. Using the results of appendix A, one finds that ρAB(0) evolves to
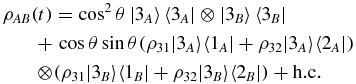
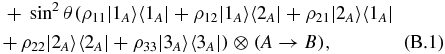
with ρij as defined in appendix A.
Appendix C.: Divisibility
Although not relevant for our present purposes, we briefly discuss the alternative non-Markovianity measure that is based on the divisibility of a quantum map Φ. We recall that a completely positive trace preserving (CPTP) map Φ(t + τ, 0) is divisible, if it can be decomposed as the product of two CPTP maps, according to Φ(t + τ, 0) = Φ(t + τ, t)Φ(t, 0). Rivas et al [17] define a map to be Markovian iff it is divisible, which amounts to require that Φ(t + τ, t) is CP [17]. It can be shown that Φ(t + τ, t) is CP iff
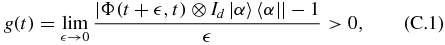
where |α〉〈α| = d−1/2∑di = 1|i〉|i〉 is a maximally entangled state of the open system—whose dynamics is ruled by Φ—and some ancillary system, both of them having dimension d. When the system's evolution is ruled by a local-in-time master equation  , then for
, then for  → 0 we can formally write
→ 0 we can formally write ![$\Phi (t+\epsilon ,t)=\exp \left[ \mathcal {L}(t)\epsilon \right]$](https://content.cld.iop.org/journals/0953-4075/45/9/095501/revision1/jpb416647ieqn84.gif) . In this case,
. In this case,
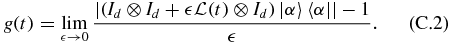
The non-Markovianity measure ![$\mathcal {N}_{{\rm RHP}} \in \left[ 0,1\right]$](https://content.cld.iop.org/journals/0953-4075/45/9/095501/revision1/jpb416647ieqn85.gif) , proposed by Rivas et al , is defined as
, proposed by Rivas et al , is defined as  , with
, with  . Now, for the kind of approach that we have followed here,
. Now, for the kind of approach that we have followed here,  is not directly applicable. The maps we have considered are obtained by tracing out some subsystem of the whole system. On the other hand, the calculation of Φ(t +
is not directly applicable. The maps we have considered are obtained by tracing out some subsystem of the whole system. On the other hand, the calculation of Φ(t +  , t)⊗Id|α〉〈α| requires that we have Φ(t +
, t)⊗Id|α〉〈α| requires that we have Φ(t +  , t)|i〉〈j| for any element |i〉〈j| of the system. Let us take, e.g., the map giving the atom–atom evolution ρaa(θ, t), equation (4). It was obtained by tracing ρAB(t) over the cavities. The space
, t)|i〉〈j| for any element |i〉〈j| of the system. Let us take, e.g., the map giving the atom–atom evolution ρaa(θ, t), equation (4). It was obtained by tracing ρAB(t) over the cavities. The space  in which ρaa(θ, t) operates is thus spanned by {|gg〉, |ge〉, |eg〉, |ee〉} and the ancilla space required for the calculation of g(t) would be a copy of
in which ρaa(θ, t) operates is thus spanned by {|gg〉, |ge〉, |eg〉, |ee〉} and the ancilla space required for the calculation of g(t) would be a copy of  . In order to calculate g(t), we thus need Φaa(t +
. In order to calculate g(t), we thus need Φaa(t +  , t)|gg〉〈gg|, Φaa(t +
, t)|gg〉〈gg|, Φaa(t +  , t)|ge〉〈ge| and so on. Such quantities cannot be unambiguously obtained from the available map Φ(t, 0): ρAB(0)↦ρAB(t) = Φ(t, 0)ρAB(0). Indeed, there are several different initial states ρAB(0) which, after tracing over the cavities, lead to the same atom–atom state, say, |gg〉〈gg|. This is of course a consequence, as pointed out by Rivas et al [17], of our having decided to be blind to one part of the whole system by tracing over that part. Nevertheless, if we want to assess—by means of its divisibility—the non-Markovianity of the effective map leading to ρaa(θ, t), then we need to restrict the general definition of
, t)|ge〉〈ge| and so on. Such quantities cannot be unambiguously obtained from the available map Φ(t, 0): ρAB(0)↦ρAB(t) = Φ(t, 0)ρAB(0). Indeed, there are several different initial states ρAB(0) which, after tracing over the cavities, lead to the same atom–atom state, say, |gg〉〈gg|. This is of course a consequence, as pointed out by Rivas et al [17], of our having decided to be blind to one part of the whole system by tracing over that part. Nevertheless, if we want to assess—by means of its divisibility—the non-Markovianity of the effective map leading to ρaa(θ, t), then we need to restrict the general definition of  , as we did with the measure
, as we did with the measure  defined by Breuer et al [14] (denoted by
defined by Breuer et al [14] (denoted by  in the main text). To this end, we proceed as follows.
in the main text). To this end, we proceed as follows.
The map ΦAB(t, 0): ρAB(0)↦ρAB(t) = ΦAB(t, 0)ρAB(0) can be obtained from the two CPTP maps ΦS(t, 0): ρS(0)↦ρS(t) = Φ(t, 0)ρS(0), S = A, B, that correspond to two open subsystems. Each ΦS(t, 0) can be expressed in terms of Kraus operators, from which one obtains [16]
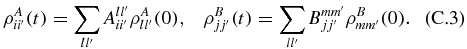
It then follows that
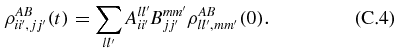
In our case,  and
and  coincide with one another, because we have taken two identical atom–cavity subsystems. Furthermore, we obtain
coincide with one another, because we have taken two identical atom–cavity subsystems. Furthermore, we obtain  for
for  → 0 directly from the Liouvillian
→ 0 directly from the Liouvillian ![$\mathcal {L}=-{\rm i}[H,\rho ]+\frac{\kappa }{2} \left( 2a\rho a^{\dagger }-a^{\dagger }a\rho -\rho a^{\dagger }a\right)$](https://content.cld.iop.org/journals/0953-4075/45/9/095501/revision1/jpb416647ieqn97.gif) , as
, as  . Replacing this in equation (C.4), we obtain the total map Φ(t, 0): ρAB(0)↦ρAB(t) = ΦAB(t, 0)ρAB(0) to second order in
. Replacing this in equation (C.4), we obtain the total map Φ(t, 0): ρAB(0)↦ρAB(t) = ΦAB(t, 0)ρAB(0) to second order in  . Tracing ρAB(t) over the cavities, we obtain
. Tracing ρAB(t) over the cavities, we obtain
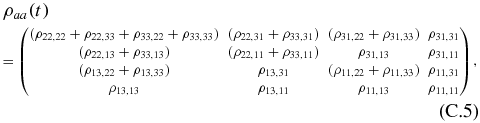
with explicit expressions for the  that are given to second order in
that are given to second order in  . The map fixing ρaa(θ, t), equation (4), is obtained for initial states of the form given by equation (3). We can thus restrict ourselves to the subspace spanned by {|11〉, |33〉} and use an ancillary system that is a replica of this subsystem, so that |α〉 = 2−1/2(|11〉⊗|11〉 + |33〉⊗|33〉). Using equation (C.4), we obtain ΦAB(|11〉〈11|), ΦAB(|11〉〈33|),ΦAB(|33〉〈11|) andΦAB(|33〉〈33|). Tracing these quantities over the cavities yields a matrix of the form of equation (C.5) in each case, for both the system and the ancilla. There is no ambiguity in this case, as both |11〉 and |33〉 correspond to zero cavity photons. With these results, we can calculate g(t) as defined by equation (C.2). It turns out that the effective map, i.e. the result of calculating
. The map fixing ρaa(θ, t), equation (4), is obtained for initial states of the form given by equation (3). We can thus restrict ourselves to the subspace spanned by {|11〉, |33〉} and use an ancillary system that is a replica of this subsystem, so that |α〉 = 2−1/2(|11〉⊗|11〉 + |33〉⊗|33〉). Using equation (C.4), we obtain ΦAB(|11〉〈11|), ΦAB(|11〉〈33|),ΦAB(|33〉〈11|) andΦAB(|33〉〈33|). Tracing these quantities over the cavities yields a matrix of the form of equation (C.5) in each case, for both the system and the ancilla. There is no ambiguity in this case, as both |11〉 and |33〉 correspond to zero cavity photons. With these results, we can calculate g(t) as defined by equation (C.2). It turns out that the effective map, i.e. the result of calculating  followed by tracing over the cavities, yields a result that differs from the identity Id⊗Id only in terms that are of second order in
followed by tracing over the cavities, yields a result that differs from the identity Id⊗Id only in terms that are of second order in  . As a consequence, g(t) = 0 for the evolution of ρaa(θ, t), which according to this restricted measure should thus be diagnosed as a Markovian one for all values of the parameters θ, ω, Ω and κ. We thus obtain a diagnosis that occasionally differs from the one based on the trace distance between states. Now, generally, whenever
. As a consequence, g(t) = 0 for the evolution of ρaa(θ, t), which according to this restricted measure should thus be diagnosed as a Markovian one for all values of the parameters θ, ω, Ω and κ. We thus obtain a diagnosis that occasionally differs from the one based on the trace distance between states. Now, generally, whenever 
 , in contrast to our result. However, we stress that such a result should be taken with a grain of salt, as it does not refer to the actual quantum map Φ(t, 0): ρAB(0)↦ρAB(t) = Φ(t, 0)ρAB(0). If our aim were to compare the two (unrestricted) measures,
, in contrast to our result. However, we stress that such a result should be taken with a grain of salt, as it does not refer to the actual quantum map Φ(t, 0): ρAB(0)↦ρAB(t) = Φ(t, 0)ρAB(0). If our aim were to compare the two (unrestricted) measures,  and
and  , then we should address the total system AB. However, in such a case, an appropriate entanglement measure like concurrence is lacking, and this precludes addressing the interplay between entanglement and non-Markovianity, which is our main concern here.
, then we should address the total system AB. However, in such a case, an appropriate entanglement measure like concurrence is lacking, and this precludes addressing the interplay between entanglement and non-Markovianity, which is our main concern here.






