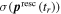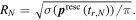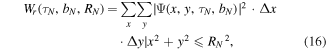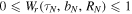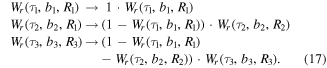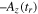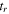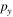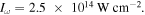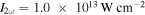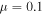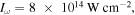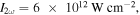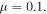Abstract
In strong-field ionization processes, two-color laser fields are frequently used for controlling sub-cycle electron dynamics via the relative phase of the laser fields. Here we apply this technique to velocity map imaging spectroscopy using an unconventional orientation with the polarization of the ionizing laser field perpendicular to the detector surface and the steering field parallel to it. This geometry allows not only to image the phase-dependent photoelectron momentum distribution (PMD) of low-energy electrons that interact only weakly with the ion (direct electrons), but also to investigate the low yield of higher-energy rescattered electrons. Phase-dependent measurements of the PMD of neon and xenon demonstrate control over direct and rescattered electrons. The results are compared with semi-classical calculations in three dimensions including elastic scattering at different orders of return and with solutions of the three-dimensional time-dependent Schrödinger equation.

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Strong-field ionization processes with subsequent recollision of the ionized electron wave packet with the parent ion can lead to recombination of the wave packet with emission of high-energy photons (high-harmonic generation) [1–3], impact ionization of a second electron (non-sequential double ionization, (NSDI)) [4, 5] or scattering of the wave packet, leading to high-energy electrons in the photoelectron momentum distribution (PMD) [6]. Due to the strong interaction of the electron with the ion, substantial structural information from the ion can be retrieved from the PMDs [7–9].
In recent years, tailoring of strong laser fields on the sub-cycle and sub-femtosecond timescale has become an important tool to gain control over electronic and nuclear dynamics in strong-field processes. Examples are polarization gating [10–13], field synthesis with parallel and orthogonal-polarized two-color (OTC) fields [14–16] and controlling/tagging of the carrier-envelope phase of few-cycle pulses [17–19]. OTC fields provide a fairly simple but powerful approach for steering the ionized electron wave packet in the field [20, 21]. Recently, this control has been used to study electron correlation in NSDI [22], the influence of the Coulomb field on the PMD [23], and interference effects between electron wave packets ionized within the same laser cycle [24].
In this study, the OTC technique is combined with velocity map imaging (VMI) spectroscopy [25] in an atypical geometry with the polarization of the (weak) steering field parallel to the detector surface and the polarization of the (strong) ionizing laser field perpendicular to it. In this configuration, changes in the momentum distribution due to the steering field change the position of the distribution on the detector and can be directly observed. Obviously, the information about the electron momenta parallel to the ionizing laser field is lost in this configuration. On the other hand, detecting scattered electrons with higher total energy is possible compared to the typical geometry of VMI spectroscopy where the ionizing field is polarized parallel to the detector surface. This is due to the fact that the electron detection is limited to a maximum energy parallel to the detector surface and the maximum energy of electrons emitted perpendicular to the ionizing field component is nearly a factor of three lower than the maximum energy of electrons emitted parallel to the ionizing laser field is the ponderomotive energy, where is the amplitude of the vector potential (atomic units will be used throughout unless otherwise specified).
We present the PMDs of neon and xenon in the aforementioned OTC field geometry and investigate how the PMDs of direct and scattered electrons behave as a function of the relative phase, between the two field components. The results are compared with three-dimensional (3D), semi-classical simulations which include scattering at multiple returns as well as to 3D simulations of the time-dependent Schrödinger equation (TDSE) within the single-active electron (SAE) approximation. By analyzing the simulated and measured results with the 'phase of the phase' method [26], we show a clear phase shift between direct and scattered electrons and demonstrate control over them. Both kinds of simulations reproduce the neon results very well. For xenon the agreement is overall good as well. However, noticeable deviations in the center of the PMD exist.
2. Experimental setup
The experimental investigation of strong-field photoionization in OTC fields is performed by focusing a Ti:Sapphire laser (λ0 = 798 nm) and its second harmonic into the interaction region of a VMI, see figure 1(a).
Figure 1. (a) Schematic of the thick-lens velocity map imaging spectrometer. The axes of the laboratory frame of reference and the orientation of the OTC fields are indicated. The red, ω, and blue, 2ω, components are linearly polarized parallel to the z- and y-axis, respectively. The polarization directions of both components are indicated by small red (ω) and blue (2ω) arrows in each figure. The effect of the orientation of the ω component is illustrated with measured examples of projections of PMDs for a linearly polarized (one-color) laser field where the polarization is parallel to y-axis (b) and parallel to z-axis (c). The former geometry has been used in numerous previous works, the latter is the subject of this paper. Due to the cylindrical symmetry of the PMDs, one can use the PMDs projection in (b) to retrieve a cut through the 3D PMD by Abel inversion. The result is shown in (d). The dashed lines/rings serve as orientation and indicate two specific momenta perpendicular to the polarization of the laser field. (e) shows how the PMD of (c) changes when a weak 2ω field is added.
Download figure:
Standard image High-resolution imageThe interferometer uses a 200 μm β-BaB2O4 (BBO) crystal, a 3000 μm calcite plate and a pair of fused silica wedges [27]. Depending on the incoming pulse energy, which is controlled using the reflection of a thin-film polarizer, the BBO converts up to 12% of the pulse energy from the fundamental pulse (frequency ω) to the orthogonally polarized pulse of twice the frequency (2ω). The calcite crystal is used to compensate the group velocity mismatch between the and fields such that the blue pulse overtakes the red one. Then the wedges are used for overlapping and fine tuning the relative phase between both fields. The overlap of both field envelopes is optimized by maximizing the total photoelectron yield from the target gas. Focusing with a mm mirror in back-focusing geometry yields peak intensities up to at the focus point in the interaction region of the VMI.
The VMI's electrostatic lens system accelerates photoelectrons towards a chevron multi-channel plate detector, which is equipped with a phosphor screen assembly. Projections of the 3D PMDs are recorded by taking images of the resulting intensity distribution on the phosphor screen with a CCD camera which has a dynamic range of 2600:1.
In order to overcome the limited dynamic range of the camera, we record a series of images with different exposure times and combine them into a high dynamic range (HDR) image for each measurement. The HDR images are generated from the individual images by replacing the signal of the overexposed pixels in the image with the longest exposure time (12 min) with the signal of the same pixel at shorter exposure time scaled to the longer exposure time. This approach allows us not only to observe PMDs in regions with high electron yield (i.e. the region of direct electrons), but also gives access to PMDs in regions where the electron yield is 4 to 5 orders of magnitude lower (e.g. in the region of scattered electrons).
The use of OTC fields entails a problem as compared to more conventional VMI measurements using a single linearly polarized field because there is no cylindrical symmetry. Thus, reconstructing the 3D PMD by applying an Abel inversion [28, 29] to the measured projection is not possible. One option to overcome this problem is to use a tomographic method [30]. However, this approach requires recording projections of the PMDs from multiple directions, which is difficult to realize for an OTC field and, in addition, increases the measurement time. The latter is particularly disadvantageous if regions with low photoelectron yield are of interest.
Here, we use a different geometry for the orientation of the polarizations, see figure 1(a), and compare the recorded PMDs to the corresponding theoretical results. We start by illustrating the difference of conventional VMI measurements for a linearly polarized one-color field and the projections that are measured and analyzed here. In figure 1(b) a typical projection from a measurement with linear polarization orientated parallel to the detector surface is shown. Applying Abel inversion leads to the cut thought the PMD shown in figure 1(d). Changing the geometry such that the linear polarization is perpendicular to the plane of the detector, results in figure 1(c) for the same interaction. The dashed rings in figure 1(c) correspond to the dashed lines in figure 1(b) and indicate two different momenta perpendicular to the polarization direction. As expected for a one-color linearly polarized field and this measurement geometry, the PMD (figure 1(c)) is rotationally symmetric. For an OTC configuration, in which the 2ω-field is parallel to the detector surface momentum changes induced by the 2ω-field are directly mapped onto the detector, see figures 1(a) and (e). As expected and readily identifiable, the rotational symmetry of the PMD is broken.
The core part of this work is recording and analyzing these PMD projections as a function of the relative phase of the fundamental and the second harmonic for different gases.
For each scan, is varied by 2π in steps of π/17 by adding fused silica to the beam path. The amount of fused silica needed to change by is 23.8 μm and the step size corresponds to adding ∼1.4 μm fused silica to the beam path. These values are confirmed by the periodicity in the observed phase-dependent yield
3. Data analysis
In order to quantify and analyze the phase-dependence of the yield, we apply the 'phase-of-the-phase' method [26] and extend it to the OTC measurements. The phase of the phase, is obtained by extracting the yield as a function of the relative phase, for each pixel, i.e. the electron yield as a function of and integrated over Then the corresponding data set of each pixel is Fourier analyzed. This results in a spectrum defined by amplitude and phase where is the frequency of the oscillating electron yield, i.e. the frequency, corresponds to an electron yield oscillating with the same frequency, as the relative phase between the ω- and 2ω-fields. Obviously, must have this periodicity. However, harmonics of higher periodicity are also possible.
The procedure is demonstrated for two example pixels in figure 2. They are marked by a red and a black cross in figures 2(d)–(f). The oscillating yield, of these two pixels is shown in figure 2(a). The Fourier transformation yields the amplitude (figure 2(b)) and the phase (figure 2(c)) of the frequency components, , for both momenta. Figure 2(d) shows that the amplitude of the fundamental phase dependence is dominating for most electron momenta. Considering only the fundamental frequency component yields figures 2(e) and (f), which show the amplitude, and the phase, In figure 2(f) the different phase-dependence of the electron yield at different momenta is very obvious.
Figure 2. (a) Phase-dependent yield, for the two specific momenta marked with red and black in panels (d)–(f). Using Fourier transformation one obtains amplitude (b) and phase (c) of the frequency components in the yield signal. (d) shows the frequency component with strongest amplitude for each momentum. The first component which oscillates with the same frequency, as the relative phase, is dominant in most cases. Its amplitude (e) and phase (f) are already meaningful representations of the underlying processes. The conspicuous spot on the left side of (d)–(f) close to corresponds to a defect on the detector surface and shall be ignored.
Download figure:
Standard image High-resolution imageWhile is the naturally expected phase-dependence which is in fact dominant for more than 70% of the pixels, frequencies of are also observed. This occurs predominantly around the region, i.e. perpendicular to the 2ω field.
The reason is as trivial as profound: corresponds to zero crossings of the vector potential of the field, which occur twice per optical cycle (figure 3(a)). In other words: a sine wave reaches its maximum only once per cycle but passes through zero twice per cycle [31]. Thus, the yield for momenta with being smaller than the maximum deflection (∼2Up of the 2ω field) oscillates twice as fast as the natural phase-dependence (see yield of example momenta in figure 3(b)).
Figure 3. (a) Calculated y-momentum distribution (linear scale, ) as function of the relative phase. (b) Normalized phase-dependent yield for different momenta The momenta are also indicated in (a) by the dashed lines. The yield of momenta inside the range of the deflection oscillates twice as fast as the yield of momenta outside of the deflection (i.e. momenta larger than the 2Up cut-off of the 2ω field).
Download figure:
Standard image High-resolution imageEven higher frequencies are due to insufficient signal to noise ratio and typically occur for large electron momenta, i.e. at low count rates.
4. Semi-classical model (SCM) and time-dependent Schrödinger equation (TDSE)
From a simplified point of view, the behavior of atoms and small molecules in the strong laser fields can intuitively be described using the SCM of strong-field ionization [32–34]. However, 3D fields including the scattering in three dimensions or multiple returns have rarely been included. Here we extend the SCM to incorporate these aspects.
The scattering of returning electrons is modeled in first Born approximation with a spherical scattering distribution according to the differential cross-section for plane-wave scattering at a Yukawa potential, [26, 35]. The shielding parameter, controls the range of the potential. A detailed description of the model and calibration of the laser field intensities is given in appendices A and B.
The results of this extended SCM are also compared to numerical solutions of the 3D TDSE. We solve it in the SAE approximation in the velocity gauge with the split-operator method on a Cartesian grid and calculate the PMD by projecting outgoing parts of the wave function on Volkov states [36]. We use a pulse envelope, corresponding to a 12-cycle pulse. For the binding of the electron to the nucleus we chose the SAE potential from Tong and Lin [37]. The values for neon are and for xenon [37, 38].
Since the singularity in the Tong–Lin potential poses problems in the numerical calculation, with both the time step and the spatial resolution required for an accurate solution of the TDSE, we modify the potential for small radii according to the procedure described in [39]. A small cut-off radius is introduced such that all nodes of the radial wave function lie within a sphere of that radius. The potential is then modified within that sphere in a smooth way such that the singularity disappears and the 2p state of the new potential coincides with the former state of the original potential for radii larger than the cut-off radius. For xenon this effectively removes the nodes of the former 5p state, making it a 2p state while conserving the ionization potential. The cut-off radius is 2 a.u., the total size of the box is 125 a.u. and the grid spacing is 0.25 a.u. For neon, the cutoff radius is 3 a.u, the total size of the box is 300 a.u. and the grid spacing is 0.39 a.u. The total propagation time is 1500 a.u. with a time step of 0.03 a.u.
For xenon we also did a calculation starting from the 1s state of a soft-core potential, with chosen for the ground state to reproduce the ionization potential,
5. Results and discussion
5.1. General structure
We start with the direct electrons, i.e. the electrons that are ionized and accelerated by the laser field but do not rescatter. For these electrons, the final momentum is to a good approximation equal to −1 times the vector potential at the time of ionization, i.e. Further, the ionization probability peaks at the zero crossing of the vector potential of the field, i.e. at the maximum of For example in the case of shown in figure 4(c), the maximum ionization probability occurs in each half cycle around etc, as indicated by the mark. Accordingly, electrons ionized at these instants will have a final momentum shifted in the y-direction by the vector potential of the field. This shifts the bulk of the PMD towards positive y-momenta, see left sides of figures 4(a) and (b).
Figure 4. Panel (a) and (b) display experiment and simulation data of neon for the deflection of electrons due to the weak 2ω-field, where the strong ω-field component is perpendicular on the detector plane. The full sequence of data for (see animated data in the the supplementary material available online at stacks.iop.org/JPB/51/015001/mmedia) clearly shows two components in the PMDs with approximately opposite phase dependence. This can be explained with the semi-classical model. (c) displays qualitatively the time-dependent ionization yield (gray shaded curve) together with the vector potential components and of the ω- and 2ω-fields. The +- and ×-mark indicates maximum and minimum amplitude of the vector potential of the 2ω-field, respectively. For appreciable ionization exists only at the position of the ×-mark, where is negative. Accordingly, the electrons will be deflected in positive direction, as indicated by the white -mark in the left halves of the panel (a) and (b). The +-mark also indicates the instant of recollision of electrons emitted at briefly after i.e. with appreciable probability. Due to at the +-mark, the rescattered electrons are deflected in negative direction. In panel (a), (b) and (d), maximum radius of the scattering sphere for the first, second and third return is indicated by the red, blue and green circle, respectively. The center of these circles is indicated by the white -marks. Panel (d) displays computed data in the plane perpendicular to the laser beam. Electrons recolliding at different will be deflected by the 2ω-field differently. According to the classical model, the center of the scattering spheres (dashed circles) is given by (white dashed curve). The direct electrons, in contrast are confined to small momenta because they are only created close to the maximum of the -field. Since the momentum of the direct electrons is given by the center of their distribution also lies on the white dashed curve. The characteristic behavior of the distribution as a function of can be seen in an animation provided in the supplementary material.
Download figure:
Standard image High-resolution imageConversely, flips the sign of the field and shifts the PMD towards negative y-momenta, see right side of figures 4(a) and (b). Further, the vector potential and resulting momentum for a relative phase of follows the path shown by the white dashed line in figure 4(d) as the ionization time is varied.
The effects of the relative phase upon the PMD of rescattered electrons are more complex. After being ionized and driven away from and then back towards the parent ion, these electrons scatter off the parent ion. This rescattering is affected by the scattering properties of the parent ion and the electron trajectory, which is modified by the ionization time and the relative phase As seen in figure 4(d), the circles, which define the maximum possible momenta in y–z-plane for scattered electrons (dotted circles) have centers that follow the white dashed line defined by the vector potential. Further, the distribution within the circle is defined by the scattering properties of the atomic potential and by the electron trajectories. The size of this circle also depends on the return energy of the electron or whether the electron is scattered on the first (red circle), second (blue circle), or third (green circle) return to the parent ion, as shown for in figures 4(b) and (d).
In general, changes of the relative phase shift the ionization time, at which maximum deflection due the second field occurs. This leads to a phase shift between different regions in the spectrum which can be visualized using the 'phase-of-the-phase' method introduced above. The SCM allows us to separate and analyze the individual contributions of the PMD. In figure 5 the phase (a)–(e) and amplitude (f)–(j) of the PMDs resulting from direct electrons and rescattered electrons is shown for neon ( ). Scattering of electrons at the first return produces the most complex phase map because the range of return times and return energies are larger compared to higher-order returns. Note that the dashed circles denote the PMD's cut-off at maximum deflection in y-direction for each process. For the direct electrons the maximum momentum in y-direction is and for the first, second, and third return of rescattered electrons and respectively. The color of the circles indicate the relative phase where the maximum deflection occurs (black: white: ). Figure 5(k) shows, in addition, where the amplitude for the direct and rescattered electrons dominates. In particular, rescattered electrons dominate for and while direct electrons dominate for Further, from the harmonic addition theorem, one expects that the phase of the total PMD will tend towards the phase of the dominant process and in regions where multiple processes contribute roughly equally, the phase will accordingly shift towards a mean phase.
Figure 5. Phase (ϕ1-) ((a)–(e)) and amplitude (-) ((f)–(j)) map of neon for direct and scattered electrons, computed with the semi-classical model for different classes of electrons. The black and white dashed circles indicate the PMD's cut-off for the relative phase for which the deflection of the electrons due to the -field is maximum. The color indicates the value of relative phase at which the maximum deflection occurs (black: white: ). (k) compares of direct and scattered electrons. Positive values (red colors) mean that the amplitude of direct electrons dominate in this region and vice versa for blue colors.
Download figure:
Standard image High-resolution image5.2. Results for neon
Phase-of-the-phase maps of neon, with the same intensities as in figure 5, are shown in figure 6 for the experiment (figure 6(a)), the semi-classical simulation (figure 6(b)) and 3D TDSE calculations (figure 6(c)). In figure 6(d) the py- and φrel-dependent yield along the py-axis is shown as a grayscale color map and is normalized independently for each py-row. The phase-of-the-phase, as a function of is superimposed for the measured (blue ), SCM (red circles) and TDSE data (green squares). One can see that the phase map roughly provides the phase at which the maximum electron yield occurs as the phase of the phase follows the white area of the grayscale map. As expected from simulation a phase shift between the region with dominantly scattered electrons and the region with dominant direct electrons is observed. Surprisingly, an additional phase shift in the region with small lateral momentum is observed in the measurement. It can be reproduced with the SCM by tuning the screening parameter μ of the Yukawa potential. For small μ (e.g. μ = 0.1) the potential becomes more Coulomb-like which lead to a peak of electron yield in forward scattering direction. For a long-range Yukawa potential, therefore, the amplitude of forward scattered electron yield may become stronger than the amplitude of direct electrons.
Figure 6. Phase maps (ϕ1) of neon: (a) measured, (b) SCM, (c) TDSE. To map the transition between different ionization processes, the measured yield, along the py-axis is displayed in panel (d) as grayscale value. The size of the slice is marked with dashed lines in (a)–(c). The amplitude is normalized to the peak value for each py-bin. The phase values derived from the phase maps are superimposed for the measured (blue +), SCM (red circles), and TDSE data (green squares). For the measured data there is a clear transition at i.e. between regions where scattered high energetic electrons dominate and the region with predominantly direct electrons The SCM and the TDSE data show quite a similar behavior.
Download figure:
Standard image High-resolution imageIn total, the measurement and both simulations show the same behavior. As expected, deviations occur in regions where the rates of direct and scattered electrons are similarly strong. There the phase of the phase, strongly depends on the chosen value for and the ratio of direct and scattered electrons.
5.3. Results for xenon
In contrast to neon, xenon shows substantially richer structures, in particular some wing-like features to the left (white box) and the right of the y-axis (figure 7(a)). These structures are also present in the semi-classical calculation (figure 7(b)) and the solution of the TDSE calculated for the 1s state of a soft-core potential (figure 7(c)). For the TDSE calculation the wings are not visible if one starts from the 2 state of the modified SAE potential (figure 7(d)). The differences in the TDSE calculations are predominantly due to the different shape of the potentials used, which have different scattering cross-sections. This demonstrates the sensitivity of the phase maps to even minor changes in the scattering cross-section. Since, as shown in figures 8 (a)–(j), the semi-classical calculation allows us to easily distinguish between direct and scattered electrons, we can relate the wing structure to scattered electrons, while the scattered electrons between the wings are overlapped by the direct electrons. Additionally, for xenon we see a substantial amount of photoelectrons with a different phase dependence, as compared to the same momentum region for neon data (white ellipse in figure 7(a)). SCM results with larger (not shown) suggest that this is due to the second return as this process has the proper phase dependence in this region.
Figure 7. Phase maps (ϕ1) of xenon. (a) Measurement, (b) SCM, (c) TDSE solution starting from 1s state of a soft-core potential, (d) TDSE results obtained for an initial 2p state of the model potential from [37, 38].
Download figure:
Standard image High-resolution imageFigure 8. Same as figure 5 but for xenon. Note the changed scaling.
Download figure:
Standard image High-resolution image5.4. Comparison and interpretation
To further highlight the differences between neon (figures 9(a), (c)) and xenon (figures 9(b), (d)) we display the two measurements side-by-side. Note the difference in the momentum scales. As expected from the simulations (figures 5 and 8), the basic structure is the same for neon and xenon. The differences in detail are primarily due to the larger scattering cross-section of xenon, which results in a larger fraction of rescattered electron as compared to neon. Additionally the lower ionization potential of xenon requires less intensity to ionize which reduce excursion distances and return energies and lead to more rescattered electrons. Differences are also seen in the central part of the spectrum, which is outside the scope of our theory. Since these features are not reproduced by SCM or TDSE, they could be due to multi-electron effects not describable by an effective potential.
Figure 9. Phase (-) and amplitude (-) map of neon (a), (c) and xenon (b), (d).
Download figure:
Standard image High-resolution image6. Conclusion
In contrast to most previous studies, a strong ω-field with a polarization perpendicular to the imaging plane is used. As compared to the conventional scheme, this technique has the advantage that electrons with almost three times higher energy can be collected. Analysis by retrieving the 'phase-of-the-phase' shows a clear phase difference between scattered and direct electrons. The phase-dependent PMDs measured with a novel scheme for OTC VMI spectroscopy show a strong dependence on the target. Using a 3D SCM that includes higher-order returns and scattering in three dimensions, good qualitative agreement with the experimental and the TDSE data is obtained for neon. However, for xenon the phase of the central structure is not fully reproduced in both kinds of calculations. For the SCM, this can be due to the approximation of the scattering with the differential cross-section of a Yukawa potential. The SCM could possibly be improved by modifying the scattering cross-section to better incorporate different targets. Regarding the TDSE calculations, the deviation may point to deficits of the shape of the potentials established in the literature. Also, the omission of multi-electron effects or the modification of the potential for small radii might be problematic. The question is whether a satisfactory effective potential exists.
Acknowledgments
This work was supported by grant PA730/4 and FR 1251/17-1 within the Priority Programme 'Quantum Dynamics in Tailored Intense Fields (QUTIF)' of the German Research Foundation (DFG).
Appendix A.: Semi-classical model (SCM)
To a certain extent, the behavior of atoms and small molecules in the linearly polarized strong laser fields can easily and intuitively be described using the SCM of strong-field ionization [32–34]. In many situations, and with a sufficiently detailed model, the agreement with the experiment allows its use for the calibration of the laser intensity or other parameters. In the SCM, 3D fields and scattering in three dimensions or multiple returns are often not included. In the following we expand the model to include these items.
Unlike common Monte Carlo simulations this approach does not calculate the trajectory of single electrons. Instead, for each ionization time (∼2500 times per cycle) the complete electron distribution due to scattering or different initial momenta is calculated and weighted with the ionization probability. This significantly reduces the calculation time, since the scattering distribution needs to be calculated only once per ionization time. Hereafter the 'electron's trajectory' describes the motion of the mean wave packet i.e. the electron's motion with zero initial velocity.
The PMD is viewed as the sum of the contributions from direct and rescattered electrons. Therefore, the momentum distribution of the photoelectrons can be expressed as the incoherent sum,
of the two contributions.
Appendix. A.1 Direct electrons
By neglecting the influence of the binding potential, the momentum of a direct electron ionized at time follows from the conservation of the canonical momentum,
with the vector potential, of the laser field, Integrating (equation (2)) from time to t leads to the trajectory of direct electrons:
Here, is the integral over following a notation similar to [40].
For direct electrons, an additional transversal spread due to an initial transversal momentum after tunneling ionization has to be added. It has the form of Gaussian,
with the ionization potential [41, 42]. Thus, the final momentum at the detector is, leading to a distribution of direct electrons
for this ionization time,
Appendix. A.2 Scattered electrons
For scattered electrons, in contrast, we include the influence of the binding potential on the trajectory by assuming just a single elastic scattering event for each rescattering time
For the rest of the trajectory, i.e. for times before rescattering, and after rescattering, the effect of the binding potential is neglected. Before scattering the trajectory is simply one of a direct electron, i.e. it has the position and the momentum For times after scattering, the momentum is which leads to the final momentum
at the detector. Here, is the new momentum after the elastic scattering event, which fulfills
Appendix. A.3 Return times
In view of the OTC pulses as they are used here, the 'condition of return' is of particular interest in dealing with rescattered electrons. This return occurs at and thus As illustrated in figure A1, the vector potential of the OTC field is chosen such that it rotates in the z–y plane. It can be written as
with being the pulse envelope, the ratio of the two (electric) field amplitudes and the relative two-color phase, which is easy to control in the experiment. Due to the long pulses, is set to 1 for the calculation.
Figure A1. Schematic of Born scattering for a specific trajectory in the two-color laser field. (a) Due to the 2ω field, the mean electron distribution of the returning electron misses the parent atom by the distance b in y-direction. Trajectories with the initial velocity will hit the parent atom (b). Using elastic Born scattering at a Yukawa potential, the return momentum is scattered onto a scattering sphere leading to a scattering distribution with momentum .
Download figure:
Standard image High-resolution imageIn order to define for a given we follow the trajectory, with the initial conditions set to zero, i.e. and search for times when the trajectory crosses the x–y-plane, i.e. The trajectory passes the ion at distance, see figure A1(a). However scattering can still occur if the initial velocity, is approximately
where is the travel time (figure A1(b)). Note, that this approach is only valid if the distribution of initial momenta only yields small momenta e.g. Otherwise the point of return needs to be calculated more carefully.
Due to the periodicity of the laser field, a given ionization time may lead to several returns with different return times, and different impact parameters, In the presented simulations, only the first three returns are considered. Thus, the return of a trajectory that starts at is characterized by the travel time, and impact parameter where can run up to 3.
The scattering is modeled as a spherical scattering distribution described by the differential cross-section, for plane-wave scattering at a Yukawa potential in first Born approximation [26, 35]
In our simulation the scattering distribution, is calculated on a discrete grid of solid angles. For discrete solid angles the total cross-section, is given by
Thus the scattering distribution is
Appendix. A.4 Weighting of the contributions
The contributions of direct and rescattered electrons with ionization time, are weighted with their ionization rate, which is proportional to the ADK tunneling rate [43]
In addition we use the empirical correction factors provided by Tong and Lin [37]
Using this weighting factor, the simulation calculates the total distribution of direct electrons, by the summation of the direct electrons distribution, (equation (5)), from all starting times, within a full laser cycle.
For the contribution of scattered electrons, weighting with only the ionization rate is not sufficient. An additional weighting factor is needed to take the wave packet spreading and wave packet displacement at each return into account. This is done by calculating the ratio of the wave packet which overlaps with the total cross-section.
First we need to describe the wave packet spreading. Using the initial velocity distribution (equation (4)) leads to the electrons' spatial distribution after travel time, of
with and If we assume a uniform transversal spreading of the electron distribution, the wave packet can be described by a normalized two dimensional Gaussian, which is displaced in y-direction by the impact parameter b:
At the origin (e.g. where the ion is located), the amplitude decreases proportional to while the decreasing of the amplitude due to the displacement is proportional to
To calculate the weighting factor, we calculate the overlap of the two dimensional wave packet (equation (15)) with the total cross-section (equation (11)), e.g. we integrate the two dimensional wave packet within radius
This leads to a weighting factor,
which is for each return.
For higher-order returns we need to take depletion of the wave packet due to scattering at previous returns into account. The depletion is approximated by simply subtracting the weighting factors of the previous returns:
Using the weighting factor and the total distribution of scattered electrons, can be calculated by the summation of the scattered electrons distribution, (equation (12)), from all starting times, within a full laser cycle.
For ionization times, at which scattering occurs, the direct electrons distribution is weighted by the amount of the wave packet which remains after scattering.
Thus, a high scattering probability leads to a weaker direct electrons distribution for those trajectories.
Appendix B.: Intensity calibration
A first application of the SCM is the calibration of the intensity of the ionizing field component. To this end, the calcite crystal is detuned such that the overlap between the pulses of different wavelength is avoided. The 2ω component now arrives after the ionizing field and thus has no effect on the PMD. This was tested by blocking the 2ω component using dichroic mirrors.
The resulting one-color momentum distribution is compared to our SCM (figure B1). The measured data is shown as blue line in figure B1(a) and on the left side of figure B1(b). The colored rings indicate the scattering spheres of the electrons with maximum return energy at the first (red), second (blue) and third (green) return from our calculation (right side of figures B1(b) and (c)). This means the radii correspond to 3.17Up, 1.54Up and 2.40Up, while the spheres are shifted by in z-direction where is the time of return. The 2Up cut-off of the ω-component is indicated by the black bar in figure B1(c). The measured momentum cut-off (figure B1(a) blue line) corresponds to the indicated red 3.17 Up ring, making it easy to calculate the intensity The simulation with this intensity (figure B1(a) green line and figure B1(b) right side) fits perfectly to the measured data. Note that for the measurement geometry (figure B1(b)) the cut-off is approximately three times lower compared to figure B1(c) where the cut-off is 10Up, which allows us to collect much more scattered electrons.
Figure B1. Calculated PMD for a one-color field in comparison to a two-color measurement (Neon) without overlap of the pulses. (a) shows the measured (blue) and calculated (green) y-momentum distribution. (b) Comparison of measured (left side) and calculated (right side) x–y-momentum distribution. The rings represent the cut-off of scattering momentum at the first (red circle), second (blue circle) and the third (green circle) return. (c) Calculated –-momentum distribution. The cut-off rings are shifted by the 2Up cut-off of the fundamental laser field (black line).
Download figure:
Standard image High-resolution imageFor the two-color case, the intensity of the 2ω component is fitted to the deflection amplitude of the PMD. This oscillation is also used to calibrate the relative phase between the two fields by comparing it to simulated direct electron spectra (Neon: ). The screening parameter μ of the Yukawa potential (equation (9)) is optimized to achieve the best fit between the measurement and the SCM
However, using the measured PMD for calibration does not result in the best fit in the phase maps, where a much smaller and for neon higher intensities ( ) lead to better results. The reason for the intensity difference may be that our assumed cut-off is near the border of the detector, where a decrease of the sensitivity is possible. With the phase map calibrated intensity, the real cut-off lies beyond the detector. However, even with a larger detector it would be hard to measure the electron yield, as the signal of it will be too low. The smaller μ result in a more Coulomb-like potential which should be more accurate for trajectories with large impact parameter. For xenon we find


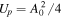
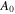


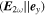

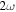

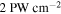
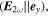
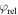
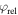
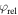
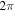
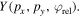
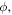




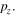



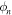
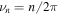

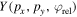

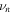
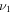
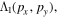
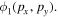



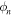


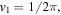
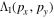

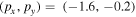
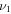
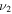
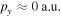

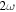


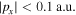
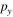
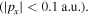





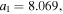
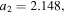

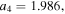
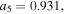
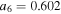
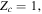

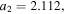

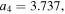
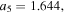


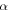

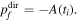

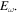

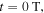
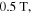


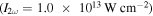

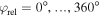
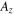


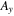


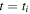


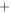
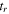

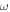
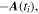
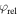
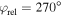
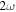

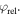

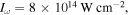
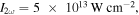
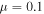
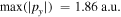
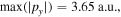
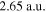

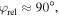
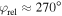
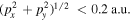

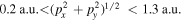


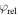

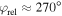

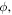



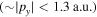
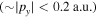

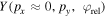


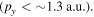


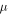


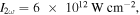
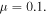


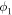
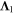


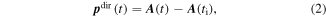
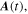

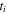
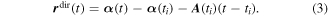


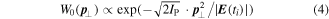
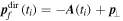
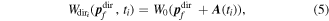




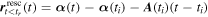




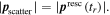

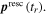

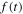


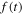


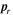

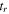

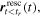

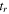
![${{\boldsymbol{r}}}_{t\lt {t}_{r}}^{{\rm{r}}{\rm{e}}{\rm{s}}{\rm{c}}}({t}_{r})=[0,y({t}_{r}),0].$](https://content.cld.iop.org/journals/0953-4075/51/1/015001/revision2/jpbaa975cieqn176.gif)
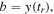
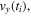


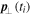


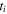




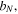



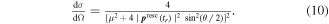


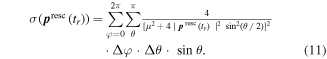


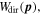



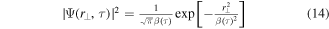

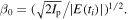
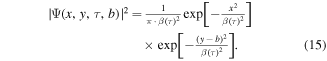
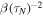

![$\exp \left[-\tfrac{{{b}_{N}}^{2}}{\beta {({\tau }_{N})}^{2}}\right].$](https://content.cld.iop.org/journals/0953-4075/51/1/015001/revision2/jpbaa975cieqn203.gif)