Abstract
The initial conditions for electron trajectories at the exit from the tunnelling barrier are often used in strong field models, for example to bridge the first and the second steps of the three-step model celebrated in this issue. Since the analytical R-matrix theory does not rely on the three-step model or the concept of the tunnelling barrier in coordinate space, obtaining the initial conditions for electron trajectories at the barrier exit is, strictly speaking, not necessary to calculate standard observables. Not necessary, but possible—especially when motivated by the occasion of this issue. The opportunity to evaluate such initial conditions emerges as a corollary of analysing sub-barrier kinematics, which includes the interplay of laser and Coulomb fields on the sub-cycle scale (see the companion paper I). We apply our results to discuss the difference in such initial conditions for co- and counter-rotating electrons liberated during strong field ionisation. We derive quantum orbits and classical trajectories describing ionization dynamics of co- and counter-rotating electrons in long-range potentials.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
The trajectory-based picture of strong field phenomena has been very inspiring and useful. It underlies our intuitive understanding of all strong field phenomena: single, double and multiple ionisation [1–5], high harmonic generation [6–10], above threshold ionisation [11–16] and related attosecond imaging techniques, such as laser-induced diffraction [17–20], holography [17, 21, 22], attoclock [23, 24], high harmonic spectroscopy [18, 25–36, 37–43], to name but a few examples. Strong field ionisation is the first step in all these phenomena.
Since the pioneering work of Keldysh [44] and PPT [45–47], the physical picture of strong field ionisation has inevitably involved complex times (see recent reveiw [48]). The complex times are associated with optical tunnelling. The barrier created by the oscillating low-frequency field and the core potential separates classically forbidden and allowed regions. The separation point in space is called 'the exit from the barrier'.
This image is compelling in low-frequency fields ω ≪ Ip, where optical tunnelling is the dominant ionisation mechanism. One reason why tunnelling emerges as the dominant mechanism is that real excitations within the potential well are strongly suppressed in the low-frequency regime. In fact, both tunnelling and multiphoton regimes of strong field ionisation in the Keldysh theory involve electron dynamics in the sub-barrier region (see [49]).
Tunnelling and associated complex times lead to complex trajectories, even in the simplest case of a short-range potential. Looking broadly, the interplay of classically allowed and classically forbidden regions of particle dynamics always leads to complex trajectories in the semiclassical limit (see e.g. Keller in [50, p 27]), see also [51, 52]). However, in those problems the 'barrier', i.e. the separation between the forbidden and the allowed regions, is time-independent. For example, in scattering theory, the semiclassical description of the Rutherford scattering [52] leads to complex trajectories due to the presence of classically inaccessible regions in the momentum space ('dynamical tunnelling'). In geometrical optics, where rays are used to assemble electromagnetic fields, representing the main term in the semiclassical expansion of the exact fields, the complex rays accurately describe electromagnetic fields on the dark side of caustics and refraction shadows, i.e. in classically forbidden regions [50, 51]. Here the role of time is played by the distance along the ray and it becomes complex once a classically forbidden region is involved. Formally, complex-valued variables originate from the fact that those kinds of trajectories are derived from action, which becomes imaginary in the classically forbidden region. The imaginary action describes exponential damping of a signal inside the classically forbidden region. For example, real-values rays are tangent to the caustic on its convex part (bright side of the caustic), while only complex-valued rays can be tangent to the caustic on its concave part (the dark side of the caustic).
In the case of strong field ionisation, complex trajectories, especially complex-valued coordinates, appear as a manifestation of the non-adiabaticity of the electron dynamics triggered by rapid changes of the tunnelling barrier due to fast oscillations of the laser field or quickly the changing field envelope, in the case of nearly single-cycle pulses. Of course, this does not make strong field complex trajectories any less 'legal' than the real-valued ones. The "complexity" of the coordinate becomes particularly acute when the coordinate-dependent Coulomb potential is included into analysis.
From the pragmatic perspective of a semiclassical theory, such as e.g. the analytical R-matrix (ARM) theory, complex electron trajectories take care of the propagation of the electron wave function in time in the same way as complex rays take care of the propagation of the electromagnetic fields in space (Keller in [50, 51]). From the practical perspective and following the tradition in the field, it is desirable to introduce effective classical, i.e. real-valued trajectories, which start at the time of the exit from the barrier with some initial conditions encoding the information about the under-the-barrier quantum dynamics, propagate in the laser and the Coulomb fields (or in a more complex field decribing the electron-core interaction) according to Newton's equations, and are uniquely linked to a given observable (e.g. the photoelectron momentum) at the detector. Establishing trajectories linked to final photoelectron momenta helps one to understand the ionization dynamics. Last but not least, such trajectories should include information about the intial orbital, e.g. the orbital momentum and its projection on the quantization axis.
This desire is a very natural one, and the question 'what is the value of the electron velocity for such trajectory at the 'exit' from the tunnelling barrier for a given final momentum [53–57]?' is hardly new. If the Coulomb potential is not included, the formal answer can be obtained with no effort and it is known since the PPT times [45–47, 58]: for the peak of the photoelectron distribution the 'exit velocity' is equal to zero. (It only means that the trajectory with zero intial velocity accurately follows the peak of the quantum phase-space distribution sufficiently far from the exit coordinate, see e.g. Ref. [59], Figure 6, and Ref. [60]). Once the Coulomb potential is taken into account, the analysis becomes more involved.
In strong fields we usually speak about Coulomb 'corrections', because the electron dynamics is dominated by the laser field. However, these 'corrections' become very significant in the sub-barrier region, where the electron comes very close to the singular Coulomb core. The problem can be solved, for example, using the ideas of the ab initio R-matrix method [61], where the configuration space around the core and outside the core is treated by applying different approximations. We apply the same trick in the ARM method [62–68], see also recent work [ 69] similar to [68 ] . Then, we have to match the solutions for the electron wave functions at the boundary of the inner and outer regions.
The ARM method starts with the time-dependent Schrödinger equation, but ends up with semiclassical expressions. Celebrating 25 years of the three-step model, we shall keep things simple in this paper, making the short-cut directly to the semiclassical picture. The semiclassical ansatz represents the electron wave function in terms of a phase (action) and an amplitude (prefactor, which is linked to the electron density). It means that we have to match both the phase and the amplitude (the gradient of the phase) at the R-matrix boundary which separates the inner and the outer regions. The key idea for matching the phase has already been given in the PPT papers [45–47, 58]. We just had to adapt it to our formalism and extend to the sub-cycle regime [62, 64]. Matching the gradient of the phase proved to be a harder task, because the gradient of the Coulomb potential—the attractive force responsible for the momentum shift—becomes very strong as we approach the core. Nevertheless, the problem was solved in [67].
In fact, the outcome of the matching procedure can be understood as specification of the time, velocity and coordinate at the effective 'entrance' to the barrier (the effective start of the electron trajectory leaving the core). For the short-range potential, this 'entrance' lies at the origin, but it is shifted from the origin in case of the the Coulomb potential. Knowing the starting position, velocity, and time allows one to find the corresponding parameters at the 'exit' from the barrier, the latter defined at the instant when the imaginary part of the time along the trajectory turns to zero.
These 'initial values' at the 'barrier entrance' do not contribute to observables in the case of ionisation from the s-states, which has been analysed within the ARM method in [65, 66, 70]. However, they are still needed if one wants to establish the 'initial conditions' at the exit from the barrier, even for s-states.
The situation changes with ionisation from states with non-zero l, m. Now the the initial velocity 'at the entrance' and the 'entrance time' directly contribute to the ionisation rates for orbitals with 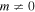 in circularly polarised fields. The contributions depend on the l, m quantum numbers of the initial orbital and leave their mark in photoelectron spectra. Since these quantities contribute to observables, they have to be calculated.
in circularly polarised fields. The contributions depend on the l, m quantum numbers of the initial orbital and leave their mark in photoelectron spectra. Since these quantities contribute to observables, they have to be calculated.
In our first paper [64] on ARM theory for ionisation in circularly polarised fields, we resorted to estimates for the 'most popular' trajectory, which is followed by the majority of the electrons and which has no non-adiabatic features (this trajectory 'yields' the peak in the photoelectron spectrum in circularly polarised fields). Later, we rigorously performed the required matching in [67]. The resulting momentum shifts, accumulated under the barrier, are intrinsically sub-cycle and sensitive to orbital geometry.
Due to the fact that we have explicitly derived the velocity, time and coordinate 'at the entrance to the barrier' in ARM formalism, we can define a unique quantum trajectory, which satisfies the Newtons equations with the Coulomb and the laser fields included, starts at the 'entrance to the barrier' and terminates at the detector with a given final momentum. The trajectory is quantum, because it evolves in complex time and space. Moreover, the evolution of the imaginary and real parts of the trajectory coordinate are now coupled via the long-range potential. This coupling persists until the end of the laser pulse, affects the population amplitudes associated with the trajectories, and reflects the fact that ionisation is not completed at the 'exit from the barrier'. For example, electrons can be trapped into Rydberg states and released later at times t > texit [65]. In other words, there is no such moment in time after which the electron dynamics is fully described by a purely classical trajectory.
However, if one insists on establishing a fully classical trajectory propagating in real time and space after the 'exit', encoding the information about the sub-barrier dynamics only in the exit velocities and exit coordinates, it is also possible. Such trajectory, while imperfect, is also uniquely defined. The imperfection is due to the missing imaginary part of the coordinate associated with the quantum trajectory and the missing coupling between its real and imaginary parts. At the time of exit from the barrier, the coordinate of the classical trajectory is set to be equal to the real part of the coordinate of the quantum trajectory. However, the velocity of classical trajectory at the exit time is not identical to the velocity of quantum trajectory at the same time—they must only coincide at the detector.
We stress again that, strictly speaking, neither the quantum nor the classical trajectory are needed to obtain observables in the ARM theory. Their purpose is different. First, they are introduced here to explore how far can we push the language of trajectories including the Coulomb and the laser field for quantitatively describing the ionisation dynamics in strong laser fields. Second, they provide insight into ionisation dynamics from current-carrying orbitals, allowing us to interpret ionisation of co- and counter-rotating electrons from the trajectory perspective.
We use atomic units (me = ℏ = ke = 1), and consider here only circularly polarised fields.
2. ARM perspective on electron velocities and coordinates at the exit from the barrier
2.1. Sub-cycle Coulomb corrections to ionisation times
In the ARM theory we include the effects of Coulomb potential  in the outer region up to the first order in Z, in the wave function's exponent (action). In the inner region, the Coulomb effects are included fully. It leads to the shift of the saddle points in the time-domain quantum integrals over the ionisation times. In particular the complex ionisation time becomes
in the outer region up to the first order in Z, in the wave function's exponent (action). In the inner region, the Coulomb effects are included fully. It leads to the shift of the saddle points in the time-domain quantum integrals over the ionisation times. In particular the complex ionisation time becomes 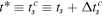 [64, 66, 67, 70]. Since the PPT times, this time is associated with the beginning of tunnelling. Here ts is the SFA ionisation time for a short-range potential, while
[64, 66, 67, 70]. Since the PPT times, this time is associated with the beginning of tunnelling. Here ts is the SFA ionisation time for a short-range potential, while  is the Coulomb correction to this time. For the same final electron momentum at the detector, the trajectory starts earlier w.r.t to the SFA (short-range) case. The correction
is the Coulomb correction to this time. For the same final electron momentum at the detector, the trajectory starts earlier w.r.t to the SFA (short-range) case. The correction  is given by equation (13) in appendix A of [71], which we rewrite here:
is given by equation (13) in appendix A of [71], which we rewrite here:
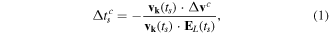
or, in the equivalent form [66, 67, 70]:
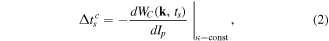
where  and the phase
and the phase 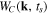 is the Coulomb correction to the SFA action in the ARM theory:
is the Coulomb correction to the SFA action in the ARM theory:
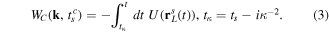
This term describes the Coulomb-laser coupling, and amounts to integrating the Coulomb potential along the trajectory 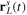 of free electron in the laser field:
of free electron in the laser field:
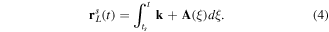
Because the Coulomb-laser coupling term originates from the outer region, any further correction to the trajectory would involve second and higher order terms in Z, which are much smaller for direct electrons and field frequency  , where Ip is the ionisation potential.
, where Ip is the ionisation potential.
2.2. Sub-cycle Coulomb corrections to the initial velocity
The initial velocity at complex ionisation time tsc enters the expression for the ionisation amplitudes [67] and rates (equations (4) and (5) in [71]) via the term 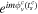 , where
, where 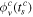 is the complex tunnelling angle,
is the complex tunnelling angle, 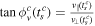 —the angle at which the electron enters the classically forbidden region. Here
—the angle at which the electron enters the classically forbidden region. Here 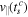 and
and  are the initial velocities parallel and perpendicular to field direction at time tsc. The perpendicular velocity is positive if it has positive projection on the final momentum. Finally, m is the magnetic quantum number of the ionising bound state. For orbitals with m = 0, this Coulomb correction to momentum has no impact on final observables at the detector, i.e. the photoelectron spectrum.
are the initial velocities parallel and perpendicular to field direction at time tsc. The perpendicular velocity is positive if it has positive projection on the final momentum. Finally, m is the magnetic quantum number of the ionising bound state. For orbitals with m = 0, this Coulomb correction to momentum has no impact on final observables at the detector, i.e. the photoelectron spectrum.
For 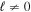 and
and 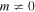 bound states, the Coulomb-laser coupling leads to a momentum shift,
bound states, the Coulomb-laser coupling leads to a momentum shift,  [67]:
[67]:
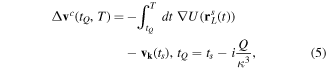
 which modifies the initial velocity at time tsc:
which modifies the initial velocity at time tsc:

Time tQ is an outcome of the matching procedure. Here Q is the effective charge of the core which describes the behaviour of the bound wave function in the classically forbidden region,  , where
, where  is the effective quantum number. For short-range potential Q = 0, ν = 0. Note that
is the effective quantum number. For short-range potential Q = 0, ν = 0. Note that  (see appendix 2, [67]). The physical meaning of this expression is as follows: the electron momentum
(see appendix 2, [67]). The physical meaning of this expression is as follows: the electron momentum  is fixed at the detector. The first term
is fixed at the detector. The first term  describes the SFA velocity at the Coulomb-corrected complex ionisation time tsc. The term
describes the SFA velocity at the Coulomb-corrected complex ionisation time tsc. The term  describes the momentum shift accumulated due to the Coulomb-laser coupling on the way from the origin to detector. Because the final momentum is fixed to be
describes the momentum shift accumulated due to the Coulomb-laser coupling on the way from the origin to detector. Because the final momentum is fixed to be  , the initial velocity subtracts
, the initial velocity subtracts  to compensate this 'future' change in velocity.
to compensate this 'future' change in velocity.
The above expressions are valid for arbitrary field geometries (for direct electrons), all electron momenta, and for all values of the Keldysh parameter γ within the applicability of the theory. The latter requires that real transitions to excited states are negligible. In practice, this of course limits the region of available frequencies and laser intensities (usually ω ≪ κ2/2).
2.3. Properties of classical and quantum trajectories
In the previous two subsections we defined the complex ionisation time and the electron velocity at this time. Both quantities directly enter the ARM expression for ionisation amplitudes and contribute to the photoelectron spectra.
Now we aim to introduce auxiliary tool—quantum and classical trajectories. They will allow us to interpret observables in terms of the Newtonian mechanics. Both quantum (complex) and classical (real) trajectories are evaluated in the first order with respect to Coulomb potential, to be consistent with the ARM approach.
The quantum trajectory starts at real coordinate  (along the axis defined by the laser field at time
(along the axis defined by the laser field at time ![${\mathfrak{R}}[{t}_{s}^{C}]$](https://content.cld.iop.org/journals/0953-4075/51/17/174002/revision1/jpbaad132ieqn28.gif) , but in the opposite direction) at the time
, but in the opposite direction) at the time 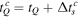 with the velocity:
with the velocity:

The velocity at any time t > tQ is:
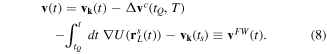
The coordinate rQ, time tQ and the respective initial velocity at this time are known due to the matching procedure. These quantities fully specify the quantum trajectory:
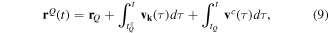
where the Coulomb velocity is 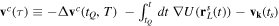 .
.
Importantly, the ARM -trajectory  which enters the argument of the Coulomb force
which enters the argument of the Coulomb force 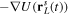 in the integral (equation (8)) is always complex, as discussed in the introduction. It remains complex, with constant imaginary part, even after the exit from the barrier during the real time evolution. It has implications for our ability to introduce an equivalent classical trajectory.
in the integral (equation (8)) is always complex, as discussed in the introduction. It remains complex, with constant imaginary part, even after the exit from the barrier during the real time evolution. It has implications for our ability to introduce an equivalent classical trajectory.
Indeed, taking into account the explicit expression for the velocity 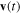 (equation (5)), we can rewrite (equation (8)) in the equivalent form:
(equation (5)), we can rewrite (equation (8)) in the equivalent form:
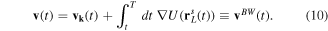
The last equation simply describes back propagation of the final momentum  from time T at the end of the pulse to arbitrary time t. The velocities in equations (equations (8) and (10)) propagated forward from time tQ and backward from time T will coincide at any point t if and only if the back propagation is performed along the complex trajectory
from time T at the end of the pulse to arbitrary time t. The velocities in equations (equations (8) and (10)) propagated forward from time tQ and backward from time T will coincide at any point t if and only if the back propagation is performed along the complex trajectory  . This is the case for the quantum trajectory.
. This is the case for the quantum trajectory.
If we neglect the imaginary part of the trajectory  during back propagation from the detector, as we have to do if we want to introduce a purely classical trajectory, we will have a velocity off-set between the inevitably quantum forward propagation (i.e. using complex ARM trajectories) from the 'under the barrier' region and the desirably classical backward propagation (i.e. using only real parts of ARM trajectories) back from the detector.
during back propagation from the detector, as we have to do if we want to introduce a purely classical trajectory, we will have a velocity off-set between the inevitably quantum forward propagation (i.e. using complex ARM trajectories) from the 'under the barrier' region and the desirably classical backward propagation (i.e. using only real parts of ARM trajectories) back from the detector.
Nevertheless, the classical trajectory is also uniquely defined. Its initial coordinate is defined by the real part of the coordinate on quantum trajectory at the exit time: ![${\mathfrak{R}}[{{\bf{r}}}^{Q}({t}_{{exit}})]$](https://content.cld.iop.org/journals/0953-4075/51/17/174002/revision1/jpbaad132ieqn37.gif) . But the exit velocity is defined by
. But the exit velocity is defined by  propagated backwards from the end of the laser pulse along the real trajectory. Such back propagation is necessary to make sure that the classical trajectory propagated from the 'barrier exit' to the detector will have correct final momentum
propagated backwards from the end of the laser pulse along the real trajectory. Such back propagation is necessary to make sure that the classical trajectory propagated from the 'barrier exit' to the detector will have correct final momentum  at time T. thus, the classical trajectory is uniquely derived from the quantum trajectory as follows:
at time T. thus, the classical trajectory is uniquely derived from the quantum trajectory as follows:
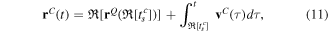
where ![${t}_{{exit}}\equiv {\mathfrak{R}}[{t}_{s}^{c}]$](https://content.cld.iop.org/journals/0953-4075/51/17/174002/revision1/jpbaad132ieqn40.gif) , and the classical velocity is obtained by propagation in real time and space:
, and the classical velocity is obtained by propagation in real time and space:
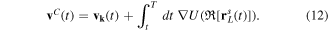
To specify how the Coulomb potential leads to coupling between the real and the imaginary parts of the ARM trajectory and how neglecting the imaginary part of the exit coordinate we remove this coupling, consider the analytical continuation of the Coulomb potential to the complex plane. The procedure has been described in detail in [65]. Here we recall the results to make the discussion more specific. For a real vector  , we have
, we have 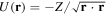 . For a complex vector,
. For a complex vector,  , we have
, we have
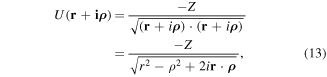
where  and
and  . We choose the branch cut of the complex square root to be infinitesimally above the negative real axis to ensure that our contour never crosses the branch cut. The real and imaginary parts of the Coulomb potential are:
. We choose the branch cut of the complex square root to be infinitesimally above the negative real axis to ensure that our contour never crosses the branch cut. The real and imaginary parts of the Coulomb potential are:
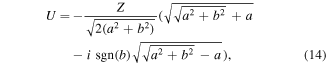
where
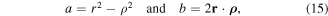
and
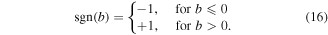
The real and imaginary parts of the Coulomb force  :
:
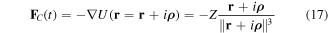
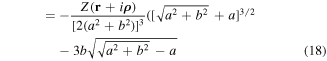
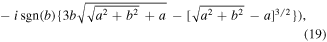
describe the evolution of the real and imaginary parts of quantum trajectory  .
.
Separating real and imaginary contributions to Coulomb force FC, we get:
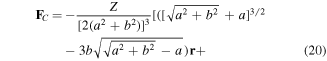
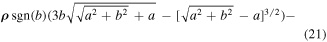
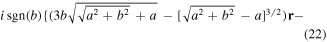
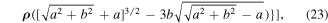
and we see the contribution of  and
and  to the real part of quantum velocity.
to the real part of quantum velocity.
The coupling between the real and the imaginary parts of the ARM trajectory due to the Coulomb force is obvious. Even though the imaginary part of the ARM trajectory is constant after the barrier exit, the real part evolves and therefore both b and a are the functions of time along the ARM trajectory. Thus, the evolution in real time is affected by the presence of the imaginary exit coordinate. Depending on the sign of the parameter  , the Coulomb force either increases or decreases in its attractive strength.
, the Coulomb force either increases or decreases in its attractive strength.
The imaginary exit coordinate is present in quantum trajectory, but absent in the classical trajectory. This mismatch leads to the off-set in their real velocities at the exit point. The presence of the imaginary component of the ARM trajectory is due to the non-adiabaticity of the electron dynamics. Thus, in circularly polarised fields the majority of electrons released from s-orbitals will follow the classical trajectory (classical and quantum trajectories coincide in this case), but the majority of co- and counter-rotating electrons (released from the orbitals with 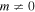 ) will follow quantum trajectories with non-zero imaginary parts. In this case, the degree of approximation that classical trajectory offers depends on the degree of non-adiabaticity of electron dynamics. We will illustrate this general picture below.
) will follow quantum trajectories with non-zero imaginary parts. In this case, the degree of approximation that classical trajectory offers depends on the degree of non-adiabaticity of electron dynamics. We will illustrate this general picture below.
3. Results
We first consider the real parts of coordinates and velocities along the quantum trajectories at the 'exit time' ![$t\,={\mathfrak{R}}[{t}_{s}^{c}]\equiv {t}_{i}^{c}$](https://content.cld.iop.org/journals/0953-4075/51/17/174002/revision1/jpbaad132ieqn52.gif) .
.
The parallel and perpendicular components of the coordinate or the velocity vector are defined w.r.t. the electric field. For velocity, these components v∥ and v⊥ are:
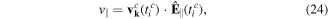
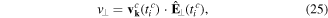
where 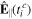 and
and  are unit vectors parallel and perpendicular to the electric field, respectively, at the Coulomb-corrected time of exit
are unit vectors parallel and perpendicular to the electric field, respectively, at the Coulomb-corrected time of exit  (the real part of the saddle point,
(the real part of the saddle point, ![${t}_{i}^{c}={\mathfrak{R}}[{t}_{s}^{c}]$](https://content.cld.iop.org/journals/0953-4075/51/17/174002/revision1/jpbaad132ieqn56.gif) ). The quantity
). The quantity  is positive if it has positive projection on the direction of the vector potential at the same time. For SFA, the time instants used are ti.
is positive if it has positive projection on the direction of the vector potential at the same time. For SFA, the time instants used are ti.
3.1. Circularly polarised fields
We first consider a few-cycle, circularly polarised laser pulse, defined via its vector potential:
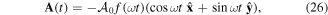
where 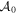 is the amplitude. The envelope profile used here is
is the amplitude. The envelope profile used here is  with Ne = 2. The peak field strength is defined as
with Ne = 2. The peak field strength is defined as  . The most dominant ionisation event happens near t = 0, which maps onto a peak at ϕk = 0 in the SFA theory. Long-range interactions lead to an offset in this mapping between the ionisation time and the momentum peak, which ARM accurately predicts for s-orbitals [66, 70]. The off-set angle is equal to
. The most dominant ionisation event happens near t = 0, which maps onto a peak at ϕk = 0 in the SFA theory. Long-range interactions lead to an offset in this mapping between the ionisation time and the momentum peak, which ARM accurately predicts for s-orbitals [66, 70]. The off-set angle is equal to ![$\omega {\mathfrak{R}}[{t}_{s}^{c}]$](https://content.cld.iop.org/journals/0953-4075/51/17/174002/revision1/jpbaad132ieqn61.gif) [66, 70].
[66, 70].
The velocities at the exit point (time ![$t={\mathfrak{R}}[{t}_{s}^{c}]={t}_{i}^{c}$](https://content.cld.iop.org/journals/0953-4075/51/17/174002/revision1/jpbaad132ieqn62.gif) ) are shown in figure 1, as a function of the final (detected) energy and angle of the photoelectron. We use the example of Yb III, interacting with
) are shown in figure 1, as a function of the final (detected) energy and angle of the photoelectron. We use the example of Yb III, interacting with 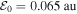 , λ = 800 nm, right circular polarised field. Superimposed on these distributions are the contour levels of the final photoelectron momentum distribution at the detector. Red solid curves are for f−3 (counter-rotating) orbital, which has the highest ionisation rate in a right-circularly polarised field. The blue dashed contours are for the f+3 (co-rotating) orbital, which has weaker photoelectron signal (see the companion paper I). Contours for both
, λ = 800 nm, right circular polarised field. Superimposed on these distributions are the contour levels of the final photoelectron momentum distribution at the detector. Red solid curves are for f−3 (counter-rotating) orbital, which has the highest ionisation rate in a right-circularly polarised field. The blue dashed contours are for the f+3 (co-rotating) orbital, which has weaker photoelectron signal (see the companion paper I). Contours for both 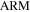 (upper rows) and SFA (lower rows) are shown.
(upper rows) and SFA (lower rows) are shown.
Figure 1. Distribution of exit velocities at the time instant  , for Yb III, at
, for Yb III, at  , λ = 800 nm, right circular polarised field. The outermost contour level corresponds to 10% electron population, the innermost to 90% electron population. For SFA,
, λ = 800 nm, right circular polarised field. The outermost contour level corresponds to 10% electron population, the innermost to 90% electron population. For SFA,  , and exit point is at SFA
, and exit point is at SFA ![${t}_{i}={\mathfrak{R}}[{t}_{s}]$](https://content.cld.iop.org/journals/0953-4075/51/17/174002/revision1/jpbaad132ieqn68.gif) . Only real part of exit velocity, corresponding to quantum trajectory is shown.
. Only real part of exit velocity, corresponding to quantum trajectory is shown.
Download figure:
Standard image High-resolution imageWe begin with the analysis of the SFA results, see figure 1 (SFA, v⊥, SFA v∥). The velocity v⊥ orthogonal to the instantaneous field at the time of exit is known to define the final energy of the photoelectron at the peak of the distribution (see e.g. [72]). Let us follow the contours, which specify the angle and energy dependence of co- and counter-rotating electrons, superimposed on the colour-coded background representing the 'exit' value of v⊥ as a function of the final angle and energy of the photoelectron (see figure 1(d)). In agreement with our expectations, we find larger v⊥ for the co-rotating electron at the peak of its momentum distribution, than for the counter-rotating electron at the peak of its momentum distribution. This non-adiabatic effect is discussed e.g. in [72]. It is responsible for the fact that counter-rotating electron (blue dashed contour) has the peak of its distribution at higher energy than the co-rotating electron (red solid contour). In the quasistatic limit, the perpendicular 'exit' velocity v⊥ for both co- and counter-rotating electrons tends to zero, removing the difference between their spectra and ionisation rates.
The longitudinal 'exit' SFA velocity v∥ (see figure 1(c)) varies as a function of the detection angle. It is zero for zero detection angle (where the maxima of both photoelecton distributions are located) and is exactly opposite for positive and negative angles. For positive detection angles, it is directed away from the core, while for negative detection angles, it is directed towards the core. This angular dependence reflects the non-adiababticity of electron dynamics due to the fast change of the magnitude of the laser field in the short pulse. In this respect, the situation becomes similar to linearly polarised fields, where non-adiabaticity of the electron response maps into non-zero longitudinal velocity for all ionisation times within the optical cycle, except for the ionisation time at the peak of the laser field.
This (envelope-related) non-adiabatic feature of the 'exit' value of v∥ already tells us that when the Coulomb potential is included, the trajectories with the SFA velocities directed towards the core can be more efficiently decelerated by the Coulomb field (and may even be trapped), than the trajectories with the SFA velocities directed away from the core. As a result, it is clear that when the Coulomb field is included, the final distributions will be more distorted (with respect to their SFA counterparts) for positive angles and less distorted for the negative angles. This is exactly what we see in figure 1(a), where the final momentum distributions are shown. They are superimposed on top of the colour-coded 'exit' velocities.
Overall, the main effect of the Coulomb potential is to 'skew' the final and the initial momentum distributions while mostly preserving the range of the 'exit' velocities arising in the short-range potential. This observation is in agreement with the standard assumptions of the Coulomb-corrected three-step models.
The range of variation of the transverse velocity component is reduced in ARM, compared to SFA, but is shifted to larger positive velocities. This is the influence of 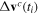 . The SFA transverse velocity sharply depends on energy, whereas the ARM velocity spreads out gradually. Long-range interactions therefore lead to bunching of the trajectories just after emerging into the continuum.
. The SFA transverse velocity sharply depends on energy, whereas the ARM velocity spreads out gradually. Long-range interactions therefore lead to bunching of the trajectories just after emerging into the continuum.
We next consider initial coordinate distribution at the barrier exit, figure 2, where the coordinates parallel and perpendicular to the electric field direction are shown. These values of the exit coordinates correspond to quantum trajectories. In both SFA and ARM case, counter-rotating (f−3) electrons have smaller parallel component of the coordinate than the co-rotating electron (f+3) (figures 2(a) and (c)). Compare this to the perpendicular coordinate distribution (figures 2(b) and (d)): counter-rotating electrons are liberated farther from the core in terms of their perpendicular displacement, than the co-rotating electrons.
Figure 2. Distribution of exit coordinates at the 'exit time'  , for Yb III, at
, for Yb III, at  , λ = 800 nm, right circular polarised field. The outermost contour level corresponds to 10% electron population, the innermost to 90% electron population. For SFA,
, λ = 800 nm, right circular polarised field. The outermost contour level corresponds to 10% electron population, the innermost to 90% electron population. For SFA, 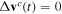 , and exit point is at SFA
, and exit point is at SFA ![${t}_{i}={\mathfrak{R}}[{t}_{s}]$](https://content.cld.iop.org/journals/0953-4075/51/17/174002/revision1/jpbaad132ieqn73.gif) . Only real part of exit coordinate corresponding to the quantum trajectory is shown.
. Only real part of exit coordinate corresponding to the quantum trajectory is shown.
Download figure:
Standard image High-resolution imageThe extent of the parallel displacement is much stronger than perpendicular displacement, and thus, overall, the co-rotating electrons are liberated at a larger distance from the core than the counter-rotating electrons.
With this information on initial velocity and coordinates, we can develop a schematic of electron trajectories after tunnelling through the barrier.
The corresponding SFA quantum orbits and long-range quantum and classical trajectories for majority of electrons are shown in figure 3, for the time duration corresponding to two cycles of the laser field after ionisation (the laser field switches off after one cycle). The curve with red solid triangles represents the SFA trajectory for f−3 orbital and the curve with the blue dashed triangles is the SFA trajectory for the f+3 orbital. The two trajectories are very close to each other, with f+3 ending up slightly farther from f−3, due to its higher momentum, as expected.
Figure 3. Real part of quantum orbits in SFA (curves with triangles), classical (curves with squares) and quantum (curves with diamonds) trajectories derived using ARM, for f−3 (solid curves) and f+3 (dashed curves) of Yb III, in a circularly polarised field. We see the sharp steering of electrons, with f−3 electrons experiencing strong counter-clockwise 'streaking' compared to f+3 electrons, in long-range potential. The real quantum trajectories differ from classical trajectories, because the dynamics of the majority of co- and counter-rotating electrons is manifestly non-adiabatic.
Download figure:
Standard image High-resolution imageWhen the long-range Coulomb interaction is switched on, however, we see a significant difference between the trajectories for the f−3 and f+3 electrons, travelling in very different directions (as one would expect from the full picture [71]). While the f+3 electrons still maintain greater distance from the core than their f−3 counterparts, the f−3 electrons show larger steering by the laser field compared to f+3 electrons.
This leads to larger offset angle in the photoelectron spectra at the detector [71]. The SFA trajectories fail to capture this essential feature.
As discussed in detail in section 2.3, we can either define the real initial conditions at the barrier exit (real part of coordinate on quantum trajectory at the exit time, real velocity obtained by back propagation from the final momentum  to real exit coordinate, see equations (11) and (12)) and then propagate them to the detector in real time, leading to the curve with with squares in figure 3(a) (classical), or we can perform propagation directly from the 'entrance to the barrier' (in complex space and time), guided by the matching scheme and leading to the quantum trajectories (equations (9) and (10)). The difference between the two after the exit point is due to imaginary exit coordinate missing in classical trajectory and present in the quantum trajectory and is a result of the coupling between the real and imaginary components of the quantum trajectories.
to real exit coordinate, see equations (11) and (12)) and then propagate them to the detector in real time, leading to the curve with with squares in figure 3(a) (classical), or we can perform propagation directly from the 'entrance to the barrier' (in complex space and time), guided by the matching scheme and leading to the quantum trajectories (equations (9) and (10)). The difference between the two after the exit point is due to imaginary exit coordinate missing in classical trajectory and present in the quantum trajectory and is a result of the coupling between the real and imaginary components of the quantum trajectories.
The coupling can be understood by considering the Coulomb force (see section 2.3) on the imaginary trajectory. Its real part depends on the parameter b(t), proportional to the imaginary part of the exit coordinate:
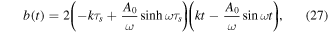
for any real t ≥ texit, τs is the imaginary part of complex SFA ionisation time ts.
For circularly polarised fields  (hence b(t) = 0) at optimal momentum, corresponding to the majority of s-electrons. However, the spectral peaks corresponding to co- and counter-rotating electrons are on the opposite sides from the peak of photoelectron spectrum for s-electrons. Thus, b > 0 for counter- and b < 0 for co-rotating electron, reflecting the fact that these electrons are not born at the peak of the laser field, i.e. their dynamics is manifestly non-adiabatic. The deviation between the classical and the real part of the quantum trajectories in the long-range potential is due to this effect.
(hence b(t) = 0) at optimal momentum, corresponding to the majority of s-electrons. However, the spectral peaks corresponding to co- and counter-rotating electrons are on the opposite sides from the peak of photoelectron spectrum for s-electrons. Thus, b > 0 for counter- and b < 0 for co-rotating electron, reflecting the fact that these electrons are not born at the peak of the laser field, i.e. their dynamics is manifestly non-adiabatic. The deviation between the classical and the real part of the quantum trajectories in the long-range potential is due to this effect.
In elliptical fields 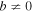 for s-orbitals and therefore co- and counter-rotating electrons are 'asymmetrically' off-set from b = 0. In this case the degree of mismatch between the classical and quantum trajectories in long-range potential depends on the magnetic number m of the orbital (i.e., whether it is co-rotating or counter-rotating w.r.t. the field).
for s-orbitals and therefore co- and counter-rotating electrons are 'asymmetrically' off-set from b = 0. In this case the degree of mismatch between the classical and quantum trajectories in long-range potential depends on the magnetic number m of the orbital (i.e., whether it is co-rotating or counter-rotating w.r.t. the field).
3.2. Elliptically polarised fields
Non-adiabaticity of ionisation is the key reason for the deviations between the classical and quantum trajectories. It is enhanced due to the application of short pulses, Coulomb-laser coupling and is, probably, best detected by looking at orbitals with large l, m. However, the ellipticity of the field offers an additional control knob: non-adiabaticity of ionisation is also enhanced by decreasing the ellipticity, because the sub-cycle variation of the field comes into play. It is particularly relevant for long pulses, where the ionisation dynamics in circularly polarised fields becomes largely adiabatic. Analysing the initial conditions for various orbitals, the differences in the evolution of quantum and classical trajectories we can clearly identify the 'degree' of non-adiabaticity of strong field ionisation. We will now focus on orbitals with lower m, l, such as s and p orbitals and longer laser pulses. As discussed earlier, 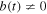 already for the majority of s electrons in elliptical fields, leading to m-dependent deviations between classical and quantum trajectories for
already for the majority of s electrons in elliptical fields, leading to m-dependent deviations between classical and quantum trajectories for  , which we illustrate here.
, which we illustrate here.
We extend the method we recently employed in [73], to include initial coordinate with Coulomb corrections due to the under the barrier dynamics.
We consider elliptically polarised short pulse with the vector potential defined as:
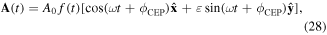
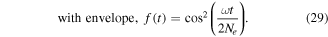
Here we choose 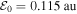 , λ = 780 nm,
, λ = 780 nm,  ,
,  , and Ne = 6 cycles. For Ar II, the ionisation potential is Ip = 27.630 eV.
, and Ne = 6 cycles. For Ar II, the ionisation potential is Ip = 27.630 eV.
The electric field defined from the vector potential of equation (29) has its major axis along the x-axis, which means that the peak of the photoelectron distribution is close to the y-axis, as is also evident from the contour plots in figures 4 and 5. The symmetry breaking around ϕk = 90° is the well-known effect of the Coulomb interaction [74, 75].
Figure 4. Distribution of exit velocity (the real part of velocity on quantum trajectory) at time instant ![$t={\mathfrak{R}}[{t}_{s}^{c}]$](https://content.cld.iop.org/journals/0953-4075/51/17/174002/revision1/jpbaad132ieqn82.gif) (
(![$t={\mathfrak{R}}[{t}_{s}]$](https://content.cld.iop.org/journals/0953-4075/51/17/174002/revision1/jpbaad132ieqn83.gif) for SFA case), for Ar II, with field parameters:
for SFA case), for Ar II, with field parameters:  , λ = 780 nm,
, λ = 780 nm,  , right-elliptically polarised field.
, right-elliptically polarised field.
Download figure:
Standard image High-resolution imageFigure 5. Distribution of exit coordinate (the real part of quantum trajectory) at time instant ![$t={\mathfrak{R}}[{t}_{s}^{c}]$](https://content.cld.iop.org/journals/0953-4075/51/17/174002/revision1/jpbaad132ieqn86.gif) (
(![$t={\mathfrak{R}}[{t}_{s}]$](https://content.cld.iop.org/journals/0953-4075/51/17/174002/revision1/jpbaad132ieqn87.gif) for SFA case), for Ar II, with field parameters:
for SFA case), for Ar II, with field parameters:  , λ = 780 nm,
, λ = 780 nm,  , right-elliptically polarised field.
, right-elliptically polarised field.
Download figure:
Standard image High-resolution image3.3. Initial conditions versus ellipticity
Figure 6 shows the perpendicular and parallel components of the exit coordinate and velocity (real parts of quantum trajectories and their respective velocities at the exit time), respectively, as a function of ellipticity for the majority of p− and p+ electrons liberated from Ar II.
Figure 6. Exit parallel and perpendicular (a) coordinate and (b) velocity, for p− and p+ electrons of Ar II, at effective field strength 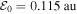 , λ = 780 nm, six-cycle, right-polarised elliptical field, real parts of quantum trajectories (solid) in long-range potential and (dashed) in short-range potential (SFA).
, λ = 780 nm, six-cycle, right-polarised elliptical field, real parts of quantum trajectories (solid) in long-range potential and (dashed) in short-range potential (SFA).
Download figure:
Standard image High-resolution imageFigure 7. (a) Timing information of most probably p− and p+ electrons, as a function of ellipticity. Red solid line is the most probable release time for p− electrons, green dashed for the p+ electrons, and blue dotted line is the difference between the two. There is a general trend of the increasing time delay between p− and p+ electrons, with increasing ellipticity. (b) Envelope effects and associated corrections for nearly single-cycle pulses, for p−, p0, and p+ orbitals, as a function of ellipticity. The effects are negligible, on the scale of 10−3 au. Field parameters: λ = 780 nm, cos2-envelope, six-cycle, right-elliptically polarised field.
Download figure:
Standard image High-resolution imageBrief analysis shows that the parallel displacement of p− electron is always higher than that of p+ electrons. Counter-rotating electrons also have higher perpendicular and parallel exit velocity (figure 6(b)). This is in contrast to circular fields, where parallel displacement for p+ electrons is higher than for the p− electrons.
The result for exit parallel velocities shown in figure 6 is particularly instructive. The parallel velocity is zero in short-range potential in the adiabatic regime, it always applies to the majority of electrons in SFA. Figure 6 shows that in long-range potentials, the parallel velocity for the majority of the p+ and p− electrons is small, but not equal to zero. The non-zero velocity is due to the non-adiabaticity of electron dynamics and subsequent sub-barrier Coulomb-laser coupling. Note that the respective result for the majority of s electrons (with the same Ip) would be squeezed in between the green and black curves for p+ and p− electrons. First, we see that for elliptically polarised fields and ellipticity in the range  , co-rotating p+ electrons have the largest non-zero initial velocities, i.e. they are the most non-adiabatic in elliptical fields. The s-electrons follow next and then, the most 'adiabatic' in elliptical fields are the p− electrons. In contrast, recall that in circularly polarised fields, the most adiabatic are the s-electrons. Indeed, for ellipticity
, co-rotating p+ electrons have the largest non-zero initial velocities, i.e. they are the most non-adiabatic in elliptical fields. The s-electrons follow next and then, the most 'adiabatic' in elliptical fields are the p− electrons. In contrast, recall that in circularly polarised fields, the most adiabatic are the s-electrons. Indeed, for ellipticity  , the exit parallel velocity is very close to zero for s and p− electrons, because the pulse we are using (for given frequency and intensity) is already sufficiently long to significantly suppress the non-adiabaticity of ionisation along the major field axis for the majority of s and p− electrons in circularly polarised fields, but not for p+ electrons. Just like in short-range potential, the non-zero parallel exit velocity reflects non-adiabaticity of ionisation dynamics in long-range potentials and the parallel velocity is equal to zero in the adiabatic limit. In adiabatic (long-wavelength) limit the ARM predictions for the photoelectron angular and energy distributions in attoclock set-up (strong field ionisation in circularly polarised fields) are remarkably accurate [70], further supporting our conclusions.
, the exit parallel velocity is very close to zero for s and p− electrons, because the pulse we are using (for given frequency and intensity) is already sufficiently long to significantly suppress the non-adiabaticity of ionisation along the major field axis for the majority of s and p− electrons in circularly polarised fields, but not for p+ electrons. Just like in short-range potential, the non-zero parallel exit velocity reflects non-adiabaticity of ionisation dynamics in long-range potentials and the parallel velocity is equal to zero in the adiabatic limit. In adiabatic (long-wavelength) limit the ARM predictions for the photoelectron angular and energy distributions in attoclock set-up (strong field ionisation in circularly polarised fields) are remarkably accurate [70], further supporting our conclusions.
In figure 8, we show the (a) real and (b) imaginary parts of the trajectories corresponding to the peak of the photoelectron spectra for the p− and p+ electrons, for  , for the SFA (triangles), classical (squares) and quantum (diamond) trajectories in the long-range potential. We take into account the impact of the Coulomb momentum shift term
, for the SFA (triangles), classical (squares) and quantum (diamond) trajectories in the long-range potential. We take into account the impact of the Coulomb momentum shift term  for the ARM quantum orbits. The difference between the SFA and the ARM trajectories is the deflection of the trajectories in the long-range potential. The effect depends on the magnetic number m of the initial bound state: counter-rotating electrons (p−) experience greater deflection by the Coulomb potential compared to the co-rotating (p+) electrons. Both p− and p+ electrons emerge from under the barrier at almost the same point in space, but p− electrons are released after the peak of the pulse (see Figure 7) and are more likely to pass closer to the core (see Figure 8). We can also see some difference between the ARM quantum trajectories and ARM classical trajectories, especially for the p+ orbital (blue dashed curves in figure 8) discussed above.
for the ARM quantum orbits. The difference between the SFA and the ARM trajectories is the deflection of the trajectories in the long-range potential. The effect depends on the magnetic number m of the initial bound state: counter-rotating electrons (p−) experience greater deflection by the Coulomb potential compared to the co-rotating (p+) electrons. Both p− and p+ electrons emerge from under the barrier at almost the same point in space, but p− electrons are released after the peak of the pulse (see Figure 7) and are more likely to pass closer to the core (see Figure 8). We can also see some difference between the ARM quantum trajectories and ARM classical trajectories, especially for the p+ orbital (blue dashed curves in figure 8) discussed above.
Figure 8. Comparison of SFA (triangles), classical (squares), and real part of quantum (diamonds) trajectories in long-range potential for (red solid) p− and (blue dashed) p+ electrons, at ellipticity 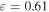 . Quantum trajectories deviate from the classical trajectories mostly for the p+ orbitals. (b) Radial coordinate for the classical (squares) and quantum (diamonds) trajectories in the long-range potential, as a function of time, after the exit from the barrier. p− electrons are liberated just after the peak of the pulse. They traverse closer to the core, leading to stronger interaction with the Coulomb potential. On the other hand, the p+ electrons are released just before the peak, and interact weaker with the core.
. Quantum trajectories deviate from the classical trajectories mostly for the p+ orbitals. (b) Radial coordinate for the classical (squares) and quantum (diamonds) trajectories in the long-range potential, as a function of time, after the exit from the barrier. p− electrons are liberated just after the peak of the pulse. They traverse closer to the core, leading to stronger interaction with the Coulomb potential. On the other hand, the p+ electrons are released just before the peak, and interact weaker with the core.
Download figure:
Standard image High-resolution image4. Adiabatic expressions
Before concluding this paper, we present simple, analytical expressions for the Coulomb momentum shift  , which is essential for describing the enhancement in ionisation of the counter-rotating versus the co-rotating electrons. We consider the adiabatic regime γ ≪ 1.
, which is essential for describing the enhancement in ionisation of the counter-rotating versus the co-rotating electrons. We consider the adiabatic regime γ ≪ 1.
Let the electric field point along the positive y-axis during the instant of ionisation, leading to the electrons drifting in the positive x-direction in the continuum. The Coulomb potential yields the correction  to velocity parallel to the electric field, and
to velocity parallel to the electric field, and  to the velocity perpendicular to the electric field.
to the velocity perpendicular to the electric field.
We assume  (where
(where  is the atomic field strength) and γ ≪ 1. For laser field strength pointing along (or near) y-axis as the electron escapes, we find the momentum shift to be defined, in the first order in Z, by the expression:
is the atomic field strength) and γ ≪ 1. For laser field strength pointing along (or near) y-axis as the electron escapes, we find the momentum shift to be defined, in the first order in Z, by the expression:
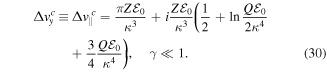
This is the approximate expression for momentum shift in the direction of the field at the instant of ionisation. The real part of this expression is equivalent to the adiabatic momentum shift outside of the barrier given by equation (78) of [64], because in the adiabatic regime, there is no sub-barrier contribution to the real Coulomb shift. The momentum shift perpendicular to the field is zero in 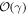 , becasue it is manifestly non-adiabatic. thus, we need to expand to higher order in the Keldysh parameter γ
, becasue it is manifestly non-adiabatic. thus, we need to expand to higher order in the Keldysh parameter γ
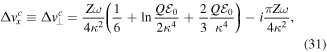
Figure 9 compares these approximate expressions with exact result equation (5). The agreement is excellent for  , because it is 'less non-adiabatic' than
, because it is 'less non-adiabatic' than  (figures 9(a) and (b)). We also note that, even though equation (30) is supposed to be valid for γ ≪ 1, we get very good agreement for γ ≃ 4, well into the non-adiabatic limit. The velocity in orthogonal direction is as non-adiabatic as it gets and one should use even more terms in the expansion w.r.t. γ to converge to
(figures 9(a) and (b)). We also note that, even though equation (30) is supposed to be valid for γ ≪ 1, we get very good agreement for γ ≃ 4, well into the non-adiabatic limit. The velocity in orthogonal direction is as non-adiabatic as it gets and one should use even more terms in the expansion w.r.t. γ to converge to  given by equation (5). However, we have found that even at the current level of approximation for velocities, the approximate expression for ionisation rates has a reasonable quality (see Figure 9).
given by equation (5). However, we have found that even at the current level of approximation for velocities, the approximate expression for ionisation rates has a reasonable quality (see Figure 9).
Figure 9. Comparison of exact expression for  , with the approximate expressions (equations (30) for
, with the approximate expressions (equations (30) for  and equation (31) for
and equation (31) for 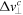 ), as function of field strength. The exact curves are shown in solid red, and approximate expressions are shown in blue dashed curves. We use Yb III, Q = 3, Ip = 0.92 au, with laser field parameters: λ = 3 μm, monochromatic circularly polarised field.
), as function of field strength. The exact curves are shown in solid red, and approximate expressions are shown in blue dashed curves. We use Yb III, Q = 3, Ip = 0.92 au, with laser field parameters: λ = 3 μm, monochromatic circularly polarised field.
Download figure:
Standard image High-resolution imageIndeed, for  , and adiabatic case, we have:
, and adiabatic case, we have:
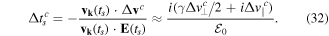
Even though γ ≪ 1, and 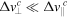 (figure 9), we still need to keep
(figure 9), we still need to keep  , as shown below.
, as shown below.
We can now calculate the complex deviation angle 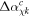 (equation (A.7) in [71]):
(equation (A.7) in [71]):
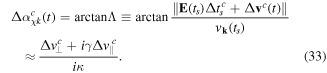
We find that  and
and  are on par.
are on par.
The Coulomb complex angle shift 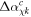 enters expressions for the quantum amplitudes via
enters expressions for the quantum amplitudes via 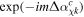 . Therefore, it is the real part of the complex momentum shift
. Therefore, it is the real part of the complex momentum shift 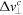 and the imaginary part of
and the imaginary part of 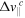 , that define the ratio of the ionisation rates for the counter- and co-rotating electrons. This is in line with expectations, as the bulk of the real part of
, that define the ratio of the ionisation rates for the counter- and co-rotating electrons. This is in line with expectations, as the bulk of the real part of  and the imaginary part of
and the imaginary part of  are mostly defined under the barrier.
are mostly defined under the barrier.
The final expression for the ratio between counter- and co-rotating electrons rates, for γ ≪ 1, is:
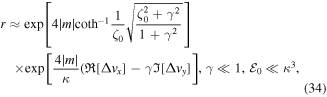
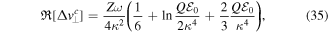
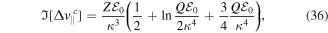
where  . The first exponential in equation (37) is the SFA ratio [72], while the second exponential is the additional m-specific contribution from the Coulomb potential, manifesting through the momentum shift
. The first exponential in equation (37) is the SFA ratio [72], while the second exponential is the additional m-specific contribution from the Coulomb potential, manifesting through the momentum shift 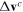 and time correction
and time correction 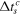 . Further simplification gives us the compact expression:
. Further simplification gives us the compact expression:
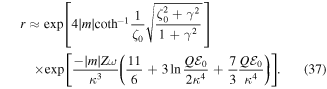
A comparison of this approximate ratio and the exact-ARM ratio is shown in figure 10, for Yb III, at m = ±3. The agreement gets better for lower m. Thus, the higher m, the more non-adiabatic terms need to be included. The overall agreement between the approximate ARM ratio equation (37) and the exact results is good. Deviation from the exact result is at most ≃8% (for 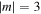 ). Therefore, equation (37) can serve as a succinct formula for the ratio of the ionisation yields of the counter- to co-rotating electrons, in the long-range potentials in non-adiabatic domain.
). Therefore, equation (37) can serve as a succinct formula for the ratio of the ionisation yields of the counter- to co-rotating electrons, in the long-range potentials in non-adiabatic domain.
Figure 10. Comparison of exact (solid curves) and approximate (dashed curves) ratio (equation (37)) of counter- to co-rotating ionisation rates, for Yb III. Field parameters: λ = 6 μm, monochromatic, right-circularly polarised field. We find very good agreement between exact and approximate results.
Download figure:
Standard image High-resolution image5. Conclusion
We have applied the ARM theory to obtain electron velocities and coordinates at the exit from the tunnelling barrier in strong field ionisation by few-cycle circularly and elliptically polarised fields.
The opportunity to derive such initial conditions emerges as a corollary of analysing sub-barrier kinematics, i.e. the interplay of laser and Coulomb fields on the sub-cycle scale.
We have derived the quantum trajectories describing the electron dynamics in long-range potential and evolving in complex time and space. We have also derived their classical counterpart: the trajectories evolving in real time and real space in long-range potential. The difference between classical and quantum trajectories is proportional to the degree of non-adiabaticity of ionisation dynamics and related to fact that the ionisation process is not completed after the 'exit' from the barrier (see the companion paper and [65]). Despite this difference, the key features that characterise the difference in the final photoelectron distributions for the co- and counter-rotating electrons are reproduced by both quantum and classical trajectories corresponding to the majority of electrons. For example, the trajectories for the counter-rotating electrons experience larger deflection by the long-range Coulomb-type potential of the core. In particular, the classical trajectories corresponding to real initial conditions (real parts of velocities and coordinates taken at real value of the saddle point for time, all Coulomb-corrected) does not seem to betray our intuition in capturing the basic physics.
We have presented analytical expressions for the ratio of the counter- to co-rotating electron yields, in the adiabatic limit, obtaining very good agreement with the exact-ARM results. These analytical expressions can be tested in experiments and used as a a guide for understanding the orbital-specific Coulomb correction.
We also clarified the misconception in the literature that ARM assumes zero initial parallel velocity at the exit from the barrier [76]. We show that (i) ARM offers a rigorous framework for establishing quantum and classical trajectories reflecting ionisation dynamics in long-range potentials, (ii) the parallel velocity is different for different ellipticities and orbitals with different l, m and thus is often non-zero, (iii) the exit parallel velocity is zero in long-range potentials in the adiabatic limit. In this, long-wavelength, limit ARM predictions for photoelectron angular and energy distributions in the attoclock set-up (strong field ionisation in circularly polarised fields) are remarkably accurate [70], further supporting our conclusions.
Acknowledgments
OS gratefully acknowledges financial support from the EU ITN MEDEA-AMD-641789-17. JK and OS gratefully acknowledge financial support from the DFG grant SM 292/2-3.










