Abstract
We review recent experimental and theoretical progress in realizing and simulating many-body phases of ultracold atoms in optical lattices, which gives access to analog quantum simulations of fundamental model Hamiltonians for strongly correlated condensed matter systems, such as the Hubbard model. After a general introduction to quantum gases in optical lattices, their preparation and cooling, and measurement techniques for relevant observables, we focus on several examples, where quantum simulations of this type have been performed successfully during the past years: Mott-insulator states, itinerant quantum magnetism, disorder-induced localization and its interplay with interactions, and topological quantum states in synthetic gauge fields.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Since the achievement of Bose–Einstein condensation (BEC) we have witnessed enormous progress in experimental and theoretical research on ultracold quantum gases [1]. In particular, optical lattices and Feshbach resonances have opened up the possibility to realize analog quantum simulators for strongly correlated electronic condensed matter systems, such as high-temperature superconductors [2, 3], but also for bosonic quantum phase transitions [4], and for exotic quantum matter, as for example color superconducting phases of dense nuclear matter in neutron stars [5, 6]. These developments build on the pioneering ideas of Feynman [7, 8], who already envisioned a universal 'digital' quantum simulator, and others [9].
Quantum simulations of this type should address relevant, possibly simplified models, containing (or at least believed to contain) the essential physics of a system. The solution, or quantitatively accurate simulation of the model should be hard or even impossible on a classical computer, using state-of-the-art algorithms, due to the exponential growth of Hilbert space of a quantum many-body system with particle number, or due to method-specific limitations such as the sign problem of quantum Monte Carlo (QMC) simulations [10]. The setup of the quantum simulator should allow for high tunability of the model parameters, an efficient preparation of the initial state, and easy readout (detection) of physical properties of the final state after time evolution or thermalization.
In this article we will review the goals, achievements and challenges of analog quantum simulations for condensed-matter-type phenomena, based on ultracold quantum gases in optical lattices, for selected examples. Other experimental platforms, such as atom chips, trapped ultracold ions or interacting photonic systems, will be beyond the scope of this article. Likewise, we will not discuss digital quantum simulations [11]. Our focus will be on models and experimental implementations, and on the role of theory, which provides benchmarks and quantitative or qualitative guidance (for example phase diagrams, critical temperatures or coupling strengths) for the design of quantum simulators.
2. Hubbard model and optical lattices
2.1. Strongly correlated electrons
A paradigm of strongly correlated electronic systems is the Hubbard model, which was proposed around 1960 by Anderson [12], Hubbard [13] and Kanamori [14], and has since then been highly successfully applied to describe a wide range of phenomena, in particular metal-insulator transitions, magnetic ordering and d-wave superconductivity [2, 3, 15].
In its simplest version for spin-1/2 fermions within a single band, the model has the form
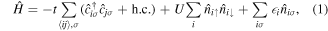
where  denotes spin,
denotes spin, 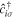 is the creation operator on lattice site i, and t the hopping matrix element between pairs of nearest-neighbor lattice sites
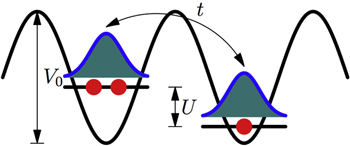
is the creation operator on lattice site i, and t the hopping matrix element between pairs of nearest-neighbor lattice sites  . For a schematic illustration, see figure 1. U is the onsite Hubbard interaction,
. For a schematic illustration, see figure 1. U is the onsite Hubbard interaction,  is the local number operator for spin σ, and
is the local number operator for spin σ, and  denotes an additional single-particle potential, modeling an inhomogeneity of the system, which could be due to disorder or due to an external potential, for example the optical trap in the case of ultracold atoms.
denotes an additional single-particle potential, modeling an inhomogeneity of the system, which could be due to disorder or due to an external potential, for example the optical trap in the case of ultracold atoms.
Figure 1. Schematic illustration of the Fermi–Hubbard model on the square lattice.
Download figure:
Standard image High-resolution imageFor most electronic solid-state systems, the simple version of the Hubbard model (1) is an idealization. Although the Coulomb interaction is screened in metallic systems, the screening length may be significantly larger than the lattice constant, and further terms such as density-dependent hopping or next-neighbor interactions can be relevant [13, 16]. Also effects of lattice vibrations and electron-phonon-coupling, which are not contained in (1), may be important for the physics under consideration. They are completely absent in optical lattices, but can be introduced by coupling to additional degrees of freedom, for example to dynamical phonons in hybrid atom-ion quantum simulators [17].
Despite its apparent simplicity, the plain Fermi–Hubbard model can only be solved exactly in one spatial dimension, analytically by the Bethe Ansatz [18] or numerically by the density-matrix renormalization group (DMRG) [19]. After decades of intense theoretical research, the low-temperature phase diagram of the 2d fermionic Hubbard model, which is believed to contain essential ingredients for the physics underlying high-temperature superconductivity [20], is not known rigorously, due to fundamental limitations of numerically exact simulation techniques such as QMC [10], or matrix product states and their generalizations [21]. At this point analog quantum simulations can provide powerful insight, via a controlled and highly tunable experimental realization of the pure model Hamiltonian based on ultracold fermions in optical lattices [22], as already earlier proposed for the bosonic version of the model [4]. These investigations are in many ways complementary to condensed matter studies. They give access to new observables, for example in situ, single-site resolved measurements of charge and spin order and correlations, both in the Mott insulator (MI) and at finite doping, for tunable repulsive or attractive interactions [23–25]. They also allow measuring real-time nonequilibrium particle and spin dynamics [26–30].
2.2. Optical lattices
Optical lattices are artificial crystals of light, formed by pairs of counterpropagating, interfering laser beams, as shown in figure 2. Due to the AC Stark effect, neutral atoms interacting with the standing light waves of an optical lattice experience an effective conservative potential, which for a simple cubic geometry has the form
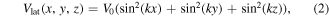
where the amplitude V0 is determined by the light intensity and the atomic polarizability [31]. 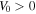 for blue detuning of the lattice lasers with respect to the atomic transition frequency, corresponding to a repulsive optical dipole potential, while
for blue detuning of the lattice lasers with respect to the atomic transition frequency, corresponding to a repulsive optical dipole potential, while  for red detuning.
for red detuning.  is the wavenumber of the lattice lasers, and the characteristic energy scale is given by the recoil energy
is the wavenumber of the lattice lasers, and the characteristic energy scale is given by the recoil energy 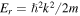 , typically in the kilohertz range, which corresponds to the kinetic energy of an atom after absorbing an optical lattice photon. For a schematic figure of a 1d optical lattice see figure 3. A wide range of different optical lattice structures has been realized, including artificial graphene [32] and frustrated geometries such as triangular or Kagome [33–35], just to name a few examples.
, typically in the kilohertz range, which corresponds to the kinetic energy of an atom after absorbing an optical lattice photon. For a schematic figure of a 1d optical lattice see figure 3. A wide range of different optical lattice structures has been realized, including artificial graphene [32] and frustrated geometries such as triangular or Kagome [33–35], just to name a few examples.
Figure 2. Cubic optical lattice, with a 2d slice shown. Arrows indicate the orthogonal polarizations of the lattice lasers, each of which is retroreflected from a mirror. Reproduced with permission from [36].
Download figure:
Standard image High-resolution imageFigure 3. Schematic figure of optical lattice with hopping t and on-site Hubbard interaction U.
Download figure:
Standard image High-resolution imageThe much larger lattice constant 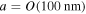 in an optical lattice, compared to
in an optical lattice, compared to 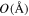 in an electronic crystal, and the lower energy scales (kHz instead of eV) lead to far longer timescales of the quantum dynamics. As a result, observing ultracold many-body quantum phases, their excitations and nonequilibrium dynamics, with single-site resolution and in real-time, has recently become possible [37, 38].
in an electronic crystal, and the lower energy scales (kHz instead of eV) lead to far longer timescales of the quantum dynamics. As a result, observing ultracold many-body quantum phases, their excitations and nonequilibrium dynamics, with single-site resolution and in real-time, has recently become possible [37, 38].
It is remarkable that even though these systems are extremely dilute gases, more than 10 000 times less dense than air, they can nevertheless show effects of strong correlations arising from the competition between two-particle interactions (resulting from s-wave scattering due to the van der Waals interaction, or from electric or magnetic dipolar interactions) and the kinetic energy. For more details, see for example the reviews [1, 39, 40].
At the same time these are very clean quantum systems, defect-free and with little dissipation resulting from spontaneous emission (which leads to an inelastic scattering rate  where Δ is the detuning, Γ the decay rate of the excited state,
where Δ is the detuning, Γ the decay rate of the excited state,  the atomic transition frequency and
the atomic transition frequency and 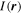 the light intensity [31]), unless dissipation is included in a controlled way, for example via losses due to ionization by an electron beam [41]. Ultracold gases in optical lattices therefore represent almost ideal closed quantum systems up to timescales of several 100 ms, when heating processes typically start to dominate.
the light intensity [31]), unless dissipation is included in a controlled way, for example via losses due to ionization by an electron beam [41]. Ultracold gases in optical lattices therefore represent almost ideal closed quantum systems up to timescales of several 100 ms, when heating processes typically start to dominate.
They are also scalable, up to hundreds of thousands of lattice sites, and therefore represent mesoscopic crystals. One should note that they are intrinsically inhomogeneous due to the additional external confinement potential, which typically arises from the Gaussian laser beam profiles and is approximately harmonic for (red-detuned) dipole traps, but can be engineered as a quasi-homogeneous 'box potential' with repulsive walls created by blue-detuned sheets of light [42]. As a result, spatial domains of different phases form, for example Fermi-liquid, band- and Mott-insulator domains, leading to 'wedding cake structures' of the density profile, which have recently been imaged in situ by quantum gas microscopy as shown in figure 4 [43]. For large systems they can be well described within a local density approximation (LDA), where every lattice site i is considered as part of a homogeneous system with effective chemical potential 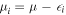 .
.
Figure 4. In situ images of the Mott metal-insulator transition and the 'wedding cake' domain structure of Fermi-liquid and insulating domains for ultracold fermionic 6Li in a 2d optical lattice. From [43]. Reprinted with permission from AAAS.
Download figure:
Standard image High-resolution image2.3. Band structure and interactions
Bloch's theorem states that due to the periodicity of the external potential, the single-particle eigenstates in an optical lattice have the form

where the function  has the same periodicity as the lattice, and α is the band index. Note that for the moment we disregard the external confinement potential, which will be included later. Here
has the same periodicity as the lattice, and α is the band index. Note that for the moment we disregard the external confinement potential, which will be included later. Here  is the quasimomentum (or crystal momentum), which for a simple cubic lattice has the domain
is the quasimomentum (or crystal momentum), which for a simple cubic lattice has the domain ![${q}_{x,y,z}\in (-\pi /a,\pi /a]$](https://content.cld.iop.org/journals/0953-4075/51/8/082001/revision3/jpbaaa31bieqn18.gif) , where
, where 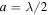 is the lattice constant. At sufficiently low temperature T, interaction strength U, and filling (particle number per site of the optical lattice), it is a good approximation to consider only the lowest Bloch band with index
is the lattice constant. At sufficiently low temperature T, interaction strength U, and filling (particle number per site of the optical lattice), it is a good approximation to consider only the lowest Bloch band with index  .
.
While the Bloch states are delocalized over the lattice, Wannier functions form a set of orthonormal single-particle states, which are maximally localized at individual lattice sites and are defined as
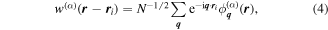
where 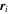 is the position of the ith lattice site and N is the total number of sites. The construction of maximally localized Wannier functions for a given optical lattice geometry is an important step towards defining the appropriate model Hamiltonian for a successful quantum simulation in optical lattices, see for example [32]. It should be noted that the optimal choice of the phases of the Bloch states in (4) for achieving maximal localization of
is the position of the ith lattice site and N is the total number of sites. The construction of maximally localized Wannier functions for a given optical lattice geometry is an important step towards defining the appropriate model Hamiltonian for a successful quantum simulation in optical lattices, see for example [32]. It should be noted that the optimal choice of the phases of the Bloch states in (4) for achieving maximal localization of  [44] is a nontrivial computational problem for non-separable lattices. Alternatively, in an efficient diagonalization-based approach, the Wannier functions can be determined as eigenstates of the band-projected position operator [32, 36]. This approach becomes particularly useful if additional disorder is present due to a spatially random potential: in this case the lattice translational invariance is broken, and no Bloch states or quasimomentum can be defined.
[44] is a nontrivial computational problem for non-separable lattices. Alternatively, in an efficient diagonalization-based approach, the Wannier functions can be determined as eigenstates of the band-projected position operator [32, 36]. This approach becomes particularly useful if additional disorder is present due to a spatially random potential: in this case the lattice translational invariance is broken, and no Bloch states or quasimomentum can be defined.
From now on we consider a single band, omitting the index α. The kinetic energy takes the form  , where
, where 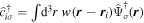 is the creation operator of a particle with mass m and hyperfine state σ on site i, and
is the creation operator of a particle with mass m and hyperfine state σ on site i, and  is the tunneling matrix element between neighboring sites. Depending on the lattice geometry, and for deep lattices with a dimensionless depth
is the tunneling matrix element between neighboring sites. Depending on the lattice geometry, and for deep lattices with a dimensionless depth 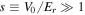 , longer-range tunneling can be neglected and the summation restricted to nearest neighbors
, longer-range tunneling can be neglected and the summation restricted to nearest neighbors  . For deep and separable lattices (1d, square, cubic) the tunneling matrix element can be approximately written as
. For deep and separable lattices (1d, square, cubic) the tunneling matrix element can be approximately written as 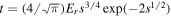 [1].
[1].
Additional two-particle interactions between atoms can be written in the form
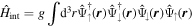
for fermions with two hyperfine ('spin') states 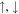 , where we have assumed that at the low energies considered here s-wave scattering with a scattering length as dominates, which can be described by a contact potential
, where we have assumed that at the low energies considered here s-wave scattering with a scattering length as dominates, which can be described by a contact potential 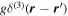 of strength
of strength 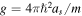 between two particles at positions
between two particles at positions  ,
,  [45]. Within the single-band approximation, which for unpolarized spin-1/2 fermions at low temperatures is valid for a total filling
[45]. Within the single-band approximation, which for unpolarized spin-1/2 fermions at low temperatures is valid for a total filling  per site and for a sufficiently deep optical lattice with
per site and for a sufficiently deep optical lattice with 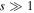 in the absence of Feshbach resonances, the dominant interaction term in the Wannier basis can be written as
in the absence of Feshbach resonances, the dominant interaction term in the Wannier basis can be written as  due to the localized nature of the Wannier states and the contact potential.
due to the localized nature of the Wannier states and the contact potential. 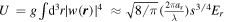 is the Hubbard interaction. In total, we obtain the single-band Fermi–Hubbard (FH) model (1) [22], where an additional trapping potential
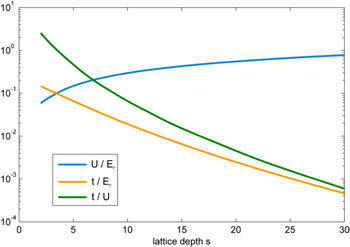
is the Hubbard interaction. In total, we obtain the single-band Fermi–Hubbard (FH) model (1) [22], where an additional trapping potential  is included, which describes the external confinement discussed previously. Note that the ratio U/t, and thus the correlation strength of the system, can be tuned freely by varying the dimensionless lattice depth s as shown in figure 5, or independently by changing as via a Feshbach resonance [46], from values
is included, which describes the external confinement discussed previously. Note that the ratio U/t, and thus the correlation strength of the system, can be tuned freely by varying the dimensionless lattice depth s as shown in figure 5, or independently by changing as via a Feshbach resonance [46], from values  to
to  . The particle density (filling) n per site is tunable by varying the confinement or the total number of atoms.
. The particle density (filling) n per site is tunable by varying the confinement or the total number of atoms.
Figure 5. The Hubbard parameters t and U and their ratio, shown as a function of the dimensionless lattice depth for 87Rb in a 812 nm optical lattice. t and t/U decay approximately exponentially for deep lattices. Reproduced with permission from [36].
Download figure:
Standard image High-resolution imageIn a similar way, the bosonic version of the Hubbard model can be derived for ultracold gases [4], written here in a spinless form:
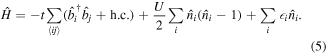
It has been previously introduced as a model for granular superconductors and 4He in porous media [47].
Even though corrections to the single-band Hubbard models (1) and (5) within the lowest band are usually small for sufficiently deep lattices with 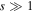 , nevertheless the increasing precision of experiments and the development of new probing techniques have allowed to observe effects beyond the standard single-band (Bose-) Hubbard model. In particular, a density dependence of the interaction parameter U has been measured by quantum phase revival spectroscopy for 87Rb [48] and in the excitation spectrum of a 133Cs MI [49]. This correction, and others such as density-dependent hopping, pair tunneling and next-neighbor interactions, have been found to arise in an effective dressed single-band representation, when contributions of higher bands are properly taken into account [36, 50, 51]. These additional interaction terms become significant for strong contact interactions, for example close to Feshbach resonances, where the scattering length as becomes comparable to the lattice constant, and are expected to lead to novel phases. Note that a simple renormalization of single-particle Wannier orbitals is not sufficient to describe these multibody effects, but instead higher-order correlations are essential [36, 51].
, nevertheless the increasing precision of experiments and the development of new probing techniques have allowed to observe effects beyond the standard single-band (Bose-) Hubbard model. In particular, a density dependence of the interaction parameter U has been measured by quantum phase revival spectroscopy for 87Rb [48] and in the excitation spectrum of a 133Cs MI [49]. This correction, and others such as density-dependent hopping, pair tunneling and next-neighbor interactions, have been found to arise in an effective dressed single-band representation, when contributions of higher bands are properly taken into account [36, 50, 51]. These additional interaction terms become significant for strong contact interactions, for example close to Feshbach resonances, where the scattering length as becomes comparable to the lattice constant, and are expected to lead to novel phases. Note that a simple renormalization of single-particle Wannier orbitals is not sufficient to describe these multibody effects, but instead higher-order correlations are essential [36, 51].
Naturally, it is also possible to realize and simulate true multi-orbital physics in optical lattices, by populating higher bands in a controlled fashion, see for example [52, 53].
2.4. Measurement
Detection of many-body states and measurement of their physical characteristics (for example the particle- or spin-density, excitation spectra, collective modes and transport) is an essential element of a quantum simulator. Experimental techniques naturally depend strongly on the 'hardware' used, which on the one hand could be a solid-state electronic crystal and on the other hand a cloud of neutral ultracold atoms in a crystal of light. While for example transport measurements of the conductance are highly convenient and common in solid-state systems, in ultracold gases they are significantly more involved, although possible [54], due to their mesoscopic and confined geometry. On the other hand, for spectroscopic measurements there exist close analogies between electronic and ultracold quantum matter. Here we give a brief overview of the most common probing techniques in ultracold atomic systems.
Time-of-flight (TOF) spectroscopy is widely applied in cold atom experiments to determine momentum distributions and to explore long-range order. An ultracold atomic gas is released from the trapping potential to expand ballistically for a time large enough that the initial size of the cloud can be neglected. Light-absorbtion imaging is then used to measure the column densities  of the expanding cloud at time t, which in principle allows to reconstruct the full 3d density distribution after TOF. If interactions can be neglected during the expansion, its average is related to the in-trap momentum distribution as
of the expanding cloud at time t, which in principle allows to reconstruct the full 3d density distribution after TOF. If interactions can be neglected during the expansion, its average is related to the in-trap momentum distribution as  where
where 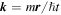 [1]. While a fast, quasi-instantaneous ramp-down of the optical lattice gives access to the full momentum distribution of the initial many-body state, alternatively a slower ramp-down ('band mapping'), which is adiabatic with respect to the band gap, can be applied to measure the Bloch quasimomentum distribution and Fermi surfaces in TOF [55]. A single-shot TOF image, resulting from the projection by quantum measurement, does in general not yield the quantum-statistical expectation value of the density distribution. Every pixel of an image measures the integrated atom density in a column along the direction of the probe light. Since the number of atoms in this column is not macroscopic, it has been shown that one can use spatial noise correlation functions, in analogy to Hanbury-Brown and Twiss interferometry [56]
[1]. While a fast, quasi-instantaneous ramp-down of the optical lattice gives access to the full momentum distribution of the initial many-body state, alternatively a slower ramp-down ('band mapping'), which is adiabatic with respect to the band gap, can be applied to measure the Bloch quasimomentum distribution and Fermi surfaces in TOF [55]. A single-shot TOF image, resulting from the projection by quantum measurement, does in general not yield the quantum-statistical expectation value of the density distribution. Every pixel of an image measures the integrated atom density in a column along the direction of the probe light. Since the number of atoms in this column is not macroscopic, it has been shown that one can use spatial noise correlation functions, in analogy to Hanbury-Brown and Twiss interferometry [56]

to detect MI states, magnetic long-range order and Fermi-superfluid (SF) pairing correlations in the many-body system. Noise correlations have been measured for bosonic and fermionic insulators in cubic lattices, where characteristic bunching and antibunching of particles was observed in TOF [57, 58]. Moreover, pair-correlated fermions in different spin states have been observed [59] and long-range antiferromagnetic (AF) order in a 1d quantum spin chain has been detected [60] by noise correlations.
Radio-frequency (RF) spectroscopy is a powerful tool for studying interaction effects [61, 62]. For a recent review on its theoretical description see [63]. Initially in state 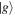 , the atoms are excited to state
, the atoms are excited to state  by the applied RF field, the wavelength of which is typically much larger than the size of the cloud, so that the corresponding momentum of the RF photon can be neglected compared to other momentum scales, such as the Fermi momentum. The number of atoms in the excited state
by the applied RF field, the wavelength of which is typically much larger than the size of the cloud, so that the corresponding momentum of the RF photon can be neglected compared to other momentum scales, such as the Fermi momentum. The number of atoms in the excited state  is then measured. One can in this way directly extract the mean-field shift of the transition due to interactions [61]. RF spectroscopy has also revealed s-wave pairing of spinful fermions due to an attractive interaction, with the emergence of a double-peak structure [64] as a response of paired fermions in the center of the harmonic trap and unpaired ones at the edges, consistent with theory [65]. The threshold energy
is then measured. One can in this way directly extract the mean-field shift of the transition due to interactions [61]. RF spectroscopy has also revealed s-wave pairing of spinful fermions due to an attractive interaction, with the emergence of a double-peak structure [64] as a response of paired fermions in the center of the harmonic trap and unpaired ones at the edges, consistent with theory [65]. The threshold energy  of the RF line shape, which can be used to determine the SF gap Δ, has been observed directly [66], in analogy with tunneling experiments in superconductors. Besides this 'plain' RF spectroscopy, a momentum-resolved version has been implemented [67], giving direct access to the fermionic spectral function
of the RF line shape, which can be used to determine the SF gap Δ, has been observed directly [66], in analogy with tunneling experiments in superconductors. Besides this 'plain' RF spectroscopy, a momentum-resolved version has been implemented [67], giving direct access to the fermionic spectral function  , where
, where 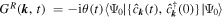 , which measures the weight of single-particle excitations of the many-body system at frequency ω and momentum
, which measures the weight of single-particle excitations of the many-body system at frequency ω and momentum  . It thus serves as a counterpart of angle-resolved photoemission spectroscopy (ARPES), which is for example applied in studies of high-
. It thus serves as a counterpart of angle-resolved photoemission spectroscopy (ARPES), which is for example applied in studies of high- superconductors [68].
superconductors [68].
A further powerful probe is Bragg spectroscopy, where two laser beams  with momenta
with momenta  and energies
and energies  cross each other at an angle, inducing a two-photon process where atoms absorb a photon from one laser and emit into the other. The atoms remain in the same internal state, but obtain a momentum and energy 'kick'. The initial and final motional states are resonantly coupled with momentum difference
cross each other at an angle, inducing a two-photon process where atoms absorb a photon from one laser and emit into the other. The atoms remain in the same internal state, but obtain a momentum and energy 'kick'. The initial and final motional states are resonantly coupled with momentum difference  , where
, where  , and energy difference
, and energy difference  . Bragg spectroscopy probes density-density correlations and, within linear response, yields the dynamical structure factor
. Bragg spectroscopy probes density-density correlations and, within linear response, yields the dynamical structure factor
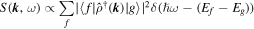
written here for T = 0, where  is the Fourier transform of the density, and
is the Fourier transform of the density, and  denote the initial (final) state of the many-body system. Bragg spectroscopy can be applied to detect the single-particle and the collective mode spectrum [63]. It has been used to characterize the structure factor and excitation spectrum of weakly and strongly interacting BECs [69–71], as well as the dynamical density- and spin-density-response of a strongly interacting Fermi gas [72, 73]. Moreover, the fully momentum-resolved excitation spectrum of a weakly interacting BEC in a cubic optical lattice has been measured [74]. By further going to the strongly correlated regime and beyond linear response, and comparing to large-scale dynamical Gutzwiller simulations, the Higgs-amplitude mode of strongly interacting bosons in a cubic lattice has been observed with Bragg spectroscopy [75].
denote the initial (final) state of the many-body system. Bragg spectroscopy can be applied to detect the single-particle and the collective mode spectrum [63]. It has been used to characterize the structure factor and excitation spectrum of weakly and strongly interacting BECs [69–71], as well as the dynamical density- and spin-density-response of a strongly interacting Fermi gas [72, 73]. Moreover, the fully momentum-resolved excitation spectrum of a weakly interacting BEC in a cubic optical lattice has been measured [74]. By further going to the strongly correlated regime and beyond linear response, and comparing to large-scale dynamical Gutzwiller simulations, the Higgs-amplitude mode of strongly interacting bosons in a cubic lattice has been observed with Bragg spectroscopy [75].
A closely related technique is lattice amplitude modulation spectroscopy [63, 76], where essentially the Bragg beams coincide with lattice beams. The optical lattice amplitude, for example in x-direction, is modulated with frequency 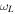 , which corresponds to adding a term
, which corresponds to adding a term  to the Hamiltonian. As a result, both the kinetic and interaction energy terms in the Hubbard models (1) and (5) are perturbed by a sinusoidal modulation. This technique was first developed to study the SF-MI transition and the excitations of bosonic lattice gases [77–79], where the broadening of the
to the Hamiltonian. As a result, both the kinetic and interaction energy terms in the Hubbard models (1) and (5) are perturbed by a sinusoidal modulation. This technique was first developed to study the SF-MI transition and the excitations of bosonic lattice gases [77–79], where the broadening of the  interference peak in TOF images is a measure of energy absorption. Because of Pauli's principle, this effect is less visible for a fermionic system, where energy absorption will only smear the step at the Fermi edge in TOF images. Therefore, it was proposed to measure instead the rate of doublon creation induced by the modulation [80]. This approach was adopted to identify the MI phase of fermions in a three-dimensional optical lattice [81], and to study nearest-neighbor correlations [82]. It has been combined with band mapping to perform multiband-spectroscopy of the full band structure of ultracold fermions in optical lattices, and to detect hopping renormalization effects due to interaction with an additional bosonic species [83].
interference peak in TOF images is a measure of energy absorption. Because of Pauli's principle, this effect is less visible for a fermionic system, where energy absorption will only smear the step at the Fermi edge in TOF images. Therefore, it was proposed to measure instead the rate of doublon creation induced by the modulation [80]. This approach was adopted to identify the MI phase of fermions in a three-dimensional optical lattice [81], and to study nearest-neighbor correlations [82]. It has been combined with band mapping to perform multiband-spectroscopy of the full band structure of ultracold fermions in optical lattices, and to detect hopping renormalization effects due to interaction with an additional bosonic species [83].
2.5. Preparation and cooling
For an excellent review on cooling and thermometry techniques in optical lattices, we refer to [84]. The standard approach towards strongly correlated many-body states in optical lattices is laser cooling, followed by evaporative cooling of the gas in a harmonic trap, and subsequent slow (ideally adiabatic) ramp-up of the lattice. For fermions, the latter leads to an adiabatic cooling effect even in the noninteracting case due to flattening of the dispersion [22], it does however by definition not reduce the entropy, which in these quasi-isolated ultracold quantum systems is the key quantity characterizing strongly correlated many-body states, for example of quantum magnetic or d-wave SF type. Interaction effects in spinful gases can enhance adiabatic cooling due to the Pomeranchuk effect [85–88], similar as in 3He. For an in-depth discussion of many-body cooling techniques in ultracold atoms and strongly correlated electron systems, see [89].
While harmonically trapped, noninteracting Fermi gases have been cooled down to 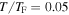 , with TF the Fermi temperature [90], for strongly interacting fermions in a 2d optical lattice
, with TF the Fermi temperature [90], for strongly interacting fermions in a 2d optical lattice  has recently been measured [23]. Stabilizing phases with quantum magnetic order in optical lattices for large systems requires low entropies per particle, for example
has recently been measured [23]. Stabilizing phases with quantum magnetic order in optical lattices for large systems requires low entropies per particle, for example  in the case of quantum antiferromagnetism in the isotropic 3d FH model. Up to now, this regime has not been accessed, with measured values roughly a factor of two higher [91, 92]. Note, however, the recent breakthrough in observing long-range AF correlations of fermions extending through a 2d lattice of about 80 sites [23].
in the case of quantum antiferromagnetism in the isotropic 3d FH model. Up to now, this regime has not been accessed, with measured values roughly a factor of two higher [91, 92]. Note, however, the recent breakthrough in observing long-range AF correlations of fermions extending through a 2d lattice of about 80 sites [23].
A major obstacle in the approach towards low-entropy many-body states in optical lattices is light-induced heating [84], arising both due to atomic recoil from spontaneous emission, and due to parametric heating from intensity- or phase noise of the lattice lasers. Moreover, non-adiabatic many-body dynamics occurs during any loading and ramp-up of the optical lattice in finite time, which can for example lead to a dynamical arrest of interacting fermions [93]. Advanced entropy redistribution schemes in optical lattices similar to the one proposed in [94] may in the future overcome these problems.
3. Mott transition
One prime example for the success of quantum simulations with ultracold atoms has been the controlled realization of pure MI transitions, both bosonic and fermionic, between a delocalized phase (Fermi liquid or SF) and a localized MI state. They are based on a competition between the kinetic energy gain due to delocalization, which is of order of the noninteracting bandwidth 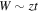 (where z is the lattice coordination number), and the local on-site Hubbard repulsion U.
(where z is the lattice coordination number), and the local on-site Hubbard repulsion U.
Originally predicted for transition metal oxides with partially filled d-shells by Peierls and Mott [95, 96], electronic MI have been the subject of intense research; for a review see [15]. They are of fundamental relevance for the physics of strongly correlated electronic systems, including transition metals, transition metal oxides, rare earth and actinide compounds, and organic conductors. For recent experimental studies on critical properties of the Mott transition in a 3d material (V2O3) and the role of lattice degrees of freedom in the transition in a quasi-2d layered organic conductor (BEDT-TTF) see [97, 98]. The effect of the lattice on the critical behavior at the Mott transition in correlated electron materials is not yet fully clarified. Moreover, doped MI are the starting point for understanding high-temperature superconductivity and the pseudogap phase in the cuprates [2, 3].
Ultracold fermions in optical lattices, on the other hand, allow a controlled and defect-free realization of the Mott transition with clear separation of fermionic and lattice degrees of freedom, and with higher tunability than the above mentioned solid-state materials. In particular, they also allow realizing the limit of a noninteracting Fermi gas in a lattice, where the completely filled Brillouin zone of a band insulator can be directly mapped out [55].
Theoretical understanding of the Mott transition has been advanced in a major way due to progress of several numerical techniques, including DMRG [19], QMC approaches [99], and in higher spatial dimensions the development of dynamical mean-field theory (DMFT) [100] and its generalization to systems with arbitrary inhomogeneity [101]. Within DMFT, the physics on lattice site i of a Fermi–Hubbard model is described by an effective local action

with the dynamical Weiss mean-field 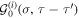 simulating the effect of all other lattice sites. This is equivalent to an effective (Anderson-type) quantum impurity model. DMFT captures the local equilibrium quantum dynamics of the lattice model in a non-perturbative way. The Weiss field is determined self-consistently from the local Dyson equation
simulating the effect of all other lattice sites. This is equivalent to an effective (Anderson-type) quantum impurity model. DMFT captures the local equilibrium quantum dynamics of the lattice model in a non-perturbative way. The Weiss field is determined self-consistently from the local Dyson equation  , in combination with the lattice Dyson equation
, in combination with the lattice Dyson equation  where the boldface notation indicates a matrix labeled by two lattice site indices. The above set of equations is closed by identifying the interacting local (impurity) Green's function with the diagonal elements of the full lattice Green's function:
where the boldface notation indicates a matrix labeled by two lattice site indices. The above set of equations is closed by identifying the interacting local (impurity) Green's function with the diagonal elements of the full lattice Green's function: 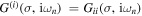 . Solving the local action (6) for the self-energy
. Solving the local action (6) for the self-energy  is computationally demanding and requires advanced quantum impurity solvers, such as the numerical renormalization group, exact diagonalization, or continuous-time QMC [100, 102]. Real-space DMFT [101] allows simulations of trapped, inhomogeneous fermionic gases in an optical lattice for experimentally realistic system sizes [103], which are not accessible by QMC calculations in the presence of a sign problem [10]. DMFT has provided a consistent picture of the Mott metal-insulator transition, with a phase diagram shown in figure 6, and has explained the emergence of a narrow quasiparticle peak in the spectrum on the metallic side [104]. Note that on bipartite lattices, perfect nesting of the Fermi surface at half filling strongly favors an AF instability, which on the square and cubic lattices at T = 0 occurs for any value of the Hubbard interaction. The resulting Néel phase masks the paramagnetic Mott transition and renders only a crossover at higher temperatures visible. Lattice frustration, for example on a triangular lattice, or due to longer-range hopping, can reduce the extent of the magnetic phase and partially recover the Mott transition, as shown schematically in figure 6.
is computationally demanding and requires advanced quantum impurity solvers, such as the numerical renormalization group, exact diagonalization, or continuous-time QMC [100, 102]. Real-space DMFT [101] allows simulations of trapped, inhomogeneous fermionic gases in an optical lattice for experimentally realistic system sizes [103], which are not accessible by QMC calculations in the presence of a sign problem [10]. DMFT has provided a consistent picture of the Mott metal-insulator transition, with a phase diagram shown in figure 6, and has explained the emergence of a narrow quasiparticle peak in the spectrum on the metallic side [104]. Note that on bipartite lattices, perfect nesting of the Fermi surface at half filling strongly favors an AF instability, which on the square and cubic lattices at T = 0 occurs for any value of the Hubbard interaction. The resulting Néel phase masks the paramagnetic Mott transition and renders only a crossover at higher temperatures visible. Lattice frustration, for example on a triangular lattice, or due to longer-range hopping, can reduce the extent of the magnetic phase and partially recover the Mott transition, as shown schematically in figure 6.
Figure 6. Schematic phase diagram of the homogeneous Fermi–Hubbard model (1) at half filling on a generic 3d lattice with bandwidth W, as obtained within DMFT. At low temperatures the system has long-range order (indicated in red), for example antiferromagnetism, which depends on the lattice structure. The orange region denotes coexisting metallic and Mott-insulating phases, with a first-order transition occurring at the dashed line, which ends in a second-order critical point, above which the Mott metal-insulator transition becomes a crossover. Reproduced with permission from [104]. © 2004 American Institute of Physics.
Download figure:
Standard image High-resolution imageIn the late 1980's it was realized that also interacting lattice bosons can undergo a Mott transition at commensurate filling, in this case into a SF, which in 3d can be described with good accuracy already on the level of a static mean-field theory [47]. In the limit of strong coupling, and at integer filling n per site, the MI many-body wavefunction is a product of local Fock states  , while in the noninteracting limit and for arbitrary n the condensate factorizes into a product of local coherent states:
, while in the noninteracting limit and for arbitrary n the condensate factorizes into a product of local coherent states: 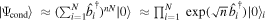 . In the visionary work [4] it was proposed to realize the SF-MI quantum phase transition with ultracold bosons in an optical lattice, which was observed for the first time in the pioneering experiment [105], where by loading 87Rb into a cubic optical lattice of variable depth, and by measuring the quasimomentum distribution as well as the excitation spectrum, the transition was clearly and reversibly identified at an interaction strength in good agreement with the mean-field prediction
. In the visionary work [4] it was proposed to realize the SF-MI quantum phase transition with ultracold bosons in an optical lattice, which was observed for the first time in the pioneering experiment [105], where by loading 87Rb into a cubic optical lattice of variable depth, and by measuring the quasimomentum distribution as well as the excitation spectrum, the transition was clearly and reversibly identified at an interaction strength in good agreement with the mean-field prediction  , where
, where  is the lattice coordination number. Later studies have established short-range phase coherence in the MI due to particle-hole excitations in accordance with theory [106], and determined the excitation spectrum with higher precision by lattice amplitude modulation [77]. A measurement of the finite-temperature phase diagram and comparison to ab-initio QMC calculations of the TOF momentum distribution was performed in [107], allowing thermometry in the presence of the lattice, and constituting a direct validation of this quantum simulator for the Bose–Hubbard model (5). The recent development of in situ imaging techniques with single-site resolution allows resolving SF and MI domain structures, measuring local particle number statistics, and extracting temperature and entropy by direct comparison to theory, which has taken the quantum simulator concept and its validation to a new level [37, 38].
is the lattice coordination number. Later studies have established short-range phase coherence in the MI due to particle-hole excitations in accordance with theory [106], and determined the excitation spectrum with higher precision by lattice amplitude modulation [77]. A measurement of the finite-temperature phase diagram and comparison to ab-initio QMC calculations of the TOF momentum distribution was performed in [107], allowing thermometry in the presence of the lattice, and constituting a direct validation of this quantum simulator for the Bose–Hubbard model (5). The recent development of in situ imaging techniques with single-site resolution allows resolving SF and MI domain structures, measuring local particle number statistics, and extracting temperature and entropy by direct comparison to theory, which has taken the quantum simulator concept and its validation to a new level [37, 38].
These experimental advances have been accompanied by theoretical progress in numerical simulations of bosonic lattice models. A bosonic version of DMFT has been developed and applied to Bose–Hubbard type models [108, 109], providing a refined picture of the Mott transition in 2d and 3d, which captures short-range coherence in the MI due to particle-hole excitations, as well as quantum magnetism in multicomponent systems. On the other hand, large-scale, quasi-exact QMC simulations of interacting bosonic models have become possible by the worm algorithm [110, 111]. DMRG allows numerically exact calculations of equilibrium properties and short-time dynamics in one spatial dimension, and can be extended to 2d as well [19].
The Mott transition of ultracold fermions has been first observed in two parallel and complementary measurements [81, 112]. While [81] focused on local signatures of the transition, measuring the double occupancy and the particle-hole excitation spectrum by lattice amplitude modulation, [112] observed the size and global compressibility of the fermionic cloud as a function of the harmonic confinement strength, and established by comparison to DMFT calculations the existence of an incompressible Mott core. Note that the crossover from metallic to MI regimes was later also observed in artificial graphene [32].
Quantum gas microscopy with single-site resolution has recently also allowed direct imaging of the fermionic MI (see figure 4), as well as determining the local particle number and variance, and the entropy per site in the paramagnetic state  in accord with theory [43]. AF correlations have also been observed, which will be discussed in section 4.
in accord with theory [43]. AF correlations have also been observed, which will be discussed in section 4.
Ultracold gases, in particular alkaline-earth-like elements, furthermore offer the possibility to study fermionic and MI physics for higher spins  , or more generally a larger number N of internal degrees of freedom, realizing higher symmetry groups such as SU(N). An SU(6) MI has been prepared in the experiment [88], where an increased adiabatic Pomeranchuk cooling effect was observed, consistent with the higher residual spin entropy per site
, or more generally a larger number N of internal degrees of freedom, realizing higher symmetry groups such as SU(N). An SU(6) MI has been prepared in the experiment [88], where an increased adiabatic Pomeranchuk cooling effect was observed, consistent with the higher residual spin entropy per site  of the MI, and in agreement with theoretical predictions based for example on high-temperature expansions [113].
of the MI, and in agreement with theoretical predictions based for example on high-temperature expansions [113].
4. Quantum magnetism
While in the paramagnetic MI particle number fluctuations are strongly suppressed, spin fluctuations are still possible, as indicated by the macroscopic residual entropy  for unit filling and spin-1/2, with the total particle number N, in the limit of vanishing hopping
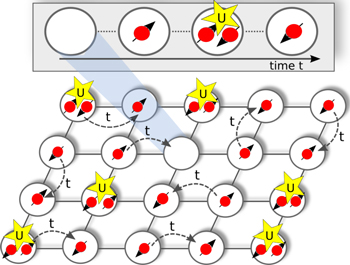
for unit filling and spin-1/2, with the total particle number N, in the limit of vanishing hopping 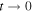 . However, virtual hopping processes lead to magnetic (super-) exchange couplings, see figure 7, which at low temperatures can remove the macroscopic degeneracy and induce long-range magnetic order, unless they are frustrated by the lattice geometry. Although quantum magnetism in solids has been investigated for a long time, important open questions remain, for example regarding the existence and characteristic properties of quantum spin liquids in frustrated geometries, where spins interact through competing exchange couplings [114]. QMC simulations of frustrated quantum spin models in any spatial dimension are problematic, even in equilibrium, due to the sign problem [10]. On the other hand, DMRG has provided a powerful approach to equilibrium properties of (frustrated) spin systems in 1d, and recently been extended to 2d systems of finite width [115]. Accurate simulations of the nonequilibrium dynamics of large interacting quantum spin systems are in general only possible by DMRG in one spatial dimension, where they are also limited to short simulation times due to an exponentially increasing truncation error [19].
. However, virtual hopping processes lead to magnetic (super-) exchange couplings, see figure 7, which at low temperatures can remove the macroscopic degeneracy and induce long-range magnetic order, unless they are frustrated by the lattice geometry. Although quantum magnetism in solids has been investigated for a long time, important open questions remain, for example regarding the existence and characteristic properties of quantum spin liquids in frustrated geometries, where spins interact through competing exchange couplings [114]. QMC simulations of frustrated quantum spin models in any spatial dimension are problematic, even in equilibrium, due to the sign problem [10]. On the other hand, DMRG has provided a powerful approach to equilibrium properties of (frustrated) spin systems in 1d, and recently been extended to 2d systems of finite width [115]. Accurate simulations of the nonequilibrium dynamics of large interacting quantum spin systems are in general only possible by DMRG in one spatial dimension, where they are also limited to short simulation times due to an exponentially increasing truncation error [19].
Figure 7. Superexchange couplings due to virtual second-order tunneling.
Download figure:
Standard image High-resolution imageCold atom quantum simulators can provide new insight into the physics of quantum spin systems, since exchange couplings and lattice geometry are highly tunable, from ferro- to antiferromagnetic, and from bipartite to frustrated. Moreover, spin–spin correlations and nonequilibrium spin dynamics can be measured in situ and in real-time [23, 26, 82, 116, 117]. In our discussion of ultracold quantum magnetism in this section we will roughly follow the historical timeline, first for theoretical predictions (derivation of superexchange, numerical simulations), then for the experimental implementations (superexchange couplings, cooling, correlations). We will discuss fermionic and bosonic systems in parallel, in order to highlight analogies.
It was proposed early that ultracold bosons and fermions with multiple hyperfine states in optical lattices can give rise to superexchange couplings and quantum magnetic order [22, 118]. While for fermions the superexchange is always AF, for bosons the sign is tunable. Consider for example a general single-band, two-component Hubbard Hamiltonian

with bosonic or fermionic statistics. As before,  denotes a spin index, labeling two hyperfine states or two different atomic species. For fermions the intra-species couplings
denotes a spin index, labeling two hyperfine states or two different atomic species. For fermions the intra-species couplings  are to be considered as infinite, which yields the standard spin-1/2 FH model. Deep in the MI, at a total filling of one particle per site (
are to be considered as infinite, which yields the standard spin-1/2 FH model. Deep in the MI, at a total filling of one particle per site ( ), and to leading order in
), and to leading order in 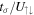 and
and  , this system can be described by the effective anisotropic Heisenberg XXZ spin Hamiltonian [118]
, this system can be described by the effective anisotropic Heisenberg XXZ spin Hamiltonian [118]

where 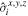 are Pauli matrices, and the sign ± applies to fermions and bosons, respectively. The longitudinal
are Pauli matrices, and the sign ± applies to fermions and bosons, respectively. The longitudinal

and transverse superexchange couplings

are tunable by the choice of the hopping amplitudes  , which can be achieved by spin-dependent optical lattices or by a mass imbalance of the two atomic species
, which can be achieved by spin-dependent optical lattices or by a mass imbalance of the two atomic species  [86]. Alternatively, the interactions
[86]. Alternatively, the interactions 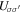 can be tuned via the s-wave scattering lengths
can be tuned via the s-wave scattering lengths 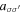 . For the case of an isotropic, spin-dependent cubic lattice loaded with spinful bosons, tuning the ratio
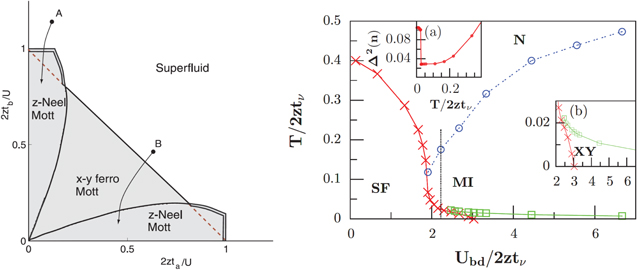
. For the case of an isotropic, spin-dependent cubic lattice loaded with spinful bosons, tuning the ratio  leads to a quantum phase transition between in-plane xy-ferromagnetism and a z-Néel antiferromagnet [119], shown in the left part of figure 8. Bosonic DMFT calculations performed at
leads to a quantum phase transition between in-plane xy-ferromagnetism and a z-Néel antiferromagnet [119], shown in the left part of figure 8. Bosonic DMFT calculations performed at  and in the full range from weak to strong coupling [87, 109] found in addition to the magnetic phases a bosonic analog of the Pomeranchuk effect [85], which implies that the system can be heated from the strongly correlated SF into the spin-disordered MI (see figure 8, right part). It has been proposed that the resulting squeezing of the local particle number fluctuations
and in the full range from weak to strong coupling [87, 109] found in addition to the magnetic phases a bosonic analog of the Pomeranchuk effect [85], which implies that the system can be heated from the strongly correlated SF into the spin-disordered MI (see figure 8, right part). It has been proposed that the resulting squeezing of the local particle number fluctuations 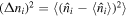 could be observed in situ by optical quantum gas microscopy as in [37, 38].
could be observed in situ by optical quantum gas microscopy as in [37, 38].
Figure 8. (left) Tunable magnetism in the ground state of two-component bosons in a cubic lattice. Reproduced from [119]. © 2003 IOP Publishing and Deutsche Physikalische Gesellschaft. Reproduced by permission of IOP Publishing. CC BY-NC-SA. (right) Finite-temperature phase diagram, including the bosonic Pomeranchuk effect indicated by the dashed line, which is also visible as a squeezing of the local particle number fluctuations shown in inset (a) with increasing temperature. Inset (b) is a zoom of the main figure around the critical point of magnetic order. Reprinted figure with permission from [87]. Copyright 2012 by the American Physical Society.
Download figure:
Standard image High-resolution imageFor ultracold fermions, on the other hand, the emergence of AF order at sufficiently low temperatures, as proposed in [22], was quantified for a 3d cubic lattice in [85], where a critical entropy per particle  was found by single-site DMFT calculations, which were however known to significantly overestimate the exact result. Later studies based on the dynamical cluster approximation and on diagrammatic Monte Carlo simulations provided a more realistic value of
was found by single-site DMFT calculations, which were however known to significantly overestimate the exact result. Later studies based on the dynamical cluster approximation and on diagrammatic Monte Carlo simulations provided a more realistic value of  for the homogeneous system [120], which is significantly lower than estimates of the entropy in recent 3d experiments, where
for the homogeneous system [120], which is significantly lower than estimates of the entropy in recent 3d experiments, where 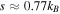 was found in the Mott core of [91], and almost the same value in [92]. Large-scale simulations based on real-space DMFT [101] have yielded magnetization and entropy distributions of spin-1/2 fermions in a cubic lattice, in the presence of a harmonic trap [103], shown in figure 9. They have also proved that emerging Néel order, or short-range AF correlations, are accompanied by an enhanced double occupancy
was found in the Mott core of [91], and almost the same value in [92]. Large-scale simulations based on real-space DMFT [101] have yielded magnetization and entropy distributions of spin-1/2 fermions in a cubic lattice, in the presence of a harmonic trap [103], shown in figure 9. They have also proved that emerging Néel order, or short-range AF correlations, are accompanied by an enhanced double occupancy  at intermediate to strong correlation strength, which provides a characteristic signature for detecting AF order.
at intermediate to strong correlation strength, which provides a characteristic signature for detecting AF order.
Figure 9. Real-space DMFT results for AF order (1st row), double occupancy D (2nd row), particle (3rd row) and entropy (4th row) densities per site, in the central plane of the Fermi–Hubbard model (1) on a cubic lattice with  and a harmonic trapping potential
and a harmonic trapping potential  with
with  . At low temperature (left column) a large antiferromagnetic core is strongly magnetized, with increasing T the AF order decays. In the 2nd, 3rd and 4th row the top half displays the respective observables in the central plane of the lattice, and the bottom half the corresponding values after integration along the z-axis. Reprinted figure with permission from [103]. Copyright 2010 by the American Physical Society.
. At low temperature (left column) a large antiferromagnetic core is strongly magnetized, with increasing T the AF order decays. In the 2nd, 3rd and 4th row the top half displays the respective observables in the central plane of the lattice, and the bottom half the corresponding values after integration along the z-axis. Reprinted figure with permission from [103]. Copyright 2010 by the American Physical Society.
Download figure:
Standard image High-resolution imageIn multiflavor mixtures of more than two different hyperfine states of fermions with repulsive interactions in a lattice, as realized with alkaline-earth elements or 173Yb [88], higher symmetry groups (such as SU(N)) can be realized, and exotic magnetic states have been prediced, for example by DMFT studies of 3-color magnetism at unit filling [121, 122]. They should be observable below critical temperatures comparable to those of spin-1/2 antiferromagnetism and may in fact have a higher critical entropy.
It has also been pointed out that an anisotropy of the system, for example an easy-axis, can raise the critical entropy significantly [86]. For bosons on a 3d cubic lattice, QMC simulations have established a critical entropy  in the (easy-axis, Ising-type) z-Néel antiferromagnet, in contrast to the lower value
in the (easy-axis, Ising-type) z-Néel antiferromagnet, in contrast to the lower value  for the easy-plane xy-ferromagnetic state [123], due to additional fluctuations of the magnetization arising from a Goldstone mode in the latter case.
for the easy-plane xy-ferromagnetic state [123], due to additional fluctuations of the magnetization arising from a Goldstone mode in the latter case.
Superexchange couplings arising from virtual hopping, illustrated in figure 7, have first been clearly observed in the experiment [124] by measurement of the coherent spin dynamics of 87Rb with two hyperfine states in a superlattice, where both sign and magnitude of the superexchange coupling can be changed by tuning the potential bias between the sublattices. Extended tunability of both Jz and 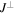 in the effective XXZ spin model (8) by additional periodic driving of the superlattice has been demonstrated in [125].
in the effective XXZ spin model (8) by additional periodic driving of the superlattice has been demonstrated in [125].
Spin–spin-correlations between neighboring sites have initially been measured by superlattice techniques [126] and by lattice amplitude modulation [127]. In this way it has been possible to detect short-range AF correlations for fermions in dimerized and anisotropic simple cubic lattices [116], where in the MI domain entropies per particle of  have been found, which is clearly below the values for isotropic cubic lattices. These techniques have more generally allowed systematic studies of the dependence of spin correlations on the lattice geometry, and of their dynamics after sudden changes of the geometry [26].
have been found, which is clearly below the values for isotropic cubic lattices. These techniques have more generally allowed systematic studies of the dependence of spin correlations on the lattice geometry, and of their dynamics after sudden changes of the geometry [26].
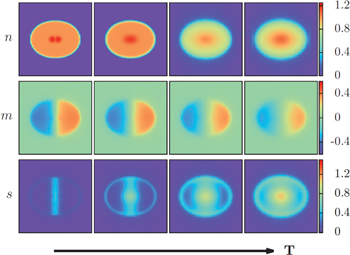
While cooling and thermometry in the presence of a lattice is a major challenge up to the present day [84], as discussed in section 2.5, significant progress has been made during the last years. The width of a transition layer between two spin domains of 87Rb in a trap, separated by a magnetic field gradient, has allowed the measurement of temperatures in the optical lattice [128]. By adiabatically reducing the gradient, it was possible to cool the system in the presence of the optical lattice down to 350 pK, with equilibration between spin and motional degrees of freedom [129]. These measurements have been quantitatively validated by real-space bosonic DMFT simulations, see the results in figure 10, taking into account the experimental geometry [87]. While magnetic order had not been achieved in the experiment [129], where temperatures were within a factor of two of the theoretically expected ordering temperature [123], the simulations of [87] showed that the adiabatic demagnetization process, which reduces the local entropy per particle in the spin-mixed regions, can drive the system into the long-range magnetically ordered phase. For a detailed discussion of magnetic cooling techniques in ultracold gases and in solid-state quantum magnets see [89].
Figure 10. Real-space distribution of the local particle density, magnetization and entropy of 2-component bosons (7) in the xy-plane of a 3d cubic optical lattice, calculated by bosonic DMFT+LDA. From left to right, temperatures are  and 0.095, respectively, with interactions
and 0.095, respectively, with interactions  and hopping amplitudes
and hopping amplitudes  , and a total number of 17 000 bosons in a harmonic trap and a magnetic field gradient. Reprinted figure with permission from [87]. Copyright 2012 by the American Physical Society.
, and a total number of 17 000 bosons in a harmonic trap and a magnetic field gradient. Reprinted figure with permission from [87]. Copyright 2012 by the American Physical Society.
Download figure:
Standard image High-resolution imageAF correlations of ultracold fermionic 6Li in a cubic optical lattice have been detected by spin-sensitive Bragg scattering, which—in analogy to the scattering of neutrons from solid-state electronic materials—measures the spin structure factor

that shows coherent enhancement in the direction  , corresponding to staggered (Néel-type) spin–spin correlations [92]. Temperatures in this experiment were estimated as 1.4 times the Néel temperature of long-range AF order, by comparison to theoretical predictions (QMC, high-temperature series) for
, corresponding to staggered (Néel-type) spin–spin correlations [92]. Temperatures in this experiment were estimated as 1.4 times the Néel temperature of long-range AF order, by comparison to theoretical predictions (QMC, high-temperature series) for  . As emphasized in [92], for the temperatures in this experiment, state-of-the-art numerical simulation techniques for the Fermi–Hubbard model approach their limit of reliability, motivating the use of an analog quantum simulator based on ultracold fermions.
. As emphasized in [92], for the temperatures in this experiment, state-of-the-art numerical simulation techniques for the Fermi–Hubbard model approach their limit of reliability, motivating the use of an analog quantum simulator based on ultracold fermions.
Very recently, AF correlations have also been measured in situ by optical quantum gas microscopy. In one-dimensional fermionic spin-1/2 Hubbard chains realized with 6Li, staggered spin correlations were observed by spin-dependent splitting in a superlattice potential [117]. Moreover, for two hyperfine states of 6Li in a 2d optical lattice, the spin–spin correlator  has been determined by in situ measurements of the particle density, in combination with selective removal of one spin state [23]. At the lowest temperatures
has been determined by in situ measurements of the particle density, in combination with selective removal of one spin state [23]. At the lowest temperatures 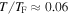 with
with 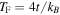 in a square lattice at half filling, long-range AF correlations extending through the entire system, up to a distance of 10 lattice sites, were observed (see figure 11), with a temperature-dependent correlation length in quantitative agreement with theory. These long-range correlations are also visible in the spin structure factor
in a square lattice at half filling, long-range AF correlations extending through the entire system, up to a distance of 10 lattice sites, were observed (see figure 11), with a temperature-dependent correlation length in quantitative agreement with theory. These long-range correlations are also visible in the spin structure factor  . They have been shown to be stable at significant hole doping of the system. Further recent in situ studies of the ultracold Fermi–Hubbard model have included the effect of spin imbalance, i.e. a finite spin polarization of the system, and observed canted antiferromagnetism [24], which would be hard to access in cuprate materials due to the very large magnetic fields required. Moreover, at finite doping these measurements were in agreement with the non-monotonic doping dependence of the magnetic susceptibility in the cuprates, while matching numerical calculations were at the limit of current state-of-the-art numerical simulation techniques. A better understanding of the magnetic response in the normal state of the Fermi–Hubbard model, which is crucial for describing the pseudogap phase of the cuprates, and thus for clarifying the mechanism of high-temperature superconductivity [2, 3], can therefore be achieved by ultracold quantum simulations in optical lattices. More recently also the attractive
. They have been shown to be stable at significant hole doping of the system. Further recent in situ studies of the ultracold Fermi–Hubbard model have included the effect of spin imbalance, i.e. a finite spin polarization of the system, and observed canted antiferromagnetism [24], which would be hard to access in cuprate materials due to the very large magnetic fields required. Moreover, at finite doping these measurements were in agreement with the non-monotonic doping dependence of the magnetic susceptibility in the cuprates, while matching numerical calculations were at the limit of current state-of-the-art numerical simulation techniques. A better understanding of the magnetic response in the normal state of the Fermi–Hubbard model, which is crucial for describing the pseudogap phase of the cuprates, and thus for clarifying the mechanism of high-temperature superconductivity [2, 3], can therefore be achieved by ultracold quantum simulations in optical lattices. More recently also the attractive  Fermi–Hubbard model has been studied with quantum gas microscopy, where charge-density-wave- and SF correlations have been measured close to half filling [25]. In the future, these studies could be extended to the Berezinskii–Kosterlitz–Thouless transition into SF long-range order at lower-temperatures [130], and to the Fulde–Ferrell–Larkin–Ovchinnikov SF state in the presence of spin imbalance [131–133]. These developments represent a breakthrough towards quantum simulations of magnetism and superconductivity of the Fermi–Hubbard model, as proposed in [22].
Fermi–Hubbard model has been studied with quantum gas microscopy, where charge-density-wave- and SF correlations have been measured close to half filling [25]. In the future, these studies could be extended to the Berezinskii–Kosterlitz–Thouless transition into SF long-range order at lower-temperatures [130], and to the Fulde–Ferrell–Larkin–Ovchinnikov SF state in the presence of spin imbalance [131–133]. These developments represent a breakthrough towards quantum simulations of magnetism and superconductivity of the Fermi–Hubbard model, as proposed in [22].
Figure 11. Long-range antiferromagnetic correlations observed in an ultracold Fermi–Hubbard system on a square lattice: (a) spin correlator  , (b) azimuthally averaged sign-corrected correlator
, (b) azimuthally averaged sign-corrected correlator 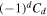 and (c) spin structure factor
and (c) spin structure factor 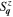 . Reprinted by permission from Macmillan Publishers Ltd: Nature [23], copyright 2017.
. Reprinted by permission from Macmillan Publishers Ltd: Nature [23], copyright 2017.
Download figure:
Standard image High-resolution imageFar-from-equilibrium magnetization dynamics has been measured as well. In one- and two-dimensional ferromagnetic Heisenberg quantum magnets, realized with two-component ultracold bosons in an optical lattice, the decay of initial spin spiral patterns, and diffusive (1d) versus superdiffusive (2d) spin transport has been observed by quantum gas microscopy [27]. Also the propagation of elementary spin excitations (magnons) and of bound states comprised of two magnons has been detected in this system [28]. Superexchange-mediated exponential decay of the magnetization for an initially prepared out-of-equilibrium AF state has been observed for a pseudospin-1/2 Bose–Hubbard model at unit filling in a 2d optical lattice [29].
Despite this impressive progress, experimental realization of long-range magnetic order induced by superexchange is still challenging due to the low entropies required. On the other hand, a quantum phase transition into an antiferromagnetically ordered state has been observed for an effective quantum Ising model [60], realized in a spinless Bose–Hubbard chain via a mapping of bosonic site-occupation to an Ising pseudospin, as proposed earlier [134]. The advantage of this approach is that the effective magnetic coupling is proportional to the hopping t, typically much larger than the superexchange scale 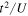 , and therefore leads to faster spin dynamics and a higher critical temperature for magnetic ordering. In this way, the one-dimensional quantum Ising model with a transverse magnetic field has been realized:
, and therefore leads to faster spin dynamics and a higher critical temperature for magnetic ordering. In this way, the one-dimensional quantum Ising model with a transverse magnetic field has been realized:
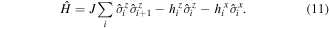
The spin-flip dynamics of the system is generated by the effective transverse magnetic field, given as 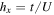 in terms of the underlying Bose–Hubbard model (5) [60]. The transition from a paramagnet to an antiferromagnet and the resulting formation of AF domains were detected by single-site resolved imaging, and via noise correlations in TOF images, following the proposal [56].
in terms of the underlying Bose–Hubbard model (5) [60]. The transition from a paramagnet to an antiferromagnet and the resulting formation of AF domains were detected by single-site resolved imaging, and via noise correlations in TOF images, following the proposal [56].
A highly promising new platform for simulating quantum spin systems is given by Rydberg-excited atoms in arrays of optical microtraps. These can be arranged in arbitrary geometries and loaded defect-free [135, 136]. They have already been used to probe the many-body dynamics of Ising-type quantum spin models with tunable interactions and system sizes of up to 51 qubits [30]. Alternatively, weak Rydberg-dressing of ground state atoms in optical lattices can be applied in order to design and investigate synthetic quantum spin lattices [137].
A further, very successful approach towards quantum simulations of magnetic long-range order is based on mapping the position-dependent phase  of a BEC onto a classical xy-spin vector
of a BEC onto a classical xy-spin vector ![${{\boldsymbol{S}}}_{i}=[\cos {\theta }_{i},\sin {\theta }_{i}]$](https://content.cld.iop.org/journals/0953-4075/51/8/082001/revision3/jpbaaa31bieqn122.gif) . It has been implemented for a triangular lattice with tunable spin-exchange couplings
. It has been implemented for a triangular lattice with tunable spin-exchange couplings  in [33]. Since in this case the exchange couplings are given by the bosonic hopping matrix elements, the associated critical temperatures for long-range order (condensate formation) are easier to access than for superexchange-induced magnetism. Both sign and magnitude of J and
in [33]. Since in this case the exchange couplings are given by the bosonic hopping matrix elements, the associated critical temperatures for long-range order (condensate formation) are easier to access than for superexchange-induced magnetism. Both sign and magnitude of J and  are independently tunable via elliptic lattice shaking, giving rise to a rich phase diagram with various magnetic phases, including ferromagnetic and spiral order, with phase transitions of first and second order [33]. Spontaneous symmetry breaking between two degenerate spiral configurations was clearly observed. In a later study, an additional Ising-type
are independently tunable via elliptic lattice shaking, giving rise to a rich phase diagram with various magnetic phases, including ferromagnetic and spiral order, with phase transitions of first and second order [33]. Spontaneous symmetry breaking between two degenerate spiral configurations was clearly observed. In a later study, an additional Ising-type  symmetry was implemented via staggered, synthetic gauge fluxes [35]. At low temperatures, the spontaneous breaking of this
symmetry was implemented via staggered, synthetic gauge fluxes [35]. At low temperatures, the spontaneous breaking of this  symmetry was observed, as well as a hysteresis-like behavior of the emerging Ising magnetization. While these impressive results arise 'only' from a classical spin Hamiltonian, they nevertheless represent successful quantum simulations of frustrated spin systems by ultracold atoms in optical lattices. Extending these studies towards low bosonic filling per site will give access to fully quantum spin models, with possible exotic spin-density wave [138] or spin-liquid ground states. The latter could be detected by measuring non-local correlation functions (for example string order, as in the spin-1 Haldane chain) with quantum gas microscopy, which has already been achieved for the string order parameter in a one-dimensional bosonic MI [139]. Note that other frustrated geometries, such as the Kagome lattice, have been realized as well [34].
symmetry was observed, as well as a hysteresis-like behavior of the emerging Ising magnetization. While these impressive results arise 'only' from a classical spin Hamiltonian, they nevertheless represent successful quantum simulations of frustrated spin systems by ultracold atoms in optical lattices. Extending these studies towards low bosonic filling per site will give access to fully quantum spin models, with possible exotic spin-density wave [138] or spin-liquid ground states. The latter could be detected by measuring non-local correlation functions (for example string order, as in the spin-1 Haldane chain) with quantum gas microscopy, which has already been achieved for the string order parameter in a one-dimensional bosonic MI [139]. Note that other frustrated geometries, such as the Kagome lattice, have been realized as well [34].
5. Disorder and localization
Disorder is of natural relevance in solids where defects are not only inevitably present but can also be introduced in a controlled way, for instance chemically during sample preparation. As a result, one observes intriguing phenomena such as localization or glassiness. Of particular interest is the interplay of disorder and interactions, which is of fundamental importance in systems as diverse as frustrated quantum magnets, or itinerant electronic systems with metal-insulator transitions due to competing interaction and disorder. Many aspects of these are not yet well understood. In this context, quantum simulations with ultracold gases offer the unique possibility to freely tune the type and strength of disorder, the strength of two-particle interactions, as well as the quantum statistics of the system. They have for the first time allowed direct imaging of an exponentially Anderson-localized wavefunction, which is impossible in a disordered metal or semiconductor. Since quantum gases in optical lattices are approximately closed quantum systems, they also give access to many-body quantum dynamics far out of equilibrium, and to probing the regime of many-body localization (MBL). In our discussion in the following we will focus on the most relevant case of quenched disorder, which is assumed to be 'frozen' on the timescale of the experiment, and on localization transitions induced by disorder and interactions.
Scattering from impurities and defects crucially affects the conducting properties of electronic materials. In two-dimensional noninteracting systems it leads to weak localization due to enhanced backscattering at any disorder strength [140, 141], while in 3d disorder can induce a metal-insulator transition due to Anderson localization of the electronic wavefunctions [142]. Here the character of the spectrum of energy eigenstates changes from continuous to a dense point spectrum. In an Anderson-localized state, a quantum particle returns with a finite probability to the position where it starts to propagate.
For noninteracting, disordered systems, a rather complete physical understanding has been obtained by powerful theoretical techniques such as the scaling theory of localization, the nonlinear σ-model and numerical simulations. For reviews see [140, 141]. The scaling theory of noninteracting localization argues that the logarithmic derivative of the dimensionless conductance  with respect to the linear system size L can be expressed as a function of
with respect to the linear system size L can be expressed as a function of  alone:
alone:

In one and two spatial dimensions one finds  always, which implies that at sufficiently large length scales only insulating behavior with localized single-particle wavefunctions can occur. In three spatial dimensions,
always, which implies that at sufficiently large length scales only insulating behavior with localized single-particle wavefunctions can occur. In three spatial dimensions,  at a critical, length-scale dependent conductance gc, which corresponds to a mobility edge between localized and extended states.
at a critical, length-scale dependent conductance gc, which corresponds to a mobility edge between localized and extended states.
Experimentally, noninteracting Anderson localization and its critical behavior have been observed in a driven quantum gas modeled by a quasiperiodic kicked rotor, where the resulting dynamical localization in momentum space is equivalent to Anderson localization in three spatial dimensions [143]. Direct imaging of localized bosonic matter-waves in a 1d disordered potential has also been achieved, both by expansion of a BEC in an optical Speckle potential [144] and by in situ imaging of localized states in a quasiperiodic, incommensurate lattice [145]. In this way, exponential Anderson localization of matter-waves  has been observed in real-space for the first time.
has been observed in real-space for the first time.
Three-dimensional fermionic Anderson localization and the emergence of a mobility edge have been observed in [146]. An exponentially localized component of the cloud with a lack of diffusion was detected, which could not be explained classically. The mobility edge Ec has been extracted from the localized fraction, and its dependence on the disorder strength Δ determined. The localization length  has been determined, and found to decrease as a function of disorder strength Δ as expected, while it increases with the temperature T.
has been determined, and found to decrease as a function of disorder strength Δ as expected, while it increases with the temperature T.
On the other hand, the regime of strong disorder combined with strong two-particle interactions still poses major open theoretical questions. It is believed that the interplay between disorder and interaction is at the core of the metal-insulator transition observed in 2d electron gases with disorder [147], which would be ruled out by the noninteracting scaling theory discussed above. A particular scenario that is amenable to quantum simulations in optical lattices, is the interplay between localization of bosons or fermions on a lattice due to strong, local repulsive interaction (the Mott transition) and Anderson localization due to disorder, which presents a major theoretical challenge due to the absence of (numerically) exact solutions, except in 1d. For a review see [148].
Significant theoretical progress on this topic has been achieved for fermions due to new developments in DMFT [100], in particular statistical DMFT [149] and typical medium theory (TMT) [150], which provide a nonperturbative approach to Mott-Anderson localization in strongly correlated Fermi systems that becomes exact in the limit of high lattice coordination number. Large-scale QMC simulations have given new insight into SF-insulator transitions for disordered and interacting bosons [111].
The disordered Bose–Hubbard model is given by (5), with onsite energies  sampled from a probability distribution
sampled from a probability distribution 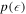 of width Δ, for example box disorder with
of width Δ, for example box disorder with  , or Speckle disorder with
, or Speckle disorder with 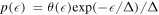 , where
, where  denotes the Heavyside function. It is a paradigmatic model for studying effects of randomness in strongly correlated bosonic systems [47], as they arise in superconducting thin films [151], for SF 4He immersed in random pores of Vycor [152] and in effective models of vortex pinning in type-II superconductors [153]. In addition to the MI, the SF and the normal phase at
denotes the Heavyside function. It is a paradigmatic model for studying effects of randomness in strongly correlated bosonic systems [47], as they arise in superconducting thin films [151], for SF 4He immersed in random pores of Vycor [152] and in effective models of vortex pinning in type-II superconductors [153]. In addition to the MI, the SF and the normal phase at  , a Bose glass (BG) phase has been predicted, which is compressible and insulating [47], and can be considered as the equivalent of the compressible Anderson insulating phase for fermions. The nature and extent of the BG has been subject to a theoretical debate, including the question whether a direct transition between MI and SF is possible for the disordered system. While DMRG studies have accurately addressed the 1d case [154], the situation in higher-dimensional lattices has been less clear. Since arithmetical averaging over disorder cannot describe the BG, a stochastic mean-field theory (SMFT) has been developed, which captures disorder-induced localization, includes non-trivial dimensional effects beyond simple mean-field scaling, is applicable in the thermodynamic limit and can efficiently include experimentally realistic Speckle disorder [155, 156]. It is based on a probabilistic description of the lattice system by a distribution function
, a Bose glass (BG) phase has been predicted, which is compressible and insulating [47], and can be considered as the equivalent of the compressible Anderson insulating phase for fermions. The nature and extent of the BG has been subject to a theoretical debate, including the question whether a direct transition between MI and SF is possible for the disordered system. While DMRG studies have accurately addressed the 1d case [154], the situation in higher-dimensional lattices has been less clear. Since arithmetical averaging over disorder cannot describe the BG, a stochastic mean-field theory (SMFT) has been developed, which captures disorder-induced localization, includes non-trivial dimensional effects beyond simple mean-field scaling, is applicable in the thermodynamic limit and can efficiently include experimentally realistic Speckle disorder [155, 156]. It is based on a probabilistic description of the lattice system by a distribution function 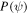 for the condensate order parameter ψ, which is determined self-consistently, as illustrated in figure 12. It allows a clear distinction of MI, SF and BG phases, based on the average condensate order parameter ψ and the compressibility
for the condensate order parameter ψ, which is determined self-consistently, as illustrated in figure 12. It allows a clear distinction of MI, SF and BG phases, based on the average condensate order parameter ψ and the compressibility  . While an analysis of the MI border based on purely onsite particle/hole excitations within SMFT predicts that a direct transition between MI and SF is possible [155], including collective excitations of the BG in the calculation of the ground state always leads to an intermediate BG phase between the MI and SF phases [156]. This has been predicted by a 'theorem of inclusions' and by QMC studies [157, 158], which also provided evidence that the transition MI-BG is of the Griffiths type.
. While an analysis of the MI border based on purely onsite particle/hole excitations within SMFT predicts that a direct transition between MI and SF is possible [155], including collective excitations of the BG in the calculation of the ground state always leads to an intermediate BG phase between the MI and SF phases [156]. This has been predicted by a 'theorem of inclusions' and by QMC studies [157, 158], which also provided evidence that the transition MI-BG is of the Griffiths type.
Figure 12. (left) Within SMFT, the lattice model is represented by an effective single-site problem, which is coupled to a bath of condensate mean-fields. Spatially random fluctuations are accounted for by a statistical distribution of the condensate order parameter ψ. Reprinted figure with permission from [155]. (right) Phase diagram of the Bose–Hubbard model for box disorder at filling n = 1 and  (hopping is denoted here as J). Note the re-entrant superfluidity indicated by the protruding Mott lobe, where increasing the disorder Δ can drive the system through a series of SF-insulator transitions. Reprinted figure with permission from [156]. Copyright 2010 by the American Physical Society.
(hopping is denoted here as J). Note the re-entrant superfluidity indicated by the protruding Mott lobe, where increasing the disorder Δ can drive the system through a series of SF-insulator transitions. Reprinted figure with permission from [156]. Copyright 2010 by the American Physical Society.
Download figure:
Standard image High-resolution imageDisorder-driven, re-entrant condensation and SF at strong interactions and constant filling has been observed both within SMFT for a lattice coordination number z = 6 [156], see figure 12, and within QMC simulations for a cubic lattice [158], although only at low temperatures, which are beyond the reach of experiments up to date [159].
In the experiment [160] an array of 1d Bose–Hubbard chains with an additional bichromatic (quasiperiodic) potential, mimicking disorder, has been realized and the excitation spectrum measured by Bragg spectroscopy. With increasing quasi-disorder, a crossover from MI to a state with vanishing long-range coherence and a flat, gapless density of excitations was found, which was interpreted as evidence for the formation of a BG phase.
An experimental realization of the 3d disordered Bose–Hubbard model with fine-grained Speckle disorder has been presented in [159, 161], where a strong reversible reduction of the condensate fraction indicates disorder-induced localization of an interacting BEC in the lattice. Additional mass transport measurements in [159] confirmed the localization scenario. The experimental data found no evidence for the disorder-induced re-entrant transition from MI to SF predicted by theory, most likely due to finite temperature effects. They were also not yet able to distinguish the MI and BG phases directly, which would require measurements of the excitation spectrum or the compressibility of the insulating state.
The combined effect of strong correlations and disorder has also been studied for fermions in the framework of the Anderson–Hubbard model, given by (1) with onsite energies  sampled from a probability distribution
sampled from a probability distribution  of width Δ. In particular, the interplay between Mott- and Anderson localization in the spin-1/2 Fermi–Hubbard model has been investigated by DMFT combined with TMT [162], where it was shown that the combined influence of interaction and disorder leads to delocalization and re-entrant metallic behaviour, see the phase diagram in figure 13. Within the TMT the typical value of the local density of states (LDOS)
of width Δ. In particular, the interplay between Mott- and Anderson localization in the spin-1/2 Fermi–Hubbard model has been investigated by DMFT combined with TMT [162], where it was shown that the combined influence of interaction and disorder leads to delocalization and re-entrant metallic behaviour, see the phase diagram in figure 13. Within the TMT the typical value of the local density of states (LDOS) 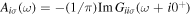 , well approximated by its geometric average
, well approximated by its geometric average ![${A}_{\sigma }{(\omega )}_{\mathrm{geom}}=\exp [\langle \mathrm{ln}{A}_{i\sigma }(\omega )\rangle ]$](https://content.cld.iop.org/journals/0953-4075/51/8/082001/revision3/jpbaaa31bieqn145.gif) , represents a mean-field for Anderson localization. It vanishes at the transition, in contrast to the arithmetically averaged or global density of states, which remains finite in the Anderson insulator. These studies were later extended to the full statistical DMFT, where a self-consistent distribution of the LDOS is determined [163], also taking into account experimentally realistic Speckle-type disorder [164]. AF correlations have also been included within DMFT+TMT [165], leading to the magnetic phase diagram in figure 14. In this case, the competition between disorder and strong correlations was found to stabilize a novel AF metallic phase for intermediate interaction strength.
, represents a mean-field for Anderson localization. It vanishes at the transition, in contrast to the arithmetically averaged or global density of states, which remains finite in the Anderson insulator. These studies were later extended to the full statistical DMFT, where a self-consistent distribution of the LDOS is determined [163], also taking into account experimentally realistic Speckle-type disorder [164]. AF correlations have also been included within DMFT+TMT [165], leading to the magnetic phase diagram in figure 14. In this case, the competition between disorder and strong correlations was found to stabilize a novel AF metallic phase for intermediate interaction strength.
Figure 13. Nonmagnetic ground state phase diagram of the disordered Fermi–Hubbard model at half filling, determined by DMFT+TMT. Reprinted figure with permission from [162]. Copyright 2005 by the American Physical Society.
Download figure:
Standard image High-resolution imageFigure 14. Magnetic ground state phase diagram of the disordered Fermi–Hubbard model at half filling, determined by DMFT+TMT. Reprinted figure with permission from [165]. Copyright 2009 by the American Physical Society.
Download figure:
Standard image High-resolution imageThe disordered Fermi–Hubbard model has been studied in a recent experiment with ultracold 40K in a cubic optical lattice with an additional Speckle potential [166]. Localization properties were measured by applying an impulse to the atomic cloud via a magnetic field gradient, and measuring the resulting center-of-mass velocity by TOF expansion. It was found that increasing disorder suppresses the resulting mass transport, which vanishes at a critical disorder strength 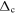 , corresponding to an Anderson metal-insulator transition. Remarkably, when in addition the Hubbard interaction U is increased, an interaction-driven delocalization transition is observed, see figure 15, thus qualitatively confirming the DMFT predictions of re-entrant metallic behavior [162–164]. No quantitative agreement was found, most likely due to the different lattice geometries investigated in experiment and theory. The additional prediction that increasing disorder can also drive delocalization, when applied to a strongly correlated MI state [162, 163] still needs to be verified experimentally, since probing transport properties in the Mott regime is more challenging. Also note that, strictly speaking, a true MI does not exist for unbounded Speckle disorder in the thermodynamic limit [164]. Remarkably, the experiment [166] observed that disorder-induced localization persists also at finite temperature, which could be an indication of MBL, which we discuss in the following.
, corresponding to an Anderson metal-insulator transition. Remarkably, when in addition the Hubbard interaction U is increased, an interaction-driven delocalization transition is observed, see figure 15, thus qualitatively confirming the DMFT predictions of re-entrant metallic behavior [162–164]. No quantitative agreement was found, most likely due to the different lattice geometries investigated in experiment and theory. The additional prediction that increasing disorder can also drive delocalization, when applied to a strongly correlated MI state [162, 163] still needs to be verified experimentally, since probing transport properties in the Mott regime is more challenging. Also note that, strictly speaking, a true MI does not exist for unbounded Speckle disorder in the thermodynamic limit [164]. Remarkably, the experiment [166] observed that disorder-induced localization persists also at finite temperature, which could be an indication of MBL, which we discuss in the following.
Figure 15. Measured critical disorder strength for the disorder-driven fermionic metal-insulator transition of ultracold 40K in a 3d optical lattice with Speckle disorder. Interaction-induced delocalization is clearly visible, as the increasing Hubbard interaction U drives the system back into the metallic phase. Reprinted figure with permission from [166]. Copyright 2015 by the American Physical Society.
Download figure:
Standard image High-resolution imageAs already remarked by Anderson in his pioneering work on localization [142], disordered and isolated quantum many-body systems may fail to act as their own heat bath. Within perturbation theory it was later shown that under its intrinsic unitary dynamics an interacting, disordered electron system without coupling to a (phonon) bath may remain localized in excited many-body eigenstates, thus violating ergodicity [167]. This phenomenon has been termed MBL and been at the focus of a considerable amount of theoretical studies, for example by exact diagonalization [168] and renormalization group methods [169]. For a recent review see [170]. A rigorous proof, involving only a single reasonable assumption, for the existence of MBL in a 1d quantum spin chain with short-range interactions has recently been given [171]. In higher spatial dimensions  the situation is much less clear from a theoretical point of view, due to the absence of analytical solutions and the challenges faced by numerical simulations of the full nonequilibrium many-body quantum dynamics.
the situation is much less clear from a theoretical point of view, due to the absence of analytical solutions and the challenges faced by numerical simulations of the full nonequilibrium many-body quantum dynamics.
While a generic, interacting Anderson insulator, like a MI, would only be insulating at T = 0, a many-body localized system has the remarkable property that it can remain strictly insulating even at finite temperature [167]. In analogy to an ideal noninteracting Anderson insulator, where all single-particle eigenstates are localized, in the case of MBL the many-body wavefunctions are considered as localized in Fock space. In addition, many-body localized systems exhibit a characteristic logarithmic spreading of entanglement, when starting from non-entangled initial conditions, which distinguishes them both from noninteracting Anderson insulators and from thermal states [170].
Analog quantum simulations with interacting ultracold bosons and fermions in disordered optical lattices have recently allowed to shed new light on MBL and the conditions under which it occurs. The breakdown of local thermalization of an ultracold fermionic ensemble in a 1d optical lattice with quasi-random disorder due to an incommensurate superlattice, described by the Aubry–André model, has been observed [172]. In this experiment, an initially prepared highly excited particle-density wave state fails to decay for sufficiently strong randomness, while the system is ergodic at weaker disorder, in agreement with DMRG simulations. In a study of coupled, identical 1d disordered tubes, MBL was found to disappear with increasing inter-tube coupling, when crossing over from one to two spatial dimensions [173]. On the other hand, [174] observed an MBL transition between thermal and localized phases of bosonic 87Rb in a fully two-dimensional disordered optical lattice, where the dynamics of an initially prepared excited state with spatial density imbalance was monitored in situ with single-site resolution (see figure 16) and the sharp onset of a finite (quasi-) steady-state imbalance at a critical disorder strength was observed, with an associated decay length scale diverging at the transition. Note that the system size in this measurement was beyond the capability of current state-of-the-art numerical simulations on classical computers. In [175] a controlled coupling to a thermal environment was introduced via dissipation due to photon scattering. In this case, the sharp MBL transition of the closed system is expected to be replaced by a crossover, similar to the effect of finite temperature on a quantum phase transition. As a result of dissipation, the excited initial state was found to decay with a rate proportional to the photon scattering.
Figure 16. Many-body localization observed in a two-dimensional disordered optical lattice. An initially prepared excited state with spatial density imbalance is evolving in time, without disorder (left subfigure (b)), and in the presence of spatial disorder (right subfigure (c)). τ denotes the tunneling time. In both (b) and (c), the left column shows single-shot images (isolated red dots are individual atoms) of the parity projected atomic distribution for the indicated evolution times. The right column displays the mean density distribution averaged over 50 different disorder potentials. In contrast to (b), traces of the initial state remain visible for all times in the disordered case. The white lines in the averaged density profiles after  highlight the difference. From [174]. Reprinted with permission from AAAS.
highlight the difference. From [174]. Reprinted with permission from AAAS.
Download figure:
Standard image High-resolution imageIt is at this stage an open question whether the MBL phenomena observed in the above discussed measurements represent a stable phase, or only a metastable localized regime, from which the system will eventually thermalize on much longer timescales beyond experimental reach [170]. The characteristic slow, logarithmic growth of entanglement entropy in MBL systems could be measured by quantum gas microscopy [176].
6. Synthetic gauge fields and topological states
The integer quantum Hall effect plays a fundamental role in modern solid-state physics [177], and has important applications, for example the definition of the resistance standard. Laughlin's Gedanken experiment [178], illustrated in figure 17, shows that the presence of chiral edge states is an inescapable consequence of the quantized transverse conductance 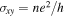 in quantum Hall insulators of finite width. Chiral edge states, which can be understood as skipping motion of electrons when their cyclotron orbits bounce off the edge, emerge at the interface between quantum Hall state and vacuum [179]. The quantum Hall conductivity can also be related to a topological invariant, the Chern number, by the TKNN formula [180]:
in quantum Hall insulators of finite width. Chiral edge states, which can be understood as skipping motion of electrons when their cyclotron orbits bounce off the edge, emerge at the interface between quantum Hall state and vacuum [179]. The quantum Hall conductivity can also be related to a topological invariant, the Chern number, by the TKNN formula [180]:  with a summation over all occupied bands, where
with a summation over all occupied bands, where 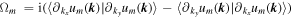 is the Berry curvature, and
is the Berry curvature, and  denotes a Bloch state with quasimomentum
denotes a Bloch state with quasimomentum  in band m. The two pictures are related by the bulk-edge correspondence [181].
in band m. The two pictures are related by the bulk-edge correspondence [181].
Figure 17. Illustration of Laughlin's Gedanken experiment and edge states, as proposed in [178]. Threading a fictitious flux Φ of exactly one flux quantum through a cylinder with a Quantum Hall insulator leads to n electrons transferred from one edge to the other, where n is the number of gapless, counterpropagating edge modes (indicated by the green arrows). Gauge invariance implies that n is related to the quantized Hall conductance as  .
.
Download figure:
Standard image High-resolution imageIf a second time-reversed copy of a bulk quantum Hall state is added, one obtains the time-reversal invariant quantum spin Hall (QSH) state, which similarly has topologically protected one-dimensional helical edge states inside insulating band gaps. The first version of a QSH effect proposed by Kane and Mele [182] consists of two time-reversed copies of Haldane's model [183], discussed below, with spin-up and spin-down coupling to effective orbital magnetic fields in opposite directions. In solid-state physics, the quantum (spin-) Hall state can be detected by measuring the quantum Hall conductivity [184], or by observing the band structure using ARPES [181]. However, in solids it is difficult to realize models with different spin components coupling to opposite magnetic fields, to measure the Berry curvature directly, or to tune the strength of two-particle interactions and to investigate their effect on topological states of matter.
Recently, novel methods have been developed for realizing synthetic gauge fields in neutral cold-atom systems, which are well suited for studying topologically non-trivial states of matter. This has been first achieved by using the Coriolis force in a rotating atomic gas [185], and later by inducing a Berry phase with Raman lasers [186, 187]. In one-dimensional systems, tunable gauge fields have been realized by an effective Zeeman lattice [188] and by dynamical driving of an optical lattice [189]. Here we will highlight developments for laser-induced tunnelling [190–194] and shaken lattices [195–197], which are powerful tools for realizing strong effective magnetic fields and topologically non-trivial states. These systems are time-periodically driven and well-controllable. Great progress has already been made in simulating paradigmatic models such as the Harper-Hofstadter (HH) [192, 193] and Haldane Hamiltonians [196].
Following the seminal proposal [190], the HH Hamiltonian, describing a quantum particle on a 2d lattice, coupling to a strong magnetic flux
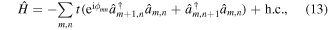
where 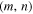 labels the sites of a square lattice, has been realized with ultracold atoms [192, 193]. The key ingredient of the HH Hamiltonian is a phase that particles acquire when hopping between sites. In optical lattices, this so-called Peierls phase
labels the sites of a square lattice, has been realized with ultracold atoms [192, 193]. The key ingredient of the HH Hamiltonian is a phase that particles acquire when hopping between sites. In optical lattices, this so-called Peierls phase  has been imprinted by laser-assisted tunneling with the setup shown in figure 18. A magnetic field gradient induces an energy offset Δ in x-direction, which is much larger than the bare tunneling strength in this direction. Therefore, hopping in x-direction is effectively inhibited. It is then recovered resonantly via laser-assisted tunneling, induced by two beams with frequency difference
has been imprinted by laser-assisted tunneling with the setup shown in figure 18. A magnetic field gradient induces an energy offset Δ in x-direction, which is much larger than the bare tunneling strength in this direction. Therefore, hopping in x-direction is effectively inhibited. It is then recovered resonantly via laser-assisted tunneling, induced by two beams with frequency difference 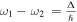 . On the other hand, Δ is much smaller than the band gap, ensuring that atoms do not occupy higher orbital states. The local optical potential induced by the two laser beams is
. On the other hand, Δ is much smaller than the band gap, ensuring that atoms do not occupy higher orbital states. The local optical potential induced by the two laser beams is  where
where 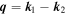 is the wave vector difference and
is the wave vector difference and 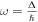 . In the high-frequency limit the system can be described by an effective time-independent Hamiltonian of the type (13), with the Peierls phase
. In the high-frequency limit the system can be described by an effective time-independent Hamiltonian of the type (13), with the Peierls phase 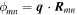 , where Rmn is the position vector of lattice site (m, n). The resulting dimensionless flux per unit cell of the lattice is given by
, where Rmn is the position vector of lattice site (m, n). The resulting dimensionless flux per unit cell of the lattice is given by 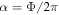 in terms of the phase Φ accumulated on a closed path around a plaquette.
in terms of the phase Φ accumulated on a closed path around a plaquette.
Figure 18. Experimental set-up for the realization of the Harper-Hofstadter Hamiltonian [192], as proposed in [190]. Two time-reversed copies of the HH Hamiltonian (13) were realized for the hyperfine states 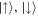 . Reprinted figure with permission from [192]. Copyright 2013 by the American Physical Society.
. Reprinted figure with permission from [192]. Copyright 2013 by the American Physical Society.
Download figure:
Standard image High-resolution imageThe implementation of the HH Hamiltonian (13) offers a platform for generating non-trivial topological states. Measurement of the Chern number of the lowest band for a flux 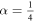 has been carried out in an all-optical set-up [194]. In response to a constant force
has been carried out in an all-optical set-up [194]. In response to a constant force 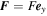 , atoms undergo Bloch oscillations in the direction of the force. If the energy bands have non-zero Berry curvature, the atom cloud experiences a net perpendicular drift [198], with an anomalous contribution to the velocity for a particle in the Bloch state
, atoms undergo Bloch oscillations in the direction of the force. If the energy bands have non-zero Berry curvature, the atom cloud experiences a net perpendicular drift [198], with an anomalous contribution to the velocity for a particle in the Bloch state 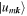 that is given by the Berry curvature as
that is given by the Berry curvature as  [199]. In this way, the Chern number of the lowest band has been determined as
[199]. In this way, the Chern number of the lowest band has been determined as 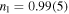 [194]. On the other hand, the detection of edge states, and the realization of a QSH state by completely filling Chern bands with ultracold fermions remain future experimental challenges.
[194]. On the other hand, the detection of edge states, and the realization of a QSH state by completely filling Chern bands with ultracold fermions remain future experimental challenges.
The Haldane model is a further pioneering model for a topological phase of matter [183], defined by the Hamiltonian
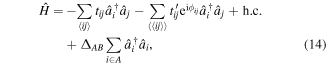
where  denote the sites of a honeycomb lattice, tij and
denote the sites of a honeycomb lattice, tij and 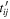 are real hopping amplitudes between pairs of nearest neighbors
are real hopping amplitudes between pairs of nearest neighbors  and next-nearest neighbors
and next-nearest neighbors 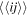 , respectively, and
, respectively, and 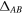 is a staggered offset between the two sublattices A and B. It illustrates that time-reversal symmetry (TRS) breaking, rather than overall non-zero flux per unit cell, is required for a finite quantum Hall conductance. The Haldane model has been realized by following the proposal [200] to shake a two-dimensional honeycomb lattice (see figure 19) on an elliptical orbit
is a staggered offset between the two sublattices A and B. It illustrates that time-reversal symmetry (TRS) breaking, rather than overall non-zero flux per unit cell, is required for a finite quantum Hall conductance. The Haldane model has been realized by following the proposal [200] to shake a two-dimensional honeycomb lattice (see figure 19) on an elliptical orbit 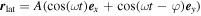 , with a non-interacting, ultracold gas of fermionic
, with a non-interacting, ultracold gas of fermionic  prepared in the lowest band [196]. The quasimomentum drift induced by the Berry curvature
prepared in the lowest band [196]. The quasimomentum drift induced by the Berry curvature 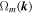 has been observed to demonstrate topological properties of the resulting effective Haldane model. Breaking of either inversion symmetry (IS) or TRS opens a gap in the band structure. IS is broken by introducing the energy offset
has been observed to demonstrate topological properties of the resulting effective Haldane model. Breaking of either inversion symmetry (IS) or TRS opens a gap in the band structure. IS is broken by introducing the energy offset 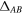 between sublattices, while TRS can be broken by changing the phase φ of the driving. As shown in the experiment, with only IS broken, the drift is zero since the Berry curvature is point anti-symmetric
between sublattices, while TRS can be broken by changing the phase φ of the driving. As shown in the experiment, with only IS broken, the drift is zero since the Berry curvature is point anti-symmetric 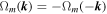 , while with only TRS broken, a finite drift arises, corresponding to a point symmetric Berry curvature
, while with only TRS broken, a finite drift arises, corresponding to a point symmetric Berry curvature 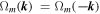 [199]. Recently the full
[199]. Recently the full  -dependence of the Chern number of a tunable honeycomb lattice has been determined by a tomographic approach, based on the dynamics after a quench of the effective Floquet band structure [197].
-dependence of the Chern number of a tunable honeycomb lattice has been determined by a tomographic approach, based on the dynamics after a quench of the effective Floquet band structure [197].
Download figure:
Standard image High-resolution imageThe above described experimental realizations of key models for topological bands provide examples for Floquet engineering, which more generally allows realizing and tuning band structures, interactions and many-body quantum states, for example via effective Floquet Hamiltonians, by time-periodic driving of single- or many-particle quantum systems [201].
Cold atoms with time-periodic driving are thus an ideal platform to study the interplay of interactions and topology. To this end, it is crucial for a topologically non-trivial ground state to have a long life-time in the presence of interactions. First experimental attempts [196, 202] in this direction are encouraging. Reference [196] observed only a 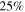 entropy increase in the MI regime by loading a balanced spin mixture of ultracold fermions into a lattice and reversing the loading procedure, compared to the situation without driving. This implies that the heating induced by driving need not be a dominating factor. Reference [202] studied the effect of different loading procedures in two and three spatial dimensions by comparing images of TOF patterns. It is found that an interacting HH SF state can be realized up to a lattice depth of
entropy increase in the MI regime by loading a balanced spin mixture of ultracold fermions into a lattice and reversing the loading procedure, compared to the situation without driving. This implies that the heating induced by driving need not be a dominating factor. Reference [202] studied the effect of different loading procedures in two and three spatial dimensions by comparing images of TOF patterns. It is found that an interacting HH SF state can be realized up to a lattice depth of 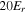 , with lifetimes that are only 2–4 times smaller than in the weakly interacting case.
, with lifetimes that are only 2–4 times smaller than in the weakly interacting case.
While noninteracting topological insulators have been the subject of intense investigations during recent years and are reasonably well understood [181], much less is known about topological bands in the presence of two-particle interactions. It is still an open question under which conditions the bulk-edge correspondence holds for interacting systems. A recently proposed effective topological Hamiltonian [203], involving only the zero-frequency Green's function of the interacting system  , allows calculating topological indices for strongly correlated fermionic systems in combination with (real-space) DMFT. In this way, the topological phase diagram for the time-reversal-symmetric fermionic Hofstadter–Hubbard model
, allows calculating topological indices for strongly correlated fermionic systems in combination with (real-space) DMFT. In this way, the topological phase diagram for the time-reversal-symmetric fermionic Hofstadter–Hubbard model
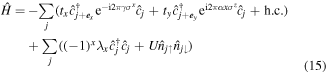
with additional spin–orbit coupling γ and a staggered potential 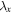 has been calculated, where
has been calculated, where 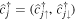 is the creation operator at site
is the creation operator at site  of a square lattice and
of a square lattice and  ,
, 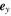 denote the primitive lattice vectors in x- and y-direction. The bulk-edge correspondence has been verified for the interaction-driven transition into the QSH state [204, 205], while exotic quantum magnetic order was found for larger interaction values, see figure 20. For bosons, on the other hand, it is an open question whether topological (Chern-) insulating states can be realized, since this requires strong interactions from the start. A recent DMFT study of the bosonic Haldane–Hubbard model established a nontrivial chiral SF phase for weak interactions, while the Chern index of the strongly correlated Mott phase, which has local plaquette currents, was found to vanish despite topologically non-trivial subbands [206]. More generally, the question is whether a topological MI, predicted in [207], can exist. Also the role of disorder, which may stabilize topological bands and induce topological Anderson insulators [208], is an open issue.
denote the primitive lattice vectors in x- and y-direction. The bulk-edge correspondence has been verified for the interaction-driven transition into the QSH state [204, 205], while exotic quantum magnetic order was found for larger interaction values, see figure 20. For bosons, on the other hand, it is an open question whether topological (Chern-) insulating states can be realized, since this requires strong interactions from the start. A recent DMFT study of the bosonic Haldane–Hubbard model established a nontrivial chiral SF phase for weak interactions, while the Chern index of the strongly correlated Mott phase, which has local plaquette currents, was found to vanish despite topologically non-trivial subbands [206]. More generally, the question is whether a topological MI, predicted in [207], can exist. Also the role of disorder, which may stabilize topological bands and induce topological Anderson insulators [208], is an open issue.
Figure 20. Phase diagram of the time-reversal-invariant Hofstadter–Hubbard model (15) with spin–orbit coupling 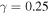 and dimensionless flux per unit cell
and dimensionless flux per unit cell  , obtained by using the effective topological Hamiltonian in combination with DMFT, for half filling and
, obtained by using the effective topological Hamiltonian in combination with DMFT, for half filling and 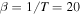 . The phases shown are band insulator (BI), quantum spin Hall insulator (QSH), and magnetically ordered Slater insulator (MOSI). Solid lines are obtained by using the full DMFT local self-energy, while the dashed line is the phase boundary between BI and QSH obtained by Hartree–Fock. Reprinted figure with permission from [205]. Copyright 2016 by the American Physical Society.
. The phases shown are band insulator (BI), quantum spin Hall insulator (QSH), and magnetically ordered Slater insulator (MOSI). Solid lines are obtained by using the full DMFT local self-energy, while the dashed line is the phase boundary between BI and QSH obtained by Hartree–Fock. Reprinted figure with permission from [205]. Copyright 2016 by the American Physical Society.
Download figure:
Standard image High-resolution imageThe QSH state discussed above, or more generally topological band insulators, as well as the Haldane spin-1 chain, are examples for symmetry-protected topological (SPT) phases, featuring a bulk gap, no exotic excitations, but nontrivial surface states which are protected by symmetry. Alternatively, intrinsic topological order may emerge in a many-body system, which is then characterized by topological ground state degeneracy, fractional excitations and topological entanglement entropy [209, 210]. Fractional (anyonic) excitations in systems with intrinsic topological order, for example a fractional quantum Hall state, could find a powerful application in topological quantum computation [211]. While SPT phases have only short-range entanglement, in phases with intrinsic topological order long-range entanglement is found. Ultracold realizations have been proposed for fractional Chern insulators, which represent the lattice analog of fractional quantum Hall states, and for which optical flux lattices may be a promising platform [212]. The resulting topological order may be detected via nonlocal correlation functions, such as string order, which has already been measured in a one-dimensional bosonic MI [139].
Since cold atom realizations of topological states are mesoscopic in size, it is an important question how topological properties and edge states are affected by the soft boundaries of the optical trapping potential. In [213] it was shown for noninteracting fermions that sharp boundaries are not required for realizing quantum Hall or QSH states in optical lattices, and that a quartic confinement potential 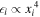 in the open direction of a cylinder geometry is already steep enough to obtain well-defined edge and bulk regions. Quasi-homogeneous bulk regions with sharp repulsive boundaries can be created by blue-detuned sheets of light [42].
in the open direction of a cylinder geometry is already steep enough to obtain well-defined edge and bulk regions. Quasi-homogeneous bulk regions with sharp repulsive boundaries can be created by blue-detuned sheets of light [42].
All current implementations of synthetic gauge fields in optical lattices are based on periodic driving with a Hamiltonian  , either by laser-assisted tunneling or time-periodic forcing [189, 192, 196], with the HH and Haldane models emerging as effective Hamiltonians in the Floquet picture [214]. Little is known yet about extending these concepts to interacting, periodically driven systems. Non-perturbative theoretical investigations along these lines [215] will be crucial for a quantitative understanding of upcoming experiments involving synthetic gauge fields and strong two-particle interactions. Moreover, the topological classification of periodically driven systems has so far only been understood for noninteracting systems [216].
, either by laser-assisted tunneling or time-periodic forcing [189, 192, 196], with the HH and Haldane models emerging as effective Hamiltonians in the Floquet picture [214]. Little is known yet about extending these concepts to interacting, periodically driven systems. Non-perturbative theoretical investigations along these lines [215] will be crucial for a quantitative understanding of upcoming experiments involving synthetic gauge fields and strong two-particle interactions. Moreover, the topological classification of periodically driven systems has so far only been understood for noninteracting systems [216].
7. Outlook
As discussed in this article, ultracold quantum simulations of strongly correlated systems have already achieved a number of impressive milestones. Future developments will likely aim at a further reduction of entropies and temperatures in optical lattices, to give access to the d-wave SF regime of the doped FH model [22], which is expected at temperatures roughly a factor of 4 below those for AF ordering [2], and could provide critical insight into the origin of high-temperature superconductivity in the cuprates. At these reduced temperatures, also more exotic types of spin and topological order can be investigated, for example in frustrated quantum magnets. The additional role of electron-phonon coupling could be studied in hybrid quantum simulators, where ultracold fermions are coupled to the tunable quantized vibrations of trapped ion crystals [17]. The fundamental open question whether many-body localized phases, arising from the interplay of disorder and interaction, can be stable in spatial dimensions higher than one, will likely be another focus of future research.
In systems of cold gases with synthetic gauge fields, the experimental realization of interacting topological states, as well as the detection of edge modes, intrinsic topological order, and fractional excitations will be of major interest.
Novel physics and quantum phases are expected and will be investigated in quantum many-body systems with long-range interactions, which can be induced by Rydberg dressing [137], by Rydberg-excited atoms in optical microtraps [30], via heteronuclear molecules [217–219] or in gases with magnetic dipolar moments [220]. Alternatively, self-organization transitions due to infinitely long-range effective interactions arise in degenerate quantum gases interacting with an optical cavity [221], where ordered states and collective excitations in the presence of additional two-particle interactions [222] and coupling to multiple cavities [223] are currently under active investigation.
There has also been remarkable progress in creating degenerate Fermi gases of alkaline-earth-like elements (for example 173Yb or 87Sr), which have long-lived, metastable excited electronic states and a large nuclear spin decoupled from the electronic angular momentum, see for example [88, 224]. These systems have moved into focus as promising new candidates for quantum simulations of lattice fermions with higher spin, orbital degeneracy or higher internal symmetry SU(N) [225]. Ultracold simulations of more exotic condensed matter systems, such as color superconductors in neutron star cores, and 'baryonic' Fermi liquids [5, 6], are thus also becoming accessible.
Acknowledgments
This work was partially supported by the Deutsche Forschungsgemeinschaft via DFG SPP 1929 GiRyd, DFG FOR 2414 and DFG SFB/TR 49.