Coulomb correlations in 4d and 5d oxides from first principles—or how spin–orbit materials choose their effective orbital degeneracies

The 5d transition metal oxide (TMO) Sr₂IrO₄ has a tetragonal crystal structure, the symmetry of which is lowered from the K₂NiF₄-type, well-known in Sr₂RuO₄ or La₂CuO₄, by an ${{11}^{\circ}}$ rotation of its IrO₆ octahedra around the $\mathbf{c}$-axis [136]. Each Ir atom accommodates 5 electrons and the standard picture neglecting spin–orbit interactions would give a '$t_{2g}^{5}$' ground state. However, this compound exhibits insulating behavior up to the highest measured temperatures, with a strongly temperature-dependent gap. The optical gap at room temperature is about 0.26 eV [137]. Below ${{T}_{\text{N}}}=240$ K, a canted-antiferromagnetic (AF) order sets in, with an effective local moment of 0.5 ${{\mu}_{\text{B}}}$/Ir, and a saturation moment of 0.14 ${{\mu}_{\text{B}}}$/Ir [138]. This phase has triggered much experimental and theoretical work [139–142], highlighting, in particular, the importance of the SOC.

Here, we focus on the paramagnetic phase, above 240 K, which is most interesting due to the persistence of the insulating nature despite the absence of magnetic order, as shown by transport measurements [15], by scanning tunneling microscopy and spectroscopy experiments [143], by angle-resolved spectroscopy [16, 144], time-resolved spectroscopy [145, 146] or optical conductivity [137].

Resonant inelastic x-ray spectroscopy (RIXS) experiments [15] proposed a picture early on in terms of ${{j}_{\text{eff}}}=1/2$ states and ${{j}_{\text{eff}}}=3/2$ states:

$$\begin{eqnarray}\begin{array}{*{35}{l}} |\,{{j}_{\text{eff}}}=\frac{1}{2},{{m}_{{{j}_{\text{eff}}}}}=+\frac{1}{2}\rangle & =+\frac{1}{\sqrt{3}}\left(|{{d}_{yz}},\downarrow \rangle +\text{i}|{{d}_{xz}},\downarrow \rangle \right)+\frac{1}{\sqrt{3}}|{{d}_{xy}},\uparrow \rangle, \\ |\,{{j}_{\text{eff}}}=\frac{1}{2},{{m}_{{{j}_{\text{eff}}}}}=-\frac{1}{2}\rangle & =+\frac{1}{\sqrt{3}}\left(|{{d}_{yz}},\uparrow \rangle -\text{i}|{{d}_{xz}},\uparrow \rangle \right)-\frac{1}{\sqrt{3}}|{{d}_{xy}},\downarrow \rangle, \\\end{array}\end{eqnarray} \tag{ 1 }$$

$$\begin{eqnarray}\begin{array}{*{35}{l}} |\,{{j}_{\text{eff}}}=\frac{3}{2},{{m}_{{{j}_{\text{eff}}}}}=+\frac{1}{2}\rangle & = & -\frac{1}{\sqrt{6}}\left(|{{d}_{yz}},\downarrow \rangle +\text{i}|{{d}_{xz}},\downarrow \rangle \right)+\sqrt{\frac{2}{3}}|{{d}_{xy}},\uparrow \rangle, \\ |\,{{j}_{\text{eff}}}=\frac{3}{2},{{m}_{{{j}_{\text{eff}}}}}=-\frac{1}{2}\rangle & = & +\frac{1}{\sqrt{6}}\left(|{{d}_{yz}},\uparrow \rangle -\text{i}|{{d}_{xz}},\uparrow \rangle \right)+\sqrt{\frac{2}{3}}|{{d}_{xy}},\downarrow \rangle, \\ |\,{{j}_{\text{eff}}}=\frac{3}{2},{{m}_{{{j}_{\text{eff}}}}}=+\frac{3}{2}\rangle & = & -\frac{1}{\sqrt{2}}\left(|{{d}_{yz}},\uparrow \rangle +\text{i}|{{d}_{xz}},\uparrow \rangle \right), \\ |\,{{j}_{\text{eff}}}=\frac{3}{2},{{m}_{{{j}_{\text{eff}}}}}=-\frac{3}{2}\rangle & = & +\frac{1}{\sqrt{2}}\left(|{{d}_{yz}},\downarrow \rangle -\text{i}|{{d}_{xz}},\downarrow \rangle \right). \\\end{array}\end{eqnarray} \tag{ 2 }$$

Since the quartet of states lies lower in energy than the doublet and the splitting between the ${{j}_{\text{eff}}}=3/2$ and ${{j}_{\text{eff}}}=1/2$ is large, neglecting any band dispersion would result in a configuration with one electron in the ${{j}_{\text{eff}}}=1/2$ state. The DFT band structure displays a dispersion of width comparable to this splitting, leaving the question a priori open again. However, the bandwidth is narrowed due to structural distortions [21], and electronic correlations can then become effective and eventually drive the compound insulation.

Since the discovery of this mechanism, other Ir-based compounds (see table 1) have been classified as spin–orbit Mott insulators (Na₂IrO₃, pyrochlores, etc...). Recent theoretical studies also predict some fluoride material [147] to be in this class. The one-orbital nature of insulating Sr₂IrO₄ has contributed to intense activities attempting to dope the compound, with the hope of inducing a superconducting state as in the cuprates. Doping-induced metal–insulator transitions and the properties of the metallic phases have therefore become a hot topic, with studies of various compounds, e.g. Sr₂IrO₄ [144, 148], (Sr_1−xLa_x)₃Ir₂O₇ [149], Ca_1−xSr_xIrO₃ [150], Ca_1−xRu_xIrO₃ [151], Sr₂Ir_1−xRh_xO₄ [152, 153], Sr₂Ir_1−xRu_xO₄ [154], Sr_xLa_11−xIr₄O₂₄ [155].

It is natural that also in metallic 4d or 5d transition metal compounds, SOC can have notable consequences. An example of a 'spin–orbit correlated metal' is the end member SrIrO₃ of the Ir-based Ruddlesden–Popper Sr_n+1Ir_nO_3n+1 series [46] but also many Ru-,Rh- or Os-based transition metal oxides (TMOs) belong to this class (see tables 1 and 2). In these compounds, correlations are important enough to renormalize the Fermi surface-, albeit in a strongly spin–orbit coupling-dependent way. The respective roles of both effects have been worked out in some detail for several compounds, among which are SrIrO₃ [46–48], Sr₂RuO₄/Ca₂RuO₄ [108, 109, 156] and Sr₂RhO₄ [19–21].

We will focus our attention in the following on Sr₂RhO₄, motivated by its structural proximity and isoelectronic nature to Sr₂IrO₄. Indeed, this TMO is the 4d counterpart of Sr₂IrO₄, both concerning structure and filling. To understand its Fermi surface requires the inclusion of both SOC and correlations [21]. It is composed of three pockets (see figure 8): a circular hole-like α-pocket around $\Gamma$, a lens-shaped electron pocket ${{\beta}_{M}}$ and a square-shaped electron pocket ${{\beta}_{X}}$ with a mass enhancement of 3.0, 2.6 and 2.2, respectively [120].

In this review, we will put Sr₂IrO₄ and Sr₂RhO₄ in parallel, shedding light on the spectral properties of these compounds and elaborating on the notion of a reduced effective (spin–orbital) degeneracy that is crucial for their properties.

Necessary conditions for realizing a j_eff picture are (1) a strong spin–orbit coupling constant and (2) an important cubic crystal field. These conditions are often met in crystalline structures where IrO₆ octahedra are present (see table 1). Similar compounds based on Ru, Rh and Os also show such j_eff states (see table 2). However, not all Ir-based structures belong to this case: we note that neither epitaxial thin films of IrO₂ [157] nor the correlated metal IrO₂ in its rutile structure [158, 159] exhibit such a ${{j}_{\text{eff}}}=1/2$ state. We will now turn to a more precise description of that picture.

The spin–orbit interaction is one of the relativistic corrections to the Schrödinger–Pauli equation arising when taking the non-relativistic limit of Dirac's equation. It introduces a coupling between the spin $\mathbf{S}$ and the motion—or, more precisely, the orbital momentum $\mathbf{L}$ in the atomic case—of the electron. In a solid described within an independent-particle picture, spin–orbit coupling has the following general form:

$$\begin{eqnarray}&&{{H}_{\text{SO}}}=\frac{\hbar}{4m_{0}^{2}{{c}^{2}}}\boldsymbol{\sigma }\centerdot \left[\boldsymbol{}\nabla V\left(\mathbf{r}\right)\times \mathbf{p}\right],\end{eqnarray} \tag{ 3 }$$

where m₀ is the electron mass, $V\left(\mathbf{r}\right)$ is the effective Kohn–Sham potential and ${{\sigma}_{i=x,y,z}}$ denote the Pauli-spin matrices. Assuming that the potential close to the nucleus has spherical symmetry, the mean value of the spin–orbit interaction on the atomic state $(n,\ell )$ takes the more common form:

$$\begin{eqnarray}&&{{H}_{\text{SO}}}={{\zeta}_{\text{SO}}}(n\ell )~\mathbf{l}\centerdot \mathbf{s},\quad \quad {{\zeta}_{\text{SO}}}(n\ell )=\frac{{{\hbar}^{2}}}{2m_{0}^{2}{{c}^{2}}}~{{\langle \frac{1}{r}\frac{\text{d}V}{\text{d}r}\rangle}_{(n,\ell )}},\end{eqnarray} \tag{ 4 }$$

where $\mathbf{S}=\frac{1}{2}\boldsymbol{\sigma }$, $\mathbf{L}=\mathbf{r}\times \mathbf{p}=\hbar ~\mathbf{l}$ and ${{\langle \ldots \rangle}_{(n,\ell )}}$ denotes the mean value of the radial quantity in the state $(n,\ell )$. Table 3 gives some values of the spin–orbit constant ${{\zeta}_{\text{SO}}}$ for 3d, 4d and 5d atoms. The SOC increases with the atomic number, explaining why spin–orbit materials are mostly found in 5d and 4d TMOs.

Table 3. Value of the spin–orbit constant ${{\zeta}_{\text{SO}}}$ in the d-valence shells of some transition metals. Data from Landolt–Börnstein database and [160] (3d), from [19, 161] (4d) and from [162] (5d).

Atom	Z	${{\zeta}_{\text{SO}}}(3d)$ (eV)	Atom	Z	${{\zeta}_{\text{SO}}}(4d)$ (eV)	Atom	Z	${{\zeta}_{\text{SO}}}(5d)$ (eV)
Fe	26	0.050	Ru	44	0.161	Os	76	0.31
Co	27	0.061	Rh	45	0.191	Ir	77	0.40
Cu	29	0.103	Ag	47	0.227	Au	79	0.42

Due to the effect of SOC, a multiplet splitting arises in the d-orbitals. Figure 2 shows the multiplet splitting of d-orbitals due to the spin–orbit coupling as a function of the strength of a cubic crystal field $\Delta =10Dq$.

Zoom In Zoom Out Reset image size

In spherical symmetry the fine structure is composed of a six-fold J  =  5/2 multiplet (in red) and a J  =  3/2 quartet of lower energy (in blue), following 'Landé's interval rule'. The presence of a cubic crystal field splits further the six-fold multiplet. Indeed, the spin–orbit interaction in the cubic basis (e_g and t_2g in green and light green, respectively, in figure 2) can be reduced to two five-dimensional submatrices:

$$\begin{eqnarray}\left(\begin{array}{c} 0 & -\text{i} & \text{i} & \sqrt{3} & -1 \\ \text{i} & 0 & -1 & -\text{i}\sqrt{3} & -\text{i} \\ -\text{i} & -1 & 0 & 0 & -2\text{i} \\ \sqrt{3} & \text{i}\sqrt{3} & 0 & 0 & 0 \\ -1 & \text{i} & 2\text{i} & 0 & 0 \\\end{array}\right).\frac{{{\zeta}_{\text{SO}}}}{2},\\ \left(\begin{array}{c} 0 & \text{i} & \text{i} & -\sqrt{3} & 1 \\ -\text{i} & 0 & 1 & -\text{i}\sqrt{3} & -\text{i} \\ -\text{i} & 1 & 0 & 0 & 2\text{i} \\ -\sqrt{3} & \text{i}\sqrt{3} & 0 & 0 & 0 \\ 1 & \text{i} & -2\text{i} & 0 & 0 \\\end{array}\right).\frac{{{\zeta}_{\text{SO}}}}{2},\end{eqnarray} \tag{ 5 }$$

in the bases $\left\{{{d}_{xz}}\uparrow,{{d}_{yz}}\uparrow,{{d}_{xy}}\downarrow,{{d}_{3{{z}^{2}}-{{r}^{2}}}}\downarrow,{{d}_{{{x}^{2}}-{{y}^{2}}}}\downarrow \right\}$ and $\left\{{{d}_{xz}}\downarrow,{{d}_{yz}}\downarrow,{{d}_{xy}}\uparrow,{{d}_{3{{z}^{2}}-{{r}^{2}}}}\uparrow,{{d}_{{{x}^{2}}-{{y}^{2}}}}\uparrow \right\}$, respectively. After diagonalization, the total angular momentum J remains a good quantum number, contrary to ${{j}_{z}}/{{m}_{j}}$ and one gets the following fine structure:

• a first quartet of J  =  5/2 states (in red) with an energy
  $$\begin{eqnarray}&&{{\varepsilon}_{\frac{5}{2}+}}=\frac{1}{4}\left(2 \Delta -{{\zeta}_{\text{SO}}}\right)+\frac{1}{4}\sqrt{{{\left(2 \Delta +{{\zeta}_{\text{SO}}}\right)}^{2}}+24\zeta _{\text{SO}}^{~~2}},\end{eqnarray}$$
• a doublet of J  =  5/2 states (in yellow) of energy
  $$\begin{eqnarray}&&{{\varepsilon}_{\frac{5}{2}-}}=+2\frac{{{\zeta}_{\text{SO}}}}{2},\end{eqnarray}$$
• a quartet of J  =  3/2 states (in light blue) with an energy
  $$\begin{eqnarray}&&{{\varepsilon}_{\frac{3}{2}}}=\frac{1}{4}\left(2 \Delta -{{\zeta}_{\text{SO}}}\right)-\frac{1}{4}\sqrt{{{\left(2 \Delta +{{\zeta}_{\text{SO}}}\right)}^{2}}+24\zeta _{\text{SO}}^{~~2}}.\end{eqnarray}$$

In the limit of strong crystal field ($\Delta \gg {{\zeta}_{\text{SO}}}$), the J  =  5/2 doublet (in yellow) remains invariant while the higher-energy quartet will tend to the usual e_g states and the lower-energy J  =  3/2 quartet will be composed of t_2g states only, with an energy of $-{{\zeta}_{\text{SO}}}/2$.

Since the SOC matrix restricted to the t_2g subspace is exactly the opposite of the SOC matrix of the p-states of a free atom, one usually labels these latter states by a j_eff quantum number in analogy with the ${{p}_{\frac{1}{2}}}$ and ${{p}_{\frac{3}{2}}}$ multiplets, leading to the expressions given in equations (1) and (2). We point out that the ${{j}_{\text{eff}}}=1/2$ doublet arises from the interplay of both cubic symmetry and SOC, whatever the strength of the crystal field. The corresponding eigenstates can indeed be written:

$$\begin{eqnarray}\begin{array}{*{35}{l}} |\frac{1}{2},+\frac{1}{2}\rangle & = & +\frac{1}{\sqrt{3}}\left(|{{d}_{yz}},\downarrow \rangle +\text{i}|{{d}_{xz}},\downarrow \rangle \right)+\frac{1}{\sqrt{3}}|{{d}_{xy}},\uparrow \rangle \\ {} & = & \frac{i}{\sqrt{6}}\left(\sqrt{5}|\frac{5}{2},-\frac{3}{2}\rangle -|\frac{5}{2},\frac{5}{2}\rangle \right), \\ |\frac{1}{2},-\frac{1}{2}\rangle & = & +\frac{1}{\sqrt{3}}\left(|{{d}_{yz}},\uparrow \rangle -\text{i}|{{d}_{xz}},\uparrow \rangle \right)-\frac{1}{\sqrt{3}}|{{d}_{xy}},\downarrow \rangle \\ {} & = & \frac{i}{\sqrt{6}}\left(\sqrt{5}|\frac{5}{2},\frac{3}{2}\rangle -|\frac{5}{2},-\frac{5}{2}\rangle \right)~ \\\end{array}\end{eqnarray} \tag{ 6 }$$

(where the right hand side is written using the J,m_J quantum numbers). This may explain the robustness of this doublet in spin–orbit compounds [163]. However, the splitting between the ${{j}_{\text{eff}}}=1/2$ and ${{j}_{\text{eff}}}=3/2$ multiplets follows the inverse Landé interval rule (with the ${{j}_{\text{eff}}}=1/2$ above the ${{j}_{\text{eff}}}=3/2$ states) only in the strong crystal field limit.

Combined density functional theory (DFT) and dynamical mean-field theory (DMFT), as pioneered in [164, 165] (for a review, see [166, 167]), has made correlated electron systems accessible to first principles calculations. Over the years, various classes of systems ranging from transition metals [168–171], their oxides [11, 172–177], sulphides [178, 179], pnictides [4, 9, 180, 181], rare earths [182–184] and their compounds [185–187], including heavy fermions [188, 189], actinides [190, 191] and their compounds [192, 193] to organics [194], correlated semiconductors [195, 196], and correlated surfaces and interfaces [197–199] have been studied with great success. Besides intensive methodological developments (see e.g. [2, 3, 167, 200–203]), recent research activities continue to extend to new classes of materials. In this context, 4d and 5d oxides have also come into focus [21, 22, 62]. In this section, we review the technical aspects related to combined DFT+DMFT calculations in the presence of spin–orbit interactions. Since the applications we later focus on are 4d and 5d oxides in their paramagnetic phases, we restrict the discussion to this case.

In DMFT, a local approximation is made to the many-body self-energy which can then be calculated from an effective atom problem, subject to a self-consistency condition (see figure 3).

Zoom In Zoom Out Reset image size

The notion of locality is understood in the sense of many-body theory as a site-diagonal form, with respect to atomic sites after representing the Hamiltonian in an atom-centered Wannier-type basis $|w_{\ell m}^{\alpha,\sigma}\rangle$, where the index α labels the atom in the unit-cell, $(\ell,m)$ the angular momentum quantum numbers of the atomic orbital and σ the spin degree of freedom. Different choices are possible for the construction of the atom-centered orbitals, and the work reviewed here is based on the construction of projected atomic orbitals subject to a subsequent orthonormalization procedure [180].

The DMFT self-consistency cycle links the local effective atom problem to the electronic structure of the solid, via the transformation matrix from the Kohn–Sham states $|\psi _{\mathbf{k}\nu}^{\sigma}\rangle$, labelled by their momentum $\mathbf{k}$ their band index ν and their spin σ, to the resulting Wannier-like local orbitals $|w_{\ell m}^{\alpha,\sigma}\rangle$. These key quantities are called projectors and denoted $P_{\ell m,\nu}^{\alpha,\sigma}\left(\mathbf{k}\right)$.

The main advantage of projector-based implementations of DFT+DMFT (see e.g. [180, 205, 206]) is that not only the DFT-based part of the calculations but also the determination of the local Green's function, used within the DMFT self-consistency condition, can be performed in any convenient basis set, and notably in the one used in the respective DFT code. Since the transformation of the DFT Hamiltonian matrix in that basis into the Kohn–Sham eigenset $|\psi _{\mathbf{k}\nu}^{\sigma}\rangle$ is known, it is sufficient to further determine the projections of the Kohn–Sham eigenstates onto the local orbitals $|w_{\ell m}^{\alpha,\sigma}\rangle$ used in the DMFT impurity problem. This is precisely the role of the projectors.

In [21], this construction was generalized to the case when spin is not a good quantum number anymore, and implemented within the framework of the DFT+DMFT implementation of [180]. Nowadays, it is available within the TRIQS/DFTTools package [207] that links the Wien2k code [208] to DMFT. We give here the main lines of this generalization of the projector-based DFT+DMFT formalism.

When taking into account SOC, the Kohn–Sham eigenstates $|{{\psi}_{\mathbf{k}\nu}}\rangle$ are built out of both spin-up and spin-down states—in a similar fashion to the previously introduced ${{j}_{\text{eff}}}=1/2$ and ${{j}_{\text{eff}}}=3/2$ atomic states. Nevertheless, we can still write them in the following Bloch form:

$$\begin{eqnarray}\begin{array}{*{35}{l}} {{\psi}_{\mathbf{k}\nu}}\left(\mathbf{r}\right) & = & \left[u_{\mathbf{k}\nu}^{\uparrow}\left(\mathbf{r}\right)+u_{\mathbf{k}\nu}^{\downarrow}\left(\mathbf{r}\right)\right]{{\text{e}}^{\text{i}\mathbf{k}\centerdot \mathbf{r}}} \\ {} & = & \phi _{\mathbf{k}\nu}^{\uparrow}\left(\mathbf{r}\right)+\phi _{\mathbf{k}\nu}^{\downarrow}\left(\mathbf{r}\right), \\\end{array}\end{eqnarray} \tag{ 7 }$$

where the index ν now runs over both spin and band indices. The state $|\phi _{\mathbf{k}\nu}^{\sigma}\rangle$ denotes the projection of the Kohn–Sham state onto its spin-σ contribution and is not an eigenstate of the Hamiltonian.

Using this decomposition, we can define the new projectors:

$$\begin{eqnarray}&&P_{\ell m,\nu}^{\alpha,\sigma}\left(\mathbf{k}\right)=\langle w_{\ell m}^{\alpha,\sigma}|{{\psi}_{\mathbf{k}\nu}}\rangle =\langle w_{\ell m}^{\alpha,\sigma}|\phi _{\mathbf{k}\nu}^{\sigma}\rangle.\end{eqnarray} \tag{ 8 }$$

We define them in the standard complex basis, but allow for a basis transformation to quantum numbers j, m_j (like ${{j}_{\text{eff}}}=1/2$ and ${{j}_{\text{eff}}}=3/2$) afterwards by means of a unitary matrix transformation in the correlated $\ell$-space:

$$\begin{eqnarray}&&P_{j,\nu}^{\alpha,{{m}_{j}}}\left(\mathbf{k}\right)=\underset{m,\sigma}{\sum}\,\mathcal{S}_{j,\ell m}^{{{m}_{j}},\sigma}\langle w_{\ell m}^{\alpha,\sigma}|{{\psi}_{\mathbf{k}\nu}}\rangle =\underset{m,\sigma}{\sum}\,\mathcal{S}_{j,\ell m}^{{{m}_{j}},\sigma}P_{\ell m,\nu}^{\alpha,\sigma}\left(\mathbf{k}\right).\end{eqnarray} \tag{ 9 }$$

The main difference with the usual implementation where spin is a good quantum number is that there are now two projectors associated with each band index ν: $P_{\ell m,\nu}^{\alpha,\sigma}\left(\mathbf{k}\right)$ with $\sigma =\uparrow,\downarrow$.

Using the decomposition (7) in the formulation of the self-consistency condition relating the lattice Green's function of the solid to the impurity model, the (inverse) Green's function of the solid is given by:

$$\begin{eqnarray}&&{{\left[{{G}^{-1}}\left(\mathbf{k},\text{i}{{\omega}_{n}}\right)\right]}_{\nu {{\nu}^{\prime}}}}=\left(\text{i}{{\omega}_{n}}+\mu -\varepsilon _{\mathbf{k}}^{\nu}\right){{\delta}_{\nu {{\nu}^{\prime}}}}-{{ \Sigma }_{\nu {{\nu}^{\prime}}}}\left(\mathbf{k},\text{i}{{\omega}_{n}}\right),\end{eqnarray} \tag{ 10 }$$

where $\varepsilon _{\mathbf{k}}^{\nu}$ are the (ν-dependent only) Kohn–Sham eigenvalues and ${{ \Sigma }_{\nu {{\nu}^{\prime}}}}\left(\mathbf{k},\text{i}{{\omega}_{n}}\right)$ is the approximation to the self-energy obtained by the solution of the DMFT impurity problem. It is obtained by 'mapping' the impurity self-energy to the local self-energy of the lattice and 'upfolding' it as:

$$\begin{eqnarray}&&{{ \Sigma }_{\nu {{\nu}^{\prime}}}}\left(\mathbf{k},\text{i}{{\omega}_{n}}\right)=\underset{\alpha,j{{j}^{\prime}}}{\sum}\,\underset{{{m}_{j}}{{m}_{{{j}^{\prime}}}}}{\sum}\,{{\left[P_{j,\nu}^{\alpha,{{m}_{j}}}\left(\mathbf{k}\right)\right]}^{\ast}}~\left[\Delta \Sigma _{\text{loc}}^{\alpha}\left(\text{i}{{\omega}_{n}}\right)\right]_{j{{j}^{\prime}}}^{{{m}_{j}}{{m}_{{{j}^{\prime}}}}}~P_{{{j}^{\prime}},{{\nu}^{\prime}}}^{\alpha,{{m}_{{{j}^{\prime}}}}}\left(\mathbf{k}\right),\end{eqnarray} \tag{ 11 }$$

with

$$\begin{eqnarray}&&\left[\Delta \Sigma _{\text{loc}}^{\alpha}\left(\text{i}{{\omega}_{n}}\right)\right]_{j{{j}^{\prime}}}^{{{m}_{j}}{{m}_{{{j}^{\prime}}}}}=\left[{{ \Sigma }_{\text{imp}}}\left(\text{i}{{\omega}_{n}}\right)\right]_{j{{j}^{\prime}}}^{{{m}_{j}}{{m}_{{{j}^{\prime}}}}}-\left[{{ \Sigma }_{\text{dc}}}\right]_{j{{j}^{\prime}}}^{{{m}_{j}}{{m}_{{{j}^{\prime}}}}}.\end{eqnarray} \tag{ 12 }$$

Here, ${{ \Sigma }_{\text{imp}}}\left(\text{i}{{\omega}_{n}}\right)$ is the impurity self-energy, expressed in the local orbitals, and ${{ \Sigma }_{\text{dc}}}$ is the double-counting correction. Consequently, the equations of the DMFT loop (see figure 3) are formally the same as in the case without SOC, but the computations now involve matrices which are double in size.

The local Green's function is obtained by projecting the lattice Green's function to the set of correlated orbitals and summing over the full Brillouin zone,

$$\begin{eqnarray}&&\left[G_{\text{loc}}^{\alpha}\left(\text{i}{{\omega}_{n}}\right)\right]_{j{{j}^{\prime}}}^{{{m}_{j}}{{m}_{{{j}^{\prime}}}}}=\underset{\mathbf{k},\nu {{\nu}^{\prime}}}{\sum}\,P_{j,\nu}^{\alpha,{{m}_{j}}}\left(\mathbf{k}\right)~{{G}_{\nu {{\nu}^{\prime}}}}\left(\mathbf{k},\text{i}{{\omega}_{n}}\right)~{{\left[P_{{{j}^{\prime}},{{\nu}^{\prime}}}^{\alpha,{{m}_{{{j}^{\prime}}}}}\left(\mathbf{k}\right)\right]}^{\ast}}.\end{eqnarray} \tag{ 13 }$$

In practice, the summation over momenta is done in the irreducible Brillouin zone only, supplemented by a standard symmetrization procedure, using Shubnikov magnetic point groups [209, 210].

The DMFT equations are solved iteratively: starting from an initial local Green's function $G_{\text{loc}}^{\alpha}\left(\text{i}{{\omega}_{n}}\right)$ (obtained from the 'pure' Kohn–Sham lattice Green's function using equation (13)), the Green's function ${{\mathcal{G}}_{0}}\left(\text{i}{{\omega}_{n}}\right)$ of the effective environment in the impurity model is constructed. The impurity model is solved, allowing the evaluation of the local self-energy of the solid (see equation (11)) and a new lattice Green's function $G\left(\mathbf{k},\text{i}{{\omega}_{n}}\right)$. The latter can then be projected again onto the correlated subset and the cycle is repeated until convergence is reached.

The present implementation is within a full-potential linearized augmented plane wave (FLAPW) framework, as realized in the Wien2k package [208]. With respect to the existing DFT+DMFT implementation [180] in this context, the main changes concern the projection technique for building the correlated orbitals: as discussed above, one has to take care of the fact that spin is no longer a good quantum number, leading to the more general construction of localized 'spin-orbitals'. The necessary modifications in the construction of the projectors are reviewed in the following.

As in the case without SOC, we still use the Kohn–Sham states within a chosen energy window $\mathcal{W}$ to form the Wannier-like functions that are treated as correlated orbitals, and the construction of the Wannier projectors is done in two steps. First, auxiliary Wannier projectors $\tilde{P}_{\ell m,\nu}^{\alpha,\sigma}\left(\mathbf{k}\right)$ are calculated—separately for each $|\phi _{\nu \mathbf{k}}^{\sigma}\rangle$ term—from the following expression:

$$\begin{eqnarray}\begin{array}{*{35}{l}} \tilde{P}_{\ell m,\nu}^{\alpha,\sigma}\left(\mathbf{k}\right) & = & \langle u_{\ell}^{\alpha,\sigma}\left({{E}_{1}}\ell \right)Y_{m}^{\ell}|{{\psi}_{\mathbf{k}\nu}}\rangle \\ {} & = & A_{\ell m}^{\nu \alpha}\left(\mathbf{k},\sigma \right)+\underset{{{n}_{\text{LO}}}=1}{\overset{{{N}_{\text{LO}}}}{\sum}}\,c_{\text{LO}}^{\nu,\sigma}C_{\ell m}^{\alpha,\text{LO}}\mathcal{O}_{\ell m,{{\ell}^{\prime}}{{m}^{\prime}}}^{\alpha,\sigma}. \\\end{array}\end{eqnarray} \tag{ 14 }$$

A description of the augmented plane wave (APW) basis can be found in [180]. We use the same notations e.g. for the coefficients $A_{\ell m}^{\nu \alpha}\left(\mathbf{k},\sigma \right)$ and the overlap matrix $\mathcal{O}_{\ell m,{{\ell}^{\prime}}{{m}^{\prime}}}^{\alpha,\sigma}$ as introduced there.

One performs an orthonormalization step in order to get the Wannier projectors $P_{\ell m,\nu}^{\alpha,\sigma}\left(\mathbf{k}\right)$. The overlap matrix $\left[O\left(\mathbf{k}\right)\right]_{(m\sigma ),\left({{m}^{\prime}}{{\sigma}^{\prime}}\right)}^{\alpha,{{\alpha}^{\prime}}}$ between the correlated $\ell$ orbitals is defined by:

$$\begin{eqnarray}\begin{array}{*{35}{l}} \left[O\left(\mathbf{k}\right)\right]_{(m\sigma ),\left({{m}^{\prime}}{{\sigma}^{\prime}}\right)}^{\alpha,{{\alpha}^{\prime}}} & = & \underset{\nu ={{\nu}_{\min}}\left(\mathbf{k}\right)}{\overset{{{\nu}_{\max}}\left(\mathbf{k}\right)}{\sum}}\,\tilde{P}_{\ell m,\nu}^{\alpha,\sigma}\left(\mathbf{k}\right)\tilde{P}_{\ell {{m}^{\prime}},\nu}^{{{\alpha}^{\prime}},{{\sigma}^{\prime}}\ast}\left(\mathbf{k}\right), \\\end{array}\end{eqnarray} \tag{ 15 }$$

leading to the final projectors:

$$\begin{eqnarray}&&P_{\ell m,\nu}^{\alpha,\sigma}\left(\mathbf{k}\right)=\underset{{{\alpha}^{\prime}},{{m}^{\prime}},{{\sigma}^{\prime}}}{\sum}\,\left\{{{\left[O\left(\mathbf{k}\right)\right]}^{-1/2}}\right\}_{(m\sigma ),\left({{m}^{\prime}}{{\sigma}^{\prime}}\right)}^{\alpha,{{\alpha}^{\prime}}}\tilde{P}_{\ell {{m}^{\prime}}\nu}^{{{\alpha}^{\prime}},{{\sigma}^{\prime}}}\left(\mathbf{k}\right),\end{eqnarray} \tag{ 16 }$$

which are then further transformed into a j,m_j basis as described above (see equation (9)).

Hubbard interactions U—obtained as the static ($\omega =0$) limit of the on-site matrix element $\langle |{{W}^{\text{partial}}}|\rangle$ within the 'constrained random phase approximation' (cRPA)—have by now been obtained for a variety of systems, ranging from transition metals [211] to oxides [204, 212–215], pnictides [181, 186, 216, 217], f-electron elements [218] and compounds [187], to surface systems [219], and several implementations within different electronic structure codes and basis sets have been done, e.g. within linearized muffin tin orbitals [211, 220], maximally localized Wannier functions [212, 216, 221] (as elaborated in [222]), or localized orbitals constructed from projected atomic orbitals [204]. The implementation into the framework of the Wien2k package [204] made it possible for Hubbard U's be calculated for the same orbitals as the ones used in subsequent DFT+DMFT calculations, and, to our knowledge, [21] was indeed the first work using in this way consistently calculated Hubbard interactions in a DFT+DMFT calculation. Systematic calculations investigating the basis set dependence for a series of correlated transition metal oxides revealed further interesting trends, depending on the choice of the low-energy subspace. In contrast to common belief until then, Hubbard interactions increase, for example, with the principal quantum number when low-energy effective models encompassing only the t_2g orbitals are employed. These trends can be rationalized by two counteracting mechanisms, the increasing extension of the orbitals with increasing principal quantum number and the less efficient screening by oxygen states [204]. We will come back to this point below, in the context of the cRPA calculations for our target compounds.

In the following, we review the specificities involved when determining the Hubbard interactions for our target spin–orbit compounds. We hereby use the same notations as in [204].

We start from the standard Hubbard–Kanamori Hamiltonian H_int which allows us to describe the interactions between t_2g orbitals within a Hamiltonian restricted to the t_2g-space:

$$\begin{eqnarray}\begin{array}{*{35}{l}} {{H}_{\text{int}}} & = & \mathcal{U}\underset{m}{\sum}\,{{n}_{m\uparrow}}{{n}_{m\downarrow}}+{{\mathcal{U}}^{\prime}}\underset{m<n,\sigma}{\sum}\,{{n}_{m\sigma}}{{n}_{n\bar{\sigma}}} \\ {} & {} & +\,\left({{\mathcal{U}}^{\prime}}-\mathcal{J}\right)\underset{m<n,\sigma}{\sum}\,{{n}_{m\sigma}}{{n}_{n\sigma}} \\ {} & {} & -\,\mathcal{J}\underset{m<n,\sigma}{\sum}\,\left[c_{m\sigma}^{\dagger}{{c}_{m\bar{\sigma}}}c_{n\bar{\sigma}}^{\dagger}{{c}_{n\sigma}}+c_{m\sigma}^{\dagger}c_{m\bar{\sigma}}^{\dagger}{{c}_{n\sigma}}{{c}_{n\bar{\sigma}}}\right], \\\end{array}\end{eqnarray} \tag{ 17 }$$

where $\mathcal{U}$ is the intra-orbital Coulomb repulsion term and ${{\mathcal{U}}^{\prime}}$ ($=\mathcal{U}-2\mathcal{J}$ with cubic symmetry) the inter-orbital Coulomb interaction which is reduced by Hund's exchange $\mathcal{J}$. (m and n run over the three t_2g orbitals and σ stands for the spin).

To draw the link between the cRPA calculations and this model Hamiltonian, the terms $\mathcal{U}$, ${{\mathcal{U}}^{\prime}}$ and $\mathcal{J}$ are understood as the Slater-symmetrized effective interactions in the t_2g subspace, related to the Slater integrals F⁰, F² and F⁴ as:

$$\begin{eqnarray}\begin{array}{*{35}{l}} \mathcal{U}={{F}^{0}}+\frac{4}{49}\left({{F}^{2}}+{{F}^{4}}\right) & \quad \text{and}\quad & \mathcal{J}=\frac{3}{49}{{F}^{2}}+\frac{20}{441}{{F}^{4}}. \\\end{array}\end{eqnarray} \tag{ 18 }$$

The last relation ${{\mathcal{U}}^{\prime}}={{F}^{0}}-\frac{2}{49}{{F}^{2}}-\frac{4}{441}{{F}^{4}}$ is redundant since ${{\mathcal{U}}^{\prime}}=\mathcal{U}-2\mathcal{J}$.

One now transforms H_int into the ${{j}_{\text{eff}}}$ basis using the unitary matrix transformation $\mathcal{S}_{j,lm}^{{{m}_{j}},\sigma}$. Keeping only density-density terms, H_int becomes:

$$\begin{eqnarray}&&{{H}_{\text{int}}}=\frac{1}{2}\underset{j,{{m}_{j}}}{\sum}\,\underset{{{j}^{\prime}},{{m}_{{{j}^{\prime}}}}}{\sum}\,U_{j{{j}^{\prime}}}^{{{m}_{j}}{{m}_{{{j}^{\prime}}}}}{{n}_{j,{{m}_{j}}}}{{n}_{j,{{m}_{{{j}^{\prime}}}}}}.\end{eqnarray} \tag{ 19 }$$

Here, the index j is a shortcut notation for the ${{j}_{\text{eff}}}=\left\{3/2,1/2\right\}$ quantum number and ${{m}_{j}}=\left\{\pm 3/2,\pm 1/2\right\}$. The reduced interaction matrix $U_{j{{j}^{\prime}}}^{{{m}_{j}}{{m}_{{{j}^{\prime}}}}}$ has the following form:

$$\begin{eqnarray}U_{j{{j}^{\prime}}}^{{{m}_{j}}{{m}_{{{j}^{\prime}}}}}=U_{j{{j}^{\prime}}}^{{{{\bar{m}}}_{j}}{{{\bar{m}}}_{{{j}^{\prime}}}}}=\left(\begin{array}{c|cc} 0 & \mathcal{U}-2\mathcal{J} & \mathcal{U}-\frac{5}{3}\mathcal{J} \\ \hline \mathcal{U}-2\mathcal{J} & 0 & \mathcal{U}-\frac{7}{3}\mathcal{J} \\ \mathcal{U}-\frac{5}{3}\mathcal{J} & \mathcal{U}-\frac{7}{3}\mathcal{J} & 0 \\\end{array}\right)\\ U_{j{{j}^{\prime}}}^{{{m}_{j}}{{{\bar{m}}}_{{{j}^{\prime}}}}}=U_{j{{j}^{\prime}}}^{{{{\bar{m}}}_{j}}{{m}_{{{j}^{\prime}}}}}=\left(\begin{array}{c|cc} \mathcal{U}-\frac{4}{3}\mathcal{J} & \mathcal{U}-\frac{8}{3}\mathcal{J} & \mathcal{U}-\frac{8}{3}\mathcal{J} \\\hline \mathcal{U}-\frac{8}{3}\mathcal{J} & \mathcal{U}-\mathcal{J} & \mathcal{U}-\frac{7}{3}\mathcal{J} \\ \mathcal{U}-\frac{8}{3}\mathcal{J} & \mathcal{U}-\frac{7}{3}\mathcal{J} & \mathcal{U}-\mathcal{J} \\\end{array}\right)\end{eqnarray} \tag{ 20 }$$

We use the standard convention that ${{\bar{m}}_{j}}$ denotes  −m_j, as is usually done for spin degree of freedom. The ordering of the orbitals $|\,j,|{{m}_{j}}|\rangle$ is: $|1/2,1/2\rangle,|3/2,1/2\rangle,|3/2,3/2\rangle$, ${{j}_{\text{eff}}}=1/2$ and ${{j}_{\text{eff}}}=3/2$ blocks are emphasized to ease the reading of the matrices.

For the solution of the quantum impurity problem we apply the continuous-time quantum Monte Carlo method (CTQMC) in the strong-coupling formulation [223]. We are able to perform calculations at room temperature ($\beta =1/{{k}_{\text{B}}}T=40$ eV⁻¹) with reasonable numerical effort. In our calculations, we typically use around $16\times {{10}^{6}}$ Monte Carlo sweeps and 28 k-points in the irreducible Brillouin zone.

Since the CTQMC solver computes the Green's function on the imaginary-time axis, an analytic continuation is needed in order to obtain results on the real-frequency axis. A continuation of the impurity self-energy using a stochastic version of the maximum entropy method [224] yields real and imaginary parts of the retarded self-energy. From those, we calculate the momentum-resolved spectral function $A\left(\mathbf{k},\omega \right)$ using partial projectors introduced in the appendix.

During the calculations we use the fully localized limit (FLL) expression for the double-counting:

$$\begin{eqnarray} &&\Sigma _{j,{{j}^{\prime}}}^{\text{dc}}=\left[\mathcal{U}\left({{N}_{c}}-\frac{1}{2}\right)-\mathcal{J}\left(\frac{1}{2}{{N}_{c}}-\frac{1}{2}\right)\right]{{\delta}_{j{{j}^{\prime}}}},\end{eqnarray} \tag{ 21 }$$

where j and ${{j}^{\prime}}$ run over the ${{j}_{\text{eff}}}$ states and N_c is the total occupancy of the orbitals. (Since each orbital is doubly degenerate in m_j, N_c/2 is used in the term containing J). Moreover, we neglect the off-diagonal terms in the local Green's functions (particularly, we neglect the term between the ${{j}_{\text{eff}}}=1/2$ and the ${{j}_{\text{eff}}}=3/2$ $|{{m}_{j}}|=1/2$ which we checked to be two orders of magnitude smaller than the diagonal terms, in the chosen basis).

The Kohn–Sham band structures of Sr₂IrO₄ and Sr₂RhO₄ within the local density approximation and in the presence of spin–orbit coupling (LDA  +  SO) are represented in figures 4(d) and (e). For Sr₂IrO₄, we use the lattice parameters measured at 295 K in [225], and for Sr₂RhO₄ those measured at 300 K in [226].

Zoom In Zoom Out Reset image size

The LDA  +  SO band structures for Sr₂IrO₄ and Sr₂RhO₄ are very similar, as a consequence of both the structural similarity and the key role of spin–orbit coupling in these compounds. The e_g-states (${{d}_{{{x}^{2}}-{{y}^{2}}}}$ in red and ${{d}_{3{{z}^{2}}-{{r}^{2}}}}$ in yellow) start at about 1–1.5 eV, and are fully separated from the t_2g-manifold which lies around the Fermi level and overlaps at lower energies with the oxygen 2p-states (black). Given the $t_{2g}^{5}$ filling and the four-atom unit cell of both compounds, a metallic solution is obtained within LDA for both Sr₂RhO₄ and Sr₂IrO₄—at variance with experiments for Sr₂IrO₄. Among the t_2g-manifold (in green), only the four highest-lying bands, highlighted in blue, cross the Fermi level: this is suggestive of the existence of a separated half-filled ${{j}_{\text{eff}}}=1/2$ -derived band, which—within a four-atom unit cell—corresponds to a quartet of bands at each k-point. We stress, however, that the true picture is much more subtle: in fact, ${{j}_{\text{eff}}}=1/2$ and ${{j}_{\text{eff}}}=3/2$ overlap (see the band structure between the $\Gamma$ and the M-point for instance) and the identification of the upper four bands as the ${{j}_{\text{eff}}}=1/2$ states is too simplistic. We will come back to this point below.

To get a better understanding of the Kohn–Sham band structures of Sr₂RhO₄ and Sr₂IrO₄, we study artificial compounds where both the structural distortions and the spin–orbit coupling have been switched off. Figures 5(b) and (c) depict the LDA band structure of such 'idealized undistorted Sr₂RhO₄ and Sr₂IrO₄'. Neglecting the rotation of about ${{10}^{\circ}}$ of their IrO₆ and RhO₆ octahedra around the c-axis leads to a K₂NiF₄-type crystal structure, like in Sr₂RuO₄, the well-known LDA band structure of which is plotted in figure 5(a).

Zoom In Zoom Out Reset image size

The similarity of the three band structures is obvious. Around the Fermi level, one distinguishes the three t_2g bands. The d_xy-band (green) reaches out to lower energies and overlaps with the oxygen 2p-states (black). The e_g-states (${{d}_{{{x}^{2}}-{{y}^{2}}}}$ in red and ${{d}_{3{{z}^{2}}-{{r}^{2}}}}$ yellow), higher in energy, cut the Fermi level in both Sr₂IrO₄ and Sr₂RhO₄ due the additional electron remaining in the d-manifold, contrary to Sr₂RuO₄, which has actually a mere $t_{2g}^{4}$-filling. The larger extension of the 5d orbitals (see figure 1) explains the wider bandwidth observed for Sr₂IrO₄ in comparison to Sr₂RhO₄: the d_xy band reaches the value of  −3.5 eV in $\Gamma$, while it remains above  −3 eV for the 4d counterparts. Another consequence of this wider extension is the stronger hybridization between the 5d states with the oxygen p-states, which are located 1 eV lower in energy in Sr₂IrO₄ than in the 4d-TMOs.

Re-introducing the effects of the spin–orbit coupling in Sr₂RhO₄ and Sr₂IrO₄ (but without considering the structural distortions) modifies these Kohn–Sham band structures to those shown in figures 4(a) and (b). The t_2g bands are the most affected, while the e_g bands are slightly shifted as a consequence of the topological change in the t_2g manifold. A detailed study of the character of these band structures confirms the decoupling between e_g and t_2g states (see also [19, 20]). The cubic crystal field at stake in these compounds is indeed much larger than the energy scale associated with the spin–orbit coupling of about ${{\zeta}_{\text{SO}}}\approx 0.4$ eV and ${{\zeta}_{\text{SO}}}\approx 0.2$ eV for Sr₂IrO₄ and Sr₂RhO₄ respectively.

The j_eff picture is thus justified in both Sr₂IrO₄ and Sr₂RhO₄: the t_2g orbitals split into a quartet of ${{j}_{\text{eff}}}=3/2$ states and a higher lying doublet ${{j}_{\text{eff}}}=1/2$ (see figure 2). Each state is doubly degenerate in $\pm {{m}_{j}}$, since we observe the system in its paramagnetic phase at room temperature and the crystal structure has a center of inversion. Therefore we still refer to them as the '${{j}_{\text{eff}}}=1/2$ band' and the two '${{j}_{\text{eff}}}=3/2$ bands' in the following. The three ${{j}_{\text{eff}}}$ bands can easily be identified: the ${{j}_{\text{eff}}}=1/2$ one (light green) lies above the two ${{j}_{\text{eff}}}=3/2$ ones (m_j  =  3/2 in light blue and m_j  =  1/2 in violet). The three j_eff bands are well-separated all along the $\mathbf{k}$-path, and more generally in the whole Brillouin zone. Since the spin–orbit coupling is half the size in Sr₂RhO₄, the splitting between the j_eff bands is reduced by a factor of 2, as one can see, for instance, at X or $\Gamma$.

To draw the link between the 'undistorted' band structures and the realistic ones, we plot in figure 4(c) the LDA  +  SO band structure of the undistorted Sr₂IrO₄ in a supercell containing four unit cells. Each band is now folded four times and we provide a scheme of the two first Brillouin zones in the ${{\mathbf{k}}_{z}}=0$ plane to understand the correspondence between the high-symmetry points of each structure.

Comparing figures 4(c) and (e) highlights the key role of the structural distortion in Sr₂IrO₄: a hybridisation between two neighboring Ir d_xy and ${{d}_{{{x}^{2}}-{{y}^{2}}}}$ orbitals via the in-plane oxygens is now allowed and pushes the t_2g and e_g bands apart. Another consequence of the distortions is the general narrowing of the j_eff bandwidth, which is of crucial importance in driving the compound insulation, as we will see below.

Finally, comparing figures 4(c) and (e) gives more insight into the nature of the four highest-lying bands (blue) of figure 4(e). Along the M  −  −X direction, each quartet of the j_eff bands remain well-separated, ${{j}_{\text{eff}}}=1/2$ and ${{j}_{\text{eff}}}=3/2$ overlap in the other direction $\Gamma -M$ and M  −  X. As a result, the ${{j}_{\text{eff}}}=3/2$ bands cross the Fermi-level closest to the $\Gamma$-point, while the other crossings are due to the ${{j}_{\text{eff}}}=1/2$ bands. The identification of the upper four bands in Sr₂IrO₄ as 'pure' ${{j}_{\text{eff}}}=1/2$ states is thus too simplistic, implying the need for a Hamiltonian containing more than one orbital in a realistic calculation.

The same mechanisms are important in Sr₂RhO₄ even though we do not display the orbital characters here: the four highest-lying bands, highlighted in blue in figure 4(d) exhibit a mixed character of type ${{j}_{\text{eff}}}=1/2$ and ${{j}_{\text{eff}}}=3/2$. Moreover, thanks to the distortions which allow the opening of a gap between t_2g and e_g bands, the LDA  +  SO Fermi surface becomes qualitatively similar to the experimental one; as shown in figure 8(a), they both contain three closed contours: a circular hole-like α-pocket around $\Gamma$, a lens-shaped electron pocket ${{\beta}_{M}}$ and a square-shaped electron pockets ${{\beta}_{X}}$. However, the striking discrepancies in the size of the pockets point out a subtle deficiency in the LDA for Sr₂RhO₄ [19, 20].

We have derived the Wannier functions associated with the ${{j}_{\text{eff}}}$ manifold for both Sr₂IrO₄ and Sr₂RhO₄, using the framework introduced in section 3.1. Because of the mixed character of the four bands that cross the Fermi level in Sr₂IrO₄ and Sr₂RhO₄, the local effective atomic problem used in the DMFT cycle must contain the three j_eff orbitals and thus accommodate five electrons. We construct Wannier functions for the j_eff orbitals from the LDA  +  SO band structure of Sr₂IrO₄ and Sr₂RhO₄, using an energy window [−3.0,0.5] eV for Sr₂IrO₄ and an energy window [−2.67;0.37] eV for Sr₂RhO₄.

Figures 6 and 7 depict the projection of these Wannier functions on the LDA  +  SO band structure. The similarities between figures 6 and 4(c) are numerous, thus confirming our previous band character analysis. Table 5 gives the decomposition of these local Wannier functions on the t_2g manifold and their respective occupation.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

To obtain deeper insights into the nature of these Wannier orbitals, table 4 gives the coefficients of the local Wannier orbitals obtained from the LDA  +  SO band structure of 'undistorted' Sr₂IrO₄ using an energy window [−3.5, 0.8] eV. The results agree well with the standard j_eff picture (see equations (1) and (2)) in both modulus and phase. Discrepancies are mostly due to the elongation of the IrO₆ along the c-axis, which introduces an additional tetragonal field between the t_2g states. This effect also explains the lifting of the degeneracy of the two ${{j}_{\text{eff}}}=3/2$ (${{m}_{j}}=\pm 1/2$ and ${{m}_{j}}=\pm 3/2$) states and implies the reason why the ${{j}_{\text{eff}}}=1/2$ is slightly more than half-filled.

Table 4. Coefficients and occupation (within LDA  +  SO) of the j_eff Wannier orbitals in 'undistorted' Sr₂IrO₄. The discrepancy between these coefficients and those given in equations (1) and (2) are due to the small elongation of the octahedra along the c-axis.

'Undistorted' Sr2IrO4	$|\frac{1}{2},\pm \frac{1}{2}\rangle$	$|\frac{3}{2},\pm \frac{1}{2}\rangle$	$|\frac{3}{2},\pm \frac{3}{2}\rangle$
$|$dxy $\uparrow \downarrow \rangle$	±0.6605	+0.7508	0
$|$dxz $\uparrow \downarrow \rangle$	±0.5309 i	−0.4670 i	−0.7071 i
$|$dyz $\uparrow \downarrow \rangle$	+0.5309	$\mp$0.4670	$\mp$0.7071
Occupation (LDA  +  SO)	1.20	1.92	1.86

Because of the hybridization between the d_xy and ${{d}_{{{x}^{2}}-{{y}^{2}}}}$ orbitals in the distorted structures, we had to define in practice 'effective ${{j}_{\text{eff}}}=1/2$ and ${{j}_{\text{eff}}}=3/2$ $|{{m}_{j}}|=1/2$ states', which remain close to the atomic j_eff picture but take into account a small amount of ${{d}_{{{x}^{2}}-{{y}^{2}}}}$ character (see table 5). The coefficients have been calculated such that the density matrix of the local atomic problem is the closest possible to the diagonal form⁴. In addition to the hybridization, the construction of the 'effective j_eff' also takes into account the tetragonal crystal field due to the elongation of the octahedra in each crystal structure; this explains the discrepancies with the standard coefficients given in equations (1) and (2). We note that the coefficients obtained for the ${{j}_{\text{eff}}}=1/2$ state of Sr₂IrO₄ are equivalent to those obtained in the AF phase in [139].

Table 5. Modulus of the coefficients of the j_eff Wannier orbitals in Sr₂IrO₄ and Sr₂RhO₄. The occupation within LDA  +  SO and the charge within LDA  +  SO+DMFT of each atomic Wannier orbital are also provided, showing how electronic correlations enhance the spin–orbital polarization.

	Sr2IrO4			Sr2RhO4
Wannier orbitals	$|\frac{1}{2},\pm \frac{1}{2}\rangle$	$|\frac{3}{2},\pm \frac{1}{2}\rangle$	$|\frac{3}{2},\pm \frac{3}{2}\rangle$	$|\frac{1}{2},\pm \frac{1}{2}\rangle$	$|\frac{3}{2},\pm \frac{1}{2}\rangle$	$|\frac{3}{2},\pm \frac{3}{2}\rangle$
$|$${{d}_{{{x}^{2}}-{{y}^{2}}}}$ $\uparrow \downarrow \rangle$	0.0388	0.0766	0	0.0100	0.0302	0
$|$d xy $\uparrow \downarrow \rangle$	0.4499	0.8889	0	0.3153	0.9485	0
$|$d xz $\uparrow \downarrow \rangle$	0.6309	0.3193	0.7071	0.6710	0.2231	0.7071
$|$d yz $\uparrow \downarrow \rangle$	0.6309	0.3193	0.7071	0.6710	0.2231	0.7071
occupation (LDA  +  SO)	1.16	1.98	1.84	1.42	1.96	1.64
charge (LDA  +  SO+DMFT)	1.02	2.00	1.98	1.26	1.98	1.76

Finally, comparing the occupation of the orbitals in tables 4 and 5 highlights again the role of the hybridisation between the d_xy and ${{d}_{{{x}^{2}}-{{y}^{2}}}}$ orbitals which pushes the band ${{j}_{\text{eff}}}=3/2$ $|{{m}_{j}}|=1/2$ further below the Fermi level close to $\Gamma$. As a result, the four bands that cross the Fermi level are formed only by the ${{j}_{\text{eff}}}=1/2$ and ${{j}_{\text{eff}}}=3/2$ $|{{m}_{j}}|=3/2$ orbitals and the ${{j}_{\text{eff}}}=1/2$ tend to be close to half-filling. Similar conclusions were drawn for the AF phase within a variational cluster approximation (VCA) approach in [140]. Similar conclusions hold for Sr₂RhO₄.

After defining the j_eff Wannier orbitals, we evaluate the local Coulomb interaction in the effective atomic problem within cRPA [204, 211], as explained in section 3.3. For reasons of computational resources, the cRPA calculations were performed in the case without distortions (without the rotations of the octahedra, hence considering only one formula-unit in a unit-cell) and without SOC. To mimic the effect of the distortions, the e_g states are shifted up to their energetic position in the presence of distortions. We find $\mathcal{U}=2.54$ eV and $\mathcal{J}=0.23$ eV for Sr₂IrO₄ and $\mathcal{U}=1.94$ eV and $\mathcal{J}=0.23$ eV for Sr₂RhO₄. These parameters lead to the following local interaction matrices for Sr₂IrO₄:

$$\begin{eqnarray}U_{j{{j}^{\prime}}}^{{{m}_{j}}{{m}_{{{j}^{\prime}}}}}=\left(\begin{array}{c|cc} 0 & 2.08 & 2.21 \\\hline 2.08 & 0 & 1.93 \\ 2.21 & 1.93 & 0 \\\end{array}\right)\end{eqnarray} \tag{ 22 }$$

$$\begin{eqnarray}U_{j{{j}^{\prime}}}^{{{m}_{j}}{{{\bar{m}}}_{{{j}^{\prime}}}}}=\left(\begin{array}{c|cc} 2.25 & 1.98 & 1.90 \\\hline 1.98 & 2.38 & 2.03 \\ 1.90 & 2.03 & 2.31 \\\end{array}\right)\end{eqnarray} \tag{ 23 }$$

and for Sr₂RhO₄:

$$\begin{eqnarray}U_{j{{j}^{\prime}}}^{{{m}_{j}}{{m}_{{{j}^{\prime}}}}}=\left(\begin{array}{c|cc} 0 & 1.48 & 1.66 \\ \hline 1.48 & 0 & 1.29 \\ 1.66 & 1.29 & 0 \\\end{array}\right)\end{eqnarray} \tag{ 24 }$$

$$\begin{eqnarray}U_{j{{j}^{\prime}}}^{{{m}_{j}}{{{\bar{m}}}_{{{j}^{\prime}}}}}=\left(\begin{array}{c|cc} 1.67 & 1.32 & 1.27 \\ \hline 1.32 & 1.86 & 1.46 \\ 1.27 & 1.46 & 1.71 \\\end{array}\right)\end{eqnarray} \tag{ 25 }$$

where the values are in eV and the ordering of the $|\,j,|{{m}_{j}}|\rangle$ orbitals is: $|1/2,1/2\rangle$, $|3/2,1/2\rangle$, $|3/2,3/2\rangle$ and ${{\bar{m}}_{j}}$ denotes  −m_j. We remind the reader that $U_{j{{j}^{\prime}}}^{{{m}_{j}}{{m}_{{{j}^{\prime}}}}}=U_{j{{j}^{\prime}}}^{{{{\bar{m}}}_{j}}{{{\bar{m}}}_{{{j}^{\prime}}}}}$ and $U_{j{{j}^{\prime}}}^{{{m}_{j}}{{{\bar{m}}}_{{{j}^{\prime}}}}}=U_{j{{j}^{\prime}}}^{{{{\bar{m}}}_{j}}{{m}_{{{j}^{\prime}}}}}$. Since we have used 'effective j_eff' Wannier orbitals instead of the standard definition given in equations (1) and (2), some discrepancies with the formulae given in equation (20) and in [22] can be observed. Contrary to common belief, the Hubbard interactions are smaller in the 4d-TMO than in its 5d-counterpart. This might seem counterintuitive at first sight, since the 5d-orbitals are more extended than the 4d ones, but finds its explanation in more efficient screening in the 4d material: As shown in figures 4(d) and (e), the hybridization between the Rh-4d states and the O-2p is weaker in Sr₂RhO₄ than in Sr₂IrO₄. Correspondingly, the energetic position of the O-2p bands is closer to the Fermi level by about 1 eV, and as a result, the Coulomb interactions are screened more efficiently in Sr₂RhO₄ than in Sr₂IrO₄, explaining the observed trend.

DFT+DMFT calculations following the procedure described in section 3.1 indeed find an insulating solution for Sr₂IrO₄ and a correlated metal for Sr₂RhO₄ [21], in agreement with experiment. The difference in the metallic versus insulating nature of Sr₂RhO₄ and Sr₂IrO₄ can be traced back to the different spin–orbital polarization in the three j_eff orbitals, which is enhanced by Coulomb correlations.

The occupations of the j_eff Wannier orbitals within LDA  +  SO and LDA  +  SO+DMFT are provided in table 5. In Sr₂IrO₄, one detects a considerable spin–orbital polarization already at the LDA  +  SO level: the four ${{j}_{\text{eff}}}=3/2$ states are almost filled with ${{n}_{3/2,|1/2|}}=1.98$ and ${{n}_{3/2,|3/2|}}=1.84$ while the ${{j}_{\text{eff}}}=1/2$ states thus slightly exceed half-filling with n_1/2  =  1.16 (as in the 'ideal undistorted' case). Taking into account Coulomb correlations within DMFT opens a gap of about 0.26 eV [21] and enhances the spin–orbital polarization, such as to fill the ${{j}_{\text{eff}}}=3/2$ states entirely, leading to a half-filled ${{j}_{\text{eff}}}=1/2$ state. This is thus the celebrated '${{j}_{\text{eff}}}=1/2$ -picture' [16], which comes out here as a result of the calculations, rather than being an input as in most model Hamiltonian calculations.

A different picture emerges for Sr₂RhO₄ according to table 5: while the spin–orbital occupations display some polarization at the LDA  +  SO level, the smaller SOC—and thus the smaller effective splitting between the j_eff bands—leads to a picture where only the ${{j}_{\text{eff}}}=3/2$ $|{{m}_{j}}|=1/2$ state is entirely filled, while both ${{j}_{\text{eff}}}=3/2$ $|{{m}_{j}}|=3/2$ and ${{j}_{\text{eff}}}=1/2$ live at the Fermi level. This spin–orbital polarization is enhanced by Coulomb correlations—just as in Sr₂IrO₄—but this enhancement is not enough to fill both ${{j}_{\text{eff}}}=3/2$ states entirely and obtain a half-filled ${{j}_{\text{eff}}}=1/2$ state. The higher effective degeneracy, together with the smaller value of $\mathcal{U}$, eventually leaves Sr₂RhO₄ metallic.

We now turn to the calculated spectral function of the spin–orbital correlated metal Sr₂RhO₄ that we analyze in comparison to experiment.

Figure 8 depicts the Fermi surface of Sr₂RhO₄ within LDA  +  SO (left panel) and LDA  +  SO+DMFT (right panel) in the ${{\mathbf{k}}_{z}}=0$ plane, on which we superimpose the experimental measurement from [120]. Table 6 gives more quantitative insight to ease the comparison between the different topologies. All three Fermi surfaces, the two theoretical ones and the experimental one, are qualitatively similar with three closed contours: a circular hole-like α-pocket around $\Gamma$, a lens-shaped electron pocket ${{\beta}_{M}}$ and a square-shaped electron pockets ${{\beta}_{X}}$. These two structures merge in the undistorted tetragonal zone (dashed blue line in figure 8) to a large electron-like pocket β.

Zoom In Zoom Out Reset image size

Table 6. Comparison of the Fermi surface (FS) parameters evaluated within LDA  +  SO, within LDA  +  SO+DMFT and ARPES [120]. For each α, ${{\beta}_{X}}$ and ${{\beta}_{M}}$ pocket, the FS volume A is defined as a percentage of the two-dimensional BZ volume (using the experimental lattice parameters (a  =  5.45 Å)). The Fermi velocity $\hbar \overline{{{v}_{\text{F}}}}$ is obtained from the slope of the band dispersion at the Fermi level. The cyclotron mass ${{m}^{\ast}}/{{m}_{e}}$ is calculated using the same method as described in [120]: ${{m}^{\ast}}\overline{{{v}_{\text{F}}}}=\hbar \sqrt{A/\pi}$.

	α			${{\beta}_{X}}$			${{\beta}_{M}}$
	LDA	DMFT	Exp.	LDA	DMFT	Exp.	LDA	DMFT	Exp.
FS volume A (% BZ)	18.4	10.1	6.1(4)	4.5	6.2	8.1(5)	10.0	7.6	7.4(4)
$\hbar \overline{{{v}_{\text{F}}}}$ (eV · Å)	1.252	0.645	0.41(4)	1.260	0.674	0.55(6)	1.260	0.674	0.61(6)
m* (me)	1.70	2.44	3.0(3)	0.83	1.83	2.6(3)	1.24	2.02	2.2(2)

Comparing figures 8(a) and (b) highlights the key role of electronic correlations: they decrease the radius of the α pocket from 0.26–0.29 ${{{\mathring{\rm A}}}^{-1}}$ to 0.21 ${{{\mathring{\rm A}}}^{-1}}$ and decrease the radius of the large β pocket from 0.69–0.72 ${{{\mathring{\rm A}}}^{-1}}$ to 0.67–0.70 ${{{\mathring{\rm A}}}^{-1}}$, thus enlarging the ${{\beta}_{M}}$ and ${{\beta}_{X}}$ pockets such that their volumes are well-reproduced within LDA  +  SO+DMFT (see table 6). As a result, the agreement between LDA  +  SO+DMFT data and the experimental measurements becomes quantitatively excellent.

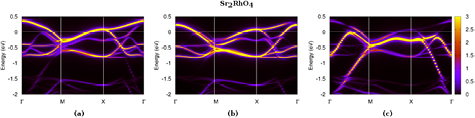
To go further in the analysis, figure 9 depicts the momentum-resolved spectral function, as well as its orbital-resolved version. The completely filled ${{j}_{\text{eff}}}=3/2$ $|{{m}_{j}}|=1/2$ state is visible (panel (d)), as well as the partially filled character of the ${{j}_{\text{eff}}}=3/2$ $|{{m}_{j}}|=3/2$ (panel (c)) and ${{j}_{\text{eff}}}=1/2$ states (panel (b)). A detailed comparison with angle-resolved photoemission data from [121] (blue dashed line on the figure) shows that the band dispersion around the Fermi level is well-reproduced, while some discrepancies are observed for the structures experimentally observed along $\Gamma -X$ and $\Gamma -M$ at lower energy. These features, reminiscent of the ${{j}_{\text{eff}}}=3/2$ $|{{m}_{j}}|=1/2$ bands, are indeed about 0.05 eV higher in energy in our calculated spectral function.

Zoom In Zoom Out Reset image size

From figures 9(b) and (c), one observes that the Fermi level is crossed by the renormalized ${{j}_{\text{eff}}}=3/2$ $|{{m}_{j}}|=3/2$ band at 0.20 ${{{\mathring{\rm A}}}^{-1}}$ along $\Gamma -X$ and at 0.21 ${{{\mathring{\rm A}}}^{-1}}$ along $\Gamma -M$, while the renormalized ${{j}_{\text{eff}}}=1/2$ band is responsible for all other crossings. This allows us to label the hole-like α-pocket as being of ${{j}_{\text{eff}}}=3/2$ $|{{m}_{j}}|=3/2$ type, whereas the two other pockets ${{\beta}_{M}}$ and ${{\beta}_{X}}$ are mostly of type ${{j}_{\text{eff}}}=1/2$. Using the quasiparticle weight of each state (Z_1/2  =  0.535 and ${{Z}_{3/2,|3/2|}}=0.675$), we evaluate the Fermi velocity at each crossing along the path $\left[\Gamma MX \Gamma \right]$: we find a huge variation in the values depending on $\mathbf{k}$ and give in table 6 their mean value over the Brillouin zone. Finally, using the same method as described in [120], we evaluate the cyclotron mass ${{m}^{\ast}}/{{m}_{e}}$ based on the approximate formula used there: ${{m}^{\ast}}\overline{{{v}_{\text{F}}}}=\hbar \sqrt{A/\pi}$. The DMFT results shown in table 6 show a substantial improvement over DFT when compared to experiments.