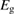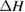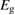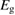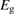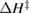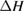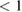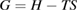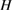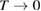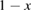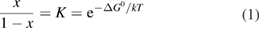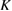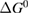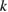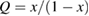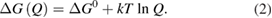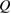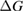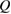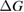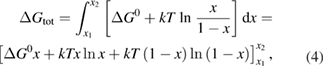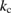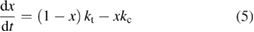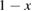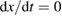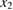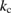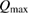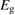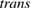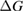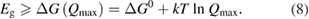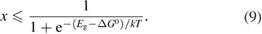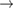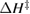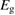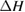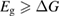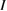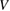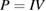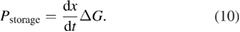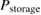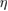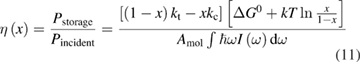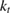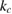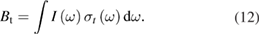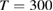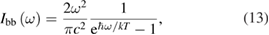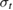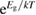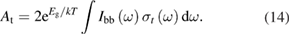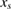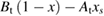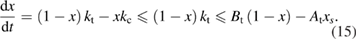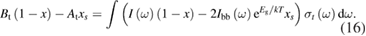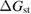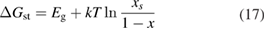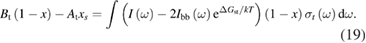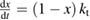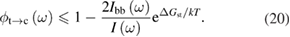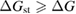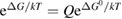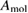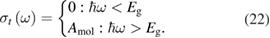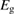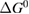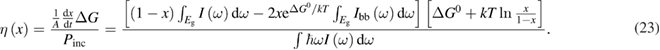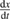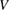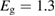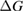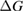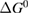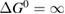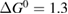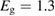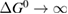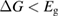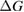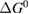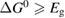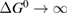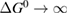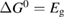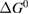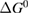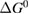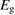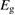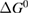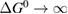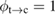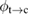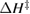Thermodynamic limits to energy conversion in solar thermal fuels

Solar thermal fuels (STFs) are an unconventional paradigm for solar-energy harvesting and storage, which provides long-term storage as chemical energy and later release as heat. Unlike in photovoltaics (PV), incident solar photons are not converted to electricity but rather drive a reversible structural change in a material. Molecules that undergo a structural change on absorption of light (photoisomerization) are referred to as 'photochromic', since in general the optical absorption spectrum will change with the new structure. (STFs have also been referred to as 'molecular solar thermal' [1].) Various classes of photochromic molecules are known, such as azobenzene, spiropyran/merocyanine, norbornadiene/quadricyclane, and fulvalene (tetracarbonyl) diruthenium [2]. The basic concept was developed decades ago [3], but available molecular materials did not have adequate performance to enable applications, with regard to metrics such as cyclability, stored energy density, visible light absorption, and cost. Modern advances in nanoscience and atomistic computation and design have given new approaches and interest in this idea, as molecular and nanoscale templates and functionalization have produced increases in stored energy density and lifetime [4–11], and performance of solution-based [1, 12] and solid-state devices [13] have been demonstrated. While current devices deliver stored energy as heat, it may also be possible to use photo-induced mechanical motion [14] to convert the stored energy to other forms [15].

The question of the actual efficiency of STF devices, taking together all the relevant material properties, is a crucial one for assessing the relevance of STFs as an approach for solar-energy conversion, especially by comparison to the more established PV, solar thermal, and solar fuels technologies. However, the efficiency has remained unclear: it has been estimated experimentally in only a few cases [1], and given only preliminary and somewhat limited theoretical analysis in the literature [6, 16, 17]. These works have focused primarily on enthalpy but not considered free energy or the key roles of chemical equilibrium, entropy, and temperature, and have relied on idealized or arbitrary parameters for simplicity. Other work has analyzed the photochemistry in detail but not overall device efficiency [3, 18], or considered schemes more general than STFs [19].

In the field of PV, the well-known work of Shockley and Queisser [20] (hereafter, SQ) bridged the gap between analysis of the specific PV materials, and analysis of general heat engines, to find an efficiency limit for the single-junction PV scheme under sunlight, with constraints not from the properties of current materials but from rigorous thermodynamics. They found that the maximum efficiency attainable for a single-junction cell at 300 K in unconcentrated sunlight is 32%, achieved for a bandgap of 1.27 eV.

In this paper, we follow the SQ analysis to derive formulae for the efficiency of STFs and their limits from rigorous thermodynamic considerations. We underscore the detailed analogy to PV, including $I$–$V$ characteristics, despite the differing device operation; show the importance of the free energy; find a limit to the quantum yield of photoisomerization; and demonstrate the possibility of attaining the same limit as SQ for conversion of solar energy to stored chemical energy in an STF device. (By contrast, previous analyses showed significantly lower limits.)

Previous to the SQ work, researchers had found PV efficiency limits based on empirical models, which could only demonstrate where the current approaches to silicon solar cells might lead, but could not show the potential of other ideas that had not yet been considered. Understanding the SQ limit suggested the benefit of new strategies for photovoltaics such as spectrum splitting, multi-junctions, intermediate bands, hot carriers, multiple exciton generation, singlet fission, etc [21], or hybrid devices using conversion to heat as well as electricity [22]. Similarly this analysis can inspire new paradigms for STFs—indeed, upconversion [23] and hybrid solar thermal devices [24] have already been examined in the context of STFs—and point the way to overcoming the limits we show here.

We begin by reviewing the SQ analysis and showing the analogy between PV and STFs. The basic processes are diagrammed in figure 1. The SQ limit considers that each photon incident on the cell is not absorbed if it is below the band gap ('below-gap losses'); if it is above the band gap, it is absorbed, but the resulting electron and hole quickly relax to the band edges and provide only energy equal to the band gap ('above-gap losses'). These two loss mechanisms are the most important, and certainly apply to STFs. Consider the schematic potential-energy surfaces for azobenzene. Initially light must have energy of at least $E_{\rm g}$ to be absorbed by trans, and then quickly loses any excess energy beyond that, as in a solar cell. However, after that further losses occur: the excitation relaxes on the excited-state surface to the minimum. De-excitation to the ground state causes a further loss, as does relaxation on the ground-state surface to cis, at an enthalpy $\Delta H$ above trans. We note that a distinction between absorption threshold and useful energy is in common with systems that relax to a dark state, such as an indirect gap in a semiconductor or a triplet molecular state.

Zoom In Zoom Out Reset image size

The simple model above does not take into account two other important loss mechanisms considered by SQ: radiative recombination, and voltage loss. While non-radiative recombination might be reducible to zero, radiative recombination is absolutely required by detailed balance: if the cell can absorb, it can emit. Thermally excited electron–hole pairs, populated according to the Boltzmann distribution at 300 K, can recombine and emit photons. Moreover, the population is dependent on the voltage, thus defining the $I$–$V$ characteristics of the cell, as a maximum-power point has to be found between the extremes of open circuit with maximum voltage but no current, and short circuit with no voltage and maximum current. The voltage loss is the difference between the open-circuit voltage and the voltage at maximum power.

Since STFs are not electrical devices, these considerations may seem unrelated, but in fact the analogy with photovoltaics can be carried quite far. Corresponding concepts are compared in table 1. To begin, consider the Gibbs free energy $G = H - TS$ of a solution of an STF molecule. For concreteness, we will refer to the stable isomer as trans and the higher-energy metastable isomer as cis, as for azobenzene, but the analysis is general. The Gibbs free energy change is the relevant thermodynamic quantity for determining the maximum amount of work that can be done by a reaction at constant pressure and temperature [25], as in the STF discharge, and its sign determines whether a process is spontaneous or not. Previous STF works have analyzed only the enthalpy $H$, thus working in some sense in a $T \rightarrow 0$ limit.

Let the fraction of molecules which are in the cis isomer be $x$ and in the trans isomer be $1 - x$. (We assume a dilute solution to ensure 'ideal solution' behavior; at high concentrations or with strong interactions between solute molecules, different equations than those below, with more parameters, may be required, such as the 'regular solution' model [25].) Then thermal equilibrium in the dark will satisfy

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \frac{x}{1 - x} = K = {\rm e}^{- \Delta G^{0} / k T} \nonumber \end{align} \tag{ 1 }$$

where $K$ is the equilibrium constant, $\Delta G^{0}$ is the difference in Gibbs free energy per molecule between cis and trans under standard conditions, $k$ is the Boltzmann constant, and $T$ is the temperature of the solution. The Gibbs free energy will vary as a function of the ratio between cis/trans fractions $Q = x/(1-x)$, according to

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \Delta G \left( Q \right) = \Delta G^{0} + k T~{\rm ln }~ Q. \nonumber \end{align} \tag{ 2 }$$

In equilibrium, $Q$  =  $K$, and then

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \Delta G \left( K \right) = \Delta G^{0} + k T~{\rm ln }~ K = 0. \nonumber \end{align} \tag{ 3 }$$

From this equation, we can observe that an STF solution in equilibrium irradiated with sunlight has initial energy storage rate of zero, since $\Delta G = 0$, even though the rate of conversion of molecules is maximum. This condition is thus analogous to the short-circuit condition for photovoltaics, since $\Delta G$ corresponds to voltage and conversion rate to current. As $Q$ increases due to the incident light, $\Delta G$ too will grow. This important effect was not considered in previous analyses [6, 16, 17]. We can integrate to find the total free energy stored, when cycling between two compositions $x_1$ and $x_2$:

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \label{eq:storage} \Delta G_{\rm tot} = \int_{x_1}^{x_2} \left[ \Delta G^{0} + k T {\rm\ ln \ } \frac{x}{1-x} \right] {\rm d}x =\nonumber \\ \left[ \Delta G^{0} x + kT x \ln x + kT \left(1 - x\right) \ln \left( 1 - x\right) \right]_{x_1}^{x_2}, \nonumber \end{align} \tag{ 4 }$$

a familiar expression from entropy of mixing, depending on temperature and fraction $x$ as well as the intrinsic molecular quantity $\Delta G^{0}$.

The rate of conversion of molecules from cis to trans, given rate constants $k_{\rm c}$ and $k_{\rm t}$ under the given illumination conditions, is

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \frac{{\rm d}x}{{\rm d}t} = \left( 1 - x \right) k_{\rm t} - x k_{\rm c} \nonumber \end{align} \tag{ 5 }$$

where

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle k_{\rm t} = \int I \left( \omega \right) \sigma_{\rm t} \left( \omega \right) \phi_{{\rm t} \rightarrow {\rm c}} \left( \omega \right) {\rm d}\omega \label{eq:k_t} \nonumber \end{align} \tag{ 6 }$$

and similarly for cis. $I$ is the incident solar photon flux (photons per time per area), which we approximate as the blackbody spectrum at 6000 K, as in the SQ analysis. $\sigma_{\rm t}$ is the absorption cross-section, and $\phi_{{\rm t} \rightarrow {\rm c}}$ is the photoisomerization quantum yield from trans to cis.

Thus the conversion rate declines over time as $1 - x$ falls and $x$ grows. Eventually a new equilibrium in the presence of the light is established, called the 'photostationary state' [26] in which ${\rm d}x/{\rm d}t = 0$, in which case the ratio of fractions must be

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle Q_{\rm max} = \left. \frac{x}{1 - x} \right|_{\rm max} = \frac{k_{\rm t}}{k_{\rm c}}. \nonumber \end{align} \tag{ 7 }$$

This ratio represents a maximum in the sense that continued irradiation will not result in further conversion of trans to cis. In fact, if the ratio were higher, incident light would actually promote a net conversion the other way, towards the photostationary state. This condition is analogous to open-circuit condition for photovoltaics, since $\Delta G$ is maximum but the conversion rate is zero. The composition of the photostationary state is key for the stored energy density, representing the maximum $x_2$ possible in equation (4) and is an important target for STF design.

The calculation of the constants $k_{\rm c}$ and $k_{\rm t}$ is complicated: while the absorption cross-section is straightforward, the quantum yield is difficult to measure experimentally, and challenging to obtain theoretically, involving calculation of non-adiabatic excited-state dynamics after light absorption [27]. The quantum yield depends sensitively on solvent and excitation energy [26], and on functionalization, which may cause sensitization, quenching, or modification of potential-energy surfaces [16, 28]. Adsorption on a metal surface [29, 30] or packed templating on carbon nanotubes [6] can dramatically reduce quantum yields, showing a key role of the environment.

However, we can put a simple limit on the photostationary state ratio, $Q_{\rm max}$, from energy conservation. Incident photons must have at least a threshold energy $E_{\rm g}$ in order to be absorbed by $trans$. Therefore, $\Delta G$ cannot exceed this value:

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle E_{\rm g} \geqslant \Delta G \left( Q_{\rm max} \right) = \Delta G^{0} + k T {\rm\ ln \ } Q_{\rm max}. \nonumber \end{align} \tag{ 8 }$$

The resulting constraint on the cis fraction in the photostationary state is

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle x \leqslant \frac{1}{1+{\rm e}^{-\left( E_{\rm g} - \Delta G^{0} \right) / k T}}. \nonumber \end{align} \tag{ 9 }$$

Thermal reversion in the ground state (cis $\rightarrow$ trans) is controlled by the barrier height $\Delta H^{\ddagger}$ (as shown in figure 1(b)), and constitutes a long-term loss of stored energy. It also forms part of the difference between $E_{\rm g}$ and $\Delta H$, which appears as a loss in the potential-energy surface, and was considered as a fundamental constraint in the work of Börjesson et al. However, considering an ensemble at finite temperature, this need not be the case. The population $x$ of products can build up, increasing their free energy, up to the limit just cited, $E_{\rm g} \geqslant \Delta G$, irrespective of $\Delta H$. Considering specifically the barrier height, we note that transition-state theory [25] for thermal reversion assumes that the molecules at the barrier are in thermal equilibrium with those in the metastable state, i.e. no free-energy difference between the top of the barrier and the product cis molecules. As a result, the barrier height $\Delta H^{\ddagger} > 0$ does not necessarily imply any loss of free energy, and need not be considered in our efficiency analysis, although of course it is critical for the storage lifetime [4].

We have identified conditions analogous to open circuit and short circuit in photovoltaics. We can continue with an analogy to the $I$–$V$ characteristics of photovoltaics. For STF, this plot is of conversion rate of molecules versus free-energy difference, with the different points on the curve corresponding to different values of $x$. The actual rate of energy storage, like $P = I V$ in an electrical device, is

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle P_{\rm storage} = \frac{{\rm d}x}{{\rm d}t} \Delta G. \nonumber \end{align} \tag{ 10 }$$

We can find the 'maximum power point' ($x$ that maximizes $P_{\rm storage}$) by solving ${\rm d}P_{\rm storage}/{\rm d}x = 0$.

The efficiency $\newcommand{\e}{{\rm e}} \eta$ is given by

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \eta \left( x \right) = \frac{P_{\rm storage}}{P_{\rm incident}} = \frac{\left[ \left(1 - x\right)k_{\rm t} - x k_{\rm c} \right] \left[\Delta G^0 + kT \ln \frac{x}{1-x}\right]} {A_{\rm mol} \int \hbar \omega I \left( \omega \right) {\rm d}\omega} \nonumber \end{align} \tag{ 11 }$$

where $A_{\rm mol}$ is an effective molecular area (which will cancel out in the final result). This equation is not a limit but an actual efficiency (assuming only independent molecules in an ideal solution) which can be computed if the properties involved are known.

Now we will consider bounds on the rate constants $k_{t}$ and $k_{c}$, depending on the photoisomerization quantum yield. We can put a simple bound on the quantum yield via consideration of fluorescence from molecules in the excited state, which is analogous to radiative electron–hole recombination in PV. An excited molecule may relax (radiatively or non-radiatively) to the ground state at any point along its path from trans to cis; at some points this relaxation will produce trans and at others will produce cis. What we can say for certain is that the vibronic states reached by initial excitation from the trans ground state can fluoresce and relax back to a trans structure, and so this process sets an upper bound on the quantum yield.

Let $B_{\rm t}$ be the rate constant for absorption by trans, the same as equation (6) if the quantum yield were unity.

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle B_{\rm t} = \int I \left( \omega \right) \sigma_{t} \left( \omega \right) {\rm d}\omega. \nonumber \end{align} \tag{ 12 }$$

Then the absorption rate is $B_{\rm t} \left( 1 - x \right)$. According to SQ's analysis and detailed balance, a similar quantity will govern radiative recombination back to trans, with the modifications:

• 1.  
  the solar photon flux is replaced by the blackbody spectral intensity at room temperature ($T = 300$ K),

  $$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle I_{\rm bb} \left( \omega \right) = \frac{2 \omega^2}{\pi c^2} \frac{1}{{\rm e}^{\hbar \omega/kT} - 1}, \nonumber \end{align} \tag{ 13 }$$
• 2.  
  there is an additional factor of 2 to account for the fact that the device can only absorb from one illuminated side but can radiate from both sides, and
• 3.  
  the emission probability is given by $\sigma_t$ multiplied by the Boltzmann factor ${\rm e}^{E_{\rm g} / kT}$ (using the energy difference between the ground and excited states of trans), as required to allow thermal equilibrium.

The radiative recombination coefficient then is

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle A_{\rm t} = 2 {\rm e}^{E_{\rm g} / kT} \int I_{\rm bb} \left( \omega \right) \sigma_{t} \left( \omega \right) {\rm d}\omega. \nonumber \end{align} \tag{ 14 }$$

Let $x_s$ be the fraction of molecules in the excited state. The net absorption rate is given by absorption minus emission: $B_{\rm t} \left( 1 - x \right) - A_{\rm t} x_s$.

The conversion rate to cis is limited by radiative recombination and non-radiative recombination along the photoisomerization pathway, as well as the reverse photoisomerization pathway after absorption by cis. We start by neglecting reverse photoisomerization, as will be further justified below. We derive an upper bound by taking the thermodynamically required radiative recombination as the only process preventing an excited trans molecule from converting to cis, so the conversion rate is equal to the net absorption rate.

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \frac{{\rm d}x}{{\rm d}t} = \left( 1 - x \right) k_{\rm t} - x k_{\rm c} \leqslant \left( 1 - x \right) k_{\rm t} \leqslant B_{\rm t} \left( 1 - x \right) - A_{\rm t} x_s. \nonumber \end{align} \tag{ 15 }$$

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle B_{\rm t} \left( 1 - x \right) - A_{\rm t} x_s = \int \left( I \left( \omega \right) \left( 1 - x \right) - 2 I_{\rm bb} \left( \omega \right) {\rm e}^{E_{\rm g} / kT} x_s \right) \sigma_{t} \left( \omega \right) {\rm d}\omega. \nonumber \end{align} \tag{ 16 }$$

We can rewrite in terms of the free-energy difference $\Delta G_{\rm st}$ between the ground and excited states.

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \Delta G_{\rm st} = E_{\rm g} + k T \ln \frac{x_s}{1 - x} \nonumber \end{align} \tag{ 17 }$$

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle x_s {\rm e}^{E_{\rm g} / kT} = \left( 1 - x \right) {\rm e}^{\Delta G_{\rm st} / kT} \nonumber \end{align} \tag{ 18 }$$

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle B_{\rm t} \left( 1 - x \right) - A_{\rm t} x_s = \int \left( I \left( \omega \right) - 2 I_{\rm bb} \left( \omega \right) {\rm e}^{\Delta G_{\rm st} / kT} \right) \left( 1 - x \right) \sigma_{t} \left( \omega \right) {\rm d}\omega. \nonumber \end{align} \tag{ 19 }$$

This is an upper bound for $\frac{{\rm d}x}{{\rm d}t} = \left( 1 - x \right) k_{\rm t}$. Comparing to the expression for $k_{\rm t}$ in equation (6), we find in fact a bound on the quantum yield of photoisomerization across the spectrum:

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \phi_{{\rm t} \rightarrow {\rm c}} \left( \omega \right) \leqslant 1 - \frac{2 I_{\rm bb} \left( \omega \right)}{I \left( \omega \right)} {\rm e}^{\Delta G_{\rm st} / kT}. \nonumber \end{align} \tag{ 20 }$$

This is expressed in terms of the free-energy difference between the ground and excited states of trans, which is not a quantity that is easily measured or controlled. Instead, we can use the inequality $\Delta G_{\rm st} \geqslant \Delta G$, which is required for the excited state to be able to drive the structural change to cis. Then

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \phi_{{\rm t} \rightarrow {\rm c}} \left( \omega \right) \leqslant 1 - \frac{2 I_{\rm bb} \left( \omega \right)}{I \left( \omega \right)} {\rm e}^{\Delta G / kT}. \nonumber \end{align} \tag{ 21 }$$

This quantum yield bound decreases as a function of conversion percentage (through ${\rm e}^{\Delta G / kT} = Q {\rm e}^{\Delta G^{0} / kT}$), and therefore makes a contribution to the $I$–$V$ characteristics of the STF. Moreover, we have shown that the quantum yield cannot reach unity even in principle, due to microscopic reversibility. This bound can be used in place of the simple assumption of $\phi_{{\rm t} \rightarrow {\rm c}} = 1$ in previous efficiency analyses.

Following the SQ approach, we can let the absorption probability for trans be 1 above the band gap and 0 below, which can be approached in practice by making the device thick enough so that all incoming light is absorbed. This is the maximum possible absorption, which will lead to the best efficiency, and implies a cross-section equal to $A_{\rm mol}$.

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \sigma_t \left( \omega \right) = \left\{\begin{array}{@{}lr@{}} 0 : \hbar \omega < E_{\rm g} \nonumber \\ A_{\rm mol} : \hbar \omega > E_{\rm g}. \end{array} \right. \nonumber \end{align} \tag{ 22 }$$

On the other hand, absorption by cis reduces the efficiency, and so we will take $\sigma_c \left( \omega \right) = 0$, the lowest possible absorption. (While quantum-mechanical sum rules require some absorption, it can be pushed arbitrarily far out of the solar spectrum to achieve a similar result.) This limit also sets the cis $\rightarrow$ trans reverse photoisomerization to zero, removing this loss from consideration. That could also happen via $\phi_{c \rightarrow t} = 0$, as for the 'one-way' photoisomerizable molecules such as dihydroazulene/vinylheptafulvene which do not exhibit a reverse process [2].

We have now a simplified model giving an upper bound to the efficiency, involving as parameters only $E_{\rm g}$ and $\Delta G^{0}$, both of which can be straightforwardly measured and computed theoretically:

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \eta \left( x \right) = \frac{\frac{1}{A} \frac{{\rm d}x}{{\rm d}t} \Delta G}{P_{\rm inc}} = \frac{\left[ \left(1 - x\right) \int_{E_{\rm g}} I \left( \omega \right) {\rm d}\omega - 2 x {\rm e}^{\Delta G^{0}/kT} \int_{E_{\rm g}} I_{\rm bb} \left( \omega \right) {\rm d}\omega \right] \left[\Delta G^0 + kT \ln \frac{x}{1-x}\right]} {\int \hbar \omega I \left( \omega \right) {\rm d}\omega}. \label{eq:final} \nonumber \end{align} \tag{ 23 }$$

The numerical solutions of the conversion rate $\frac{{\rm d}x}{{\rm d}t}$ versus free-energy difference $\Delta G$, a curve analogous to $I$-$V$ characteristics, are shown in figure 2 for the case $E_{\rm g} = 1.3$ eV and various values of $\Delta G^{0}$. Changing $\Delta G^{0}$ has little effect on the conversion rate at fixed $\Delta G$, but it strongly affects the maximum $\Delta G$ attainable (at the photostationary state). This maximum $\Delta G$ increases with $\Delta G^{0}$ but saturates at 1.1 eV and the curves become indistinguishable beyond that. The power is also plotted as a function of $x$, which shows a slow rise and steep fall. The smallest $x$ where power generation occurs is the thermal population, which of course decreases with increasing $\Delta G^{0}$. The value of $x$ at which the maximum power is attained falls with increasing $\Delta G^0$, showing a trade-off between maximum rate of energy storage and the maximum amount of energy that can be stored (as in equation (4)).

Zoom In Zoom Out Reset image size

In PV, power electronics can be used to vary the resistive load across the device in order to operate close to the maximum power point. In STF, we need to control the cis fraction to do the equivalent. For example, the rate at which the solution flows through a plate where it is exposed to the sun [1] can be optimized (given the charging rate) in order to keep the solution near the maximum power point, if one wished to achieve the maximum energy storage rate. Of course, doing so would result in quite a small conversion percentage and thus not be the best choice for energy storage density. An alternate possibility is controlling cis fraction via differential solubility or density of the two isomers in a liquid phase.

Consider the case $\Delta G^{0} \rightarrow \infty$. This is consistent with the requirement that free energy decreases, which stipulates only $\Delta G < E_{\rm g}$ (as we used for the limit on the photostationary state). In this limit, for a given $\Delta G$, $x$ goes to 0, removing the loss of absorption due to depletion of the trans molecules, and remarkably reducing the efficiency equation to one equivalent to SQ (following the translation of concepts in table 1):

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \eta_{\Delta G^{0} \rightarrow \infty} \left( \Delta G \right) = \frac{\left[ \int_{E_{\rm g}} I \left( \omega \right) {\rm d}\omega - 2 {\rm e}^{\Delta G/kT} \int_{E_{\rm g}} I_{\rm bb} \left( \omega \right) {\rm d}\omega \right] \Delta G } {\int \hbar \omega I \left( \omega \right) {\rm d}\omega}. \nonumber \end{align} \tag{ 24 }$$

For lesser values of $\Delta G^{0}$, the efficiency is reduced due to trans depletion, but $\Delta G^{0} \geqslant E_{\rm g}$ is sufficient to obtain almost the maximum efficiencies. These results are plotted in figure 3, exhibiting the maximum of 32% at 1.27 eV for $\Delta G^{0} \rightarrow \infty$. Comparing to the experimentally estimated efficiency of 0.07% for the Ru-dithiafulvalene system [1], it is clear there is the possibility of great improvement in STFs.

Zoom In Zoom Out Reset image size

High-throughput screening of molecules for STF applications has already begun, using azobenzene derivatives [7] and later norbornadiene/quadricyclane derivatives [31]. These works have assessed their candidates only by considering parameters separately, or with regard to the older attempt at an efficiency limit [17]. Our improved and more fundamental limit enables a more powerful screening without unnecessary assumptions. We reassess the azobenzene derivatives of [7] in figure 4, using the estimated $E_{\rm g}$ (as PBE Kohn–Sham gap +0.9 eV, as in that work) and $\Delta G^{0}$ as the total energy difference (neglecting effects of vibrational entropy or volume changes). We observe that several molecules indeed come very close to the maximum efficiency limit. Many of the molecules have a large enough $\Delta G^0$ to reach the maximum efficiency for their $E_{\rm g}$, but their potential efficiency is limited by having too large $E_{\rm g}$. Therefore, smaller $E_{\rm g}$ should be a design goal to find improved STF molecules.

Zoom In Zoom Out Reset image size

We underscore numerous important new aspects in our approach to understanding STF efficiency limits. We do not assume a quantum yield $\phi_{{\rm t} \rightarrow {\rm c}} = 1$ but in fact derived an upper bound for $\phi_{{\rm t} \rightarrow {\rm c}}$ dependent on the extent of charging. We showed that the ground-state barrier to thermal reversion, $\Delta H^{\ddagger}$, does not inherently cause a loss and does not enter into our final limit. We demonstrated the critical importance of the free energy, not just the enthalpy, because of the effect of temperature and entropy of mixing. Most importantly, we found that thermodynamic considerations provide the same 32% efficiency limit, as same optimal band gap, as in the SQ analysis.

This analysis of the fundamental limits to STF efficiency helps to benchmark candidate materials and devices against potential performance, identify the weak points that are most important to improve, and focus thinking on applications by showing what is the best performance we can expect. Our results demonstrate that STFs may match the peak efficiencies of PV (despite the much lower performance of current STF devices), although further losses may occur in conversion of the stored chemical energy, into e.g. electricity. This level of performance is very promising for applications where heat will be used directly [32], and also where the storage feature is particularly valued. We believe this thermodynamic approach to STF efficiency could enable the development of new STF materials and paradigms, and provides new insights into photochemistry generally, for example by demonstrating the existence of limits to quantum yield regardless of details of reaction pathways.

We would like to acknowledge helpful discussions with Alexie Kolpak, Yun Liu, Tim Kucharski, and Jee Soo Yoo. This work was supported by the US Advanced Research Projects Agency—Energy under grant DE-AR0000180.