Abstract
We first review the shell evolution in exotic nuclei driven by nuclear forces. We then demonstrate that the underlying mechanism played by the balance of the tensor and central components in the effective nucleon–nucleon interaction is crucial when describing shape coexistence. This effect will be referred to as type II shell evolution, while the shell evolution passing through a series of isotopes or isotones is denoted as type I. We describe type II shell evolution in some detail for the case of the 68Ni nucleus as an example. We present how the fission dynamics can be related to enhanced deformation triggered by type II shell evolution, at its initial stage. It is suggested that the island of stability may be related to the suppression of this mechanism.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Shape coexistence is one of the most interesting and mysterious subjects in nuclear physics and has been studied extensively for a long period. Early works include Morinaga's suggestion, made in 1956, about the structure of 16O [1]. Among more recent studies, the coexistence of triple shapes of 186Pb was reported by Andreyev et al [2]. Review articles have been published, for instance, by Wood et al [3] and more recently by Heyde and Wood [4], providing good coverage of the extensive studies on this topic. On the other hand, there remain open and/or unexplored questions.
In this paper, we discuss the shape coexistence mainly from the viewpoint of the nuclear shell model, paying particular attention to its relation on the changes in the energies of single-particle orbits, called 'shell evolution' due to nuclear forces. Shape coexistence has been discussed by a variety of theoretical methods/models, as presented in this Focus Issue. They include the successful description within the shell model (see Heyde et al [5, 6]), where the combined effects of the pairing, monopole and quadrupole interactions were presented. We shall move ahead so that the effects of the tensor force component of the effective nucleon–nucleon (NN) interaction, particularly its monopole component, are highlighted. Those effects have been shown to play crucial roles in the shell evolution in exotic nuclei [7]. We demonstrate that the same basic mechanism as the shell evolution enhances and/or stabilizes the shape coexistence in a novel way. We then explain how the fission dynamics can be related to this mechanism, referring to the 'island of stability' as the case in which this mechanism is suppressed.
2. Shell evolution and monopole interaction
The nuclear shell model originates in the shell structure and its magic numbers proposed by Mayer and Jensen [8, 9]. The magic numbers (corresponding to major closed shells) proposed with the independent particle shell model [8, 9] have been considered to be constants for all nuclei, taking the values 2, 8, 20, 28, 50, 82, 126, .... This paradigm of the magic-number constancy has worked very well for stable nuclei and their neighborhood, but is being challenged for exotic nuclei. Here, exotic nuclei mean atomic nuclei with an unbalanced ratio N/Z, with N (Z) being the neutron (proton) number, and have short half lives due to this feature. In contrast, stable nuclei have a well-balanced ratio N/Z (from 1 for 4He up to 1.5 for 208Pb) and have infinite (or almost infinite) life times.
This shell structure is certainly a valid starting point in stable nuclei. However, as more neutrons are added within a given isotope chain, nuclei move to the right on the Segrè chart and enter the region of exotic nuclei. The shell structure may change, or evolve. Moreover, the same mechanism will be shown to be one of the keys to understand/describe shape coexistence. We therefore start by discussing the mechanism of shell evolution.
The canonical (or standard) shell structure/magic numbers can be obtained basically by using a harmonic oscillator potential and spin–orbit splitting. This model already includes a large fraction of the nuclear forces. We shall now discuss effects in medium (not included in a simple one-body central potential).
2.1. Monopole interaction
We start with a single-particle orbit, characterized by its angular momentum j, on top of a doubly closed shell (or core). Its single-particle energy is denoted as  . In the case of one nucleon + core system, if this nucleon is on the orbit j,
. In the case of one nucleon + core system, if this nucleon is on the orbit j,  consists of the kinetic energy and the effects of nuclear forces from all nucleons in the core. In the case of a one nucleon outside a stable closed-shell nucleus, the
consists of the kinetic energy and the effects of nuclear forces from all nucleons in the core. In the case of a one nucleon outside a stable closed-shell nucleus, the  are well described by the standard shell-model structure. As the nucleus moves away from such a case with more neutrons (i.e., neutron-rich exotic nuclei),
are well described by the standard shell-model structure. As the nucleus moves away from such a case with more neutrons (i.e., neutron-rich exotic nuclei),  will change in general. A smooth A (= Z + N) dependence arises, but the change is gradual and minor. The kinetic-energy part changes very gradually as a function of A, and is assumed, in this article, to remain unchanged within the region of interest on the Segrè chart [10]. The
will change in general. A smooth A (= Z + N) dependence arises, but the change is gradual and minor. The kinetic-energy part changes very gradually as a function of A, and is assumed, in this article, to remain unchanged within the region of interest on the Segrè chart [10]. The  can change, however, due to nuclear forces, as N (or Z) changes.
can change, however, due to nuclear forces, as N (or Z) changes.
We show how to calculate this change. For this purpose, we first introduce the monopole component of a general two-body interaction 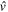 [11, 12, 13, 14]. The monopole matrix element is defined as
[11, 12, 13, 14]. The monopole matrix element is defined as

with j and 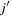 shorthand notation for (n, l, j) of the orbit, μ and
shorthand notation for (n, l, j) of the orbit, μ and 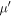 being their magnetic substates, respectively, and
being their magnetic substates, respectively, and 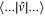 standing for the two-body matrix element. This expression is a general one, and
standing for the two-body matrix element. This expression is a general one, and 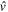 implies a general two-body interaction. The monopole matrix element is obtained, for a given pair of orbits j and
implies a general two-body interaction. The monopole matrix element is obtained, for a given pair of orbits j and  , as the average over all possible orientations of the two-particle states,
, as the average over all possible orientations of the two-particle states, 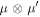 . The denominator in equation (1) is the number of such two-particle states. This average property then becomes,
. The denominator in equation (1) is the number of such two-particle states. This average property then becomes,
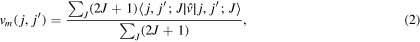
where J denotes the angular momentum resulting from the angular momenta of the two orbits, as 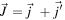 . The factor
. The factor  is the degeneracy of the two-particle states having the same value of J. In the latter equation, some J values can be forbidden by the antisymmetrization, but this is not the case if only the proton-neutron monopole interaction is considered. From the monopole matrix element, one can derive the monopole component,
is the degeneracy of the two-particle states having the same value of J. In the latter equation, some J values can be forbidden by the antisymmetrization, but this is not the case if only the proton-neutron monopole interaction is considered. From the monopole matrix element, one can derive the monopole component,  , of the interaction
, of the interaction  , which can be called the monopole interaction.
, which can be called the monopole interaction.
The monopole interaction we discuss in the present contribution is limited, almost exclusively, to the one between a proton and a neutron. We then obtain

where the orbit j refers to a proton and 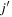 to a neutron, or vice versa. The (total) monopole interaction, consisting of not only this proton–neutron interaction but also the proton–proton and the neutron–neutron interactions, is an important part of the original interaction
to a neutron, or vice versa. The (total) monopole interaction, consisting of not only this proton–neutron interaction but also the proton–proton and the neutron–neutron interactions, is an important part of the original interaction 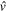 . The remaining part is called the multipole interaction, in order to distinguish it from the monopole interaction. The multipole interaction is often expressed as
. The remaining part is called the multipole interaction, in order to distinguish it from the monopole interaction. The multipole interaction is often expressed as 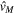 , and it includes in particular the quadrupole interaction.
, and it includes in particular the quadrupole interaction.
2.2. Effect of monopole interaction
The most important effect of the monopole interaction is the change in the single-particle energy of the orbit j due to the occupancy of the orbit 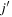 . Calculating the expectation value of the operator
. Calculating the expectation value of the operator 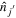 with respect to a many-body reference state, we obtain,
with respect to a many-body reference state, we obtain,

where 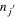 stands for the expectation value
stands for the expectation value 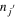 =
= 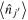 . This equation means that the single-particle energy of the orbit j is changed in proportion to
. This equation means that the single-particle energy of the orbit j is changed in proportion to 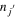 . This relation leads to a very amusing feature: the effects of the multipole interaction vanish if the shell (or orbit)
. This relation leads to a very amusing feature: the effects of the multipole interaction vanish if the shell (or orbit) 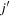 is completely filled, whereas this effect of the monopole interaction not only remains finite but also maximal.
is completely filled, whereas this effect of the monopole interaction not only remains finite but also maximal.
An interesting issue is related to the type of monopole interaction, with changing the nuclear forces. As an extreme case, if  is isotropic with infinite range,
is isotropic with infinite range, 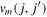 does not depends on j or
does not depends on j or  , being a constant. If
, being a constant. If 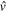 is an attractive force,
is an attractive force, 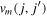 takes a constant negative value. This implies that if more neutrons occupy the orbit
takes a constant negative value. This implies that if more neutrons occupy the orbit 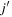 , all proton orbits j become more bound to the same extent. In other words, the proton shell is conserved but becomes more deeply bound.
, all proton orbits j become more bound to the same extent. In other words, the proton shell is conserved but becomes more deeply bound.
On the other hand, if 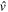 is given by a δ-function with a strength parameter,
is given by a δ-function with a strength parameter, 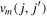 becomes sensitive to the overlap between the wave function of the orbit j and that of the orbit
becomes sensitive to the overlap between the wave function of the orbit j and that of the orbit 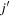 . This implies that if more neutrons occupy the orbit
. This implies that if more neutrons occupy the orbit 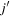 , proton orbits j become more bound to different extents. In other words, the ordering of the single-particle proton orbits in a given shell may change to a certain extent while they become more deeply bound as a whole.
, proton orbits j become more bound to different extents. In other words, the ordering of the single-particle proton orbits in a given shell may change to a certain extent while they become more deeply bound as a whole.
These are properties that one can expect from different central forces, while the actual situation should be somewhere in between. We point out a common feature that if the nuclear force, 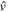 , is an attractive central force, the monopole effect depicted in equation (4) is always attractive for all orbits j.
, is an attractive central force, the monopole effect depicted in equation (4) is always attractive for all orbits j.
3. Shell evolution due to nuclear forces
As shown in the previous section, the monopole interaction changes the shell structure through the mechanism shown in equation (4). These shifted single-particle energies and the multipole interaction, such as the quadrupole interaction, will act within a given model space. Although the multipole interaction does not change, their effects can be different for different single-particle energies. For instance, for the same quadrupole interaction, the quadrupole deformation will change due to the shell evolution. Thus, the shell evolution can affect various properties of nuclei. We note that single-particle energies here mean so-called spherical ones, as the mechanism in equation (4) is scalar. On the other hand, such spherical single-particle energies (obtained from appropriate reference states) are relevant not only to spherical states but also to all kinds of deformed states, because they represent the effects of the monopole interaction. We note also that the monopole and multipole interactions are parts of the Hamiltonian, and their effects are automatically included if the Hamiltonian is diagonalized.
3.1. Type I shell evolution
We start by considering a chain of isotopes. If more neutrons are added beyond a closed shell, the nucleus moves to the right on the Segrè chart. We now take a filling scheme where neutrons occupy the lowest possible single-particle orbits. As more neutrons (or protons) occupy the orbit 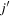 at the Fermi level, its occupation number
at the Fermi level, its occupation number  increases (see equation (4)). Thus, type I shell evolution can occur. In subsection 2.2, this case was discussed with an extremely simple force–an infinite-range central force. We then found that the shell structure does not change, but the whole shell becomes more bound. We now study the shell evolution due to another component of nuclear force.
increases (see equation (4)). Thus, type I shell evolution can occur. In subsection 2.2, this case was discussed with an extremely simple force–an infinite-range central force. We then found that the shell structure does not change, but the whole shell becomes more bound. We now study the shell evolution due to another component of nuclear force.
3.2. Shell evolution due to tensor force
The tensor force has been known for a long time, and its effects were studied from many angles. Those studies include an extraction of the tensor-force component in the empirical nucleon–nucleon interaction by Schiffer and True [15], a derivation of microscopic effective NN interaction (i.e., the so-called 'G-matrix interaction') including second-order effects of the tensor force by Kuo and Brown [16], calculations of magnetic moments also including second-order tensor-force contributions by Arima and his collaborators [17] and by Towner [18], and so-called TOSM calculations of halo nuclei [19].
The robust, systematic and first-order effects of the tensor force on the shell structure have, however, been discussed since 2005 [7]. We present the basic properties of the monopole interaction of the tensor force, by using an illustrative example. Figure 1(a) shows proton orbits and a neutron orbit. The proton orbits are spin-orbit partners

where l denotes the orbital angular momentum, and 1/2 represents the spin. As shown in [7] with an intuitive picture, the coupling between 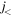 and
and 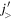 orbits is attractive for the tensor force. On the other hand, the coupling between
orbits is attractive for the tensor force. On the other hand, the coupling between 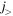 and
and 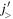 is repulsive as well as the coupling between
is repulsive as well as the coupling between 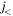 and
and 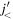 . (For a more elaborate intuitive explanation, see [20].) In figure 1(a), a neutron
. (For a more elaborate intuitive explanation, see [20].) In figure 1(a), a neutron 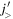 orbit is shown on top of the core. Figure 1(b) illustrates how the tensor force works if two neutrons occupy this
orbit is shown on top of the core. Figure 1(b) illustrates how the tensor force works if two neutrons occupy this 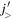 orbit. Due to the repulsive monopole interaction (red wavy line), the single-particle energy of the proton
orbit. Due to the repulsive monopole interaction (red wavy line), the single-particle energy of the proton 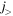 orbit is raised. On the other hand, owing to the attractive monopole interaction (blue wavy line), the single-particle energy of the proton
orbit is raised. On the other hand, owing to the attractive monopole interaction (blue wavy line), the single-particle energy of the proton 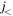 orbit is lowered. These changes combined produce the reduction of spin-orbit splitting.
orbit is lowered. These changes combined produce the reduction of spin-orbit splitting.
Figure 1. Illustration of the type I and II shell evolutions. Wavy lines indicate tensor force. Closed (open) circles denote neutron particles (holes).
Download figure:
Standard image High-resolution imageSince the monopole effect is linear, four neutrons in the 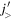 orbit as shown in figure 1(c) double the effect exhibited in figure 1(b). Thus, the proton spin-orbit splitting becomes smaller and smaller, as more neutrons occupy the
orbit as shown in figure 1(c) double the effect exhibited in figure 1(b). Thus, the proton spin-orbit splitting becomes smaller and smaller, as more neutrons occupy the 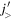 orbit.
orbit.
This change of the shell structure is very different from the changes discussed in subsection 2.2. In the former, the sign of the effect changes for different combinations of the orbits, whereas the sign is the same in the latter. Thus, the tensor force produces a very unique monopole interaction, which may show various shell evolutions with significant changes such as the disappearance of known magic numbers, the appearance of new magic numbers, the crossing of two orbits, etc, which provide intriguing research programs [20, 22, 23].
We note that the actual values of monopole matrix element depend on the radial wave functions of the orbits j and 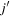 in equation (3) also in the case of the tensor force. Large magnitudes are expected between the same orbits (
in equation (3) also in the case of the tensor force. Large magnitudes are expected between the same orbits (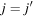 ) or between spin-orbit partners, as well as for a pair of orbits both having no radial node and high orbital angular momenta close to each other [7].
) or between spin-orbit partners, as well as for a pair of orbits both having no radial node and high orbital angular momenta close to each other [7].
The tensor-force component has been included in various types of nuclear models, including those based on the spin-tensor decomposition [24, 25], those based on the mean-field models [26, 27, 28, 29, 30, 31, 32, 33], while the tensor force was not activated before these works [34].
One typical case of the application of the tensor-force-driven shell evolution is shown in figure 2, taken from [21]. Here, from 90Zr to 100Sn, the number of protons in the 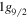 orbit increases from 0 to 10. The neutron orbits on top of the N = 50 core change their single-particle energies, as shown in figure 2. There are two sets of calculated results: one (solid lines) is obtained with the central and tensor forces, while the other (dashed lines) is only with the central force. Note that the tensor force used in figure 2 was obtained from the π-meson + ρ-meson exchange potential [35, 21], and that the central force here is of a Gaussian type, which can reproduce basic properties of the central part of microscopic effective NN interactions based on G-matrix calculation [36] (see [21] for details). We mention some important features: (i) the
orbit increases from 0 to 10. The neutron orbits on top of the N = 50 core change their single-particle energies, as shown in figure 2. There are two sets of calculated results: one (solid lines) is obtained with the central and tensor forces, while the other (dashed lines) is only with the central force. Note that the tensor force used in figure 2 was obtained from the π-meson + ρ-meson exchange potential [35, 21], and that the central force here is of a Gaussian type, which can reproduce basic properties of the central part of microscopic effective NN interactions based on G-matrix calculation [36] (see [21] for details). We mention some important features: (i) the 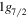 and
and 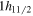 orbits come down together if the central force only is taken. In contrast, these two orbits exhibit an increasing energy splitting approaching Z = 50 if the tensor force is included. The lowering of the
orbits come down together if the central force only is taken. In contrast, these two orbits exhibit an increasing energy splitting approaching Z = 50 if the tensor force is included. The lowering of the 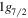 orbit has been known experimentally [37, 38], which is consistent with a significant monopole effect of the tensor force. The stronger coupling between the proton
orbit has been known experimentally [37, 38], which is consistent with a significant monopole effect of the tensor force. The stronger coupling between the proton 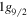 orbit and the neutron
orbit and the neutron 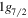 orbit was discussed as an enhanced effect of the proton-neutron central (
orbit was discussed as an enhanced effect of the proton-neutron central (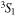 ) force by Federman and Pittel [39], which is consistent with the central-force contribution in figure 2.
) force by Federman and Pittel [39], which is consistent with the central-force contribution in figure 2.
Figure 2. Shell evolution of neutrons from Z = 40 to 50. Taken from figure 3 of [21].
Download figure:
Standard image High-resolution imageWe mention, from a more general viewpoint, that the strong attraction between proton–neutron spin–orbit partners was noticed in relation to the onset of deformation in Zr isotopes [40]. The monopole interaction between proton  orbit and neutron
orbit and neutron 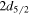 orbit was discussed for the description of Zr-Sr isotopes in [41] by using the empirical interaction introduced in [15]. Such monopole effects presented in earlier works without mentioning the tensor force, e.g., [39, 40, 41, 42, 43, 44], can be understood now quite consistently as consequences of the shell evolution mainly due to the tensor force.
orbit was discussed for the description of Zr-Sr isotopes in [41] by using the empirical interaction introduced in [15]. Such monopole effects presented in earlier works without mentioning the tensor force, e.g., [39, 40, 41, 42, 43, 44], can be understood now quite consistently as consequences of the shell evolution mainly due to the tensor force.
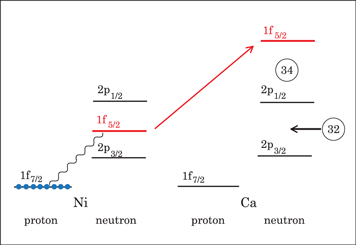
A recent typical example of the shell evolution is the appearance of a new magic number N = 34. Figure 3 shows the shell evolution for the neutron orbits in the pf shell from Ni to Ca. In Ni, there are eight protons on top of the Z = 20 core, and they are assumed to be in the 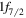 orbit. Due to the strong attractive interaction between the
orbit. Due to the strong attractive interaction between the 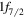 proton and
proton and 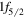 neutron orbits where the tensor and central forces contribute additively, the addition of protons lowers the energy of the neutron
neutron orbits where the tensor and central forces contribute additively, the addition of protons lowers the energy of the neutron 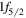 orbit. This is the case for Ni isotopes, where the
orbit. This is the case for Ni isotopes, where the 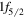 orbit is located between the
orbit is located between the 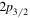 and
and 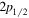 orbits. In the Ca isotopes, the proton
orbits. In the Ca isotopes, the proton 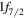 orbit is unoccupied, so there is a vanishing monopole shift for the
orbit is unoccupied, so there is a vanishing monopole shift for the 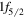 orbit. This moves the neutron
orbit. This moves the neutron 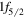 orbit upwards even above the
orbit upwards even above the 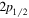 orbit, leaving a gap at N = 32 and creating another gap at N = 34. Thus, N = 34 becomes a magic number for the Ca isotopes. In this argument, the
orbit, leaving a gap at N = 32 and creating another gap at N = 34. Thus, N = 34 becomes a magic number for the Ca isotopes. In this argument, the 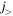 -
- 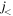 proton–neutron coupling within a major shell is important, and is the mechanism for the shell evolution between Ca and Ni. (This was basically the prediction in [13] in 2001, as the corresponding text is quoted as 'we can predict other magic numbers, for instance, N = 34 associated with the
proton–neutron coupling within a major shell is important, and is the mechanism for the shell evolution between Ca and Ni. (This was basically the prediction in [13] in 2001, as the corresponding text is quoted as 'we can predict other magic numbers, for instance, N = 34 associated with the  interaction'.) The experimental investigation of the N = 34 magic number in the Ca isotopes, however, had been infeasible for a long time, casting doubt over this magic number [45]. In 2013, finally, the 2+ excitation energy was measured in the Radioactive Isotope Beam Factory (RIBF) [46] consistently with an N = 34 gap. The N = 32 gap in the Ca isotopes was investigated experimentally in ISOLDE in 1985 in terms of the 2+ excitation energy [47]. The magic structures of Ca isotopes attracted much attention in recent years [48]–[64].
interaction'.) The experimental investigation of the N = 34 magic number in the Ca isotopes, however, had been infeasible for a long time, casting doubt over this magic number [45]. In 2013, finally, the 2+ excitation energy was measured in the Radioactive Isotope Beam Factory (RIBF) [46] consistently with an N = 34 gap. The N = 32 gap in the Ca isotopes was investigated experimentally in ISOLDE in 1985 in terms of the 2+ excitation energy [47]. The magic structures of Ca isotopes attracted much attention in recent years [48]–[64].
Figure 3. Schematic illustration of shell evolution from Ni back to Ca for neutron orbits. Light blue circles exhibit protons. The wavy line is the interaction between the proton 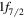 orbit and the neutron
orbit and the neutron 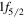 orbit. The numbers in circles indicate (semi-) magic numbers.
orbit. The numbers in circles indicate (semi-) magic numbers.
Download figure:
Standard image High-resolution imageWe here comment that the tensor force in the free space like the one obtained from one-π-meson + one-ρ-meson exchange potential does not change much after the renormalization procedures for the short-range repulsion and the in-medium corrections, as referred to as renormalization persistency [21, 65]. The tensor-force component of the effective NN interaction can be obtained by its spin-tensor decomposition [66]–[71] also. The tensor forces obtained by different approaches are expected to be rather similar at least at the level of the monopole interaction for the valence shell because of the renormalization persistency. Thus, we can discuss rather well general features of the monopole effects of the tensor force.
4. Type II shell evolution and shape coexistence
4.1. Type II shell evolution
Figure 1(d) depicts the basic idea of type II shell evolution, where particle–hole excitations occur for neutrons from the orbit 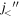 to the orbit
to the orbit 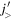 . Because of the rule of the tensor-force monopole interaction, the occupancy of the particle orbit
. Because of the rule of the tensor-force monopole interaction, the occupancy of the particle orbit 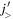 reduces the proton
reduces the proton 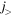 -
- 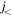 splitting. This is identical to what takes place in figure 1(b). In addition, the creation of holes in the neutron
splitting. This is identical to what takes place in figure 1(b). In addition, the creation of holes in the neutron 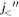 orbit brings about another effect. It decreases the effect of the tensor-force monopole interaction from the fully occupied
orbit brings about another effect. It decreases the effect of the tensor-force monopole interaction from the fully occupied  orbit. In other words, equation (4) is changed by the ordinary particle-hole transformation to
orbit. In other words, equation (4) is changed by the ordinary particle-hole transformation to

where 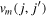 is the same as in equation (4) and
is the same as in equation (4) and 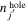 stands for the number of holes in the orbit
stands for the number of holes in the orbit  . Note that
. Note that 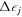 implies the difference from the value for the configuration with the fully occupied (no-hole)
implies the difference from the value for the configuration with the fully occupied (no-hole)  orbit.
orbit.
In the case of figure 1(d), as  due to the general rule, the neutron hole in the orbit
due to the general rule, the neutron hole in the orbit 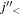 lowers the proton
lowers the proton 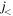 orbit. By the same mechanism working oppositely, the proton
orbit. By the same mechanism working oppositely, the proton 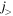 orbit is raised by the neutron particle in the orbit
orbit is raised by the neutron particle in the orbit 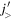 and neutron holes in the orbit
and neutron holes in the orbit 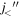 . Combining all these effects, the proton spin–orbit splitting between
. Combining all these effects, the proton spin–orbit splitting between 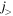 -
- 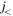 is reduced by even more than in figure 1(b). We emphasize that similarly to the situation shown in figure 1(c), the change is doubled due to the linearity of the monopole effect, if there are 4p−4 h excitation as shown in figure 1(e). This reduction, of course, depends on the orbits involved. If favorable combinations are involved, the final effect can be quite significant. We now discuss such examples.
is reduced by even more than in figure 1(b). We emphasize that similarly to the situation shown in figure 1(c), the change is doubled due to the linearity of the monopole effect, if there are 4p−4 h excitation as shown in figure 1(e). This reduction, of course, depends on the orbits involved. If favorable combinations are involved, the final effect can be quite significant. We now discuss such examples.
4.2. Structure of 68Ni
Figure 4(a) shows levels of 68Ni [72]. These levels are calculated by using the Monte Carlo shell model (MCSM) [74, 75] by using the K computer facility [72]. The model space consists of the full pf shell + 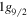 +
+ 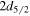 without any truncation. The variance extrapolation ensures the accuracy of the result [76]. The shell-model Hamiltonian was modified A3DA, which is a combination of G-matrix effective interaction, phenomenologically tuned bare single-particle energies and two-body matrix elements [75, 72]. The level scheme and E2 properties of other Ni isotopes are presented in [72] with a salient systematic agreement with experiment [73, 87, 88], suggesting the validity of the shell-model Hamiltonian. While there have been many studies on 68Ni [77]–[89], we shall focus on messages contained in the calculated results of [72].
without any truncation. The variance extrapolation ensures the accuracy of the result [76]. The shell-model Hamiltonian was modified A3DA, which is a combination of G-matrix effective interaction, phenomenologically tuned bare single-particle energies and two-body matrix elements [75, 72]. The level scheme and E2 properties of other Ni isotopes are presented in [72] with a salient systematic agreement with experiment [73, 87, 88], suggesting the validity of the shell-model Hamiltonian. While there have been many studies on 68Ni [77]–[89], we shall focus on messages contained in the calculated results of [72].
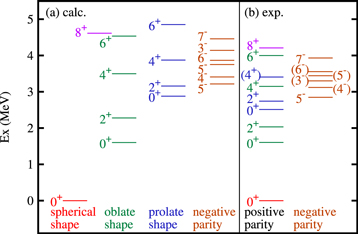
Calculated positive-parity levels of 68Ni are classified according to their shapes: spherical, oblate or prolate. The shape assignment is made based on the intrinsic quadrupole moments of primary MCSM basis vectors as explained below and also in [72]. The separation in specific bands is consistent with the enhanced E2 transitions. The present calculation exhibits rather good agreement with the data shown in figure 4(b) [73, 87, 88]. The appearance of three different shapes within a narrow energy range points towards the presence of shape coexistence.
Figure 4. Energy levels of 68Ni (a) calculated by the Monte Carlo shell model [72] and (b) obtained by experiments [73, 87, 88]. Taken from figure 2 of [72].
Download figure:
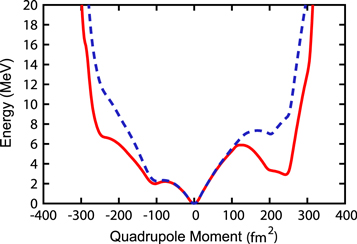
Standard image High-resolution imageFigure 5 shows the three-dimensional total energy surface calculated from the same shell-model Hamiltonian by the constrained Hartree–Fock method [90]. The constraint is by the values of the intrinsic quadrupole moments, Q0 (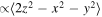 ) and Q2 (
) and Q2 (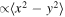 ), where the x, y and z coordinates are taken in the intrinsic frame [90]. The energy here means that of constrained Hartree–Fock ground state for a given set of Q0 and Q2 values. Figure 5 gives a global view of the structure of 68Ni. The absolute minimum is obtained at the spherical shape. Moving to the oblate direction along the axially-symmetric shape, there appears a shoulder. On the other hand, in the direction to the prolate shape, one encounters a huge barrier and a pronounced local minimum beyond it.
), where the x, y and z coordinates are taken in the intrinsic frame [90]. The energy here means that of constrained Hartree–Fock ground state for a given set of Q0 and Q2 values. Figure 5 gives a global view of the structure of 68Ni. The absolute minimum is obtained at the spherical shape. Moving to the oblate direction along the axially-symmetric shape, there appears a shoulder. On the other hand, in the direction to the prolate shape, one encounters a huge barrier and a pronounced local minimum beyond it.
Figure 5. Three dimensional total energy surface of 68Ni. A similar figure was shown in [88]. Schematic images of the spherical, oblate and prolate shapes are shown along the axes.
Download figure:
Standard image High-resolution imageThe shell-model eigenstate in the MCSM is represented by a superposition of 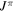 projected MCSM basis vectors. These MCSM basis vectors themselves are deformed Slater determinants, and are generated through Monte Carlo and variational processes [75]. As they can be characterized by the intrinsic quadrupole moments, Q0 and Q2, they can be plotted on the total energy surface according to their Q0 and Q2 values. This analysis (called T-plot later) in [72] indicates that the
projected MCSM basis vectors. These MCSM basis vectors themselves are deformed Slater determinants, and are generated through Monte Carlo and variational processes [75]. As they can be characterized by the intrinsic quadrupole moments, Q0 and Q2, they can be plotted on the total energy surface according to their Q0 and Q2 values. This analysis (called T-plot later) in [72] indicates that the 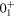 ,
, 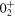 and
and 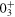 states have their major basis vectors located around the spherical absolute minimum, the oblate shoulder and the prolate local minimum, respectively. Note that the plots of these basis vectors are scattered as a consequence of various quantum fluctuations (see [72]). Thus, we can relate the
states have their major basis vectors located around the spherical absolute minimum, the oblate shoulder and the prolate local minimum, respectively. Note that the plots of these basis vectors are scattered as a consequence of various quantum fluctuations (see [72]). Thus, we can relate the 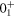 ,
,  and
and 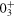 shell-model eigenstates to specific regions on the total energy surface, such as the spherical, oblate and prolate ones.
shell-model eigenstates to specific regions on the total energy surface, such as the spherical, oblate and prolate ones.
We now concentrate on the shape change along the axially symmetric deformation axis. Figure 6 is a simpler version of figure 5, presenting the same energy for the states of the axial symmetry (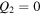 ), as a function of Q0. The
), as a function of Q0. The  ground state corresponds to the spherical absolute minimum. In this situation, the Z = 28 and N = 40 closed shell is kept well. Figure 7 shows the occupation number of each orbit for the three 0+ states. The breaking of the closed shell in the
ground state corresponds to the spherical absolute minimum. In this situation, the Z = 28 and N = 40 closed shell is kept well. Figure 7 shows the occupation number of each orbit for the three 0+ states. The breaking of the closed shell in the 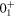 state is only minimal, with about one neutron excited from the pf shell to the
state is only minimal, with about one neutron excited from the pf shell to the  orbit in average. The
orbit in average. The 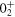 state contains more excitations from the closed shell, with about one proton from the
state contains more excitations from the closed shell, with about one proton from the 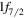 to the upper pf shell and more than two neutrons to the
to the upper pf shell and more than two neutrons to the 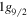 orbit. Thus, the relative excitation with respect to the
orbit. Thus, the relative excitation with respect to the 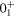 state is about two: about one proton and about one neutron. This is a usual excitation pattern, and the
state is about two: about one proton and about one neutron. This is a usual excitation pattern, and the 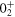 state shows a modest oblate deformation. For the
state shows a modest oblate deformation. For the 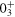 state, the situation is very different: nearly three protons are excited from the
state, the situation is very different: nearly three protons are excited from the 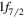 orbit and more than four neutrons are excited across N = 40 gap. Here, the relative excitation from the
orbit and more than four neutrons are excited across N = 40 gap. Here, the relative excitation from the  state is about six nucleons: three protons and three neutrons. It is clear that such particle–hole excitations produce a large deformation in the
state is about six nucleons: three protons and three neutrons. It is clear that such particle–hole excitations produce a large deformation in the 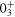 state. What mechanism can make it possible?
state. What mechanism can make it possible?
Figure 6. Total energy surfaces with the axially-symmetric deformation for 68Ni. The red solid line indicates the calculated result obtained from the present full Hamiltonian, while the blue dashed line the result suppressing type II shell evolution (see the text).
Download figure:
Standard image High-resolution imageFigure 7. (a) Proton and (b) neutron occupation numbers in 68Ni. Taken from figure 4 of [71].
Download figure:
Standard image High-resolution imageThe answer is in type II shell evolution within the nucleus 68Ni. In the 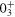 state, there are about four neutron particles in the
state, there are about four neutron particles in the 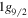 orbit, leaving four neutron holes in the pf shell: these can be approximately partitioned into two in the
orbit, leaving four neutron holes in the pf shell: these can be approximately partitioned into two in the 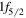 and another two in the
and another two in the 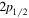 . Both the
. Both the 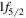 and
and 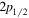 orbits are
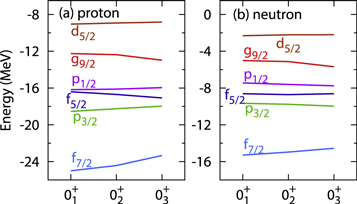
orbits are 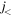 orbits. According to the situation discussed in figure 1(d), the monopole shift implies a reduction in the proton spin–orbit splitting. Figure 8 shows the single-particle energy of each orbit for the
orbits. According to the situation discussed in figure 1(d), the monopole shift implies a reduction in the proton spin–orbit splitting. Figure 8 shows the single-particle energy of each orbit for the 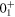 ,
, 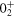 and
and 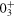 states. The effects discussed in calculating the monopole shifts with equations (4) and (6) are included using the actual values of
states. The effects discussed in calculating the monopole shifts with equations (4) and (6) are included using the actual values of 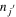 and
and 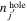 . The most remarkable change in the proton and neutron single-particle energies between the
. The most remarkable change in the proton and neutron single-particle energies between the  and
and 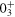 states is the splitting between proton
states is the splitting between proton 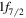 and
and 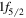 . This is about 9 MeV for the
. This is about 9 MeV for the 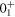 state, which is reduced to about 6 MeV for the 0+3 state. This change is what one can expect from type II shell evolution. A large spin-orbit splitting generally prevents the nucleus from deformation, and tends to make it more spherical. The type II shell evolution hinders this function. Thus, large prolate deformation becomes possible.
state, which is reduced to about 6 MeV for the 0+3 state. This change is what one can expect from type II shell evolution. A large spin-orbit splitting generally prevents the nucleus from deformation, and tends to make it more spherical. The type II shell evolution hinders this function. Thus, large prolate deformation becomes possible.
Figure 8. (a) Proton and (b) neutron single-particle energies for the shell-model 0+ eigenstates of 68Ni.
Download figure:
Standard image High-resolution imageIn fact, this is a self-consistency mechanism. Once particle-hole excitations favoring type II shell evolution occur, protons lose resistance against the tendency for deformation to occur. This makes the proton sector more deformed, resulting in a stronger deformation also in the neutron sector. A stronger deformation enhances neutron particle–hole excitations, which then favors type II shell evolution. Thus, the self-consistent solution is achieved with an unusual amount of deformation and particle–hole excitations. This shows up for the 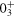 state. This is a nonlinear process, too. The mechanism introduced here is consistent with figure 6: once a large deformation is imposed as the constraint, neutron particle–hole excitations occur more easily, making the proton sector less resistant against deformation through the proton–neutron interaction.
state. This is a nonlinear process, too. The mechanism introduced here is consistent with figure 6: once a large deformation is imposed as the constraint, neutron particle–hole excitations occur more easily, making the proton sector less resistant against deformation through the proton–neutron interaction.
The probabilities of various configurations reflect such an unusual feature. Figures 9–11 show the probability of each particle–hole configuration, for the three 0+ states. Figure 9 depicts the probabilities of the 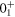 state with concentrations on the 0p−0 h configuration as well as a modest contribution from neutron 2p−2 h with proton 0p−0 h configurations. Figure 10 presents a different pattern with the highest peak of proton 0p−0 h neutron 2p−2 h configuration. Finally, in figure 11, major peaks are shifted to multi-particle multi-hole configurations. It is noted that certain intermediate configurations are absent, because a larger amount of particle–hole excitations brings about more binding energy as a consequence of the nonlinear nature of type II shell evolution.
state with concentrations on the 0p−0 h configuration as well as a modest contribution from neutron 2p−2 h with proton 0p−0 h configurations. Figure 10 presents a different pattern with the highest peak of proton 0p−0 h neutron 2p−2 h configuration. Finally, in figure 11, major peaks are shifted to multi-particle multi-hole configurations. It is noted that certain intermediate configurations are absent, because a larger amount of particle–hole excitations brings about more binding energy as a consequence of the nonlinear nature of type II shell evolution.
Figure 9. Probabilities of configurations of the 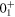 state of 68Ni.
state of 68Ni.
Download figure:
Standard image High-resolution imageFigure 10. Probabilities of configurations of the 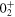 state of 68Ni.
state of 68Ni.
Download figure:
Standard image High-resolution imageFigure 11. Probabilities of configurations of the 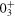 state of 68Ni.
state of 68Ni.
Download figure:
Standard image High-resolution imageThe crucial role played by type II shell evolution can be visualized by introducing another Hamiltonian where it is suppressed by tuning particular two-body matrix elements. In the present case, we reset 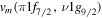 and
and 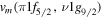 in equation (3) so that both of them are equal to the average of their original values. We reset
in equation (3) so that both of them are equal to the average of their original values. We reset 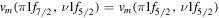 similarly. This modification removes mainly the tensor-force contributions from the relevant monopole interactions, while the contributions of the central force remain nearly unchanged. The resultant total energy surface is included in figure 6 (blue dashed line), exhibiting significant differences from the one obtained by the original Hamiltonian. The difference is negligible near the spherical shape, because neutron particle–hole excitations occur only modestly. However, once the deformation becomes stronger, type II shell evolution sets in and the energy is lowered, creating a pronounced local minimum. Note that through this mechanism, both the spherical and prolate minima remain stable because the barrier is kept high near the spherical shape.
similarly. This modification removes mainly the tensor-force contributions from the relevant monopole interactions, while the contributions of the central force remain nearly unchanged. The resultant total energy surface is included in figure 6 (blue dashed line), exhibiting significant differences from the one obtained by the original Hamiltonian. The difference is negligible near the spherical shape, because neutron particle–hole excitations occur only modestly. However, once the deformation becomes stronger, type II shell evolution sets in and the energy is lowered, creating a pronounced local minimum. Note that through this mechanism, both the spherical and prolate minima remain stable because the barrier is kept high near the spherical shape.
5. Extension to other nuclei
Shape coexistence has been known experimentally in many nuclei [4]. Amongst the many nuclei, the Pb isotopes are well known, including the most interesting 186Pb nucleus [2]. These nuclei may well be understood by extending the shell–model methods applied before to the Ni isotopes. Figure 12 displays Pb version of type II shell evolution. In 68Ni, neutron particle–hole excitations from the  orbit to the
orbit to the 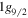 orbit yield the reduction of the proton spin-orbit splitting. Figure 12 suggests that in the Pb isotopes, neutron particle–hole excitations from the
orbit yield the reduction of the proton spin-orbit splitting. Figure 12 suggests that in the Pb isotopes, neutron particle–hole excitations from the 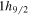 orbit to the
orbit to the 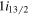 orbit will cause a similar effect. In the proton sector, the reduction of the
orbit will cause a similar effect. In the proton sector, the reduction of the 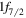 -
-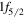 energy splitting was the key in describing the appearance of the shape coexistence in 68Ni. This mechanism now implies a reduction of the
energy splitting was the key in describing the appearance of the shape coexistence in 68Ni. This mechanism now implies a reduction of the  -
-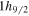 splitting for the shape coexistence in Pb isotopes. It is of much interest to find out what results will be obtained for the Pb neutron deficient nuclei and neighboring nuclei with this scope. Work along these lines is in progress.
splitting for the shape coexistence in Pb isotopes. It is of much interest to find out what results will be obtained for the Pb neutron deficient nuclei and neighboring nuclei with this scope. Work along these lines is in progress.
Figure 12. Schematic illustration of type II shell evolution and associated reduction of the proton spin–orbit splitting in Pb isotopes. Green bent arrow indicates neutron particle–hole excitations. Dashed lines stand for Fermi energies.
Download figure:
Standard image High-resolution imageThere should be many other cases comparable with the Ni and Pb regions, where, for instance, the role of protons and neutrons can be interchanged. Such studies have been started, for instance, in Zr and Sn regions with intriguing results expected.
6. Fission and the island of stability
Figure 6 exhibits the total energy surface along the axially-symmetric deformation for 68Ni. Figure 6 then demonstrates that multi-particle multi-hole excitations can give rise to lowering the height of the barrier between the spherical minimum and the prolate local minimum, and can lower also the prolate minimum. This is a quite notable effect, and one may consider a possible relevance to the study of the fission dynamics [91]–[93]. The description of the fission has made enormous progress so far, but might miss the basic picture at its very initial stage, particularly for the spontaneous fission [94]–[97]. Figure 13 displays the total energy surface along the axially-symmetric deformation for an unspecified heavy or superheavy nucleus. The blue dashed curve in figure 13 represents schematically a standard picture. The transition from the ground state to a strongly deformed local minimum is usually considered to trigger spontaneous fission. Thus far, it has been argued that in theory, the barrier is too high and/or the local minimum is also too high. If one considers the possibility that spin-orbit splitting might be reduced in an appreciable way in certain relevant nuclei due to specific multi-particle multi-hole excitations (type II shell evolution), the barrier and local minimum can come down as a consequence of enhanced deformation energy similarly to figure 6. Figure 13 illustrates schematically this scenario. The blue dashed line represents what can be expected from existing calculations where type II shell evolution is basically absent. It could be conceivable that type II shell evolution may result in a shift of the total energy surface, as shown by red solid line.
Figure 13. Schematic picture of total energy surface for an unspecified heavy or superheavy nucleus. The blue dashed line represents some conventional result, while the red solid line includes an additional contribution from type II shell evolution associated with particular particle–hole excitations.
Download figure:
Standard image High-resolution imageThe present idea leads us to the possibility of initiating a fission process by exciting neutrons from the core, for instance, by photons (e.g. a gamma-ray laser). Such speculations are quite amusing and intriguing, but the outcome is reserved to the future.
The island of stability may then be considered as a case of reduced fission probability due to the suppression of the present mechanism by the Pauli principle, for instance. Note that the fission may be the primary decay mode for certain heavy and super heavy nuclei.
7. Summary
In summary, we have presented how type II shell evolution driven by the tensor force can contribute to the appearance and stability of shape coexistence. Due to type II shell evolution, the single-particle energies can be re-arranged with reduced spin-orbit splitting. This implies weaker resistance against deformation, and a strongly deformed local minimum may occur. This picture seems to be reasonable and applicable in the Ni isotopes, as far as the comparison with experiment has been carried out. The enhanced tendency to deformation can be connected with the initial stage of the fission where the transition to a strongly deformed shape is needed and type II shell evolution certainly helps. The suppression of this mechanism might lead to the hindrance of the fission in certain nuclei and the consequent emergence of the island of stability.
Thus, further studies on the shape coexistence are very important in a wide scope.
Acknowledgments
We would like to thank Drs T Suzuki, Y Utsuno and N Shimizu for their contributions to the works shown in this article. We are grateful to Dr Y Aritomo for providing useful comments on fission. This work was supported in part by Grants-in-Aid for Scientific Research (23244049). It was supported in part by HPCI Strategic Program (hp150224), in part by MEXT and JICFuS as a priority issue (Elucidation of the fundamental laws and evolution of the universe) to be tackled by using Post 'K' Computer, and also by CNS-RIKEN joint project for large-scale nuclear structure calculations.