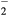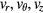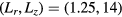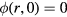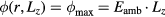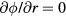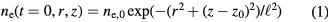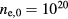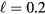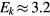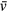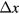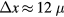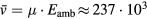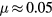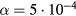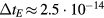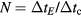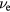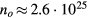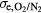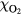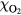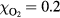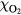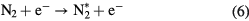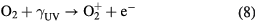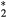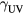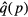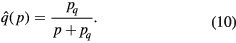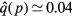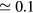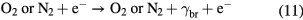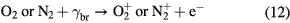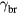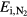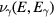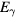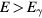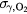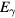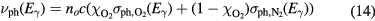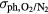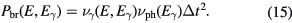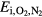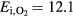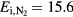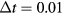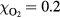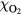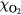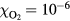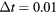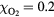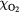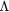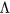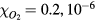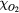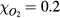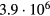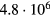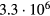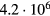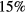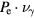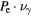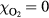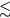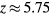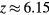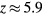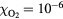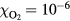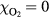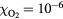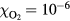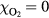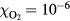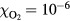The influence of bremsstrahlung on electric discharge streamers in N₂, O₂ gas mixtures

Streamers are thin, ionized plasma channels formed by ionization waves in an electrified gas [1–8]. They are thought to facilitate the formation and propagation of the lightning leader channel [9–13], and are the main discharge modes of sprites in the mesosphere, of black jets in the stratosphere and of gigantic jets flashing from clouds to the ionosphere [5, 14–20].

Negative polarity streamers move against the electric field in the direction of electron acceleration and can propagate in all gases by means of electron impact collisions. Positive streamers move against the electron acceleration and require an alternative ionization source to feed the discharge. In air, O₂ is ionized by UV photons emitted by excited N₂ [21–25]. The photons are unaffected by the field and can create electrons in all directions. The electrons ahead of the ionization wave are accelerated into the wave and facilitate its propagation [10]. The above suggests that in a pure N₂ gas, positive streamers should not develop. Nevertheless, experiments show their formation even for impurity levels of O₂ down to 1 ppm achieved in gases used in experiments [26].

Experimental gases are not free of charged particles because free electrons are continuously created by cosmic rays and radiation from natural radioactivity. Free electrons are lost via attachment to neutrals, creating negative ions, and some are recycled via detachment from negative ions. One 3D fluid simulation shows that the UV process is effective down to 1 ppm O₂ in agreement with experiments on streamer properties if the background density of O$_{2}^{-}$ is 10⁷–10⁹ cm⁻³ [27]. This, however, is orders of magnitude above the natural density of small ions at cloud altitudes [28]. A later fluid simulation in 2D cylindrical symmetry found that at 1 ppm O₂ the results depend on the spatial resolution of the simulation, the finer resolution showing that the UV process alone does not allow for positive streamers. It was suggested that there is less than one oxygen molecule per cell, making the fluid approximation questionable. In that case, the influence of UV photons is uncertain because of the low oxygen density and positive streamers were found to require high background ionization densities [24].

Here, we explore an alternative ionization mechanism: when electrons are accelerated in the electric field of a streamer they may emit bremsstrahlung photons when they are scattered off the air nuclei [29–31] or shell electrons [32, 33], and the photons may ionize the neutral molecules provided their energy is above the ionization energy [34]. Although bremsstrahlung is usually considered for electron energies of many keV and higher, the cross section for photon emission increases with decreasing electron energy [35]. In air, the rates of this process is 2–3 orders of magnitude smaller than UV ionization, however, at small concentrations of O₂ it may be comparable or larger.

Using particle simulations we study, to our knowledge for the first time, bremsstrahlung effects on streamer propagation at various O₂ concentrations, considering both positive and negative polarities. In all cases we perform and compare two simulations, one with and one without bremsstrahlung, in order to understand bremsstrahlung- relative to UV photo ionization.

In section 2 we describe the simulation model and the initial conditions and in section 3 we present the electron impact, UV- and bremsstrahlung processes. In section 4 we present the results of the simulations and in section 5 we provide some additional discussions.

We perform our simulations with a 2.5D Monte Carlo particle-in-cell code with two spatial coordinates (r,z) and three coordinates (${{v}_{r}},{{v}_{\theta}},{{v}_{z}}$) in velocity space. The simulation domain is cylindrically symmetric $\left({{L}_{r}},{{L}_{z}}\right)=\left(1.25,14\right)$ mm with 150 grid points in r and 1200 grid points in z. Thus, the grid sizes in r and z direction are approximately 8 μm and 11 μm comparable to the grid sizes used in [24, 36]. Since we use a particle code, updating the position of electrons and photons as well as the collision with air molecules is independent of the actual grid. The background gas is immobile at a constant density. Ions are also immobile whereas electrons are accelerated by the instantaneous, local electric field. The interactions of electrons with the neutral molecules include ionization, elastic and inelastic scattering, attachment and detachment, as well as UV and bremsstrahlung emissions using the formulation of [31, 37]. The electric field is updated by solving the Poisson equation on the grid, accounting for space charge effects. The model also includes photon generation, transport and ionization, discussed in section 3.

At the boundaries (z  =  0,L_z) we choose the Dirichlet condition for the electric potential $\phi (r,0)=0$ and $\phi \left(r,{{L}_{z}}\right)={{\phi}_{\text{max}}}={{E}_{\text{amb}}}\cdot {{L}_{z}}$, and at (r  =  0,L_r) the Neumann condition $\partial \phi /\partial r=0$ where E_amb is the ambient electric field. Electrons and photons that leave the domain are written off. We initiate a streamer with a charge neutral ionization patch at the center of the domain. The electron density has a Gaussian distribution:

$$\begin{eqnarray}&&\begin{array}{*{35}{l}} {{n}_{\text{e}}}(t=0,r,z)={{n}_{\text{e},0}}\exp (-({{r}^{2}}+{{(z-{{z}_{0}})}^{2}})/{{\ell}^{2}}) \end{array}\end{eqnarray} \tag{ 1 }$$

with a peak density ${{n}_{\text{e},0}}={{10}^{20}}$ m⁻³, width $\ell =0.2$ mm centered at z₀  =  7 mm. The neutral density corresponds to standard temperature (T  =  300 K) and pressure (p  =  1 atm) (we here use the same values for STP as in [24]). Simulations are conducted in nitrogen–oxygen mixtures with 20% oxygen (air), with 1 ppm oxygen, and in pure nitrogen. The ambient electric field is pointing towards  −z and has a magnitude of 3E_k, where ${{E}_{k}}\approx 3.2$ MVm⁻¹ is the conventional breakdown field at STP. This field magnitude is a compromise between a need to reduce computational time by accelerating electrons fast into the energy regime relevant for the bremsstrahlung process, and the fields expected in stages of laboratory or atmospheric discharges [37, 38]. The simulation domain and initial condition of the particle density are shown in figure 1.

Zoom In Zoom Out Reset image size

The code uses two different time steps. One defines the time between two updates of the electric field. It is restricted by the Courant condition:

$$\begin{eqnarray}&&\begin{array}{*{35}{l}} \Delta {{t}_{E}}\lesssim \alpha \Delta x{{{\bar{v}}}^{-1}} \end{array}\end{eqnarray} \tag{ 2 }$$

where $\bar{v}$ is the mean velocity of electrons in the background field, $\Delta x$ the mesh size, and α a parameter smaller than one. In the present paper we use $\Delta x\approx 12~\mu$m, $\bar{v}=\mu \cdot {{E}_{\text{amb}}}\approx 237\cdot {{10}^{3}}$ ms⁻¹, with the electron mobility $\mu \approx 0.05$ m² V⁻¹s⁻¹, and $\alpha =5\cdot {{10}^{-4}}$; hence $\Delta {{t}_{E}}\approx 2.5\cdot {{10}^{-14}}$ s. The second time step relates to the time between collisions. It is the time step of particle position and velocity updates, and collision processes. It is defined by the Nambu scheme:

$$\begin{eqnarray}&&\begin{array}{*{35}{l}} \Delta {{t}_{\text{c}}}<{{\left({{N}_{\text{c}}}{{\gamma}_{\text{max}}}\right)}^{-1}} \end{array}\end{eqnarray} \tag{ 3 }$$

where ${{\gamma}_{\text{max}}}$ is the maximum of the total electron collision frequency and N_c the number of collision types taken into account. Generally, the second time step is smaller than the first one, which allows $N= \Delta {{t}_{E}}/ \Delta {{t}_{\text{c}}}$ collisions and particle updates between two updates of the electric field.

Each electron is actually a 'computer' electron with a weight of w electrons. To increase resolution and to limit computer resources we have implemented an adaptive particle scheme [37] conserving the charge distribution as well as the electron energy and momentum. To reduce computational noise we have also implemented a splitting scheme for computer-electrons solely populating one grid cell yielding maximal 100 new computer-electrons with reduced weight.

We now discuss the three processes through which an electron with energy E can create a secondary electron: directly by impact collision or indirectly by UV- and bremsstrahlung photoionization. They are implemented in the simulation code with a Monte Carlo scheme. The aim of the discussion is to understand their relative importance.

The ionization frequency for impact collisions, ${{\nu}_{\text{e}}}$, is

$$\begin{eqnarray}&&\begin{array}{*{35}{l}} {{\nu}_{\text{e}}}(E)={{n}_{o}}v\left({{\chi}_{{{\text{O}}_{2}}}}{{\sigma}_{\text{e},{{\text{O}}_{2}}}}(E)+\left(1-{{\chi}_{{{\text{O}}_{2}}}}\right){{\sigma}_{\text{e},{{\text{N}}_{2}}}}(E)\right) \end{array}\end{eqnarray} \tag{ 4 }$$

where ${{n}_{o}}\approx 2.6\cdot {{10}^{25}}$ m⁻³ is the density of air at STP, v the velocity of the incident electron with energy E and ${{\sigma}_{\text{e},{{\text{O}}_{2}}/{{\text{N}}_{2}}}}$ the cross sections of impact ionization of molecular nitrogen and oxygen [39–41]. The parameter ${{\chi}_{{{\text{O}}_{2}}}}$ is the relative abundance of oxygen molecules and (1-${{\chi}_{{{\text{O}}_{2}}}}$) of nitrogen molecules, i.e. ${{\chi}_{{{\text{O}}_{2}}}}=0.2$ in air. The cross sections of oxygen and nitrogen are almost the same, hence the impact ionization frequency is weakly dependent on ${{\chi}_{{{\text{O}}_{2}}}}$. The probability of an ionization event during a time step $\Delta t$ is then:

$$\begin{eqnarray}&&\begin{array}{*{35}{l}} {{P}_{\text{e}}}(E)\approx {{\nu}_{\text{e}}}(E) \Delta t \end{array}.\end{eqnarray} \tag{ 5 }$$

New electrons are created not only through electron impact ionization, but also indirectly through ionization of oxygen by photons emitted from excited states of nitrogen:

$$\begin{eqnarray}\begin{array}{*{35}{l}} {{\text{N}}_{2}}+{{\text{e}}^{-}} & \to & \text{N}_{2}^{\ast}+{{\text{e}}^{-}} \end{array}\end{eqnarray} \tag{ 6 }$$

$$\begin{eqnarray}\begin{array}{*{35}{l}} \text{N}_{2}^{\ast} & \to & {{\text{N}}_{2}}+{{\gamma}_{\text{UV}}} \end{array}\end{eqnarray} \tag{ 7 }$$

$$\begin{eqnarray}\begin{array}{*{35}{l}} {{\text{O}}_{2}}+{{\gamma}_{\text{UV}}} & \to & \text{O}_{2}^{+}+{{\text{e}}^{-}} \end{array}\end{eqnarray} \tag{ 8 }$$

with N$_{2}^{\ast}$ an excited state of N₂ and ${{\gamma}_{\text{UV}}}$ the UV photon,

For this process we follow [37, 42] and adopt the model of Zheleznyak [21]. It accounts for wavelengths in the UV range between 980 Å and 1025 Å, corresponding to photon energies from 12.10 to 12.65 eV. It is a band that does not interact with N₂ and exclusively ionizes molecular oxygen and is considered the dominant path where photoionization operates in air discharges. The photons are radiated isotropically and ionize at distances related to their mean free path [37]. The number of UV ionization events is estimated from the number of electron impact ionization events. The probability of UV ionization, P_UV, is a function of the ambient pressure, p:

$$\begin{eqnarray}&&\begin{array}{*{35}{l}} {{P}_{\text{UV}}}\left(\,p\right)=\xi \hat{q}\left(\,p\right){{P}_{\text{e}}} \end{array}\end{eqnarray} \tag{ 9 }$$

where ξ is the relative number of events that lead to UV ionization in the absence of quenching and $\hat{q}\left(\,p\right)$ is the quenching factor

$$\begin{eqnarray}&&\begin{array}{*{35}{l}} \hat{q}\left(\,p\right)=\frac{{{p}_{q}}}{p+{{p}_{q}}}. \end{array}\end{eqnarray} \tag{ 10 }$$

The quenching pressure is p_q  =  30 Torr  =0.04 bar for the singlet states of N₂ [21] giving $\hat{q}\left(\,p\right)\simeq 0.04$ at STP. The parameter ξ depends on the abundance of oxygen and is $\simeq 0.1$ in air.

For bremsstrahlung we have:

$$\begin{eqnarray}\begin{array}{*{35}{l}} {{\text{O}}_{2}}~\text{or}~{{\text{N}}_{2}}+{{\text{e}}^{-}} & \to & {{\text{O}}_{2}}~\text{or}~{{\text{N}}_{2}}+{{\gamma}_{\text{br}}}+{{\text{e}}^{-}} \end{array}\end{eqnarray} \tag{ 11 }$$

$$\begin{eqnarray}\begin{array}{*{35}{l}} {{\text{O}}_{2}}~\text{or}~{{\text{N}}_{2}}+{{\gamma}_{\text{br}}} & \to & \text{O}_{2}^{+}~\text{or}~\text{N}_{2}^{+}+{{\text{e}}^{-}} \end{array}\end{eqnarray} \tag{ 12 }$$

where ${{\gamma}_{\text{br}}}$ is the emitted bremsstrahlung photon. The cross sections for reactions (11) are given in e.g. [29–31, 35], they are almost identical for nitrogen and oxygen.

In this process we follow all bremsstrahlung photons above 12.1 eV in their motion through the ambient gas. For both UV and bremsstrahlung photons, a photon is fully absorbed during an ionization event and the kinetic energy of the emitted electron is the energy of the incident photon minus the binding energy of the electron.

The probability of bremsstrahlung ionization (12) is the convolution of the probability of producing a bremsstrahlung photon by an incident electron with the probability of subsequent photoionization. The highest energy the photon can have is the incident electron energy, E, and the lowest energy of interest is the binding energies of the neutral molecules, ${{E}_{\text{i},{{\text{O}}_{2}}}}$ and ${{E}_{\text{i},{{\text{N}}_{2}}}}$. The frequency, ${{\nu}_{\gamma}}\left(E,{{E}_{\gamma}}\right)$, that photons in the energy bin ${{E}_{\gamma}}$ are created from an electron with energy $E>{{E}_{\gamma}}$ is:

$$\begin{eqnarray}&&\begin{array}{*{35}{l}} {{\nu}_{\gamma}}\left(E,{{E}_{\gamma}}\right)={{n}_{o}}v\left({{\chi}_{{{\text{O}}_{2}}}}{{\sigma}_{\gamma,{{\text{O}}_{2}}}}\left(E,{{E}_{\gamma}}\right)+\left(1-{{\chi}_{{{\text{O}}_{2}}}}\right){{\sigma}_{\gamma,{{\text{N}}_{2}}}}\left(E,{{E}_{\gamma}}\right)\right) \end{array}\end{eqnarray} \tag{ 13 }$$

where ${{\sigma}_{\gamma,{{\text{O}}_{2}}}}$ and ${{\sigma}_{\gamma,{{\text{N}}_{2}}}}$ are the cross sections of bremsstrahlung depending on the photon energy [29, 30, 43]. The frequency at which photons with energy ${{E}_{\gamma}}$ photoionize the gas is:

$$\begin{eqnarray}&&\begin{array}{*{35}{l}} {{\nu}_{\text{ph}}}\left({{E}_{\gamma}}\right)={{n}_{o}}c\left({{\chi}_{{{\text{O}}_{2}}}}{{\sigma}_{\text{ph},{{\text{O}}_{2}}}}\left({{E}_{\gamma}}\right)+\left(1-{{\chi}_{{{\text{O}}_{2}}}}\right){{\sigma}_{\text{ph},{{\text{N}}_{2}}}}\left({{E}_{\gamma}}\right)\right) \end{array}\end{eqnarray} \tag{ 14 }$$

where c is the speed of light and ${{\sigma}_{\text{ph},{{\text{O}}_{2}}/{{\text{N}}_{2}}}}$ the total cross section of photoionization [43]. The probability of photoionization via bremsstrahlung in a time step $\Delta t$ is then:

$$\begin{eqnarray}&&\begin{array}{*{35}{l}} {{P}_{\text{br}}}\left(E,{{E}_{\gamma}}\right)={{\nu}_{\gamma}}\left(E,{{E}_{\gamma}}\right){{\nu}_{\text{ph}}}\left({{E}_{\gamma}}\right) \Delta {{t}^{2}}. \end{array}\end{eqnarray} \tag{ 15 }$$

The total ionization frequency including all photons in the range ${{E}_{\text{i},{{\text{O}}_{2}},{{\text{N}}_{2}}}}$ to E is:

$$\begin{eqnarray}&&\begin{array}{*{35}{l}} {{P}_{\text{br}}}(E)=\frac{1}{E-{{E}_{\text{i},{{\text{O}}_{2}},{{\text{N}}_{2}}}}}{\int}_{{{E}_{\text{i},{{\text{O}}_{2}},{{\text{N}}_{2}}}}}^{E}{{\nu}_{\gamma}}\left(E,{{E}_{\gamma}}\right){{\nu}_{\text{ph}}}\left({{E}_{\gamma}}\right) \Delta {{t}^{2}}\text{d}{{E}_{\gamma}}. \end{array}\end{eqnarray} \tag{ 16 }$$

In the equation we have used a short hand notation where the lower limit of integration is ${{E}_{\text{i},{{\text{O}}_{2}}}}=12.1$ eV for the oxygen contribution and ${{E}_{\text{i},{{\text{N}}_{2}}}}=15.6$ eV for the nitrogen contribution.

The probabilities of the three processes to generate ionization are shown in figure 2 as functions of incident electron energy for $\Delta t=0.01$ ps, a time interval in the order of a Monte Carlo time step. The curves are for STP conditions with ${{\chi}_{{{\text{O}}_{2}}}}=0.2$ (air) and with 10⁻⁶. Impact ionization and bremsstrahlung induced ionization are each represented by a single curve as their probabilities depend weakly on ${{\chi}_{{{\text{O}}_{2}}}}$. In pure nitrogen, UV ionization is nonexistent and otherwise we assume it proportional to ${{\chi}_{{{\text{O}}_{2}}}}$ according to (9). We see from the figure that impact ionization dominates, and when in air, that UV ionization is orders of magnitudes larger than bremsstrahlung ionization. At lower ambient pressures, as at higher altitudes, UV quenching will decrease and UV ionization increases to even higher values relative to bremsstrahlung ionization. We further note that for ${{\chi}_{{{\text{O}}_{2}}}}={{10}^{-6}}$, bremsstrahlung induced ionization dominates over UV ionization.

Zoom In Zoom Out Reset image size

The figure also shows the mean free path $\Lambda$ of electrons for the impact ionization process (full) and the mean free path of photons for the photoionization process as function of the photon energy (dot). Since photoionization is the dominant process for photons between 10 and 1 keV, the dotted curve approximately also shows the mean free path of a photon in air. For photon energies below 1 keV the mean free path for photoionization ranges from 0.1 mm to 1 cm. In comparison, the mean free path of UV photons with energies of approximately 15.6 eV, is smaller than 1 mm. Hence, photoionization by bremsstrahlung photons with energies above 15.6 eV covers a wider spatial range than the photoionization by UV photons with energies of up to 15.6 eV.

We add here that the treatment of UV photoionization, in previous literature [37, 42] and here, is not consistent because it assumes that photons above 12.65 eV will not ionize the gas because they are assumed to be absorbed by N₂ [7, 44]. As a consequence, in previous models, only photons with energies between 12.1 and 12.65 eV, are supposed to ionize oxygen whereas there is no UV photoionization of molecular nitrogen at all. Yet, we find that bremsstrahlung photons with energies above 12.65 eV indeed create ionization. At this point we are not able to offer a more consistent model for UV ionization.

Streamer simulations were carried out for three oxygen mixing ratios, ${{\chi}_{{{O}_{2}}}}=0.2,{{10}^{-6}}$ and 0. To understand the influence of bremsstrahlung, the simulations were conducted with and without bremsstrahlung. The electron density is shown in figure 3 in the (r,z) domain at three time steps (columns) and for the three mixing ratios (rows). In all panels the left half of each domain shows results with bremsstrahlung and the right half without. The electric field (3E_k) is pointing downwards such that the positive polarity is propagating downwards and the negative upwards. The maximum time simulated is given by the time that boundaries of the domain begin to interfere with the results. As supplementary material we provide movies showing the complete temporal evolution of the electron density. We note here that the actual shape of the electron density profile may look different if they had been simulated with a three dimensional Monte Carlo code, but that the filaments which we observe would still exist and that in the following the overall microphysical interpretation of the observed phenomena is independent of the dimensionality of the used Monte Carlo code.

Zoom In Zoom Out Reset image size

The top row is for ${{\chi}_{{{O}_{2}}}}=0.2$ where UV ionization dominates over bremsstrahlung ionization. We see that both polarities propagate with ionization well ahead of the streamer body. This is caused by UV ionization, and since it reaches the boundaries rather quickly, the simulations are halted after 0.49 ns. Interestingly, although the probability of bremsstrahlung ionization is lower than UV ionization by an order of magnitude or more, when bremsstrahlung is included, both polarities appear to propagate slower with less ionization ahead of the streamer body. The velocities of the streamer fronts are shown in figure 4 as functions of time. We see how the streamers accelerate as they form, reaching  ≈$3.9\cdot {{10}^{6}}$ m s⁻¹ and  ≈$4.8\cdot {{10}^{6}}$ m s⁻¹ for the positive and negative polarities without bremsstrahlung and  ≈$3.3\cdot {{10}^{6}}$ m s⁻¹ and  ≈$4.2\cdot {{10}^{6}}$ m s⁻¹, i.e.  ≈$15 \%$ lower, when bremsstrahlung is included.

Zoom In Zoom Out Reset image size

It has been suggested that streamer velocities depend on the radius of the streamers and the electric field magnitude at the streamer front [45]. The field structure in our streamers is shown in the r,z-plane in figure 5 for the same times and in the same format as for the densities in figures 3(a)–(c). The electric field magnitude and the geometry of the streamer fronts do not appear significantly different, however both densities and fields have higher levels of fluctuations than seen in fluid codes. We discuss later if this is a numerical effect or a real physical effect. Figure 6 shows the electric field profile in (a) air and (b) with 1 ppm oxygen only as a function of z after different time steps with and without bremsstrahlung. The shape of the field in air resembles the shape of the electric field given in the previous literature, e.g. in [37]. We observe that the field at the streamer head declines smoothly; the field increase from the interior to the streamer heads happens within approximately 100 μm which is much larger than the grid size of approximately 10 μm. This indicates that the grid size is fine enough to resolve the field gradients sufficiently well.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

Turning instead to the electron energies, we find a clue. In figure 7 the cumulative probability P_e to have electrons and the rate ${{P}_{\text{e}}}\cdot {{\nu}_{\gamma}}$ of bremsstrahlung photon production with energies above E with and without bremsstrahlung is shown at t  =  0.12 ns (a) and 0.49 ns (b). We see that at the earlier time, the high-energy tail above approximately 10 eV is more pronounced when bremsstrahlung is excluded. We interpret this as an effect of increased energy loss of electrons to bremsstrahlung photons. Hence, these electrons are lost from the subset of precursor electrons and there is less electron impact ionization and according to our model less UV photoionization. Since UV photoionization in air is one of the driving forces for streamer propagation [22], this implies a less significant acceleration of the streamer front if the bremsstrahlung process is turned on. We observe this tendency already for time steps when the electric field is the same with and without bremsstrahlung (a), but this effect is still present for later times (b).

Zoom In Zoom Out Reset image size

In the above, we have discussed the influence of bremsstrahlung in air where UV ionization dominates over bremsstrahlung ionization. We next turn to gas mixtures at low levels of oxygen corresponding to the two lower rows of figure 3. Here we see a completely different picture with the branching of the negative streamer fronts and also the positive fronts that propagate with difficulty, as expected. To explore further the processes at the fronts we first turn to the positive tips which are shown in figure 8 for the same time steps as in figure 3 with ${{\chi}_{{{\text{O}}_{2}}}}={{10}^{-6}}$ in the top row and ${{\chi}_{{{\text{O}}_{2}}}}=0$ at the bottom. From the right part of the panels which are without bremsstrahlung, we see that the positive streamer front is not moving during the time of this simulation, in agreement with simulations of others, as described earlier. In the top row, we see that the small amount of oxygen has the effect of building a thick space charge region in the tip where the field reaches values above 6E_k. It is possible that the layer will break down and sub-streamers be formed if the simulations are run for longer duration. On the left half of the plots, which includes bremsstrahlung, we see a markedly different dynamics of sub-streamers emerging from the front, propagating and branching into new sub-streamers. It is most noticeable when oxygen is included (top), but also appears to some extent with no oxygen (bottom). The electric field at the tips of these sub-streamers reaches almost 10E_k, a value that allows electrons to be accelerated to 100 eV where the cross sections for ionization maximize, and even above into the runaway regime.

Zoom In Zoom Out Reset image size

For the case of no oxygen and with bremsstrahlung (bottom, left half of each panel) sub-streamers are also formed, but propagate slower. One sub-streamer is developing from the edge of the flattening streamer front and propagates radially and perpendicular to the ambient field. The exact location and development of sub-streamers are of course a stochastic problem in a situation with few ionization events. However, our results overall suggest that the apparent contradiction between experiments that show that positive streamers propagate in nitrogen–oxygen admixtures with $\lesssim$1 ppm oxygen and simulations showing no propagation [24, 27] is resolved by including bremsstrahlung into the simulations.

We next study in more detail the formation of the first sub-streamer appearing in the nitrogen-oxygen mixture with a 1 ppm oxygen. In figure 9 we have combined the density (top row), the electric field distribution (middle) and the electron energies (bottom) at t  =  0.25,0.36 and 0.43 ns. All electrons at positions below z  =  7 are plotted as a function of their energies. On the left panel, electrons reach about 80 eV in the streamer front that is being established, with a few electrons at higher energies. Electrons are also present ahead of the streamer front down to $z\approx 5.75$. These are electrons in the sub-streamer channel that is being formed from a few localized electrons from bremsstrahlung induced photoionization, accelerating towards the front creating new electrons by impact ionization. They are seen in the density plot of the top row, but are at first too few in number to affect the electric field. In the middle panel, the main streamer front has grown and the electrons have reached higher energies and higher numbers in the front ($z\approx 6.15$). The sub-streamer has also developed. It has retracted a little in z, but the number of electrons has increased significantly, thus affecting the electric field distribution; however, their energies are modest. In the right column, the streamer front is now located in the sub-streamer, with a large number of electrons around $z\approx 5.9$ and with high energies, reaching well above 100 eV. At later times, the sub-streamer branches as shown in figure 8. Comparing the results with and without bremsstrahlung we conclude that bremsstrahlung facilitates the propagation of positive streamer fronts and the acceleration of electrons to energies reaching into the runaway regime.

Zoom In Zoom Out Reset image size

The electric field distribution of the negative streamer fronts are shown in figure 10 at times corresponding to figure 3 for ${{\chi}_{{{\text{O}}_{2}}}}={{10}^{-6}}$ in the top row and ${{\chi}_{{{\text{O}}_{2}}}}=0$ at the bottom. We see a similar picture as for the positive front, with negative streamer channels forming with high electric fields at their tips. This basic structure is independent of bremsstrahlung and UV ionization and must be fundamental to electron impact ionization. However, when photoionization is added, either from UV or bremsstrahlung photons, the branches (or sub-streamers) grow more readily. The photoionization creates seed electrons ahead of the streamer front and these lead to further ionization. The key to the difference between nitrogen admixed with low oxygen contents and of air is simply the relatively large amount of photoionization in air which prevents streamer branching, at least during the short time of our simulations.

Zoom In Zoom Out Reset image size

If one considers the probabilities of photoionization via oxygen versus bremsstrahlung (figure 2) it is surprising that oxygen concentrations at the level of ${{\chi}_{{{\text{O}}_{2}}}}={{10}^{-6}}$ can make such a difference to streamer dynamics as the probability is 1–2 orders lower than for bremsstrahlung. We can understand this effect by looking at the total number of (real) electrons in the simulation domain as a function of time, as shown in figure 11. We show the numbers for bremsstrahlung only (${{\chi}_{{{\text{O}}_{2}}}}=0$), UV photoionization only without bremsstrahlung (${{\chi}_{{{\text{O}}_{2}}}}={{10}^{-6}}$) and for both processes together (${{\chi}_{{{\text{O}}_{2}}}}={{10}^{-6}}$). When the two processes are taken separately, we see that the electron numbers are similar, with a slightly higher number with bremsstrahlung. As shown by figure 2(a), the dominant mechanism for the production of new electrons in the considered gas mixtures, is electron impact ionization. Thus the important role of UV photoionization or bremsstrahlung induced photoionization is not to create a large amount of ionization, but to catalyze impact ionization. If the two processes are taken together, however, the number density grows more rapidly because of the additional possibility of electron creation and their effect is more than just catalytic.

Zoom In Zoom Out Reset image size

A final point to be made concerns the production of high-energy electrons. As noted in the discussion of positive sub-streamers, these focus the electric field to very high values at the streamer tips, creating patches of high densities and fields dislocated from the main streamer body. One example is shown in the top, right panel of figure 10 for the case without bremsstrahlung. These regions accelerate electrons to energies up to  ≈4 keV, in our simulations. The high-energy fluxes appear not to be sensitive to the bremsstrahlung process or the concentrations of oxygen.

It appears that the bremsstrahlung process may solve the enigma of how positive streamers may propagate in pure or almost pure nitrogen. There may, of course, be other effects that allow this propagation, for instance cosmic ray ionization of the nitrogen gas that creates seed electrons ahead of a positive streamer [27], just as bremsstrahlung from the the streamer electrons does in our simulations. One should also remember that, although these simulations follow the complete physics including electron dynamics, there are limits to the resolution of electrons, which can be coalesced to larger computer- electrons. To minimize this problem we have adapted the scheme of [37] in the way described in section 2. Nevertheless, when the results depend on few ionization events, the stochastic nature cannot be ignored. To this we offer the following considerations. As figure 5 demonstrates, the stochastic nature leads to rather noisy field tips at the streamer heads in air after 0.49 ns. However, the noise is present independent of the inclusion of the bremsstrahlung process and, hence, does not affect our conclusions. We here also note that we implemented a splitting scheme of superelectrons as described in section 2, thus the production of the filaments presented in figures 3(f) and (i) is rather physical than due to pure computational noise.

The simulations presented here are for a background field of 3E_k which may be considered rather large. We have chosen this value to accelerate the physics thereby reducing the computational time. At lower fields we expect the overall conclusion to stand, that is that bremsstrahlung facilitates the propagation of positive streamer fronts, that both negative and positive fronts move slower in air when bremsstrahlung is included and that sub-streamers are formed at low oxygen levels. The electric fields in the fronts of the streamers and sub-streamers may, however, be reduced in magnitude and the acceleration of electrons less pronounced.

The research leading to these results has received funding from the People Programme (Marie Curie Actions) of the European Union's Seventh Framework Programme (FP7/2007–2013) under REA grant agreement no 609405 (COFUNDPostdocDTU).