Abstract
The previously presented analytical model of a transversely diode-pumped alkali metal vapour laser (A.I. Parkhomenko, A.M. Shalagin, Quantum Electronics, 2015, Vol. 45, No. 9, pp 797 – 806) is refined and expanded. Analytical formulas are derived describing the operation of a high-intensity laser at an almost arbitrary buffer gas pressure and taking into account radiation losses in the resonator. Comparison of the results of calculations of the laser energy characteristics by analytical formulas with the results of numerical calculations of other authors shows very good agreement.
Export citation and abstract BibTeX RIS
| A.I. Parhomenko Institute of Automation and Electrometry, Siberian Branch, Russian Academy of Sciences, prosp. Akad. Koptyuga 1, 630090 Novosibirsk, Russia |
| e-mail: par@iae.nsk.su |
| A.M. Shalagin Institute of Automation and Electrometry, Siberian Branch, Russian Academy of Sciences, prosp. Akad. Koptyuga 1, 630090 Novosibirsk, Russia; Novosibirsk State University, ul. Pirogova 2, 630090 Novosibirsk, Russia |
| e-mail: shalagin@iae.nsk.su |
1. Introduction
In recent years, diode-pumped alkali metal vapour lasers have been intensively investigated experimentally and theoretically [1–5]. A great interest in these lasers is reasonably associated with their ability to generate cw radiation of very high power, while demonstrating a high conversion efficiency of pump radiation into laser radiation.
The maximum output of an alkali metal vapour laser has been achieved in work [4], where the creation of a longitudinally diode-pumped caesium vapour laser with closed-cycle laser-active medium circulation is reported. In cw mode, the laser radiation power was 1 kW with a conversion efficiency of pump energy into laser energy amounting to 48%.
Obtaining significantly higher powers requires the scaling of the process. In our opinion, the geometry with transverse pumping is optimal for scaling. In this geometry, the power of the generated radiation increases in proportion to the length of the laser. The idea of a transversely diode-pumped alkali metal vapour laser was patented [6] and first implemented in [7]. A theoretical model of such a laser was first proposed by Komashko and Zweiback [8]. The laser operation was described in [8] by a rather complex system of differential equations, which was solved numerically in the approximation of the effective absorption cross section of pump radiation. Yang et al. [9] developed a somewhat different numerical model of the laser than that presented in work [8]. The equations in [9] were solved numerically on the assumption that the population levels of the atoms of the active medium do not depend on the coordinate along the resonator axis, i.e., they are constant along the propagation direction of the laser output.
In paper [10], we developed an analytical model of a transversely diode-pumped alkali metal vapour laser, which describes the operation of the laser in the practically important case of high radiation intensity but at a sufficiently high buffer gas pressure and in the absence of radiation loss in the resonator. The aim of the present paper is to expand the analytical model [10] for the possibility of describing the generation of a high-intensity laser at an almost arbitrary buffer gas pressure and taking into account radiation losses in the resonator.
2. Equations describing the operation of a laser
An alkali metal vapour laser operates in accordance with a three-level scheme (Fig. 1). The laser cycle includes optical excitation of the D2 (2S1/2 – 2P3/2) transition, the population of the 2P1/2 level in collisions of alkali metal atoms at the 2P3/2 level with the buffer gas particles, and laser generation at the D1 (2P1/2 – 2S1/2) transition. In Fig. 1, the levels 2S1/2, 2P1/2 and 2P3/2 are denoted by figures 1, 2 and 3, respectively.
Figure 1. Diagram of energy levels and transitions in alkali metal atoms. The straight line shows the transition caused by pump radiation, the wavy line corresponds to the laser transition and curved lines indicate collisional transitions.
Download figure:
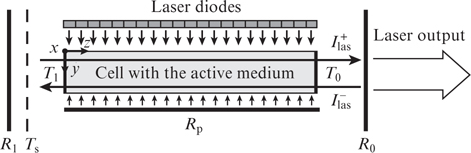
Standard imageFigure 2. Scheme of a transversely diode-pumped alkali metal vapour laser.
Download figure:
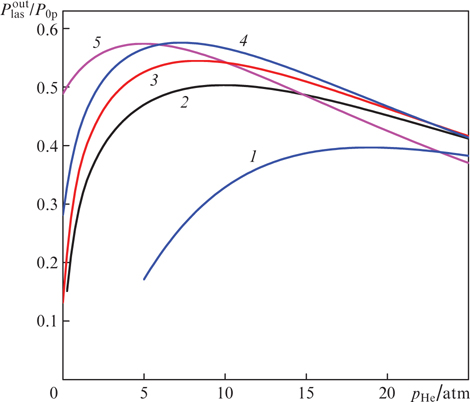
Standard imageFigure 3. Effect of the parameter Ny0 on the conversion efficiency. The calculation parameters are I0p = 3 kW cm−2, Δω/(2πc) = 3 cm−1, T = 395 K, pCH4 = 0.1 atm, Rp = 0.99, R0 = 0.3, R1 = 0.99, T0 = 0.99, T1 = 0.99, Ts = 0.99, ωp = ω31, ωlas = ω21; (1, 1') Ny0 = 13.5 × 1013, (2, 2') 18 × 1013 and (3, 3') 9 × 1013 cm−2. Solid curves are the results of calculation in the first approximation in the parameter bϰp, dashed curves – calculation in the approximation b = 0.
Download figure:
Standard imageLet us consider the operation of a transversely diode-pumped alkali metal vapour laser. The scheme of the laser is shown in Fig. 2. To simplify the analysis, we assumed that a cell with alkali metal vapours and buffer gases has the form of a rectangular parallelepiped with edges z0 (length), y0 (width) and x0 (height). Pump laser diodes are arranged on one side of the cell. Their radiation enters the cell in the xz plane and propagates in the y direction. For a more efficient utilisation of the pump energy, a plane mirror is mounted on the other side of the cell, which reflects the pump radiation passing through it (the reflection coefficient of the mirror, Rp) back to the cell. The resonator consists of two plane mirrors with reflection coefficients R0 and R1. The transmission coefficients of the cell windows are T0 and T1. The radiation energy losses in the resonator (due to the diffraction of light at the edges of the mirrors, due to the geometric imperfection of the resonator, due to the scattering of light in the medium by inhomogeneities) are taken into account by introducing the effective transmittance Ts. The value of Ts characterises the relative losses of the radiation energy in the resonator in one pass, excluding the transmission losses of the windows. It is assumed that the losses of Ts are localised in front of the rear mirror R1. Laser radiation is coupled out of the cell in the xy plane through a semitransparent mirror with a reflection coefficient R0 and propagates in the z direction. For simplicity, we assume that the intensity distribution of pump radiation is uniform in the xz plane (at the input to the cell). In this case, as a consequence, the intensity distribution of laser radiation is also uniform along the height of the cell (along the x axis).
Under steady-state conditions, absorption of pump radiation and amplification of laser radiation are described by the equations:
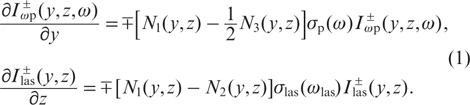
Here, 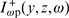 and
and  are the spectral densities of the pump radiation power at a frequency ω, propagating along the y axis and in the opposite direction (after reflection by the mirror), respectively;
are the spectral densities of the pump radiation power at a frequency ω, propagating along the y axis and in the opposite direction (after reflection by the mirror), respectively;  and
and 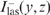 are the intensities of laser radiation propagating along the z axis and in the opposite direction, respectively; N1(y, z), N2(y, z) and N3(y, z) are the populations of levels 1, 2 and 3; σp(ω) is the absorption cross section of pump radiation; and σlas(ωlas) is the absorption cross section of laser radiation with frequency ωlas. The absorption cross sections are found from the formulas:
are the intensities of laser radiation propagating along the z axis and in the opposite direction, respectively; N1(y, z), N2(y, z) and N3(y, z) are the populations of levels 1, 2 and 3; σp(ω) is the absorption cross section of pump radiation; and σlas(ωlas) is the absorption cross section of laser radiation with frequency ωlas. The absorption cross sections are found from the formulas:
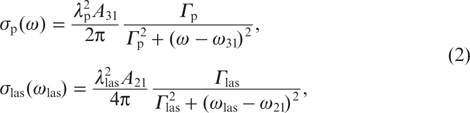
where λp and λlas are the centre wavelengths of pump radiation and laser radiation; A31 and A21 are the spontaneous emission rates (the first Einstein coefficients) for 3 – 1 and 2 – 1 transitions; Γp = A31/2 + γ31 and Γlas = A21/2 + γ21 are the homogeneous half-widths of 3 – 1 and 2 – 1 transition lines, respectively; γ31 and γ21 are the collision half-widths of 3 – 1 and 2 – 1 transition lines; ω31 and ω21 are the frequencies of 3 – 1 and 2 – 1 transitions. Equations (1) are supplemented by boundary conditions describing the change in radiation intensities on the mirror surface in the course of reflection and propagation through the cell windows:
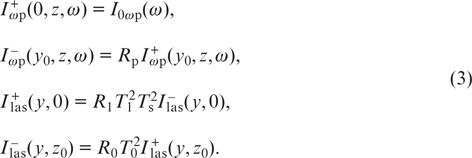
The populations of levels 1, 2 and 3 in equations (1) are found from the balance equations. In the steady-state case, these equations have the form:
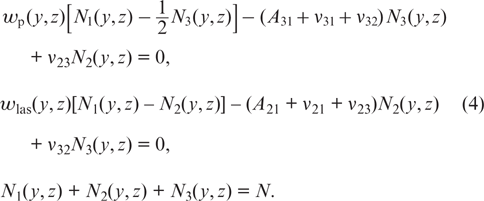
Here, N is the total concentration of active atoms; collision frequencies ν32 and ν23 describe collisional mixing between levels 3 and 2; collision frequencies ν31 and ν21 describe inelastic collision transitions along the 3 → 1 and 2 → 1 channels; and wp(y, z) and wlas(y, z) are the probabilities of induced transitions under the action of pump radiation and generated laser radiation, respectively. We assume that pump radiation has a spectrum of arbitrary width, and generated laser radiation is monochromatic. Then

where ωp is the centre frequency of the pump radiation spectrum; and
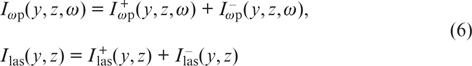
is the total spectral power density of pump radiation inside the cell and the total intensity of laser radiation inside the cell, respectively. The collision frequencies ν32 and ν23, due to the principle of detailed balance, are related by the expressions
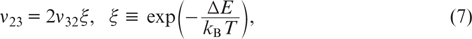
where ΔE = ħω32 is the energy difference between levels 3 and 2; and T is the temperature of the gas mixture inside the cell.
From the system of algebraic equations (4) we find the populations of levels:

and population differences characterising laser generation and pump absorption:
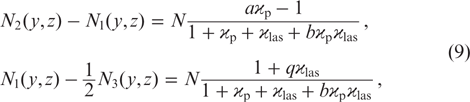
where
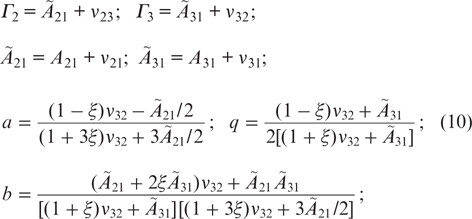
Ã31 and Ã21 are the transition frequencies from levels 3 and 2 as a result of spontaneous emission and collisional transitions to the ground state; and Γ3 and Γ2 are the total transition frequencies from levels 3 and 2 as a result of spontaneous emission and collisions. The quantities ϰp ≡ ϰp(y, z) and ϰlas ≡ ϰlas(y, z) are defined as
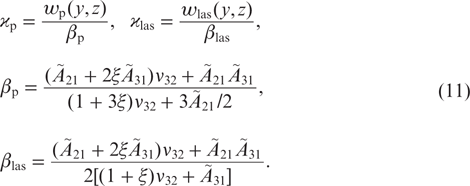
They denote the saturation parameters, since each of them characterises the degree of population equalisation at the 3 – 1 or 2 – 1 transition in the absence of the second field.
Taking into account relations (9), differential equations (1), describing the operation of the laser, have the form:
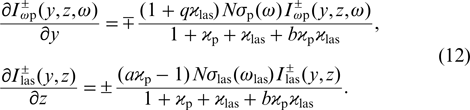
As follows from the equations for  in (12), lasing occurs when the condition aϰp > 1 is fulfilled. To ensure effective generation (aϰp ≫ 1), one must meet the conditions
in (12), lasing occurs when the condition aϰp > 1 is fulfilled. To ensure effective generation (aϰp ≫ 1), one must meet the conditions
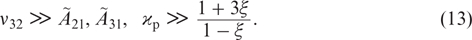
The first condition in (13) is satisfied with a large margin at a sufficiently high pressure of the buffer gas (∼1 atm and higher). To fulfil the second condition, the spectral power density of pump radiation must be sufficiently high. Under these conditions, pumping produces an extremely large population inversion at the laser transition.
3. Relationship between integral characteristics of radiations
The system of differential equations (12) describing the laser operation can be solved only by numerical methods. Nevertheless, it is possible, without solving it, to obtain a practically important relationship between the integral characteristics of radiations.
We will show how this relationship directly follows from Eqns (12). Integrating the difference between the third (for  ) and fourth (for
) and fourth (for  ) equations in (12) over the cell volume (with respect to x, y, z), taking into account formulas (5) and (11) for wlas and ϰlas, for the output power of laser radiation coupled out of the cell
) equations in (12) over the cell volume (with respect to x, y, z), taking into account formulas (5) and (11) for wlas and ϰlas, for the output power of laser radiation coupled out of the cell

we obtain an expression
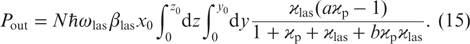
Hereafter, we assume that in the considered geometry of the transversely pumped laser, laser radiation is generated in the entire cell volume V = x0 y0 z0.
The intensity  of laser radiation emerging from the resonator through a semitransparent mirror with a reflection coefficient R0 is given by the expression
of laser radiation emerging from the resonator through a semitransparent mirror with a reflection coefficient R0 is given by the expression
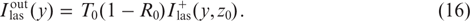
The output power  of laser radiation emerging from the resonator through a semitransparent mirror is defined as the integral of the intensity over the beam cross section:
of laser radiation emerging from the resonator through a semitransparent mirror is defined as the integral of the intensity over the beam cross section:

Let us find the relationship between the powers 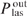 (17) and Pout (15). From the last two equations in (12) we obtain the expression
(17) and Pout (15). From the last two equations in (12) we obtain the expression
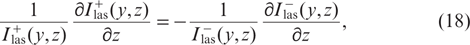
from which it follows that the product 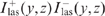 does not depend on z. In particular, the relation
does not depend on z. In particular, the relation
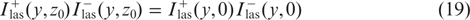
is valid. The integrand in (14), taking into account (16), (19) and boundary conditions (3), has the form
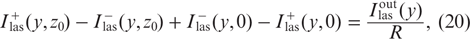
where
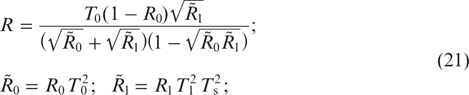
Expressions (14), (15), (17) and (20) yield the relationship between the powers 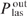 and Pout (15):
and Pout (15):
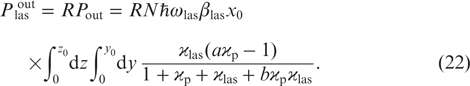
Let us write the difference between the second (for 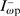 ) and first (for
) and first (for  ) equations in (12) and integrate it with respect to the frequency ω. Taking into account formulas (5) and (11) for wp and ϰp, we obtain an expression
) equations in (12) and integrate it with respect to the frequency ω. Taking into account formulas (5) and (11) for wp and ϰp, we obtain an expression

where
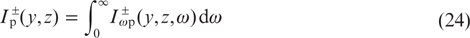
are the total intensities of pump radiation propagating along the y axis (the superscript '+') and in the opposite direction (after reflection by the mirror, the superscript '–'). Integrating equation (23) over the cell volume, we obtain for the absorbed pump power
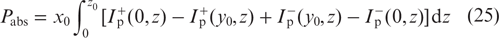
an expression
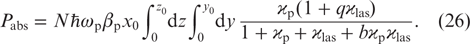
Below we will take into account that the total losses of the pump power for spontaneous emission and collisional quenching in the cell volume are given by a fairly obvious relationship:
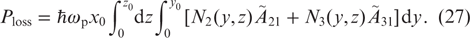
Taking into account formulas (8) for the population levels, expression (27) has the form
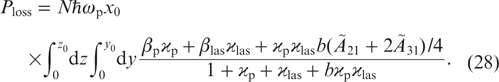
From (22), (26), and (28) we obtain the expression

relating the output power  of laser radiation coupled out from the resonator with the absorbed pump power Pabs and the pump power losses Ploss due to spontaneous emission and collisional quenching.
of laser radiation coupled out from the resonator with the absorbed pump power Pabs and the pump power losses Ploss due to spontaneous emission and collisional quenching.
The pump power loss Ploss during the laser operation arises both due to the loss of spontaneous emission and collisional quenching and due to the unabsorbed pump power

where P0p is the pump power at the entrance to the cell. Taking this relation into account, formula (29) for the laser radiation power can also be represented in the form
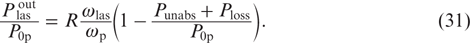
The ratio of the laser power to the pump power, 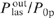 , characterises the efficiency of the conversion of pump radiation into laser radiation, and the ratio of radiation frequencies ωlas/ωp is the quantum efficiency of this conversion. For alkali metal vapours it is close to unity (95% for caesium, 98% for rubidium and 99.5% for potassium), which ensures a high efficiency of alkali metal vapour lasers. The conversion efficiency of pump radiation into laser radiation
, characterises the efficiency of the conversion of pump radiation into laser radiation, and the ratio of radiation frequencies ωlas/ωp is the quantum efficiency of this conversion. For alkali metal vapours it is close to unity (95% for caesium, 98% for rubidium and 99.5% for potassium), which ensures a high efficiency of alkali metal vapour lasers. The conversion efficiency of pump radiation into laser radiation 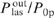 the higher, the smaller the relative total pump power losses (Punabs + Ploss)/P0p.
the higher, the smaller the relative total pump power losses (Punabs + Ploss)/P0p.
4. High intensity of laser radiation
The system of differential equations (12) describing the laser operation can be solved in general only numerically. In our previous work [10], an analytical solution of Eqn (12) was obtained for the case of high laser radiation intensity and a sufficiently high buffer gas pressure, which is reduced to the fulfilment of conditions
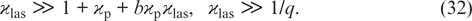
The first condition means both a high intensity of laser radiation (a large saturation parameter ϰlas, not only in comparison with unity, but also in comparison with a saturation parameter for pump radiation ϰp) and a high pressure ensuring a small parameter b such that bϰp ≪ 1. In order to satisfy the second condition in (32), a sufficiently large saturation parameter ϰlas (in particular, for rubidium atoms 1/q ≈ 5) is also needed.
In paper [10], based on approximation (32), we left in equation (12) only ϰlas in the denominator and discarded unity in the first equation of (12) in the numerator in comparison with qϰlas. As a result, the equations were greatly simplified and an analytical solution was obtained.
In the present paper we remove the strict restriction bϰp ≪ 1 and find out the influence of the term bϰp ϰlas in the denominators of equations (12) on the lasing characteristics at not very high buffer gas pressures. Instead of restrictions (32), we impose weaker restrictions:
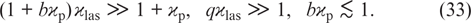
When conditions (33) are satisfied, differential equations (12) have the form:
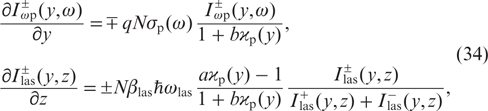
where the saturation parameter ϰp is independent of the coordinate z and is given, in accordance with (5), (6), (11), by the expression
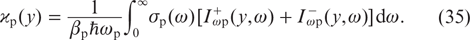
Solving the equations for the laser radiation intensities in (34) with allowance for the boundary conditions (3), we obtain the expression for  :
:
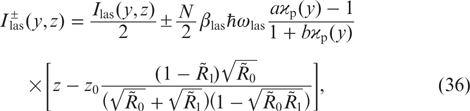
where Ilas(y, z) is the total intensity of laser radiation inside the cell, determined by the formula
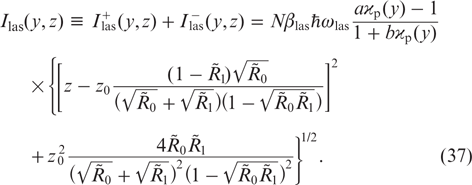
If the effective reflection coefficients of the mirrors, 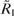 and
and 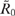 , are close to unity, then, according to (37), the laser radiation intensity Ilas inside the cell is almost constant along the z axis of the resonator. From formulas (16) and (36) we find the laser output intensity
, are close to unity, then, according to (37), the laser radiation intensity Ilas inside the cell is almost constant along the z axis of the resonator. From formulas (16) and (36) we find the laser output intensity
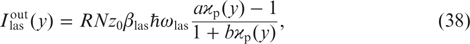
where R is given by the formula in (21).
Next, to solve the problem, we need to find the saturation parameter ϰp(y), determined by the first two equations for the spectral power densities of pump radiation  in (34). We will solve these equations by the method of successive approximations with respect to the small quantity bϰp. For b = 0 (zeroth approximation), the first two equations in (34) have the form [10]:
in (34). We will solve these equations by the method of successive approximations with respect to the small quantity bϰp. For b = 0 (zeroth approximation), the first two equations in (34) have the form [10]:
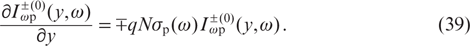
According to [10], the solution of equations (39), taking into account boundary conditions (3), is given by the expressions
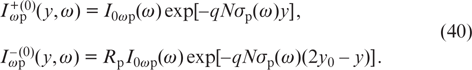
In the next approximation, the first two equations in (34) have the form
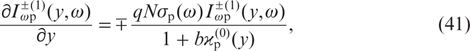
where the initial approximate value of the saturation parameter 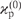 is given by the expression
is given by the expression
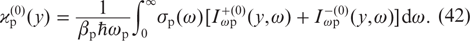
The solution of equations (41) with allowance for boundary conditions (3) is given by the expression:
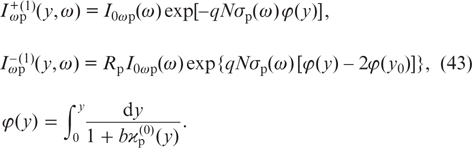
As the final expression for the saturation parameter ϰp, we have the expression obtained on the basis of relation (43):
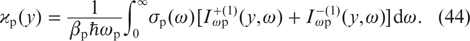
Thus, formulas (38) and (44) describe the operation of a diode-pumped alkali metal vapour laser in the practically important case of a sufficiently high intensity of laser radiation and a weak restriction from below on the buffer gas pressure (for bϰp ≲ 1).
5. Analysis of lasing characteristics
To further define the calculations using the above formulas, it is necessary to specify the spectral power density I0ωp(ω) of the pump diodes at the cell input. We assume that at the input to the cell the pump radiation spectrum is Gaussian:
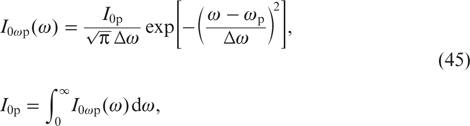
where I0p is the pump radiation intensity at the cell input; and Δω is the half-width (at the level 1/e) of the pump radiation spectrum.
From (43), taking into account (45) for the total spectral power density Iωp(y, ω) of pump radiation inside the cell, we obtain the relation
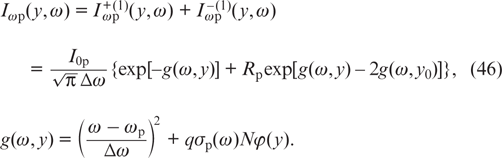
The saturation parameter 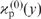 (42) that appears in the formula for the function φ(y) is given by the expression
(42) that appears in the formula for the function φ(y) is given by the expression
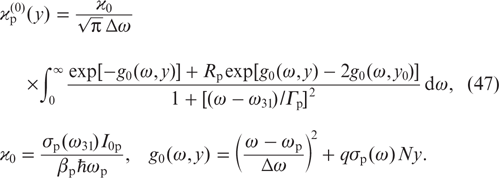
Using (46), we find the total intensity of pump radiation inside the cell:
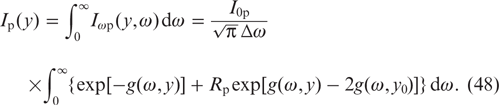
The saturation parameters ϰp(y) and ϰlas(y, z) under the conditions in question are given by the expressions:
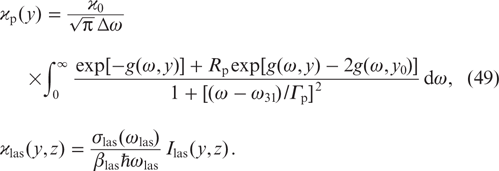
For the laser output power, from expression (17), using (38), we obtain
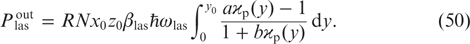
Note here the following important circumstance. Analysis shows that on the right-hand side of formula (50) the concentration N of active particles and cell width y0 enter only in the combination Ny0. This means that, under the condition Ny0 = const, the change in the cell width does not affect the laser output power  .
.
For the pump power losses due to spontaneous emission and collisional quenching in the cell volume, from (28), when conditions (33) are satisfied, we find the expression

For the absorbed pump power in the cell volume, from expression (26), when conditions (33) are satisfied, we obtain the expression
We will calculate the energy characteristics of the laser using the formulas given above. Let the active medium in the laser cell be rubidium atoms, and a mixture of helium and methane be used as a buffer gas. Methane is usually used for effective collisional mixing between excited levels 3 and 2 in alkali metal atoms [1]. Helium is added to increase the collisional broadening of the D2 line in order to make more efficient use of broadband emission from pump diodes [1].
We specify the initial parameters required for the calculation. For rubidium atoms, according to the NIST database [11], the rates of radiative transitions are A21 = 3.6 × 107 s−1, A31 = 3.8 × 107 s−1, transition wavelengths are λ21 = 794.8 nm, λ31 = 780.0 nm and the energy difference ΔE between levels 3 and 2 is 237.6 cm−1. Collisional broadening for rubidium atoms in a helium buffer gas is as follows [12]: γHe(D1) = 9.45 MHz Torr−1 for the D1 line and γHe(D2) = 10.0 MHz Torr−1 for the D2 line. For rubidium atoms in a methane buffer gas, collisional broadening is as follows [12]: γCH4(D1) = 14.55 MHz Torr−1 for the D1 line and γCH4(D2) = 13.1 MHz Torr−1 for the D2 line.
To find the collision frequency ν32, we used the following cross sections for the collisional transitions between the fine components of the excited state of rubidium atoms: σ32(He) = 0.103 × 10−16 cm2 for rubidium atoms in helium [13] and σ32(CH4) = 42 × 10−16 cm2 for rubidium atoms in methane [14]. Because of the small cross section σ32(He), a molecular gas is added to the buffer mixture.
For the cross sections σ31(CH4) and σ21(CH4) of the collisional quenching of excited levels 3 and 2 of rubidium atoms interacting with methane, Zameroski et al. [15] experimentally obtained values not exceeding 1.9 × 10−18 cm2. In calculating collision frequencies ν31 and ν21, we assumed that σ31(CH4) = σ21(CH4) = 1.9 × 10−18 cm2. For rubidium atoms colliding with helium atoms, the collisional quenching cross sections are extremely small (σ31(He), σ21(He) ⩽ 3 × 10−20 cm2 [16]), and therefore quenching due to interaction with helium can be neglected.
We assume below in the calculation that the centre frequency of the pump radiation spectrum and the laser radiation frequency coincide with the frequencies of 3 – 1 and 2 – 1 transitions, respectively: ωp = ω31, ωlas = ω21. The cell should be designed in such a way that the alkali metal vapour enters it through the side branches so that the concentration N of active particles inside the cell is set by the temperature of these branches containing an alkali metal and is not related to the temperature T of the gas mixture inside the cell.
We first consider the effect of the correction associated with the term bϰp in the denominators of equations (34) on the lasing characteristics. This correction should be taken into account at not very high pressures of the buffer gas, when the parameter bϰp is not too small. In the case of a sufficiently high buffer gas pressure, the parameter bϰp is very small (bϰp ≪ 1) and can be neglected in Eqns (34) (we can assume b = 0). In this case, 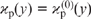 and the analytical formulas given above, which describe lasing, coincide with the formulas obtained previously in [10] (it should be noted that in [10] we neglected the energy losses in the resonator, which are taken into account in this paper by introducing the transmission coefficients T0 and T1 of the cell windows and the effective transmittance Ts, which differ from unity).
and the analytical formulas given above, which describe lasing, coincide with the formulas obtained previously in [10] (it should be noted that in [10] we neglected the energy losses in the resonator, which are taken into account in this paper by introducing the transmission coefficients T0 and T1 of the cell windows and the effective transmittance Ts, which differ from unity).
Figure 3 shows the results of calculations using formula (50) (with a correction for the parameter bϰp and without it) for the conversion efficiency of pump radiation into laser radiation  (pump radiation power P0p = x0 z0 I0p) as a function of the helium buffer gas pressure pHe at different values of the parameter Ny0 (the number of active atoms in the cell in a gas column of width y0 with a unit cross section). The methane buffer gas pressure pCH4 was assumed fixed and equal to 0.1 atm. Condition (33) of applicability of formula (50) with the parameters corresponding to Fig. 3 is met if the cell is sufficiently long (if z0 ≫ y0). Thus, for example, for the parameters corresponding to curve (1) in Fig. 3, as well as for z0 = 10y0 and pHe = 10 atm [a maximum on curve (1)], relations (1 + bϰp) ϰlas ⩾ 14 (1 + ϰp), qϰlas ⩾ 29, bϰp ⩽ 0.53 hold true. It is clear from Fig. 3 that the conversion efficiency
(pump radiation power P0p = x0 z0 I0p) as a function of the helium buffer gas pressure pHe at different values of the parameter Ny0 (the number of active atoms in the cell in a gas column of width y0 with a unit cross section). The methane buffer gas pressure pCH4 was assumed fixed and equal to 0.1 atm. Condition (33) of applicability of formula (50) with the parameters corresponding to Fig. 3 is met if the cell is sufficiently long (if z0 ≫ y0). Thus, for example, for the parameters corresponding to curve (1) in Fig. 3, as well as for z0 = 10y0 and pHe = 10 atm [a maximum on curve (1)], relations (1 + bϰp) ϰlas ⩾ 14 (1 + ϰp), qϰlas ⩾ 29, bϰp ⩽ 0.53 hold true. It is clear from Fig. 3 that the conversion efficiency 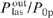 depends monotonically on the pressure pHe and the parameter Ny0 and reaches a maximum value
depends monotonically on the pressure pHe and the parameter Ny0 and reaches a maximum value 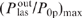 at some optimal helium pressure
at some optimal helium pressure 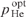 and some optimal parameter (Ny0)opt. If the parameter Ny0 deviates from the optimal value [it corresponds to curve (1) in Fig. 3] in the direction of its increase [curve (2)] or decrease [curve (3)], the laser efficiency decreases dramatically. As can be seen from Fig. 3, the allowance for the correction for the parameter bϰp can both reduce [cf. curves (1) and (1'), (3) and (3')] and increase [cf. curves (2) and (2')] the calculated values of
and some optimal parameter (Ny0)opt. If the parameter Ny0 deviates from the optimal value [it corresponds to curve (1) in Fig. 3] in the direction of its increase [curve (2)] or decrease [curve (3)], the laser efficiency decreases dramatically. As can be seen from Fig. 3, the allowance for the correction for the parameter bϰp can both reduce [cf. curves (1) and (1'), (3) and (3')] and increase [cf. curves (2) and (2')] the calculated values of 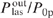 . The effect of the correction on the calculated value of
. The effect of the correction on the calculated value of 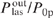 is small for the optimal value of the parameter Ny0 [cf. curves (1) and (1')] and becomes significant when Ny0 deviates from the optimum value [cf. curves (2) and (2'), (3) and (3')].
is small for the optimal value of the parameter Ny0 [cf. curves (1) and (1')] and becomes significant when Ny0 deviates from the optimum value [cf. curves (2) and (2'), (3) and (3')].
Let us consider in more detail the effect of the correction on the calculated value 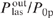 at the optimal value of the parameter Ny0. At a helium pressure pHe = 10 atm, the calculated values of
at the optimal value of the parameter Ny0. At a helium pressure pHe = 10 atm, the calculated values of  with correction for the parameter bϰp [curve (1)] and without correction [curve (1')] are 0.503 and 0.512, respectively, i.e., the relative change is 0.018. The parameter bϰp(y) is a decreasing function of y. For the parameters corresponding to curve (1) in Fig. 3, and at a pressure pHe = 10 atm, we have bϰp(0) = 0.530 and bϰp(y0) = 0.268. Thus, with the optimal value of the parameter Ny0, the correction for the parameter bϰp leads to a relative change in the conversion efficiency
with correction for the parameter bϰp [curve (1)] and without correction [curve (1')] are 0.503 and 0.512, respectively, i.e., the relative change is 0.018. The parameter bϰp(y) is a decreasing function of y. For the parameters corresponding to curve (1) in Fig. 3, and at a pressure pHe = 10 atm, we have bϰp(0) = 0.530 and bϰp(y0) = 0.268. Thus, with the optimal value of the parameter Ny0, the correction for the parameter bϰp leads to a relative change in the conversion efficiency 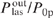 by an amount much smaller than the parameter bϰp itself. Let us explain this somewhat surprising fact on the basis of the dependences of the laser radiation intensity on the coordinate y. Then, the reason for a more significant difference of curves (2') and (3') from (2) and (3) in Fig. 3 becomes clear.
by an amount much smaller than the parameter bϰp itself. Let us explain this somewhat surprising fact on the basis of the dependences of the laser radiation intensity on the coordinate y. Then, the reason for a more significant difference of curves (2') and (3') from (2) and (3) in Fig. 3 becomes clear.
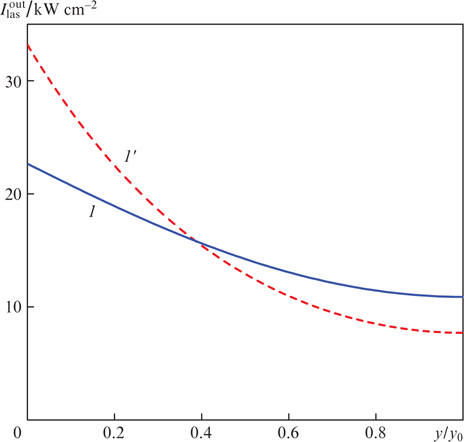
The correction for the parameter bϰp has a much stronger effect on the local laser radiation intensity. Figure 4 shows the laser radiation intensity  as a function of the coordinate y along the cell width for the parameters corresponding to curves (1) and (1') in Fig. 3 and for a helium pressure pHe = 10 atm. It can be seen that taking the correction into account leads to a smoother dependence of
as a function of the coordinate y along the cell width for the parameters corresponding to curves (1) and (1') in Fig. 3 and for a helium pressure pHe = 10 atm. It can be seen that taking the correction into account leads to a smoother dependence of  : the intensity decreases from one side of the cell (at y = 0) and increases from the other side (at y = y0). Relative changes in intensity near the two sides of the cell have different signs and turn out to be of the order of magnitude of bϰp. Note here the following circumstance. The laser radiation power
: the intensity decreases from one side of the cell (at y = 0) and increases from the other side (at y = y0). Relative changes in intensity near the two sides of the cell have different signs and turn out to be of the order of magnitude of bϰp. Note here the following circumstance. The laser radiation power 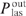 is an integral characteristic (17), i.e., it is proportional to the area under curves (1) and (1') in Fig. 4. The difference in the areas under these curves characterises the effect of the correction for the parameter bϰp on the calculated value of the laser radiation power. As a result, we see that locally the influence of the parameter bϰp is quite appreciable, but for the integral characteristic
is an integral characteristic (17), i.e., it is proportional to the area under curves (1) and (1') in Fig. 4. The difference in the areas under these curves characterises the effect of the correction for the parameter bϰp on the calculated value of the laser radiation power. As a result, we see that locally the influence of the parameter bϰp is quite appreciable, but for the integral characteristic 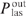 it is strongly suppressed due to the proximity of the areas under the curves. In the case of pairs of curves (2) and (2'), (3) and (3') in Fig. 3, the situation is such that for the corresponding values of the parameter Ny0, the dependences, similar to those in Fig. 4, give comparable differences between both local (with and without bϰp) and integral values of power.
it is strongly suppressed due to the proximity of the areas under the curves. In the case of pairs of curves (2) and (2'), (3) and (3') in Fig. 3, the situation is such that for the corresponding values of the parameter Ny0, the dependences, similar to those in Fig. 4, give comparable differences between both local (with and without bϰp) and integral values of power.
Figure 4. Laser radiation intensity  as a function of the y coordinate. The calculation parameters are I0p = 3 kW cm−2, Δω/(2πc) = 3 cm−1, T = 395 K, pHe = 10 atm, pCH4 = 0.1 atm, Ny0 = 13.5 × 1013 cm−2, z0 = 10y0, Rp = 0.99, R0 = 0.3, R1 = 0.99, T0 = 0.99, T1 = 0.99, Ts = 0.99, ωp = ω31, ωlas = ω21. Curve (1) shows the results of calculation in the first approximation in the parameter bϰp, curve (1') – calculation in the approximation b = 0.
as a function of the y coordinate. The calculation parameters are I0p = 3 kW cm−2, Δω/(2πc) = 3 cm−1, T = 395 K, pHe = 10 atm, pCH4 = 0.1 atm, Ny0 = 13.5 × 1013 cm−2, z0 = 10y0, Rp = 0.99, R0 = 0.3, R1 = 0.99, T0 = 0.99, T1 = 0.99, Ts = 0.99, ωp = ω31, ωlas = ω21. Curve (1) shows the results of calculation in the first approximation in the parameter bϰp, curve (1') – calculation in the approximation b = 0.
Download figure:
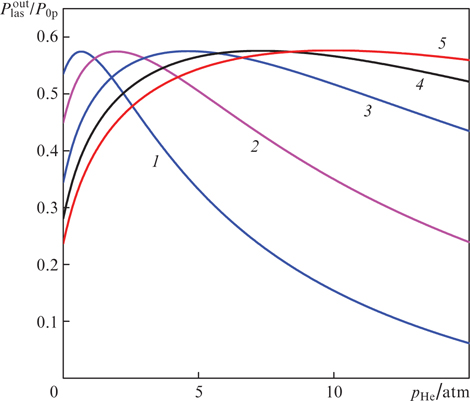
Standard imageMethane is added to the buffer mixture for rapid collisional mixing between upper levels 3 and 2 in the alkali metal atoms so that at a not too high buffer gas pressure the first effective generation condition is satisfied in (13) (ν32 ≫ Ã21, Ã31). The influence of the pressure of the methane buffer gas on the conversion efficiency of pump radiation into laser radiation at optimum values of the parameter Ny0 is illustrated in Fig. 5. It can be seen that the addition of methane to the buffer mixture significantly improves the conversion efficiency and greatly reduces the optimum helium pressure  , at which the efficiency
, at which the efficiency 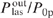 reaches its maximum value. Thus, in the absence of methane in the buffer mixture, the maximum efficiency
reaches its maximum value. Thus, in the absence of methane in the buffer mixture, the maximum efficiency  is attained at a high helium pressure
is attained at a high helium pressure  [curve (1) in Fig. 5], while an increase in methane pressure pCH4 to 0.5 atm increases the efficiency maximum (up to 0.58), attained at a lower helium pressure
[curve (1) in Fig. 5], while an increase in methane pressure pCH4 to 0.5 atm increases the efficiency maximum (up to 0.58), attained at a lower helium pressure 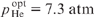 [curve (4) in Fig. 5].
[curve (4) in Fig. 5].
Figure 5. Effect of the methane buffer gas pressure pCH4 on the conversion efficiency at optimum values of the parameter Ny0. The calculation parameters are I0p = 3 kW cm−2, Δω/(2πc) = 3 cm−1, T = 395 K, Rp = 0.99, R0 = 0.3, R1 = 0.99, T0 = 0.99, T1 = 0.99, Ts = 0.99, ωp = ω31, ωlas = ω21; (1) pCH4 = 0, Ny0 = 17.0 × 1013 cm−2, (2) pCH4 = 0.1 atm, Ny0 = 13.5 × 1013 cm−2, (3) pCH4 = 0.2 atm, Ny0 = 12.1 × 1013 cm−2, (4) pCH4 = 0.5 atm, Ny0 = 10.8 × 1013 cm−2 and (5) pCH4 = 2 atm, Ny0 = 9.5 × 1013 cm−2.
Download figure:
Standard imageThe conversion efficiency 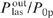 depends monotonically on the helium pressure pHe and the parameter Ny0 and reaches a maximum value
depends monotonically on the helium pressure pHe and the parameter Ny0 and reaches a maximum value 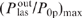 at some optimal helium pressure
at some optimal helium pressure  and some optimal parameter (Ny0)opt. Figure 6 shows the results of calculations of the quantities
and some optimal parameter (Ny0)opt. Figure 6 shows the results of calculations of the quantities 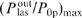 ,
,  and (Ny0)opt as functions of methane pressure pCH4 for two values of the intensity I0p and half-width Δω of the pump radiation spectrum chosen so that the spectral power density of pump radiation I0p/Δω remained unchanged. One can see from Fig. 6a that the maximum conversion efficiency is achieved at an optimum methane pressure
and (Ny0)opt as functions of methane pressure pCH4 for two values of the intensity I0p and half-width Δω of the pump radiation spectrum chosen so that the spectral power density of pump radiation I0p/Δω remained unchanged. One can see from Fig. 6a that the maximum conversion efficiency is achieved at an optimum methane pressure 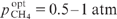 . Figure 6a also shows the calculated values of
. Figure 6a also shows the calculated values of 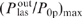 in approximation b = 0 [curves (1') and (2'), for which the initial calculation parameters are the same as for curves (1) and (2), respectively]. It can be seen from a comparison of curves (1) and (1'), (2) and (2') that at an optimum helium pressure
in approximation b = 0 [curves (1') and (2'), for which the initial calculation parameters are the same as for curves (1) and (2), respectively]. It can be seen from a comparison of curves (1) and (1'), (2) and (2') that at an optimum helium pressure 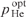 and optimum parameter (Ny0)opt, the effect of correction for the parameter bϰp on the calculated values of
and optimum parameter (Ny0)opt, the effect of correction for the parameter bϰp on the calculated values of 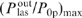 is small.
is small.
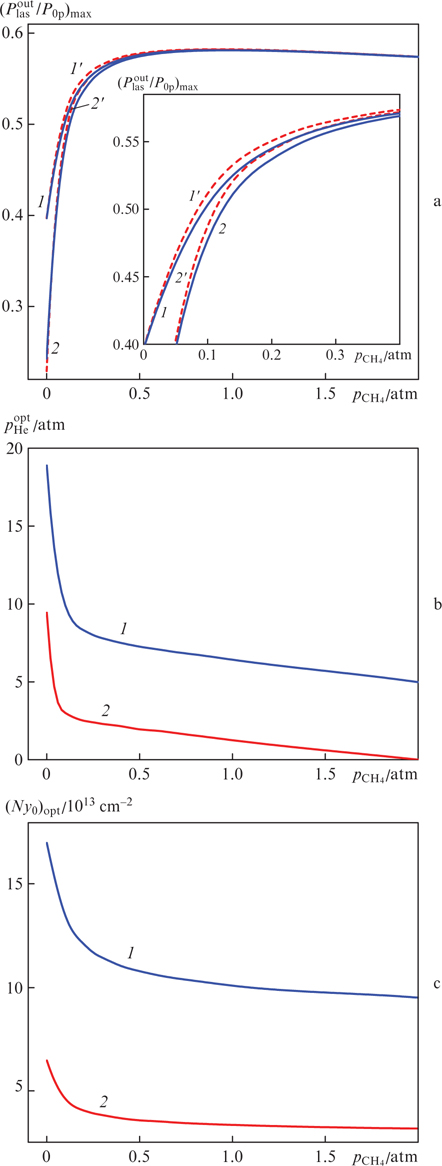
Figure 6. (a) Dependences of the maximum conversion efficiency of pump radiation into laser radiation  on the methane pressure pCH4 at optimum parameters of (Ny0)opt and optimum helium pressures pHe [curves (1') and (2') show the results of calculation in the approximation b = 0, the calculated parameters are the same as for curves (1) and (2), respectively; the inset shows on a larger scale the left upper part of Fig. 6a], (b) dependence of the optimum helium pressure pHe on the methane pressure pCH4 at optimum parameters of (Ny0)opt and (c) dependences of the optimum parameter (Ny0)opt on the methane pressure pCH4 at the optimum helium pressures pHe. The calculation parameters are T = 395 K, Rp = 0.99, R0 = 0.3, R1 = 0.99, T0 = 0.99, T1 = 0.99, Ts = 0.99, ωp = ω31, ωlas = ω21; (1) I0p = 3 kW cm−2, Δω/(2πc) = 3 cm−1 and (2) I0p = 1 kW cm−2, Δω/(2πc) = 1 cm−1.
on the methane pressure pCH4 at optimum parameters of (Ny0)opt and optimum helium pressures pHe [curves (1') and (2') show the results of calculation in the approximation b = 0, the calculated parameters are the same as for curves (1) and (2), respectively; the inset shows on a larger scale the left upper part of Fig. 6a], (b) dependence of the optimum helium pressure pHe on the methane pressure pCH4 at optimum parameters of (Ny0)opt and (c) dependences of the optimum parameter (Ny0)opt on the methane pressure pCH4 at the optimum helium pressures pHe. The calculation parameters are T = 395 K, Rp = 0.99, R0 = 0.3, R1 = 0.99, T0 = 0.99, T1 = 0.99, Ts = 0.99, ωp = ω31, ωlas = ω21; (1) I0p = 3 kW cm−2, Δω/(2πc) = 3 cm−1 and (2) I0p = 1 kW cm−2, Δω/(2πc) = 1 cm−1.
Download figure:
Standard imageConsider the following important circumstance. Numerical analysis shows that for a given spectral power density of pump radiation I0p/Δω and selected optimal values of  ,
, 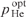 and (Ny0)opt at different Δω, the lasing efficiency is the same (Fig. 6a). For example, the spectral power density of pump radiation is the same for curves (1) and (2) in Fig. 6a (I0p/[Δω/(2πc)] = 1 kW cm−1), and therefore for these curves the maximum of the ratio
and (Ny0)opt at different Δω, the lasing efficiency is the same (Fig. 6a). For example, the spectral power density of pump radiation is the same for curves (1) and (2) in Fig. 6a (I0p/[Δω/(2πc)] = 1 kW cm−1), and therefore for these curves the maximum of the ratio  is the same and equal to 0.58 [at pCH4 ⩾ 0.5 atm, the difference between curves (1) and (2) is so slight that they merge and become indistinguishable by the naked eye].
is the same and equal to 0.58 [at pCH4 ⩾ 0.5 atm, the difference between curves (1) and (2) is so slight that they merge and become indistinguishable by the naked eye].
It can be seen from Figs 6b and 6c that the optimum helium pressure 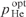 and the optimal parameter (Ny0)opt decrease monotonically with increasing methane buffer gas pressure. At the same time, smaller values of the half-width Δω of the pump radiation spectrum correspond to smaller values of
and the optimal parameter (Ny0)opt decrease monotonically with increasing methane buffer gas pressure. At the same time, smaller values of the half-width Δω of the pump radiation spectrum correspond to smaller values of 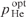 and (Ny0)opt, which is quite obvious.
and (Ny0)opt, which is quite obvious.
Figure 7 illustrates the above statement that for the same spectral power density of pump radiation and optimum values of (Ny0)opt, 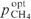 and
and  , the maximum conversion efficiency of pump radiation into laser radiation
, the maximum conversion efficiency of pump radiation into laser radiation 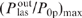 being the same. For curves (1), (2), (3), (4) and (5), the spectral output power density is the same (I0p/[Δω/(2πc)] = 1 kW cm−1) and the same are the maxima of the ratios
being the same. For curves (1), (2), (3), (4) and (5), the spectral output power density is the same (I0p/[Δω/(2πc)] = 1 kW cm−1) and the same are the maxima of the ratios 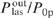 (equal to 0.58), which are attained at pHe = 0.7, 2, 4.6, 7.3 and 10 atm, respectively. At these pressures, the ratio of the half-width Δω of the pump spectrum to the homogeneous half-width Γp of the 3 – 1 transition line (Δω/Γp = 1.5) and the ratio Ny0/I0p = 3.6 × 1013 kW−1 are the same for all the curves.
(equal to 0.58), which are attained at pHe = 0.7, 2, 4.6, 7.3 and 10 atm, respectively. At these pressures, the ratio of the half-width Δω of the pump spectrum to the homogeneous half-width Γp of the 3 – 1 transition line (Δω/Γp = 1.5) and the ratio Ny0/I0p = 3.6 × 1013 kW−1 are the same for all the curves.
Figure 7. Conversion efficiency of pump radiation into laser radiation as a function of helium buffer gas pressure with the same spectral power density of pump radiation I0p/Δω and optimal values of (Ny0)opt and 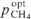 . The calculation parameters are T = 395 K, pCH4 = 0.5 atm, Rp = 0.99, R0 = 0.3, R1 = 0.99, T0 = 0.99, T1 = 0.99, Ts = 0.99, ωp = ω31, ωlas = ω21; (1) I0p = 0.5 kW cm−2, Δω/(2πc) = 0.5 cm−1, Ny0 = 1.8 × 1013 cm−2, (2) I0p = 1 kW cm−2, Δω/(2πc) = 1 cm−1, Ny0 = 3.6 × 1013 cm−2, (3) I0p = 2 kW cm−2, Δω/(2πc) = 2 cm−1, Ny0 = 7.2 × 1013 cm−2, (4) I0p = 3 kW cm−2, Δω/(2πc) = 3 cm−1, Ny0 = 10.8 × 1013 cm−2 and (5) I0p = 4 kW cm−2, Δω/(2πc) = 4 cm−1, Ny0 = 14.4 × 1013 cm−2.
. The calculation parameters are T = 395 K, pCH4 = 0.5 atm, Rp = 0.99, R0 = 0.3, R1 = 0.99, T0 = 0.99, T1 = 0.99, Ts = 0.99, ωp = ω31, ωlas = ω21; (1) I0p = 0.5 kW cm−2, Δω/(2πc) = 0.5 cm−1, Ny0 = 1.8 × 1013 cm−2, (2) I0p = 1 kW cm−2, Δω/(2πc) = 1 cm−1, Ny0 = 3.6 × 1013 cm−2, (3) I0p = 2 kW cm−2, Δω/(2πc) = 2 cm−1, Ny0 = 7.2 × 1013 cm−2, (4) I0p = 3 kW cm−2, Δω/(2πc) = 3 cm−1, Ny0 = 10.8 × 1013 cm−2 and (5) I0p = 4 kW cm−2, Δω/(2πc) = 4 cm−1, Ny0 = 14.4 × 1013 cm−2.
Download figure:
Standard imageFigure 8 shows the intensities of laser radiation 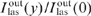 and pump radiation Ip(y)/Ip(0) as functions of coordinate y. The intensity profiles were calculated for such parameters of Ny0 and helium and methane pressures, at which the conversion efficiency of pump radiation into laser radiation
and pump radiation Ip(y)/Ip(0) as functions of coordinate y. The intensity profiles were calculated for such parameters of Ny0 and helium and methane pressures, at which the conversion efficiency of pump radiation into laser radiation 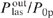 has the highest value. It can be seen that the laser radiation intensity decreases more rapidly with increasing y than the pump radiation intensity. The numerical analysis shows that for a given spectral power density of pump radiation I0p/Δω but at different Δω and optimum values of the methane and helium pressures as well as the parameter Ny0, the intensity profiles of laser radiation and pump radiation do not depend separately on Δω and I0p.The spectral power density of pump radiation is the same for all the curves in Fig. 7 (I0p/[Δω/(2πc)] = 1 kW cm−1). At optimum helium pressures (at the points of the curve maxima in Fig. 7), the intensity profiles of laser radiation and pump radiation are described by curves (1) and (2) in Fig. 8. Each of these curves actually contains five curves with the same parameters as for Fig. 7 and the corresponding optimum helium pressures.
has the highest value. It can be seen that the laser radiation intensity decreases more rapidly with increasing y than the pump radiation intensity. The numerical analysis shows that for a given spectral power density of pump radiation I0p/Δω but at different Δω and optimum values of the methane and helium pressures as well as the parameter Ny0, the intensity profiles of laser radiation and pump radiation do not depend separately on Δω and I0p.The spectral power density of pump radiation is the same for all the curves in Fig. 7 (I0p/[Δω/(2πc)] = 1 kW cm−1). At optimum helium pressures (at the points of the curve maxima in Fig. 7), the intensity profiles of laser radiation and pump radiation are described by curves (1) and (2) in Fig. 8. Each of these curves actually contains five curves with the same parameters as for Fig. 7 and the corresponding optimum helium pressures.
Figure 8. Intensities of (1) laser radiation 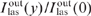 and (2) pump radiation Ip(y)/Ip(0) as functions of the coordinate y with the constant pump power spectral density I0p/Δω and optimal values of (Ny0)opt,
and (2) pump radiation Ip(y)/Ip(0) as functions of the coordinate y with the constant pump power spectral density I0p/Δω and optimal values of (Ny0)opt, 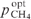 and
and 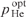 . The calculated parameters are the same as for curves (1), (2), (3), (4) and (5) in Fig. 7 at points of their maxima for the helium pressure pHe = 0.7, 2, 4.6, 7.3 and 10 atm, respectively.
. The calculated parameters are the same as for curves (1), (2), (3), (4) and (5) in Fig. 7 at points of their maxima for the helium pressure pHe = 0.7, 2, 4.6, 7.3 and 10 atm, respectively.
Download figure:
Standard imageLet us compare the results of calculations of the laser energy characteristics obtained numerically in [9] with the results of our calculations using analytical formulas. In considering the possibility of creating a megawatt rubidium vapour laser, Yang et al. [9] used the following parameters of the working medium and pump radiation: T = 380 K, N = 9.34 × 1012 cm−3, z0 = 50 cm, x0 = y0 = 5.5 cm, pHe = 3.24 atm, pCH4 = 0.683 atm, I0p = 3.7 kW cm−2, Δω/(2πc) = 1.97 cm−1, ωp = ω31, Rp = 0.99, R0 = 0.3, R1 = 0.99, T0 = 0.99, T1 = 0.99, Ts = 0.99. The influence of the spatial overlap of the laser radiation and pump fields on the lasing efficiency was taken into account in [9] by introducing the parameter ηmode = Vlas/V = 0.96 (Vlas is the laser volume in the cell). With these parameters, Yang et al. [9] obtained the conversion efficiency of pump radiation into laser radiation  and the ratio of the absorbed pump power to the total pump power Pabs/P0p = 0.725. The corresponding calculations by our analytical formulas for the same parameters of the working medium and pump radiation yield (after multiplying by ηmode = 0.96)
and the ratio of the absorbed pump power to the total pump power Pabs/P0p = 0.725. The corresponding calculations by our analytical formulas for the same parameters of the working medium and pump radiation yield (after multiplying by ηmode = 0.96)  , Pabs/P0p = 0.730. The results of calculations of the laser energy characteristics by analytical formulas are in very good agreement with the results of numerical calculations [9]. Such a good agreement is achieved only when the correction is taken into account for the parameter bϰp. Calculation by simpler analytical formulas in the approximation b = 0 gives not so good agreement with the results of paper [9]:
, Pabs/P0p = 0.730. The results of calculations of the laser energy characteristics by analytical formulas are in very good agreement with the results of numerical calculations [9]. Such a good agreement is achieved only when the correction is taken into account for the parameter bϰp. Calculation by simpler analytical formulas in the approximation b = 0 gives not so good agreement with the results of paper [9]: 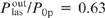 , Pabs/P0p = 0.780. Note that in Ref. [9], not all the parameters of the working medium of a megawatt laser are optimal. According to our calculations, if the concentration of rubidium atoms is increased to 17.8 × 1012 cm−3 and the helium pressure is raised to 5.25 atm with the other parameters unchanged, the conversion efficiency will increase to 0.66.
, Pabs/P0p = 0.780. Note that in Ref. [9], not all the parameters of the working medium of a megawatt laser are optimal. According to our calculations, if the concentration of rubidium atoms is increased to 17.8 × 1012 cm−3 and the helium pressure is raised to 5.25 atm with the other parameters unchanged, the conversion efficiency will increase to 0.66.
6. Conclusions
We have developed an analytical model of a transversely diode-pumped alkali metal vapour laser, which describes the laser generation in the practically important case of a sufficiently high intensity of laser radiation and with a weak restriction from below on the buffer gas pressure. This restriction is removed by taking into account the correction for the parameter bϰp. In the case of a sufficiently high buffer gas pressure, the parameter bϰp is very small (bϰp ≪ 1) and can be neglected (it can be assumed that b = 0) in the equations describing the laser operation. This case was considered earlier in our work [10]. The analytical solution of the differential equations that describe the laser generation makes it possible to determine exhaustively any energy characteristics of the laser and to find the optimum parameters of the working medium and pump radiation (temperature, buffer gas pressure and composition, intensity and width of the pump spectrum).
The conversion efficiency of pump radiation into laser radiation  is described by an analytical formula in which the concentration N of active particles and the cell width y0 enter only in the combination Ny0. The efficiency
is described by an analytical formula in which the concentration N of active particles and the cell width y0 enter only in the combination Ny0. The efficiency 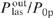 depends nonmonotonically on the parameter Ny0, as well as on the pressure of helium pHe and methane pCH4 and reaches a maximum value
depends nonmonotonically on the parameter Ny0, as well as on the pressure of helium pHe and methane pCH4 and reaches a maximum value  at some optimum parameter (Ny0)opt and some optimal pressures
at some optimum parameter (Ny0)opt and some optimal pressures 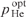 and
and 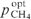 . It is important to note that at the given spectral power density of pump radiation I0p/Δω and selected optimal values of (Ny0)opt,
. It is important to note that at the given spectral power density of pump radiation I0p/Δω and selected optimal values of (Ny0)opt, 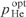 and
and 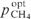 for different Δω, the lasing efficiency is the same. Calculations using analytical formulas show that the conversion efficiency
for different Δω, the lasing efficiency is the same. Calculations using analytical formulas show that the conversion efficiency 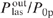 reaches 69% with the spectral power density of pump radiation I0p/[Δω/(2πc)] = 2 kW cm−1.
reaches 69% with the spectral power density of pump radiation I0p/[Δω/(2πc)] = 2 kW cm−1.
Analytical formulas for intensities of laser radiation 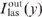 and pump radiation Ip(y) are obtained as functions of the coordinate y along the width of the cell. The laser radiation intensity decreases with increasing y faster than the pump radiation intensity. At a given spectral power density of pump radiation I0p/Δω, but for different Δω and corresponding optimum values of the methane and helium pressures, as well as the parameter Ny0, the intensity profiles of laser radiation and pump radiation do not depend separately on Δω and I0p.
and pump radiation Ip(y) are obtained as functions of the coordinate y along the width of the cell. The laser radiation intensity decreases with increasing y faster than the pump radiation intensity. At a given spectral power density of pump radiation I0p/Δω, but for different Δω and corresponding optimum values of the methane and helium pressures, as well as the parameter Ny0, the intensity profiles of laser radiation and pump radiation do not depend separately on Δω and I0p.
Allowance for the correction for the parameter bϰp can both reduce and increase the calculated values of  . The effect of the correction on the calculated value of
. The effect of the correction on the calculated value of 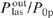 is small for the optimal value of the parameter Ny0 and becomes significant when Ny0 deviates from the optimum value. With the optimal value of the parameter Ny0, the correction for the parameter bϰp leads to a relative change in the conversion efficiency of pump radiation into laser radiation
is small for the optimal value of the parameter Ny0 and becomes significant when Ny0 deviates from the optimum value. With the optimal value of the parameter Ny0, the correction for the parameter bϰp leads to a relative change in the conversion efficiency of pump radiation into laser radiation  by a value that is much smaller than the parameter bϰp itself. At the same time, the correction for the parameter bϰp exerts a much stronger effect on the local value of the laser radiation intensity
by a value that is much smaller than the parameter bϰp itself. At the same time, the correction for the parameter bϰp exerts a much stronger effect on the local value of the laser radiation intensity 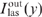 . Taking the correction into account leads to a smoother dependence of
. Taking the correction into account leads to a smoother dependence of 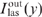 : the intensity decreases from one side of the cell (at y = 0) and increases from the other side (at y = y0). The relative changes in intensity near the two sides of the cell have different signs and turn out to be of the order of magnitude of bϰp.
: the intensity decreases from one side of the cell (at y = 0) and increases from the other side (at y = y0). The relative changes in intensity near the two sides of the cell have different signs and turn out to be of the order of magnitude of bϰp.
Acknowledgements
The work was supported by the integrated programme of fundamental research of the Siberian Branch of the Russian Academy of Sciences (RAS) (Integration and Development Programme No. II.2P as part of the RAS programme, Project No. II.2P/II.10-13) and RF President's Grants Council (State Support to Leading Scientific Schools Programme, Grant No. NSh-6898.2016.2).