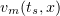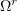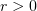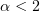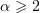Abstract
The method of Galerkin approximations is employed to prove the existence of a strong global (in time) solution of a doubly nonlinear parabolic equation in an unbounded domain. The second integral identity is established for Galerkin approximations, and passing to the limit in it an estimate for the decay rate of the norm of the solution from below is obtained. The estimates characterizing the decay rate of the solution as 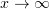 obtained here are used to derive an upper bound for the decay rate of the solution with respect to time; the resulting estimate is pretty close to the lower one.
obtained here are used to derive an upper bound for the decay rate of the solution with respect to time; the resulting estimate is pretty close to the lower one.
Bibliography: 17 titles.
Export citation and abstract BibTeX RIS
This research was carried out with the support of the Russian Foundation for Basic Research (grant nos. 10-01-00118-a and 13-01-00081-a).
§ 1. Introduction
Let  be a domain in
be a domain in  ,
, 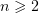 . We consider the first mixed problem
. We consider the first mixed problem

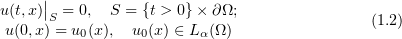
for a doubly nonlinear parabolic equation in the cylindrical domain 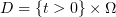 .
.
Here,
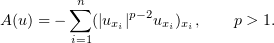
The existence and uniqueness of the solution of this problem was examined by Lions [1], Raviart [2], Grange and Mignot [3], Bamberger [4], Alt and Luckhaus [5], Bernis [6] and others. For the most part, these problems were dealt with on a bounded domain  and a bounded time interval
and a bounded time interval ![$[0,T]$](https://content.cld.iop.org/journals/1064-5616/204/9/1239/revision1/msb_204_9_1239ieqn7.gif) with arbitrary
with arbitrary 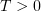 . The strong solution of this problem in a bounded domain
. The strong solution of this problem in a bounded domain  was found by Raviart by replacing the evolution derivative with a difference relation. The existence of a weak solution in an unbounded domain
was found by Raviart by replacing the evolution derivative with a difference relation. The existence of a weak solution in an unbounded domain 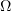 was proved by Bernis, who applied a limiting procedure to the solutions built by Grange and Mignot on bounded domains. However, working with a weak solution involves a difficulty consisting, for example, in examining the decay of the solution as
was proved by Bernis, who applied a limiting procedure to the solutions built by Grange and Mignot on bounded domains. However, working with a weak solution involves a difficulty consisting, for example, in examining the decay of the solution as 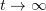 . Bamberger proved the uniqueness of a strong positive solution of the problem.
. Bamberger proved the uniqueness of a strong positive solution of the problem.
In this paper, Galerkin approximations are employed in the conventional way to construct a strong solution of the problem across the whole time interval 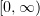 (the domain
(the domain 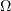 may be unbounded). In [7], this type of solution was constructed on a bounded interval
may be unbounded). In [7], this type of solution was constructed on a bounded interval ![$[0,T]$](https://content.cld.iop.org/journals/1064-5616/204/9/1239/revision1/msb_204_9_1239ieqn14.gif) for any
for any  . The ideas of [7] were used in [8] to construct a solution of an anisotropic parabolic equation for
. The ideas of [7] were used in [8] to construct a solution of an anisotropic parabolic equation for 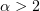 on a bounded time interval.
on a bounded time interval.
Derivation of the estimates we need for the Galerkin approximations is facilitated by the fact that they are smooth functions; then passing to the limit we can extend these estimates to the solution of problem (1.1), (1.2). In particular, for the equation
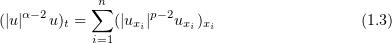
on a bounded domain 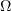 , with
, with 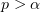 , it will be shown that
, it will be shown that
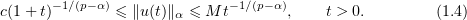
Conceptually, these results continue the studies started by Gushchin [9] on the behaviour of solutions of linear parabolic equations for large  . The left-hand side of estimate (1.4) with
. The left-hand side of estimate (1.4) with  was obtained by Alikakos and Rostamian in [10] for the Cauchy problem. Tedeev [11] obtained analogous estimates for the solution of a high-order quasi-linear equation. Sharp, two-sided estimates for the decay rate of the norm of the solution to a linear and a quasi-linear parabolic equation in an unbounded domain were established by Kozhevnikova [12] and Karimov and Kozhevnikova [13], and for an anisotropic parabolic equation with
was obtained by Alikakos and Rostamian in [10] for the Cauchy problem. Tedeev [11] obtained analogous estimates for the solution of a high-order quasi-linear equation. Sharp, two-sided estimates for the decay rate of the norm of the solution to a linear and a quasi-linear parabolic equation in an unbounded domain were established by Kozhevnikova [12] and Karimov and Kozhevnikova [13], and for an anisotropic parabolic equation with 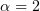 , by Kozhevnikova and Mukminov [14]. Nearly sharp estimates for the solution of an anisotropic parabolic equation with
, by Kozhevnikova and Mukminov [14]. Nearly sharp estimates for the solution of an anisotropic parabolic equation with 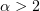 were obtained in [8] (a solution on a bounded time interval).
were obtained in [8] (a solution on a bounded time interval).
§ 2. Statements of the main results
We define the space 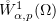 to be the completion of
to be the completion of 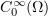 in the norm
in the norm
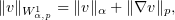
where
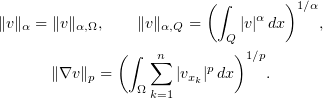
We also let 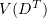 , where
, where  and
and 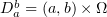 , denote the completion of
, denote the completion of 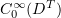 in the norm
in the norm
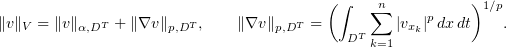
Definition. A generalized solution of problem (1.1), (1.2) is a function  in the space
in the space 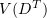 for all
for all 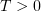 and satisfying the identity
and satisfying the identity
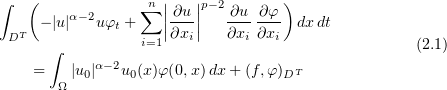
for all 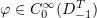 .
.
Here and below, 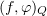 denotes the value of a distribution
denotes the value of a distribution 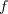 at an element
at an element 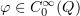 , where
, where 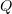 is a domain in
is a domain in 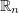 or in
or in 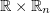 . However, in formula (2.1), it is assumed that
. However, in formula (2.1), it is assumed that 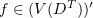 .
.
We shall write a function  as
as  or
or  when there is no ambiguity.
when there is no ambiguity.
Throughout we assume that 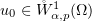 .
.
Theorem 1. Let  for all
for all  . Then there exists a generalized solution
. Then there exists a generalized solution 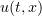 of problem (1.1), (1.2) such that
of problem (1.1), (1.2) such that
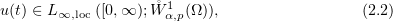
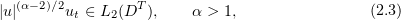
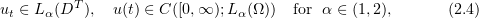
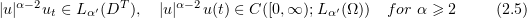
for all 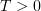 . Here,
. Here,  .
.
Bamberger [4] defined a strong solution by the condition 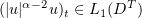 and proved, in particular, that if
and proved, in particular, that if
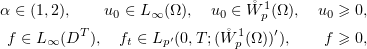
where 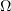 is a bounded domain, then the problem has at most one strong solution. He also showed that this solution
is a bounded domain, then the problem has at most one strong solution. He also showed that this solution 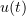 vanishes for
vanishes for 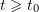 , provided that
, provided that 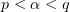 ,
, 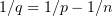 .
.
It is easily checked that the solution in Theorem 1 is strong.
The paper [10] puts forward a series of assertions (not all of them are fully justified) about the behaviour of the solution of the Cauchy problem for the equation

The following upper and lower bounds for the solution of the Cauchy problem were obtained under the assumption that 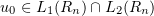 and
and  .
.
The upper estimates read as follows:
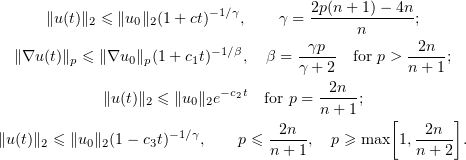
The lower estimates are as follows:
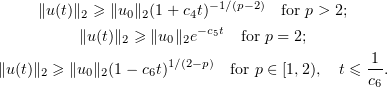
In [15] the following estimate for the solution of the Cauchy problem for equation (2.6) for any 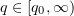 is given, under the assumption that
is given, under the assumption that 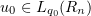 :
:
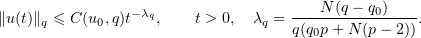
The paper [11] looks at the problem
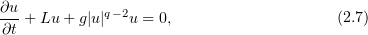
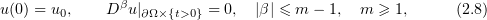
where
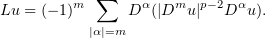
(In fact [11] deals with somewhat more general equations.) A solution  in the space
in the space ![$ L_p(0,T; \mathring{W}_p^m(\Omega)) \cap C([0,T];L_2(\Omega))\cap L_q(D^T)$](https://content.cld.iop.org/journals/1064-5616/204/9/1239/revision1/msb_204_9_1239ieqn60.gif) ,
, 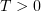 , is considered under the assumption that
, is considered under the assumption that 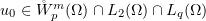 . In particular, the following bounds were proved for a bounded domain
. In particular, the following bounds were proved for a bounded domain 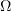 :
:
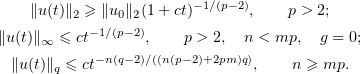
Above we have only given basic results on the behaviour of the solutions of equations (2.6), (2.7). For more detailed results the reader is referred to the book [16].
The remaining assertions of the present paper are established under the assumption that 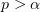 . In Theorems 2–5, a domain
. In Theorems 2–5, a domain 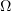 may be bounded or unbounded. For an unbounded
may be bounded or unbounded. For an unbounded 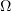 , it is assumed that the initial function has bounded support
, it is assumed that the initial function has bounded support
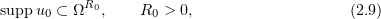
where 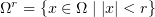 .
.
Theorem 2. Let 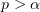 . Assume that condition (2.9) is satisfied and that the initial function
. Assume that condition (2.9) is satisfied and that the initial function  is bounded. Then there exist a positive number
is bounded. Then there exist a positive number 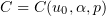 and a bounded solution
and a bounded solution  of problem (1.3), (1.2) such that, for all
of problem (1.3), (1.2) such that, for all  ,
,
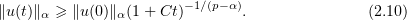
Below we shall need the characteristic function of the layer between two concentric spheres
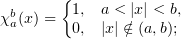
when 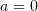 or
or  the limit indices will be omitted:
the limit indices will be omitted: 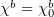 ,
, 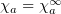 .
.
The proof of the lower bound when 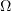 is unbounded depends heavily on the following fact.
is unbounded depends heavily on the following fact.
Theorem 3. Let  , let (2.9) be satisfied, and let
, let (2.9) be satisfied, and let  be a generalized solution of problem (1.3), (1.2) with bounded initial function
be a generalized solution of problem (1.3), (1.2) with bounded initial function  . Assume that
. Assume that 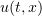 satisfies properties (2.2)–(2.5). Then
satisfies properties (2.2)–(2.5). Then 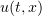 is also bounded and there exist positive numbers
is also bounded and there exist positive numbers 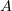 and
and  such that
such that
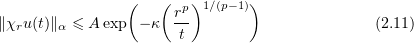
for all  ,
, 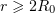 .
.
To prove Theorem 3 we shall employ the maximum principle (see § 5).
For 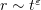 , estimate (2.11) becomes trivial. Hence, we need a different estimate in order to bound the decay rate of the solution from above. We shall assume that the origin lies on the boundary of
, estimate (2.11) becomes trivial. Hence, we need a different estimate in order to bound the decay rate of the solution from above. We shall assume that the origin lies on the boundary of  . Also let
. Also let 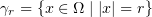 ,
, 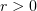 .
.
Consider the following geometrical characteristic of the unbounded domain 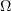 . We set
. We set
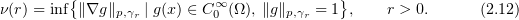
Assume that the domain 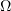 satisfies the condition
satisfies the condition

For example, this condition is satisfied for a domain lying inside some cone.
Theorem 4. Let 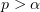 and let (2.9) and (2.13) be satisfied. Then there exist positive numbers
and let (2.9) and (2.13) be satisfied. Then there exist positive numbers 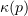 ,
, 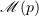 and a generalized solution
and a generalized solution 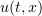 of problem (1.3), (1.2) such that
of problem (1.3), (1.2) such that
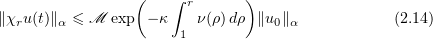
for all  ,
, 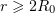 .
.
Let 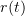 be an arbitrary positive function satisfying the inequality
be an arbitrary positive function satisfying the inequality

for all 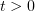 . Clearly, such a function always exists.
. Clearly, such a function always exists.
Theorem 5. Let 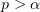 . Assume that (2.9) and (2.15) are satisfied. Then there exist a positive number
. Assume that (2.9) and (2.15) are satisfied. Then there exist a positive number 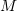 and a solution
and a solution 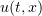 of problem (1.3), (1.2) in a domain
of problem (1.3), (1.2) in a domain 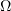 lying inside some cone (of aperture
lying inside some cone (of aperture 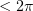 ) such that
) such that
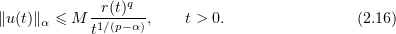
If the domain 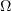 satisfies the condition
satisfies the condition
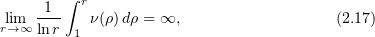
then we can set 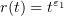 ,
,  , and (2.16) assumes the form
, and (2.16) assumes the form

Taking 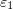 sufficiently small,
sufficiently small,  can be made arbitrarily close to zero. The exponent in the last estimate is close to the exponent
can be made arbitrarily close to zero. The exponent in the last estimate is close to the exponent 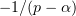 in the lower bound (2.10).
in the lower bound (2.10).
As an example, consider the domain of revolution
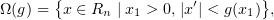
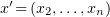 , with a positive function
, with a positive function  . The only requirement imposed on
. The only requirement imposed on  is that the set
is that the set  be a domain and that
be a domain and that
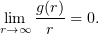
For these domains, one can easily prove the relation
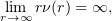
from which condition (2.17) follows.
§ 3. Proof of the existence theorem
Under the above assumptions on  we have
we have

In particular, 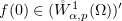 .
.
3.1. The case  .
.
Consider a sequence  of linearly independent functions whose linear hull is dense in
of linearly independent functions whose linear hull is dense in  . We set
. We set  . Galerkin approximations to the solution will be sought in the form
. Galerkin approximations to the solution will be sought in the form
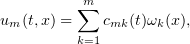
where the functions 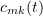 are determined from the equations
are determined from the equations
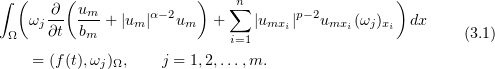
The numbers 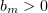 will be chosen later. We claim that equations (3.1) can be solved for the derivatives
will be chosen later. We claim that equations (3.1) can be solved for the derivatives 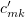 . Clearly, they are as follows:
. Clearly, they are as follows:
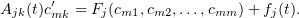
For each 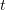 , the coefficient matrix
, the coefficient matrix
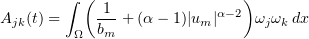
is a Gram matrix of the system of linearly independent vectors  ,
, 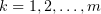 , and hence is invertible. From equations (3.1) with initial conditions
, and hence is invertible. From equations (3.1) with initial conditions 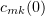 , chosen so that
, chosen so that 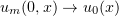 in
in  , we find the functions
, we find the functions 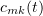 . At first, these functions are determined on a short time interval. Then, the fact that the Galerkin approximations are bounded (to be proved later) lets us define them on an infinite time interval. The numbers
. At first, these functions are determined on a short time interval. Then, the fact that the Galerkin approximations are bounded (to be proved later) lets us define them on an infinite time interval. The numbers  will be chosen so as to have
will be chosen so as to have 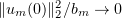 as
as  .
.
Now we proceed to estimate the Galerkin approximations. Multiplying equations (3.1) by  and summing, this gives
and summing, this gives
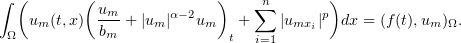
Integrating with respect to 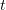 shows that
shows that
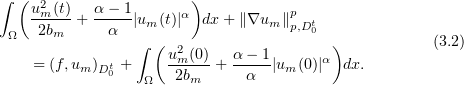
The last integral on the right is bounded by a constant independent of 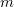 , thanks to the above convergences. Further, for
, thanks to the above convergences. Further, for 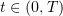 we have
we have
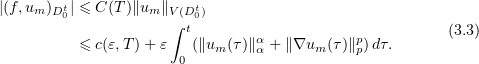
Hence, from (3.2) and Gronwall's lemma we see that the sequence 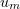 is bounded in the spaces
is bounded in the spaces ![$C([0,T];L_{\alpha }(\Omega))$](https://content.cld.iop.org/journals/1064-5616/204/9/1239/revision1/msb_204_9_1239ieqn140.gif) and
and 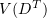 for all
for all  by the constant
by the constant 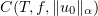 , which remains unchanged if the sequence
, which remains unchanged if the sequence  is replaced by a larger one
is replaced by a larger one  .
.
Now we multiply equations (3.1) by  and sum:
and sum:
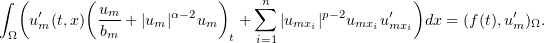
Integrating with respect to  shows that
shows that
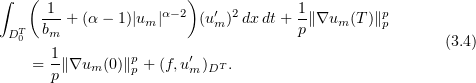
Integrating the last term by parts, we obtain

Note that
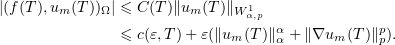
Further, since 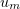 is bounded in the space
is bounded in the space  , we have
, we have

Now we find from (3.4) that, for any 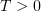 , the sequence
, the sequence 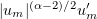 is bounded in
is bounded in 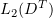 and that the sequence
and that the sequence  is bounded in
is bounded in ![$C([0,T]; L_p(\Omega))$](https://content.cld.iop.org/journals/1064-5616/204/9/1239/revision1/msb_204_9_1239ieqn154.gif) . Using the diagonal process, we can now choose a subsequence
. Using the diagonal process, we can now choose a subsequence  which is weakly convergent in these spaces. For brevity of notation we shall omit the subscript
which is weakly convergent in these spaces. For brevity of notation we shall omit the subscript  :
:
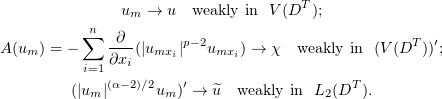
The convergence holds for any  , and the limit functions agree in their common domain of definition. Consequently, we have convergence for any
, and the limit functions agree in their common domain of definition. Consequently, we have convergence for any 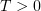 .
.
Below it will be shown that  ,
,  and that the function
and that the function  is a generalized solution of problem (1.1), (1.2). We will proceed in three steps, which we will also need later in the subsequent analysis.
is a generalized solution of problem (1.1), (1.2). We will proceed in three steps, which we will also need later in the subsequent analysis.
Step 1. The sequence  is bounded in the space
is bounded in the space  on any finite interval:
on any finite interval:

We fix a countable dense subset 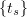 of
of ![$[0,\infty]$](https://content.cld.iop.org/journals/1064-5616/204/9/1239/revision1/msb_204_9_1239ieqn165.gif) . We can assume that
. We can assume that 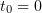 . Given any bounded domain
. Given any bounded domain 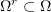 with smooth boundary, the embedding
with smooth boundary, the embedding  is compact. Hence, using the diagonal process we can choose a subsequence
is compact. Hence, using the diagonal process we can choose a subsequence 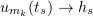 converging strongly in
converging strongly in  for all natural
for all natural  . Choosing, if necessary, a further subsequence (and dropping the subscripts), we assume that
. Choosing, if necessary, a further subsequence (and dropping the subscripts), we assume that  almost everywhere in
almost everywhere in  for any
for any  . In particular, for
. In particular, for 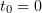 we have
we have 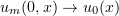 almost everywhere in
almost everywhere in  .
.
For the next step we require the following result.
Lemma 1. Let the sequence ![$v_m(t)\!\in \! C([0,T];L_2(\Omega))$](https://content.cld.iop.org/journals/1064-5616/204/9/1239/revision1/msb_204_9_1239ieqn178.gif) satisfy the following properties:
satisfy the following properties:
- 1)
 converges almost everywhere in
converges almost everywhere in  for each
for each  and some
and some  ;
; - 2)the sequence
 is bounded in
is bounded in  for each
for each  .
.
Then it contains a subsequence 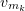 converging to the function
converging to the function  in the space
in the space ![$C([0,T];L_1(\Omega ^r))$](https://content.cld.iop.org/journals/1064-5616/204/9/1239/revision1/msb_204_9_1239ieqn188.gif) , and
, and 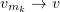 almost everywhere in
almost everywhere in 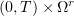 .
.
Proof. The sequence 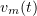 is equicontinuous in
is equicontinuous in  in the space
in the space 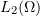 :
:
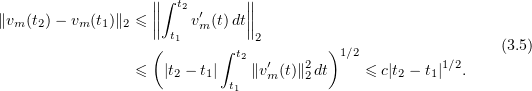
Next, the sequence 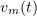 is bounded in the space
is bounded in the space ![$C([0,T];L_2(\Omega))$](https://content.cld.iop.org/journals/1064-5616/204/9/1239/revision1/msb_204_9_1239ieqn195.gif) . Consequently, it contains a subsequence
. Consequently, it contains a subsequence 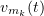 converging weakly in
converging weakly in 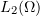 for the same
for the same 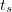 as above. Along with the almost everywhere convergence in
as above. Along with the almost everywhere convergence in 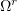 , this implies strong convergence in
, this implies strong convergence in  for any
for any 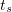 (see [1], Ch. 1, § 12.2). We again write
(see [1], Ch. 1, § 12.2). We again write 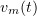 for
for  .
.
For a bounded domain 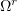 , it follows easily from (3.5) that
, it follows easily from (3.5) that 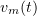 is a uniformly Cauchy sequence in the norm
is a uniformly Cauchy sequence in the norm 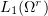 :
:
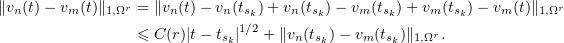
Choosing a finite grid  of small spacing and then increasing
of small spacing and then increasing  and
and 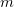 , we ensure that the right-hand side is uniformly small in
, we ensure that the right-hand side is uniformly small in  .
.
Thus, we see that 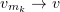 in
in ![$C([0,T];L_1(\Omega ^r))$](https://content.cld.iop.org/journals/1064-5616/204/9/1239/revision1/msb_204_9_1239ieqn212.gif) for any
for any  . The convergence also takes place in
. The convergence also takes place in  . Hence, one may select a subsequence converging in
. Hence, one may select a subsequence converging in  almost everywhere. The lemma is proved.
almost everywhere. The lemma is proved.
Step 2. We apply Lemma 1 to the sequence  . Since
. Since  is arbitrary and
is arbitrary and 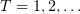 , we can apply the diagonal process to select a subsequence
, we can apply the diagonal process to select a subsequence  converging in
converging in 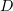 almost everywhere. Hence, the sequence
almost everywhere. Hence, the sequence 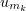 converges almost everywhere in
converges almost everywhere in 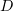 to
to  (see [1], Ch. 1, § 1.4, Lemma 1.3). We quote this result.
(see [1], Ch. 1, § 1.4, Lemma 1.3). We quote this result.
Lemma 2. Let  be a domain in
be a domain in 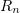 or in
or in 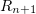 . Assume that a sequence
. Assume that a sequence  converges to
converges to  almost everywhere in
almost everywhere in  and is bounded in
and is bounded in  . Then
. Then 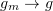 weakly in
weakly in 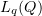 .
.
Clearly, this result, which is stated in [1] for bounded domains, also holds for unbounded domains.
From Lemma 2 it also follows that  weakly in
weakly in  for any
for any 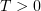 . Given a fixed
. Given a fixed  , the convergence
, the convergence 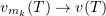 in
in  implies that there is a subsequence convergent almost everywhere in
implies that there is a subsequence convergent almost everywhere in 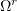 for all
for all  . Hence,
. Hence,
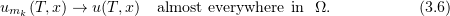
The sequence 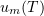 is bounded in the space
is bounded in the space  , and hence we can choose a subsequence such that
, and hence we can choose a subsequence such that
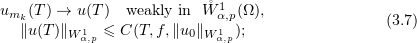
also, if 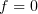 , then the constant
, then the constant 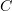 depends only on
depends only on  . The constant
. The constant  is monotone in
is monotone in  , so this proves (2.2).
, so this proves (2.2).
Further,
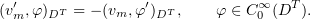
Passing to the limit, we get
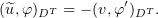
It follows that 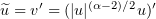 .
.
We claim that the sequence  is bounded in
is bounded in 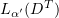 . Indeed,
. Indeed,
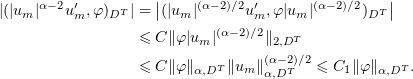
Hence we can assume that 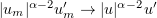 weakly in
weakly in  . As a result,
. As a result,  . We also have
. We also have
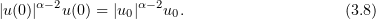
In fact, in Step 1 we noted that 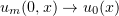 converges almost everywhere in
converges almost everywhere in 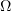 . Now,
. Now, 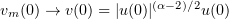 in
in 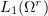 ,
, 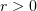 , by Lemma 1, thereby proving (3.8).
, by Lemma 1, thereby proving (3.8).
Step 3. We will now prove the equality  . For this we need some integral relations. We multiply equation (3.1) by the smooth function
. For this we need some integral relations. We multiply equation (3.1) by the smooth function  , integrate over
, integrate over 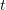 , and let
, and let  , denoting
, denoting 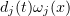 by
by 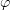 in the resulting expression:
in the resulting expression:
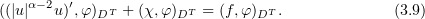
We note that
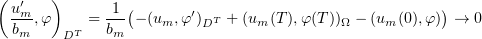
as 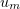 is bounded in
is bounded in ![$C([0,T];L_{\alpha }(\Omega))$](https://content.cld.iop.org/journals/1064-5616/204/9/1239/revision1/msb_204_9_1239ieqn266.gif) and
and 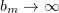 . Clearly, any function from
. Clearly, any function from 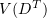 can be approximated by linear combinations
can be approximated by linear combinations
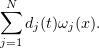
Hence, (3.9) also holds for functions from the space 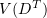 . So, in view of (3.8),
. So, in view of (3.8),  will be a generalized solution of problem (1.1), (1.2) if we prove that
will be a generalized solution of problem (1.1), (1.2) if we prove that 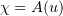 .
.
Note that 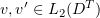 implies that
implies that ![$v\in C([0,T];L_2(\Omega))$](https://content.cld.iop.org/journals/1064-5616/204/9/1239/revision1/msb_204_9_1239ieqn273.gif) and that
and that ![$\Vert u(t)\Vert _\alpha \in C([0,T])$](https://content.cld.iop.org/journals/1064-5616/204/9/1239/revision1/msb_204_9_1239ieqn274.gif) ,
,  . Substituting the function
. Substituting the function  into (3.9), this gives
into (3.9), this gives
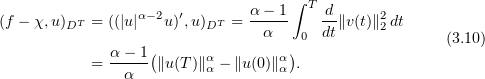
Our next argument depends on the operator 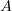 being monotone. It is readily verified that
being monotone. It is readily verified that
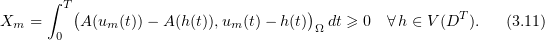
From equations (3.1) it is easily seen that
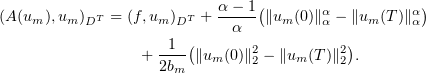
Hence,
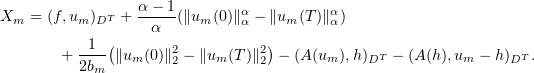
Consequently, since 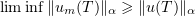 , by (3.6)
, by (3.6)
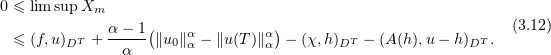
Applying (3.10) shows that
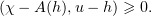
Setting 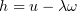 ,
, 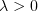 ,
, 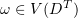 , we have
, we have

Letting 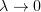 , we see that
, we see that  for any
for any 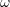 . Hence,
. Hence, 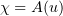 .
.
3.2. The case  .
.
Galerkin approximations to the solution will be sought in the previous form, but now the functions 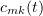 are determined from the equations
are determined from the equations
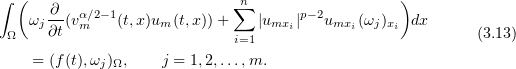
Here, the functions 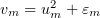 are introduced for regularization; the numbers
are introduced for regularization; the numbers  will be chosen later. We claim that equations (3.13) can be solved with respect to the derivatives
will be chosen later. We claim that equations (3.13) can be solved with respect to the derivatives  . Clearly, they are as follows
. Clearly, they are as follows
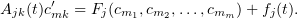
For each 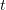 , the coefficient matrix
, the coefficient matrix
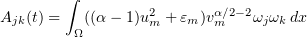
is a Gram matrix of the system of linearly independent vectors  ,
,  , and hence is invertible. From equations (3.13) with initial conditions
, and hence is invertible. From equations (3.13) with initial conditions 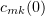 , chosen so that
, chosen so that 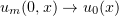 in the space
in the space 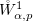 , we find the functions
, we find the functions 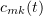 .
.
Now we estimate the Galerkin approximations. Multiplying equations (3.13) by 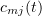 and summing, we find that
and summing, we find that
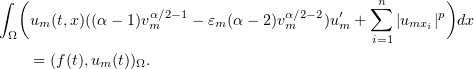
We have  and
and 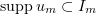 , and hence, integrating with respect to
, and hence, integrating with respect to 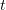 shows that
shows that
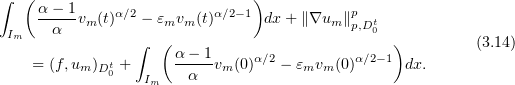
Since the sets  are bounded, we may choose
are bounded, we may choose  to satisfy
to satisfy
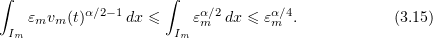
Now the last integral on the right of (3.14) is bounded by a constant independent of 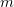 , thanks to the above convergences. As before, inequality (3.3) holds. Hence, using (3.14) and Gronwall's lemma it follows that the integrals
, thanks to the above convergences. As before, inequality (3.3) holds. Hence, using (3.14) and Gronwall's lemma it follows that the integrals 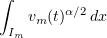 are uniformly bounded in
are uniformly bounded in 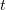 and
and 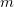 , and hence so is the sequence
, and hence so is the sequence 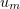 in the spaces
in the spaces ![$C([0,T];L_{\alpha }(\Omega))$](https://content.cld.iop.org/journals/1064-5616/204/9/1239/revision1/msb_204_9_1239ieqn309.gif) and
and 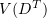 for all
for all 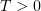 .
.
We now multiply equations (3.13) by 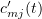 and sum:
and sum:
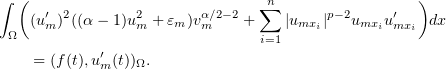
Integrating over 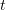 gives
gives
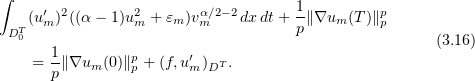
As before,  . In addition,
. In addition, 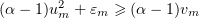 . Setting
. Setting
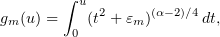
it follows from (3.16) that the sequence  is bounded in
is bounded in 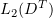 and the sequence
and the sequence  is bounded in
is bounded in ![$C([0,T];L_p(\Omega))$](https://content.cld.iop.org/journals/1064-5616/204/9/1239/revision1/msb_204_9_1239ieqn319.gif) . In view of the above results, we can choose a subsequence
. In view of the above results, we can choose a subsequence 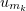 that is weakly convergent in the spaces specified below. For brevity, the subscript
that is weakly convergent in the spaces specified below. For brevity, the subscript  will be dropped:
will be dropped:

Repeating Steps 1–3, as adapted to the new setting, we will be able to prove that 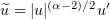 .
.
Proceeding as in Step 1, we can assume (dropping the subscripts) that the sequence 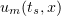 converges almost everywhere in
converges almost everywhere in 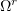 for each
for each 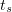 .
.
At Step 2, Lemma 1 is applied to the sequence 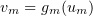 to produce a subsequence converging almost everywhere in
to produce a subsequence converging almost everywhere in 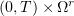 . Since
. Since 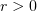 ,
, 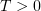 are arbitrary, the diagonal process can be applied to extract a subsequence
are arbitrary, the diagonal process can be applied to extract a subsequence  converging almost everywhere in
converging almost everywhere in 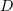 . The sequence of inverse functions
. The sequence of inverse functions  converges pointwise. Now, Lemma 2 shows that the sequence
converges pointwise. Now, Lemma 2 shows that the sequence  converges almost everywhere to
converges almost everywhere to  in
in 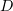 . Hence, we have proved that
. Hence, we have proved that
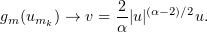
Moreover,  .
.
As in the case 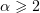 , (3.6) and (3.7) are satisfied for a fixed
, (3.6) and (3.7) are satisfied for a fixed  .
.
For 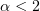 , the sequence
, the sequence 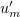 is bounded in
is bounded in 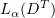 . Indeed, using (3.16),
. Indeed, using (3.16),
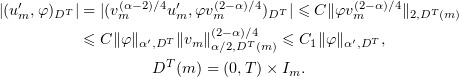
Hence, we can assume that 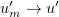 weakly in
weakly in 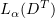 ,
,  , and so
, and so 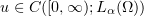 . This proves (2.4).
. This proves (2.4).
At Step 3, our aim is to show that 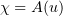 . For this purpose we shall need some integral relations. We multiply equations (3.13) by a smooth function
. For this purpose we shall need some integral relations. We multiply equations (3.13) by a smooth function 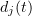 , integrate with respect to
, integrate with respect to 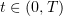 , and then integrate the first term by parts. Now, writing
, and then integrate the first term by parts. Now, writing 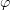 for
for 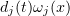 , we have
, we have
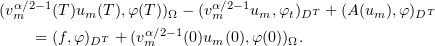
We note that
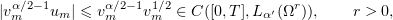
since 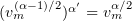 is a bounded sequence in
is a bounded sequence in ![$C([0,T];L_1(\Omega ^r))$](https://content.cld.iop.org/journals/1064-5616/204/9/1239/revision1/msb_204_9_1239ieqn352.gif) . Hence, we can choose a subsequence to ensure that
. Hence, we can choose a subsequence to ensure that  weakly in
weakly in  and
and 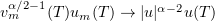 weakly in
weakly in  . That the limit functions have exactly this form is justified by the fact that, as we said above, the subsequence
. That the limit functions have exactly this form is justified by the fact that, as we said above, the subsequence 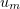 converges almost everywhere in
converges almost everywhere in 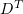 and almost everywhere in
and almost everywhere in 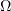 for
for  (see (3.6)). Now making
(see (3.6)). Now making  , in view of (3.8) it follows that
, in view of (3.8) it follows that
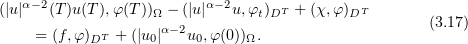
As in the case  , we show that this equality is satisfied for all functions
, we show that this equality is satisfied for all functions  . Relation (3.17) also means that
. Relation (3.17) also means that  is a generalized solution of problem (1.1), (1.2), provided that
is a generalized solution of problem (1.1), (1.2), provided that  .
.
Substituting 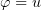 into (3.17), we see that
into (3.17), we see that
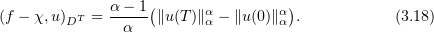
Our next argument depends on 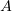 being monotone. Using equations (3.14), it is easily seen that
being monotone. Using equations (3.14), it is easily seen that
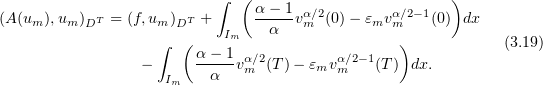
Employing inequality (3.15), by (3.19) we have
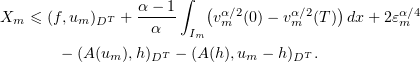
Now (3.12) follows because 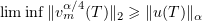 and
and 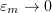 . Finally, a similar argument as in the case
. Finally, a similar argument as in the case  shows that
shows that 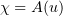 .
.
The proof of Theorem 1 is complete.
§ 4. Proof of Theorem 2
Assume now that  and that a domain
and that a domain  is bounded. Our aim is to estimate the decay rate of the solution to problem (1.3), (1.2) from below as
is bounded. Our aim is to estimate the decay rate of the solution to problem (1.3), (1.2) from below as 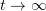 .
.
4.1. The case  .
.
We define
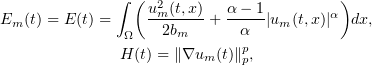
dropping the subscripts where possible. After differentiating with respect to 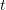 , for
, for  formula (3.2) assumes the form
formula (3.2) assumes the form

Differentiating (3.4), we obtain
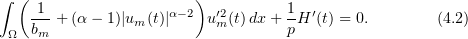
The following estimates hold:
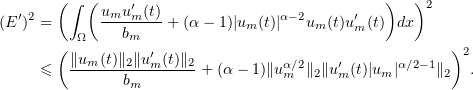
Applying the Cauchy-Schwarz inequality for the inner product in  , this gives
, this gives
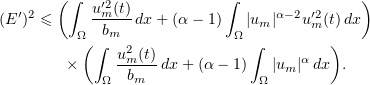
Hence,

Using (4.1), we rewrite this as follows:

As a result,  , or, on integrating,
, or, on integrating,
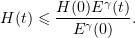
Consequently,
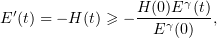
or
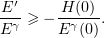
It follows that
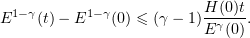
Thus,

In view of (3.7), for fixed 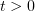 and
and  if the domain is bounded one may choose a subsequence
if the domain is bounded one may choose a subsequence  which converges strongly in the space
which converges strongly in the space 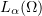 . The functions
. The functions
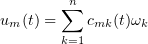
lie in the linear hull of the functions 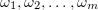 . In a finite-dimensional space all the norms are equivalent, and hence
. In a finite-dimensional space all the norms are equivalent, and hence

We choose numbers 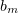 so as to have
so as to have 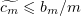 . Now
. Now
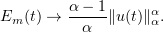
Passing to the limit in (4.4) as  , we obtain
, we obtain
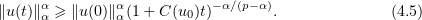
4.2. The case  .
.
In this case we set
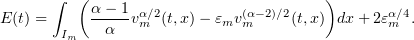
Note that (3.15) implies that 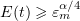 .
.
Differentiating (3.14) with respect to 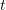 and rewriting it for
and rewriting it for  , this establishes
, this establishes

From (3.16) it follows that
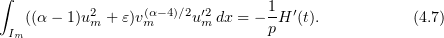
For any 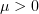 , clearly
, clearly
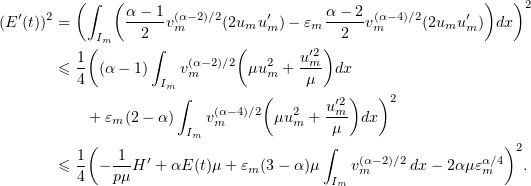
In view of (3.15),
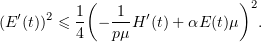
Now (4.3) follows by minimizing the right-hand side over  .
.
The rest of the proof is similar to the case  .
.
We claim that the estimate (4.5), in the case of a bounded domain 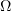 , is sharp. To prove this, we need the following Friedrichs-Steklov-type inequality
, is sharp. To prove this, we need the following Friedrichs-Steklov-type inequality
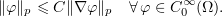
We note in passing that the following Friedrichs-Steklov inequality holds for an unbounded domain located inside a cone:

For  , we have
, we have
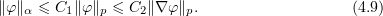
Differentiating (3.10) or (3.18) with respect to 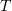 and employing (4.9) for
and employing (4.9) for  , we see that
, we see that
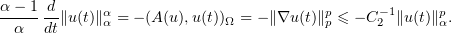
Solving this differential inequality, we obtain the estimate

which proves that (4.5) is sharp.
4.3. An unbounded domain.
Our aim here is to derive (4.5) for the solution of problem (1.3), (1.2) in the case when 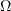 is unbounded.
is unbounded.
We let 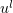 ,
,  , denote the solutions in
, denote the solutions in  with fixed initial function
with fixed initial function 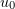 . We can assume that these solutions are extended by zero outside
. We can assume that these solutions are extended by zero outside 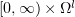 . Using (3.7), we have the estimate
. Using (3.7), we have the estimate
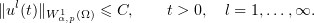
Using the properties of the solutions 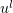 listed in Theorem 1, we can choose a subsequence
listed in Theorem 1, we can choose a subsequence  such that
such that  weakly in
weakly in 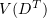 as
as 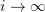 for all
for all 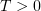 , and then, applying Steps 1–3, prove that the limit function
, and then, applying Steps 1–3, prove that the limit function 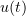 is a generalized solution of problem (1.3), (1.2).
is a generalized solution of problem (1.3), (1.2).
Further, given a fixed 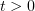 we can assume that
we can assume that  weakly in
weakly in 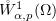 as
as  . As the embedding
. As the embedding 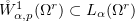 is compact,
is compact, 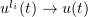 strongly in
strongly in 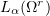 as
as 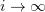 for any
for any 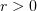 .
.
By (2.11), for any  there exists
there exists  such that
such that

Estimate (4.5) holds for 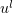 . Now
. Now
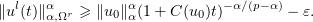
Using the strong convergence in 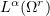 , we pass to the limit as
, we pass to the limit as  and then as
and then as  . Thus, we have now proved (2.10) for an unbounded domain
. Thus, we have now proved (2.10) for an unbounded domain 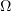 as well.
as well.
The proof of Theorem 2 is complete.
§ 5. Proof of Theorem 3
For the sake of completeness we recall the maximum principle to be used in the proof of Theorem 3. Note that the inequality 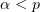 is not used in the proof of the maximum principle.
is not used in the proof of the maximum principle.
Proposition. Let 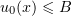 ,
, 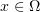 ,
,  . Then a generalized solution of problem (1.1), (1.2) with properties (2.2)–(2.5) is bounded:
. Then a generalized solution of problem (1.1), (1.2) with properties (2.2)–(2.5) is bounded:

Proof. The truncation 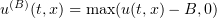 of a function
of a function 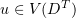 is known to lie in the same space (see, for example, [17], Ch. 2, § 4, Lemmas 4.1–4.3).
is known to lie in the same space (see, for example, [17], Ch. 2, § 4, Lemmas 4.1–4.3).
Assume first that 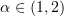 . That the function
. That the function 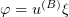 can be substituted into (3.17) is justified by the passage to the limit; here
can be substituted into (3.17) is justified by the passage to the limit; here 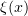 is a Lipschitz function with bounded support. We have
is a Lipschitz function with bounded support. We have
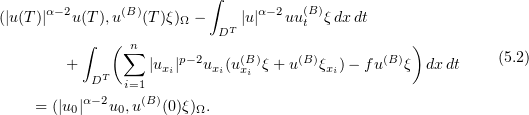
We choose 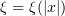 , where
, where
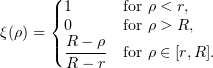
In this case, 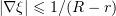 . Note that
. Note that 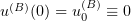 . We have
. We have 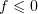 , and hence
, and hence
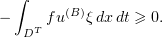
Further,
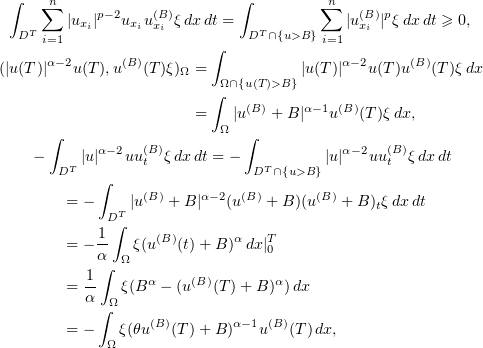
where 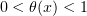 . Thus, (5.2) implies that
. Thus, (5.2) implies that
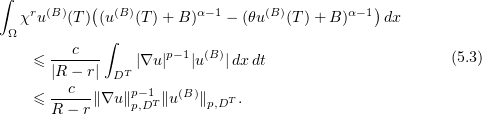
Without loss of generality we may assume that 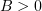 . Since
. Since ![$u\in C([0,T];L_{\alpha }(\Omega))$](https://content.cld.iop.org/journals/1064-5616/204/9/1239/revision1/msb_204_9_1239ieqn443.gif) , we have
, we have 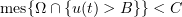 ,
, ![$t\in [0,T]$](https://content.cld.iop.org/journals/1064-5616/204/9/1239/revision1/msb_204_9_1239ieqn445.gif) . Hence,
. Hence,  ,
, ![$t\in [0,T]$](https://content.cld.iop.org/journals/1064-5616/204/9/1239/revision1/msb_204_9_1239ieqn447.gif) (see, for example, [17], Ch. 2, § 1, inequality (2.12)). So, the right-hand side of (5.3) tends to zero as
(see, for example, [17], Ch. 2, § 1, inequality (2.12)). So, the right-hand side of (5.3) tends to zero as  . Therefore,
. Therefore,
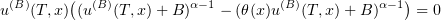
for almost all 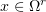 . Hence,
. Hence, 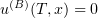 almost everywhere in
almost everywhere in  . This proves (5.1) since
. This proves (5.1) since 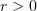 and
and 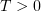 are arbitrary.
are arbitrary.
When 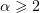 , we have to substitute
, we have to substitute 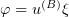 into (3.9) and proceed according to the above scheme. For example, we transform the first integral in (3.9) (putting
into (3.9) and proceed according to the above scheme. For example, we transform the first integral in (3.9) (putting 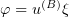 ):
):
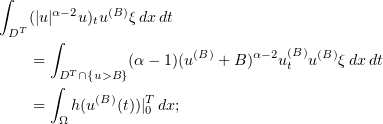
here 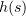 ,
, 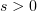 , is a monotonic function:
, is a monotonic function: 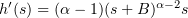 . The rest of the argument proceeds as above.
. The rest of the argument proceeds as above.
Proof of Theorem 3. Assume first that 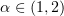 . We set
. We set 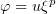 , where the function
, where the function  will be chosen later. Substituting
will be chosen later. Substituting 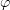 into (3.17) with
into (3.17) with 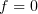 , we have
, we have
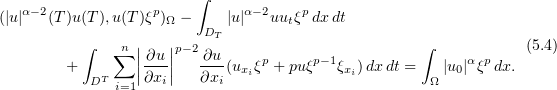
By choosing the functions 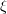 so that the supports of the functions
so that the supports of the functions 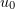 and
and  are disjoint, we can assume that the right-hand side of (5.4) is zero. Next, using Young's inequality,
are disjoint, we can assume that the right-hand side of (5.4) is zero. Next, using Young's inequality,
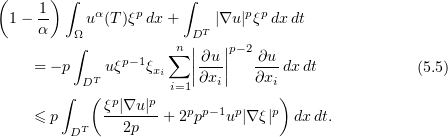
For  , the same result is obtained by substituting
, the same result is obtained by substituting  into (3.9).
into (3.9).
Let 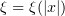 ,
,  for
for 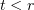 ,
, 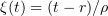 for
for ![$t\in (r,r+\rho]$](https://content.cld.iop.org/journals/1064-5616/204/9/1239/revision1/msb_204_9_1239ieqn474.gif) , and
, and 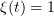 for
for 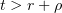 . Also let
. Also let  be such that
be such that 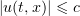 . Then
. Then
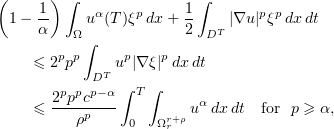
where we have set  , and the superscript
, and the superscript  will be omitted. It follows that
will be omitted. It follows that
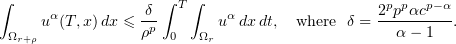
Setting
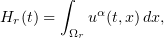
we have

In view of (3.10), the function 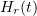 is bounded; that is,
is bounded; that is,  for all
for all  ,
,  . Hence, by (5.6),
. Hence, by (5.6),
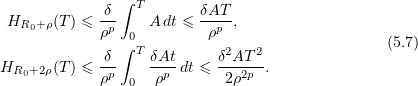
Proceeding by induction and applying Stirling's formula, this gives
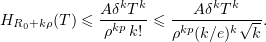
Let 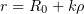 . Then
. Then
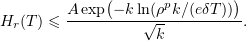
We choose 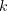 so that
so that  . Then
. Then
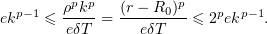
As a result,
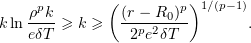
Consequently,
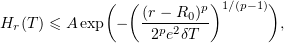
which implies (2.11). If  cannot be chosen as required, the inequality
cannot be chosen as required, the inequality ![$\smash[b]{\dfrac{(r-R_0)^p}{e\delta T}<e}$](https://content.cld.iop.org/journals/1064-5616/204/9/1239/revision1/msb_204_9_1239ieqn489.gif) holds, and estimate (2.11) is trivial.
holds, and estimate (2.11) is trivial.
The proof of Theorem 3 is complete.
§ 6. An upper estimate for the norm of the solution
Our aim in this section is to prove Theorems 4 and 5.
6.1. Proof of Theorem 4.
Let 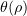 ,
, 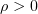 , be an absolutely continuous function equal to 1 for
, be an absolutely continuous function equal to 1 for 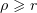 , to 0 for
, to 0 for  , linear for
, linear for ![$\rho \in [R_0,2R_0]$](https://content.cld.iop.org/journals/1064-5616/204/9/1239/revision1/msb_204_9_1239ieqn494.gif) and satisfying the equation
and satisfying the equation
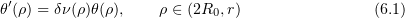
(the constant  will be specified below). Solving this equation, we find, in particular, that
will be specified below). Solving this equation, we find, in particular, that
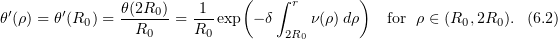
For any function 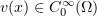 it follows from the definition of
it follows from the definition of 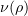 that
that
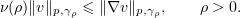
Multiplying by 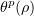 and integrating over
and integrating over ![$\rho \in [a,b]$](https://content.cld.iop.org/journals/1064-5616/204/9/1239/revision1/msb_204_9_1239ieqn499.gif) , we derive the inequality
, we derive the inequality
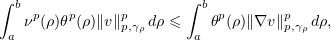
which now holds for any function 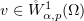 . For
. For 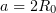 and
and 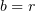 , we rewrite the last inequality as follows
, we rewrite the last inequality as follows
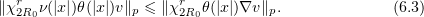
Substituting  into (5.5), we have
into (5.5), we have
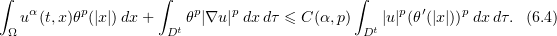
Using (6.1), (6.2), one easily reduces (6.4) to the form
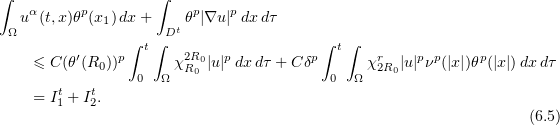
Applying (4.8) with 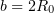 and using (3.18), it follows that
and using (3.18), it follows that
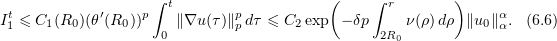
Using (6.3) shows that
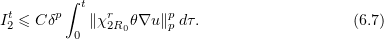
Taking 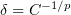 and combining (6.5)–(6.7), we obtain
and combining (6.5)–(6.7), we obtain
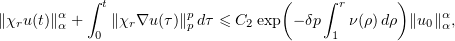
thereby proving inequality (2.14).
The proof of Theorem 4 is complete.
6.2. Proof of Theorem 5.
We choose a positive number 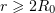 . Setting
. Setting
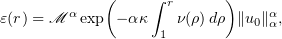
in view of (2.14), we have
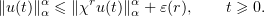
By (4.8),
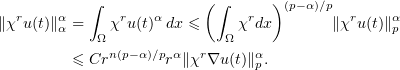
Setting  with an appropriate factor
with an appropriate factor  , we have
, we have
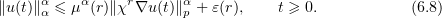
Let 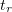 denote a point in the interval
denote a point in the interval  such that
such that 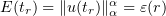 . If
. If  for any
for any 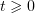 , we let
, we let  . Since the function
. Since the function  is monotone nonincreasing for
is monotone nonincreasing for  , we have
, we have 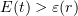 . Now (6.8) implies that
. Now (6.8) implies that
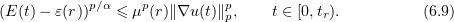
Differentiating (3.18) with respect to  , we see that
, we see that
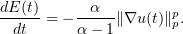
Next, in view of (6.9),
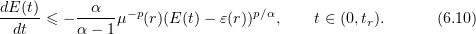
Solving this differential inequality, we obtain
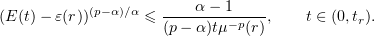
The substitution  into the last inequality shows that, for
into the last inequality shows that, for 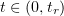 ,
,
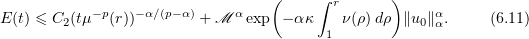
Note that, for  , the inequality
, the inequality 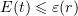 holds and estimate (6.11) is also valid.
holds and estimate (6.11) is also valid.
In (6.11) we set 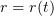 and use (2.15):
and use (2.15):
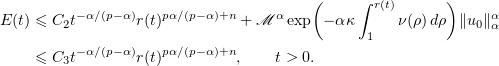
This proves inequality (2.16).
The proof of Theorem 5 is complete.