Table of contents

We prove the local representability and local finite basis property of varieties of associative rings and algebras over an arbitrary associative-commutative Noetherian ring .

We consider classes of uniformly bounded convex functions defined on convex compact bodies in  and satisfying a Lipschitz condition and establish the exact orders of their Kolmogorov, entropy, and pseudo-dimension widths in the -metric. We also introduce the notions of pseudo-dimension and pseudo-dimension widths for classes of sets and determine the exact orders of the entropy and pseudo-dimension widths of some classes of convex bodies in relative to the pseudo-metric defined as the -dimensional Lebesgue volume of the symmetric difference of two sets. We also find the exact orders of the entropy and pseudo-dimension widths of the corresponding classes of characteristic functions in -spaces, .

We prove that sets of zero modulus with weight  (in particular, isolated singularities) are removable for discrete open -maps if the function  has finite mean oscillation or a logarithmic singularity of order not exceeding on the corresponding set. We obtain analogues of the well-known Sokhotskii-Weierstrass theorem and also of Picard's theorem. In particular, we show that in the neighbourhood of an essential singularity, every discrete open -map takes any value infinitely many times, except possibly for a set of values of zero capacity.

Under certain natural assumptions on cohomology of a complex projective fibred threefold with semi-stable degenerations, we prove the Grothendieck standard conjecture  of Lefschetz type on the algebraicity of the operators  and . In particular, is true if at least one of the following conditions holds: 1) the generic fibre of some -parameter holomorphic family is birationally equivalent to either a ruled surface, an Enriques surface, or a K3-surface, 2) all the fibres of  are smooth surfaces of Kodaira dimension .

We prove theorems on the exact asymptotic behaviour of the integrals

for 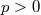and 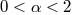for two random processes 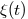, namely, the Wiener process and the Brownian bridge, and obtain other related results. Our approach is via the Laplace method for infinite-dimensional distributions, namely, Gaussian measures and the occupation time for Markov processes.