Abstract
We study the long-time behaviour of solutions to the periodic problem for a non-linear Sobolev-type equation. In the case of non-small initial perturbations we get estimates for the decay as a function of time. In the case of small initial data we prove an asymptotic formula for solutions to the periodic problem for a non-linear Sobolev-type equation.
Export citation and abstract BibTeX RIS
§ 1. Introduction
In this paper we study the long-time asymptotic behaviour of solutions to the periodic problem for the non-linear Sobolev-type equation
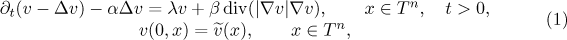
where 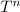 is the
is the 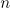 -dimensional torus (that is, the cube
-dimensional torus (that is, the cube ![$\Omega =([-\pi ,\pi ])^{n}$](https://content.cld.iop.org/journals/1064-5632/77/2/313/revision1/izv_77_2_313ieqn3.gif) with natural identification of the appropriate faces),
with natural identification of the appropriate faces),  and
and 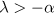 ,
, 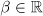 . We consider spatially
. We consider spatially 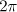 -periodic solutions
-periodic solutions 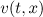 of (1) with
of (1) with 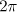 -periodic initial data
-periodic initial data 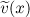 .
.
Note that the evolution of the mean value  can easily be calculated as
can easily be calculated as

where 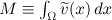 is the mean value of the initial perturbation
is the mean value of the initial perturbation 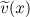 . Changing the variables by
. Changing the variables by
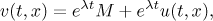
we get the periodic problem
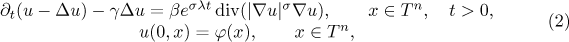
whose initial data 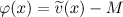 have zero mean value, and with
have zero mean value, and with 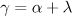 . By the assumption
. By the assumption 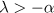 we have
we have 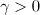 . Thus, in what follows we study the periodic problem (2) with
. Thus, in what follows we study the periodic problem (2) with 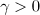 ,
,  and
and

Sobolev-type equations [1] describe various physical processes and have been studied in many papers. The monograph [2] gives a comprehensive survey of the modern theory of linear and non-linear Sobolev-type equations along with a derivation of linear higher-order Sobolev-type modelling equations arising in the theory of plasma and the description of quasistationary processes in electromagnetic continua. The long-time asymptotics of solutions to the Cauchy problem for non-linear Sobolev-type equations with various types of non-linearities was studied in the book [3] and the survey [4].
Many publications are devoted to the study of space-periodic problems. For example, asymptotic stability of stationary periodic solutions of Fisher's equation was proved in [5], the periodic problem for the Hopf equation was studied in [6], and the long-time asymptotic behaviour of solutions to the periodic problem for the Burgers equation was obtained in [7]. Some decay estimates for the solutions to the Korteweg–de Vries–Burgers equation with periodic initial data having zero mean value have been found in [8]. It was also proved there that the asymptotic behaviour is determined by higher-order harmonics. The papers [9], [10] contain a proof of the existence and uniqueness of global-in-time solutions to the periodic problem for the Landau–Ginzburg equation as well as decay estimates with respect to time in various norms. Explicit periodic solutions to the Landau–Ginzburg equation have been found in [11]. The global existence and decay estimates with respect to time for solutions to the periodic problem for the Kuramoto–Sivashinsky equation were obtained in [12]. For the Benjamin–Bona–Mahoney–Peregrin–Burgers equation, the existence of global solutions and energy decay estimates with respect to time have been established in [13]. The periodic problem for the Boussinesq equation was studied in [14]. The long-time behaviour of solutions to the periodic problem for systems of conservation laws was studied in [15], [16]. In [17] the authors consider the issues of existence and blow-up of solutions to the periodic problem for the Camassa–Holm equation. Asymptotic formulae for the solutions to the periodic problem for various non-linear equations have been obtained in [18].
As far as we know, the long-time behaviour of solutions to the periodic problem for the non-linear Sobolev-type equation (1) has not been treated before. Our aim is to prove the asymptotic formulae for the solutions to the periodic problem for the non-linear Sobolev-type equation (1).
We introduce some notation. Let
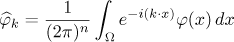
be the Fourier coefficients of a  -periodic function
-periodic function 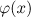 . As usual, by
. As usual, by 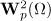 we denote the Sobolev space with norm
we denote the Sobolev space with norm
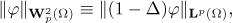
where 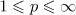 , and we write
, and we write 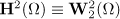 . We denote by
. We denote by 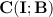 the space of continuous functions from a temporal interval
the space of continuous functions from a temporal interval  to a Banach space
to a Banach space 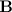 . We denote various constants by the same symbol
. We denote various constants by the same symbol 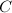 .
.
Using the Duhamel principle, we rewrite the periodic problem (2) in the form of an integral equation

where the Green operator 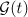 can be formally represented as a Fourier series
can be formally represented as a Fourier series
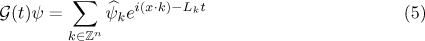
with ![$\smash[t]{L_{k}=\frac{\gamma |k|^{2}}{1+|k|^{2}}}$](https://content.cld.iop.org/journals/1064-5632/77/2/313/revision1/izv_77_2_313ieqn30.gif) . By a global-in-time solution of the periodic problem (2) we mean a solution
. By a global-in-time solution of the periodic problem (2) we mean a solution 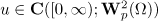 of the corresponding integral equation (4).
of the corresponding integral equation (4).
We now state the main result of this paper.
Theorem 1. Let 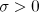 and
and  . Suppose that
. Suppose that 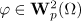 ,
, 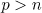 for
for 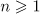 , and the norm
, and the norm 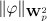 is sufficiently small. Then there is a unique global-in-time solution
is sufficiently small. Then there is a unique global-in-time solution 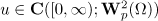 to the periodic problem (2). It satisfies the estimate
to the periodic problem (2). It satisfies the estimate
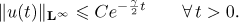
For equations (2) with 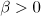 we can relax the requirement that the initial data should be small. For simplicity we consider only the case when
we can relax the requirement that the initial data should be small. For simplicity we consider only the case when  .
.
Theorem 2. Let 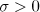 ,
,  and
and 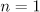 . Suppose that
. Suppose that  . Then there is a unique solution
. Then there is a unique solution 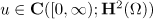 to the periodic problem (2). Moreover, it satisfies the decay estimate
to the periodic problem (2). Moreover, it satisfies the decay estimate
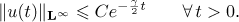
In the following theorem we obtain an asymptotic expansion of the solution. We put 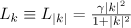 .
.
Theorem 3. Let 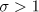 and
and  . Suppose that
. Suppose that 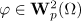 ,
, 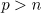 for
for 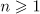 , and the norm
, and the norm  is sufficiently small. Then there are numbers
is sufficiently small. Then there are numbers 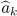 (the Fourier coefficients of the function
(the Fourier coefficients of the function  defined in (16) below) such that the following asymptotic formula holds:
defined in (16) below) such that the following asymptotic formula holds:
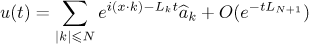
as 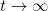 uniformly with respect to
uniformly with respect to  , where
, where 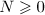 .
.
In the next section we obtain some preliminary estimates for the Green operator of the periodic problem for the linear Sobolev-type equation and prove the global existence of solutions to the periodic problem for the non-linear equation (1). In the three subsequent sections we prove Theorems 1–3 respectively.
§ 2. Preliminary estimates
Consider the periodic problem for the linear Sobolev-type equation

where the right-hand side 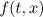 and the initial perturbation
and the initial perturbation 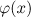 are
are 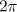 -periodic functions of the spatial variable
-periodic functions of the spatial variable  . Using Fourier series, we can formally write the Green operator
. Using Fourier series, we can formally write the Green operator 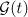 in the form (5). Therefore the solution to the periodic problem for the linear Sobolev-type equation (6) can be written by means of the Duhamel formula as
in the form (5). Therefore the solution to the periodic problem for the linear Sobolev-type equation (6) can be written by means of the Duhamel formula as
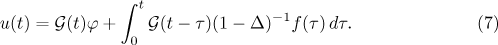
We first estimate the solution to the linear periodic problem (6) in terms of the Lebesgue norms in 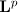 ,
, 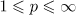 . We introduce two projectors
. We introduce two projectors
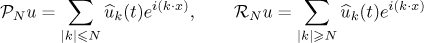
for 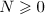 . Then
. Then 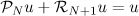 for every
for every 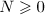 .
.
Lemma 1. Suppose that 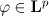 and
and 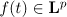 for
for 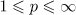 . Then for
. Then for 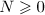 and
and 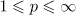 we have
we have
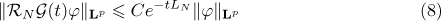
for all  ,
,
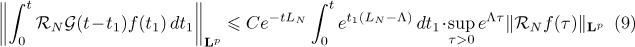
for all 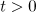 if
if 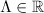 , and
, and
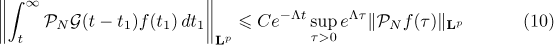
for all  if
if 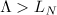 .
.
Proof. We write the representation
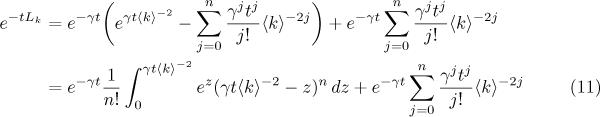
for 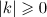 , where
, where 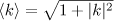 . Note that the remainder term
. Note that the remainder term
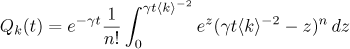
satisfies the estimate
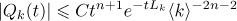
for 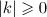 . We put
. We put 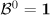 and define the operators
and define the operators
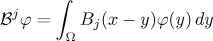
with kernels
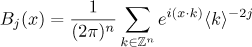
for 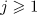 , and the remainder operator
, and the remainder operator 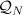 ,
,
with kernel
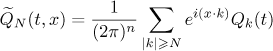
such that by (11) we have the representation
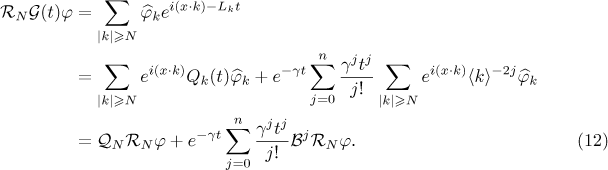
Then 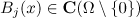 and we have
and we have
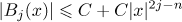
for all 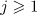 and
and  (see [19], Theorem 2.17). We also have
(see [19], Theorem 2.17). We also have
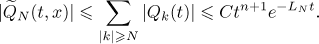
Therefore
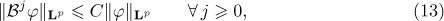
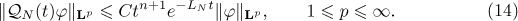
Thus, by (13) and (14), we obtain from (12) that

Since 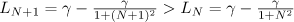 and
and
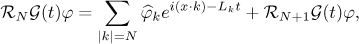
we get estimate (8) in the lemma:
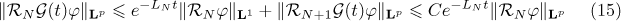
for all  . We similarly have
. We similarly have
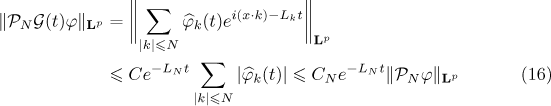
for all  . Using (15) and (16), we obtain
. Using (15) and (16), we obtain
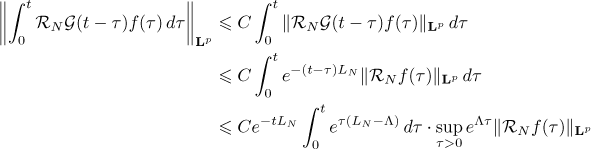
for all  if
if 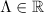 . We similarly get
. We similarly get
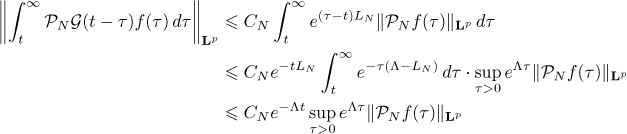
for all 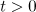 if
if 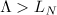 . □
. □
In the following lemma we establish the local-in-time existence of solutions of the periodic problem (2).
Lemma 2. Let 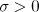 and
and 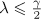 . Suppose that
. Suppose that 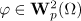 and
and 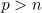 for
for 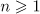 . Then for some time
. Then for some time 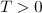 there is a unique solution
there is a unique solution ![$u\in \mathbf {C}([0,T];\mathbf {W}_{p}^{2}(\Omega ))$](https://content.cld.iop.org/journals/1064-5632/77/2/313/revision1/izv_77_2_313ieqn100.gif) of the periodic problem (2).
of the periodic problem (2).
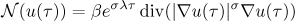
and consider the integral equation (4):

By (3) we have  and
and 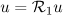 . Consider the ball
. Consider the ball
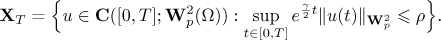
For all 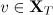 we define the map
we define the map
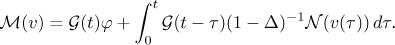
We claim that 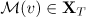 . Indeed, the Sobolev embedding theorem (see [20]) yields that
. Indeed, the Sobolev embedding theorem (see [20]) yields that 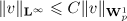 if
if 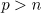 for
for 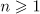 . Hence,
. Hence,
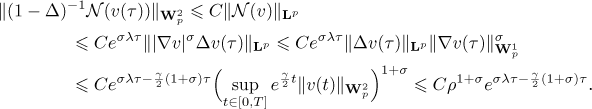
In view of estimate (8) in Lemma 1 we have
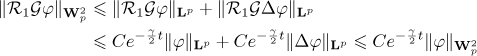
for all 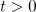 . Using estimate (9) in Lemma 1 for
. Using estimate (9) in Lemma 1 for 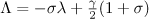 , we get
, we get
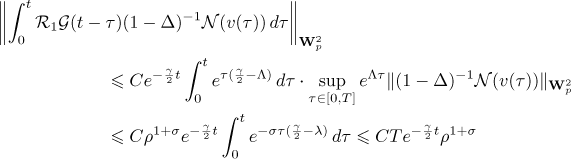
for all ![$t\in [0,T]$](https://content.cld.iop.org/journals/1064-5632/77/2/313/revision1/izv_77_2_313ieqn110.gif) since
since 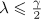 . It follows that
. It follows that 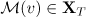 for a suitable choice of
for a suitable choice of 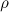 and
and  .
.
We now claim that 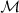 is a contraction. Indeed, as above, we have
is a contraction. Indeed, as above, we have
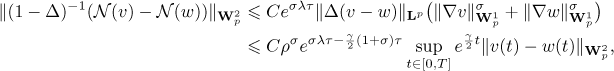
whence we deduce from estimate (9) in Lemma 1 that
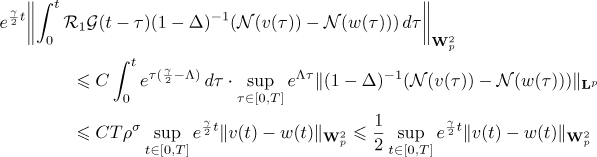
for all ![$t\in [0,T]$](https://content.cld.iop.org/journals/1064-5632/77/2/313/revision1/izv_77_2_313ieqn116.gif) if
if 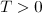 is chosen sufficiently small. Thus
is chosen sufficiently small. Thus 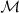 is a contraction in the space
is a contraction in the space 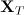 and, therefore, there is a unique solution
and, therefore, there is a unique solution ![$u\in \mathbf {C}([0,T];\mathbf {W}_{p}^{2}(\Omega ))$](https://content.cld.iop.org/journals/1064-5632/77/2/313/revision1/izv_77_2_313ieqn120.gif) of the periodic problem (2). □
of the periodic problem (2). □
§ 3. Proof of Theorem 1
Consider the ball

of a small radius 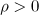 . As in the proof of Lemma 2, we can see that
. As in the proof of Lemma 2, we can see that  is a contraction in the space
is a contraction in the space 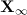 . Hence there is a unique global-in-time solution
. Hence there is a unique global-in-time solution 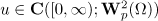 of the periodic problem (2). This solution satisfies the estimate
of the periodic problem (2). This solution satisfies the estimate

for all 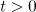 . By the Sobolev embedding theorem, this yields the estimate in the theorem. □
. By the Sobolev embedding theorem, this yields the estimate in the theorem. □
§ 4. Proof of Theorem 2
Multiplying the one-dimensional version
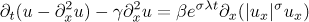
of equation (2) by 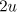 and integrating over
and integrating over 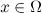 , we get
, we get
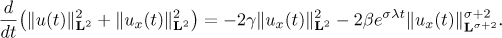
In a similar vein, multiplying (2) by 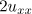 and integrating over
and integrating over 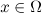 , we get
, we get
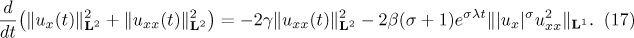
In particular, the norm 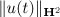 is bounded for all
is bounded for all 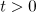 . Using estimate (11) and the standard extension of solutions, we find that there is a global-in-time solution
. Using estimate (11) and the standard extension of solutions, we find that there is a global-in-time solution 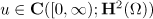 of the periodic problem (2).
of the periodic problem (2).
By Parseval's identity we have
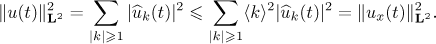
We similarly have 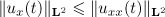 . Hence it follows from (17) that
. Hence it follows from (17) that
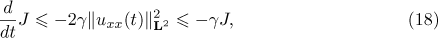
where 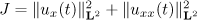 . Integrating (18) with respect to
. Integrating (18) with respect to  , we get the estimate
, we get the estimate
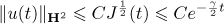
for all 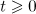 . Theorem 2 now follows from the Sobolev embedding theorem. □
. Theorem 2 now follows from the Sobolev embedding theorem. □
§ 5. Proof of Theorem 3
We put
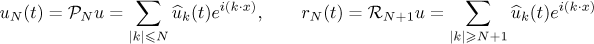
for 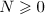 . Thus we get a representation
. Thus we get a representation  . It follows from the integral equation (4) that
. It follows from the integral equation (4) that
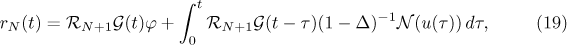
where 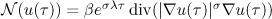 . We define the space
. We define the space
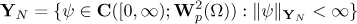
with the norm
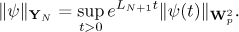
We now use induction to prove that

for all 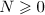 . Since
. Since  and
and 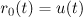 , the estimate (20) for
, the estimate (20) for 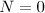 can be obtained in the same way as in the proof of Lemma 1. Suppose that (20) holds for
can be obtained in the same way as in the proof of Lemma 1. Suppose that (20) holds for 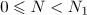 and consider
and consider  .
.
By estimate (8) in Lemma 1 we have
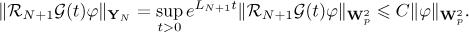
Using estimate (9) in Lemma 1, we find that
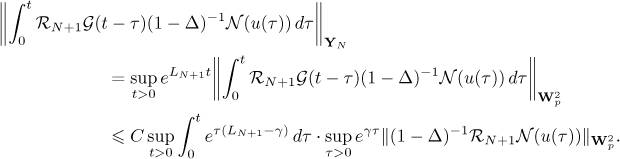
By the Sobolev embedding theorem (see [20]) we have 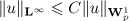 for
for 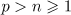 , whence
, whence
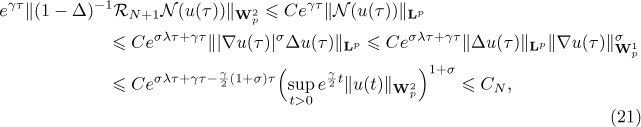
because 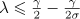 . It follows that
. It follows that
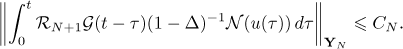
Thus estimate (20) holds for all  .
.
We now find the asymptotics of the solution. We put
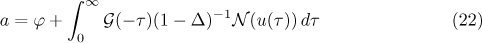
and write the representation

for  . By estimate (10) in Lemma 1 we have
. By estimate (10) in Lemma 1 we have
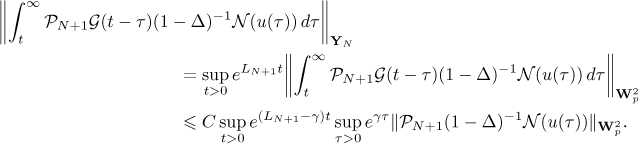
As in (21), we have the estimate
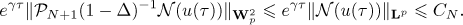
Therefore we get
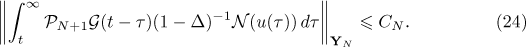
Furthermore, since
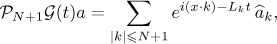
we obtain the following asymptotic formula from (20), (23), (24):
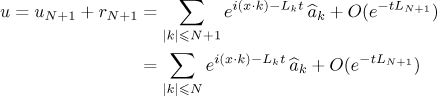
as 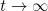 uniformly with respect to
uniformly with respect to 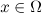 . □
. □



