Abstract
We consider the problem of best uniform approximation of real continuous functions  by simple partial fractions of degree at most
by simple partial fractions of degree at most  on a closed interval
on a closed interval  of the real axis. We get analogues of the classical polynomial theorems of Chebyshev and de la Vallée-Poussin. We prove that a real-valued simple partial fraction
of the real axis. We get analogues of the classical polynomial theorems of Chebyshev and de la Vallée-Poussin. We prove that a real-valued simple partial fraction  of degree
of degree  whose poles lie outside the disc with diameter
whose poles lie outside the disc with diameter  , is a simple partial fraction of the best approximation to
, is a simple partial fraction of the best approximation to  if and only if the difference
if and only if the difference 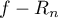 admits a Chebyshev alternance of
admits a Chebyshev alternance of  points on
points on  . Then
. Then  is the unique fraction of best approximation. We show that the restriction on the poles is unimprovable. Particular cases of the theorems obtained have been stated by various authors only as conjectures.
is the unique fraction of best approximation. We show that the restriction on the poles is unimprovable. Particular cases of the theorems obtained have been stated by various authors only as conjectures.
Export citation and abstract BibTeX RIS
§ 1. Introduction. Statement of results
We study the best uniform approximation of real-valued continuous functions on closed intervals of the real axis by real-valued simple partial fractions (s. f.). Recall that a real-valued simple partial fraction  of degree
of degree  ,
,  , is the logarithmic derivative of an algebraic polynomial of degree
, is the logarithmic derivative of an algebraic polynomial of degree  with real coefficients:
with real coefficients:
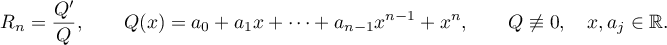
Thus 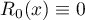 and
and
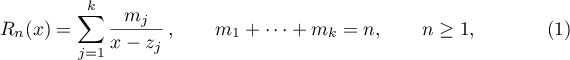
where the poles  are all pairwise- distinct zeros of the polynomial
are all pairwise- distinct zeros of the polynomial  , and the numbers
, and the numbers  are their multiplicities. Clearly, the zeros are symmetric with respect to the real axis and the multiplicities of complex- conjugate zeros coincide.
are their multiplicities. Clearly, the zeros are symmetric with respect to the real axis and the multiplicities of complex- conjugate zeros coincide.
Consider a simple partial fraction of order at most  of the best uniform approximation of a function
of the best uniform approximation of a function  on a closed interval
on a closed interval ![$S=[x_0-r,x_0+r]$](https://content.cld.iop.org/journals/1064-5632/79/3/431/revision1/IZV_79_3_431ieqn13.gif) ,
,  . We denote it by
. We denote it by
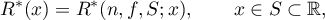
and sometimes call this fraction optimal.
Simple partial fractions were used by Macintyre and Fuchs (1940), Gonchar (1950s) and Dolzhenko (1960s) in connection with extremal problems in classes of rational functions. As an independent tool of approximation, simple partial fractions were first used by V. I. Danchenko and D. Ya. Danchenko (1999). The theory of approximation by simple partial fractions and their modifications was further developed by V. I. Danchenko, Borodin, Kosukhin, Protasov, Kayumov, Novak and others. Some of these papers are listed in the references. For example, analogues of the classical polynomial theorems of Mergelyan, Jackson, Bernshtein, Zygmund, Dzyadyk and Walsh were obtained for s. f. (see [1], [2]). On the other hand, there are a number of principal approximative properties that do not hold for polynomials. One such property of simple partial fractions is the possibility of approximation on unbounded sets (see [3]–[6]).
Another principal feature is that the fraction  is, generally speaking, non-unique and cannot be characterized by the number of alternance points 1 for
is, generally speaking, non-unique and cannot be characterized by the number of alternance points 1 for  . The non-uniqueness of
. The non-uniqueness of  even in the presence of an alternance of
even in the presence of an alternance of  points (as well as the non-necessity of such an alternance for the best approximation) was first shown in [7] by an example for
points (as well as the non-necessity of such an alternance for the best approximation) was first shown in [7] by an example for 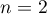 . This example was completely generalized to
. This example was completely generalized to  in [8] and to arbitrary
in [8] and to arbitrary 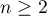 in [9]. Thus for s. f. there is no exact analogue of Chebyshev's classical theorem on alternance (see [10], p. 69). Our main result (Theorem 1) is an analogue of Chebyshev's theorem under an additional restriction on the poles of the simple partial fraction that delivers the alternance. Many authors have sought such an analogue, and a number of general conjectures were stated in [11]–[14]. Some of them will be established here for the first time.
in [9]. Thus for s. f. there is no exact analogue of Chebyshev's classical theorem on alternance (see [10], p. 69). Our main result (Theorem 1) is an analogue of Chebyshev's theorem under an additional restriction on the poles of the simple partial fraction that delivers the alternance. Many authors have sought such an analogue, and a number of general conjectures were stated in [11]–[14]. Some of them will be established here for the first time.
The following conjecture of V. I. Danchenko [12] is still open: for every continuous function  , the fraction
, the fraction  is unique and is characterized by an alternance of
is unique and is characterized by an alternance of  points whenever the degree
points whenever the degree  is sufficiently large. This conjecture has been proved only for constant functions
is sufficiently large. This conjecture has been proved only for constant functions  (see [7], [15], [16]). We note that the problem of the best approximation of constants by simple partial fractions is one of the possible analogues of Chebyshev's problem on the monic polynomial of a given degree with least deviation from zero.
(see [7], [15], [16]). We note that the problem of the best approximation of constants by simple partial fractions is one of the possible analogues of Chebyshev's problem on the monic polynomial of a given degree with least deviation from zero.
We now state our results. Let  be a continuous real function on the closed interval
be a continuous real function on the closed interval ![$S=[x_0-r,x_0+r]$](https://content.cld.iop.org/journals/1064-5632/79/3/431/revision1/IZV_79_3_431ieqn13.gif) , and let
, and let  be the closed disc with diameter
be the closed disc with diameter  :
:
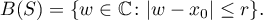
Theorem 1. If all poles of a real-valued s. f.  of degree
of degree  of the form (1) lie outside the disc
of the form (1) lie outside the disc  , then
, then  if and only if the difference
if and only if the difference  admits an alternance of
admits an alternance of  points on
points on  . In this case
. In this case  is the unique fraction of best uniform approximation in the class of all s. f. of degree at most
is the unique fraction of best uniform approximation in the class of all s. f. of degree at most  . The condition on the position of the poles cannot be weakened.
. The condition on the position of the poles cannot be weakened.
The impossibility of weakening the condition on the poles means that if at least one pair of complex- conjugate poles of the fraction of best approximation lies in the disc  , then, generally speaking, the best approximation is non-unique and is not characterized by an alternance of
, then, generally speaking, the best approximation is non-unique and is not characterized by an alternance of  points in
points in  . Examples are given in §2.
. Examples are given in §2.
In Theorem 1, the degree of the s. f. of best approximation is fixed (and is equal to  ). In the next theorem we get rid of this restriction as far as the sufficiency of the alternance is concerned. The condition also seems to be redundant as far as the necessity of the alternance and the uniqueness of the best approximation are concerned.
). In the next theorem we get rid of this restriction as far as the sufficiency of the alternance is concerned. The condition also seems to be redundant as far as the necessity of the alternance and the uniqueness of the best approximation are concerned.
Theorem 2. If a simple partial fraction  of degree
of degree  has no poles in the disc
has no poles in the disc  and the difference
and the difference  has an alternance of
has an alternance of  points on
points on  , then
, then 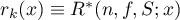 .
.
Theorem 2 is proved in §4. Theorem 1 is proved in §3 (sufficiency of the alternance) and §5 (necessity of the alternance and uniqueness of the best approximation).
Remark 1. In the case of  distinct poles of
distinct poles of  , Theorem 1 was stated and proved by the author in [14] (sufficiency of the alternance) and [17] (necessity of the alternance and uniqueness of the best approximation). We now do not require all poles to be distinct. This form of the criterion was announced by the author in [16]. Novak [11] had earlier proved an analogue of Theorem 1 in the case of
, Theorem 1 was stated and proved by the author in [14] (sufficiency of the alternance) and [17] (necessity of the alternance and uniqueness of the best approximation). We now do not require all poles to be distinct. This form of the criterion was announced by the author in [16]. Novak [11] had earlier proved an analogue of Theorem 1 in the case of  distinct real poles except for the uniqueness assertion. The proofs in [11], [14], [17] make essential use of the determinant identity (8), which was conjectured (in other terminology) in [11] and verified only for small
distinct real poles except for the uniqueness assertion. The proofs in [11], [14], [17] make essential use of the determinant identity (8), which was conjectured (in other terminology) in [11] and verified only for small  . The author has learned that (8) was proved for all
. The author has learned that (8) was proved for all  by Borchardt (see [18], Russian p. 18). This promotes the previous results from conjectures to fully fledged theorems. In this paper we also use Borchardt's identity.
by Borchardt (see [18], Russian p. 18). This promotes the previous results from conjectures to fully fledged theorems. In this paper we also use Borchardt's identity.
Remark 2. For  it is still an open question whether one can replace the disc in Theorem 1 by a smaller figure containing the closed interval
it is still an open question whether one can replace the disc in Theorem 1 by a smaller figure containing the closed interval  . Such a replacement is impossible for
. Such a replacement is impossible for  because of the non-uniqueness example in [7], where the poles of each s. f. of degree 2 of the best approximation to
because of the non-uniqueness example in [7], where the poles of each s. f. of degree 2 of the best approximation to  ,
, ![$x\in [-1,1]$](https://content.cld.iop.org/journals/1064-5632/79/3/431/revision1/IZV_79_3_431ieqn39.gif) , lie precisely on the unit circle.
, lie precisely on the unit circle.
Remark 3. The requirement of the continuity of  in Theorem 1 is redundant in the following sense. Let
in Theorem 1 is redundant in the following sense. Let  and
and  be bounded functions. We put
be bounded functions. We put  and say that points
and say that points  of the closed interval
of the closed interval  form a generalized alternance on
form a generalized alternance on  for the difference
for the difference  if every point
if every point  is contained in an arbitrarily small subinterval
is contained in an arbitrarily small subinterval  such that at least one of the two following alternances holds:
such that at least one of the two following alternances holds:
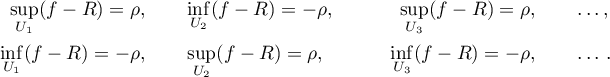
If we define the alternance in this way, then Theorem 1 holds for all bounded functions  . Only the slightest changes are needed in the proof.
. Only the slightest changes are needed in the proof.
As an application of Theorem 1, we consider the problem of the best approximation of continuous functions  whose modulus is small on the interval
whose modulus is small on the interval ![$x\in [-1,1]$](https://content.cld.iop.org/journals/1064-5632/79/3/431/revision1/IZV_79_3_431ieqn44.gif) . We recall that Kosukhin [2] established, under very general assumptions, a connection between the least deviations from polynomials and simple partial fractions. To state his result in the case of approximation on
. We recall that Kosukhin [2] established, under very general assumptions, a connection between the least deviations from polynomials and simple partial fractions. To state his result in the case of approximation on ![$[-1,1]$](https://content.cld.iop.org/journals/1064-5632/79/3/431/revision1/IZV_79_3_431ieqn45.gif) , we put
, we put

( is fixed). Let
is fixed). Let  (resp.
(resp.  ) be the least deviation on
) be the least deviation on ![$[-1,1]$](https://content.cld.iop.org/journals/1064-5632/79/3/431/revision1/IZV_79_3_431ieqn45.gif) of
of  from simple partial functions of degree at most
from simple partial functions of degree at most  (resp. of
(resp. of  from algebraic polynomials of degree at most
from algebraic polynomials of degree at most  ) and let
) and let  be the uniform norm on
be the uniform norm on ![$[-1,1]$](https://content.cld.iop.org/journals/1064-5632/79/3/431/revision1/IZV_79_3_431ieqn45.gif) . Put
. Put 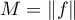 . Then the following estimate holds (see [2]):
. Then the following estimate holds (see [2]):
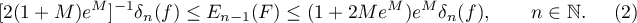
By definition we have  , where
, where ![$R^*(x)\equiv R^*(n,f,[-1,1];x)$](https://content.cld.iop.org/journals/1064-5632/79/3/431/revision1/IZV_79_3_431ieqn54.gif) . Therefore,
. Therefore,
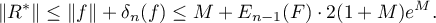
Furthermore, it is proved in [19] that the poles of every s. f.  of degree
of degree  satisfying the condition
satisfying the condition 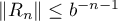 for some
for some  lie in the exterior of the ellipse
lie in the exterior of the ellipse
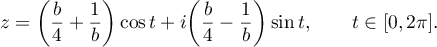
The interior of this ellipse contains the unit disc if 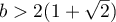 . Therefore we obtain the following corollary from Theorem 1 and the previous estimates.
. Therefore we obtain the following corollary from Theorem 1 and the previous estimates.
Corollary 1. Suppose that the following inequality holds for some constants ![$c\in[-1,1]$](https://content.cld.iop.org/journals/1064-5632/79/3/431/revision1/IZV_79_3_431ieqn58.gif) (see the definition of
(see the definition of  ,
, 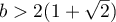 and
and  :
:
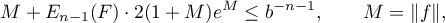
and the s. f. ![$R^*(n,f,[-1,1];x)$](https://content.cld.iop.org/journals/1064-5632/79/3/431/revision1/IZV_79_3_431ieqn61.gif) has degree
has degree  . Then the best approximation is unique and the difference
. Then the best approximation is unique and the difference  admits an alternance consisting of
admits an alternance consisting of  points of
points of ![$[-1,1]$](https://content.cld.iop.org/journals/1064-5632/79/3/431/revision1/IZV_79_3_431ieqn45.gif) .
.
In §2 we apply this result to a concrete function  (see the example in §2.4). Note that if this inequality holds, then the function itself has small modulus since we necessarily have
(see the example in §2.4). Note that if this inequality holds, then the function itself has small modulus since we necessarily have  .
.
A lower bound for the least deviation can be obtained from the following analogue of de la Vallée-Poussin's polynomial theorem (see [10], pp. 63–64).
Theorem 3. If the poles of a s. f.  of degree
of degree  lie outside the disc
lie outside the disc  and there are
and there are  points
points  on the closed interval
on the closed interval  such that
such that  ,
,  ,
, 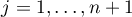 , then
, then
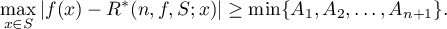
Theorem 3 is proved in §4. Note that Theorem 3 with  was obtained in [11] (see also [14]) under some additional assumptions (see Remark 1). Here we get rid of these restrictions.
was obtained in [11] (see also [14]) under some additional assumptions (see Remark 1). Here we get rid of these restrictions.
The most important auxiliary tool in the proofs of Theorems 1–3 is the following Theorem 4, which can be deduced from Borchardt's identity. Theorem 4 is of independent interest. In particular, it asserts that the functions (3) below satisfy the Haar condition on  . We recall some terminology in this connection (see [10], pp. 79–88).
. We recall some terminology in this connection (see [10], pp. 79–88).
Continuous complex functions  satisfy the Haar condition on a compact set
satisfy the Haar condition on a compact set 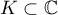 (containing more than
(containing more than  points) if every generalized polynomial of the form
points) if every generalized polynomial of the form  with constants
with constants  (not all equal to 0) has no more than
(not all equal to 0) has no more than  distinct zeros on
distinct zeros on  . Clearly, this condition is equivalent to the inequality
. Clearly, this condition is equivalent to the inequality  for any
for any  distinct points
distinct points  . Haar showed that it is also equivalent to the uniqueness of the polynomial
. Haar showed that it is also equivalent to the uniqueness of the polynomial  of least deviation for all continuous functions
of least deviation for all continuous functions  on
on  . In particular, if the functions
. In particular, if the functions  are real and satisfy the Haar condition on a compact set
are real and satisfy the Haar condition on a compact set  , then the system
, then the system  is called a Chebyshev system on
is called a Chebyshev system on  . Chebyshev's alternance theorem and some other results in the theory of approximation by algebraic polynomials can be transferred verbatim to the case of Chebyshev systems.
. Chebyshev's alternance theorem and some other results in the theory of approximation by algebraic polynomials can be transferred verbatim to the case of Chebyshev systems.
We consider a system of  functions of the form
functions of the form
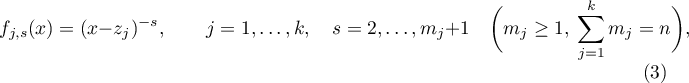
where  are distinct points which are situated symmetrically with respect to the real axis, and with every point
are distinct points which are situated symmetrically with respect to the real axis, and with every point  we associate a number
we associate a number  such that
such that 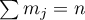 and the numbers
and the numbers  associated with complex- conjugate
associated with complex- conjugate  are equal to each other.
are equal to each other.
Theorem 4. If the numbers  in the definition of the system (3) of
in the definition of the system (3) of  functions lie outside the disc
functions lie outside the disc  , then the sum of the multiplicities of the zeros on
, then the sum of the multiplicities of the zeros on  of the generalized polynomial
of the generalized polynomial 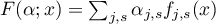 with arbitrary numerical coefficients
with arbitrary numerical coefficients  , not all equal to
, not all equal to  , does not exceed
, does not exceed  .
.
Theorem 4 is proved in §6. We mention separately the case when the functions (3) are real-valued. In this case Theorem 4 yields the following corollary.
Corollary 2. If the numbers  in the definition of the system (3) are real and lie outside the closed interval
in the definition of the system (3) are real and lie outside the closed interval  , then the functions (3) form a Chebyshev system on
, then the functions (3) form a Chebyshev system on  .
.
This assertion was first proved in [11] (see also [14], [17]) in the case when  , that is, for the system of functions
, that is, for the system of functions  with
with  distinct real poles
distinct real poles  , under the assumption that the identity (8) holds.
, under the assumption that the identity (8) holds.
Unlike the Haar condition, the property of the system (3) stated in Theorem 4 restricts the sum of the multiplicities of the zeros of 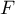 . In what follows we call this property the strengthened Haar condition. Chebyshev systems possessing this property (see [20], Russian p. 58) are referred to as
. In what follows we call this property the strengthened Haar condition. Chebyshev systems possessing this property (see [20], Russian p. 58) are referred to as 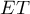 -systems, while arbitrary Chebyshev systems are alternatively referred to as
-systems, while arbitrary Chebyshev systems are alternatively referred to as  -systems.
-systems.
Using Theorem 4, we prove in §3 the following theorem on the uniqueness of the solution of the multiple interpolation problem. We recall that an interpolating s. f. need not be unique, in contrast to the interpolating polynomial. This was first observed for the simple interpolation problem in [21] and [11], where one can also find some uniqueness conditions in terms of the table of interpolation nodes. The issue of the unique solubility of the interpolation problem was further treated in [13], [14], [22] and elsewhere.
Theorem 5. If a real-valued s. f.  of degree
of degree  of the form (1) with all poles lying outside the disc
of the form (1) with all poles lying outside the disc  interpolates a table with
interpolates a table with  pairwise- distinct nodes
pairwise- distinct nodes  of total multiplicity
of total multiplicity  , that is,
, that is,
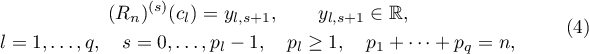
then  is the unique interpolating fraction in the class of all s. f. of degree
is the unique interpolating fraction in the class of all s. f. of degree 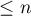 for all possible nodes
for all possible nodes  , values
, values  and multiplicities
and multiplicities  .
.
§ 2. Examples relating to the main theorem
In §§2.1–2.3 we establish the unimprovability of the condition on poles in Theorem 1. In §2.4 we give an example relating to Corollary 1. The example in §2.5 concerns the case when the best approximation is attained at a s. f. with one pole.
2.1.
We show by an example that if at least one pair of complex- conjugate poles of a s. f. possessing an 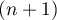 -point alternance lies in the disc
-point alternance lies in the disc  , then the fraction need not be optimal.
, then the fraction need not be optimal.
Consider a s. f.  of degree
of degree  with poles
with poles  and
and  , and take the interval
, and take the interval ![$[-1,1]$](https://content.cld.iop.org/journals/1064-5632/79/3/431/revision1/IZV_79_3_431ieqn45.gif) for
for  . Clearly, the second pair of poles lies outside the closed unit disc, and the first pair lies inside.
. Clearly, the second pair of poles lies outside the closed unit disc, and the first pair lies inside.
The function  has exactly five points of local extremum on
has exactly five points of local extremum on ![$[-1,1]$](https://content.cld.iop.org/journals/1064-5632/79/3/431/revision1/IZV_79_3_431ieqn45.gif) :
:
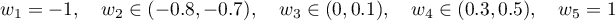
(alternately minima and maxima) and takes the following values  at these points:
at these points:
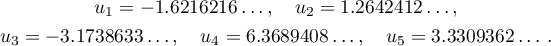
We put  and define a continuous piecewise-linear function
and define a continuous piecewise-linear function  by letting it be constant on the intervals
by letting it be constant on the intervals
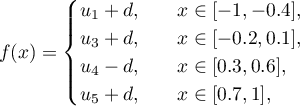
and connecting the neighbouring endpoints of these intervals by straight lines on the remaining part of ![$[-1,1]$](https://content.cld.iop.org/journals/1064-5632/79/3/431/revision1/IZV_79_3_431ieqn45.gif) .
.
By construction, the  points
points  form an alternance for
form an alternance for  on
on ![$[-1,1]$](https://content.cld.iop.org/journals/1064-5632/79/3/431/revision1/IZV_79_3_431ieqn45.gif) and we have
and we have ![$\max_{x\in[-1,1]}|f(x)-R(x)|=d$](https://content.cld.iop.org/journals/1064-5632/79/3/431/revision1/IZV_79_3_431ieqn108.gif) . Nevertheless,
. Nevertheless,  is not a fraction of best approximation for
is not a fraction of best approximation for  . For example, we easily verify that the s. f.
. For example, we easily verify that the s. f.  with poles
with poles 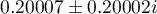 and
and  is a better approximation to
is a better approximation to  :
: ![$\max_{x\in[-1,1]}|f(x)-\widetilde{R}(x)|=1.4427864\ldots<d$](https://content.cld.iop.org/journals/1064-5632/79/3/431/revision1/IZV_79_3_431ieqn112.gif) .
.
2.2.
The hypothesis of Theorem 1 on the position of the poles does not hold in the known examples of non-uniqueness of best approximation (see [7]–[9]). We recall that for every 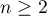 (see [7], [8] for small
(see [7], [8] for small  and [9] for arbitrary
and [9] for arbitrary  ) one can find an interval
) one can find an interval 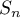 , a continuous function
, a continuous function 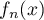 and a family (with parameter
and a family (with parameter  ) of simple partial fractions
) of simple partial fractions  of degree
of degree  such that every fraction
such that every fraction  provides the best approximation of
provides the best approximation of  in the class of all s. f. of degree at most
in the class of all s. f. of degree at most  on
on 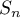 . Moreover, there is a value
. Moreover, there is a value 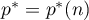 of the parameter such that
of the parameter such that  has exactly
has exactly  alternance points on
alternance points on 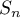 . For all other values of the parameter, the alternance contains fewer than
. For all other values of the parameter, the alternance contains fewer than  points.
points.
Thus, if the condition on the position of the poles does not hold, then
(a) neither 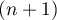 -point alternance nor uniqueness can be guaranteed for the optimal fraction;
-point alternance nor uniqueness can be guaranteed for the optimal fraction;
(b) an 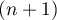 -point alternance does not guarantee uniqueness.
-point alternance does not guarantee uniqueness.
The conclusions (a), (b) hold even in the case when only one pair of complex- conjugate poles of the fraction lies in the disc 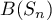 (for example, this is obvious when
(for example, this is obvious when  ).
).
2.3.
Following [13], [8], we construct for every 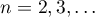 an example showing that if all poles of the fraction lie in the disc
an example showing that if all poles of the fraction lie in the disc  , then even the presence of an alternance of
, then even the presence of an alternance of  points does not guarantee that the approximation is optimal.
points does not guarantee that the approximation is optimal.
It is proved in [13] that for all  and
and  there are real polynomials
there are real polynomials  and
and  of degree
of degree  which are positive on
which are positive on ![$S=[x_0-r,x_0+r]$](https://content.cld.iop.org/journals/1064-5632/79/3/431/revision1/IZV_79_3_431ieqn13.gif) and such that the polynomial
and such that the polynomial  has exactly
has exactly 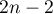 simple zeros on the interval
simple zeros on the interval  .
.
Indeed, suppose for example that  is even, choose points
is even, choose points  on the interval
on the interval  and put
and put
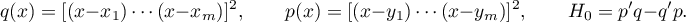
The polynomial 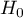 has at least
has at least  distinct zeros on the closed interval
distinct zeros on the closed interval ![$[x_1,x_m]$](https://content.cld.iop.org/journals/1064-5632/79/3/431/revision1/IZV_79_3_431ieqn131.gif) . These are the
. These are the  zeros
zeros  and at least one zero on each of the
and at least one zero on each of the  intervals
intervals  (since the signs of the derivatives
(since the signs of the derivatives  coincide). We similarly see that
coincide). We similarly see that 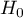 has at least
has at least  distinct zeros on
distinct zeros on ![$[y_1,y_m]$](https://content.cld.iop.org/journals/1064-5632/79/3/431/revision1/IZV_79_3_431ieqn137.gif) . Since the polynomial
. Since the polynomial 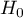 is of degree
is of degree 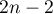 , it has no zeros other than those listed, and all the listed zeros are simple. Putting
, it has no zeros other than those listed, and all the listed zeros are simple. Putting  and
and  , where
, where  is arbitrarily small, we see that the polynomials
is arbitrarily small, we see that the polynomials  and
and  are positive and, by continuity, the polynomials
are positive and, by continuity, the polynomials  and
and 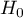 have the same number of zeros on
have the same number of zeros on  , that is,
, that is, 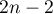 zeros. (A similar, but more involved, argument works for odd
zeros. (A similar, but more involved, argument works for odd  .)
.)
Since  is small, it follows by continuity that all zeros of
is small, it follows by continuity that all zeros of  and
and  lie inside the disc
lie inside the disc  .
.
We now repeat an argument in [8]. Let  ,
,  , be the zeros of
, be the zeros of  enumerated in ascending order. Putting also
enumerated in ascending order. Putting also 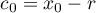 and
and 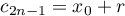 , we have
, we have 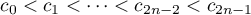 .
.
By construction, all the poles of the simple partial fractions  and
and  lie inside the disc
lie inside the disc  but outside the closed interval
but outside the closed interval  , and the difference
, and the difference  has exactly
has exactly 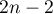 simple zeros on
simple zeros on  and preserves sign on each of the
and preserves sign on each of the  intervals
intervals  ,
,  . This sign alternates from one interval to another.
. This sign alternates from one interval to another.
There is no loss of generality in assuming that 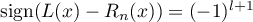 for
for 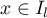 ,
, 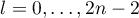 . We fix an arbitrary number
. We fix an arbitrary number  and define a continuous real-valued function
and define a continuous real-valued function  by the following (easily achievable) conditions:
by the following (easily achievable) conditions:
1) 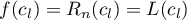 ,
,  ;
;
2)  for
for 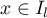 ,
,  ;
;
3)  ,
,  .
.
Clearly, the deviation of the s. f.  from
from  on
on  is equal to
is equal to 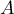 and the difference
and the difference 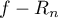 has an alternance on
has an alternance on  consisting of the
consisting of the  points
points 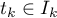 . However,
. However,  is not optimal because, by construction, the deviation of the s. f.
is not optimal because, by construction, the deviation of the s. f. 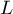 from
from  is strictly less than
is strictly less than 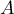 .
.
2.4.
Consider the family of functions
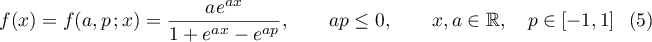
(where 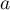 and
and  are parameters). The condition
are parameters). The condition  guarantees that these functions are continuous for all
guarantees that these functions are continuous for all  (
( ) and monotone increasing (
) and monotone increasing (![$f\,'(x)= a^2e^{ax}(1- e^{ap})\times [1+ e^{ax}-e^{ap}]^{-2}\ge 0$](https://content.cld.iop.org/journals/1064-5632/79/3/431/revision1/IZV_79_3_431ieqn167.gif) ). For example, the family (5) contains all constants:
). For example, the family (5) contains all constants: 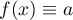 for
for  . If
. If 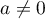 , then
, then  and
and 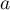 have the same sign. Therefore, by monotonicity,
have the same sign. Therefore, by monotonicity,
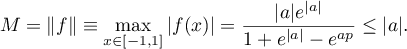
We fix a parameter ![$p\in[-1,1]$](https://content.cld.iop.org/journals/1064-5632/79/3/431/revision1/IZV_79_3_431ieqn171.gif) and put
and put  in the definition of
in the definition of 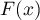 (see §1). Then it can easily be seen that
(see §1). Then it can easily be seen that  . We use the following estimate for
. We use the following estimate for  (see [23], Russian pp. 229–230). If
(see [23], Russian pp. 229–230). If 
 everywhere on
everywhere on ![$[-1,1]$](https://content.cld.iop.org/journals/1064-5632/79/3/431/revision1/IZV_79_3_431ieqn45.gif) , then
, then

Since in our case  , we obtain
, we obtain
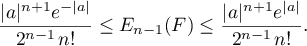
Using this and (2), we find a bound for the least deviation from  :
:
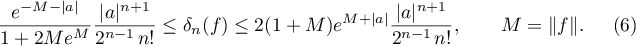
This estimate has exact order in  . In particular, we obtain an estimate of exact order for the least deviations in the problem of the best approximation of constants.
. In particular, we obtain an estimate of exact order for the least deviations in the problem of the best approximation of constants.
Thus we have the following assertion whose last part follows from Corollary 1, the inequality  and the upper bound in (6).
and the upper bound in (6).
Proposition 1. For all ![$p\in[-1,1]$](https://content.cld.iop.org/journals/1064-5632/79/3/431/revision1/IZV_79_3_431ieqn171.gif) and
and  with
with  , the least deviation of a s. f. of degree at most
, the least deviation of a s. f. of degree at most  from a function
from a function  of the form (5) satisfies the estimate (6), and this estimate is of exact order. If the s. f.
of the form (5) satisfies the estimate (6), and this estimate is of exact order. If the s. f.  of the best approximation of
of the best approximation of  has degree
has degree  for
for  , then the best approximation is unique and the difference
, then the best approximation is unique and the difference  has an alternance of
has an alternance of  points on
points on ![$[-1,1]$](https://content.cld.iop.org/journals/1064-5632/79/3/431/revision1/IZV_79_3_431ieqn45.gif) .
.
2.5.
Suppose that  is an algebraic polynomial of degree at most
is an algebraic polynomial of degree at most  and the poles of a real-valued s. f.
and the poles of a real-valued s. f.  of the form (1) lie outside the disc
of the form (1) lie outside the disc  . By Theorem 1 and Chebyshev's alternance theorem, the equality
. By Theorem 1 and Chebyshev's alternance theorem, the equality 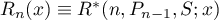 holds if and only if
holds if and only if 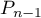 has the least deviation from
has the least deviation from  on
on  among all polynomials of degree at most
among all polynomials of degree at most  . Then
. Then 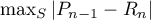 coincides with
coincides with  (the least deviation of s. f. of degree at most
(the least deviation of s. f. of degree at most  from
from 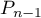 ) and
) and  (the least deviation of polynomials of degree at most
(the least deviation of polynomials of degree at most  from
from  ); compare with [13].
); compare with [13].
Theorem 2 enables us to strengthen this assertion. Namely, suppose that the poles of a s. f.  of degree
of degree  lie outside the disc
lie outside the disc  . If
. If 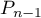 is a polynomial of least deviation from
is a polynomial of least deviation from  on
on  , then
, then  is a s. f. of degree
is a s. f. of degree 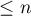 of least deviation from
of least deviation from 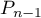 on
on  , and the magnitude of this deviation is
, and the magnitude of this deviation is 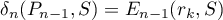 .
.
We now calculate the deviation in the case of the interval ![$[-1,1]$](https://content.cld.iop.org/journals/1064-5632/79/3/431/revision1/IZV_79_3_431ieqn45.gif) and a unipolar s. f.
and a unipolar s. f.  ,
,  . For real
. For real 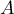 and
and  we have
we have ![$E_{n-1}(A/(x- a),[-1,1])=|A|(a-\sqrt{a^2-1})^{n-1}/(a^2-1)$](https://content.cld.iop.org/journals/1064-5632/79/3/431/revision1/IZV_79_3_431ieqn192.gif) (this follows from [10], pp. 70–72, where this quantity is found for
(this follows from [10], pp. 70–72, where this quantity is found for  ). Using this and what was said above, we obtain the following result for the polynomial
). Using this and what was said above, we obtain the following result for the polynomial 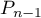 of least deviation from the fraction
of least deviation from the fraction  of degree
of degree  :
:
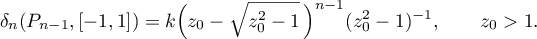
§ 3. Sufficiency of the alternance
In this section we use Theorem 4 to prove the sufficiency of the alternance in Theorem 1. We also prove Theorem 5.
Theorem 4 is applied to simple partial fractions by means of the following lemma, which was obtained by the author [13] in the case of  distinct points
distinct points  . We state the lemma for all simple partial fractions, although it will be used only for real-valued ones.
. We state the lemma for all simple partial fractions, although it will be used only for real-valued ones.
Lemma 1. Suppose that  , where
, where  is a polynomial of degree
is a polynomial of degree  of the form
of the form

 are distinct points and
are distinct points and  are positive integers. Then for every s. f.
are positive integers. Then for every s. f.  of degree at most
of degree at most  there are
there are  uniquely determined numbers
uniquely determined numbers  such that
such that
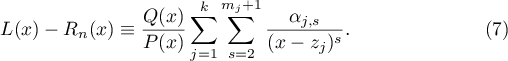
Proof. We have 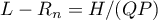 , where
, where  . Regard the formula
. Regard the formula 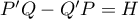 as a differential equation for an unknown polynomial
as a differential equation for an unknown polynomial  of degree
of degree  with known polynomials
with known polynomials  (of degree
(of degree  ) and
) and  (of degree
(of degree 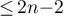 ). Integrating this equation, we obtain
). Integrating this equation, we obtain

Clearly, each zero of  of multiplicity
of multiplicity  is also a zero of
is also a zero of  of multiplicity at least
of multiplicity at least 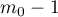 . Therefore
. Therefore  for some polynomial
for some polynomial  , and the (unique) partial fraction expansion of the regular fraction
, and the (unique) partial fraction expansion of the regular fraction  is given by
is given by
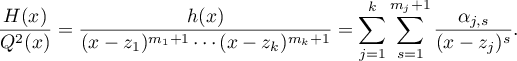
Note that the coefficients  of the fractions
of the fractions  must necessarily be equal to zero (otherwise integration gives an uncancellable logarithm, contrary to the requirement that `
must necessarily be equal to zero (otherwise integration gives an uncancellable logarithm, contrary to the requirement that ` is a polynomial'). Thus we have the identity
is a polynomial'). Thus we have the identity
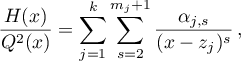
which proves the lemma. 
Here are some corollaries of Theorem 4. In their statements we assume that the s. f.  are real-valued. Hence the points
are real-valued. Hence the points  in the definition of
in the definition of  (see Lemma 1) must be situated symmetrically with respect to the real axis, and the positive integers
(see Lemma 1) must be situated symmetrically with respect to the real axis, and the positive integers  must be equal for conjugate
must be equal for conjugate  .
.
Corollary 3. If all poles of a s. f.  of degree
of degree  of the form (1) lie outside the disc
of the form (1) lie outside the disc  , and if
, and if  is another real-valued s. f. of degree at most
is another real-valued s. f. of degree at most  , then the sum of the multiplicities of the zeros of
, then the sum of the multiplicities of the zeros of  on
on  does not exceed
does not exceed  . In particular, the difference
. In particular, the difference  has at most
has at most  distinct zeros on
distinct zeros on  .
.
Proof. We have  for
for 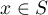 . Hence it follows from Lemma 1 that each zero of multiplicity
. Hence it follows from Lemma 1 that each zero of multiplicity  of
of  is also a zero of multiplicity
is also a zero of multiplicity  of the sum on the right-hand side of (7). But this sum is a polynomial in the system of functions (3) and, by Theorem 4, cannot have more than
of the sum on the right-hand side of (7). But this sum is a polynomial in the system of functions (3) and, by Theorem 4, cannot have more than  roots on
roots on  (counting multiplicities).
(counting multiplicities). 
Theorem 5 is merely a restatement of Corollary 3.
Corollary 4. If all poles of a s. f.  of degree
of degree  of the form (1) lie outside the disc
of the form (1) lie outside the disc  , then the sum of the multiplicities of the zeros of the first derivative of
, then the sum of the multiplicities of the zeros of the first derivative of  on
on  does not exceed
does not exceed  . In particular,
. In particular, 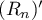 has no more than
has no more than  distinct zeros on
distinct zeros on  .
.
Proof. It follows from Corollary 3 that the polynomial  has at most
has at most  zeros on
zeros on  (counting multiplicities) if
(counting multiplicities) if  is a real polynomial of degree
is a real polynomial of degree  all of whose roots lie outside
all of whose roots lie outside  and
and  is another real polynomial of degree at most
is another real polynomial of degree at most  . Putting
. Putting 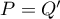 in the definition of
in the definition of  , we conclude that the polynomial
, we conclude that the polynomial 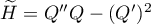 has at most
has at most  roots on
roots on  (counting multiplicities). It remains to note that
(counting multiplicities). It remains to note that 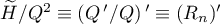 .
. 
Corollary 5. (sufficiency of the alternance) Suppose that  is a continuous function on the closed interval
is a continuous function on the closed interval  , the poles of a s. f.
, the poles of a s. f.  of degree
of degree  of the form (1) lie outside the disc
of the form (1) lie outside the disc  , and the difference
, and the difference 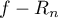 has an alternance of
has an alternance of  points on
points on  . Then
. Then  .
.
Proof. Suppose that 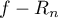 admits an alternance
admits an alternance  of
of  points on the interval
points on the interval ![$S\,{=}\,[x_0-r,x_0+r]$](https://content.cld.iop.org/journals/1064-5632/79/3/431/revision1/IZV_79_3_431ieqn219.gif) . Assume that there is a s. f.
. Assume that there is a s. f. 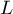 of degree
of degree  providing a better approximation to
providing a better approximation to  on
on  than
than  :
:  . At the points of alternance we have
. At the points of alternance we have
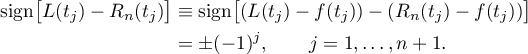
In particular, the function  is continuous on
is continuous on  and changes sign on each of the
and changes sign on each of the  closed intervals
closed intervals ![$[t_j,t_{j+1}]$](https://content.cld.iop.org/journals/1064-5632/79/3/431/revision1/IZV_79_3_431ieqn221.gif) . Hence it has at least
. Hence it has at least  distinct zeros on the interval
distinct zeros on the interval  . By Corollary 3 it follows that
. By Corollary 3 it follows that 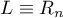 . This contradicts the assumption that
. This contradicts the assumption that 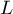 is a better approximation to
is a better approximation to  .
. 
§ 4. The case of approximation by fractions of degree less than 
In this section we prove Theorems 2, 3. Since a straightforward application of the method used in §3 becomes cumbersome when the order of the approximating s. f. is less than  , we prove Theorems 2, 3 in another way.
, we prove Theorems 2, 3 in another way.
Proof. of Theorem 2 When  the theorem coincides with Corollary 5 (see §3). Let us prove that an alternance of
the theorem coincides with Corollary 5 (see §3). Let us prove that an alternance of  points guarantees the best approximation of
points guarantees the best approximation of  by
by  even for
even for  .
.
Assume the opposite: there is a s. f.  of degree at most
of degree at most  which provides a better approximation, that is,
which provides a better approximation, that is, 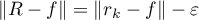 , where
, where  (here and in what follows,
(here and in what follows,  is the uniform norm for the closed interval
is the uniform norm for the closed interval  ). We introduce the notation
). We introduce the notation
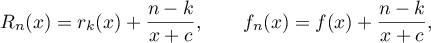
where  ,
,  . For every such
. For every such  , the simple partial fraction
, the simple partial fraction  is a best approximation to
is a best approximation to  . This follows from Corollary 5 since the degree of
. This follows from Corollary 5 since the degree of  is equal to
is equal to  , all its poles lie outside
, all its poles lie outside  , and the difference
, and the difference  has an alternance of
has an alternance of  points on
points on  because of the identity
because of the identity  and the presence of such an alternance for
and the presence of such an alternance for  .
.
By the triangle inequality we have the following chain:
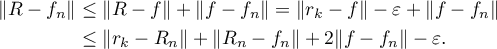
Clearly, 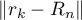 and
and  decrease to zero as
decrease to zero as  . Hence there is a
. Hence there is a 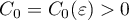 such that
such that  for all
for all  . Thus for every
. Thus for every  we have
we have
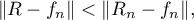
contrary to the assumption that  is a best approximation of
is a best approximation of  . Therefore our assumption is false and
. Therefore our assumption is false and  is indeed a best approximation to
is indeed a best approximation to  .
. 
Proof. of Theorem 3 When  the theorem is proved by contradiction in the same way as Corollary 5. We claim that the case
the theorem is proved by contradiction in the same way as Corollary 5. We claim that the case  can easily be reduced to the case
can easily be reduced to the case  as in the proof of Theorem 2. Indeed, given
as in the proof of Theorem 2. Indeed, given  and
and  , we construct a fraction
, we construct a fraction  and a function
and a function  as above. It follows from the hypothesis of Theorem 3 and the identity
as above. It follows from the hypothesis of Theorem 3 and the identity  that we have
that we have 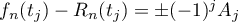 ,
,  ,
, 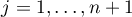 , at the points
, at the points  of the interval
of the interval  . Since all the poles of the s. f.
. Since all the poles of the s. f.  of degree
of degree  lie outside the disc
lie outside the disc  and, since the theorem is already known for fractions of degree
and, since the theorem is already known for fractions of degree  , the following bound holds for all
, the following bound holds for all  (see the proof of Theorem 2):
(see the proof of Theorem 2):
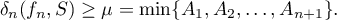
Here and in what follows we write  for the least deviation of simple partial fractions of degree at most
for the least deviation of simple partial fractions of degree at most  from the function
from the function 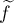 on
on  .
.
Let 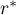 be a s. f. of degree
be a s. f. of degree 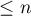 of best uniform approximation to
of best uniform approximation to  on
on  . Assume that
. Assume that  , where
, where  . Let
. Let  be a positive number such that
be a positive number such that 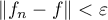 for all
for all  . Then, by our assumption,
. Then, by our assumption,
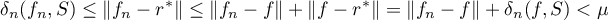
for  . This contradicts the inequality
. This contradicts the inequality  . Hence
. Hence  .
. 
§ 5. Necessity of the alternance. Uniqueness of the best approximation
Here we prove the remaining assertions in Theorem 1. To simplify the notation, we assume that ![$S=[-1,1]$](https://content.cld.iop.org/journals/1064-5632/79/3/431/revision1/IZV_79_3_431ieqn246.gif) (the case of an arbitrary closed real interval
(the case of an arbitrary closed real interval ![$S=[x_0-r,x_0+r]$](https://content.cld.iop.org/journals/1064-5632/79/3/431/revision1/IZV_79_3_431ieqn13.gif) is reduced to this by the linear transformation
is reduced to this by the linear transformation 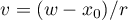 ).
).
Necessity of the alternance of  points. Suppose that the poles of the s. f.
points. Suppose that the poles of the s. f.  of degree
of degree  of the best approximation to a continuous function
of the best approximation to a continuous function  on
on ![$[-1,1]$](https://content.cld.iop.org/journals/1064-5632/79/3/431/revision1/IZV_79_3_431ieqn45.gif) lie outside the disc
lie outside the disc ![$B([-1,1])$](https://content.cld.iop.org/journals/1064-5632/79/3/431/revision1/IZV_79_3_431ieqn248.gif) , and let
, and let ![$d=\max_{x\in[-1,1]}|f(x)-R_n(x)|$](https://content.cld.iop.org/journals/1064-5632/79/3/431/revision1/IZV_79_3_431ieqn249.gif) be the least deviation.
be the least deviation.
Assume that 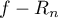 has an alternance of only
has an alternance of only  points on
points on ![$[-1,1]$](https://content.cld.iop.org/journals/1064-5632/79/3/431/revision1/IZV_79_3_431ieqn45.gif) . Then there are points
. Then there are points  such that
such that
1)  for all
for all  ;
;
2) for every  the difference
the difference 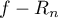 attains an extremal value
attains an extremal value  on the closed interval
on the closed interval ![$[x_j,x_{j+1}]$](https://content.cld.iop.org/journals/1064-5632/79/3/431/revision1/IZV_79_3_431ieqn256.gif) .
.
We note that the extremum on ![$[x_j,x_{j+1}]$](https://content.cld.iop.org/journals/1064-5632/79/3/431/revision1/IZV_79_3_431ieqn256.gif) ,
,  , is necessarily attained at an interior point while the extremum on
, is necessarily attained at an interior point while the extremum on ![$[x_1,x_2]$](https://content.cld.iop.org/journals/1064-5632/79/3/431/revision1/IZV_79_3_431ieqn258.gif) (resp.
(resp. ![$[x_m,x_{m+1}]$](https://content.cld.iop.org/journals/1064-5632/79/3/431/revision1/IZV_79_3_431ieqn259.gif) ) may also be attained at the endpoint
) may also be attained at the endpoint 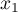 (resp.
(resp.  ).
).
We first consider the case when 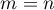 . Define the following
. Define the following  -tuple of points
-tuple of points 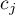 :
:
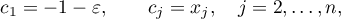
where  is small so that the poles of the s. f.
is small so that the poles of the s. f.  lie outside the disc
lie outside the disc 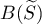 with diameter
with diameter ![$\widetilde{S}=[-1-\varepsilon,1+\varepsilon]$](https://content.cld.iop.org/journals/1064-5632/79/3/431/revision1/IZV_79_3_431ieqn265.gif) . For all
. For all  of sufficiently small modulus, the problem of interpolating the
of sufficiently small modulus, the problem of interpolating the  -node table
-node table
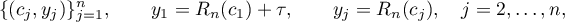
by simple partial fractions of degree 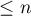 has a unique solution
has a unique solution  . The degree of
. The degree of 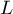 is equal to
is equal to  , and the poles of
, and the poles of 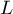 lie outside the disc
lie outside the disc 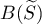 . This follows by continuity from Theorem 5 (see §1) since the only solution of the interpolation problem for
. This follows by continuity from Theorem 5 (see §1) since the only solution of the interpolation problem for 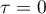 is the s. f.
is the s. f. 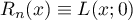 .
.
Furthermore, by Theorem 5, the graphs of 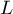 and
and  for small
for small  have no intersections on
have no intersections on  except for the nodes
except for the nodes  , and all of them are simple zeros of the difference
, and all of them are simple zeros of the difference  . Hence the function
. Hence the function 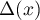 , whose modulus can be made arbitrary small on
, whose modulus can be made arbitrary small on  by an appropriate choice of
by an appropriate choice of 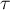 , preserves its sign on each of the intervals
, preserves its sign on each of the intervals 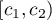 ,
,  ,
,  ,
, ![$(c_n,1+\varepsilon]$](https://content.cld.iop.org/journals/1064-5632/79/3/431/revision1/IZV_79_3_431ieqn279.gif) , and this sign alternates as we pass from any interval to the next. We can choose the sign of
, and this sign alternates as we pass from any interval to the next. We can choose the sign of 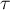 so that
so that ![$\max_{x\in[-1,1]}|f(x)-L(x;\tau)|<d$](https://content.cld.iop.org/journals/1064-5632/79/3/431/revision1/IZV_79_3_431ieqn280.gif) . This contradicts the optimality of
. This contradicts the optimality of  and hence proves the necessity of the existence of an alternance of
and hence proves the necessity of the existence of an alternance of  points.
points.
It remains to consider the case when  . We reduce it to the previous case by complementing the
. We reduce it to the previous case by complementing the  -tuple (defined as above) of the points
-tuple (defined as above) of the points 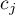 ,
,  , with points
, with points 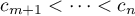 in the interval
in the interval 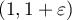 . This proves the necessity of the alternance.
. This proves the necessity of the alternance.
The uniqueness of the best approximation is proved in the same way as Corollary 5 (see §3) with the following difference. If the s. f.  of degree
of degree  with poles outside
with poles outside  and another s. f.
and another s. f. 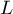 of degree
of degree 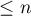 are fractions of least deviation from
are fractions of least deviation from  on
on  , then the existence of an alternance of
, then the existence of an alternance of  points for
points for 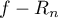 on
on  (which has been just proved) means that the difference
(which has been just proved) means that the difference  has at least
has at least  zeros on
zeros on  (counting multiplicities). More precisely, the sum of the number of simple zeros and twice the number of multiple zeros is not smaller than
(counting multiplicities). More precisely, the sum of the number of simple zeros and twice the number of multiple zeros is not smaller than  (compare [13]). By Theorem 5 we have
(compare [13]). By Theorem 5 we have 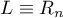 . This completes the proof of Theorem 1.
. This completes the proof of Theorem 1.
§ 6. Proof of Theorem 4
We divide the proof of Theorem 4 into three parts (cases). In the first and second parts we show that the system (3) satisfies the Haar condition on  for
for  and
and  respectively. In the third part we study the general case of the strengthened Haar condition. Note that the Haar condition for
respectively. In the third part we study the general case of the strengthened Haar condition. Note that the Haar condition for  was verified in [14], but we reproduce this proof (that uses the identity (8)) for the sake of completeness.
was verified in [14], but we reproduce this proof (that uses the identity (8)) for the sake of completeness.
It is convenient to prove the Haar condition (a particular case of Theorem 4) in terms of certain determinants. The fixed numbers  will be referred to as poles (not points) in contrast with the variable points
will be referred to as poles (not points) in contrast with the variable points  appearing in the statement of the Haar condition (see §1).
appearing in the statement of the Haar condition (see §1).
Theorem 4'. Suppose that for each of  distinct poles
distinct poles  of the system of functions (3), which are situated symmetrically with respect to the real axis, we are given a number
of the system of functions (3), which are situated symmetrically with respect to the real axis, we are given a number  such that
such that 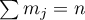 , and conjugate
, and conjugate  correspond to equal
correspond to equal  . If all the poles
. If all the poles  lie outside the disc
lie outside the disc  , then the determinant
, then the determinant
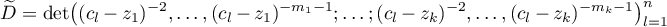
is different from zero for any  distinct points
distinct points  .
.
Case 1 (the main case):  . We denote the
. We denote the  -tuples of the points
-tuples of the points  and poles
and poles  by
by

Since  for all
for all  , the system of functions (3) takes the form
, the system of functions (3) takes the form  , and the Haar condition is written as the inequality
, and the Haar condition is written as the inequality
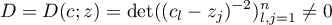
for all  -tuples of distinct points
-tuples of distinct points  on the closed interval
on the closed interval  . To prove this inequality, we use the following identity of Borchardt (1855), which was stated in the monograph [18] on permanents of matrices. (The permanent of a square matrix is the function calculated by the rule of expanding the determinant but taking the sign `plus' of every product of entries independently of the parity of the corresponding permutation.)
. To prove this inequality, we use the following identity of Borchardt (1855), which was stated in the monograph [18] on permanents of matrices. (The permanent of a square matrix is the function calculated by the rule of expanding the determinant but taking the sign `plus' of every product of entries independently of the parity of the corresponding permutation.)
Borchardt's identity. For any disjoint  -tuples
-tuples  and
and 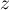 of complex numbers we have
of complex numbers we have

where 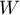 and
and  are the determinant and permanent of the matrix
are the determinant and permanent of the matrix  respectively.
respectively.
The following expansion for the determinant  is known ([10], p. 29):
is known ([10], p. 29):
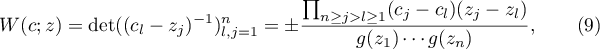
where the sign 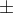 depends only on
depends only on  , and
, and 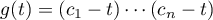 . In our case, the points
. In our case, the points  and the poles
and the poles  are pairwise distinct, whence the factor
are pairwise distinct, whence the factor 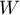 in (8) is different from 0.
in (8) is different from 0.
The inequality  is established in Lemma 2 below. It holds for more general
is established in Lemma 2 below. It holds for more general  -tuples
-tuples  and
and 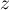 than in the inequality
than in the inequality 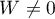 . The lemma will be proved in §7 (compare [14]). Thus we arrive at the desired inequality
. The lemma will be proved in §7 (compare [14]). Thus we arrive at the desired inequality 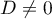 , which expresses the Haar condition for
, which expresses the Haar condition for  distinct poles.
distinct poles.
Lemma 2. The permanent  of the matrix
of the matrix  is non-zero for any
is non-zero for any  -tuple
-tuple  of points in
of points in  (not necessarily distinct) and any
(not necessarily distinct) and any  -tuple
-tuple 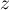 of poles lying outside the disc
of poles lying outside the disc  symmetrically with respect to the real axis (not necessarily distinct).
symmetrically with respect to the real axis (not necessarily distinct).
Case 2 (the general case in Theorem 4'):  . We consider two basic subcases in detail.
. We consider two basic subcases in detail.
Subcase 2.1: a real pole 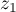 is equipped with a number
is equipped with a number  , and the poles
, and the poles  are equipped with numbers
are equipped with numbers  . (We note that here the number
. (We note that here the number  of distinct poles is equal to
of distinct poles is equal to  since
since 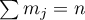 .) The functions in the system (3) take the form
.) The functions in the system (3) take the form
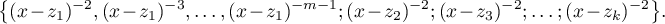
The determinant in the Haar condition is correspondingly written as
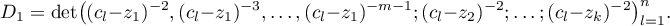
We claim that 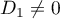 for all pairwise- distinct points
for all pairwise- distinct points  .
.
Indeed, take  pairwise- distinct points
pairwise- distinct points  situated symmetrically with respect to the real axis and satisfying the equalities
situated symmetrically with respect to the real axis and satisfying the equalities  ,
,  , ... ,
, ... , 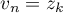 . Using them and the points
. Using them and the points  , we construct an auxiliary determinant
, we construct an auxiliary determinant  , where
, where  . It is easily seen that
. It is easily seen that
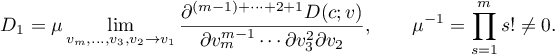
The identity (8) enables us to replace  in this expression by
in this expression by  . We expand the derivative of this product into a sum by Leibniz' formula. Each summand is a multiple of some derivative of
. We expand the derivative of this product into a sum by Leibniz' formula. Each summand is a multiple of some derivative of  . We easily see from the definition of
. We easily see from the definition of  that the limiting values of all relevant derivatives of
that the limiting values of all relevant derivatives of  (except possibly for the highest) are equal to zero because each of these limiting values is a determinant with at least two equal columns. Hence,
(except possibly for the highest) are equal to zero because each of these limiting values is a determinant with at least two equal columns. Hence,
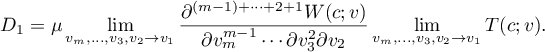
But the limit of the permanent  is different from zero by Lemma 2 (whose hypothesis allows for coincidence of some points inside each of the two
is different from zero by Lemma 2 (whose hypothesis allows for coincidence of some points inside each of the two  -tuples of arguments). It remains to prove that the limit
-tuples of arguments). It remains to prove that the limit 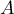 of the derivative of the determinant
of the derivative of the determinant 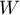 is non-zero. This limit can be written more conveniently as
is non-zero. This limit can be written more conveniently as
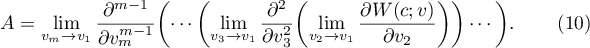
We see from (9) that
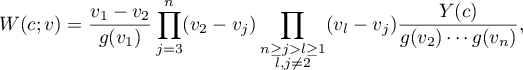
where 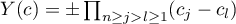 . We find the value of the innermost bracket in the limiting equality (10):
. We find the value of the innermost bracket in the limiting equality (10):
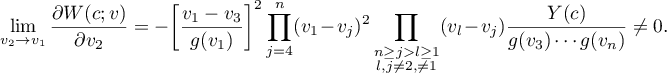
Then we calculate the limit of the second derivative of the resulting expression with respect to 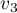 and so on. Each differentiation gives rise to a non-zero quantity since one can easily see that the limit (as
and so on. Each differentiation gives rise to a non-zero quantity since one can easily see that the limit (as 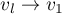 ) of the derivative of order
) of the derivative of order  with respect to
with respect to 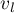 is taken from a function of the form
is taken from a function of the form  , where
, where 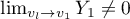 . Hence
. Hence 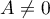 , as required.
, as required.
Thus Theorem 4' holds under the hypotheses of Subcase 2.1.
Subcase 2.2: complex-conjugate poles 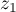 and
and  are equipped with equal numbers
are equipped with equal numbers  , and the remaining poles
, and the remaining poles  are equipped with numbers
are equipped with numbers  . Here
. Here 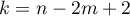 . As above, we denote the determinant in the Haar condition for the corresponding system of functions by
. As above, we denote the determinant in the Haar condition for the corresponding system of functions by  and consider an auxiliary determinant
and consider an auxiliary determinant  with pairwise- distinct points
with pairwise- distinct points  situated symmetrically with respect to the real axis and satisfying the equalities
situated symmetrically with respect to the real axis and satisfying the equalities  ,
,  ,
,  ,
,  , ... ,
, ... , 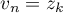 . Note that the determinant
. Note that the determinant  coincides (up to a non-zero factor
coincides (up to a non-zero factor  ) with the limit
) with the limit
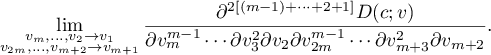
Using (8), (9) and Lemma 2, we now see that 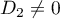 .
.
Thus Theorem 4' holds under the hypotheses of Subcase 2.2. In the general case 2, the theorem is proved by successive application of the scheme used in the two basic subcases to each pole with 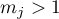 . This completes the proof of Theorem 4'.
. This completes the proof of Theorem 4'.
Case 3 (the general case of Theorem 4). Here the polynomial in the system of functions (3) may have multiple zeros. Consider the homogeneous system of equations for the coefficients  obtained from (7) in view of the multiple interpolation conditions (4). It suffices to verify that the determinant
obtained from (7) in view of the multiple interpolation conditions (4). It suffices to verify that the determinant  of this system is non-zero. We easily see that
of this system is non-zero. We easily see that  is equal to the limit of a certain derivative of the determinant
is equal to the limit of a certain derivative of the determinant  (see the statement of Theorem 4') with respect to the variables
(see the statement of Theorem 4') with respect to the variables  . For example, if the nodes
. For example, if the nodes  in the conditions (4) are simple and the node
in the conditions (4) are simple and the node  is double, then
is double, then 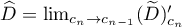 . Arguing as above, we see that
. Arguing as above, we see that  . This proves Theorem 4 (the strengthened Haar condition).
. This proves Theorem 4 (the strengthened Haar condition).
§ 7. Proof of Lemma 2
Here we reproduce the corresponding proof from [14] almost verbatim. As in [14], we only consider the case when ![$S=[-1,1]$](https://content.cld.iop.org/journals/1064-5632/79/3/431/revision1/IZV_79_3_431ieqn246.gif) . Let
. Let  be the number of those real numbers
be the number of those real numbers  that are smaller than
that are smaller than  (if some of the
(if some of the  coincide, then we count each of them).
coincide, then we count each of them).
When all the numbers  are real, the signs of all summands in the expansion of
are real, the signs of all summands in the expansion of  are equal to
are equal to  and, therefore,
and, therefore,  (this was observed in [11]).
(this was observed in [11]).
Suppose that there is at least one pair of complex- conjugate numbers  . Reorder the
. Reorder the  in such a way that their list begins with all pairs of complex- conjugate numbers and ends with real numbers. Take
in such a way that their list begins with all pairs of complex- conjugate numbers and ends with real numbers. Take 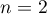 . Under our assumptions we have
. Under our assumptions we have  ,
, 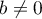 , and the numbers
, and the numbers  and
and 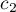 range over
range over ![$[-1,1]$](https://content.cld.iop.org/journals/1064-5632/79/3/431/revision1/IZV_79_3_431ieqn45.gif) . We calculate the permanent
. We calculate the permanent  directly:
directly:

Since  , it follows that the inequality
, it follows that the inequality  holds for all
holds for all  ,
, 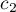 in
in ![$[-1,1]$](https://content.cld.iop.org/journals/1064-5632/79/3/431/revision1/IZV_79_3_431ieqn45.gif) if and only if
if and only if
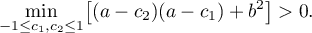
We easily see that the minimum is attained at the points  and is equal to
and is equal to  . Under the hypotheses of the lemma with
. Under the hypotheses of the lemma with ![$S=[-1,1]$](https://content.cld.iop.org/journals/1064-5632/79/3/431/revision1/IZV_79_3_431ieqn246.gif) we have
we have 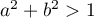 (the points
(the points 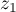 and
and  lie outside the closed unit disc). Therefore
lie outside the closed unit disc). Therefore 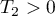 . This proves the lemma for
. This proves the lemma for 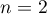 .
.
We now suppose that 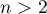 . The determinant
. The determinant  can be written by Laplace's theorem (see, for example, [24], p. 129) in the form
can be written by Laplace's theorem (see, for example, [24], p. 129) in the form
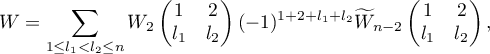
where  is the minor of order 2 formed by the entries of
is the minor of order 2 formed by the entries of  situated at the intersection of the first and second columns and
situated at the intersection of the first and second columns and  th and
th and  th rows, and
th rows, and  is the complementary minor of order
is the complementary minor of order 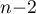 . Thus, by the definition of the permanent, we have
. Thus, by the definition of the permanent, we have
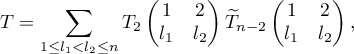
where 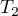 and
and  are the permanents of those submatrices whose determinants are equal to
are the permanents of those submatrices whose determinants are equal to  and
and  respectively.
respectively.
We claim that in our situation all the products  have the same sign
have the same sign  and, therefore, the sum
and, therefore, the sum  is non-zero. Indeed, by what was said above, we have
is non-zero. Indeed, by what was said above, we have
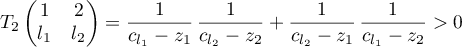
for all ![$c_{l_1},c_{l_2}\in [-1,1]$](https://content.cld.iop.org/journals/1064-5632/79/3/431/revision1/IZV_79_3_431ieqn364.gif) . Therefore the sign of the product
. Therefore the sign of the product 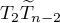 is equal to the sign of
is equal to the sign of  . If all
. If all  are real except for
are real except for 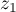 and
and  , then we have seen that
, then we have seen that  . If
. If 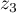 ,
,  is the next pair of complex- conjugate poles, then the previous argument works for the permanent
is the next pair of complex- conjugate poles, then the previous argument works for the permanent  . After several iterations, factoring out only positive factors at every step, we exhaust all pairs of complex- conjugate
. After several iterations, factoring out only positive factors at every step, we exhaust all pairs of complex- conjugate  . Hence only sums with real
. Hence only sums with real  remain, and the total sign is
remain, and the total sign is  . The lemma is proved.
. The lemma is proved.
Footnotes
- 1
We recall that points
 of
of  form a Chebyshev alternance (in what follows, simply an alternance) on
form a Chebyshev alternance (in what follows, simply an alternance) on  for the difference of two continuous functions
for the difference of two continuous functions  and
and  if
if  ,
,  , where
, where  .
.






