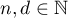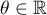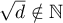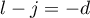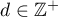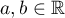Abstract
Using a new integral construction combining the idea of symmetry suggested by the second author in 2007 and the integral introduced by Marcovecchio in 2009, we obtain a new bound for the approximation of 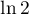 by numbers in the field
by numbers in the field 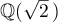 .
.
Export citation and abstract BibTeX RIS
| The research was partially supported by the Russian Foundation for Basic Research (project no. 12-01-00171). |
§ 1. Introduction. Integral construction. Arithmetic part
The object of this paper is to prove the following result.
Theorem 1. Let  ,
, 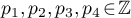 ,
, 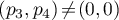 ,
, 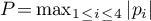 , and
, and 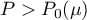 . Then the following inequality holds:
. Then the following inequality holds:
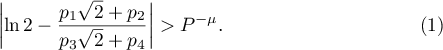
A similar bound for 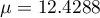 was obtained in [1], and this result was improved in [2]; the corresponding value of
was obtained in [1], and this result was improved in [2]; the corresponding value of  was
was  .
.
The derivation of the new bound (1) is related to an application of the following integral construction. Let  ,
,  ,
,  ,
,  and
and 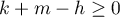 . Let
. Let 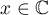 ,
, 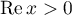 and
and 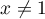 . Consider the integral
. Consider the integral
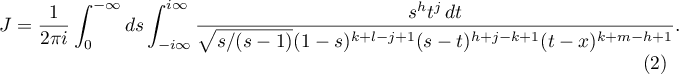
The result in Theorem 1 is obtained by taking

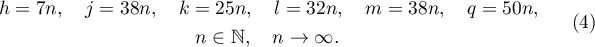
The integral (2) differs from the integral introduced by Marcovecchio in [3], p. 148, formula (5), only by the factor 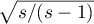 in the denominator of the integrand. The integral (2) was considered for the first time in [4]. To make the picture complete, we describe a brief scheme of some transformations of this integral (see [4], Russian pp. 484, 485). We denote the integrand of (2) by
in the denominator of the integrand. The integral (2) was considered for the first time in [4]. To make the picture complete, we describe a brief scheme of some transformations of this integral (see [4], Russian pp. 484, 485). We denote the integrand of (2) by  . Then
. Then

Evaluating the residue in (5) and making the change 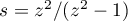 in the integral with respect to the variable
in the integral with respect to the variable  , we obtain the relation
, we obtain the relation
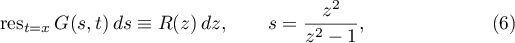
where
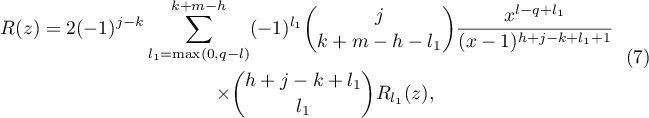

By choosing for 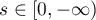 a value
a value 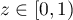 , we see from (5) and (6) that
, we see from (5) and (6) that

We write
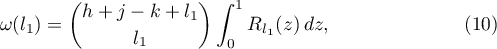
let  be the ring of numbers of the form
be the ring of numbers of the form 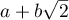 , where
, where 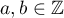 , and for positive integers
, and for positive integers  write
write 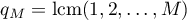 with
with 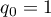 .
.
Lemma 1. Let 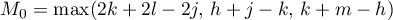 ,
,  . Then the following representation holds for all
. Then the following representation holds for all 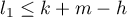 :
:
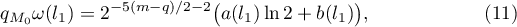
where the 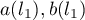 belong to
belong to 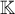 .
.
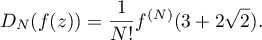
Since the integrand (8) of the integral in (10) is even, we have the following expansion into a sum of simplest fractions:
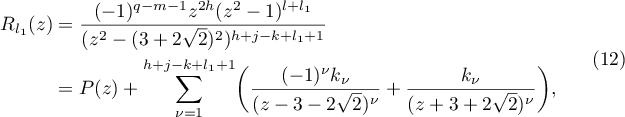
where ![$P(z)\in\mathbb{K}[z]$](https://content.cld.iop.org/journals/1064-5632/82/3/549/revision1/IZV_82_3_549ieqn39.gif) ,
, 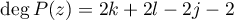 , and, moreover,
, and, moreover,
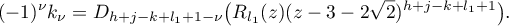
By Leibniz' formula, we see from (12) that
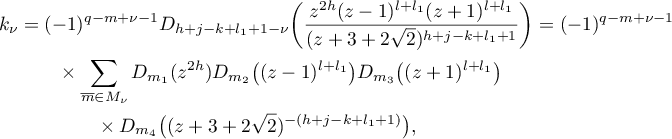
where
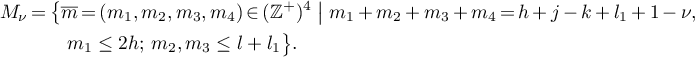
Therefore,
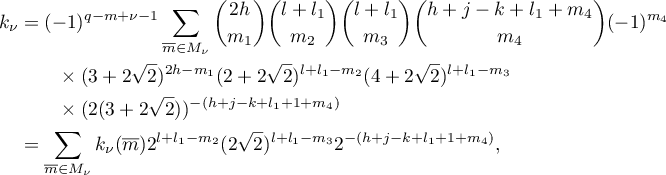
where the 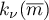 belong to
belong to 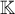 .
.
However, 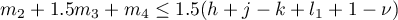 . Hence,
. Hence,
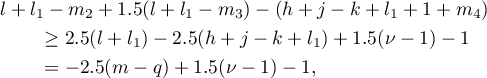
that is,
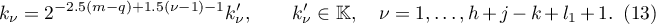
By (12), we have
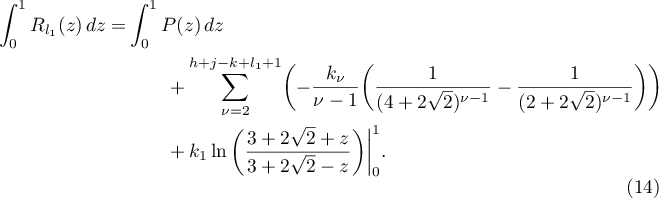
Obviously,
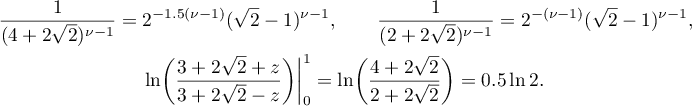
Further, it follows from the definition of  that
that 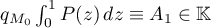 . It can also readily be seen that
. It can also readily be seen that
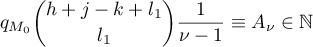
for all  . Then it follows from (13) and (14) that
. Then it follows from (13) and (14) that
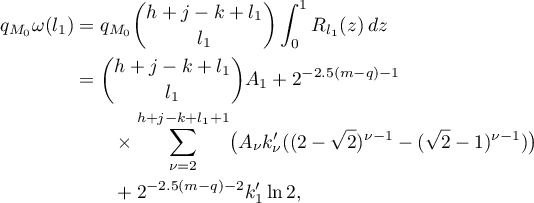
whence, since  , (11) follows.
, (11) follows. 
Corollary 1. The integral (2) admits the following representation for  :
:
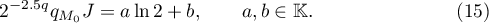
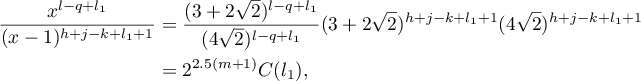
where 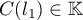 . Applying Lemma 1, we see from (7) and (9) that
. Applying Lemma 1, we see from (7) and (9) that
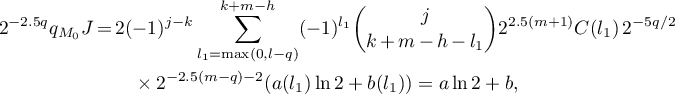
where 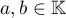 , and this proves Corollary 1.
, and this proves Corollary 1. 
Along with the family of parameters (4), we shall use a more general situation in which
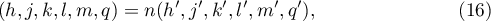
where 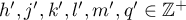 . It is convenient to denote the integral (2) for parameters of the form (16) and for
. It is convenient to denote the integral (2) for parameters of the form (16) and for  of the form (3) as follows:
of the form (3) as follows:
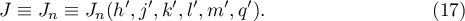
For the family of parameters (16) we write
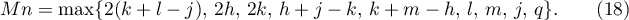
Let 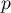 be a prime,
be a prime, 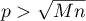 , and
, and 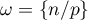 the fractional part of the number
the fractional part of the number 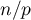 . Consider the inequalities
. Consider the inequalities
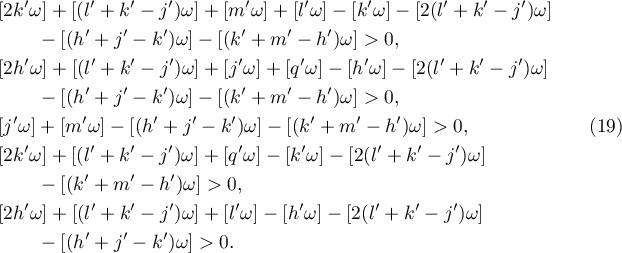
We denote by 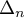 the product of all primes
the product of all primes 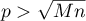 such that
such that 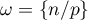 satisfies at least one of the inequalities (19). The following lemma sharpens the result obtained in Corollary 1.
satisfies at least one of the inequalities (19). The following lemma sharpens the result obtained in Corollary 1.
Lemma 2. When  the integral (17) admits the representation
the integral (17) admits the representation
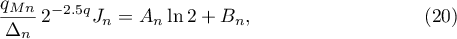
where 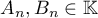 ,
, 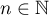 .
.
Proof. The representation (20) follows from (15) by the standard procedure of refining the denominator (see, for example, Lemma 3 in [6]). The inequalities (19) were obtained for the integral (2) for the first time in [4], Russian p. 491, inequalities (11). The inequalities (19) differ somewhat from those considered, for the same purpose, by Marcovecchio in [3], inequalities (31). 
The following lemma contains the final version of a linear form of the form (20) which we shall use to prove Theorem 1.
Lemma 3. The following representation holds ( see (17)):
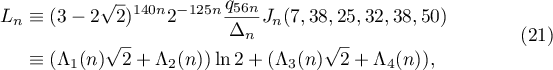
where the 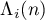 belong to
belong to 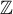 and
and 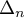 is defined by the inequalities (19) for the family of parameters (4).
is defined by the inequalities (19) for the family of parameters (4).
Proof. It was proved in [4], equation (10), that the equation  holds (see (17)), that is,
holds (see (17)), that is,
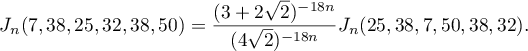
For the family of parameters (4) we have from (18) that
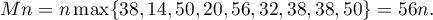
However, then
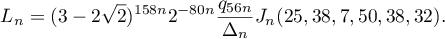
By Lemma 2,

where 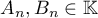 , which implies (21).
, which implies (21). 
We conclude §1 by proving the following important lemma.
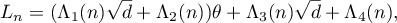
where the 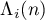 belong to
belong to 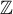 , and let
, and let 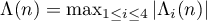 . Let
. Let
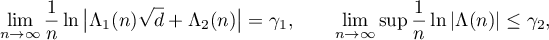
and for some constant 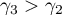 and every
and every 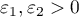 let there be an
let there be an 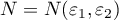 such that the following inequalities hold for every
such that the following inequalities hold for every 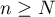 and at least one of the values
and at least one of the values 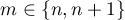 :
:
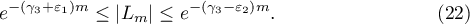
Further, let 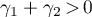 ,
, 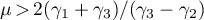 ,
, 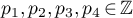 ,
, 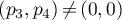 ,
,  and
and 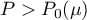 . Then
. Then
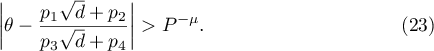
Proof. We fix a 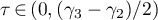 such that
such that 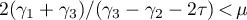 and write
and write
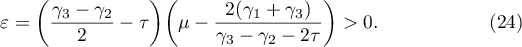
Let us choose 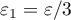 ,
, 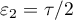 ,
, 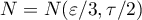 in the inequalities (22). We introduce an
in the inequalities (22). We introduce an 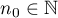 , where
, where 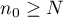 and the following family of conditions holds: for all
and the following family of conditions holds: for all 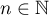 ,
, 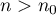 ,
,



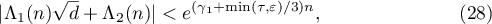



Let  and
and 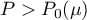 . We define
. We define 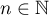 ,
, 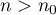 , by the inequalities
, by the inequalities
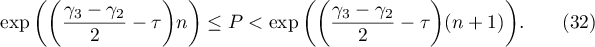
Then the inequalities (22) hold for at least one of the values 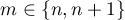 . We write (see (25))
. We write (see (25))
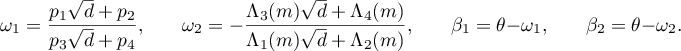
Let us first consider the case in which the inequalities (22) hold for 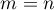 . Two situations are possible:
. Two situations are possible: 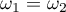 ,
, 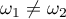 .
.
1) Let 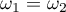 . We have
. We have
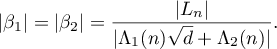
We have 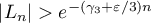 by (22), and
by (22), and 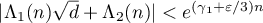 by (28). Hence, by (32), the condition
by (28). Hence, by (32), the condition 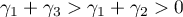 and the inequality (24) yield that
and the inequality (24) yield that
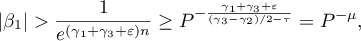
which coincides with the inequality (23).
2) Let 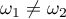 . We consider
. We consider
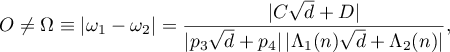
where
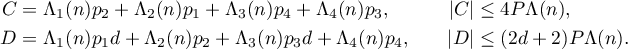
Obviously,
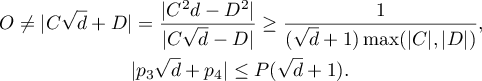
Therefore,

We claim that
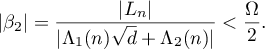
By the inequality (33), it suffices to prove that
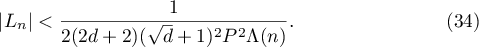
Applying the inequalities (22), (26), (32), (27) and (29), we obtain that
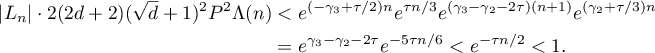
This proves the inequality (34), and therefore 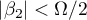 . However,
. However, 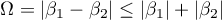 . Hence,
. Hence, 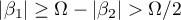 . Using the inequalities (33), (26), (27), (28) and (32) in succession and taking into account that
. Using the inequalities (33), (26), (27), (28) and (32) in succession and taking into account that 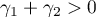 , we have
, we have
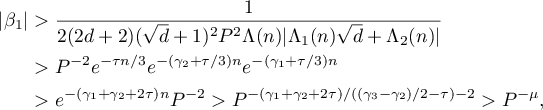
which coincides with the inequality (23).
Let us now consider the case in which the inequalities (22) hold for 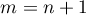 . Again, two situations are possible:
. Again, two situations are possible: 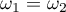 ,
, 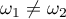 .
.
3) Let 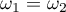 . As in part 1), we have
. As in part 1), we have

Applying the inequalities (22), (28) and (30), we obtain that

4) Let 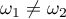 . The arguments here are similar to that in part 2), where
. The arguments here are similar to that in part 2), where 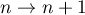 , in particular, in the inequalities (33) and (34). Applying the inequalities (22), (26), (32) and (27), we obtain that
, in particular, in the inequalities (33) and (34). Applying the inequalities (22), (26), (32) and (27), we obtain that
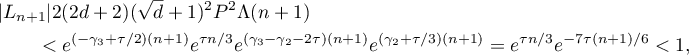
which proves the inequality (34) with 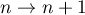 , and simultaneously the inequality
, and simultaneously the inequality 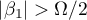 . Then, applying the inequalities (26), (27), (28), (31) and (32) in succession, we obtain
. Then, applying the inequalities (26), (27), (28), (31) and (32) in succession, we obtain
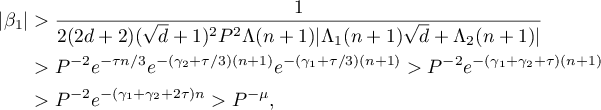
which coincides with the inequality (23).
This completes the proof of the lemma. 
Remark 1. Assertions similar to Lemma 4 were used in [1], [2] and [5].
§ 2. Asymptotics
To prove Theorem 1, we shall apply Lemma 4 to the linear form (21). We need to evaluate the constants 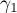 ,
,  and
and  . In this section, we evaluate
. In this section, we evaluate 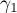 and
and  and, in the next section, the constant
and, in the next section, the constant  . To evaluate both the constants
. To evaluate both the constants 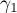 and
and  , we apply the saddle-point method. We have (see (17) and (21))
, we apply the saddle-point method. We have (see (17) and (21))
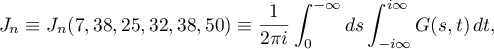
where
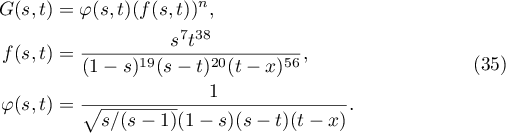
The saddle points are the solutions of the system 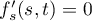 ,
, 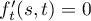 that differ from the zeros of the function
that differ from the zeros of the function  . In [4], Russian p. 492, equations (12), this system was solved in the general case for the integral (17). For the function
. In [4], Russian p. 492, equations (12), this system was solved in the general case for the integral (17). For the function  written above we have three saddle points:
written above we have three saddle points:
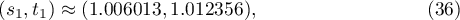
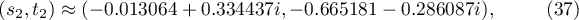
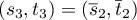 , the complex conjugate of
, the complex conjugate of  . We write
. We write 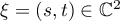 .
.
Lemma 5. Let 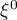 be a non-degenerate saddle point of the function
be a non-degenerate saddle point of the function  , let
, let 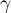 be a two-dimensional smooth complex manifold with boundary, let
be a two-dimensional smooth complex manifold with boundary, let 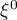 be an interior point of
be an interior point of 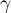 , let the functions
, let the functions 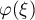 and
and  be holomorphic at the point
be holomorphic at the point 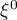 , and let also
, and let also 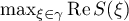 be attained only at the point
be attained only at the point 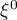 , let
, let
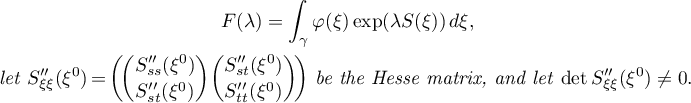
Then, as  ,
,
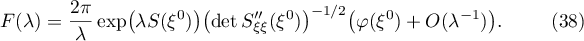
Proof. This assertion is proved in the Fedoryuk's monograph [7], p. 259, Proposition 1.1. 
Lemma 6. For the linear form (21) we have the equation
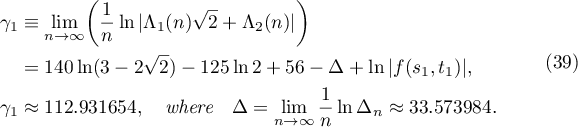
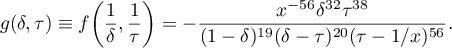
Let 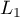 be the circle
be the circle 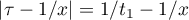 and
and  the circle
the circle 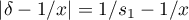 . We note that, by (3) and (36), we have
. We note that, by (3) and (36), we have 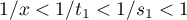 . Obviously,
. Obviously, 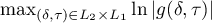 is attained only at the point
is attained only at the point  . We denote by
. We denote by 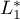 the image of the circle
the image of the circle 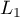 under the map
under the map 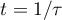 and by
and by  the image of the circle
the image of the circle  under the map
under the map  . Then it follows from the definition of the function
. Then it follows from the definition of the function  that
that 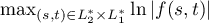 is attained only at the point
is attained only at the point 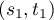 . For the integral
. For the integral 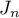 , by (35), we have
, by (35), we have

where 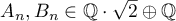 (see Corollary 1).
(see Corollary 1).
We claim that
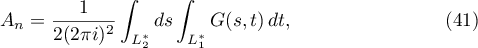
where the circles 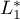 and
and  are traversed in the positive direction. Equations of the form (41) are standard and occur in many papers, for example, in [3] and [8].
are traversed in the positive direction. Equations of the form (41) are standard and occur in many papers, for example, in [3] and [8].
In the proof of Lemma 1, for the integral in (10) we have, by (12) and (14)
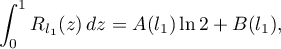
where 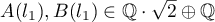 ,
,  and
and 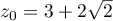 , and then it follows from (7), (9) and (40) that
, and then it follows from (7), (9) and (40) that 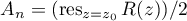 . Applying (6), we obtain
. Applying (6), we obtain
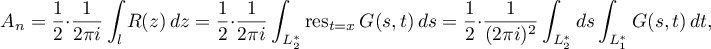
where 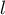 stands for the contour going around the point
stands for the contour going around the point  in the positive direction and mapping onto the circle
in the positive direction and mapping onto the circle  under the map
under the map 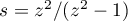 . Thus, the formula (41) is proved.
. Thus, the formula (41) is proved.
Let 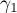 be a small arc of the circle
be a small arc of the circle 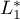 with centre at the point
with centre at the point  , let
, let  be a small arc of the circle
be a small arc of the circle  with centre at the point
with centre at the point 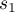 , let
, let 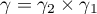 , let
, let 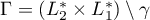 ; let
; let 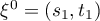 , and let
, and let  . We can define some branch
. We can define some branch 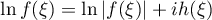 on
on  holomorphic at the point
holomorphic at the point 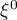 .
.
It follows from (35) and (36) that 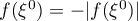 , and therefore one can choose
, and therefore one can choose  . Further, the function
. Further, the function 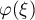 is holomorphic at the point
is holomorphic at the point 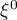 since
since  ,
,  . Obviously,
. Obviously, 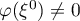 . By (41) we have
. By (41) we have

We apply Lemma 5 to the first integral in (42) with 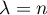 and
and 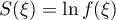 . The conditions of Lemma 5 are satisfied, since the remaining non-degeneracy condition for the saddle point
. The conditions of Lemma 5 are satisfied, since the remaining non-degeneracy condition for the saddle point 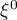 can readily be verified:
can readily be verified: 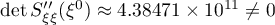 . Then by (38) we obtain
. Then by (38) we obtain
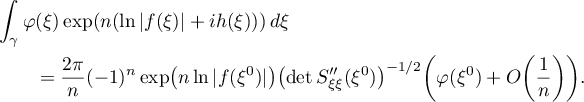
We estimate the second integral in (42) trivially:
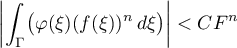
for some positive constant 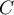 . Then
. Then 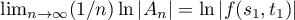 .
.
To complete the proof of the lemma, it remains to evaluate the limit
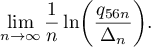
We note that 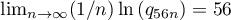 and evaluate
and evaluate 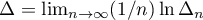 . Let us write out the inequalities (19) for the family of parameters (4):
. Let us write out the inequalities (19) for the family of parameters (4):
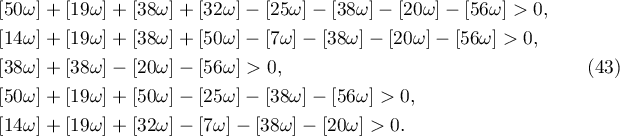
The set  of numbers
of numbers 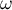 satisfying at least one of the inequalities (43) has the form
satisfying at least one of the inequalities (43) has the form

Let 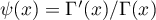 , where
, where  stands for the gamma function. Then, in the standard way (see Lemma 6 in [9]), we obtain
stands for the gamma function. Then, in the standard way (see Lemma 6 in [9]), we obtain
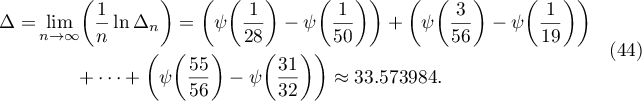
This completes the proof of the lemma. 
Lemma 7. For the linear form (21) let
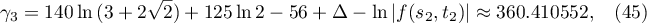
where the function 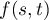 is defined in (35), the point
is defined in (35), the point  is of the form (37), and
is of the form (37), and 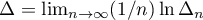 is evaluated in (44).
is evaluated in (44).
Futher, let 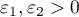 . Then there is an
. Then there is an  ,
, 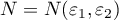 , such that the following inequalities hold for all
, such that the following inequalities hold for all 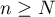 and for at least one of the values
and for at least one of the values 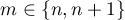 :
:
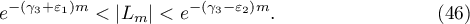
Proof. Let 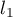 be a ray, in the complex plane
be a ray, in the complex plane  , which issues from zero and passes through the point
, which issues from zero and passes through the point  and let
and let 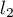 be an analogous ray, in the plane
be an analogous ray, in the plane 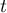 , which passes through the point
, which passes through the point 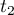 . By (35), we have
. By (35), we have
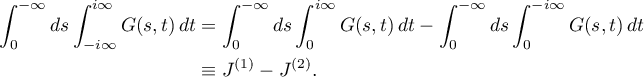
Let 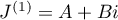 . Then
. Then  , that is,
, that is, 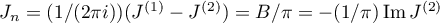 . Let us move the integration with respect to
. Let us move the integration with respect to  in the integral
in the integral 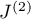 :
: 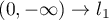 , and let us similarly move the integration with respect to the variable
, and let us similarly move the integration with respect to the variable 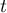 :
: 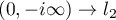 . Since there are no singular points of the integrand in the domains between the indicated rays, it follows that
. Since there are no singular points of the integrand in the domains between the indicated rays, it follows that 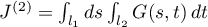 . Hence,
. Hence,

As in Lemma 6, we write  and
and 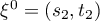 .
.
Simple computer calculations show that 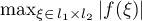 is attained only at the point
is attained only at the point 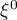 . Let
. Let 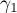 be a small segment of
be a small segment of 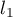 containing
containing  as an interior point, let
as an interior point, let  be a similar segment of
be a similar segment of 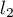 containing
containing 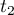 as an interior point, and let
as an interior point, and let 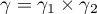 ,
, 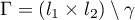 and
and  .
.
As in Lemma 6, one can apply Lemma 5 to the integral  , since
, since
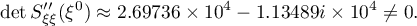
In our situation, the equation (38) becomes
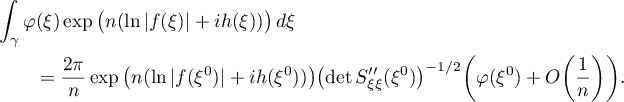
We have 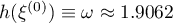 . Let
. Let 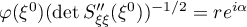 ,
, 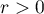 . Then (see (47))
. Then (see (47))

Obviously,
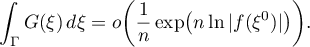
Let us write 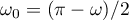 . We claim that for every
. We claim that for every 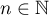
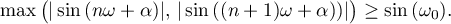
Indeed, let 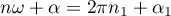 ,
, 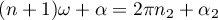 , where
, where 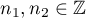 ,
, 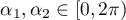 . If
. If 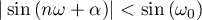 , then
, then
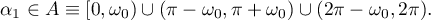
In this case, 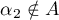 , that is,
, that is, 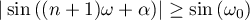 . Let
. Let 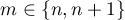 be the value for which
be the value for which 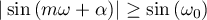 . We choose
. We choose 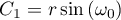 and
and 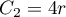 . Then for
. Then for 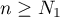 , we obtain from (17) that the integral
, we obtain from (17) that the integral 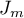 has the bounds
has the bounds
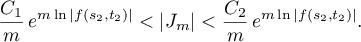
Since 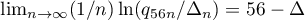 , it follows that for all
, it follows that for all 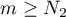 we have
we have
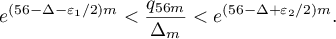
Let 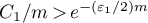 ,
, 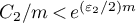 and
and 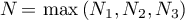 for all
for all 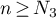 . Then, by (21), for
. Then, by (21), for 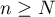 we have
we have
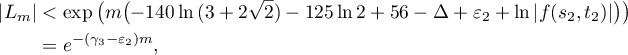
and similarly 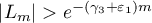 . This completes the proof of the lemma.
. This completes the proof of the lemma. 
§ 3. Evaluation of the constant  . Completion of the proof of Theorem 1
. Completion of the proof of Theorem 1
For the integral (2) we consider the function
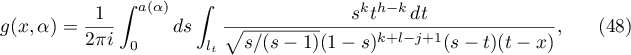
where  ,
, 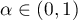 ,
,  is the circle in the complex plane
is the circle in the complex plane 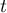 whose diameter is the segment
whose diameter is the segment ![$[{x}/{2},2x]$](https://content.cld.iop.org/journals/1064-5632/82/3/549/revision1/IZV_82_3_549ieqn208.gif) on the real line, and the integration with respect to
on the real line, and the integration with respect to  is carried out in the negative direction.
is carried out in the negative direction.
In this section, we write
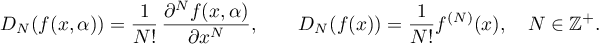
In the following lemma we establish a relationship between the function 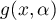 and the integral (2).
and the integral (2).
Lemma 8. The integral (2) and the function (48) satisfy the relation

where 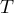 is the operator
is the operator  .
.
Proof. By (48), we obtain in the standard way (see, for example, [3], pp. 167–169) that
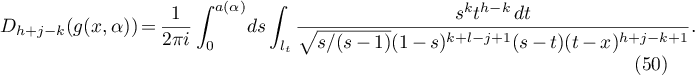
In (50) we make the change of variables 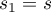 ,
, 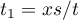 . For all
. For all 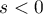 we obtain the integration with respect to the variable
we obtain the integration with respect to the variable  in the negative direction over the circle
in the negative direction over the circle 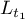 whose diameter is the segment
whose diameter is the segment ![$[2s,{s}/{2}]$](https://content.cld.iop.org/journals/1064-5632/82/3/549/revision1/IZV_82_3_549ieqn216.gif) . Further,
. Further,  ,
, 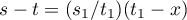 and
and 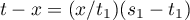 . Therefore,
. Therefore,
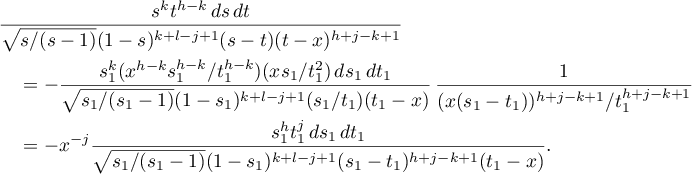
The formula (50) becomes
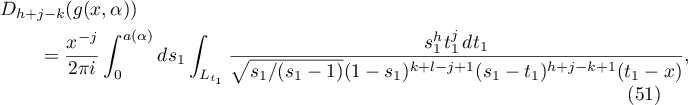
where the integration over 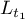 is carried out in the positive direction.
is carried out in the positive direction.
Let us multiply both the sides of the identity (51) by 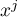 and apply the operator
and apply the operator 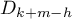 to both sides. One can now replace the integration over
to both sides. One can now replace the integration over 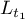 by integration over the line
by integration over the line 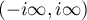 since both integrals are equal to
since both integrals are equal to 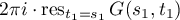 . Finally, passing to the limit as
. Finally, passing to the limit as 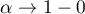 , we obtain the identity (49).
, we obtain the identity (49). 
Our next task is to evaluate the function 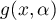 .
.
Lemma 9. The function (48) satisfies the relation
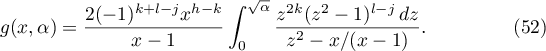
Proof. We evaluate the inner integral in (48) using Cauchy's residue theorem:
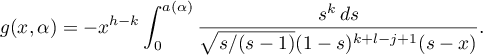
Let us make the change 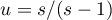 in the integral thus obtained. Setting
in the integral thus obtained. Setting  ,
,  ,
, 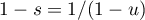 and
and ![$u\in[0, \alpha]$](https://content.cld.iop.org/journals/1064-5632/82/3/549/revision1/IZV_82_3_549ieqn229.gif) , we obtain
, we obtain
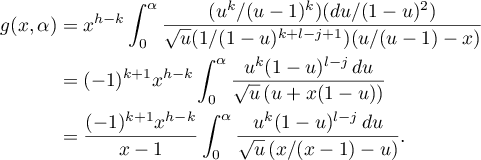
Finally, let us make the change  ,
, ![$z\in[0, \sqrt{\alpha}\,]$](https://content.cld.iop.org/journals/1064-5632/82/3/549/revision1/IZV_82_3_549ieqn231.gif) . We have
. We have
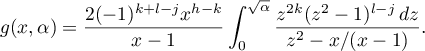
This completes the proof of the lemma. 
The following lemma gives a representation of the integral (2) in a form convenient for the evaluation of the constant  . We restrict ourselves to the case
. We restrict ourselves to the case  , which holds for the family (4) of parameters.
, which holds for the family (4) of parameters.
Lemma 10. Let  . Then the integral (2) satisfies the relation
. Then the integral (2) satisfies the relation
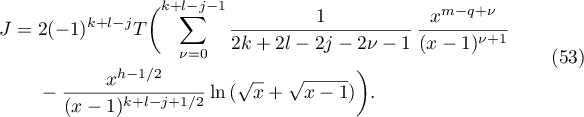
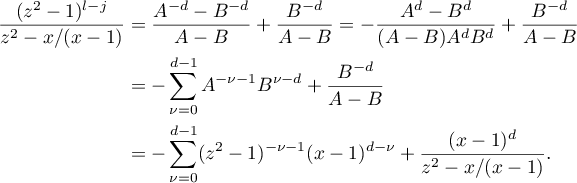
Further,
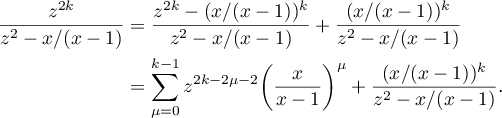
Therefore,
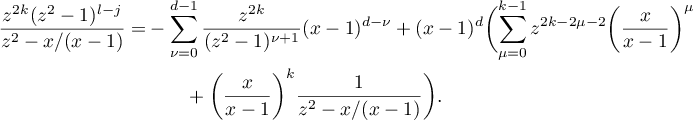
Hence, it follows from (52) that
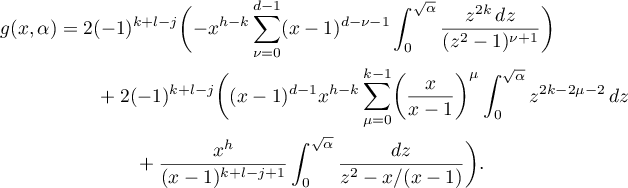
By (49), we have
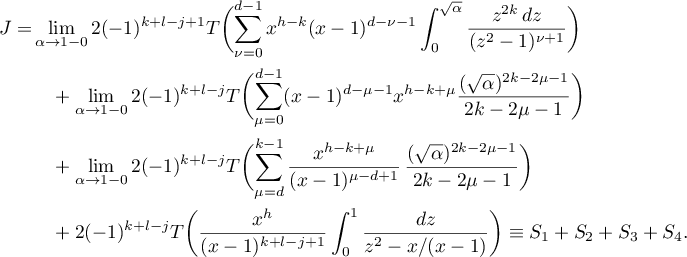
We claim that 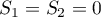 . Consider the sum
. Consider the sum 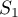 . For all
. For all 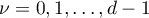 , we obtain from Leibniz' formula that
, we obtain from Leibniz' formula that
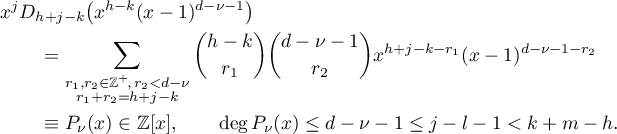
Therefore, 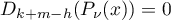 . Hence,
. Hence, 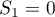 . Similarly,
. Similarly, 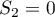 . Further, in the sum
. Further, in the sum 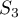 we set
we set 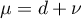 ,
, 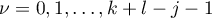 . Then
. Then

Finally,
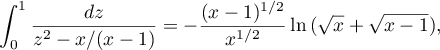
that is,
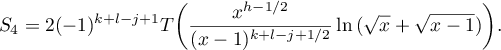
We have  , which coincides with the assertion of the lemma.
, which coincides with the assertion of the lemma. 
To evaluate the integral (2) by applying the formula (53), two more lemmas will be useful.
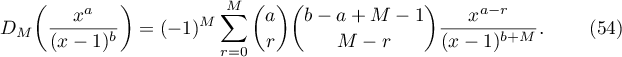
Proof. We proceed by induction on  . When
. When 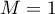 we have
we have
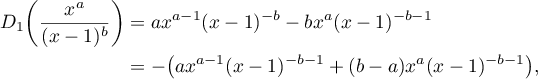
which coincides with (54) when 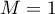 .
.
Let us make the induction step 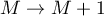 . Using the induction assumption, we obtain
. Using the induction assumption, we obtain
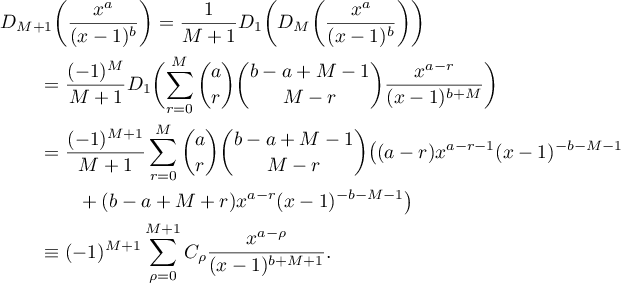
We write
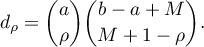
We need to prove that  for all
for all  .
.
The following equation holds:
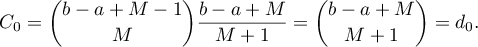
Further,
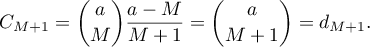
Finally, when ![$\rho\in[1, M]$](https://content.cld.iop.org/journals/1064-5632/82/3/549/revision1/IZV_82_3_549ieqn253.gif) we need to show that
we need to show that
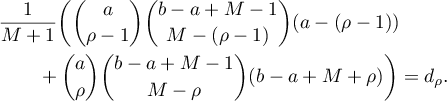
Consider two cases.
1. Let  . Here
. Here
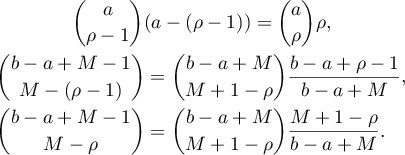
Therefore,
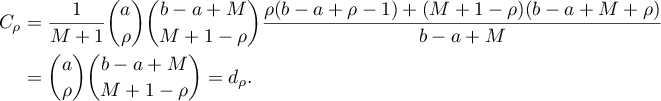
2. Let 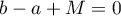 . Here
. Here
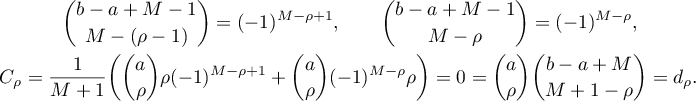
This completes the proof of the lemma. 
Lemma 12. The following equation holds for every  and for arbitrary analytic functions
and for arbitrary analytic functions 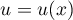 and
and 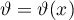 :
:

Proof. By the definition of the operator 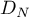 , it suffices to show that
, it suffices to show that
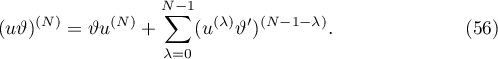
In turn, to prove the formula (56), it suffices to prove that the coefficients of 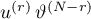 ,
, 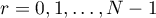 , on both the sides of the equation (56) coincide, that is,
, on both the sides of the equation (56) coincide, that is,
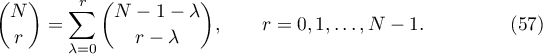
We shall prove this by induction on 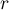 . When
. When 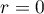 we have
we have
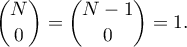
To carry out the induction step 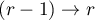 , note that
, note that
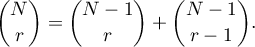
By the induction assumption,
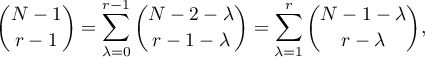
and then the equation (57) holds. 
In what follows, it is useful to note the asymptotics of generalized binomial coefficients:
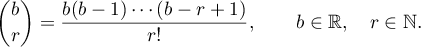
For  we introduce the function
we introduce the function
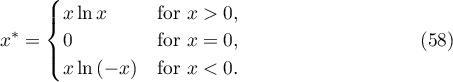
Obviously, the function 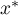 is odd.
is odd.
Lemma 13. Let 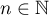 ,
,  ,
, 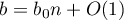 ,
, 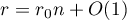 ,
, 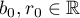 ,
,  and
and 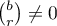 . Then the following equation holds:
. Then the following equation holds:
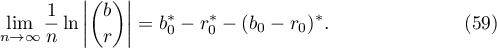
Proof. It is clear that 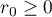 . If
. If 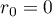 , then
, then
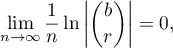
and the formula (59) holds. Let 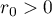 everywhere below. We consider several cases.
everywhere below. We consider several cases.
1) Let 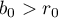 . The following formula holds:
. The following formula holds:

It follows from Stirling's formula that  as
as  . Taking into account that
. Taking into account that 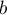 ,
,  ,
, 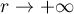 as
as  , we obtain
, we obtain
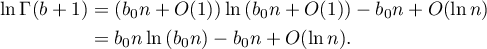
Similar formulae hold for 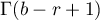 and
and  . Therefore,
. Therefore,
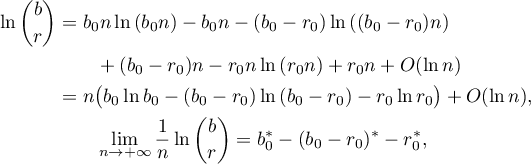
and the formula (59) is proved in the case under consideration.
2) Let 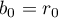 . Here
. Here
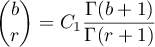
for some constant 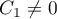 , and the formula (59) is verified trivially.
, and the formula (59) is verified trivially.
3) Let  . In this case,
. In this case,
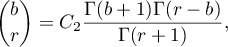
where, as above, the constant 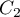 is non-zero,
is non-zero,
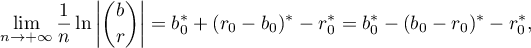
and we have used the fact that the function (58) is odd.
4) Let 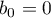 . As in cases 2) and 3), the following equation holds:
. As in cases 2) and 3), the following equation holds:
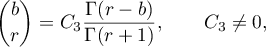
that is,
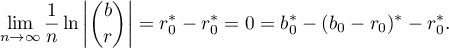
The last case remains.
5) Let 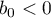 . Here
. Here
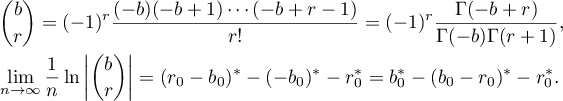
This completes the proof of the lemma. 
Let us apply the results thus obtained to the linear form (21). We first evaluate the integral 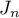 in (35) using the formula (53):
in (35) using the formula (53):
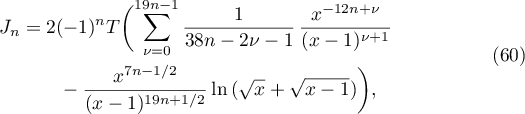
where 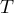 stands for the operator
stands for the operator 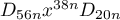 .
.
We write  and
and
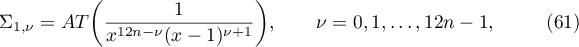
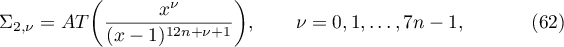
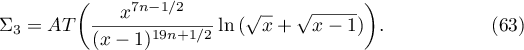
Then it follows from (21) and (60)–(63) that
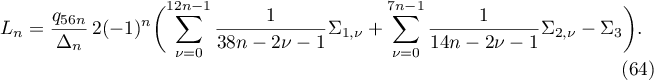
Let us combine the evaluation of the operators 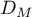 by the ordinary Leibniz formula and by the formula (54). In the latter case, we denote the operator
by the ordinary Leibniz formula and by the formula (54). In the latter case, we denote the operator 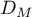 by
by 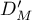 .
.
Let us begin with the evaluation of  . We have
. We have
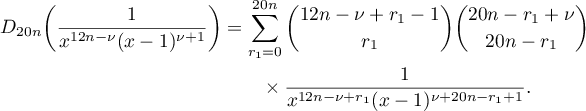
By Lemma 11,
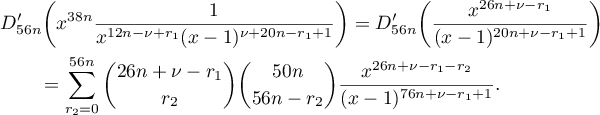
Non-zero summands occur in the last sum only when ![$r_2\in[6n, 26n+\nu-r_1]$](https://content.cld.iop.org/journals/1064-5632/82/3/549/revision1/IZV_82_3_549ieqn294.gif) . Further, it follows from (3) that
. Further, it follows from (3) that

Therefore, it follows from (61) for  that
that

Let us now evaluate  for
for 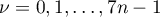 . We write
. We write
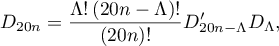
where 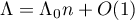 ,
,  , will be chosen below to optimize the bound for
, will be chosen below to optimize the bound for  .
.
We have
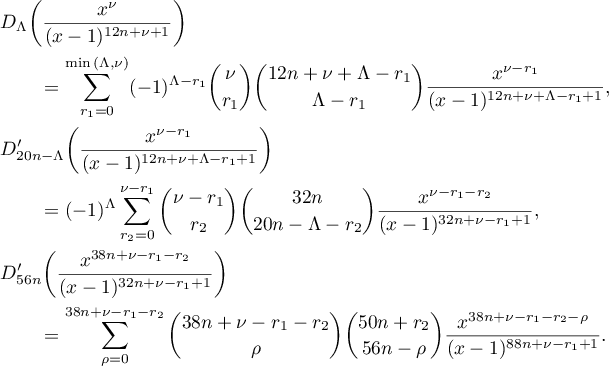
As in the evaluation of  , we have
, we have
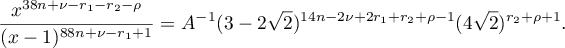
Therefore, it follows from (62) that
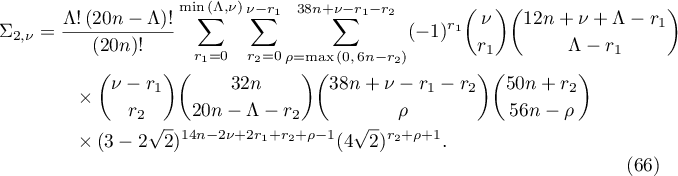
Finally, let us calculate the value of  using Lemma 12. We write
using Lemma 12. We write
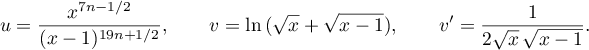
Then
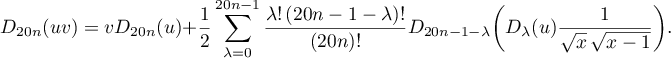
Similarly,

We note that 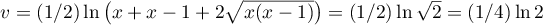 .
.
Hence, the coefficient at 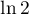 in the linear form (21) is
in the linear form (21) is
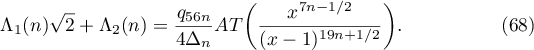
Remark 2. The formula (68) enables one to find the constant 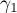 (see Lemma 6) using the terms of some positive series rather than by applying the saddle-point method. The former method is very simple, and therefore it is popular. It has been used many times in recent years; see, for example, [3], [6] and [9]. Therefore, we restrict ourselves to rather brief comments.
(see Lemma 6) using the terms of some positive series rather than by applying the saddle-point method. The former method is very simple, and therefore it is popular. It has been used many times in recent years; see, for example, [3], [6] and [9]. Therefore, we restrict ourselves to rather brief comments.
Since  , it follows that
, it follows that
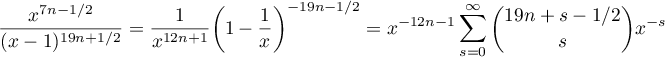
is a convergent series. Therefore, differentiating termwise, we obtain the positive series
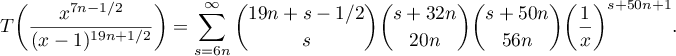
The desired asymptotic behaviour is given by the maximal term of the series. Let us find this term by solving the equation
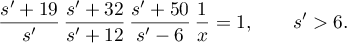
We have 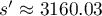 . Correspondingly, the index of the maximal term of the series is
. Correspondingly, the index of the maximal term of the series is 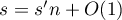 . Therefore, as in the papers indicated above,
. Therefore, as in the papers indicated above,
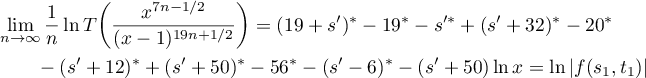
by Lemma 13, and, using the equation (68) we obtain the result coinciding with that of Lemma 6. We note that the reasoning used in Remark 2 does not involve the evaluation of the constant  .
.
Let us return to the proof of Theorem 1. The first term in the sum (67) is evaluated in the same way as 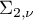 , where
, where 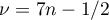 . The half-integer value of
. The half-integer value of  enables us to extend the bounds of variation of
enables us to extend the bounds of variation of 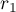 ,
, 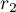 ,
, 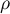 . Instead of (66), we obtain
. Instead of (66), we obtain
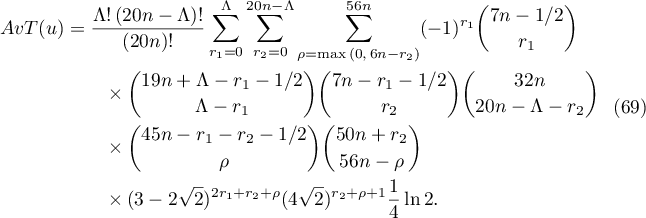
Let us now evaluate the summands 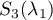 in the sum in (67). As above, let
in the sum in (67). As above, let
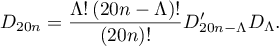
We obtain in succession
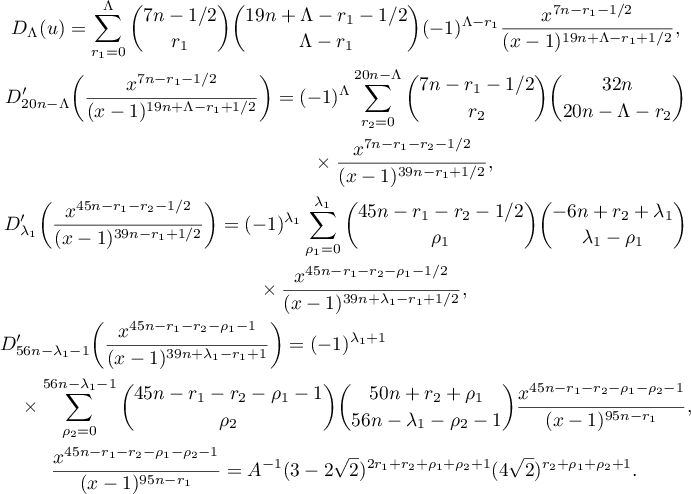
Therefore,
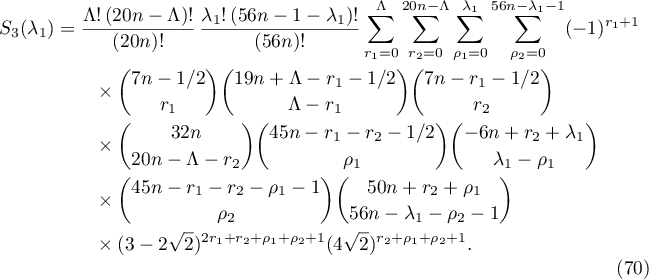
It remains to evaluate 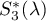 . Let
. Let
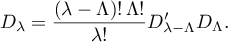
We obtain in the standard way that

Thus, in the second case, we have

All the summands in (64) evaluated using the formulae (65), (66), (70) and (71) are of the form 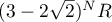 or
or 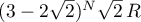 , and the summands in the formula (69) are of the form
, and the summands in the formula (69) are of the form  or
or  , where
, where 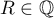 and
and 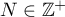 . We note that
. We note that 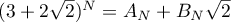 and
and 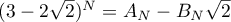 for
for  , where
, where 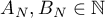 . Correspondingly,
. Correspondingly, 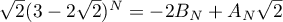 . Obviously,
. Obviously,  .
.
The total number of summands in  is estimated as
is estimated as  . Thus, for
. Thus, for  we have the bound
we have the bound 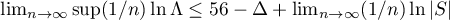 , where
, where 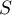 is the summand of maximal modulus among all above sums after replacing
is the summand of maximal modulus among all above sums after replacing 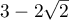 by
by 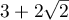 . The asymptotic behaviour of the binomial coefficients is calculated using Lemma 13.
. The asymptotic behaviour of the binomial coefficients is calculated using Lemma 13.
Computer calculations show that the corresponding maximal summand is attained in the sum (69) for the following values of parameters: 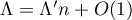 ,
, 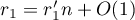 ,
, 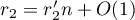 and
and 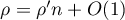 , where
, where
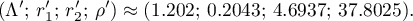
Hence by Lemma 13, it follows from (69) that
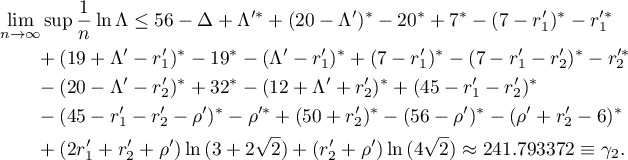
Then, by Lemma 4, the inequality (1) holds for

This completes the proof of Theorem 1.
§ 4. Concluding remarks
4.1. The number 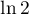 occupies a special position in the theory of Diophantine approximation. As Nesterenko said in the paper [9], ``
occupies a special position in the theory of Diophantine approximation. As Nesterenko said in the paper [9], ``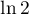 is a natural model for comparing the different methods developed for estimating the irrationality exponent for logarithms of rational numbers''. The best estimate for the irrationality measure of the number
is a natural model for comparing the different methods developed for estimating the irrationality exponent for logarithms of rational numbers''. The best estimate for the irrationality measure of the number 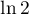 is due to Marcovecchio [3]:
is due to Marcovecchio [3]:  , and the estimate for the measure of quadratic irrationality is due to Polyansky [10]:
, and the estimate for the measure of quadratic irrationality is due to Polyansky [10]: 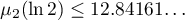 . For obvious reasons, the estimate obtained in this paper is between these values.
. For obvious reasons, the estimate obtained in this paper is between these values.
4.2. In [1], to obtain an estimate of the form (1), the classical hypergeometric construction with integer parameters was used, while in [2] an analogous integral (but with half-integral parameters) was applied. In essence, the integral (2) is a linear combination of hypergeometric integrals with half-integral parameters (see the equations (7)–(9) in this paper). This linear combination is arranged in such a way that the coefficients of the corresponding linear form (see (35) and (21)) have a relatively small common denominator. We note that an integral of the form (2) was first applied in the paper [6] to obtain a new bound for the irrationality measure of the number 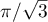 .
.
4.3. The use of a combined differentiation with the help of Lemma 11, which enables us to reduce the value of the constant  , also makes an important contribution.
, also makes an important contribution.
4.4. The most difficult and laborious part of the work was to obtain a sufficiently small value of the constant  . It is probable that the bound given in this paper is not definitive and that the methods developed in §3 can be improved.
. It is probable that the bound given in this paper is not definitive and that the methods developed in §3 can be improved.
4.5. The first author has obtained several new results using the integral (2). In particular, he managed to improve the bound for the approximation of the number 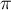 by numbers in the field
by numbers in the field 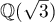 . These results are currently being prepared for publication.
. These results are currently being prepared for publication.
The authors dedicate this paper to the centenary jubilee of Professor A. B. Shidlovskii, who was the teacher of the second author for many years.