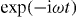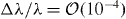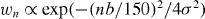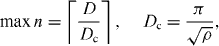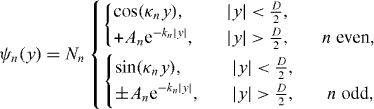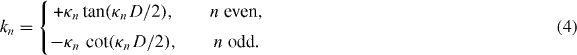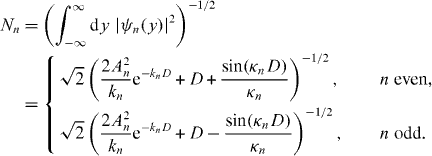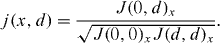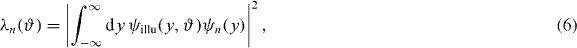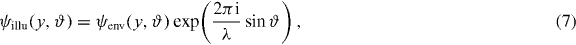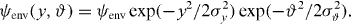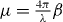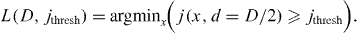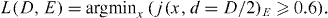Coherence filtering of x-ray waveguides: analytical and numerical approach

X-ray microscopy offers the advantage of imaging extended samples in three dimensions (3D) without sectioning, staining or slicing. However, in the hard x-ray spectral range, favorable in terms of penetration and focal depth, the resolution is severely limited by lens fabrication. To overcome this limitation, coherent x-ray imaging techniques have been developed [1–4], which enable the quantitative reconstruction of the electron density [5] beyond the fabrication limit of optical components.

Physicists from different disciplines are joining forces to fully exploit the vast field of coherent x-ray techniques; for a comprehensive overview of the state of scientific knowledge, see the New Journal of Physics' focus issue 'x-ray beams with high coherence' [6]. Plenty of topics can be found there, including accelerator physics [7–13], optics and algorithms [5, 14, 15] and applications for material science [16–22], and topics at the border of physics, biology and chemistry [23–26].

Coherent methods can also be used to reconstruct the illumination wave field, so that aberrations, figure errors and finite point spread functions become significantly less restrictive. Coherent imaging can be divided into two classes: (A) coherent diffraction imaging (CDI), where the data are recorded in the Fraunhofer far-field regime [27], and (B) propagation imaging based on the recording of the Fresnel near-field intensity distribution [28, 29]. While the latter (B) has some similarities to a projection radiography, the first (A) is similar to a conventional diffraction experiment.

The decisive difference of both types with respect to the conventional counterparts lies in the coherence properties of the illuminating beam, which enable numerical image formation (calculation) without any lens between the sample and the detector. In (A), reconstruction algorithms are based on support constraints implemented in simple error reduction schemes [30] or on more elaborate schemes [31, 32], including the overlap constraints of the so-called ptychographic algorithms [33]. Ptychography is capable of reconstructing the unknown complex-valued illumination function as well as the unknown object through the beam [34–37]. However, the idea of a fully coherent beam represents an idealization that is hardly encountered in practice. The effect of partial coherence in x-ray optics has been addressed in [3, 29, 38–41] and more specifically in the field of coherent imaging by Nugent and coworkers based on modal representations of the illuminating wave field [42, 43]. These new methods include knowledge of the partial coherence in reconstruction algorithms, allowing for polychromatic sources, and have only recently been demonstrated experimentally.

One of the remaining challenges in this field is, therefore, to control the coherence properties of the beam, and to delineate the coherence requirements more precisely for given parameters. As is well known, incoherent illumination and coherent illumination are two limiting classes, which never occur in reality. The concept of partial coherence of wave fields, which can be quantified by the mutual coherence and the mutual intensity functions, adequately describes the issue and can be used for optical design and data analysis in a given coherent imaging application. Coherence propagation and filtering can be calculated by solving the wave equations for the field correlation functions, i.e. the mutual coherence or the mutual intensity functions. Compared to the limiting case of full coherence, where the field alone is needed, this changes the dimensionality of the problem by a factor of two. Suitable methods to control and predict wave-front distortion and spatial coherence are needed [1, 2, 7]. Experimentally, interferometric methods have been developed [44–47] to quantify the mutual intensity function J(x₁,x₂) or the complex degree of coherence $j(x_1,x_2)=J_{12}/\sqrt {J_{11}J_{22}}$, and hence the visibility v = |j|. On the numerical and analytical side, coherence properties also have to be taken into account efficiently.

In this work, a simple, variable and robust approach is used for numerical coherence simulations to study the coherence propagation and filtering properties in focused hard x-ray beams; see figure 1. Starting from a discretized source plane, an ensemble average of stochastic realizations of optical fields with random phase relationships is used to evaluate the spatial coherence in any plane perpendicular to the optical axis. We then use this approach to simulate the spatial coherence properties of focused x-ray beams and coherence filtering by x-ray waveguides (WGs). The latter offers a direct comparison between analytical and numerical solutions, which is a very useful validation of the approach chosen here.

Zoom In Zoom Out Reset image size

Different methods can be used for coherence filtering, ranging from simple slits and pinholes acting as spatial filters, to combined optics with high-aperture focusing devices. The special example of WGs is a paradigmatic case, since only a discrete set of guided modes can propagate over the entire length of the WG, whereas radiative modes are quickly absorbed by the cladding. This characteristic set of guided modes can be varied systematically and calculated analytically for simple geometries, to the advantage of conceptual clarity. X-ray WGs have been realized as planar structures, guiding the beam along 1D, and as channel WGs for 2D guiding. In the 2D case, channel cross-sections down to 35 nm × 75 nm have been achieved by e-beam lithography, while 1D WGs down to 9 nm have been fabricated by thin film sputtering. For imaging, prefocusing the undulator beam into the WG is necessary, e.g. by high-gain Kirkpatrick–Baez (KB) mirror systems optimized for high flux density. In recent experiments, the beam diameter was reduced from typical values in the range of 100–200 nm to values below 15 nm by the insertion of the x-ray WG into the mirror focus [48, 49]. In proportion to the reduction in focal spot size, the numerical aperture of the projection imaging system is increased and hence also the maximum resolution. At the same time, the spatial coherence is significantly increased, as shown further below.

This paper is organized as follows. In section 2, the degree of coherence j(x₁,x₂) is defined by ensemble averages of stochastic optical fields; in sections 3 and 4, analytical expressions for the coherence properties of WGs are developed and evaluated. These results are then compared with numerical simulations in section 5. Section 6 presents a simulation on a combined optical system with the WG positioned in the KB focus; the paper closes with the conclusions and an outlook in section 7.

The propagation of coherent light waves is well understood and several numerical techniques exist for the simulation and optimization of optical systems. Depending on the Fresnel number, geometry and aspect ratios, either differential equations [51], integral equations [52] or Fourier space calculations [53] are carried out. Specific approximations are applied to, e.g., periodic media such as crystals [54], multilayer Lause lenses [55] or thin lenses [56]. Classical wave optical models assume that the light field can be described by an amplitude and phase, which can then be propagated along the optical axis, with intensity calculated as the modulus squared of the field. To account for finite coherence, the mutual intensity, as defined below, takes the role of amplitude [38, 39, 41]. It can be propagated by similar wave optical methods—but it is defined in twice as many dimensions: while amplitude and intensity are functions of one space–time point, mutual intensity is a function of two space–time points. This increases computational costs significantly.

In this paper, we use a different approach to model spatial partial coherence, based on stochastic realization of stationary fields [57], which turns out to be flexible, conceptually simple and numerically efficient for our purposes. The approach 'simulates' a spatially extended source by a discrete set of individual emitters, and can take correlations of the emitters into account. For convenience we will only consider 2D models for x-rays, but the theory can easily be generalized to the 3D case. Furthermore, we restrict the treatment to quasi-monochromatic waves, described by a time harmonic term $\exp (-\mathrm {i}\omega t)$ with mean frequency ω. Actual deviations from the time harmonic term result in finite bandwidth and coherence time τ. In the following, we assume that within the short time interval τ all contributing sources emit with a random, but fixed, phase relation. One 'coherence time later', new phase relations are present. The discussion of temporal and spatial coherence can then be decoupled, and only the spatial coherence properties will be considered here. The assumption of quasi-monochromatic x-rays is justified in many cases: the incoming synchrotron radiation is usually monochromatized by crystal monochromators, with a typical bandwidth in the range of $\Delta \lambda /\lambda =\mathcal {O}(10^{-4})$.

The mutual intensity J(x₁,x₂) of the optical field u(x) at two points x₁ and x₂ is then defined as

$$\begin{eqnarray} J(x_1,x_2) &= u(x_1)u^\ast(x_2). \end{eqnarray}\noindent \tag{ 1 }$$

This deterministic expression is appropriate for the superposition of perfectly correlated sources. In reality, partial coherence effects are important due to fluctuating phase relations between sources, which have to be accounted for by a suitable average. Formulated in the time domain, each wave train adds up coherently, within the time window τ of temporal coherence corresponding to the experimental monochromaticity. For x-rays with typical frequencies of 10¹⁸ Hz and a relative bandwidth of 10⁻⁴, we have τ ∼ 10⁻¹⁴ s, well beyond the response time of detectors. Many such short temporal time windows must then be averaged to describe the experimental result measured within macroscopic accumulation times. Here, these fluctuations are incorporated into the modeling scheme by the assumption of ergodicity, averaging the above quantity over many stochastic realizations with randomly distributed phases. Hence ensemble averages of mutual intensities for phase fluctuating fields are considered, as described now.

Each point source emits a field u_n(x). For each realization, these fields have a random but fixed phase relation, given by random coefficients c_n, such that the resulting field at any position is computed from coherent superpositions

$$\begin{eqnarray} U(x) &= \sum_n w_n c_n^{\rm rand} u_n(x). \end{eqnarray} \tag{ 2 }$$

The intensities or mutual intensities corresponding to many such superpositions are then averaged. The amplitude of a finite source is taken into account by a deterministic (but freely variable) envelope for the point sources, parameterized by the real-valued weighting coefficients w_n above. For example, below we will use a Gaussian envelope with a variable source size, without the need to recalculate the fields u_n itself.

As a model for synchrotron undulator sources, the elementary fields u_n are created by virtual point sources along the undulator source size. The great number of electrons and bunches, which are—to first approximation—uncorrelated, each emit short wave-trains with random phases. Residual correlations could easily be included in the approach by adding correlations in coefficients c_n ≈ c_n±1, using a Markov chain approach. The average mutual intensity is then

$$\begin{eqnarray*} J_{\rm e}(x_1,x_2) &= \left\langle U(x_1)U^\ast(x_2)\right\rangle_{\rm ensemble}, \end{eqnarray*}$$

and the degree of coherence j(x₁,x₂) reads

$$\begin{eqnarray}j(x_1,x_2) &= \frac{J_{\rm e}(x_1,x_2)}{\sqrt{J_{\rm e}(x_1,x_1)J_{\rm e}(x_2,x_2)}}. \end{eqnarray}\noindent \tag{ 3 }$$

By averaging 10³–10⁴ ensembles, the model was in good agreement with analytical theory, as tested for simple configurations, and faster to evaluate than, for example, generalized Fresnel–Kirchhoff integrals, which need twice as many dimensions for the propagation of J.

This ensemble averaging is only useful for 'normal' synchrotron sources and rather long exposure times (milliseconds and longer). At free electron lasers, either already working or currently being built, single-shot experiments promise significant spatial coherence properties, which would correspond to single realizations of stochastic superpositions. By using appropriate 'seeding', even strong correlations between individual pulses are prospected [12].

As an example of this approach, we have calculated the partially coherent x-ray intensity J_e(y,y) and the degree of coherence j(0,y), for one point at the focus and the second point in the focal plane at a distance y. Parameters were taken for the KB mirror system of the beamline P10 (holography endstation), PETRA III, Hamburg. The extended source was modeled by 301 equidistant point sources over ±15σ. The sources' envelopes were modeled by Gaussian weighting factors $w_n\propto \exp (-(nb/150)^2/4\sigma^2)$ for the amplitude superpositions (2). Fresnel–Kirchhoff's integral of diffraction was evaluated at 500 points in the focal plane, and included 50 000 random points on the mirrors' surfaces. For the stochastic averaging, an ensemble consisting of 10 000 random amplitudes and phases has been used. Since the ensemble average consists of mutually independent calculations, it is massively parallelizeable on modern graphics cards. This is important if hundreds of planes parallel to the focus plane are considered, to obtain data in the defocus regions. Figure 2 shows simulated curves for (a,b) the horizontal and vertical focus, the partially coherent intensity distribution in the focal region of the vertical setup (c) and the expected focus size and coherence length (d), as a function of the effective source size σ.

Zoom In Zoom Out Reset image size

Experimental data on vertical focus profiles have been obtained by scanning a Ge/Mo/C/Mo/Ni-x-ray WG as described in [48] with a 35 nm guiding layer vertically through the beam. A first experiment after commissioning carried out in November 2010 at a photon energy of 15 keV and with the P10 undulator source operated in a high-β section yielded a broadened focus size of ≈470 nm, consistent with simulations assuming a greatly enlarged effective source size of σ ≈ 40–48 μm (figure 2(e)). A second measurement at 13.8 keV carried out in April 2011 with the source in low-β mode showed excellent agreement with the simulated focus cut for the nominal source size (figure 2(f)), σ_v = 6 μm.

In fact, a diffraction limited focal spot size of 117 nm (full-width at half-maximum (FWHM)) was measured. Since neither the ring operation mode nor the photon energy would explain such a large difference in the vertical focus profile, we attribute the broadening effect mainly to vibrations in the optical setup during the first experiment, namely in the liquid nitrogen cooling system of the first monochromator crystal, which had in the meantime been optimized (flow parameters).

Note that other factors cannot be excluded, including, not in last place, alignment and motor scanning precision. We stress that comparison of experimental results and numerical simulation has been instrumental in benchmarking the optical system. In all these simulations, measured figure errors of the mirrors have been taken into account [49]. Further details of the instrument and first commissioning results are given in [50, 58].

X-ray WGs support a discrete set of guided modes plus infinitely many radiative modes. Here we only address the guided modes, since radiative modes are strongly absorbed by the cladding material. For simplicity, we assume air/vacuum as a guiding layer. The number of guided modes for a rectangular WG depends only on the guiding layer thickness D and the materials' index of refraction. For simplicity, we can reduce the discussion to a single cladding material, with the guiding layer consisting of air or vacuum. The number of modes is then given by the ratio of the thickness D and a critical material-dependent thickness D_c, rounded up to the next integer

$$\begin{eqnarray*} &&{\rm max}\,n = \left\lceil\frac{D}{D_{\mathrm{c}}}\right\rceil,\quad D_{\rm c} = \frac{\pi}{\sqrt{\rho}}, \end{eqnarray*}$$

where ρ is 4πr₀ times the electron density of the cladding material (ρ_Si ≈ 0.0248 nm⁻²) [59] with the Thompson's scattering length r₀ = 2.82 × 10⁻¹⁵ m. As is usual in hard x-ray optics, the index of refraction has been expressed in terms of electron density, which is valid as long as the photon energy is far away from absorption edges. In the case of WGs with a non-vacuum guiding layer, the electron density has to be replaced by the contrast in electron density between the guiding layer and cladding. Generalizations including interlayers are also possible.

For silicon WGs with a vacuum (air) guiding layer, the critical thickness is D_c ≈ 19.96 nm, so WGs with D = 10–70 nm as considered in this treatment support one to four modes [51, 60]. The modes ψ_n(y) can be calculated in a straightforward manner for WGs with sharp boundaries (i.e. a step profile of the index of refraction), resulting in

$$\begin{eqnarray*} \psi_n(y) = N_n \left\{\begin{array}{@{}ll@{}} \left\{\begin{array}{@{}lcc@{}} \displaystyle \cos(\kappa_ny), &\quad |y|<\frac{D}{2}, \\[3pt] + A_n\mathrm{e}^{-k_n|y|}, &\quad |y|>\frac{D}{2}, &\quad n\ {\rm even},\end{array}\right.\\[12pt] \displaystyle \left\{\begin{array}{@{}lcc@{}} \sin(\kappa_ny), &\quad |y|<\frac{D}{2},\\[3pt] \displaystyle \pm A_n\mathrm{e}^{-k_n|y|}, &\quad |y|>\frac{D}{2}, &\quad n\ {\rm odd},\end{array}\right.\end{array}\right.\end{eqnarray*}\noindent$$

where the parameters A, k and κ have to be determined numerically by solving the following transcendental equation to respect boundary conditions at the interface and at infinity:

$$\begin{eqnarray} \displaystyle k_n = \left\{\begin{array}{@{}cc@{}} + \kappa_n\tan(\kappa_n D/2) ,&\quad n\ {\rm even},\\[6pt] \displaystyle - \kappa_n\,\cot(\kappa_n D/2) ,&\quad n\ {\rm odd}. \end{array}\right. \end{eqnarray}\noindent \tag{ 4 }$$

The parameters are

$$\begin{eqnarray*} k_n &=& \sqrt{m_n},\qquad \kappa_n = \sqrt{\rho-m_n}, \\[6pt] \displaystyle A_n &=& \left\{\begin{array}{@{}lc@{}} \cos(\kappa_n D/2) \mathrm{e}^{k_n D/2}, & n\ {\rm even}, \\[6pt] \displaystyle \sin(\kappa_n D/2) \mathrm{e}^{k_n D/2}, & n\ {\rm odd}. \end{array}\right.\end{eqnarray*}\noindent$$

The transcendental equation can be solved by nested intervals: starting with some guessed mode parameter m₀, (4) may not be fulfilled; depending on k − κ tan(κD/2) or k + κ_ncot(κ_nD/2), the mode value m can be adjusted within some interval. For the next iteration, this interval is bisected. If the true m_n(D) of the searched mode is within the first, properly guessed, interval, we can solve (4) with arbitrary accuracy and thus obtain numerical values for the parameters A_n, k_n and κ_n. The start intervals m_n(D) have been found by trial and error [59]. A normalization constant N_n ensures that the integral over all intensity is 1 for each mode:

$$\begin{eqnarray*} N_n &= \left(\int_{-\infty}^\infty{\rm d}y\, \left|\psi_n(y)\right|^2\right)^{-1/2} \\ &= \begin{cases}{ \sqrt{2}\left( \frac{2A_n^2}{k_n} \mathrm{e}^{-k_nD} + D + \frac{\sin(\kappa_nD)}{\kappa_n} \right)^{-1/2} ,& $n$ {\rm even}, \\ \sqrt{2}\left( \frac{2A_n^2}{k_n} \mathrm{e}^{-k_nD} + D - \frac{\sin(\kappa_nD)}{\kappa_n} \right)^{-1/2} ,&$n$ odd. }\end{cases}\end{eqnarray*}$$

We now define the mutual intensity J(y₁,y₂)_x ≡ J((x₁ = x,y₁),(x₂ = x,y₂)) per mode as

$$\begin{eqnarray} J_n(y_1,y_2)_x &= \lambda_n(x)\psi_n(y_1)\psi_n^\ast(y_2),\end{eqnarray}\noindent \tag{ 5 }$$

with the occupation numbers λ_n. The index x shall account for the fact that along the optical axis, the occupation numbers decrease by absorption in the cladding. In fact, absorption in the cladding can be taken into account by an effective absorption coefficient, as discussed in the next section, leading to a decrease with x, which is different for each mode, since the fraction of intensity in the cladding is mode dependent. Then the degree of coherence j(x,d) ≡ j((x₁ = x,y₁ = 0),(x₂ = x,y₂ = d)) can be defined as

$$\begin{eqnarray*} j(x,d) &= \frac{J(0,d)_x}{\sqrt{J(0,0)_xJ(d,d)_x}}.\end{eqnarray*}\noindent$$

Since the modes ψ_n are mutually incoherent [7], this can be written as

$$\begin{eqnarray*} j(x,d) &= \frac{\sum_n\lambda_n(x)\psi_n(0)\psi_n^\ast(d)}{\sqrt{\sum_n\lambda_n(x)|\psi_n(0)|^2\cdot\lambda_n(x)|\psi_n(d)|^2}}.\end{eqnarray*}\noindent$$

Let us first consider the degree of coherence for illustrative examples of model occupation numbers. Figure 3 shows j(d) for increasing occupations of higher modes. Depending on the number of modes excited, we observe first full coherence (only one mode), then a decreasing degree of coherence (the first and second modes excited), a function j(d) with a zero and finite values deep in the cladding (first three modes). Finally, the fourth mode then bends the tail of the function towards zero.

Zoom In Zoom Out Reset image size

In this section, actual occupation numbers λ_n for the WG modes are calculated for different parameterized illumination conditions. Notably, we consider a plane wave illumination field with a Gaussian envelope, and at different inclination angles with respect to the WG axis. This is a simple parameterized model for the experimental situation encountered in front coupling of x-ray WGs, where a pre-focused synchrotron beam is coupled into a WG from its front side with the goal of filtering the spatial coherence. In this model, the evolution of j(x,y) as a function of propagation can be calculated semi-analytically, with the transcendental equation (4) and the following integrals solved numerically. As a result, the required lengths of WG devices needed for a given degree of coherence can be obtained.

An arbitrary wave-front can be expanded into a set of plane waves with appropriate angles of incidence. For each such plane wave, the impinging energy of the wave-field is either captured by the guided modes or lost in the radiative modes not considered here. The occupation number λ_n(ϑ) of the nth mode at an angle ϑ is given by an overlap integral with the illumination function ψ_illu(y,ϑ) [61, 62]:

$$\begin{eqnarray} \lambda_n(\vartheta) &= \left|\int_{-\infty}^\infty{\rm d}y\, \psi_{\rm illu}(y,\vartheta) \psi_n(y)\right|^2, \end{eqnarray} \tag{ 6 }$$

$$\begin{eqnarray} \psi_{\rm illu}(y,\vartheta) &= \psi_{\rm env}(y,\vartheta) \exp\!\left(\frac{2\pi \mathrm{i}}{\lambda}\sin\vartheta\right),\end{eqnarray} \tag{ 7 }$$

where ψ_env(y,ϑ) is some envelope function, for example a 2D Gaussian

$$\begin{eqnarray*} \psi_{\rm env}(y,\vartheta) &= \psi_{\rm env} \exp(-y^2/2\sigma_y^2) \exp(-\vartheta^2/2\sigma_\vartheta^2).\end{eqnarray*}$$

The modulus squared in (6) is due to the fact that in (5) we have defined λ_n as a measure of intensity, not amplitude. For finite integral limits and a more realistic model, we limit the incoming beam by setting σ_y = 5D and σ_ϑ = 5 mrad; the former yields a finite illumination beam, whereas the latter restricts the angular spectrum. The small value of 5 mrad is reasonable since the angular acceptance of x-ray WGs is limited by the critical angle ϑ_c. For silicon at photon energies of E = 12.4 keV, we have ϑ_c = 2.52 mrad. The value σ_y = 5D corresponds to beam sizes in the range of about 100 nm to 1 μm (FWHM), which is reasonable with good or moderate pre-focusing accessible at synchrotron radiation sources. If the illumination consists of plane waves under different angles, the integrated occupation number λ_n is

$$\begin{eqnarray} \lambda_n &= \int{\rm d}\vartheta\,\lambda_n(\vartheta). \end{eqnarray} \tag{ 8 }$$

The integrations are carried out numerically by Riemann sums. As the integration limits, ±5σ_y and ±2σ_ϑ have been chosen. For the Riemann sums, the integration domain was divided into 1000 × 500 (in y and ϑ) points.

The modes are subject to absorption, since a finite fraction of the energy is transported inside the cladding material. If the index of refraction is written as n = 1 − δ + iβ, the linear absorption coefficient for Beer–Lambert's law is $\mu =\frac {4\pi }{\lambda }\beta$, and the propagated occupation numbers λ_n(x) are

$$\begin{eqnarray*} \lambda_n(x) &= \lambda_n\mathrm{e}^{-\mu_nx}. \end{eqnarray*}$$

Here the effective absorption μ_n of mode n is given by the fraction of intensity inside the cladding,

$$\begin{eqnarray} \mu_n &= \mu(E)\left(\int_{y\,\in\,{\rm cladding}}{\rm d}y\,|\psi_n(y)|^2\right)\Big/\left(\int\kern-2pt{\rm d}y\,|\psi_n(y)|^2\right),\end{eqnarray} \tag{ 9 }$$

and μ(E) is a tabulated value depending on photon energy and cladding material. In figures 4(a)–(c), the relative occupation numbers λ_1–4 for WG guiding layer thicknesses D = 10–70 nm (i.e. one to four modes) are shown (a) right at the entrance and after (b) 500 μm and (c) 1500 μm of propagation. Figures 4(d)–(f) show the degree of coherence for three WGs with D = {30,50,70} nm and propagation distances x = {0 500 1500 6000} μm. As can be seen, the degree of coherence increases considerably with propagation distance, resulting from the stronger absorption of higher modes and the resulting smaller spectrum of mode occupation numbers.

Zoom In Zoom Out Reset image size

Now we address the question of which WG length is required for a certain degree of coherence, filtered by mode damping. Higher modes are subject to a higher effective absorption than lower modes, since more of their energy is dissipated inside the cladding material. In figure 5(a), the required length L as a function of guiding layer thickness D is shown, if we ask for a minimum degree of coherence between the optical axis and the interface:

$$\begin{eqnarray*} L(D,j_{\rm thresh}) &= {\rm argmin}_x\!\Big(j(x,d=D/2) \geqslant j_{\rm thresh}\Big). \end{eqnarray*}$$

The different curves in figure 5(a) correspond to j_thresh = {0.4,0.6,0.8}. If we ask for a highly coherent wave-field like j ⩾ 0.8 everywhere inside the guiding layer, a three-mode WG needs to be 4–8 mm long (silicon, 12.4 keV). Figure 5(b) shows the required WG length for a fixed j_thresh = 0.6, but for different photon energies E = {8,12.4,17,24} keV:

$$\begin{eqnarray*} L(D,E) &= {\rm argmin}_x\,(j(x,d=D/2)_E \geqslant 0.6). \end{eqnarray*}$$

As can be seen, three-mode WGs need to be more than 12 mm long if we ask for a moderate degree of coherence at high energies, while lengths of about 2 mm suffice for lower energies.

Zoom In Zoom Out Reset image size

In the semi-analytical treatment presented so far, we have only considered guided modes. However, radiative modes can also affect the coherent properties of the beam. By a numerical propagation of the illumination, based on the parabolic wave equation as described in [60, 63], the field inside the WG can be simulated. We now generalize this method to model coherence properties also: incoming plane waves under different angles are each propagated individually, yielding—itself fully coherent—wave fields u_n (the index n stands for individual plane waves). These fields are then averaged stochastically as outlined in section 2—thus the mutual intensity and the degree of coherence as defined by (1) and 3) can be obtained.

Figure 6(a) shows the intensity of a D = 50 nm WG, illuminated coherently by a single plane wave; a partially coherent ensemble average of 2401 plane waves with angles distributed equidistantly within the interval −3 mrad ⩽ ϑ ⩽ 3 mrad is shown in figure 6(b). The simulated WG has a length of L = 1 mm and the wavelength is λ = 0.1 nm. In figure 6(f), the intensity and degree of coherence after the WGs exit are shown in the form of iso-curves.

Zoom In Zoom Out Reset image size

Similar simulations have been carried out for WGs with D = {30,50,70} nm and L = 5 mm. From these data, the degree of coherence has been evaluated as a function of propagation length, as explained above. The results are shown in figures 6(c)–(e). Compared to the semi-analytical treatment and figures 4(d)–(f), the effect of radiative modes now becomes visible: the very low degree of coherence at the entrance of the WGs results from illumination by a partially coherent set of plane waves. But after a few hundreds of micrometers of propagation, j is significantly enhanced, and after one millimetre, it is comparable to the analytical values.

The mode composition of the propagated fields can be determined by a Fourier analysis (fast Fourier transform along the axis of propagation) [48, 60]. By this method, we can obtain the occupation numbers of numerically propagated fields, even if the analytical approach is no longer possible, as in the case of more general models with tapered [63] or fluctuating [59] channels.

So far we have studied the coherence properties of x-ray WGs if illuminated by their full angular acceptance; in experiments with pre-focused synchrotron beams the angular spectrum of the incoming waves is reduced to, say, ±1 mrad or lower. Additionally, focusing optics such as mirrors may act as spatial frequency filters and, furthermore, enhance the coherence length in the focal plane. If the WG is placed in the defocus, even higher degrees of coherence in the illumination are possible, yet the intensity is reduced.

We have modeled the coherence properties of a horizontally focusing mirror (HFM) at the holography endstation at the beamline P10 at PETRA III [49] and compared the simulation to experimental data. Figure 7(a) shows simulated intensity pattern (color-coded) and degree of coherence (iso-lines at j = {0.4,0.6,0.8}) within a defocus region of ±1 mm. The simulation incorporates a measured height deviation profile of the HFM; the photon energy is E = 7.9 keV, or in terms of wavelength, λ = 0.157 nm. In figure 7(b), the focused field was coupled into a WG (guiding layer size D = 50 nm; length L = 2 mm). Figures 7(c)–(f) show cuts of the intensity and degree of coherence at several positions: panel (c) is in the mirror's focal plane; the spot size of about ≈220 nm is only partially coherent, since the degree of coherence decreases rapidly. On the other hand, in the center of the WG (e), the intensity distribution is confined to a region of ≈50 nm, while the degree of coherence is nearly 1 and only decreases far in the cladding. The intensity and degree of coherence in a defocus of 1 mm behind the mirror's focus plane (d) and 0.1 mm behind the WG's exit show similar behavior: the defocused beam size of 2 μm is only partially coherent; hence, structures smaller than 1 μm are good samples for CDI applications; in the WG filtered case, all intensity is (nearly) coherent. This results in measurements with lower dose, since no 'incoherent energy' is deposited in the sample.

Zoom In Zoom Out Reset image size

A numerical approach to model spatial coherence in x-ray optics, in particular to model free propagation, reflective focusing and waveguiding of synchrotron radiation, has been used. The method is based on an ensemble average of individual sources and explicit simulation of elementary fields, followed by an average of the associated mutual intensities. We have calculated the partially coherent focus fields of typical focusing mirrors as well as the evolution of the degree of coherence in x-ray WGs, which can be used as coherence filtering devices.

While coherence filtering has been exploited, e.g. in coherent x-ray imaging, this paper fills a gap in the precise modeling of the filtering effects. Apart from its applications, WG modes are also a good test bed for coherence methods, since analytical and numerical results can easily be compared. In fact, mode theory and our statistical approach are in good agreement, the latter even accounting for radiative modes that are neglected in the analytical treatment. The length of WG required to obtain a given degree of coherence can now be determined and optimized. The proposed numerical scheme also allows for complicated geometries and real-structure effects such as non-perfect surfaces and interfaces. Instead of straightforward calculations of mutual intensity, such as a generalized Fresnel–Kirchhoff integral in twice as many dimensions, only a single integral needs to be calculated for some tens or hundreds of point sources. The stochastic averaging can be carried out very efficiently by modern computational techniques such as programmable graphic cards.

As the next step, the incorporation of the modeled partial coherence effects into reconstruction algorithms for coherent imaging can be envisioned.

The source code used to simulate the present results is provided as supplementary data and can be used on the basis of proper citation of this work. An animation showing fluctuating intensity in a partially coherent focused beam is provided for comprehension. Both the supplementary data and the animation are available at .

We gratefully acknowledge financial support by the Deutsche Forschungsgemeinschaft (DFG) through Sonderforschungsbereich 755 Nanoscale Photonic Imaging and the German Ministry of Education and Research under grant numbers 05KS7MGA and 05K10MGA. For support at beamtimes we thank our colleagues of the Institut für Röntgenphysik and Michael Sprung from the P10 beamline at PETRA III.