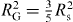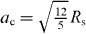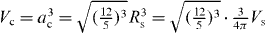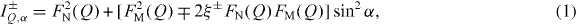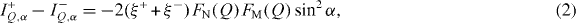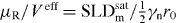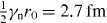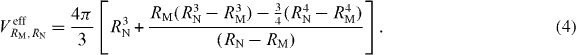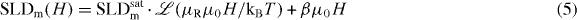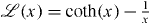Quantitative spatial magnetization distribution in iron oxide nanocubes and nanospheres by polarized small-angle neutron scattering

Physical properties of nanosized magnetic objects have been intensively investigated for both technological and scientific reasons [1, 2], with possible applications in high-density magnetic data storage, biomedical applications such as cancer treatment by hyperthermia [3], contrast agents for magnetic imaging [3–5] and in electronic and mechanical engineering [6–8]. Whereas the implementation of nanomagnetic properties into technological applications is progressing rapidly, understanding the microscopic origin of phenomena such as magnetization enhancement or decrease and magnetic anisotropy is fundamentally challenging and needs intensive research. The spatial magnetization density in such nanoparticles is both related to surface and shape anisotropies and to structural and magnetic surface disorder. Many investigations on surface spin disorder and nanoparticle magnetization were performed using spatial averaging and macroscopic probes such as superconducting quantum interference device (SQUID) magnetometry [9, 10], and the presence of a magnetically disordered surface layer is commonly concluded from reduced [11–14] and unsaturated magnetization at high fields [13–15]. X-ray and neutron diffraction studies have revealed magnetic domain sizes smaller than the structural correlation length [16, 17]. The commonly accepted model of magnetism in nanoparticles thus consists of a particle core with bulk-like magnetization and a surface shell of canted or disordered magnetic moments [18, 19]. Theoretical models complement these results [12, 13] and propose a spin structure that accounts for interatomic superexchange interaction as well as surface and magnetocrystalline anisotropies [20, 21]. Microscopically, spin disorder in maghemite nanoparticles has been investigated by x-ray magnetic circular dichroism (XMCD) and Mössbauer spectrometry, revealing a higher degree of canting on octahedral sites [22, 23]. A combination of NMR and Mössbauer spectroscopies suggests a reduced magnetization in the core, attributed to reversed moments and a frustrated topology [24]. However, a quantitative description of the spatial distribution of the magnetization in nanoparticles has not yet been given.

Neutron scattering is a volume-sensitive microscopic probe that does not disturb the magnetization state and can provide both quantitative and spatially resolved experimental access to the nanoparticle spin structure. The spatially resolved microscopic magnetization distribution is correlated with the magnetic nanoparticle form factor through Fourier transformation and is accessible only by polarized small-angle neutron scattering (SANS) in contrast to diffraction which yields spatially averaged site-specific moments. Earlier studies on cobalt ferrofluids [25] were based on a core shell model, without discriminating the nonmagnetic organic ligand shell and a possible magnetic dead layer at the particle surface. In order to resolve surface-related structural details, well-dispersed samples of highly monodisperse nanoparticles are required. Recently, spin canting in assemblies of interacting magnetic nanoparticles has been reported [26, 27].

In this paper, we present the first microscopic and quantitative investigation so far of the spatial magnetization distribution within dilute, non-interacting particles of different shapes. The magnetization profile is determined by polarized SANS in an applied magnetic field. For the quantitative determination of the magnetization, the field dependence of the magnetic SANS is evaluated. Consistent with averaged macroscopic measurements, we present the first evidence for spatially resolved spin canting in non-interacting nanoparticles and the influence of nanoparticle shape on the spatial magnetization distribution. Our findings explain the reduced nanoparticle magnetization commonly found by macroscopic methods.

Oleic acid-capped maghemite nanospheres and truncated nanocubes were produced by a modification of the thermal decomposition method [28–30]. The average particle size and statistical size distribution over both local and global scales have been determined by transmission electron microscopy (TEM) and small-angle x-ray scattering (SAXS) at the beamline B1, HASYLAB, respectively. By TEM, a particle radius of 4.6(2) nm for the spheres and an edge length of 8.6(6) nm for the cubes are obtained⁸.

SAXS measurements were carried out with an incident energy of 12 keV and two different detector distances of 935 and 3635 mm. The data were recorded on a PILATUS 300k detector, radially averaged and normalized to absolute units by the use of glassy carbon as a reference material. In order to take into account the resolution in the magnitude of the scattering vector, Q, a wavelength spread of Δλ/λ = 5 × 10⁻⁵ and an overall angular resolution parameter of dθ = 0.3 mrad were implemented in SAXS refinements. As experimental parameters such as the beam size and sample thickness may also contribute to the Q resolution, the obtained particle size distribution can be regarded as the upper limit of the real particle size distribution. Refinement of the nanosphere SAXS data presented in figure 1 according to a spherical form factor results in a particle radius of 4.96(1) nm and a lognormal size distribution with 5.5(1)% full-width at half-maximum (FWHM). The nanocube data were refined according to a spherical form factor, yielding a spherical radius of 5.33(1) nm along with a lognormal size distribution with 7.2(2)% FWHM. Fits with a cubic form factor taking into account a slight truncation of the cube corners indicated that no additional information could be extracted due to the orientational averaging of the particles in dispersion. The deviation between the data and the fit for the nanocubes at small Q is due to the onset of a structure factor, and the small Q range was thus excluded for refinement. In order to rule out interparticle interactions during the determination of magnetization distribution, dilute nanoparticle dispersions that do not reveal any structure factor were chosen for the polarized SANS experiment (see footnote ⁸). A link between the spherical radius obtained using the spherical form factor and the cubic edge length can be established using the radius of gyration, R_G, which may generally be obtained in the limit of low Q according to the Guinier approximation. The radius of gyration is given by $R_{\mathrm {G}}^2 = \frac {3}{5} R_{\mathrm {s}}^2$ for a dense sphere and $R_{\mathrm {G}}^2 = \frac {1}{4} a_{\mathrm {c}}^2$ for a cubic particle. The cubic edge length a_c is thus calculated from the determined spherical radius R_s by $a_{\mathrm {c}} = \sqrt {\frac {12}{5}} R_{\mathrm {s}}$. The determined spherical radius by SAXS of 5.33(1) nm thus corresponds to an edge length of a perfect cubic particle of 8.26(2) nm, which is in good agreement with the TEM results. This further confirms the cubic particle shape observed by TEM. Due to the rotational average of the dispersed nanoparticles and for simplification of the more complex refinements of the polarized SANS data, the nanocube SANS data in this study are described primarily by spherical form factors and conversion into cubic scales is performed via the radius of gyration. Accordingly, the conversion of a particle volume determined by small-angle scattering is performed by $V_{\mathrm {c}} = a_{\mathrm {c}}^3 = \sqrt {(\frac {12}{5})^3} R_{\mathrm {s}}^3 = \sqrt {(\frac {12}{5})^3} \cdot \frac {3}{4 \pi } V_{\mathrm {s}}$. The excellent agreement of experimental SAXS data and the simple form factor model for both nanospheres and nanocubes as well as of the particle sizes determined by TEM and SAXS gives a clear indication of the chemical homogeneity of the inorganic nanoparticle core.

Zoom In Zoom Out Reset image size

The polarized SANS by dispersions of 0.14 vol-% nanospheres and nanocubes in d₈-toluene was measured at room temperature at D22, ILL, using 6 Å neutron wavelength and a horizontal magnetic field of ⩽1.5 T. The scattering cross-sections for a dilute system of non-interacting particles aligned in an external field [25, 31] allow for determination of the magnetic form factor via magnetic contrast variation by varying the incident neutron polarization:

$$\begin{equation} I^{\pm}_{Q,\alpha} = F_{\mathrm{N}}^2(Q) + [F_{\mathrm{M}}^2(Q) \mp 2 \xi^{\pm} F_{\mathrm{N}}(Q)F_{\mathrm{M}}(Q)] \sin^2\alpha, \end{equation} \tag{ 1 }$$

$$\begin{equation} I^{+}_{Q,\alpha}-I^{-}_{Q,\alpha} = - 2 (\xi^{+}+\xi^{-}) F_{\mathrm{N}}(Q)F_{\mathrm{M}}(Q) \sin^2\alpha, \end{equation} \tag{ 2 }$$

$$\begin{equation} I^{+}_{Q,\alpha}+I^{-}_{Q,\alpha} = 2 F_{\mathrm{N}}^2(Q) + 2 F_{\mathrm{M}}^2(Q) \sin^2\alpha, \end{equation} \tag{ 3 }$$

where α is the azimuthal angle between the scattering vector Q and the applied magnetic field direction, F_N and F_M are the nuclear and magnetic scattering amplitudes, respectively, and ξ⁺ = P, ξ⁻ = Pε with P = 0.89 being the degree of polarization of the incident neutrons and ε = 0.99 the flipper efficiency. While important for the determination of the magnetic scattering contribution in equations (1) and (2), this correction is negligible (ξ⁺ ∼ ξ⁻) in equation (3). F_M scales with the magnetic scattering length density (SLD_m), which depends on the projection of the magnetic moment onto a plane perpendicular to Q.

3.1. Nuclear form factor

For the determination of the spatial magnetization distribution, the purely nuclear form factor was first determined with good precision and compared to the SAXS results. Knowing the nuclear form factor parameters allows for refinement of the purely magnetic scattering contribution in the polarized SANS. Due to the angular dependence of the magnetic scattering terms in equation (1)–(3), the pure nuclear scattering can be separated by SANS with Q∥H (i.e. α = 0) in a saturating magnetic field, where all particle spins are aligned. For better statistics, we integrated a 10° sector around α =  0 in (I⁺_Q,α + I⁻_Q,α) (H =  1.5 T); see figure 2. The obtained purely nuclear scattering cross-sections given in figure 2 have been refined according to a spherical core shell form factor. The obtained scattering length density (SLD) of the inorganic nanoparticle core of 6.76(5) and 6.60(5) × 10¹⁰ cm⁻² for spheres and cubes, respectively, are consistent with the values expected for bulk magnetite, 6.96 × 10¹⁰ cm⁻², and maghemite, 6.68 × 10¹⁰ cm⁻², and thus confirm the precision of sample concentration and data normalization to absolute units. The radii of the inorganic particle core of R_N = 4.97(2) and 5.44(5) nm for the spheres and cubes, respectively, with fixed lognormal size distributions are in agreement with the SAXS results, although these were different dispersions gained from the same batch. The oleic acid ligand shell thickness dR is determined to be 1.48(1) and 1.43(2) nm, respectively. The determined radius for the nanocubes corresponds to an edge length of 8.43(8) nm, in excellent agreement with SAXS and TEM. The consistent characterization results of the studied nanoparticle samples by TEM, SAXS and purely nuclear SANS provide a robust view of the purely nuclear structure with a defined particle shape, chemical uniformity of the inorganic nanoparticle core and negligible interparticle interactions in the SANS dispersions. The chemical composition of the nanoparticles is maghemite rather than magnetite, as indicated by the determined scattering length density, the lattice parameters and vacancy concentration (see footnote ⁸), and supported by the isomer shift observed by Mössbauer spectroscopy [32]. In combination with the excellent monodispersity, these samples are distinguished as suitable model systems for the investigation of the quantitative spatial magnetization distribution.

Zoom In Zoom Out Reset image size

3.2. Magnetization distribution

Different models of the magnetic form factor were used for the determination of the spatial magnetization distribution inside the inorganic particle core; see figure 3. In the case of a uniform magnetization distribution, the magnetic form factor is given by a spherical form factor of R_M = R_N (figure 3(a)). For a magnetic particle with reduced magnetic core size, two independent approaches were considered. An entirely nonmagnetic shell results in the contrast profile depicted in figure 3(b). The magnetic form factor corresponds to a spherical form factor with R_M < R_N and a sharp magnetization decrease at the edge of the magnetic core R_M. A more realistic gradual decrease of the magnetization towards the particle surface could be ascribed to canted spins near the surface. The magnetization profile, figure 3(c), is composed of a uniform magnetization within a magnetic core of R_M < R_N decreasing linearly and approaching 0 at the surface, R_N. The only fit parameter for the first model is SLD_m, whereas for both models containing a reduced magnetic core size, two parameters, R_M and SLD_m, are refined independently.

Zoom In Zoom Out Reset image size

The magnetic form factor was refined for both nanospheres and nanocubes using two strategies. First, the magnetic contrast variation by the incident neutron polarization allows for a simultaneous refinement of the magnetic scattering contribution in the I⁺_Q and I⁻_Q cross-sections (equation (1)). Alternatively, the magnetic–nuclear cross term, derived from I⁺_Q − I⁻_Q, can be refined (equation (2)). As the nuclear form factor is known and |F_M|² ≪ |F_N|², the two approaches should be equivalent. Our refinements yield the same results with both approaches, which indicates self-consistency. Figure 4 exemplarily presents the refinements of the nanosphere scattering data according to the magnetization distribution model given in figure 3(c). The radius of the uniformly magnetized core R_M is determined to be 4.74(6) and 4.77(8) nm for the spheres and cubes, respectively. Consistently for spheres and cubes, we thus find a surface layer of lower magnetization (R_M < R_N). For the spheres, the models of a nonmagnetic surface layer (figure 3(b)), and a linear magnetization decrease in this surface layer, (figure 3(c)), are equivalent according to the reduced sum of square differences, χ²_red, given in figure 3. For the cubes, the latter model is preferred as the difference in ndf·χ²_red is significant at the 5% level of confidence [33, 34] (ndf is the number of degrees of freedom).

Zoom In Zoom Out Reset image size

The observation of a magnetic nanoparticle volume smaller than the nuclear volume can be compared with macroscopic results. We define the effective magnetic volume, V^eff, related to the total particle magnetic moment μ_R and the determined magnetization in the nanoparticle core, $\mu _{\mathrm {R}}/V^{\mathrm {eff}} = \mathrm {SLD}_{\mathrm {m}}^{\mathrm {sat}}/\frac {1}{2}\gamma _{\mathrm {n}} r_0$, where γ_n is the gyromagnetic factor of the neutron and r₀ the classical electron radius, $\frac {1}{2} \gamma _{\mathrm {n}} r_0 = 2.7\,{\rm fm}$. For a linear decrease of the magnetization at the surface, figure 3(c), V^eff depends on both R_M and R_N:

$$\begin{equation} V^{\mathrm{eff}}_{R_{\mathrm{M}},R_{\mathrm{N}}} = \frac{4\pi}{3} \left[R_{\mathrm{N}}^3 + \frac{R_{\mathrm{M}}(R_{\mathrm{N}}^3-R_{\mathrm{M}}^3)-\frac{3}{4}(R_{\mathrm{N}}^4-R_{\mathrm{M}}^4)}{(R_{\mathrm{N}} - R_{\mathrm{M}})}\right].\end{equation} \tag{ 4 }$$

The V^eff of the spheres and cubes is determined to be 480(9) and 497(13) nm³ (after conversion via the radius of gyration), respectively, in excellent agreement with the magnetic particle volumes determined from macroscopic measurements of 484(2) and 508(1) nm³ (see footnote ⁸), respectively.

The difference between R_N and R_M yields a surface thickness of 0.3(1) nm for the nanospheres. For the nanocubes, the R_M found relates to an edge length of 7.4(1) nm (see footnote ⁸) and a surface thickness of 0.52(7) nm, significantly larger than that observed for the spheres. The decreasing magnetization at the surface may result either from spin canting due to structural deviations and symmetry breaking or from reduced atomic magnetic moments. In the Mössbauer spectral analysis of the same nanoparticles, no significant contribution from iron with reduced moment is observed [32]. The reduced magnetization found close to the nanoparticle surface can thus be due only to a canting of the surface spins away from the applied magnetic field direction. The considerably larger thickness of the surface layer found for the nanocubes is probably a direct consequence of the cubic shape anisotropy, related to a larger spin canting at the cube corners [35].

After the magnetization profile has been determined qualitatively in a high magnetic field, evaluation of the field dependence of the SLD_m further provides quantitative information on the magnetization in the nanoparticle core. The SLD_m measures the orientation of the superparamagnetic particles in the applied magnetic field

$$\begin{equation} \mathrm{SLD}_{\mathrm{m}}(H) = \mathrm{SLD}_{\mathrm{m}}^{\mathrm{sat}} \cdot \mathscr{L}(\mu_{\mathrm{R}} \mu_0H/\mathrm{k}_{\mathrm{B}}T) + \beta \mu_0H \end{equation}\noindent \tag{ 5 }$$

with the Langevin function $\mathscr {L}(x) = \coth (x) - \frac {1}{x}$, where μ_R is the integral particle moment, H the applied magnetic field, μ₀ the magnetic permeability in vacuum, k_B the Boltzmann constant, T the temperature and β a phenomenological term related to excess magnetic susceptibility observed in superparamagnetic nanoparticle systems [13]. The magnetic field dependence of SLD_m in the particle core as obtained by refinement of the form factor model in figure 3(c) is shown in figure 5. The saturation SLD_m determined by equation (5) is converted into the magnetization and the atomic magnetic moments via M_v = 2μ^⊥_Fe/V_m = SLD^sat_m/(γ_nr₀/2) with V_m the molecular volume of a Fe₂O₃ formula unit, M_v the magnetization, and μ^⊥_Fe the average magnetic moment per iron atom in the ferrimagnetic iron oxide perpendicular to Q. By this approach, we obtain an average moment of 0.76(1) and 0.77(1)μ_B per iron at the center of the spheres and cubes, respectively.

Zoom In Zoom Out Reset image size

Spatially averaged atomic magnetic moments are obtained from macroscopic magnetization measurements by conversion of the integral moment μ_R with the nuclear particle volume determined by SANS. The obtained macroscopic average iron moments of 0.705(4) and 0.680(4)μ_B for the spheres and cubes, respectively (see footnote ⁸), are in good agreement with [30] and are significantly lower than the theoretical spin-only bulk maghemite moment of 1.25μ_B (0 K) (figure 5, inset). As maghemite does not exist in bulk, but exists only in nanosized form, the bulk magnetic moment is only accessible theoretically. Taking into account the temperature dependence according to the Bloch law, which amounts to a magnetization reduction of ∼20% between 0 and 300 K in the studied particle size range [36], a bulk theoretical moment of ∼1μ_B at room temperature is estimated. The macroscopic experimental results are significantly smaller than the theoretical moment. This observation is in agreement with earlier studies of the particle size-dependent magnetization [37] as well as Monte Carlo simulations of the magnetic structure of maghemite and magnetite particles based on a 3D classical Heisenberg Hamiltonian [20, 21]. As expected from the lower magnetization found at the particle surface, the core atomic magnetic moment obtained in our polarized SANS study is significantly larger than the average macroscopic moment (figure 5, inset). The integral particle moments are consistent for both methods. However, the core magnetic moment is still significantly lower than that in the bulk material. The possible effect of a reduction of the Curie temperature as found experimentally and theoretically for magnetite nanoparticles [38, 39] is very small in the studied particle size range and thus cannot account for the largely reduced magnetic moment found in the nanoparticle core. Instead, we suspect that this indicates a certain degree of magnetic disorder even in the particle core, as may result from intermediate stoichiometry or lattice strain [11]. X-ray diffraction reflection broadening indeed indicates such lattice strain (see footnote ⁸).

In conclusion, the present study gives the first microscopic and quantitative insight into the spatial magnetization distribution within non-interacting magnetic nanoparticles. We find a surface shell of gradually decreasing magnetization in chemically uniform iron oxide nanoparticles and attribute this to an increased tendency for spin canting towards the surface. Evidence for spin canting in the case of magnetically interacting nanoparticle surfaces has been reported [26], and this canting might be assumed to explain the difference in average magnetic moment found macroscopically in nano- and bulk materials [13]. The quantitative analysis presented here reveals that even the atomic magnetic moments in the particle core are significantly lower than expected. We thus conclude that the low magnetization observed macroscopically in nanoparticles results partially from spin canting at the surface, but to a much larger extent from reduced magnetization inside the uniform nanoparticle core. This has important consequences as the generally accepted model of magnetism in nanoparticles has to be further refined to account for our observations. Moreover, we have provided solid experimental data which can now serve as a test bed for advanced theoretical modeling. Whereas the core magnetic moment is found to be essentially independent of the particle shape, we observe a substantial influence of the particle shape on the thickness of the magnetically depleted surface. We attribute the gradual decrease in magnetization in the particle shell to a combination of both surface and shape anisotropies.

We acknowledge the ILL, HASYLAB/DESY and APS for the provision of neutron and synchrotron beamtime at D22, B1 and 6-ID-D, respectively, and the German National Academic Foundation for financial support (to SD).