Abstract
In this paper, we show that a fast switch is able to lead a complex dynamical system to being asymptotically stable, although this system is completely unstable in every switch duration and even the associated connection matrices are randomly selected. Importantly, we define some new exponents by which we can figure out the essential patterns that guarantee the stability of fast switching systems, and besides, their calculations need little computational cost. More interestingly, we show the efficiency of some random switches in inducing stability through a comparison of the systems with different switch connection matrices and switch durations, and we give a design method for obtaining higher efficient random switch rules. We also investigate the generalization of the obtained results to a more realistic case where the switch obeys some renewal process.
GENERAL SCIENTIFIC SUMMARY Introduction and background. Four decades ago, May (1972 Nature 238 413) proposed an ecological model of a complex dynamical system, where the simple constraint of the population size and interaction strength was established for its asymptotical stability. In the last two decades, models of complex dynamical systems or networks have attracted a great deal of attention in various scientific communities due to their broad applications in describing real dynamical phenomena: stability, periodic rhythm, chaos and synchronization. In addition to the static configurations in modeling, time-varying or even random configurations are necessarily imported because of the omnipresently environmental fluctuations and intrinsic stochastic perturbations to systems. Here we show that stability of the complex dynamical system in the physical sense can be more efficiently achieved when a random and fast switch are simultaneously taken into account.
Main results. Some exponents that require little computational cost are novelly designed to show the essential patterns that guarantee stability in both deterministic and random systems with fast switch configurations. In each switch duration, the system can be completely unstable and the connection matrices can take values along some probability density function. It is found that the systems with random configurations are much easier to stabilize or synchronize, where the probability density function plays a crucial role. We further discuss the generalization of the obtained results to the case of the switch obeying renewal process.
Wider implications. This paper suggests that a proper set of random switches could be used to stabilize complex dynamical systems. It is expected to illustrate that environmental fluctuations or stochastic perturbations could be beneficial for producing dynamical phenomena, which corresponds to particular functions possessed by a real system even with a huge population size.
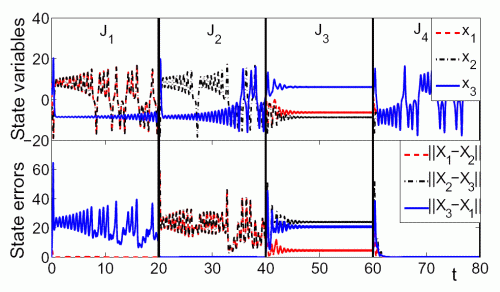 Figure. The dynamics of the first state variables xi and the state errors ||xi − xj|| for the three coupled Lorenz system systems, where i ≠ j = 1, 2, 3. In the first two time durations
Figure. The dynamics of the first state variables xi and the state errors ||xi − xj|| for the three coupled Lorenz system systems, where i ≠ j = 1, 2, 3. In the first two time durations  , static couplings are used; in
, static couplings are used; in  , a periodic-switching coupling is used; in final duration
, a periodic-switching coupling is used; in final duration 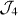 where the synchronization is achieved, a random-switching coupling with a particular probability density is utilized.
where the synchronization is achieved, a random-switching coupling with a particular probability density is utilized.
1. Introduction
Models of complex dynamical systems have attained a great deal of attention in various scientific communities simply because of their broad applications in describing real dynamical phenomena including physical motions, chemical reactions, biological or ecological evolutions, and even encoding and decoding procedure through neuronal activities [1–6]. Such types of models are always characterized by numerous interacting components. Mathematically, the interactions among the components are described by a set of connection matrices. One simple model of a complex dynamical system was proposed by May in the early 1970s, where a simple constraint on the model size and the coupling strength was established for its asymptotical stability [6, 7]. More recently, a series of investigations following and developing May's model have appeared, including studies of the time-delay influence and the realistic interactions influence on the stability of complex dynamical systems [8–11].
Although the connection matrix in May's model is random, it never changes with time once the initial time is fixed. It can always be observed in real systems that, due to the environmental fluctuations and intrinsic stochastic perturbations, the interactions among the individuals are not static but vary either slowly or quickly and even randomly. Thus, it is reasonable to introduce time-varying or switching connection matrices in modeling. Actually, many works of this kind have appeared in the literature, where it can be found that a fast switch may be beneficial for the stability of the complex dynamical networks [12–15] and also that systems with switching configurations can generate a variety of dynamical behaviors different from those observed in nonswitching systems [16, 17]. The former finding was further used to show the onset of synchronization among moving chaotic agents [18]. However, systematic discussions of the randomly time-varying and switching systems are few. One significant result of this kind is on the synchronization of the blinking networks, where an on–off (two-valued) random switch is considered [19, 20]. Also some condition for synchronization or stability needs a high cost in order to compute all the eigenvalues of the average connection matrices over an uncertain period of time [12–15].
This paper is therefore aimed at considering a complex dynamical system whose connection matrices are switched either randomly or deterministically. Some exponents that request little computational cost are designed to show the essential patterns that guarantee the stability in fast switching systems. Indeed, in each switch duration, the random dynamical system can be completely unstable and the connection matrices can take values along some continuously valued probability density function (PDF). More interestingly, through a comparison, the systems with randomly switching connection matrices are found to be much easier to stabilize or synchronize, where the form of the corresponding PDF plays a crucial role. We give a design method for obtaining higher efficient random switch rules. We also discuss the generalization of the obtained results to the case when the switch obeys some kind of renewal process [25, 26].
2. Examples showing the efficiency of a random switch
To begin, we consider the Lorenz system
with a simple and linear feedback control: F = Sq(x,y,z)⊤, where Sq is a 3 × 3 gain matrix selected from a matrix set and q = 1,2,3. Without the control, the Lorenz system exhibits chaotic dynamics, as shown, respectively, in the time periods in figure 1. With a static control, i.e. the gain matrix Sq is fixed as either one of the three matrices in all the time, the controlled Lorenz system is stabilized to some equilibria, as shown, respectively, in the periods , and in figure 1. However, for the origin (x = y = z = 0), the static control is not stable yet, since its instability can be verified simply by a positive eigenvalue of the matrix , the Jacobian matrix of the controlled Lorenz system around the origin. Also in figure 1, with a deterministic-switching control, i.e. the gain matrix is selected periodically among Se1, Se2 and Se3 with a switch duration 0.001, the controlled Lorenz system is stabilized to the equilibrium in the period . Nevertheless, this stabilized equilibrium is not the steady state of the uncontrolled Lorenz system, and the origin is still unstable. Strikingly, as shown in the period in figure 1, the unstable origin can be indeed stabilized when the random-switching control is adopted, i.e. the gain matrix is selected stochastically among Se1,2,3 with respective probabilities p1,2,3 and a switch duration 0.001.
Figure 1. The dynamics produced by the controlled chaotic Lorenz system through static controls (in, respectively, time durations , and ), a deterministic-switching control (in ) and a random-switching control (in ). The matrices in are designed as and . The probabilities for the random-switching control are selected as p1 = p2 = 0.2 and p3 = 0.6.
Download figure:
Standard imageSecondly, we consider the synchronization among three coupled Lorenz systems:
where each state variable xi = (xi,yi,zi)⊤ and L is the vector field of the Lorenz system as shown above. The coupling matrix Sq = {Sijq} is a 3 × 3 Laplacian matrix selected from a matrix set . As shown in figure 2, in the first two time durations , the synchronization cannot be realized when the connection matrix Sq is fixed as one of the matrices in . Either matrix in therefore belongs to unstable coupling. Furthermore, the synchronization cannot be surely achieved in the time duration if Sq is selected periodically between Ss1 and Ss2 with a switch duration 0.01. Interestingly, the chaotic synchronization can be realized in the last duration if Sq is selected stochastically between Se1,2 with respective probabilities p1,2 as shown in the caption of figure 2. Here, the random switch shows the special capability of realizing chaotic synchronization among coupled nonlinear systems.
Figure 2. The dynamics of the first state variables xi and the state errors ∥xi − xj∥ for the three coupled Lorenz system systems, where i ≠ j = 1,2,3. In the first two time durations , static couplings are used; in , a periodic-switching coupling is used; in final duration where the synchronization is achieved, a random-switching coupling is utilized. The matrices in are designed as and . The probabilities for the random-switching coupling are selected as p1 = 1/3 and p2 = 2/3.
Download figure:
Standard image3. Mathematical configuration of the model
The above simulation results show the capability and efficiency of a random switch among unstable controls in the stabilization or synchronization of complex dynamical systems to an unstable steady state or chaotic state of the original system. To fully illustrate the phenomenon observed above, we consider an m-dimensional complex dynamical system which is described by
with an initial condition . Here is an index function of the switching rule, which can be either random or deterministic. Moreover, the connection matrix Sσ(t) describes the switching interactions among the m-components of the system, and it takes a matrix value when the index and t belongs to the switch duration , where the time sequence satisfies 0 < Tk = tk − tk−1 ⩽ T and t0 = 0. During each switch duration, system (1) becomes simply linear and the interaction matrix can take a matrix value either randomly or deterministically.
For example, the linearization around the origin of the controlled Lorenz system we considered above can be regarded as a particular case of system (1), when the connection matrix Sσ(t) in system (1) is set as the Jacobian matrix of the controlled Lorenz system around origin, namely . Here, the index function σ(t) = q for and tk = 0.001k, and Seq is the gain matrix as defined above. More concretely, when the static control is used for the Lorenz system, σ(t) = q is fixed as one of the three numbers {1,2,3} for all t∈[0,+∞). When the deterministic-switching control is considered, the periodic index function is taken as σ(t) = q = 1 + (k mod 3) for and all . When the random-switching control is adopted, σ(t) = q in each takes a value from {1,2,3} with respective probabilities p1,2,3. Moreover, like the coupled Lorenz systems we investigated above and by adopting the variational technique along some steady synchronization manifold [1, 4, 21–24], most complex dynamical network systems of physical relevance which are described by the linear or nonlinear dynamical systems
could also be formulated into some kind of switching linear systems as system (1). For these systems, the eigenvalues of the coupling matrix Sijσ(t) contribute to the finally formulated connection matrix Sσ(t) as defined in system (1). In addition, May's model [7] could be even regarded as a specific case of system (1) since for his model every ik in system (1) is identical, but each element of the identical Sik = S is selected randomly.
To investigate the asymptotical stability of the switching system (1), we write the solution of this system as
for t∈[tk,tk+1). Here, each matrix is written decomposedly as I + SikTk + FikTk, where I is an identical matrix and Fik needs to be estimated later. Also, in what follows, we need a matrix decomposition: Sik = Dik + Aik, where Dik stands for the diagonals of Sik and the other elements constitute Aik whose diagonals are all 0. This decomposition plays a crucial role in establishing an exponent as well as criteria for guaranteeing the stability in sufficiently fast switching systems (1). With this decomposition, each matrix eSikTk can be further written as
In what follows, we are to establish feasible conditions that guarantee the asymptotical stability of system (1), that is, x(t) → 0 as t → + ∞ in the sense of probability one for a random complex dynamical system, or x(t) → 0 as t → + ∞ for a deterministic system.
4. The case of random complex systems
For a random complex dynamical system, we consider that the elements of Sik are randomly and independently selected in each switch duration . More technically, for each fixed ik, Sik is supposed to be a random and independent matrix S(ω) = D(ω) + A(ω), and thus its elements Sij(ω) (or Dij(ω) and Aij(ω)) become random variables on the probability space . In particular, ω∈Ω0 and each Sij(·) maps Ω0 into an interval . For example, the blinking complex networks investigated in [19, 20] are of specific switching systems with each Sij(ω) taking two discrete values with probabilities pij and 1 − pij. Indeed, each Sij(ω) is allowed to take multiple or continuously distributed values, obeying some PDF ρ(Sij) whose compact support is . In fact, this kind of interaction among the components is even ubiquitous in the real world.
Now, we are in a position to establish the conditions that ensure asymptotical stability of the solution of system (1) in the physical sense (i.e. in the sense of probability one). First, as mentioned above, we make an estimation (E):
where ∥·∥ denotes the Euclidean norm, and the last inequality holds if the upper bound of the switch duration T is sufficiently small, such that T < T* = (mM)−1. Secondly, for the random system (1), , set above, can be regarded as a stochastic process on , where , the natural filtration of xk, satisfies for all k. Thus, we estimate the conditional expectation as follows:
where ∥·∥1 represents the 1-norm, and for all ik are identical to since in every duration the elements of the connection matrix obey the same probability distributions as assumed above. Moreover, the independence property of the random matrix selected in each duration and T < T* are used for obtaining the formula after the third equality, and the estimation (E) ensures the formula after the second inequality. Therefore, the nonnegative stochastic process becomes a super-martingale provided that α∈(0,1), that is, conditions (RS): χr < 0 and
are satisfied. Indeed, with these conditions and according to the theory of martingale [25, 26], is convergent to a nonnegative random variable, denoted by ζ, in the sense of probability one. Note that
from the above estimation. Therefore, through recursive arguments and from Fatou's lemma [25, 26], it follows that the random variable ζ = 0 in the sense of probability one, which therefore yields a conclusion that the asymptotical stability of the solution x(t) produced by the random system (1) is ensured in the physical sense if conditions (RS) are satisfied.
Here, we further provide some illustrations of conditions (RS). Note that the exponent χr represents the expectation of some combination of the connection matrix elements. The condition χr < 0 thus means, from the viewpoint of probability, that the diagonal elements need to be negatively dominant in columns; in other words, the self-interacting intensity of each component in a complex system should be negatively stronger on average than the summation of its incoming interacting intensities. Generally, the larger the size of the system, the stronger the self-interacting intensity that is required to satisfy the condition. As is well known, for a nonrandom matrix, diagonally negative dominance implies that its eigenvalues are all located in the left-half complex plane. Nevertheless, the condition χr < 0 we established above does not lead surely to this kind of eigenvalues distribution for the matrix randomly selected in every duration . Indeed, it allows that the random matrix be unstable for almost every ik. For example, consider a complex system with a 2 × 2 random connection matrix S(ω) in which the diagonals and for i,j = 1,2 and i ≠ j. Here, ξij(ω) are mutually independent and continuous random variables, which obey the uniform distribution on [0,1]. The function is a discrete random vector taking values { − θ,0.1} and {0.1,−θ}(θ > 0), respectively, with probabilities p and 1 − p. For this example, the above-designed exponent
so that χr < 0 yields
Hence, for each ω, the matrix S(ω) is unstable with at least one positive eigenvalue, which is numerically verified in figure 3(a) for θ = 3 and p = 0.5. Therefore, in such a case, the random dynamical system (1) is unstable in every switch duration . However, according to the conclusion obtained above, we can still realize the asymptotical stability in the physical sense for such a system provided that the other condition is fulfilled (figure 3(b)). Interestingly, this shows that a sufficiently fast switch can induce stability in some kind of not only unstable but also random complex dynamical systems.
Figure 3. (a) The PDF of the maximal eigenvalue of the random matrix S(ω) shows its instability in each switch duration. (b) The asymptotically stable trajectories of system (1) with randomly selected initial values from [−1,1] and randomly selected switch Tk < 0.1. (c) The upper bound decreases with an increase of the system size m. Here, m∈[10,100] with a step size 10, each Sij obeys the uniform distribution on [−1,1] independently, and one of the diagonals is selected to subtract m2 with a probability m−1, so that χr = −0.5(m + 1) < 0. The analytical bounds , despite being smaller, are qualitatively consistent with the numerical bounds.
Download figure:
Standard imageFurthermore, the analytically obtained upper bound is strongly dependent on the system size m as well as on the maximal range M of all the random variables. The larger the size of the system, the faster the switching speed required for asymptotical stability. Figure 3(c) further shows this relation numerically, which is qualitatively consistent with the analytical bounds. Also, it is mentioned that the proposed exponent χr, as well as the upper bound , needs little computational cost if the probability distributions for the elements of the connection matrix are specified. In particular, we can compute the exponent directly through
as long as ρij, the a priori or a posteriori PDFs on the interacting intensities among the components in real systems, are given. Hence, determination of the stability of a fast switching system no longer needs a high-cost computation of the matrix eigenvalues or the Lyapunov exponents over an uncertain period of time [12–14].
5. The case of deterministic complex systems
For a deterministic system, the switching rule of the connection matrix is fixed in advance. Accurately, Sσ(t) takes values along the sequence Sik in every switch duration for , where both sequences and {ik} are given deterministically, and Sik takes values from an allowable matrix set that can contain a finite or infinite number of elements. For example, consider an allowable matrix set that contains only two unstable matrices: and , so that . Set and ik = 1 + (k mod 2) for . Then, the constructed switching rule makes system (1) switch periodically between the two unstable subsystems.
Now, a question arises: 'Can we still stabilize a system of this kind when the speed of the deterministically-fixed switch is adjusted to be sufficiently fast?'. Although the answer to this question is positive, which could be found in [12–14], we, through a particular argument below, establish some more direct and relaxable conditions to answer the question. Only with the conditions established below we are able to make a comparison and identify which kind of switch is more efficient at stabilization. Hence, we consider the other system as follows:
where the smaller the value of , the faster the switching speed. System (2) therefore could be regarded as an accelerated model of system (1). In the following discussion, suppose the original duration Tk∈[η,1] for simplicity; otherwise, we can insert some time instants without changing the real switching rules. Denote the switch duration of system (2) by Tdk. Then . For system (2), we still adopt the matrix decomposition utilized for system (1) and analogously implement the argument performed in the estimation (E). Then, we obtain if and δ ≪ 1, so that the decomposed matrices satisfy
Here and throughout, and Xn denotes a matrix. We further estimate the solution of system (2) around t = t(k+1)N with some integer N as follows:
where we need two conditions: namely condition (DS1):
for any integer k ⩾ k0 ⩾ 0 and some constant c > 1 with cζ1 < 1, and condition (DS2):
with . The notation ⊛hXh above represents an insertion of the matrix Xh into the position h of the matrix multiplication in front of this notation. Using the above estimation technique recursively, we finally obtain the asymptotical stability of the solution x(t) of the deterministic system (2)if both conditions (DS1) and (DS2) are satisfied.
Next, we interpret the two conditions (DS1) and (DS2). On the one hand, condition (DS1) can be transformed as
for all integer k ⩾ k0. Here, the negativity of the exponent χd implies that the time average of the matrix diagonals along the allowable connection matrix set is required to be sufficiently negative. This condition is somewhat analogous to χr < 0 for the random complex system, where, however, not AM but the average absolute value of the off-diagonal entries is taken into account. Moreover, the smallest switch duration η, named the dwell time of system (1), also restricts the value of χd. Thus, the condition for deterministic systems is somewhat stronger than that for random systems. Note also that the negativity of the maximal time average does not necessarily imply the stability of each allowable connection matrix. Still consider the example provided earlier in this section. Correspondingly, η = AM = 1 and m = N = 2. Therefore, the exponent χd = −0.5 < 0, although both connection matrices are unstable.
On the other hand, condition (DS2) seems to be complicated; however, it actually implies a sufficiently small value of . To intuitively see this, we depict in figure 4(a) the interval of with the parameters of the above-imported example. Although this interval is narrow, with χd < 0, it implies that we are able to stabilize the system if the speed of the deterministic switch is sufficiently fast (figure 4(b)). Therefore, the question posed above is answered completely.
Figure 4. (a) The difference Δ between the terms on the respective sides of the inequality in condition (DS2) with c = 1.5. Here, Δ > 0, i.e. , implies the validity of this condition. (b) The asymptotically stable trajectories of system (2) with the parameters of the example considered in section 3. Here, the length of each switch duration is taken as Tk ≡ 0.03 < Tδ and initial conditions are randomly selected from [−1,1].
Download figure:
Standard image6. The efficiency of randomness
We use concrete examples to further illustrate the efficiency of random complex systems in a fast switch-induced stability. Consider the complex dynamical system (1) which randomly or periodically switches among the three-dimensional connection matrices: and . These matrices are all unstable. When the switch duration is set to be sufficiently short and the switch probabilities for the matrices are given by p, q and 1 − p − q, the stability region for these probabilities is depicted analytically through conditions (RS), shown by the triangle region in figure 5(a). However, as shown in figure 5(b), the stability cannot be realized in the system that switches periodically among the three matrices S1,2,3. Thus, stability induced by fast switching is more easily realized in random complex systems. In fact, as the switch speed increases, some random switches are capable of inducing the system trajectory to more frequently visit the stable manifold generated by a proper combination of the connection matrices, which therefore leads to the negatively dominant diagonals in the probability sense. Nevertheless, the deterministic switch rarely possesses such an advantage when the switching order of the connection matrices is specified in advance. Also in figure 5(a), the stability region through the numerical experiment for all 500 times is depicted. The numerically obtained region is broader than the analytical region since conditions (RS) are only sufficient. In addition, not every but a proper designed PDF is suitable for stabilizing the random complex system. As shown in figures 5(a) and (b), even the simple uniform probabilities cannot ensure the stability. Finally, the above analyses also illustrate why the particularly designed random-switching control is capable of stabilizing the Lorenz system to the unstable origin in the previous section.
Figure 5. (a) The regions of the probabilities p and q in which the stability is ensured for the example in section 4. Here, the triangle (red) region is obtained by conditions (RS), while the lightly shaded (yellow) region is obtained by the numerical experiment for all 500 times. (b) The divergent trajectories for the systems having, respectively, periodic switch and random switch with the uniform probabilities p = q = 3−1 (marked by a dot outside the shaded region in (a)). The initial conditions are randomly selected from [−1,1], and Tk ≡ 0.01 in both (a) and (b). (c) The PDF ρ(T) of the renewal process Tk, where and ξ obeys a standard normal distribution. (d) The asymptotically stable trajectories with the random switch produced by the PDF shown in (c).
Download figure:
Standard image7. The switch obeying a renewal process
In the real world, the switch often obeys some renewal process, unlike the bounded switch duration used in the above discussion. For example, those intervals between potential spikes emitted by neurons usually satisfy either the Poisson distribution or some other distributions [5, 27]. In fact, all the results can be generalized analytically to such a case if some additional conditions on the PDF of the process are taken into account. The detailed and analytic generalization will be included in our future work. Here, to illustrate it numerically, we consider the example used in figures 3(a) and (b). Instead, Tk of the switch is supposed to be a renewal process obeying the PDF specified in figure 5(c). As shown in figure 5(d), the asymptotical stability can be realized in the physical sense if there exists a number Tc ∼ M−1 such that is sufficiently small. This means that to obtain the stability, the switch needs to be sufficiently fast most of the time and is allowed to be slow occasionally.
8. Concluding remarks
We have defined some exponents by which we are able to analytically identify the essential patterns that guarantee the stability or synchronization of complex dynamical systems with either a deterministically or a randomly switching configuration. The analysis of these exponents has allowed us to describe the capacity and efficiency of the random switch for stabilizing or synchronizing a complex dynamical system which is indeed unstable in every switch duration. Also we have emphasized the possibility of generalizing the obtained results to the more realistic case when the switch obeys some kind of renewal process. We believe that all the results obtained in this paper are of practical use for the analysis and modulation of the dynamical behaviors of some real complex systems involving random fluctuations.
Acknowledgments
This work was supported by the LMNS, the NNSF of China (grant no. 10971035), Shanghai Shu-Guang Program (no. 10SG02), Tracked Rising-Star Program (no. 11QH1400200) and New Century Excellent Talents Program (no. NCET-11-0109) and the Spanish Ministry of Science and Innovation under project no. FIS2009-09898.





















![$S^\mathrm{e}_{1}= [2~ -\!2~ 0; 2~ -\!2~ 0;2~ -\!2~ 0],~S^\mathrm{e}_{2}= [0~ -\!2.7~ 3\sqrt{2}/5; 0~ -\!2.7~ 3\sqrt{2}/5; 0~ -\!2.7~ 3\sqrt{2}/5]$](https://content.cld.iop.org/journals/1367-2630/14/8/083022/revision1/nj424578ieqn16.gif)
![$S^\mathrm{e}_{3} = [-1/3~ -\!15.1~ -\!\sqrt{2}/5; -\!142/3 ~ 47/30 ~ -\!\sqrt{2}/5; -\!1/3 ~ 47/30 ~ -\!\sqrt{2}/5]$](https://content.cld.iop.org/journals/1367-2630/14/8/083022/revision1/nj424578ieqn17.gif)









![$S^\mathrm{s}_{1}= [-8~ 8~ 0; 8~ -\!8~ 0;0~ 0~ 0]$](https://content.cld.iop.org/journals/1367-2630/14/8/083022/revision1/nj424578ieqn28.gif)
![$S^\mathrm{s}_{2}= [-4~ 0~ 4; 0~ 0~ 0; 4~ 0~ -\!4]$](https://content.cld.iop.org/journals/1367-2630/14/8/083022/revision1/nj424578ieqn29.gif)


















![$\mathcal {J}= [-M,M]\subset \mathbb {R}$](https://content.cld.iop.org/journals/1367-2630/14/8/083022/revision1/nj424578ieqn44.gif)







![$\mathbb {E}[D_{i_k}^{ii} +\sum _{j=1}^m\big |A_{i_k}^{ji}\big|]$](https://content.cld.iop.org/journals/1367-2630/14/8/083022/revision1/nj424578ieqn50.gif)
![$\mathbb {E}[D^{ii}+\sum _{j=1}^m\big |A^{ji}\big | ]$](https://content.cld.iop.org/journals/1367-2630/14/8/083022/revision1/nj424578ieqn51.gif)
























![$S_{1}=[1 ~ 1;1 ~-\!4 ]$](https://content.cld.iop.org/journals/1367-2630/14/8/083022/revision1/nj424578ieqn70.gif)
![$S_{2}=[ -4 ~ 1 ;1 ~ 1 ]$](https://content.cld.iop.org/journals/1367-2630/14/8/083022/revision1/nj424578ieqn71.gif)






![$T^{d}_k\in \big [\eta \tilde {T}, \tilde {T}\big ]$](https://content.cld.iop.org/journals/1367-2630/14/8/083022/revision1/nj424578ieqn77.gif)













![$S_{1}=[-\!9~ 0~ 2; 0~ 2~ 0; 2~ 0~ 2],~S_{2}=[2~0~2; 0~ 2~ 0; 2~ 0~-\!9]$](https://content.cld.iop.org/journals/1367-2630/14/8/083022/revision1/nj424578ieqn85.gif)
![$S_{3}=[2~0~ 2; 0~ -\!9~ 0; 2~ 0~ 2]$](https://content.cld.iop.org/journals/1367-2630/14/8/083022/revision1/nj424578ieqn86.gif)


