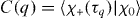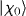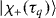Abstract
When generated in molecules, high-order harmonics can be emitted through different ionization channels. The coherent and ultrafast electron dynamics occurring in the ion during the generation process is directly imprinted in the harmonic signal, i.e. in its amplitude and spectral phase. In aligned N2 molecules, we find evidence for a fast variation of this phase as a function of the harmonic order when varying the driving laser intensity. Basing our analysis on a three-step model, we find that this phase variation is a signature of transitions from a single- to a multi-channel regime. In particular, we show that significant nuclear dynamics may occur in the ionization channels on the attosecond timescale, affecting both the amplitude and the phase of the harmonic signal.
1. Introduction
High-order harmonic generation (HHG) is a spectacular, highly nonlinear response of molecules irradiated with a strong laser field. During the interaction, a valence electron is (i) liberated through tunnel ionization, (ii) accelerated by the laser electric field in the continuum and finally (iii) driven back to the ionic core, leading to the recombination and emission of coherent extreme ultraviolet (XUV) radiation [1, 2]. HHG emission thus results from the interferences between the initial ground state and the recolliding electronic wave packet. The latter presents a combination of remarkable properties, i.e. ultrashort de Broglie wavelength and ultrashort duration. Probing of the structure and dynamics of the emitting molecule itself is therefore achievable with both sub-angström spatial and attosecond (10−18 s) temporal resolutions [3]. The detailed understanding of this self-probing process, combined with pump–probe and molecular alignment techniques, has led to many breakthroughs in recent years: orbital reconstruction [4–7], observation of ultrafast molecular dynamics [8–10] and time-resolved study of ultrafast chemical processes [11].
In various situations, spectral intensity minima and corresponding phase jumps appear in the emitted harmonic signal. Until now, three classes of minima related to either structural or dynamical features have been observed in HHG. The first type of minima, referred to as 'Cooper-like', involves destructive interferences originating from the nodal structure of the ground state and possibly involving different angular momentum components of the unbound electron wave packet when it recombines with the ground state [12]. The position of such minima is independent of any laser parameter—especially the intensity (IL) [13]. The second type, called 'structural', appears, e.g., when destructive interferences occur between XUV emissions from a two-center type of molecule [14, 15]. Structural minima are characteristic of the recombination dipole moment (RDM) of a given channel and their positions do not change with the laser parameters [14, 16], but they are sensitive to the molecular alignment angle θ with respect to the laser polarization [17–19]. The third type of minima, referred to as 'dynamical', is present when several molecular orbitals (channels) contribute to HHG. In the specific situations where two contributions end up with a π-phase difference and thus interfere destructively, a marked minimum appears in the harmonic spectrum. Varying either the driving laser intensity IL or wavelength λL shifts their relative phase and thus modifies the spectral position of dynamical minima [20, 21].
The discrimination between the different types of minima is therefore based on three main experimental parameters: θ, IL and λL. However, the interplay between different types of minima simultaneously present in the harmonic spectra may complicate severely the retrieval of information and leads to controversies. For instance, in CO2 the observed minimum was first attributed to a structural effect [17–19], then to a dynamical effect due to its change of spectral position with IL [20] and finally to a combination of both [21, 22]. In N2, most studies found a minimum close to 40 eV barely moving with varying θ, IL and λL [21, 23, 24]. Simulations using the quantitative rescattering theory indicated that a single orbital contribution and macroscopic propagation effects could be responsible for it [25]. However, a recent study found a 'small' change in spectral position when varying θ and IL [26]. The authors attributed it to multi-orbital contributions, although their model was not able to reproduce the observed harmonic spectrum.
The so-called dynamical minima indicate that several orbitals, typically the valence molecular orbitals (HOMO-1, etc) lying close below the highest-occupied one (HOMO), are high enough energetically to contribute to the tunneling process (step (i)). The molecular ion is then left in a coherent superposition of the ground (X) and excited states (A, B etc) that evolves during the continuum excursion (step (ii)) prior to recombination (step (iii)). All these ionization channels finally contribute to the harmonic emission [20, 27] which encodes the ultrafast dynamics occurring in the molecular ion, giving access, e.g., to the rearrangements occurring in the electronic shells within less than one laser cycle [28, 29]. In order to access both structural and dynamical information, it is thus of great interest to identify the different channel contributions to HHG. In the above-described studies, this has been done almost exclusively using harmonic intensity measurements [17, 18, 21, 22, 27, 30, 31].
A more advanced characterization of the harmonic emission is thus required to identify better the different channel contributions. Recent measurements of harmonic ellipticity contrasted with simulations led to the conclusion that there is a single efficiently contributing channel in N2 in special generating conditions [29, 32, 33]. The variation of the harmonic phase with the recollision angle has also been used to identify the main contributing channel in CO2 [20].
In this paper, we show that the measurement of the harmonic spectral phase is particularly well-suited for extracting information on multi-orbital contributions. By varying the laser intensity IL, we find evidence for a control of the relative weight of the ionization channels from the HOMO (channel X) and from the HOMO-1 (channel A) contributing to the HHG in N2, up to a situation where the A channel contribution is considerably reduced. In our simulations, we identify two mechanisms for explaining the measured non-trivial phase evolution. Firstly, the difference in continuum dynamics of the two channels controls the harmonic phase in the cutoff region. Secondly, the remarkably fast—sub-cycle—nuclear dynamics occurring on an attosecond timescale in the A channel strongly affects its contribution to HHG. Section 2 is devoted to the phase measurements of harmonics generated in N2. Section 3 deals with the two-orbital model we developed and the interpretation of the experimental results. Finally, the conclusions are presented in section 4.
2. Experimental results
Our experimental setup allows non-adiabatic alignment [34] of the N2 molecules, followed by attosecond pulse generation and characterization in amplitude and phase (details can be found in [5]). In the present work, the alignment laser pulse was stretched to 120 fs, with a constant intensity of 5 × 1013 W cm−2, in order to maximize the degree of alignment at half-revival, which was estimated to be . The 55 fs generating pulse then drives HHG at the half-revival. Care was taken to ensure detection of only the short trajectories' contribution to HHG [35, 36]: firstly, the gas jet was placed ≈3 mm after the laser focus in order to phase match only these contributions; secondly, an iris set 0.8 m downstream cut the outer part of the harmonic beam, where the long trajectories are expected to dominantly contribute. Harmonic phase characterization was performed using the RABBIT technique [37] that yields the group delay (GD) at the even ordered side bands (SB): GDq = (ϕq+1 − ϕq−1)/2ωL, where ϕq±1 are the phases of two consecutive odd harmonics and ωL is the fundamental laser frequency.
Our procedure for tracing multi-orbital contributions is the following. We measure the spectral phase of harmonics generated in Ar (ionization potential IArp = 15.7 eV) and in N2 (IHOMOp = 15.6 eV) under the same experimental conditions. Argon provides a very useful reference for two reasons. Firstly, the phase of its RDM (step (iii)) does not vary much over our considered spectral range [38] so that the harmonic phase is determined by the continuum dynamics (step (ii)). The latter leads to a quadratic variation of the spectral phase and thus to a linear GD in the plateau region corresponding to the recollision times of the electron trajectories [39], as shown in figure 1(a). Secondly, the slope of the GD curves (atto-chirp) is inversely proportional to the driving laser intensity and provides quite an accurate estimate of the effective intensity in the generating medium [39, 40]. Fitting the data in figure 1(a) and making a comparison with strong-field approximation (SFA) calculations [39, 41, 42] gives intensities in the range 0.7–1.3 × 1014 W cm−2. Comparable Ip and the same generation conditions would ensure that the continuum dynamics for all harmonic orders is the same in Ar and N2 if only the HOMO (channel X) contributed. In that case, their harmonic phase difference should contain only the phase of the HOMO RDM. Therefore, any distortion of the harmonic phase difference when varying the laser intensity IL can be attributed unambiguously to lower-lying orbitals. This technique is very general and applies whatever the value of the relative phase between the different contributing channels is.
Figure 1. Group delays measured in Ar (a) and in N2 for θ = 90° (b), for different driving laser intensities indicated in units of 1014 W cm−2. All curves are vertically shifted in order to have the same origin of 1100 as at SB16. Horizontal dashed lines are plotted in order to emphasize the difference between the GDs of Ar and N2. Each curve represents a typical GD curve from a group of curves obtained on different days within a small range of ΔIL around the central intensity value.
Download figure:
Standard imageWe show in figure 1(b) typical GD curves measured in N2 for a recollision angle of 90° (the generating beam polarization was orthogonal to that of the alignment beam). This angle is expected to maximize the contribution of the HOMO-1 (channel A, IHOMO−1p ≈ 17 eV) due to its symmetry [27]. Following the above procedure, GD curves for Ar and N2 taken the same day in the same conditions (IL) are used to calculate the harmonic phase difference, dubbed in the following as the 'calibrated phase'. To increase the confidence in the results, this phase difference was averaged over typically five data taken on different days within small IL intervals. The results are plotted in figure 2(a).
Figure 2. Harmonic phases (a) and intensities (b) measured for N2 at θ = 90° calibrated with the corresponding Ar quantities (see text). All phases are moved to 0 at H15.
Download figure:
Standard imageFor the lowest intensities (IL = 0.7–0.9 × 1014 W cm−2), the GDs measured in N2 vary linearly in the plateau region (cf figure 1(b)), like the corresponding Ar curves (cf figure 1(a)). This translates into a similar phase behavior for both IL. Since the increase in IL introduced only a slight deviation between the two curves, we conclude that the channel X is dominant at these intensities. Increasing further IL, the GD curves of N2 deviate more and more from the GD curves of Ar, with values smaller than in Ar below SB26 and larger above. The resulting calibrated phases show a fast decrease at intermediate harmonic orders and a re-increase at high orders (cf figure 2(a)). This produces a minimum that becomes deeper, reaching −0.7π rad, while shifting towards higher harmonic orders (from H25 to H27–29) when IL is increased. This fast evolution with IL is a clear signature of the growing contribution from channel A. The transition between the two regimes occurs around 1 × 1014 W cm−2, which may explain the mixed behavior of the phase at this IL. A striking fact is that, when calibrating the harmonic intensity spectra measured in N2 by those measured in Ar, we find a broad minimum around H19–23 that does not depend on intensity (cf figure 2(b)). In previous works, this led to the conclusion that a single orbital contributes in this spectral region [21]. Only very recently, a study using mid-IR lasers observed an IL-dependent spectral minimum that was related to multi-orbital contributions [31]. Our measurements show that phases are much more sensitive to multi-orbital dynamics than the harmonic intensity spectra. To interpret further the observed phase behavior and spectrally resolve the multichannel contributions to the measured data, we have developed an SFA-based model aimed at a qualitative interpretation, which will be presented in the next section.
3. Theoretical model and interpretation
In our approach, the radiative molecular dipole is expressed as a sum over the complex amplitudes for the uncoupled X and A channels. Each amplitude is a product of factors issued from the three-step model [38]. In the following, we study for each step the factors governing the relative amplitude of channels X and A.
We show in figure 3(a) the ratio of the square roots of the tunnel ionization rates γX,A(θ = 90°,q), relative to step (i). They are computed with a method recently developed by Murray et al [43]. For each harmonic order q, we used the instantaneous field strength at the ionization time corresponding to the short trajectories. It turns out that the ratio of the ionization rates slowly varies with the order q, but strongly depends on IL: the higher the intensity, the larger the weight of the A channel.
Figure 3. Variation of the relative amplitudes of the X and A channels as a function of the harmonic order at different intensities: (a) square root of tunneling rate ratio γA/γX at θ = 90°. (b) Modulus (solid) and phase ΔΦ (dash) of the continuum amplitude ratio aA/aX. (c) Modulus (solid) and phase (dash) of the autocorrelation function CA; the corresponding axes are left and right for modulus and phases, respectively. IL = 0.7 (red), 1 (black) and 1.3 (blue) ×1014 W cm2.
Download figure:
Standard imageIn figure 3(b), the modulus |aA(q)/aX(q)| and the phase of the continuum amplitude ratio aA/aX are shown. These complex amplitudes account for both the spread and the accumulated phase of the electron wave packet during its excursion in the continuum (step (ii)) through each ionizing channel. These quantities and all the requested timings are evaluated using 'atomic' SFA calculations [41, 42] with Ips adjusted to those of the HOMO and HOMO-1 of N2. In analyses based on single-channel descriptions [4, 19, 38], the continuum amplitude aX(q) is expected to disappear when calibrating the dipole by a reference atom. However, in our multichannel formalism, calibration with Ar removes this amplitude only in the channel X, leaving a ratio aA/aAr ≃ aA/aX in the channel A. We found that the modulus of this ratio, close to unity for lower harmonics, displays a sudden jump at a definite order depending on IL. These jumps occur between the different cutoff locations of the channels X and A, and significantly increase the weight of the latter. The relative phase ΔΦ decreases almost linearly toward the channel A cutoff and then remains constant. This is reminiscent of the evolution with the harmonic order of the short trajectory duration τq since ΔΦ ≈ ΔIpτq = (IHOMOp − IHOMO−1p)τq [5]. This phase also characterizes the coherent superposition of the X and A states as it evolved until recombination time.
To model the recombination step (iii) in molecules, one must in principle take into account both the electronic and the nuclear parts of the total molecular wavefunction. The nuclear part is important when fast nuclear motion occurs during the electron excursion in the continuum, i.e. when the ionic Born–Oppenheimer energy surface is significantly shifted away from the ground state surface [44, 45]. The Born–Oppenheimer energy surfaces on which the nuclear wavefunctions are propagated are obtained by fitting Morse potential functions to 'exact' potential energy surfaces [46]. Assuming vertical transitions, this is accounted for in a given channel by the autocorrelation function , where represents the fundamental vibrational state of N2 and represents the nuclear wave packet as it evolves on the ionic energy surface during the electron excursion time τq [44] on the sub-fs timescale. C(q) is, in general, complex valued and thus contributes a phase to the harmonic dipole [9]. While it is known that the autocorrelation function weakly affects HHG through channel X in N2 (CX ≈ 1) [45], we found that its impact is far from being negligible for channel A. The corresponding autocorrelation function |CA|, displayed in figure 3(c), decreases significantly until the cutoff region where it remains constant; there, it lowers the contribution of channel A by a factor larger than 2 in intensity. The recently published results of Farrell et al [47] showed a similar influence of channel A, when analyzing the harmonic's spectral intensity generated in H2O/D2O molecules. In addition, we remark that CA(q) also introduces an additional phase close to −0.3π that varies slowly with order q. Such a phase, not taken into account in all previous studies in N2 [5, 24, 26, 27, 29, 30], is large enough to significantly modify the interference between the two channels.
The electronic recombination is described by the RDMs dX,A,Ar, calculated from field-free atomic or molecular orbitals given by GAMESS [48] (using a minimal 6-31G basis set) and continuum plane waves (PW). We checked that the dipole ratios dA/dX evaluated with PWs or using accurate scattering waves (SW) [38] have the same behavior at θ = 90°. The ratio of their respective amplitudes varies in a similar way on the spectral range and does not differ by more than a factor of 1.5. In addition, the phase difference coming from SW RDMs varies by only 0.1π throughout the spectral range. Its influence is therefore considerably less than that of other phase factors, e.g. the continuum phase ΔΦ.
All these contributions obviously vary in a different manner with q. Nevertheless, their relative weight can finally be evaluated via the expression of the dipole calibrated by Ar and projected onto the θ direction
Note that all factors depend on both q and IL, except dX,A,Ar, which depends on q only.
The total amplitude ratio |DA/DX|, shown in figure 4(a) for θ = 90°, exhibits a transition from a main channel X contribution at low harmonic orders to a dominant channel A at high orders. The observed jumps are clear imprints of the continuum amplitude ratio (cf figure 3(b)). Inclusion of the autocorrelation functions lowers the A contribution over the whole range, in agreement with the above analysis.
Figure 4. Variation with harmonic order at θ = 90° for different intensities of: (a) |DA/DX|, (b) and (c) Φcalt, i.e. Φt calibrated and rotated. Simulations are performed with (solid) and without (dash) autocorrelation functions; the color keys are the same as in figure 3.
Download figure:
Standard imageFigure 4(b) shows the phase Φt of the normalized DN2 dipole (equation (1)) as a function of q. At low orders, while the dipole from the HOMO is preponderant (≈1:0.7; cf figure 4(a)), the phase variation mainly comes from the change in continuum phase ΔΦ. At intermediate orders, although dampened by the amplitude factors, the transition between the channels X and A due to the different cutoff extensions strengthens the contribution of ΔΦ, responsible for the intensity dependence of Φt. At high orders, the evolution of Φt is mainly governed by the phase of DA and thus by the phase of the HOMO-1 RDM dA, the continuum phase ΔΦ and the phase of CA (≈− π/4). In order to make a comparison with the experimental trend shown in figure 2(a), we calibrated both the phases at H15 and the GDs at SB16, according to the experimental procedure.
Qualitative agreement of Φcalt with the experimental results is observed, with a decrease of the phase with intensity (cf figure 4(c)). The phase increase measured at high orders is partially retrieved when taking into account the autocorrelation functions that significantly modify the general trend. However, it is still not sufficient to fully explain the re-increase of the molecular phase at high harmonic orders, which we interpret to be a 'revival' of the HOMO phase, as the contribution of the HOMO-1 vanishes due to the gradual decrease of the autocorrelation function in the channel A with q. We checked that averaging over the experimental angular distribution leads to the same conclusions. Finally, other factors not included in our theory may bring additional spectral phase distortions, such as coupling between different ionization channels [29]. This emphasizes the need for a thorough characterization of the harmonic signal in order to identify and separate the nuclear and electronic ultrafast dynamics on the sub-fs timescale.
4. Conclusion
In conclusion, we have found that the relative amplitudes of the contributions of different ionization channels to HHG can be controlled through a fine-tuning of the laser intensity. More precisely, in N2 we attribute the non-trivial HHG phase behavior over the spectral range to variations of the X- and A-channel relative amplitudes and phases. An analysis of the harmonic spectral phase in the region of the amplitude minimum thus revealed unexpected features not visible in the intensity-independent minimum. This opens up perspectives at several levels. Firstly, this should benefit the selection of single channels in order to better resolve structural and dynamical effects in HHG or when exploiting the harmonic dipole, e.g. for orbital tomographic reconstruction. Secondly, a control over the weight of ionization channels should provide insights into the electron dynamics occurring within the ion during tunnel ionization. Thirdly, the uncovered channel-dependent nuclear dynamics found in this work opens the possibility for interferometric measurement of the phase of the autocorrelation function, which could be explored over longer timescales using long trajectories or mid-IR laser fields. This also extends the field of HHG-based ultra-fast measurements to the study of correlated vibronic motion possibly launched by non-Frank–Condon transitions.
Acknowledgments
We thank R Murray and P Breger for their help with simulations and the experiments in CEA, respectively. We acknowledge financial support from the EU-FP7-ATTOFEL and ANR-09-BLAN-0031-01.




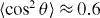


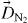

![$\Delta \Phi (q)=\arg [a_{\rm {A}}(q)]-\arg [a_{\rm {X}}(q)]$](https://content.cld.iop.org/journals/1367-2630/14/2/023062/revision1/nj414433ieqn3.gif)