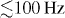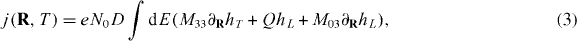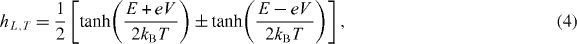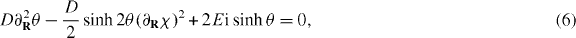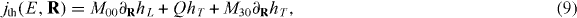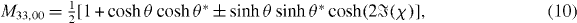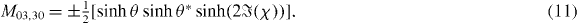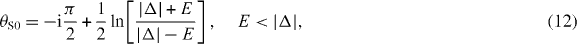Coherent nonlocal correlations in Andreev interferometers

For a single normal metal in contact with a superconductor, a quasiparticle with energy E (with respect to the Fermi energy) less than the energy of the superconducting gap Δ cannot propagate into the superconductor. In the case of a singlet superconductor it instead combines with a quasiparticle of energy −E of opposite spin polarity in the normal metal to form a Cooper pair in the superconductor. The removal of the second quasiparticle can be thought of as leaving behind a quasihole that propagates in the opposite direction, so that one can consider the first quasiparticle being reflected as a quasihole with the concomitant generation of a Cooper pair in the superconductor, in a process called Andreev reflection [1]. If two normal metals are connected to the same superconductor, one can have a nonlocal version of Andreev reflection, so long as the distance between the two normal metals is less than or comparable to the superconducting coherence length ξ_S [2, 3]. This is illustrated schematically in figure 1(c), where injection of a quasiparticle from one normal metal into the superconductor leads to the emission of a hole of opposite spin polarity into the second normal metal. The nonlocal version of Andreev reflection has been termed crossed Andreev reflection (CAR) [4]. Experimentally, it can be observed by injecting a quasiparticle current from one of the normal metals into the superconductor, which will give rise to a negative voltage at the second normal metal with respect to the superconductor. This voltage is nonlocal in the sense that no current flows through the junction between the second normal metal and the superconductor.

Zoom In Zoom Out Reset image size

The additional complexity of this geometry gives rise to a second process, illustrated schematically in figure 1(d), that can also lead to a nonlocal voltage in response to the injected quasiparticle current. The injected quasiparticle can enter the superconducting condensate as half of a Cooper pair if a vacancy in the quasiparticle occupancy is simultaneously created by the ejection of a quasiparticle into the second normal metal with the same spin and energy as the injected one. Again this process, known as elastic cotunneling (EC) [3], only occurs if the distance between the two normal metals is less than or comparable to ξ_S. EC leads to a nonlocal voltage on the second normal metal in response to a quasiparticle current injected from the first normal metal that is positive when measured with respect to the superconductor. In the case when the transparencies of the NS interfaces are low (i.e. in the tunneling regime), the contributions of the CAR and EC processes are predicted to be equal and, since they are of opposite sign, no net nonlocal voltage should be observed [3]. For higher-transparency interfaces, or in the presence of interactions, the EC contribution is predicted to be larger than the CAR contribution [5–7], so that the net nonlocal signal is positive. Nonlocal signals arising from these processes have been measured in linear, singly connected samples by a number of groups (including ours) [8–11], with both ferromagnets and conventional metals placed in contact with the superconductor.

One of the predictions regarding these nonlocal processes is that the mutual interaction with the superconductor coherently couples the quasiparticles in the two spatially separated normal metals, so that quasiparticles in the separate normal metals are in a coherent entangled state. In the experiments on linear samples mentioned above, only the scattering processes at the normal/superconductor (or ferromagnet/superconductor) interfaces and the interactions in the superconductor were relevant, with no measurements carried out that would be sensitive to the long-range phase coherence between the normal metals. Our goal in initiating the experiments discussed here was to demonstrate this coherence by modulating the quantum phase of the quasiparticle wave functions in one normal metal while monitoring the nonlocal voltage, with respect to the superconductor, on the second normal metal. To modulate the phase of the wave function, the first normal metal was embedded in a loop that formed an Andreev interferometer, shown schematically in figure 1(b). By threading an Aharonov–Bohm flux Φ through the area of the Andreev interferometer, one can modulate the phase of the quasiparticle wave function in the embedded normal metal, with a fundamental period corresponding to the superconducting flux quantum Φ₀ = h/2e [12, 13]. Our experiments demonstrate that in establishing phase coherence around the Andreev interferometer the nonlocal CAR/EC voltage signals observed in previous experiments are effectively shorted out by the simply connected geometry. However, if a nonequilibrium quasiparticle distribution is produced in the normal section of the interferometer loop while preserving phase coherence around it, nonlocal, phase-coherent oscillations are measured in the normal leads that are not part of the interferometer, but are connected to it through superconducting wires of lengths comparable to ξ_S. As we will show below, these oscillations are the result of a spatially nonuniform nonequilibrium supercurrent in the normal arm of the interferometer, which leads to phase-coherent quasiparticle currents being injected into the superconductor that produce flux-dependent voltages in the nonlocal leads via the CAR/EC mechanisms.

The samples studied were composed of 99.999% pure Al and Au, which served as the superconductor (S) and normal metal (N), respectively. Samples were fabricated by conventional electron-beam lithography with the metals deposited by thermal evaporation with a typical thickness of 50 nm. An in situ O₂⁺ plasma etch was performed prior to the Au deposition to ensure surface adhesion to the Si/SiO₂ substrate, and an Ar⁺ etch prior to the Al deposition to ensure clean NS interfaces. Low-temperature measurements of the NS interfaces yielded a contact resistivity of 1.9 Ω μm², comparable to the Sharvin resistivity. While several samples were fabricated and measured, we shall restrict ourselves here to the discussion of the measurements on two samples. Figures 1(a) and 2(a) show SEMs of these samples, which have slightly different designs. From previous experience with similarly deposited films in our group, the superconducting phase coherence length ξ_S in the Al is typically of the order of 100–130 nm. For the normal metal, two length scales are relevant. The first is the Thouless length $L_{{\rm T}} = \sqrt {\hbar D/k_{{\rm B}} T}$, where D is the electron diffusion constant in the normal metal, and T is the temperature [14]. For the superconducting proximity effect, L_T is also the superconducting coherence length in the normal metal. From measurements on simultaneously deposited long wires, D ∼ 100 cm² s⁻¹, giving L_T ∼ 275 nm at T = 1 K, and close to 2 μm at ∼20 mK, near the base temperature for our measurements. The second relevant length scale is the electron phase coherence length L_ϕ. If the length of the normal arm of the Andreev interferometer is appreciably longer than L_ϕ, any phase-coherent effects are expected to be significantly suppressed. In addition, the length of the normal metal arm of the interferometer has to be less than both L_ϕ and L_T to sustain a Josephson current in the loop. In the first samples we fabricated, an example of which is shown in figure 2(b), L_ϕ was of the order of 600 nm at the base temperature of our refrigerator, as determined from weak localization measurements on co-evaporated long normal wires. This length is shorter than the length of the normal metal arm of the interferometer (∼1.5 μm), so that no phase-coherent effects could be observed, nor would any circulating supercurrent be expected even at the base temperature of our measurements. Subsequent devices were fabricated after thoroughly cleaning the thermal evaporator used for depositing the Au films (figure 1(a) shows an example of such a sample), and weak localization measurements on a simultaneously evaporated Au wire confirmed that L_ϕ exceeded 8 μm at our lowest temperatures, so that phase-coherent effects were observed, and a circulating supercurrent established in the normal arm of the interferometer. As we shall see below, the presence or absence of long-range phase coherence in the normal arm of the loop significantly affects the nonlocal signals that were observed.

Zoom In Zoom Out Reset image size

The samples were cooled in an Oxford dilution refrigerator and measured using low-frequency (${\lesssim }100\,{\rm Hz}$) lock-in amplifier detection in conjunction with modified Adler–Jackson resistance bridges [15], with radio-frequency-filtered wiring to avoid heating from extraneous noise sources. Small resistance offsets of the order of 100 mΩ can be introduced by the resistance bridges, and were subtracted from the data after calibrating the voltages detected with conventional four-probe lock-in measurements. In some measurements a dc current was summed with the ac modulation current in order to measure the differential resistance dV/dI of the samples.

Figure 2(d) shows the measured nonlocal and local differential resistance of the sample of figure 2(b) at 20 mK. The current, consisting of a small ac component superposed on the dc current, is introduced through the normal arm of the interferometer, and taken out either through the superconducting arm of the interferometer (for the nonlocal measurement) or the dangling superconducting side arm (for the local measurement), as shown in figure 2(c). Voltages on nonlocal leads, each spaced by a few hundreds of nanometers, are measured relative to the superconductor potential. The first configuration is similar to the nonlocal CAR/EC measurement configurations in linear samples [10]. The differential resistance as a function of dc current is similar to what has been observed for linear samples: a large peak due to charge imbalance at high current bias, and a small but finite positive differential resistance at zero bias due to CAR/EC for the probes closest to the point at which current is injected into the superconductor. Both the charge imbalance peak and the CAR/EC peaks are suppressed as the distance between the probe and the current path increases, with the CAR/EC peaks showing a much more rapid decay, consistent with their expected suppression on the length scale of ξ_S. The equivalent 'local' measurement configuration (see figure 2(c)) shows almost identical behavior (figure 2(d)), except for the lower value of the critical current due to a different current path in the superconductor. The equivalence of the two current paths is not surprising as the only requirement for seeing charge imbalance and EC/CAR effects is that a quasiparticle current should be injected into the superconductor, the subsequent path of the current in the superconductor having no effect.

As mentioned above, L_ϕ for this sample was short (∼600 nm) even at our base temperature, much shorter than the normal metal arm of the interferometer, and hence no phase-coherent effects were observed. For example, conventional four-terminal magnetoresistance measurements of Andreev interferometers should show oscillations with a fundamental period of Φ₀ if L_ϕ is longer than the normal metal arm, but no such oscillations were observed for this sample. In order to examine phase-coherent effects we fabricated additional samples with L_ϕ much longer than the length of the normal arm of the interferometer at our base temperature. We focus on one such device, with geometry identical to that shown in figure 1(a), although similar qualitative and quantitative results were observed in other devices. Figure 3(a) shows the conventional four-terminal differential resistance of this device at 14 mK. Large magnetoresistance oscillations of period Φ₀ and amplitude 40% of the total resistance were observed, consistent with the expected phase coherence around the loop. As expected, these oscillations are symmetric with respect to the applied magnetic flux, with a minimum at zero applied flux. Figure 3(b) shows the nonlocal differential resistance measured on the same sample in a configuration similar to the data in figure 2(d). Contrary to expectations based on experiments of linear samples and the sample of figure 2, no nonlocal differential resistance was observed. The disappearance of previously observed nonlocal signals is not entirely understood; however, as is detailed below, once phase coherence is established around the loop, nonlocal voltages cannot be explained by only considering a segment of the loop. The quasiparticle conversion processes that were isolated at one NS interface of the loop in the sample lacking phase coherence are now correlated with conversions at the other NS interface, resulting in a vanishing of the EC/CAR voltages measured in earlier experiments.

Zoom In Zoom Out Reset image size

Although these previously observed voltages cannot be used to examine phase coherence of the EC and CAR processes, nonlocal phase coherence can be exhibited through other measurements. The data shown in figures 3(a) and (b) are taken using only ac currents of 20 and 100 nA, respectively. If a small dc current is superimposed on the ac current, oscillations in the nonlocal differential resistance with a fundamental period of Φ₀ appear, as shown in figure 3(c). The measurement configuration for these data is identical to the measurement configuration for the data of figure 3(b): the only difference is the addition of a dc current. The sign of the oscillations reverses if the dc current is reversed. The oscillations have a sawtooth waveform reminiscent of the expected form of the oscillations of the supercurrent in a superconducting ring just below its critical temperature. As we shall see, this similarity goes deeper, as the origin of these oscillations lies in the nonequilibrium persistent current in the Andreev interferometer.

Before we go into the physical origin of the oscillations, however, it is useful to discuss some of their important experimental features. Firstly, while a nonlocal signal is established on a normal lead that is not part of the loop using the measurement configuration of figures 3(b) and (c), it turns out that the path of the applied current is not particularly important, as long as it contains a dc component that intersects the normal section of the loop. The green curve in figure 4(a) shows data from a nonlocal measurement configuration where the applied current does not even enter the superconductor, yet large oscillations in the differential resistance are seen. In fact, we have used a number of different probe configurations to source and drain the applied current, and in all configurations where a dc current intersects some part of the normal section of the loop an oscillating nonlocal differential signal is observed [16], albeit with different amplitudes.

Zoom In Zoom Out Reset image size

Secondly, the amplitude of the oscillations diminishes rapidly with distance from the loop, similar to the expected decrease in amplitude of nonlocal CAR and EC signals, where the nonlocal signal is expected to show an exponential decay with distance governed by the superconducting coherence length ξ_S. The black curve in figure 4(a) shows data taken with the normal probe closest to the ring (essentially on the Andreev interferometer itself). With all other parameters being the same, the amplitude of the oscillations on this probe is approximately a factor of 6 larger than the signal on the probe off the loop, a rapid decay over a length of ∼110 nm. While we have not done a detailed length dependence on this sample, this rapid decay with length, which is reminiscent of the data on the linear sample and the sample of figure 2, suggests that CAR/EC plays a role in explaining the results.

Thirdly, the amplitude of the oscillations depends strongly on the magnitude of the dc current. To demonstrate this, we show in figure 4(b) the differential resistance dV/dI as a function of the dc current, using the near probe configuration of figure 4(a), with the sample biased at a flux of ±Φ₀/4, where the amplitude of the response is close to its maximum. The most striking aspect of these data is that the differential resistance is antisymmetric both in the applied magnetic flux as well as the applied dc current. As a function of dc current, the differential resistance amplitude initially increases, reaches a maximum at about ±250 nA and then decreases when the amplitude of the dc current is increased further. There is also a hint of oscillatory behavior for both negative and positive dc current. The fact that the oscillations are seen clearly at low temperature and low dc current but attenuate at higher dc currents and over distances of the order of ξ_S implies that these nonlocal voltages are not due to non-equilibrium charge imbalance effects.

Finally, the sign of the oscillations depends on which probes are used for measuring the voltage. Figure 4(c) shows two curves corresponding to voltage probes on the top and bottom of the interferometer; the current path for both curves is the same. The oscillations are nominally identical, but reverse in sign. We also note that the oscillations are purely antisymmetric with respect to the applied flux, since we can accurately determine the zero of applied field using the oscillations in the local resistance of the device.

The experimental signatures discussed above point to the important role of the circulating persistent current in the Andreev interferometer induced by the applied magnetic flux in explaining the results observed: like the nonlocal oscillations, this persistent current is antisymmetric in the flux; the difference in sign between the oscillations measured using the left and right normal electrodes shown in figure 4(c) is consistent with a circulating current going into one NS interface and out of the other; and the sawtooth waveform of the oscillations is similar to the flux dependence of the circulating persistent current. We discuss below possible explanations for these similarities.

Flux-dependent oscillations in the nonlocal differential resistance in the presence of a finite dc current have been observed before in NS heterostructures [17, 18], and have been ascribed to thermoelectric effects [19, 20]. Many of the experimental signatures of these earlier experiments are similar to those in the present experiments, so it is worth discussing the possibility that the effects we observe are due to thermoelectric phenomena in NS structures.

Figure 5(a) shows a schematic representation of one of the devices measured in these earlier experiments, the so-called parallelogram Andreev interferometer [17]. The sample was designed specifically for measuring the thermopower of the Andreev interferometer in a classic thermoelectric measurement configuration. One end of the interferometer is heated with a dc current as shown in the figure. The leads that inject and drain the current (the 'heater' of the sample) are designed to be much longer than the inelastic electron scattering length at the lowest measurement temperature, so that the quasiparticle distribution in the middle of this heater wire (and consequently at one end of the interferometer) is in the form of an equilibrium Fermi distribution, but with an elevated effective electron temperature T_e. This distribution results in a temperature gradient in the sample as shown schematically by the coloring in figure 5(a). Since T_e should not depend on the direction of the dc current I_dc, T_e(I_dc) is an even function of I_dc. In order to measure the thermoelectric voltage generated by this elevated electron temperature, one needs to measure the difference between the voltage generated at the other end of the interferometer and the voltage generated at a counterelectrode, as shown in figure 5(a). The counterelectrode is chosen to have a small thermoelectric coefficient which does not vary as a function of the applied flux: for these experiments, a plain Au wire was chosen as the counterelectrode. The thermal voltage generated in response to the elevated electron temperature is given by

$$\begin{equation} V_{{\rm th}} = \int_{T_{{\rm b}}}^{T_{{\rm e}}(I)} (S_{{\rm A}} - S_0)\, {\rm d}T, \end{equation} \tag{ 1 }$$

where S_A is the thermopower of the interferometer, S₀ is the thermopower of the counterelectrode (which is neglected in the subsequent analysis since it is small and does not vary as a function of Φ) and T_b is the temperature of the 'cold' end of the thermometer, assumed to be the base temperature of the measurement. (In the first experiments, the effective electron temperatures in the device were estimated from heat flow equations [17, 21]; in subsequent experiments, the electron temperatures were directly measured using local proximity effect thermometers [22].) For greater sensitivity, an ac technique is used by superposing a small, low-frequency ac current on top of I_dc and measuring the resulting ac voltage with a lock-in amplifier. This has the effect of measuring the differential of V_th, i.e.

$$\begin{equation} \frac{{\rm d}V_{{\rm th}}}{{\rm d}\,I} = S_{{\rm A}} \frac{{\rm d}T_{{\rm e}}}{{\rm d}\, I}, \end{equation} \tag{ 2 }$$

where we have taken S₀ = 0. Since T_e(I) is symmetric in I_dc, dT_e/dI is antisymmetric in I_dc; thus, the thermoelectric signature is a nonlocal differential resistance dV_th/dI that is antisymmetric in the dc current. This was indeed what was observed in the earlier experiments.

Zoom In Zoom Out Reset image size

Theoretical explanations of the origin of the oscillatory thermopower in the parallelogram interferometers have focused on imbalances in the supercurrent that circulates in the Andreev interferometer in response to the applied flux [19, 20, 23]. Specifically, it has been proposed that there is a difference in the supercurrent at the two NS interfaces due to the temperature gradient, so that the supercurrent that is injected from the superconductor into the normal arm of the interferometer is not the same as the supercurrent that flows from the normal arm back to the superconductor at the second NS interface. The difference between these two supercurrents is made up by a quasiparticle current that flows along the long normal arms of the device, resulting in a thermoelectric voltage. As the supercurrent oscillates periodically and antisymmetrically with the applied flux, so the quasiparticle current and the resulting thermal voltage also oscillate periodically and antisymmetrically with applied flux. This model appears to provide a reasonable explanation of the experimental results for the parallelogram interferometers, where the thermopower oscillations are antisymmetric with respect to applied flux. However, it cannot explain the symmetric thermopower oscillations observed in the so-called 'house' interferometers. To our knowledge, no satisfactory explanation for the symmetric thermopower oscillations in these interferometers has so far been formulated.

Figure 5(b) shows a schematic representation of one particular measurement configuration of the sample of figure 1(a) that showed the largest oscillatory signal with applied flux. It can be seen that this configuration is similar in some respects to the thermopower measurement configuration of figure 5(a), except that the 'sample' is now one half of the interferometer, and the 'counterelectrode' is the other half. A second difference is that the length of the 'heater' in the current experiments is comparable to the electron inelastic scattering length, so that a current in the heater will generate a nonequilibrium quasiparticle distribution along its length rather than an equilibrium Fermi distribution with an elevated temperature as in the sample of figure 5(a). Although the difference in distribution is important, we shall gloss over this point for the present discussion, returning to it later, and think of I_dc as simply generating a thermal gradient as shown in figure 5(b). In terms of the theoretical model for the antisymmetric thermopower oscillations discussed above, it should be noted that the symmetry of the sample geometry of figure 5(b) implies that both NS interfaces are at the same temperature, so that the central assumption of the thermoelectric model of a difference in the supercurrent through the two NS interfaces does not apply. However, we shall show later that the nonequilbrium quasiparticle distribution generated in the normal arm of the interferometer does lead to a spatial variation of the total supercurrent along the normal arm, and it is this spatial variation that leads to the nonlocal oscillations that are observed.

A second key experimental observation in the present experiments also argues against an explanation based solely on a thermoelectric effect. This is the fact that nonlocal oscillations can be detected using not only a normal probe attached to the interferometer, but also a nonlocal one placed off the interferometer loop. These are the two probe measurement configurations shown in figure 4(a). In the quasiclassical model used to describe thermoelectric effects, the electronic wave functions on the far normal probe are not sensitive to the phase difference at the two ends of the normal arm of the interferometer, as they are connected to the interferometer at only one point and hence cannot be modulated by the external flux.

While it is in principle possible that the oscillations observed on the nonlocal probe are due to a small heat current along the superconductor between the interferometer and nonlocal probes, we can show experimentally that no such current accounts for the oscillations. Figure 5(c) shows a measurement configuration where the dc current is injected along the nonlocal probe, and figure 5(d) the results of this configuration. If there were appreciable heat conduction in the small superconducting section, one would expect to see oscillations of the differential resistance as measured on the probe joined to the interferometer: none are observed to the level of the noise in the measurement. A second piece of evidence that local heating along the superconductor is negligible is shown in figure 6. In the two configurations of figures 6(a) and (b) the current is sent to either the left or right lead that intersects the interferometer while the voltage of the right nonlocal probe is measured relative to the superconductor potential. Since the dc current only marginally intersects the normal section of the interferometer, the observed oscillations (figures 6(c) and (d)) are very small. However, their amplitudes are indistinguishable within the noise resolution of our measurement. If the nonlocal oscillations had their origin in local heating, the configurations of figures 6(a) and (b) would not produce the same results. Finally, experiments and theoretical calculations show that the thermal conductance, like the electrical conductance, is symmetric in the flux, so that any excess heat current would also be expected to be symmetric in the flux.

Zoom In Zoom Out Reset image size

Rather than a heat current, the origin of the oscillations could be explained as arising from excess quasiparticle electrical currents that are injected into the short superconducting sections between the interferometer and nonlocal probes, which then make their way into the nonlocal probes. The quasiparticle currents might be expected to decay rapidly in the superconductor on the scale of ξ_S. In our view, this is essentially equivalent to the picture of nonlocal CAR/EC effects in response to a quasiparticle current being injected into the superconductor. However, it is the mechanism of generation of this quasiparticle current that must be explained.

The quasiparticle current arises from a subtle effect associated with the influence of a nonequilibrium quasiparticle distribution on the persistent current induced in the Andreev interferometer by the external magnetic field. In the quasiclassical theory of superconductivity in the diffusive limit, the current through the normal arm of the interferometer can be written as [24]

$$\begin{equation} j(\mathbf{R},T) = e N_0 D \int {\rm d}E (M_{33} \partial_{\mathbf{R}} h_T + Q h_L + M_{03} \partial_{\mathbf{R}} h_L), \end{equation} \tag{ 3 }$$

where N₀ is the quasiparticle density of states at the Fermi energy, D is the diffusion constant, T is the temperature, M₃₃ and M₀₃ are normalized diffusion coefficients that depend on the spatial coordinate R and Q is the spectral supercurrent, which is independent of R in the normal metal arm in our geometry. h_T and h_L are R-dependent quasiparticle distribution functions that have the equilibrium form

$$\begin{equation} h_{L,T} = \frac{1}{2} \left[ \tanh \kern-2pt\left(\frac{E+eV}{2k_{{\rm B}} T}\right) \pm \tanh\kern-2pt \left(\frac{E-eV}{2k_{{\rm B}} T}\right) \right], \end{equation} \tag{ 4 }$$

where E is the energy of the quasiparticle, and V is the voltage. The first term in equation (3) gives the quasiparticle contribution to the total current, the second term gives the supercurrent contribution and the third term, which is typically much smaller than the other two, is related to the conversion of supercurrent into quasiparticle current.

In equilibrium, V =0, h_T (E) = 0 and h_L(E) is related to the usual quasiparticle Fermi function f₀(E) by h_L(E) = 1 − 2f₀(E). The total current through the normal arm of the interferometer then has only a contribution from the supercurrent from the integral of Qh_L over energy. The dependence of this supercurrent on the external flux Φ arises from the dependence of Q on Φ. Since Q is independent of R (∂_RQ = 0), the total supercurrent in the normal arm is also independent of R, i.e. the supercurrent is constant along the normal arm of the interferometer.

The application of a dc current as shown in figure 3(a) will result in a modification of the distribution functions h_L and h_T . A modification of h_L will result in a change in the supercurrent in the normal arm through the second term in equation (3). The change can be dramatic, even reversing the sign of the supercurrent, as demonstrated by experiments on the so-called tunable π-junctions [25–27]. As the normal parts of these junctions were very short, theoretical analyses of these experiments assume that h_L, although modified from its equilibrium value, is still constant along the length of the normal wire, so that the total supercurrent along the wire is also constant since ∂_RQ = 0. However, our self-consistent numerical simulations show that this assumption is not correct, i.e. h_L does vary along the length of the wire, so that its value at the center of the wire (see figure 3(a)) is different from its value near the NS interfaces.

For detailed numerical simulations, we start with the Usadel equations for quasiclassical superconductivity using the so-called θ parameterization, with the geometry as shown in figure 7(a). This geometry consists of four normal metal wires of length L that meet at a single node at one of their ends. At the other end, two of the wires are connected to normal reservoirs, across which a voltage V is applied symmetrically, modeling the dc current applied to our sample. The other two wires are connected to superconducting reservoirs whose potential is 0 (V =0), but across which a phase difference Δϕ can be applied symmetrically, modeling the phase difference introduced by the application of a magnetic flux in the Andreev interferometer. In what follows, we shall use the notation of [24]. The Usadel equations in the normal wire can be written as

$$\begin{equation} \partial_{\mathbf{R}} j_{{\rm S}}(E, \mathbf{R})=0 \end{equation} \tag{ 5 }$$

and

$$\begin{equation} D\partial_{\mathbf{R}}^2 \theta - \frac{D}{2} \sinh 2 \theta (\partial_{\mathbf{R}} \chi)^2 + 2E{\rm i} \sinh \theta = 0, \end{equation} \tag{ 6 }$$

where χ is the complex, gauge-invariant phase, and

$$\begin{equation} j_{{\rm S}}(E, \mathbf{R}) = \sinh^2 \theta(E,\mathbf{R}) \partial_{\mathbf{R}} \chi(E, \mathbf{R}). \end{equation} \tag{ 7 }$$

The spectral supercurrent Q discussed above is related to j_S by Q = −ℑ(j_s). We also define a spectral electronic current

$$\begin{equation} j(E,\mathbf{R}) = M_{33} \partial_{\mathbf{R}} h_{T} + Q h_L + M_{03} \partial_{\mathbf{R}} h_L \end{equation} \tag{ 8 }$$

and a spectral thermal current

$$\begin{equation} j_{\rm th}(E,\mathbf{R}) = M_{00} \partial_{\mathbf{R}} h_L + Q h_{T} + M_{30} \partial_{\mathbf{R}} h_{T}, \end{equation} \tag{ 9 }$$

so that the total electronic and thermal currents are given by integrals of these expressions over energy, as in equation (3). The normalized diffusion coefficients M_ij are given by

$$\begin{equation} M_{33,00} = \textstyle\frac{1}{2} [1 + \cosh \theta \cosh \theta^* \pm \sinh \theta \sinh \theta^* \cosh(2 \Im(\chi)], \end{equation} \tag{ 10 }$$

and

$$\begin{equation} M_{03,30}=\pm \textstyle\frac{1}{2} [ \sinh \theta \sinh \theta^* \sinh (2 \Im(\chi))]. \end{equation} \tag{ 11 }$$

The spectral electronic current and the spectral thermal current are conserved in the normal wires, i.e. ∂_Rj(E,R) = 0 and ∂_Rj_th(E,R) = 0. These last two equations combined with equations (5) and (6) form a set of four equations that need to be solved simultaneously in all four normal wires in the schematic geometry shown in figure 7(a).

Zoom In Zoom Out Reset image size

In order to do this, we first solve equations (5) and (6) for the complex θ and χ using a numerical relaxation technique. The boundary conditions for these equations at the normal contacts are that θ and χ vanish. We assume that the phase difference Δϕ induced by the external magnetic field is dropped symmetrically across the two superconducting reservoirs, so that the phase is Δϕ/2 at one superconducting contact and −Δϕ/2 at the other superconducting contact. The boundary condition for θ at a superconducting reservoir is given by

$$\begin{equation} \theta_{\rm S0} = -{\rm i} \frac{\pi}{2} + \frac{1}{2}\ln \!\left[ \frac{|\Delta | + E}{|\Delta | -E} \right], \quad E<|\Delta |, \end{equation} \tag{ 12 }$$

$$\begin{equation} \theta_{\rm S0} = \frac{1}{2} \ln \left[ \frac{E+ |\Delta |} {E-|\Delta | } \right], \quad E>|\Delta |, \end{equation} \tag{ 13 }$$

where Δ is the gap in the superconducting reservoir. Finally, the boundary condition at the node where all four normal wires meet is that θ and χ are continuous and that the sum of their derivatives along all four wires at the node vanishes.

Figures 7(b) and (c) show the spectral supercurrent Q and the normalized diffusion coefficient M₃₃ (which determines part of the quasiparticle current in equation (3)) as a function of energy E/E_c and the distance x/L along one of the wires connected to a superconducting reservoir. The phase difference Δϕ has been set to π/2, corresponding to a quarter of a superconducting flux quantum, near where the maximum of the oscillations were observed in the experiment. The superconducting reservoir is at x/L = 1, and the node where all four wires meet is at x/L = 0. As expected, while Q oscillates as a function of E, it is independent of the position x along the wire, since ∂_RQ(E,R) = 0. Figures 7(d)–(f) show the distribution function h_L for the same wire section for applied voltages of V/E_c = 0, V/E_c = 3 and V/E_c = 10, respectively. For V =0, h_L varies with E but not with x, so that the total supercurrent, which is given by the integral over energy of the convolution of the spectral supercurrent Q and h_L (equation (3)), is also independent of x. For V ≠0, however, h_L is a function of x. Under these conditions, the total supercurrent is no longer constant; however, since the total current (given by the sum of all terms in equation (3)) must be constant, the difference is taken up by an induced quasiparticle current.

Since the supercurrent oscillates periodically as a function of the applied flux, the nonequilibrium quasiparticle current will also oscillate periodically. Figure 8(a) shows the quasiparticle current and supercurrent calculated numerically from the first and second terms in equation (3) as a function of the phase difference Δϕ between the two superconducting reservoirs. The voltage applied between the two normal reservoirs is V =3E_c. Note that the functional form of the supercurrent is sinusoidal, while the quasiparticle current tends more towards a sawtooth form, although not as pronounced as in the experiments. This discrepancy likely arises because the Josephson coupling between the two NS interfaces in the experiment is stronger than assumed in the simulations; quantitatively, this implies that E_c is larger than our estimate based on the measured electronic diffusion coefficient of a coevaporated normal metal wire.

Zoom In Zoom Out Reset image size

The numerical simulations show that a quasiparticle current is injected (or extracted) from the superconducting reservoirs when a finite voltage is applied between the normal reservoirs. In order to explain the nonlocal differential resistance observed in the experiments, we assume that this nonequilibrium quasiparticle current in turn results in a nonlocal voltage on the spatially separated normal metal leads through CAR and EC. The induced quasiparticle current flows into one NS interface and out of the other NS interface, giving rise to nonlocal voltages of opposite sign at the two NS interfaces, as is seen in the experiment. The amplitude of these voltages would depend on the CAR and EC coefficients. Figure 8(b) shows the supercurrent as a function of V for a fixed phase difference of π/2, corresponding to a flux of Φ₀/4, near where the maximum in the oscillation amplitude is observed (figure 7(a)). The supercurrent has the oscillatory form discussed earlier, which arises from the oscillatory behavior of the spectral supercurrent shown in figure 6(b) and has been predicted and observed in previous experiments as mentioned earlier. In order to facilitate comparison with our experiment, we show on the same plot the differential of the calculated quasiparticle current with the applied voltage, which is proportional to the nonlocal differential resistance due to CAR and EC arising from the nonequilibrium quasiparticle current. As can be seen from figure 7(b), this nonlocal differential resistance also oscillates as a function of the applied bias. In fact, it is very similar to the oscillations that we observe experimentally as a function of the dc current (see figure 4(b)), showing that our theoretical model does indeed describe the physics.

However, there is one aspect of the experimental data that is still not understood. A nonlocal signal arising from CAR and EC should be observed when a quasiparticle current is injected into the superconductor from the normal metal, even if only an ac current is used, as in the original nonlocal CAR and EC experiments on linear samples. As we have seen in our experiments, nonlocal signals are not observed under these conditions if a supercurrent can be sustained between the two NS interfaces (figure 3(b)). One might argue that the quasiparticle current is quickly converted into a supercurrent in the normal arm of the interferometer, so that only a supercurrent is injected into the superconductor. However, experiments on other samples [28] indicate that the quasiparticle current does not appreciably interact with the supercurrent over fairly long length scales. Another potential explanation is that in the strong Josephson coupling regime between the NS interfaces there is a minigap in the normal arm of the loop, meaning that at energies below the minigap, there are no quasiparticles and hence no CAR or EC. This aspect of our data requires further study.

In conclusion, we have conducted experiments demonstrating the existence of nonlocal phase coherence between two normal metals linked by a superconductor. The generation of the nonlocal signals has necessitated injecting a small dc current into the normal arm of an Andreev interferometer. Using a quasiclassical model that includes the spatial dependence of quasiparticle current and supercurrent along this section of the interferometer, we have shown how a non-equilibrium quasiparticle distribution created by this dc current can lead to a changing supercurrent along the length of the normal section. The supercurrent-to-quasiparticle current conversion that occurs in this section, along with the coherent CAR and EC processes, accounts for the observed nonlocal signals. The similarity of the sample geometry and measurement results to previously performed studies of thermopower in Andreev interferometers suggests that the interplay between supercurrent and non-equilibrium quasiparticle distribution in our model may be an important mechanism for understanding these earlier studies.

We thank Manan Mehta for help with the graphics. This work was funded by the US National Science Foundation under grant number DMR- 1006445.