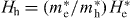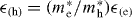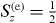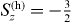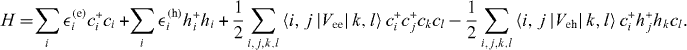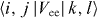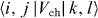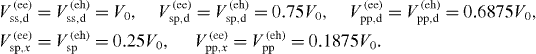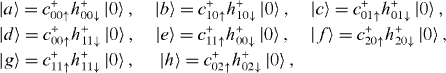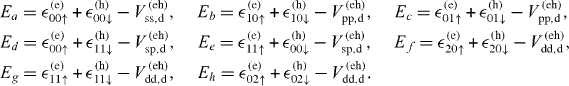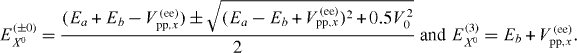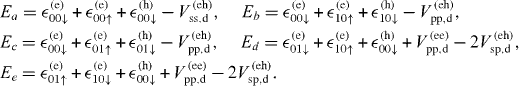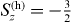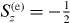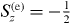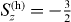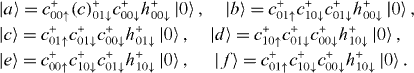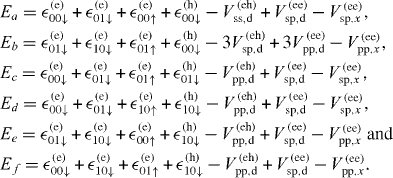Abstract
The photoluminescence of annealed CdxZn1−xSe quantum dots (QDs) under the influence of an external magnetic field has been studied in this paper. Post-growth annealing was performed for different annealing times. Above a critical annealing time, the QD luminescence shows a pronounced red-shift of the Zeeman split magnetic subcomponents. This observation is in contrast to the blue-shift caused by the diamagnetic behavior that is usually observed in non-magnetic QDs. We attribute our finding to the paramagnetism caused by the mixing of heavy and light hole states. Hence, post-growth thermal annealing treatment might be employed to render undoped epitaxial QDs intrinsically magnetic in a controlled manner. Two theoretical models were developed: a few-particle model to account for excitonic complex effects and a multiband calculation that describes the valence band hybridization. Contrasting the two models allowed us to unambiguously elucidate the nature of such an effect.
The zero-dimensional ground states of the electron and the hole in non-magnetic semiconductor quantum dots (QDs) typically have zero angular momentum and exhibit the diamagnetic response of spin split states to an external magnetic field [1, 2]. To realize magnetic QDs, usually paramagnetic ions are incorporated into the host lattice, e.g. Mn2+ [3–5]. In non-magnetic QDs, the spin properties are mainly determined by the electron and the heavy hole (hh) spins. Their counterparts, the light holes (lh), are commonly believed to play only a minor role in the exciton ground state due to the lifting of lh–hh degeneracy provoked by strain fields and quantum confinement. However, by modifying the dimensions and composition of the QDs, the lh can contribute to the exciton ground state [6] and, as proved here, effectively tune the exciton magnetic behavior. In this peper, we show how to control the intrinsic QD magnetism by means of thermal annealing (TA), taking into account the presence of extra charges and exchange effects as well as the total angular momentum tuning of the ground state.
We have studied the annealed CdxZn1−xSe QDs' growth by molecular beam epitaxy [7]. It is found that their composition and size are modified by rapid thermal annealing (RTA). The variation of the c-lattice map and Cd-content at TTA = 500 °C as a function of annealing time, tTA, is shown in figure 1. After each TA-step, low-temperature (about 2K) photoluminescence (PL) spectra were recorded by immersing the sample in a He-bath cryostat. The QDs were excited with the 405 nm line of a solid state continuous-wave laser.
Figure 1. Left-hand panels: c-lattice maps obtained from GPA analysis of off-axis HREM images (a) BTA and (b) after tTA = 40 s. The color scale corresponds to variations of the lattice constant within the range 0.565–0.665 nm. (c) Theoretical (dark line) and experimental (red dots) data match of the Cd-content versus tTA.
Download figure:
Standard imageHigh-resolution transmission electron microscopy (HRTEM) was carried out. Cross-sectional images, obtained before thermal annealing (BTA) and after various annealing steps (tTA = 10 s and tTA = 40 s), allowed determination of the Cd-content with annealing time, as displayed in figure 1(c). The variation of the lattice parameters along the growth direction was obtained from high-resolution off-axis images taken after tilting the sample by 10° around the z-axis from the [110] zone axis. The images have been analyzed by the geometrical phase method [8–10], which allowed us to obtain the lattice parameter along the growth direction. This lattice parameter can be put in correspondence with the Cd content, assuming that the in-plane lattice parameter is fixed by the substrate and that the unstrained lattice parameter and the elastic constants of CdxZn1−xSe can be linearly interpolated between CdSe and ZnSe [6]. Using the color scale of the image, the Cd compositions BTA and after RTA were estimated to be about 70 and 15%, respectively.
Such a process led to the peculiar magnetic behavior of the exciton recombination. In figure 2(a), the centers of gravity of the PL subcomponents at various annealing steps are plotted against the magnetic field. The error bars in figure 2 were estimated using different methods to obtain the centroids of a subset of 12 PL spectra. For each PL spectrum we determined: the plain centroid, the centroid of a fitted Gaussian, the centroid of a fitted asymmetric Gaussian and the maximum of the asymmetric Gaussian. The largest difference between the shifts obtained with different methods is 0.4 meV. The standard deviations of the fitted energies are one order of magnitude smaller. The PL spectra before TA and after the annealing step (TTA = 500 °C,t = 30 s) at a magnetic field of B = 0,3 and 6 T are shown in figures 2(b) and (c), respectively. The curve corresponding to the non-annealed QDs displays the expected diamagnetic blue-shift of QD lines with magnetic field. Such an observation is in strong contrast to the red-shift detected for QDs subjected to TA. In this paper, we have addressed theoretically two hypotheses that may provide conditions for tuning the effective magnetic shift: (i) the effects of extra charges in the exciton complex [11] and (ii) inter-subband hybridization due to strain relaxation and confinement attenuation. The first hypothesis is based on the fact that native defects in semiconductor selenides produce extra electrons [12], while the second hypothesis considers the hybridization of the hh ground state.
Figure 2. (a) Magnetic shift given by as a function of the magnetic field for the PL measured: BTA and after tTA = 20 s, tTA = 30 s and tTA = 40 s of TA. Multiple QD spectra at various magnetic fields: (b) BTA and (c) after tTA = 30 s.
Download figure:
Standard imageLet us first discuss the role of extra negative charge and its effect on the spin polarization [11]. In nominally-n-doped CdxZn1−xSe QDs, normally there are resident electrons inside QDs, due to the ionization of dopants [12]. Therefore, depending on the initial charge (the number of electrons) in QDs, either a neutral—or negatively charged—exciton complex may be formed after the laser excitation in the magneto-PL measurement. Then, to understand the magneto-optical properties of the QDs, we systematically investigate neutral, singly and doubly charged excitons, denoted by X−n, corresponding to n = 0,1,2, respectively. As is well known, the carriers (electrons and holes) in QDs are confined in all three dimensions, leading to a discrete energy spectrum of the electronic states. Both the quantum level spacing ΔE and charging energy EC depend on the dimensions of the dot. For a disc, for instance, they can be estimated by ΔE = ℏ2/(m*e(h)R2) and EC = e2/(8 0
0 rR), respectively, where R is the disc radius, m*e(h) and
rR), respectively, where R is the disc radius, m*e(h) and  r are the electron (hole) effective mass and dielectric constant of the QD, e is an electron charge and ℏ is the reduced Planck constant. Nevertheless, the ΔE and EC possess very different QD-size dependences. In the strong confinement regime, the single-particle energies dominate such that the Coulomb energies can be treated as a first-order perturbation to the single-particle energies. Then the diamagnetic shift of X−n excitons is proportional to B2 in the limit where the electron (hole) cyclotron frequencies ω(j)c = eB/m*j ≪ ω(j)0, where j = e,h, B is the magnetic field and ω(0)(j) is the characteristic frequency of a parabolic confining potential for the electron (hole). Thus, the magneto-PL peak position presents a usual diamagnetic shift that is independent of the exciton charge. In the weak confinement regime, however, the Coulomb energies may dominate over the single-particle energies. The excitonic diamagnetic shift must depend on surplus charge [14]. In the intermediate regime, the neutral exciton energy increases quadratically with B. However, the addition of electrons to the neutral exciton leads to a significant decrease of the blue-shift. Therefore, the interplay of energy quantization and charge quantization may lead to new phenomena.
r are the electron (hole) effective mass and dielectric constant of the QD, e is an electron charge and ℏ is the reduced Planck constant. Nevertheless, the ΔE and EC possess very different QD-size dependences. In the strong confinement regime, the single-particle energies dominate such that the Coulomb energies can be treated as a first-order perturbation to the single-particle energies. Then the diamagnetic shift of X−n excitons is proportional to B2 in the limit where the electron (hole) cyclotron frequencies ω(j)c = eB/m*j ≪ ω(j)0, where j = e,h, B is the magnetic field and ω(0)(j) is the characteristic frequency of a parabolic confining potential for the electron (hole). Thus, the magneto-PL peak position presents a usual diamagnetic shift that is independent of the exciton charge. In the weak confinement regime, however, the Coulomb energies may dominate over the single-particle energies. The excitonic diamagnetic shift must depend on surplus charge [14]. In the intermediate regime, the neutral exciton energy increases quadratically with B. However, the addition of electrons to the neutral exciton leads to a significant decrease of the blue-shift. Therefore, the interplay of energy quantization and charge quantization may lead to new phenomena.
From HRTEM, the typical height (measured along the growth direction) and the in-plane radius of the as-grown QDs (BTA) were measured to be Lz ≃ 1–2 nm and R ≃ 9–10 nm, respectively. An average Cd-content for the QDs layer of x ≃ 70% was also determined (see in figure 1(c)). After RTA, the typical QD size has cylindrical symmetry, i.e. with Lz ≃ 6–7 nm and R ≃ 10–11 nm and the Cd-content rapidly converging to x ≃ 15%. These data indicate that RTA induces changes in the geometry of QDs, reducing the strength of the quantum confinement of carriers. Consequently, the annealing process may change the role of single-particle energy and Coulomb interaction affecting the magneto-PL spectrum. Reasonably, one may guess that few-body interaction in the QDs results in the paramagnetic response of the QD ground state. In order to quantitatively understand the role of few-body interactions in the paramagnetic shift, we now address theoretically the effects of Coulomb interactions and electron charging on the excitonic diamagnetic shift. Both electrons and a valence-band hole are treated in this section in the single-band effective-mass approximation. Within this approximation, the single-particle states in the xy-plane for both an electron with spin σe = 1/2 and a valence heavy hole with σh = 3/2 can be well described by with energy , shown schematically in figure 3(a), and characterized by angular momenta le = ne − me and lh = mh − nh, where j = e, h, nj and mj are quantum numbers, and σ(j)z is the spin projection of the electron/hole, gj is the Landé g-factor of the electron/hole,
If the symmetry m*eω(e)0 = m*hω(h)0 is assumed, the Hamiltonian for the hole then becomes , where H*e is the complex conjugate of He. In this case, the relation between electron and hole energies is and the hole wave functions are the complex conjugate of those of the electron. The energy is measured in effective Rydberg (R*y = (2m*e/ 2r)Ry) and the length in effective Bohr radius (a*B = (
2r)Ry) and the length in effective Bohr radius (a*B = ( r/m*e)a0), where Ry and a0 are the Rydberg (13.56 eV) and Bohr radius (0.529 1 Å), respectively. In the calculations, we adopted the same parameters as those used in the neutral exciton case presented in [6], and disregarded the anisotropy parts of the electron–hole exchange interactions.
r/m*e)a0), where Ry and a0 are the Rydberg (13.56 eV) and Bohr radius (0.529 1 Å), respectively. In the calculations, we adopted the same parameters as those used in the neutral exciton case presented in [6], and disregarded the anisotropy parts of the electron–hole exchange interactions.
Figure 3. (a) Electron and hole shell structures (B = 0). (b) Basic two-particle configurations, corresponding to L = 0, , . Red up- and black down-arrows indicate electrons and holes, respectively.
Download figure:
Standard imageThe excitons X−n are correlated states of electrons in the conduction band and a hole in the valence band. Denoting the single-particle states as i = (nj,mj,σ(j)z), the Hamiltonian of the exciton X−n may be written in compact form as
Here, c+i (ci) is the creation (annihilation) operator of an electron in state i and h+i (hi) is the pair of hole operators. The first two terms in the Hamiltonian H account for the single-particle energies of electrons and holes, while the two-body Coulomb matrix elements and measure the electron–electron (ee) and electron–hole (eh) interactions. We determine the eigenenergies and eigenfunctions of the X−n complex in the configuration-interaction (CI) approach, using all possible configurations. The ee and eh scattering introduces both diagonal and off-diagonal elements in the Hamiltonian, given the configuration admixture. To reach the desirable precision of the ground state of the X−n complex, we utilize the s-, p- and d-shells in CI calculations, as shown in figure 3(a). In addition, to simplify calculation and avoid artificial anticrossings, the whole Hilbert space has been divided into several subspaces according to (L, S(e)z, S(h)z), where L = L(e) + L(h) is the total angular momentum of the X−n complex, S(e)z and S(h)z are the z-projections of the total spin of electrons and holes, and L(e) and L(h) are the total angular momentum of electrons and holes in a given configuration. In this work, we restrict our attention to symmetric interactions, i.e. . Below, we list relevant Coulomb matrix elements in units of V0. To elucidate the physics, we shall refer to the matrix elements by specifying which type of carrier, which shell and whether direct or exchange scattering is involved. For example, V(ee)pp,d and V(ee)pp,x denote electron–electron direct and exchange scattering involving two electrons on a p-shell, i.e. and . The p-shell eh scattering matrix elements V(eh)pp are equal to equivalent ee exchange matrix elements V(ee)pp,x. The p- to s-shell eh scattering matrix elements V(eh)ps are equal to equivalent ee exchange matrix elements V(ee)ps,x. This list of Coulomb matrix elements illustrates the relative importance of different processes.
To study the X0, the two-particle configurations are generated by
as shown in figure 3(b), where |0〉 is the vacuum. They are coupled by Coulomb interactions. Then the diagonal elements of the X0 Hamiltonian are evaluated by
The off-diagonal elements can also be obtained analytically in a similar manner. It is worth noting that the first three configurations with low energy contribute significantly to the exciton ground-state energy, and the other states with higher energy involving either an electron or a hole or both of them on a d-shell contribute little to the exciton ground state and are not essential for the effect discussed here. Hence, they can be neglected in the qualitative discussion, but they are all included in our numerical calculations. Under this assumption, the neutral exciton energies can be estimated qualitatively by
To study the X−1, three-particle configurations have to be generated. Although all possible configurations are included in our numerical calculations, for simplification purposes, we only illustrate the configurations involving s- and p-shells in the rest of this paper. Under this restriction, the three-particle configurations belonging to L = 0, S(e)z = 0, , for example, are generated by
as shown in figure 4(a). Based on these configurations, the matrix of the X−1 Hamiltonian contains diagonal elements given by
In a similar way, the off-diagonal elements can also be obtained. Then the energy spectrum and wave functions of X−1 can be obtained by the diagonalization of this matrix.
Figure 4. (a) Basic three-particle configurations with L = 0, S(e)z = 0, . (b) Basic four-particle configurations, corresponding to L = −1, , . Red up- and blue down-arrows denote electrons and black down-arrows represent holes.
Download figure:
Standard imageThe energy spectrum of the X−2 exciton has also been calculated by means of the CI method. In comparison with the two previous cases (neutral and singly charged excitons), the number of configurations increases dramatically. Consequently, the number of Coulomb interaction terms becomes high. To illustrate how to create the four-particle configurations which is an essential part in CI calculations, the configurations belonging to L = −1, , have been selected and shown in figure 4(b). These configurations can be generated as follows:
The diagonal elements of the Hamiltonian are the following:
In a similar way, the off-diagonal elements can also be obtained analytically.
The resulting energy spectra for negatively charged excitons: (i) 1 hole + 2 electrons (X−1) and (ii) 1 hole + 3 electrons (X−2), are displayed in figures 5(a) and (b). The corresponding emission energies as a function of the relative cyclotron frequency are shown in figures 5(c) and (d). For the lower-energy states, a negative slope with the magnetic field growth has been obtained for the trion X−1 at higher fields. However, the corresponding three-particle configuration, involved in this transition, corresponds to an electron in a p-shell excited state, thus with reduced probability. Thus, the observed red-shift of cannot be ascribed to the few-body interactions due to the local imbalance of carriers produced by defects.
Figure 5. Calculated energy spectrum of charged excitons: (a) X−1, (b) X−2, as a function of the cyclotron frequency. (c) and (d) Calculated optical emission energies for the transitions X−1 → e and X−2 → 2e, respectively. The transitions for σ+ and σ− polarized emissions are shown.
Download figure:
Standard imageIn order to comprehend the paramagnetic behavior observed, a multiband k.p calculation [6] was developed for QDs with modulated size and Cd-composition. Before RTA, there is a large mismatch between CdSe and ZnSe lattice parameters; however, such a difference is relaxed after RTA as shown in the upper panels of figure 1. Thus, the strain relaxation must be considered. In our modeling, we considered geometrical and composition-based changes of QDs caused by the annealing process.
Calculations performed within the multiband Luttinger Hamiltonian model, plus strain corrections, show that for the parameters of the as-grown QD, the hole ground state is purely hh in character. However, our multiband calculations revealed that for certain values of Lz, R and Cd-content, the hole ground state assumes a hybrid character with contributions from several higher-lying states having different angular (l) and magnetic (m) quantum numbers. The main contribution to such a hybrid ground state comes from the lh states. Due to the lateral confinement, by increasing Lz, the QD ground state assumes an lh character due to its higher effective mass in the xy-plane. In contrast, for a pure hh-state, m = 0, the hybrid state, due to contributions from the higher-lying states, acquires a non-zero magnetic quantum number. It is this non-zero value of m along with the mean spin momentum j, that is responsible for the observed paramagnetic dispersion of the exciton transition in RTA-treated QDs. Therefore, taking into account the hybridization of the ground hole state, the calculated trends of for different values of Lz are shown in the main panel of figure 6(a). The iso-probability surfaces of the ground state and of such a hybrid state are shown on the top and bottom of the panel, respectively.
Figure 6. (a) The calculated shift for different combinations of QD parameters for a fixed radius R = 10 nm. The ground state QD exciton formed by a heavy hole always shows the diamagnetic shift with positive (BTA). (b) The calculated shift at B = 6 T as a function of the QD height for R = 10 nm. The inset shows the experimental evolution of the magnetic shift with increasing annealing time at B = 6 T [6].
Download figure:
Standard imageIt is important to note that, for the condition BTA (when x ≃ 70%), the strong confinement along Lz separates the hh and lh subbands. Thus, a variation of Cd-content within the range 15–70%, for Lz = 1–2 nm, leaves the hh–lh coupling practically unaffected, and the hh ground state remains pure. For larger values of Lz = 4–6 nm, this is not the case. Given the rapid stabilization of the Cd-content at x ≃ 15% at tTA < 10 s, as experimentally demonstrated by the HRTEM measurements displayed in figure 1(c), we fixed x = 15% and R = 10 nm in all the calculations. The trends toward negative shifts of , obtained experimentally in figure 2, are reproduced for the ground state of the e–h pair, as displayed in figure 6(b), after keeping B = 6 T constant and varying Lz. For comparison, the corresponding experimental evolution of the magnetic shift with annealing time [6] has been displayed in the inset of this figure. For a fixed B, non-monotonic behavior of with Lz (and tTA in the experiment) is observed due to the intertwining of two opposite effects: [6] for larger Lz, the hh and lh subbands approach each other (increasing the hybridization), while their anticrossing is shifted toward lower fields. Since the hh–lh coupling depends on B, the latter effect reduces the relative strength of this interaction.
In summary, the paramagnetic behavior of the QD ground state has been induced by RTA and detected by PL in a magnetic field. The interplay of lateral and longitudinal quantization, along with the tuning of band parameters by composition, leads to a valence band hybrid ground state. It is therefore inferred that QD-size and composition-dependent hybridization imparts to the hole ground state a non-zero orbital angular momentum and, in turn, results in the paramagnetic optical response of the QD excitons, independently of the number of extra charges. Paramagnetic regimes have been visible also for QDs of other compounds, i.e. InAs/GaAs (001) [13]. Here, we demonstrated that post-growth TA treatment might be employed to render non-magnetic epitaxial QDs intrinsically magnetic in a controlled manner. In QD superlattices, such paramagnetic states might boost the ferromagnetic ordering of QD spins.
Acknowledgment
We acknowledge financial support from the DFG, the State of Bavaria, the Brazilian agencies FAPESP, CNPq and CAPES and the Chilean CONICYT/PBCT.







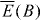
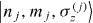
![$\epsilon _{n_{j},m_{j}, \sigma _{z}^{(j)}}=(n_{j}+m_{j}+1) \Omega _{j}+\frac {1}{2} \left [\left (n_{j}-m_{j}\right )+ \frac {1}{2} g_{j} m_{j}^{\ast } \sigma _{z}^{(j)}\right ] \omega _{\mathrm {c}}^{(j)}$](https://content.cld.iop.org/journals/1367-2630/14/4/043038/revision1/nj413120ieqn3.gif)