Abstract
In superconducting films under an applied dc current, we analyze experimentally and theoretically the influence of engineered pinning on the vortex velocity at which the flux-flow dissipation undergoes an abrupt transition from low to high resistance. We argue, based on a nonuniform distribution of vortex velocity in the sample, that in strongly disordered systems the mean critical vortex velocity for flux-flow instability (i) has a nonmonotonic dependence on magnetic field and (ii) decreases as the pinning strength is increased. These findings challenge the generally accepted microscopic model of Larkin and Ovchinnikov (1979 J. Low. Temp. Phys. 34 409) and all subsequent refinements of this model which ignore the presence of pinning centers.
GENERAL SCIENTIFIC SUMMARY Introduction and background. It is known that superconductors dislike magnetic fields but may agree to a compromise—allowing the field to penetrate in the form of quantized units of flux, i.e. vortices. Since vortex motion leads to dissipation, recent decades have witnessed an enormous effort to trap them and increase the maximum electrical current that a superconductor can sustain before vortices start to move, Jc. However, to date, Jc can still reach only a small fraction of the maximum theoretically permitted value, the depairing current. This is an enduring problem at the very core of any future technological progress.
Main results. In this paper, we propose a mechanism to explain the experimentally limited Jc. It is based on two main ingredients always present in superconducting systems, namely (i) disorder in the pinning landscape and (ii) anisotropic deformation of swiftly moving vortices. The first ingredient ensures a broad distribution of vortex velocities, particularly the formation of vortex rivers surrounded by static vortices. Once these localized vortex flows are developed, the second ingredient causes vortex instability, overheating the entire system and thereby limiting the critical current.
Wider implications. This paper stresses the relevance of disorder and pinning at the microscopic scale to determine the vortex depinning transition. In addition, it demonstrates that vortex instability transitions are strongly affected by pinning, a feature that has eluded most theoretical works until now. Therefore, our results will encourage researchers to look beyond Jc, widening the range of currents above Jc where low dissipation can be sustained.
1. Introduction
The quest for enlarging the dissipationless regime of superconductors has led to a progressive enhancement of the vortex pinning strengths in recent decades and to a continuous effort at understanding the microscopic pinning mechanisms [1]. In addition to the maximal current that a superconductor can sustain before starting to dissipate, Jc, it is technologically relevant to know how far above Jc the dissipation remains reasonably low. This information directly concerns the tolerance of a superconducting system to current fluctuation close to the depinning current [2]. In a seminal paper, Larkin and Ovchinnikov [3] showed theoretically that this dissipation region above Jc is limited by a maximum vortex velocity beyond which the damping force acting on vortices decreases. This decrement, in turn, accelerates the vortex motion and eventually gives rise to a sudden increase of dissipation. The microscopic picture at high vortex velocities corresponds to a migration of quasiparticles out of the vortex core, resulting in a shrinkage of the effective core size and therefore in a lower damping force [4, 5].
In their original formulation, Larkin and Ovchinnikov assumed a homogeneous distribution of quasiparticles which led them to predict a field-independent critical vortex velocity v*. This assumption holds as long as the diffusion of nonequilibrium quasiparticles exceeds the distance between vortices, i.e. at high enough magnetic fields. Later on, Doettinger et al [6] argued that this assumption should be considered as a necessary condition to trigger the instability, which allowed them to explain the observed systematic increase of v* with decreasing magnetic field. Further refinements of the Larkin–Ovchinnikov (LO) model to include the unavoidable overheating of quasiparticles with respect to the sample were carried out by Bezuglyj and Shklovskij [7]. In [7], it was shown that this effect does not modify the tendency of v* to increase as the external field, H, decreases. Even though this particular v*(H) dependence has been extensively corroborated experimentally by many independent groups in intermediate- and high-field regimes [8–14], Grimaldi et al [15] recently observed the opposite trend at low fields, i.e. v* decreasing with decreasing H.
In this work, we demonstrate that this unexpected behavior can result from the presence of vortex pinning and disorder, ingredients that have not been included in any of the previous theoretical models.
2. Pinning model
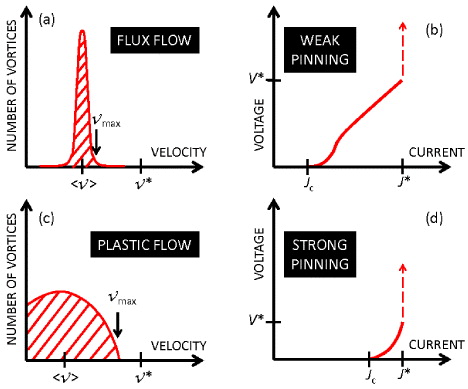
The assumption of no pinning corresponds to a δ-function-like vortex velocity distribution and a free flux flow with zero critical current [17]. In this case, an increase of current produces a shift of the velocity distribution to higher mean values until the vortex instability is triggered at v*, for all vortices simultaneously. In disordered systems, this situation can be realized in the vortex liquid state, in a weak pinning regime or at high enough fields and currents such that the vortex–vortex interaction exceeds the vortex–pinning interaction. Here, increasing the current J above Jc produces a shift of the velocity distribution toward higher mean values 〈v〉 and progressively narrows the distribution peak. This sharp distribution of vortex velocities corresponds to a linear flux-flow regime, as shown in figures 1(a) and (b), respectively. Once the system reaches a current value J* such that 〈v〉 ∼ v*, vortex instability takes place [14, 17].
Figure 1. Schematic representation of different dynamic regimes. Velocity distribution for the case of flux flow (a) and plastic flow (c). Expected current–voltage characteristics for weak (b) and strong (d) pinning strengths. The critical current density Jc indicates the onset of dissipation, whereas the instability current J* and critical voltage V* indicate where vortex instability takes place.
Download figure:
Standard imageThe introduction of strong pinning and disorder substantially modifies the previous picture. On the one hand, the presence of disorder is expected to broaden the velocity distribution and extend the nonlinear regime for currents above the critical value [13]9. This is schematically shown in figure 1(c). On the other hand, strong pinning increases the critical current and causes the vortex instability likely to appear within a nonlinear V (I) regime (see figure 1(d)). This is particularly true if the instability current J* does not depend strongly on pinning, a fact which we will demonstrate experimentally and theoretically further below. Most importantly, the broadening of the velocity distribution implies a sizable separation between the measured average velocity 〈v〉 and the maximal attainable vortex velocity vmax. In this plastic vortex flow regime, the system will inevitably reach the instability point at a lower vortex velocity than expected, practically when vmax ∼ v*. In this case, the condition of homogeneous quasiparticle distribution in the whole sample (the basis for the LO model) has to be dropped and instead homogeneous quasiparticle distribution only along the paths where vortices flow has to be considered [5, 15, 19–22]. This simple argument lead us to conclude that the stronger the pinning the lower the measured critical velocity becomes.
This analysis enables us to formulate another finding, one of our main results, which concerns the critical velocity as a function of applied magnetic field H. In the LO model, the assumption of a homogeneous quasiparticle distribution holds if the distance v*τ (τ
(τ being the quasiparticle relaxation time) over which the quasiparticles diffuse is larger than the intervortex spacing a(H)∝H−1/2. Obviously, this leads to v*∝H−1/2 (see, e.g., [9] for details). However, in the presence of strong pinning, this dependence changes dramatically.
being the quasiparticle relaxation time) over which the quasiparticles diffuse is larger than the intervortex spacing a(H)∝H−1/2. Obviously, this leads to v*∝H−1/2 (see, e.g., [9] for details). However, in the presence of strong pinning, this dependence changes dramatically.
Indeed, as the magnetic field increases the vortex density and the vortex–vortex interaction increase, which in turn effectively decreases the pinning. This narrows the vortex velocity distribution, and the measured critical velocity increases. Further increasing H, the assumption of homogeneous quasiparticle distribution at the critical velocity becomes justified again, and the standard LO scenario of v* decreasing with increasing field is recovered. This is in agreement with recent experimental reports of Grimaldi et al [15, 16] showing that in Al and Nb films at low fields, v* increases with increasing field.
This behavior at low fields is clearly unexpected within the standard LO picture and its subsequent refinements.
3. Time-dependent Ginzburg–Landau simulations
In order to provide compelling evidence in favor of the above-described picture, we performed theoretical simulations using the time-dependent Ginzburg–Landau (GL) theory, with a model and numerical procedure identical to those described in [20]. The samples were thin superconducting stripes of aluminum (taking coherence length ξ(0) = 100 nm, inelastic scattering time τin = 10 ns and relaxation constant u = 5.79) of size 10 × 10 μm2, with a regular square array of square pinning sites of size 150 × 150 nm2 and a lattice period of 600 nm. The pinning was realized through suppressed critical temperature inside the pinning sites, differing by the coefficient ζ from the rest of the sample. Obviously, for lower ζ the overall Tc of the sample decreases. For that reason, we used the same reduced temperature T/Tc(H = 0) for comparison between samples with different ζ and thus different pinning strengths. For each sample, we first calculated the I–V curves for different applied fields H, and identified the jump in voltage from the low to the high dissipative regime. The last value of current before the jump was labeled as the instability current j* and the value of voltage upon the jump was taken as the critical voltage V*. Both these quantities are plotted against the magnetic field in figures 2(a) and (b) for samples with different pinning strengths. There we clearly show that j* is weakly dependent on the pinning strength, while V* decreases in magnitude, both in agreement with our introductory analysis. Furthermore, we use the experimental estimate of average velocity as V*/H and plot it as a function of magnetic field in figure 2(c). We find the exact dependence of 〈v〉(H) as explained in the previous paragraph, clearly different at low magnetic field from the LO scenario.
Figure 2. The results of the Ginzburg–Landau theory for a thin Al superconducting stripe with a regular square array of pinning sites (as described in the text). Inside the pinning site, the critical temperature is suppressed by a factor ζ compared to the rest of the sample. All curves are obtained at the same reduced temperature of 0.9Tc(H = 0), where Tc(H = 0) is different for different ζ. Panels (a)–(c) show, respectively, the instability current j*, the critical voltage V* and the average critical velocity estimated as V*/H, as a function of applied magnetic field H (scaled to 'matching' field H1, which provides exactly one quantum of flux per pinning site). The current is normalized to cΦ0/8π2λ2ξ and the voltage is normalized to ℏ/2eτGL.
Download figure:
Standard image4. Experimental results
Experimental evidence for our claims is provided by measuring the voltage–current characteristics of a 50 nm thick Al superconducting film deposited on top of an array of permalloy (FeNi) square rings as shown in the leftmost panel of figure 3. It has been demonstrated that these magnetic templates represent a very convenient and flexible way to change the pinning strength by simply changing the magnetic state of the rings [23, 24]. This feature stems from the possibility to arrange the individual magnetic domains along each leg of the square rings in such a way that they produce either a very weak or very strong stray field at the corners [26]. Magnetic force microscopy images of these extreme cases are shown in the middle panel of figure 3 (magnified to enhance the contrast), corresponding to the so-called vortex state with a weak stray field, and the rightmost panel of figure 3, corresponding to the onion state with a strong stray field. This magnetic template is separated from the superconducting film by an insulating 5 nm Si layer in order to avoid proximity effects. The line width of each individual square ring is 150 nm, the thickness 25 nm and the lateral size d = 1 μm. Neighboring rings are separated by 70 nm, thus making the period of the magnetic template d = 1.07 μm. This separation corresponds to a matching field H1 = 1.808 mT at which there is one vortex per unit cell. In order to guarantee a homogeneous current distribution [25], the Al film was evaporated onto a predefined photoresist mask patterned into a transport bridge aligned with one of the sides of the square rings. For a direct comparison, patterned and nonpatterned Al films were co-evaporated.
Figure 3. (a) Atomic force microscopy image showing the topography of the magnetic template consisting of Py square rings. (b) Magnetic force microscopy image showing the magnetic field emanating from the square rings in the vortex state. The intensity has been magnified to become comparable to the intensity shown in (c) for rings in the onion state. In all panels, the white bars indicate 1 μm scale.
Download figure:
Standard imageIn figure 4, the experimental V (I) data are reported to compare with (middle and lower panels) and without (upper panel) the presence of artificial pinning centers. It is evident that these V (I) curves are highly nonlinear in the presence of artificial pinning with respect to the reference plain film. It is well known that Joule heating can be a possible mechanism inducing flux-flow instability, so that in our experiments we have previously performed a systematic study on the influence of self-heating (see [13] and references therein). Since unavoidable self-heating may affect experimental data, we also took into account self-heating by considering the Bezuglyj–Shklovskij [7] approach for the term of quasiparticle overheating, leading to the estimate of the threshold magnetic field value BT = 20 mT. In other words, heating effects become crucial for B > BT, clearly out of the low-field range investigated in this work. In addition, we derived from the V (I) data the dissipated power P* = I*V*, which is an increasing function of the magnetic field. This is the experimental evidence that thermal effects are not determining the instability points. In fact, if this was the case of thermal runaway, P* should be independent of magnetic field [27].
Figure 4. Experimental V (I) data at T/Tc(H = 0) = 0.89. In the upper panel, the V (I) is related to a plain Al film; in the middle and lower panels, the V (I) is related to an Al film deposited on top of the magnetic template with rings in the vortex and onion states, respectively.
Download figure:
Standard imageIn figure 5, we summarize the main results of the transport measurements comparing the response of a plain (nonpatterned) Al bridge with the Al bridge on top of the magnetic landscape for two different states, namely the vortex and the onion states. Figure 5(a) shows the critical current density Jc obtained with a voltage criterion of 1 μV as a function of reduced field H/H1 for the three cases and at the same reduced temperature T/Tc(H = 0) = 0.89. A clear difference in the critical current is found among the three samples, the lowest being for the plain film in the entire field range, whereas the onion state exhibits the highest Jc (and therefore the strongest pinning) for fields above H/H1 > 0.2. The fact that Jc for the rings in vortex state crosses over the one for the onion state at low field can be attributed to the suppression of the superconducting order parameter due to the strong stray fields at the corners of the rings. For simplicity, we focus on the field range H/H1 > 0.2, although the analysis is also valid for H/H1 < 0.2. The use of micromagnets as tunable pinning centers has been described in detail in [28].
Figure 5. Comparison of the critical current density Jc (a), instability current density J* (b) and critical velocity v* (c) between a plain Al film, an Al film deposited on top of the magnetic template with rings in the vortex state and an Al film deposited on top of the magnetic template with rings in the onion states. The inset shows a zoom-in of the critical current density and critical voltage for the onion state at a particular submatching field.
Download figure:
Standard imageFigure 5(b) shows the instability current density J* at which the voltage undergoes an abrupt transition toward a higher dissipation branch. Note that despite the huge variation of Jc among the studied samples, only small changes in the instability current J* appear. This finding again validates our model depicted in figures 1(b) and (d), where an increase of pinning only changes Jc but leaves J* almost unaltered. This indicates that J*, rather than the depairing current, represents the upper bound for the maximum achievable critical current. The most remarkable result is the field dependence of the critical velocity, shown in figure 5(c), obtained from the measured critical voltage V* divided by the magnetic field. All features from our introductory analysis and the theoretical simulation (figure 2(c)) are clearly reproduced in these curves. In particular, the fact that there is a decrease of Jc by changing the pinning implies an increase of v*. This latter effect is shown in more detail in the inset of figure 5 where both the critical current density (right axis) and the critical voltage (left axis) are plotted in a field range around the submatching condition H/H1 = 0.5. Here, instead of changing the pinning by switching between different magnetic states, we change the effective pinning by simply sweeping the magnetic field. Each time that the density of vortices is commensurate with the density of pinning sites (matching condition) the vortex lattice arranges itself in a very ordered state that leads to a minimum of the vortex–vortex interaction and therefore to a maximum pinning efficiency. Detuning the field from this condition leads to a rapid weakening of the pinning properties. It is worth mentioning that at low temperatures and magnetic fields or in the vicinity of a matching condition, the critical voltage is close to zero and the inequality Jc ⩽ J* becomes an identity.
It is interesting to note that in figure 5, the condition H = 0 corresponds to no vortices induced externally but does not prevent vortices being induced by the underlying magnetic template. Indeed, at H = 0 completely different scenarios apply for the Al plain film, the film with modulated weak pinning produced by the rings in the vortex state and the strong pinning produced by the rings in the onion state. For instance, for the sample with rings in the onion state, vortex–antivortex pairs are induced by the local intense field [29] and even at H = 0, the entire sample is populated with these pairs. This is in agreement with the fact that at H = 0, the critical voltage V* is finite (not zero) and thus Jc indicates the onset of vortex motion. In contrast to that, for the sample with rings in the vortex state at H = 0, the V(I) curves show a sudden jump from V =0 state (pinning) to the normal state, with no hint of a dissipation tail in between these two regimes. The latter effect can be attributed to the departing transition rather than indicating vortex motion. These considerations omit the effect produced by the self-field which can become important at zero external field and high currents.
Another point that we would like to emphasize is that the superconducting layer (50 nm) is evaporated on top of the magnetic template (20 nm), which implies an important corrugation of thickness modulation. As discussed above, the instabilities take place within a nonlinear V (I) regime indicative of a plastic-like flow of vortices. The microscopic image probably corresponds to a filamentary displacement of vortices, a sort of vortex river, crossing the width of the sample. Since the path that these vortex rivers follow is probably defined by the maximum stress in the vortex lattice, which in turn results from a delicate balance between vortex distribution and the pinning landscape, they may not be exactly reproducible each time. This is just a speculative argument that remains to be verified. In any case, the overall response of the system and the values of I* and V* are very much reproducible.
5. Conclusions
To summarize, we have investigated the influence of vortex pinning on the instability current I* and the critical voltage V* in Al superconducting films. Based on a simple model, where the effects of pinning strength and disorder are explicitly incorporated, we conclude that the critical velocity is always underestimated in the strong pinning limit. This effect leads to an unconventional, very strong decrease of measured v* followed by its increase as the field increases, unforeseen within the widely established LO model. Additionally, our model predicts a decrease of critical velocity as the pinning strength rises. We confirm this prediction theoretically using the Ginzburg–Landau theory and experimentally by switching from weak to strong pinning in a superconducting sample with a tunable magnetic landscape. Moreover, we also underline that our findings are independent of the particular choice either of the superconducting material or of the pinning mechanism [15, 16]. As another fact of importance, we found that the instability current J* is practically insensitive to changes in pinning strength, contrary to the critical current. Therefore J* should be regarded as an upper limit for the maximum achievable Jc.
Acknowledgments
This work was supported by the Methusalem Funding of the Flemish Government, the ESF-NES program, the Belgian Science Policy (IAP) and the Fund for Scientific Research-Flanders (FWO-Vlaanderen). AVS, GRB and WG received individual support from FWO-Vlaanderen. GG acknowledges support from the research project L.R. N5 of Regione Campania. VM acknowledges financial support from the US NSF, grant no. ECCS-0823813. We acknowledge J Van de Vondel for a critical reading of the manuscript.
Footnotes
- 9
It has been theoretically demonstrated by Faleski et al [18] via molecular dynamic simulations that a bimodal distribution of velocities can also be expected in the case of strong disorder. Nevertheless, this assumption leads to a similar conclusion as that achieved in this paper.




 t, 17, B-4000 Sart Tilman, Belgium
t, 17, B-4000 Sart Tilman, Belgium