Resonant charging and stopping power of slow channelling atoms in a crystalline metal

High energy ions impinging on a surface and aligned with low index crystallographic directions can penetrate to great depths before colliding with a target ion and initiating a damage cascade. For example, a 40 keV Xe ion can reach micron depths in crystalline tungsten, but only 0.02 microns in the amorphous form [1]. This channelling phenomenon is exploited in implantation technologies in semiconductor device fabrication [2] and hardening tool steels by nitrogen implantation [3]. Channelling is key to the interpretation of high energy ion scattering and recoil spectrometry [4]. It also plays a key role in irradiation damage of crystalline materials where incident high energy neutrons in a reactor may displace host atoms exceptionally large distances, significantly increasing the size of the damaged region [5].

Glancing collisions with host atoms confine the trajectory of a channelling ion so most of its energy is lost through electronic excitation [2]. The retarding force thus generated is called the electronic 'stopping power' dE/dx. Most theoretical investigations of electronic stopping treat the host as a homogeneous electron gas, incorporating the discrete crystal structure only indirectly through its influence on the dielectric function. In the slow ion regime, with ionic energies below 100 keV per atomic mass unit, linear dielectric response theory [6, 7] and molecular collision theory [8] predict a stopping power proportional to velocity and dependent on the charge state of the channelling ion [9, 10].

30 years ago Datz et al [12] observed resonant peaks in the probability of excitation processes for swift channelling ions with energies of more than 1.5 MeV amu⁻¹ in silver and gold crystals. These resonances were predicted by Okorokov to occur when the potential on the ion, periodic in time and space, excited electronic transitions between its core states [13, 14]. Since the transitions are between states on the same ion its charge state changes only if ionization occurs, although there may be a degree of electron delocalization. Such resonances in swift heavy ions have since been studied in detail [15, 16].

The theoretical treatment of slow ions is more complicated, because characteristic excitation energies lie within the valence band of the target. The local electronic structure of the ion–target system must be taken into account and cannot be reduced to an interaction of a distinct projectile with a spatially homogeneous background medium. Experimental data are sparse, but reveal interesting features, such as a foil-thickness dependence of the charge on channelling ions, explained only with phenomenological or ad hoc models [11, 38].

In this paper we find, through direct simulation, a resonance involving transitions between delocalized valence band states and localized states established between a 'slow' channelling ion and its nearest neighbours. Since these transitions involve a localization of valence electrons onto the channelling ion, the resonance is associated with a net negative charging of the channelling ion, in contrast to [12]. We find, furthermore, that our charge resonance is associated with a reduction in the stopping power.

Direct simulation of channelling MeV self ions in a transition metal crystal, treating electronic excitations explicitly, is computationally demanding. Stopping power may be computed using a quantum mechanical treatment of the electrons in the static limit [17], but one should really allow time for a steady state charge distribution to be established in the frame of the moving ion. This may take several femtoseconds, during which the ion moves many lattice spacings—a 1 MeV copper ion travels at 0.8 au (17.5 Å fs⁻¹) and we find it necessary to use a 116 Å long simulation cell in order to reach a steady state before the channelling ion crosses the cell boundary. The required system sizes are currently unachievable using first principles techniques: time-dependent density functional theory (DFT) studies of these phenomena are restricted to systems of hundreds of atoms [18–20] in which further finite-size effects may also impact the simulation results [21].

By contrast, tight binding (TB) allows us to retain a fully quantum mechanical description of the electrons and their interaction with ions, but in a simpler representation that enables the simulation of orders of magnitude larger systems and for longer periods of time than is the case with DFT. This is the approach to simulating non-adiabatic, quantum, electron dynamics we have developed in our earlier simulations of radiation damage in metals [21–28].

TB starts from the observation that cohesion occurs as orbitals of atoms overlap. It describes the states in a solid as giant molecular orbitals comprising a linear combination of atomic orbitals. The electronic Hamiltonian can then be expressed as a matrix containing off-diagonal elements that can be interpreted as describing quantum mechanical electron hops between orbitals on nearby atoms. For covalent systems, cohesion is naturally understood in terms of bonds, the energy of which has two contributions in TB: a binding part that is the product of a bond order and a hopping matrix element, and a repulsive part represented by a pair potential. In simple terms the bond order is a measure of how many electrons are contributing to the bond, and lies between 0 and 1: for a saturated covalent bond it has the value 1. More precisely, it is one half the difference between the number of electrons occupying bonding states and anti-bonding states formed between the two atoms forming the bond [29]. The same model can be applied to metals, the difference being that each atom has more bonds, but each one has a bond order less than 1: the metallic bond is an unsaturated covalent bond [30]. The electronic contribution to the force one atom exerts on a neighbour is the product of the bond order and the gradient of the hopping integral between them; this is the Hellmann–Feynman theorem expressed in the language of TB. As we shall see, exciting electrons out of their ground state reduces the bond order, thus modifying both the energy of the system and the forces experienced by atoms. It is a reduction because the number of electrons in bonding states is reduced while the number of electrons in anti-bonding states is increased through the excitation.

In this way our TB model is the simplest possible that captures the essential physics: (a) the electrons are treated quantum mechanically, without making the Born–Oppenheimer approximation so that they may become excited, (b) the electronic and ionic degrees of freedom are fully coupled, (c) the discrete atomic structure of the metal is treated explicitly and dynamically, and (d) the model is sufficiently simple it can treat thousands, even tens of thousands, of ions in a metal dynamically and their electrons. Any model simpler than our TB model would sacrifice at least one of these four essential features.

In section 2 we show that there is pronounced charge accumulation on the moving ion over a well-defined velocity range. The charge localization results from the stimulated occupation of localized defect states above the Fermi level, and we show that first order perturbation theory is sufficient to predict the dependence of the charging on ion velocity.

In section 3 we compute the stopping power of the channelling ion in our model system, and show that the charge resonance always leads to a reduction in the stopping power.

Semi-classical Ehrenfest dynamics describes non-adiabatic electronic effects accurately when ionic velocities are high [22]. Ions are treated as classical particles moving in a 'mean field' generated by the electrons; the electrons in turn evolving via the time-dependent Schrödinger equation [21, 31].

We use a single band TB Hamiltonian that has metallic electronic properties and the mechanical and structural properties of copper [32]. The binding energy can be written as a second order Taylor expansion about a reference one-electron density 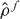$\hat {\rho }^f$ [33, 34],

$$\begin{equation} E_{\mathrm{B}} = 2\, {\mathrm{Tr}}[ (\hat{\rho}-\hat{\rho}^f) \hat{H}_0 ] + \Phi\left(\left\{ \vec{r} \right\} ; \hat{\rho}^f \right) + \epsilon \left[ \hat{\rho} - \hat{\rho}^f; U,V \right]. \end{equation} \tag{ 1 }$$

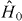$\skew3\hat {H}_0$ is the Kohn–Sham Hamiltonian evaluated at the reference density; the 2 is for spin-degeneracy; the electrostatic and exchange-correlation energies are represented by the adiabatic pairwise ion–ion interaction Φ [35], and approximates the second functional derivatives of the energy:

$$\begin{equation} \epsilon \left[ \hat{\rho} - \hat{\rho}^f ; U,V \right] = \frac{1}{2} U \sum_a q_a q_a + \frac{1}{2} \sum_{a,b\neq a} z_{ab} q_a q_b. \end{equation} \tag{ 2 }$$

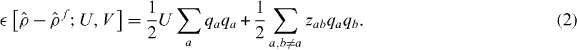
where if |a〉 is the local orbital on atom a, then 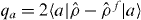$q_a = 2 \langle a | \hat {\rho } - \hat {\rho }^f | a \rangle$ is the excess number of electrons on ion a, U measures the onsite electrostatic repulsion energy, and z_ab is an electrostatic interaction regularized at short range [36]

$$\begin{equation} z_{ab} = \frac{e^2}{4\pi \epsilon_0} \left[ r_{ab}^2 + {\left(\frac{e^2}{4\pi \epsilon_0\,V} \right)^2} \right]^{-\frac{1}{2}}. \end{equation} \tag{ 3 }$$

The full self-consistent Hamiltonian is 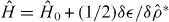$\skew3\hat {H} = \skew3\hat {H}_0 + (1/2) {\delta \epsilon }/{\delta \hat {\rho }^{*}}$. In addition z_ab is tapered to zero at half the simulation cell side length to avoid spurious interactions between an ion and its periodic replicas. Efficient metallic screening means charges are present only in the immediate vicinity of the channelling ion and this truncation is well converged. We vary U and V to explore the impact of electron-electron interactions—a realistic choice for copper is U ≈ V ≈7 eV [37].

We take a simulation cell of 7 × 9 × 32 fcc unit cells, totalling 8064 atoms, with periodic boundary conditions. An unrelaxed tetrahedral self-interstitial is introduced, and the initial electronic density matrix is found self-consistently from the Hamiltonian with a canonical electron temperature of 1000 K. The interstitial is then given an instantaneous velocity along the long axis of the [001] channel. The channelling ion therefore has the same size and electronic orbitals as a bulk ion, and the mass of a copper ion (63.5 amu or 6586 eV fs² A⁻²). The host atoms are kept stationary. The impulse imparted by a channelling ion to its neighbours is small—so the unrelaxed interstitial is the relevant configuration for channelling ions at these speeds. Letting host atoms move is not expensive, but preserving strict translational symmetry of the channel simplifies interpretation of the non-adiabatic energy transfer.

Our results indicate a steady state is reached after 4–6 fs, consistent with charge equilibration seen experimentally after 7 fs even for initially highly charged ions [38]. Figure 1 shows the steady state charge distributions at a range of ion energies. The centre of the screening charge lags behind the channelling ion, in agreement with linear response models [6, 39, 40].

Zoom In Zoom Out Reset image size

The bond energy, electrostatic energy and charge on the channelling ion oscillate with the frequency at which the ion passes its neighbours. We compute bounds for each quantity studied (figure 2), and then use least-squares fitting to extract the mean or gradient. An analysis of charge and stopping power behaviour follows.

Zoom In Zoom Out Reset image size

Figure 3(a) shows that at low velocity (<5 Å fs⁻¹) the charge distribution in the frame of the moving ion remains close to the ground state. At the highest velocities considered (>15 Å fs⁻¹) electrons start to be stripped from the ion. But the most striking feature is the charge accumulation on the moving ion at velocities between 5 and 15 Å fs⁻¹, with the position of the maximum depending on the intraionic energy U. The dependence on V is much less pronounced, with V =0 (no interionic electrostatic interactions) and V =7 eV (screened at short-range) showing very similar line shapes. We interpret the origin of this charging effect with a simple perturbation theory analysis.

Zoom In Zoom Out Reset image size

We view the channelling ion as a periodic perturbation to the perfect crystal Hamiltonian, each frequency component ω of which may excite electronic transitions through energy ℏω. This is analogous to the periodic perturbation on the channelling ion responsible for core excitations considered by Okorokov [13, 14].

The charge accumulation does not require that the ion travel ballistically through the lattice, only that characteristic frequencies are present which excite electrons to and from localized states on the ion. An unrelaxed oscillating interstitial atom should capture much of the same physics, and is amenable to analysis with time-dependent perturbation theory.

Let 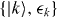$\left \{ |k\rangle , \epsilon _k \right \}$ be the eigenstates and eigenvalues of the unperturbed non-self-consistent perfect crystal, and 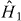$\skew3\hat {H}_1$ be the perturbation due to an unrelaxed self-interstitial vibrating with frequency ω. In the channelling case, the dominant frequency Ω is set by the time taken for the channelling ion to move between equivalent interstitial positions. Fermi's Golden Rule (FGR) gives us the number of electrons transferred to the orbital on the oscillating ion c:

$$\begin{equation} \Delta q_c(\Omega,t) \approx \, \sum_{k,k'} s(k,k' \,; \Omega) \zeta_c(k,k') \, t , \end{equation} \tag{ 4 }$$

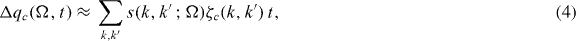
where s(k,k',Ω) is the transition rate from state k' to k,

$$\begin{equation} s(k,k' \,; \Omega) = 2 \times \frac{ 2 \pi }{\hbar} | \langle k' | \hat{H}_1 | k \rangle |^2 \, \left[ \delta\left(\epsilon_{k} - \epsilon_{k'} - \hbar \Omega \right) + \delta\left(\epsilon_{k} - \epsilon_{k'} + \hbar \Omega \right) \right] , \end{equation} \tag{ 5 }$$

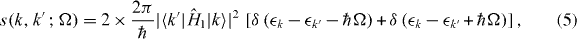
the leading 2 being for spin degeneracy, and ζ_c(k,k') is the charge transfer,

$$\begin{equation} \zeta_c(k,k') = f(k) (1 - f(k')) (\left| \langle k' | c \rangle \right|^2 - \left| \langle k | c \rangle \right|^2 ). \end{equation} \tag{ 6 }$$

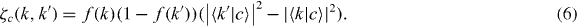
f(k) is the initial occupation of state k. We have omitted some purely oscillatory terms of second order in 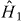$\skew3\hat {H}_1$ due to off-diagonal matrix elements $\langle k'|\hat {\rho }|k\rangle ,\,k'\neq k$.

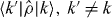At low speeds, this frequency stimulates transitions only near the Fermi level. However, key features in the local density of states (figure 4(a)) are instantaneous bonding and anti-bonding states localized on the moving ion and its neighbours. These features are not artifacts of our simplified electronic structure and are evident in more accurate DFT calculations (see below). The splitting of these states is large because the distance between the channelling ion and its immediate neighbours is small—varying between 50 and 61% of the ideal separation. Above a critical speed, the dominant frequency is sufficient to promote electrons from delocalized states below the Fermi level into the anti-bonding defect states above the band, thus localizing electrons on the channelling ion and its neighbours. At still higher speeds this charge localization is reversed when electrons are excited from the localized bonding state resonance near the bottom of the band to delocalized states above the Fermi level.

Zoom In Zoom Out Reset image size

The results of the FGR analysis of equation (4) are plotted in figure 4(b), together with points from non-self-consistent channelling simulations (U = V =0). The oscillator frequency is equated with the frequency of the ion's passage between equivalent ionic configurations, Ω = 2π|v|/d, where d = 1.805 Å, the distance between tetrahedral points in the 〈100〉 channel. The position and shape of the charge resonance is well reproduced, indicating that perturbation theory captures the mechanism of charge transfer. Charge accumulation indeed occurs when the oscillator excites electrons from delocalized states below the Fermi level to the localized anti-bonding defect state. At higher frequencies electrons are excited from the localized bonding resonance state to unoccupied states above the Fermi level. The net effect is a charging resonance in a narrow window of frequencies.

At higher frequencies still there is an important and illuminating difference between perturbation theory and the channelling simulations. Above ℏΩ = 35 eV, the only available electronic transitions are from the localized bonding resonance state to the anti-bonding defect state centred on the interstitial. For the vibrating ion these excitations yield no net charge transfer, and so FGR predicts no further change in ion charge state. But when the ion is channelling, localized anti-bonding states are created, occupied, and left behind in a trail that only gradually delocalizes (figure 1). This will occur when 2π/Ω is less than the time (≈0.1 fs) for an electron to hop from the moving ion to a channel ion and back, corresponding to a speed of ≈20 Å fs⁻¹. At these frequencies an oscillating ion is not a good representation of a channelling ion.

The inclusion of intraionic electrostatic interactions raises the energy of the anti-bonding defect state when it becomes occupied. By varying the onsite electrostatic repulsion energy U we find that the maximum charge accumulation for a self-consistent Hamiltonian occurs at a channelling speed shifted by Δv/d ≈ Uδq(v)/h, where δq(v) = q(v) − q(0) is the excess electron count accumulated in the defect state when the ion moves at speed v. This can be seen in figure 3(a).

To check that the existence of localized states is not an artifact of our simplified Hamiltonian we have computed the local electronic structure around a channelling ion using DFT. Computing the electronic structure appropriate for a relaxed self-interstitial is routine, but when unrelaxed the short bond lengths introduce some technical issues. We have computed the local density of states in a sphere centred on a channelling ion in copper (figure 5) with the projector augmented-wave (PAW) method [41] using Vasp [42]. The sphere radius was taken to be 1.12A, which would be space filling if the tetrahedral bonding environment were repeated. Convergence was found using a 108 + 1 atom cell, using an 8 × 8 × 8 Monkhorst–Pack grid with 1600 bands and a 900 eV kinetic energy cutoff. It is necessary to include 3p electrons as well as 3d and 4s in the valence band, as while these states are well separated in energy, there is significant spatial overlap which leads to additional resonances near the Fermi level [43]. We have found similar resonances and localized states in several other metals containing an unrelaxed interstitial using the same calculation method, suggesting these features are indeed generally present.

Zoom In Zoom Out Reset image size

The computed stopping power is plotted in figure 3(b). At speeds up to 5 Å fs⁻¹ it increases with speed as dE/dx ≈ b|v|. A least-squares fit indicates the coefficient b is 0.44 ± 0.01 eV Å⁻² fs, compared with b = 0.636 ± 0.004 eV Å⁻² fs obtained by simulations of radiation damage cascades [23]. The difference is due to the greater range of environments experienced by moving ions in cascades [21].

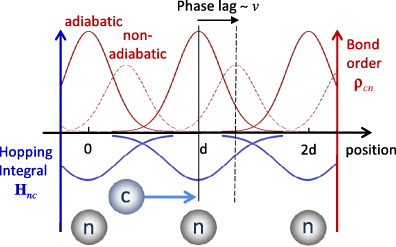
The stopping power is given by the average Hellmann–Feynman force 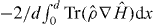$-2/ d\!\int _0^d {\mathrm {Tr}}(\hat {\rho } \nabla \skew3\hat {H}) {\mathrm {d}} x$, where d is the repeat distance along the channel. The integral is zero if electrons are able to respond in phase with the periodic variation of the Hamiltonian. In this adiabatic limit the channelling ion has to be moving sufficiently slowly. At larger channelling speeds a small phase lag develops between the periodic variations of the bond orders to the channelling ion and the Hamiltonian. Here we have the origin of the initial linear increase of the stopping power with the speed of the channelling ion in the non-adiabatic case. This is illustrated schematically in figure 6. Above the charge resonance the occupation of localized anti-bonding states and the emptying of localized bonding states both reduce the bond orders to the channelling ion. Consequently the stopping power is always expected to fall below the linear relationship at the onset of the charge resonance, as seen in figure 3(b), irrespective of whether the anti-bonding states are occupied before the bonding states are emptied or vice versa.

Zoom In Zoom Out Reset image size

A notable feature in figure 3(b) is the closeness of the lines with V zero and nonzero. This suggests that, as expected, plasmons play only a minor role in the stopping power at these velocities [44]. This is confirmed in the inset to figure 3(b): we find our single orbital TB model has a plasma frequency of 13.7 eV, stimulated by a channelling velocity of 5.96 A fs⁻¹. While some energy is lost to plasmons around this frequency, the maximum contribution is only 0.2% of the total.

We have performed simulations of slow heavy ions channelled in a model metal at energies from 1 keV to 1 MeV, using a self-consistent Hamiltonian explicitly dependent on atomic positions. We have discovered a resonance in the charge of a slow channelling ion which reduces the electronic stopping power below the usual linear dependence on the channelling ion speed. In our model the charge resonance first appears when the frequency of the variations of the Hamiltonian experienced by the channelling ion matches the energy required to excite electrons in delocalized states near the Fermi energy to anti-bonding states localized on the channelling ion. The charge on the channelling ion is subsequently reduced at higher channelling speeds by excitation of electrons from bonding states localized on the channelling ion into delocalized states. Whether the onset of the resonance is triggered, as here, by electronic excitation from delocalized states to localized anti-bonding states, or excitation from localized bonding states to delocalized states, depends on the relative location of the defect states and the Fermi-level. At sufficiently small band-fillings or where the defect states are shifted in energy the order of these excitation processes may be reversed. The channelling ion will then become more positively charged at the resonance. Regardless of whether the channelling ion becomes more positively or negatively charged at the resonance the stopping power is always reduced below the linear relationship with the speed of the channelling ion.

This phenomenon has parallels to the Okorokov effect and resonant electron capture processes, but it is not equivalent: the electronic states involved here are neither those of the atomic projectile nor those of the bulk target, because they are unique to the full electronic structure of the projectile-target combination. The charge resonance that we describe is thus a product of physics that is absent in the earlier models used to explain resonant excitation processes of channelling ions.

We have confirmed the existence of localized bonding and anti-bonding states at a stationary, unrelaxed, self-interstitial in copper using density functional theory. Although these states mix with delocalized band states of the same energy they remain sharply localized on the interstitial and its nearest neighbours, as might be expected in view of the exceptionally short bonds to an unrelaxed self-interstitial. The width of the resonance in copper is ∼0.1 eV, giving an estimated lifetime of h/E ∼ 40 fs—significantly longer than the charging timescale. Similar first principles calculations of static, unrelaxed, interstitial defects may be carried out to determine whether charge resonances are expected during channelling of those interstitial defects in other host metals.

The possibility of a wide variety of behaviour for different projectile–target combinations suggests that the effect predicted by our simulations could potentially be detected in thin foil experiments, in which memory of the charge state achieved in the bulk is retained in the emerging projectiles.

Our results have been obtained and explained with a simple model that explores the physics of channelling in a metal. Our model correctly captures the physics of a time-evolving system of classical ions and quantum mechanical electrons. The qualitative features in the electronic structure on which our results depend have been confirmed with DFT calculations. However, our simulations should not be viewed as providing a quantitative stopping power for a specific ion–target pair. The stopping power in chemically specific systems may be modelled directly with time-dependent DFT techniques using our procedures once computing resources become sufficient to treat the thousands of atoms these simulations require. It will be very interesting to see whether time-dependent ab initio techniques recover our predicted resonances in the charge and stopping power on the channelling ion.

Calculations were performed on Hector and IC-HPC. DRM and CPR were supported by EPSRC grant number EP/C524403. We thank Tchavdar Todorov for his valuable insight in many useful discussions.