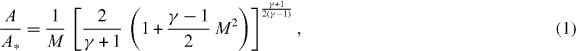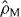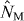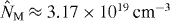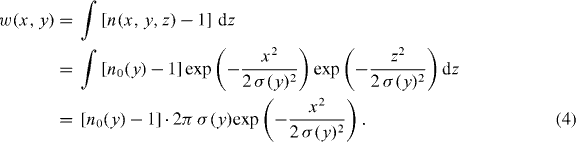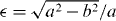Abstract
A method is presented for improving the brilliance of laser-produced soft x-ray sources that are based on pulsed gas jets as the targets. The conversion efficiency of laser energy into soft x-ray radiation is enhanced by locally increasing the particle density of the target species. This is achieved by applying a small background pressure to the supersonic flow emanating from a nozzle. In this manner, a supersonic jet with a so-called barrel shock system is formed. On passing the shocks, particles become locally concentrated, forming high-density regions that are used as the targets. An estimate of possible increases in particle densities is provided. The jet flow is then analyzed experimentally by Schlieren imaging, thus visualizing the spatial shock structure. Additionally, a quantitative measurement of the gas density is made using a Hartmann–Shack wavefront sensor. The beneficial effect of the applied background gas on plasma generation is clearly more prominent than its absorbing effect on the photons originating from the plasma. This is shown for a nitrogen target with helium as the background gas. A plasma, generated behind the barrel shock in the nitrogen jet, emits monochromatic photons at a wavelength of 2.88 nm. The peak brilliance of the source is increased by an order of magnitude, resulting in 3.15 × 1016 photons (mm2 mrad2 s)−1.
1. Introduction
Laser-produced extreme ultraviolet (EUV) and soft x-ray sources are of increasing technical and explorative interest: they provide radiation for next-generation semiconductor lithography [1] and represent the basis of many research areas such as surface analysis by reflectometry/scatterometry [2] or NEXAFS spectroscopy [3, 4]. Furthermore, generation of photons in the water window (λ = 2.3–4.4 nm) enables building of a compact x-ray microscope, surpassing the resolution achievable by conventional microscopy [5].
Solids, liquids or gases are used as the laser targets, each offering certain advantages and disadvantages. The use of solids or liquids results in comparatively bright and small plasmas whose spatial extension is of the order of several tens of μm [6–8]. The main drawback of these materials is the inevitable production of debris, which can severely damage the optics in the beam path. Additionally, preparation of liquid targets requires considerable technical and experimental effort. These problems can be avoided by using gaseous targets, with the drawback of a smaller photon yield and relatively large plasma sizes of several hundreds of μm [9].
When a gas target is used, a pulsed gas jet is typically expanded supersonically into a vacuum since absorption length of soft x-rays in gases is very small. After exiting the nozzle the density of the gas drops rapidly in all directions. For the generation of a plasma, the laser pulse is focused, preferably into a region with a high particle density, i.e. as close as possible to the nozzle without damaging it. Nevertheless, a certain nozzle degradation always occurs, due to the proximity to the plasma. A more confined density distribution has been achieved by using concentric nozzles. Here, the target gas jet is laterally guided by a jet of another species. Reabsorption by the surrounding species is low when a gas with a high transparency for the generated soft x-rays is used such as, for example, helium [10].
In the present study, a different approach is used to recompress the target gas jet at longer distances from the nozzle. The basic idea is that the density of a gas increases on passing through a shock wave. For example, high densities prevail in a shock layer formed ahead of an obstacle placed in a supersonic flow. However, shock layers are very thin and thus plasmas would again be created close to a solid surface. Therefore the formation of shock waves is caused by applying a background pressure in the chamber into which the gas expands from the nozzle. The supersonic expansion of the gas is then constrained by the presence of the background gas. As a consequence of the background pressure, shocks are generated, leading to an increase of the local particle density. In the radial direction the jet is enclosed by an oblique shock. Due to its shape, it is referred to as a 'barrel shock'. On crossing the barrel shock, streamlines are turned toward the jet axis, thus resulting in a lateral confinement of the jet. In the axial direction the lateral barrel structure is terminated by a 'Mach disc'. This term denotes a practically normal shock of disc-like shape [11]. Focusing the laser beam into a high-density region behind one of these shocks, a higher number of gas atoms can be ionized, resulting in a brighter and smaller plasma. Since the plasma is generated further away from the nozzle, degradation effects are also prevented. In the following, the possibility of exploiting these shock structures to create plasmas suitable for producing soft x-rays of high brilliance is studied.
2. A soft x-ray source
The setup of a standard soft x-ray source based on gas targets is used [4]. It basically consists of a piezo-electrically operated Proch–Trickl gas valve [12] mounted on a vacuum chamber, and a driving Nd:YAG laser (fundamental wavelength 1064 nm, pulse energy 800 mJ and pulse duration 6 ns). The intensity profile of the laser beam, measured by a CCD camera, reveals a beam diameter (determined through 1/e2 decay) of 5.9 mm, corresponding to a power density of 4.9 × 108 W cm−2. The beam is focused into the gas jet by a lens with a focal length of f = 80 mm. Thus, the diameter of the beam decreases to 45 μm at its waist position, where it reaches a maximum power density of 8.4 × 1012 W cm−2. Plasma production takes place as soon as a critical power density of ≈1012 W cm−2 is reached (i.e. shortly before the focus) at a sufficiently large particle density [13]. This initiates multiphoton ionization of the target gas followed by avalanche ionization, creating large numbers of free electrons.
The gas is expanded through a divergent nozzle of conical shape. Over a length of 1 mm its diameter increases from the throat diameter d* = 0.3 mm to the exit diameter de = 0.5 mm. The nozzle is opened for a period of 1 ms, generating an underexpanded supersonic jet that expands from stagnation pressures ps of up to 16 bar into vacuum, i.e. the background pressure pb is as low as 10−4 mbar. The laser is focused into the gas as soon as the jet flow is steady. The position where the plasma is produced is located 500 μm, i.e. one diameter de, behind the nozzle exit (cf the typical position of plasma indicated in figure 1 top). Although the density is highest at the nozzle exit the plasma should not be generated closer to the nozzle because of growing degradation effects.
Figure 1. Schematic representation of the plasma generation; top: a standard setup with pb = 10−4 mbar; bottom: a modified setup with pb > 10 mbar.
Download figure:
Standard imageIn the approach pursued in the present study, the background pressure pb is increased to several tens of mbar in order to generate a barrel shock in the supersonic jet. For this purpose, helium is utilized as background gas due to its high transmittivity to photons generated by the plasma. In addition, the length of the optical path through helium of the resulting soft x-rays is minimized by differential pumping. Another advantage of using helium as a surrounding gas is its large first ionization energy (24.6 eV) compared to that of nitrogen (14.5 eV). Thus, the critical power density to drive ionization by the incident laser beam is higher for helium, which ensures that only the target species nitrogen is ionized. Behind the shock system generated in the jet the gas density increases. In this manner, regions involving high densities of the target gas are obtained at comparably large distances from the nozzle. Thus the plasma can be generated further away from the nozzle exit, cf figure 1 bottom. By employing different target gases, various spectra can be obtained in the EUV and soft x-ray ranges. Noble gases with high atomic numbers such as xenon, argon or krypton are broadband emitters, while oxygen or nitrogen each produce several narrow lines. Corresponding spectra can be found in figure 2, produced by a laser comparable to that described above and captured with a soft x-ray spectrometer, which is described in detail in [4]. Here, nitrogen is used in combination with a titanium filter, delivering a monochromatic emittance at λ = 2.88 nm in the water window, corresponding to the transition 1s2–1s2p of the valence electron of the N5+ ion.
Figure 2. The emission spectra characteristic of various target gases, captured with a soft x-ray spectrometer.
Download figure:
Standard image3. Characterization of the supersonic jet and the plasma
3.1. Properties of the gas jet
The gas jet is characterized for obtaining information about the location of the shock waves and the density distribution in the jet. In this manner, positions suitable for generating x-ray plasmas will be determined. First, a rough estimate of achievable particle densities is provided based on one-dimensional flow theory and empirical correlations for highly underexpanded jets. Then, two different experimental methods have been employed: on the one hand, Schlieren images have been taken to gain highly resolved information on the structure of the supersonic flow. On the other, a Hartmann–Shack wavefront sensor has been applied to attain quantitative values of the particle density, but at a comparably lower resolution. In the following, the theoretical estimate and the experimental procedures of the two measurements are described in detail.
3.1.1. Theoretical estimates
The expansion of a gas into a chamber of low pressure results in the formation of distinct shock waves only if the background pressure is high enough. For a fixed stagnation pressure this means that the nozzle pressure ratio ps/pb needs to be sufficiently small. Then the flow can be considered as a continuum and shock waves can be treated as discontinuities across which the shock relations of gas dynamics apply. With increasing the nozzle pressure ratio (caused by decreasing the background pressure), shocks begin to thicken. Eventually, they can no longer be considered as individual shocks but the background gas interacts directly with the exhaust gas. This has been called the scattering regime [14]. For a gas exhausting from a sonic orifice, Muntz et al[14] have introduced a rarefaction parameter ξ = d* (ps·pb)(1/2)/T that is formed with the diameter d* of the orifice, the stagnation and background pressures and a temperature that is taken to be the stagnation temperature (T = 293 K) in the following. Besides the condition of a sufficiently small nozzle pressure ratio in order to find shock waves, this parameter classifies the flow into a scattering and a continuum regime based on the density of the gases. If the density of the background gas is too low, distinct shock waves do not evolve. After Muntz et al, gas exhausting from an orifice is in the scattering regime when ξ < ξl = 2 k σ−2s and in the continuum regime for ξ ≳ ξc = 0.01 N (m K)−1 (for nitrogen). Here, k is the Boltzmann constant and the collision diameter σs is the mean value of that of the jet gas (σs,N2 = 417 pm) and the background gas (σs,He = 233 pm) [15]. For the lowest stagnation pressure (ps = 10 bar) used in the present study, this yields pb,l ≈ 2 × 10−4 mbar and pb,c ≈ 1 mbar. For pb < pb,l the scattering regime is obtained and for pb > pb,c the jet is in the continuum regime where barrel shocks are present. Here, a background pressure of 10−4 mbar is used to represent the scattering regime, and background pressures pb ⩾ 50 mbar are used for the continuum regime. Within the latter regime, the Mach disc approaches the nozzle with increasing background pressure pb (at constant stagnation pressure). This results in an increase of the pressure behind the Mach disc because the pressure ahead of the Mach disc also increases when approaching the nozzle. For this reason, background pressures much larger than the critical value of pb,c ≈ 1 mbar were considered in the present investigation.
An upper limit of maximum particle densities achievable behind the Mach disc is now derived as follows. Within the barrel shock where the flow is not affected by the background gas, the flow can be approximated by a radially expanding source flow. The virtual center of the source flow is assumed to coincide with the location of the apex of the cone with respect to the nozzle geometry. Critical conditions corresponding to a Mach number M = 1 are reached at the throat of the nozzle, i.e. at the upstream end of the physical nozzle. Here, the throat is located a distance r* = 1.5 mm behind the virtual source that coincides with the apex of the cone corresponding to the nozzle (cf section 2).
In the expanding flow the Mach number M is connected with the cross sectional area A of the flow by the well-known area relation of gas dynamics:
where γ is the ratio of the specific heats and A* the throat area. For diatomic gases (γ = 7/5), the Mach number at the nozzle exit (where A = Ae) is equal to Me ≈ 2.6. As mentioned before, the structure of the shock system depends on the nozzle pressure ratio. For sonic nozzles and pressure ratios 15 < ps/pb < 17 000, the distance yM between the nozzle exit and the Mach disc is given by the correlation yM/de = 0.67 (ps/pb)1/2 [16].
In the isentropic flow within the barrel shock, the density ρ is a function only of the Mach number and the stagnation density ρs:
Further, the density right behind the Mach disc is given by the normal shock relation
where the index 'M' denotes the conditions at the Mach disc and the hat symbol the conditions after the shock.
Based on these considerations, a rough estimate of the density behind the Mach disc is now provided. Here, a case is considered that has also been the subject of a quantitative measurement (see below): ps = 10 bar, pb = 170 mbar, i.e. ps/pb = 58.8. The correlation for the location of the Mach disc yields yM = 2.6 mm. The distance rM of the Mach disc from the center of the source flow considered here is thus the sum of the distance of the source from the throat, the length of the nozzle and the distance of the Mach disc from the nozzle exit, i.e. rM ≈ 5.1 mm. At the Mach disc the dimensionless area of the source flow is then given by AM/A* = (rM/r*)2 = 11.56 and the area relation yields MM ≈ 4.1. Using relations (2) and (3), the density ahead of the Mach disc is ρM ≈ 0.0255ρs, and after passing the shock it is . Here, the nitrogen expanding from a reservoir at room temperature (Ts = 293 K) is considered. The stagnation density ρs is readily obtained by way of the ideal gas equation. Particle densities N are related to the density via the molecular weight and the Avogadro constant. This results in particle densities ahead (NM) and after ( ) the shock of NM ≈ 6.87 × 1018 cm−3 and . Note that these values are upper limits. The estimate is based on correlations for sonic nozzles. Here, however, a conical nozzle is used. The jet exiting the nozzle is highly underexpanded. This results in expansion waves propagating into the radially expanding source flow. Furthermore, viscous effects can cause a separation of the flow at the nozzle throat, resulting in a smaller effective critical cross sectional area and thus stronger expansion. Both effects result in a reduction of the density.
3.1.2. Schlieren imaging
Schlieren imaging is a common technique in fluid dynamics which enables one to qualitatively measure density gradients [17]. The experimental setup is shown in figure 3. A pinhole (diameter d = 100 μm) is illuminated by white light, and a focusing lens collimates the resulting beam, which then travels in the z-direction through the depicted gas distribution. The plane spanned by the x- and y-axes that contains the axis of the jet is imaged to a CCD camera at z = 2f1 + 2f2 by a 4f setup (exposure time 50 μs). Here, imaging lenses with focal lengths of f1 = 160 mm and f2 = 300 mm are used. A knife edge is moved close to the focal spot in between the two lenses, eliminating half of the spatial frequencies in the Fourier plane. The orientation of the blade determines which direction of the density gradient will become visible. For example, as depicted in figure 3, a knife edge aligned with the x-axis generates a change in intensity proportional to the gradient of the refractive index corresponding to the density gradient . Note, however, that in the Schlieren pictures shown below, the knife edge is aligned with the y-axis so that density gradients within the jet are visualized in the radial direction, thus emphasizing the barrel shock.
Figure 3. Experimental setup for producing Schlieren images. The dotted lines represent the path of light traveling through a constantly distributed refractive index. The dashed line indicates a light ray which is refracted by the varying distribution of gas density below the nozzle, thus hitting the knife edge and darkening the image. Replacing the CCD camera with a Hartmann–Shack sensor and removing the knife edge also allows monitoring of the wavefront deformations.
Download figure:
Standard image3.1.3. Hartmann–Shack measurement
A Hartmann–Shack wavefront sensor [18, 19] is used to obtain quantitative information on the density distribution in the supersonic gas jet [20]. The experimental setup is mostly the same as that depicted in figure 3 for Schlieren imaging. However, the knife edge is removed and the CCD camera is replaced by the wavefront sensor. An initially plane wavefront of a test beam that travels through the target gas is deformed due to the spatial variation of the refractive index n(x,y,z) and thus also of the density. The sensor splits the test beam into many subbeams by an array of micro lenses, each producing a spot on a CCD camera. The positions of the spots contain the information of the wavefront gradient. Thus the deformation of the wavefront can be recovered. The spatial resolution Δx of the deformation in the x-direction of a measured wavefront is equal to the pitch of the micro lens array dx = 150 μm divided by the magnification factor M = f2/f1 = 1.88 of the 4f setup, yielding Δx = 80 μm.
The particle density distribution N(x,y) is recovered from a measured shape w(x,y) of a deformed wavefront as follows. The test beam integrates n(x,y,z) over the propagation direction z of the light beam, resulting in a difference w(x,y) in the optical path. The distribution of the particle density is now obtained by assuming that in a plane corresponding to a constant y = y0, n(x,y0,z) is approximated by a rotationally symmetric Gaussian shape with a maximum value n0(y0) = n(0,y0,0). Then the deformation of the wavefront reads
The standard deviation σ(y) of n(x,y,z) is determined from the shape of the measured deformation of the wavefront w(x,y) by a Gaussian fit. The distribution of the refractive index in a plane containing the jet axis (z = 0) is recovered by
Conversion of the refractive index n(x,y,0) into a particle density N is done by using the Lorentz–Lorenz formula [21]
where α, the polarizability of the considered gas particles, is derived using the ideal gas law and the values n = 1.000 2974 and N = 2.69 × 1019 cm−3 for nitrogen under normal conditions (at a temperature of 273.15 K and a pressure of 1013 mbar). In this, the surrounding helium atmosphere is neglected because of its low refractive index, which amounts to only a few per cent as compared to that of the nitrogen jet.
3.2. Characterization of the plasma
The peak brilliance B of a pulsed monochromatic light source is defined by
where NPh denotes the number of photons emitted during the duration τ of a single pulse, per solid angle θ, originating from an area A. Here, τ = 6 ns, which equals the duration of the exciting laser pulse. The number of photons per solid angle is determined by using a calibrated XUV photo diode (International Radiation Detectors, AXUV100). The plasma is imaged by a phosphor-coated CCD camera in combination with a titanium-filtered pinhole. This delivers the intensity distribution of radiation at λ = 2.88 nm. Here, the luminescent area A is approximated by an ellipsoidal shape with the semiaxes a and b. Then A = πa b, where a and b are defined as the full-widths at half-maximum of the intensity distribution in the x- and y-direction. The uniformity of the plasma is characterized by its eccentricity . Examples of intensity images are shown in figure 6 in combination with the corresponding Schlieren images of the gas jet for the case of both, gas issuing into vacuum and gas issuing into a background gas and thus forming a jet with barrel shocks.
4. Results and discussion
First, the gas jet and the effect of a background pressure on the resulting flow structure are investigated using the techniques described in the previous section. Depending on the stagnation and background pressure, the gas jet may form various shapes, which are discussed in the following (cf figure 4). In previous studies of laser-produced x-ray sources the nozzle was operated in the range ps = 10–16 bar at a background pressure of pb = 10−4 mbar, i.e. practically without any background gas. In this case, the emerging flow is in the scattering regime and does not show any discontinuities. Independently of ps the density distribution has a maximum value at the nozzle exit and rapidly falls in all directions. Corresponding Schlieren images taken with the knife edge aligned with the y-axis can be found in figure 4, e.g. for ps = 10 bar in figure 4(a).
Figure 4. Schlieren images indicating the supersonic flow structure of a N2 jet as a function of stagnation and background pressure (flow direction: top → bottom, the knife edge is aligned with the nozzle axis): (a) an example of the scattering regime showing no internal structures of the jet; (b) arrow indicating the position of a Mach disc in continuum flow; (b) → (c) increasing background pressure, (b) → (d) increasing stagnation pressure.
Download figure:
Standard imageWith rising background pressure, particle collisions increasingly affect the gas jet and retard its free expansion. At a certain distance from the nozzle, this results in a shock which is directly connected to a sudden decrease of the Mach number M. At the same time, the local particle density increases. This becomes evident in regions in the Schlieren images that show strong changes in intensity, implying high density gradients. As can be seen, for example, in figure 4(b), the shape of the resulting shock structure resembles a barrel; for this reason it is referred to as a barrel shock. In the downstream direction the barrel shock is terminated by a Mach disc, which is indicated in the Schlieren image by an arrow (figure 4(b)). In the present Schlieren pictures, the Mach disc is reproduced only weakly because the knife edge was aligned perpendicular to the disc, i.e. only density gradients in the x-direction (parallel to the disc) were detected. Increasing pb, as from figures 4(b) to (c), results in a confinement of the gas flow towards the nozzle axis; the lateral shocks approach each other and the Mach disc moves upstream. In contrast to this, increasing ps has the opposite effect, i.e. the radius of the barrel shock and the width σ of the density distribution increase and the Mach disc moves downstream, cf figures 4(b)–(d). These two opposite effects allow generation of the same shock structure at different combinations of the pressures, provided that the ratio ps/pb stays constant.
In figure 5, wavefront and Schlieren measurements are compared with each other. Good agreement can be observed between the results of both techniques. The resulting particle density N(x,y) shows the mean gas distribution inside the gas jet. In the downstream direction, along the nozzle axis, N first decreases and then increases again up to a maximum value of Nmax = 9.76 × 1018 cm−3. This value is of the same order of magnitude but smaller than the estimate obtained in section 3.1.1. As described in section 3.1.3 the high value of the density right behind a shock cannot be resolved by the wavefront measurement. Furthermore, the estimate provides an upper limit of the particle density. This explains why values of the estimated densities, both of the maximum and the minimum, are higher than the corresponding measured values. Behind the first Mach disc the wave-like behavior of the particle density is repeated at lower density values. The maxima coincide approximately with the positions where the lateral shocks interfere, forming a Mach disc.
Figure 5. Left: wavefront and Schlieren images of the N2 jet (ps = 10 bar) which expands into a He atmosphere (pb = 170 mbar); right: particle density distribution N(x,y) of the N2 jet in the plane z = 0.
Download figure:
Standard imageThe effect of an increase in target gas density on the plasma generation is exemplarily illustrated in figure 6 for a stagnation pressure of ps = 10 bar. Taking advantage of the barrel shock, obviously the brightness of the plasma is raised, whereas its size has decreased in the direction of the incident laser beam. Due to the increased target density, there are more emitters of soft x-ray radiation in the same volume. Besides, the absorption rate of laser energy is raised. Thus, the power density of the beam decreases more rapidly below its critical value and no further atoms are ionized. This confines the size of the plasma in the beam direction and explains its smaller size. Another mechanism causing the reduced size might be plasma defocusing [22]. Due to an increased plasma density, a stronger defocusing effect can be expected, limiting the ionization region. During the experiments it turned out that generation of plasma right below the Mach disc, where the density is expected to be at a maximum, is not the optimal position. It was found that even brighter and smaller plasmas occur when the laser is focused onto the edge of the jet at a location slightly above the Mach disc and after the barrel shock (cf figure 6). This behavior may be caused by reabsorption of soft x-rays by the surrounding nitrogen particles. The barrel shock is enclosed by a thin supersonic compressed layer, which becomes thicker at the Mach disc [11], leading to increased reabsorption.
Figure 6. Pinhole camera images, indicating plasma intensities at λ = 2.88 nm, superimposed on Schlieren images of the gas jet at ps = 10 bar; left: under vacuum conditions; right: in an ambient He atmosphere (background pressure pb = 170 mbar).
Download figure:
Standard imageIn order to study the effect on the brilliance depending on the location of plasma generation with respect to shock structures in the jet, the latter were varied by changing the background pressure at a constant stagnation pressure (ps = 10 bar). By lowering pb the radius of the barrel shock is increased; conversely, with increasing pb, the radius of the barrel shock decreases. Thus, with the location of the focus of the laser beam fixed, its relative location with respect to high-density regions behind the shocks is changed. In figure 7, intensity distributions of the plasma are shown for various background pressures pb. In this, the location of plasma generation is kept constant. An optimum is found at pb = 170 mbar (cf figure 6).
Figure 7. Pinhole camera images of plasmas at a stagnation pressure of ps = 10 bar for various background pressures pb.
Download figure:
Standard imageUnexpectedly, increasing both ps and pb while preserving the pressure ratio ps/pb, does not lead to a considerable further increase of the brilliance of the source. Approaching high pressure values (ps → 16 bar), quite the reverse happens: the plasma appears even darker. It can be assumed that, in fact, more soft x-ray photons are generated since the target density is increased. However, the density of the background gas is increased as well, which leads to higher reabsorption of the generated photons. The latter effect seems to dominate the former. It is expected that further efforts at differential pumping can shorten the path length of the soft x-rays through the outer helium gas so that the brilliance of the source can be further increased.
Parameters characterizing the plasma in the optimal case are now compared with those of a plasma produced near the nozzle exit with a jet in the scattering regime. In both cases the same stagnation pressure of ps = 10 bar is considered. Regarding the shape of the resulting plasma, which is represented by its luminescent area, it can be seen that the radiating area is reduced by a factor of 0.71 to A = 0.063 mm2, and its eccentricity decreases slightly from  = 0.91 to
= 0.91 to  = 0.80 when a barrel shock is present. This results in better brilliance and improves the coherence properties due to a smaller source size and a more uniform shape. The number of photons emitted per pulse and solid angle from the nitrogen plasma at a wavelength of λ = 2.88 nm is raised by a factor of 7.1 to a value of 1.2 × 1013 sr−1. Based on these values the peak brilliance can be computed. One finds an improvement by a factor of 10 to a value of B = 3.15 × 1016 photons (mm2 mrad2 s)−1. This clearly demonstrates the advantage of utilizing the density increase across a barrel shock system. An overview of the characteristic parameters of the plasma is given in table 1.
= 0.80 when a barrel shock is present. This results in better brilliance and improves the coherence properties due to a smaller source size and a more uniform shape. The number of photons emitted per pulse and solid angle from the nitrogen plasma at a wavelength of λ = 2.88 nm is raised by a factor of 7.1 to a value of 1.2 × 1013 sr−1. Based on these values the peak brilliance can be computed. One finds an improvement by a factor of 10 to a value of B = 3.15 × 1016 photons (mm2 mrad2 s)−1. This clearly demonstrates the advantage of utilizing the density increase across a barrel shock system. An overview of the characteristic parameters of the plasma is given in table 1.
Table 1. Comparison of plasma emission characteristics at λ = 2.88 nm obtained with a nitrogen jet issuing into vacuum (no barrel shock) and into a background gas (with barrel shock).
| Without barrel shock | With barrel shock | Factor | |
|---|---|---|---|
| Radiating area (mm2) | 0.088 | 0.063 | 0.71 |
| Eccentricity (–) | 0.91 | 0.80 | 0.88 |
| Photons/(solid angle · pulse) (sr−1) | 1.66×1012 | 1.18×1013 | 7.10 |
| Peak brilliance (mm−2 mrad−2 s−1) | 3.15×1015 | 3.15×1016 | 10.0 |
5. Conclusion
Laser-produced plasmas based on gas targets serve as versatile and nearly debris-free soft x-ray sources at a table-top size. In this paper, a method has been shown by which the brilliance of gas targets can be improved. To this end, a background pressure is applied to the volume into which the gas jet issues. For the example of an underexpanded supersonic nitrogen jet as a target, the resulting barrel shock has been qualitatively visualized by Schlieren photography. The corresponding density distribution was obtained by a quantitative Hartmann–Shack measurement. Measured values of the shock location and particle densities are of the same order of magnitude as those of a first estimate that was partly based on correlations. The size of the resulting intensity distribution of the plasma is reduced by a factor of 0.71 and its shape becomes more uniform, thus improving the coherence properties or the source. At the same time, the number of photons per solid angle at λ = 2.88 nm is raised by a factor of 7.1. In this manner the brilliance of the source is increased by a factor of 10.0 to B = 3.15 × 1016 photons (mm2 mrad2 s)−1. Even greater increases may be obtained by using hydrogen as the background gas since H2 shows a 13 times lower absorption of the generated x-rays compared to He [23]. However, for safety reasons H2 has not been employed here. A further increase in the plasma's brilliance is to be expected with increasing the stagnation and background pressure. An essential condition for achieving this is an improvement in the differential pumping system in order to lower the reabsorption of the soft x-rays by the background gas.
Acknowledgments
We gratefully acknowledge support from the Deutsche Forschungsgemeinschaft within SFB755 'Nanoscale Photonic Imaging'.