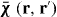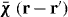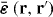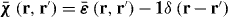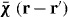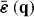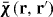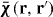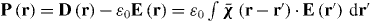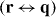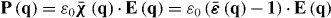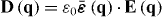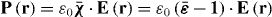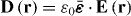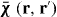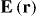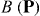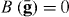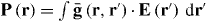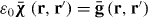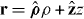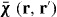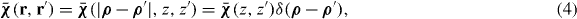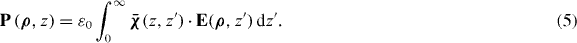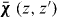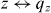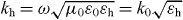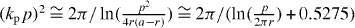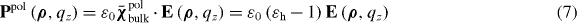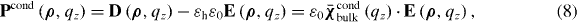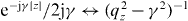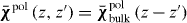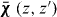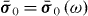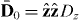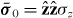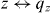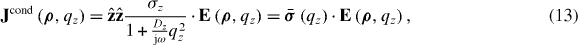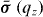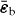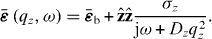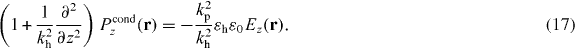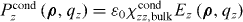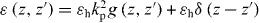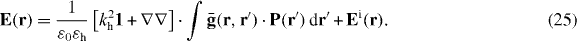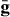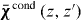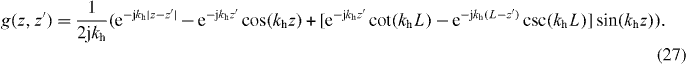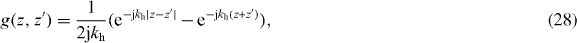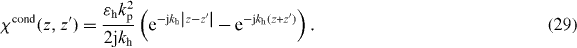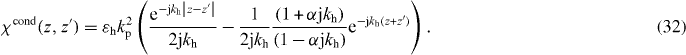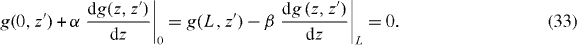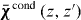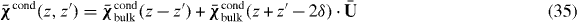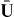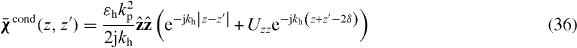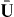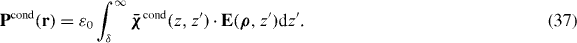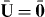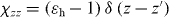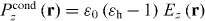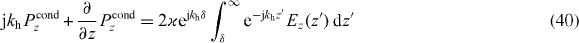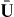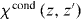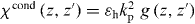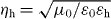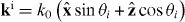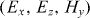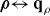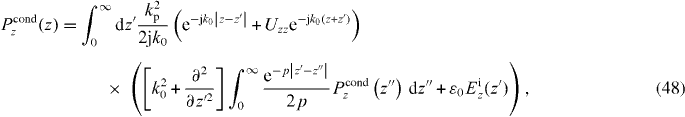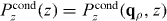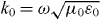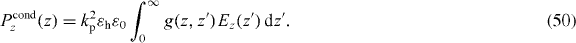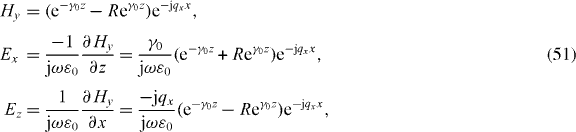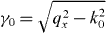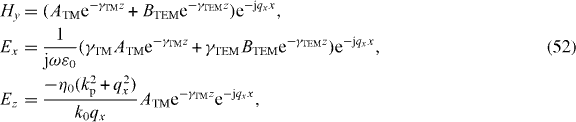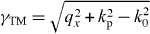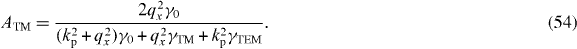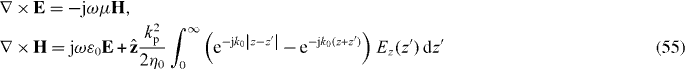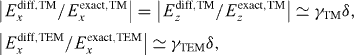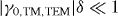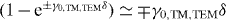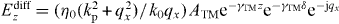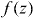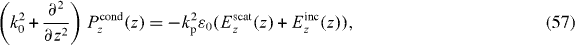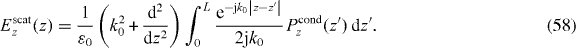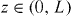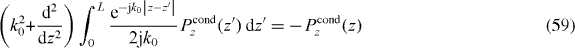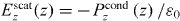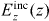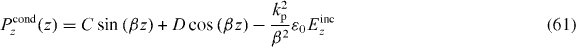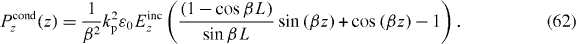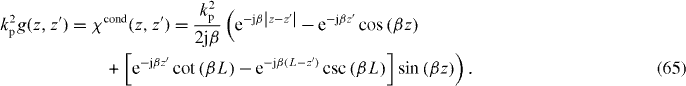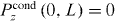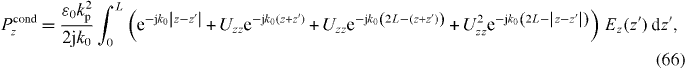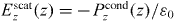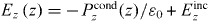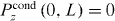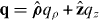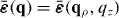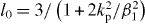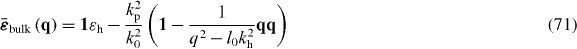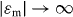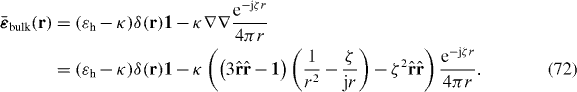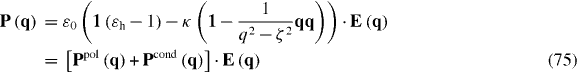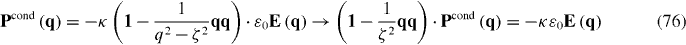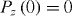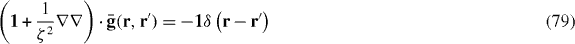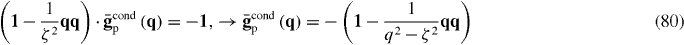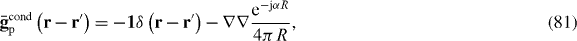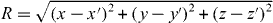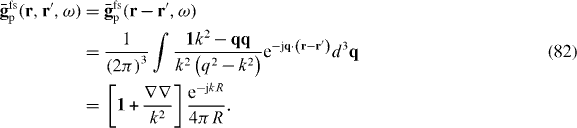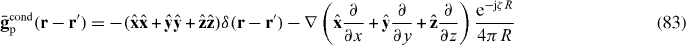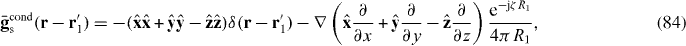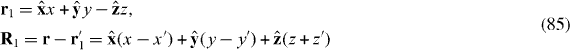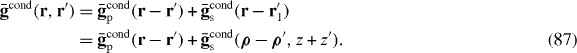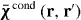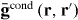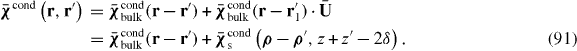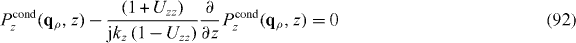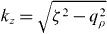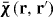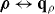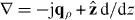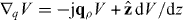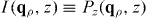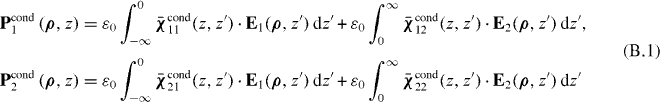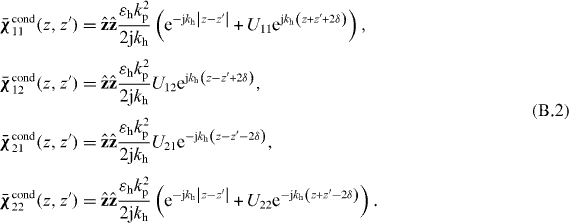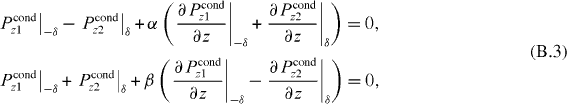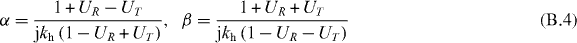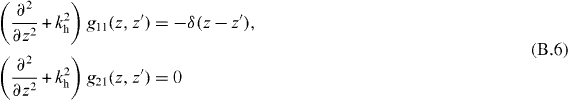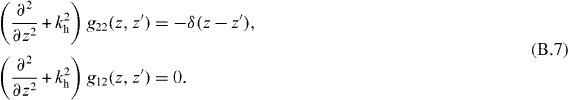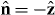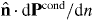Non-local susceptibility of the wire medium in the spatial domain considering material boundaries

The interaction of electromagnetic waves and wire media has been of interest for many years [1–3], driven by applications utilizing artificial plasma [4, 5], epsilon-near-zero materials [6, 7], negative refraction [8, 9], wave canalization [10, 11] and other uses. When the period of the wires is small compared to wavelength, the structure can be considered as a homogeneous (homogenized) medium. Early models of wire media neglected spatial dispersion of the homogenized material, but it has more recently been shown that non-local effects are very strong for wire media and often cannot be ignored [12–15]. However, the incorporation of spatial dispersion greatly complicates the analysis of wave–object interaction problems. For material half-space problems and related multi-region problems involving laterally infinite, finite-thickness material layers, the usual technique is to expand the field in all regions in terms of the waves that can propagate in each region as if it were infinite, and then enforce the usual boundary conditions and additional boundary conditions (ABCs) that account for the extra waves generated in non-local materials [13, 16, 17]. A considerable body of work has shown that this technique provides solutions that agree well with measurement and full-wave modeling (i.e. brute-force numerical codes that explicitly consider the individual wires rather than a homogenized medium) [14, 18–20]. Another technique is based on solving the drift-diffusion equation [21, 22] resulting in an integro-differential equation that usually requires numerical solution, but which is easily applied to various two- and three-dimensional (3D) objects [23–25].

A key property of bounded non-local materials is that polarization and electric field are related by the susceptibility tensor $\bar{\boldsymbol{\chi}}\left ( \mathbf{r},\mathbf{r}^{\prime }\right )$, rather than the tensor $\bar{\boldsymbol{\chi}}\left ( \mathbf{r-r}^{\prime }\right )$ which holds for translationally invariant media (alternatively, electric displacement and field are related by the tensor $\bar{\boldsymbol{\varepsilon}}\left (\mathbf{r,r}^{\prime }\right )$, where $\bar{\boldsymbol{\chi}}\left (\mathbf{r},\mathbf{r}^{\prime }\right ) =\bar{\boldsymbol{\varepsilon}}\left (\mathbf{r},\mathbf{r}^{\prime }\right ) -\mathbf{1}\delta \left ( \mathbf{r}-\mathbf{r}^{\prime }\right )$ and 1 is the identity dyadic). Whereas determination of $\bar{\boldsymbol{\chi}}\left ( \mathbf{r}-\mathbf{r}^{\prime }\right )$ or $\bar{\boldsymbol{\varepsilon}}\left (\mathbf{r}-\mathbf{r}^{\prime }\right )$ is a relatively straightforward task starting from the transform-domain permittivity $\bar{\boldsymbol{\varepsilon}}\left( \mathbf{q}\right)$(the quantity usually known) [25], there have been few attempts to determine $\bar{\boldsymbol{\chi}}\left(\mathbf{r},\mathbf{r}^{\prime }\right )$, which must incorporate information about the boundary. One aim of this work is to show that, when material response and field are related by a linear differential equation, a 'local' Green function for the same geometric region provides the quantity $\bar{\boldsymbol{\chi}}(\mathbf{r},\mathbf{r}^{\prime})$ (equivalently, the permittivity); information about the boundary is included by enforcing the ABC on the Green function. We explicitly show this for the case of an homogenized wire medium. The other aim of the work is to show that the two previously described methods for homogenized wire media (the wave expansion and drift-diffusion methods, both which avoid the need to know $\bar{\boldsymbol{\chi}}(\mathbf{r},\mathbf{r}^{\prime})$) are, in fact, equivalent, and are also equivalent to a third method that utilizes $\bar{\boldsymbol{\chi}}(\mathbf{r},\mathbf{r}^{\prime})$ decomposed into a principal and reflection term that provides insight into the permittivity as well as the required ABCs. Non-local wire medium material boundaries in the space domain are also discussed in [26]. Some aspects of boundary conditions for interfaces of homogenized media are discussed in [27, 28]. Although the material in this work is for homogenized materials, interface conditions and the idea of a transition layer (discussed below) have also come up for periodic structures [29, 30].

For a translationally invariant, homogeneous, non-local medium, $\mathbf{P}\left ( \mathbf{r}\right ) =\mathbf{D}\left ( \mathbf{r}\right )-\varepsilon _{0}\mathbf{E}\left ( \mathbf{r}\right ) =\varepsilon _{0}\int \bar{\boldsymbol{\chi}}\left ( \mathbf{r-r}^{\prime }\right )\cdot \mathbf{E}\left ( \mathbf{r}^{\prime }\right )\,\mathrm {d}\mathbf{r}^{\prime }$, such that in the spatial transform domain $\left ( \mathbf{r}\leftrightarrow \mathbf{q}\right )$, $\mathbf{P}\left ( \mathbf{q}\right ) =\varepsilon _{0}\bar{\boldsymbol{\chi}}\left ( \mathbf{q}\right ) \cdot \mathbf{E}\left (\mathbf{q}\right ) =\varepsilon _{0}\left ( \bar{\boldsymbol{\varepsilon}}\left ( \mathbf{q}\right ) -\mathbf{1}\right ) \cdot \mathbf{E}\left (\mathbf{q}\right )$ and $\mathbf{D}\left ( \mathbf{q}\right ) =\varepsilon _{0}\bar{\boldsymbol{\varepsilon}}\left ( \mathbf{q}\right ) \cdot \mathbf{E}\left ( \mathbf{q}\right )$. Of course, for a local material $\mathbf{P}\left ( \mathbf{r}\right ) =\varepsilon _{0}\bar{\boldsymbol{\chi}}\cdot \mathbf{E}\left ( \mathbf{r}\right ) =\varepsilon _{0}\left (\bar{\boldsymbol{\varepsilon}}-\mathbf{1}\right ) \cdot \mathbf{E}\left (\mathbf{r}\right )$ and $\mathbf{D}\left ( \mathbf{r}\right ) =\varepsilon _{0}\bar{\boldsymbol{\varepsilon}}\cdot \mathbf{E}\left ( \mathbf{r}\right )$.

For a finite material region the above non-local relations will not hold, and more general relations are required [16, 17]:

$$\begin{equation} \mathbf{D}(\mathbf{r}) =\varepsilon_{0}\int\bar{\boldsymbol{\varepsilon}}( \mathbf{r,r}^{\prime}) \cdot \mathbf{E}\left( \mathbf{r}^{\prime}\right)\,\mathrm{d}\mathbf{r}^{\prime}, \end{equation} \tag{ 1 }$$

$$\begin{equation} \mathbf{P}( \mathbf{r}) =\varepsilon_{0}\int\bar{\boldsymbol{\chi}}( \mathbf{r,r}^{\prime}) \cdot\mathbf{E}(\mathbf{r}^{\prime})\,\mathrm{d}\mathbf{r}^{\prime}. \end{equation} \tag{ 2 }$$

In this case, the material response must take into account the material boundary—it cannot be derived simply from the bulk response. For natural materials, surface effects can be accounted for using a microscopic model; in a fully quantum mechanical treatment the current–current or density–density response can be used [16, 31, 32], and the Boltzmann equation is often used in a semi-classical treatment [33]. However, these methods are often not feasible due to the complexity of the problem and a lack of knowledge of the true surface conditions present. Often, it suffices to use a macroscopic, phenomenological method [16, 17]. In the following, for homogenized wire media we develop the non-local material response that accounts for a material boundary from a macroscopic perspective.

The first main point of the paper is to show that in many cases $\bar{\boldsymbol{\chi}}\left ( \mathbf{r,r}^{\prime }\right )$ can be determined by a Green function for the given geometry containing a simple (local) material. In fact, this is the case when $\mathbf{P}\left ( \mathbf{r}\right )$ and $\mathbf{E}\left ( \mathbf{r}\right )$ are related by a linear differential equation. Indeed, if

$$\begin{equation} \begin{array}{ll} \displaystyle \mathcal{L}\mathbf{P}( \mathbf{r}) =\mathbf{E}\left( \mathbf{r}\right) ,\\ \displaystyle B\left( \mathbf{P}\right) =0, \end{array} \end{equation} \tag{ 3 }$$

where $\mathcal {L}$ is a linear differential operator and $B\left (\mathbf{P}\right )$ are boundary conditions, then one can define a Green function $\mathcal {L}\bar{\mathbf{g}}\left ( \mathbf{r},\mathbf{r}^{\prime }\right ) =\mathbf{1}\delta \left ( \mathbf{r}-\mathbf{r}^{\prime }\right )$, $B\left ( \bar{\mathbf{g}}\right ) =0$ such that $\mathbf{P}\left ( \mathbf{r}\right ) =\int \bar{\mathbf{g}}\left (\mathbf{r,r}^{\prime }\right ) \cdot \mathbf{E}\left ( \mathbf{r}^{\prime }\right )\,\mathrm {d}\mathbf{r}^{\prime }$. Therefore, since one may consider the electric field to be arbitrary, by (2) we have $\varepsilon _{0}\bar{\boldsymbol{\chi}}\left ( \mathbf{r,r}^{\prime }\right )=\bar{\mathbf{g}}\left ( \mathbf{r,r}^{\prime }\right )$. Below we illustrate this for the explicit case of a wire medium half-space and slab, although the same procedure also holds for natural non-local materials.

For simplicity, we will first consider a material half-space, as depicted in figure 1, and concentrate on the susceptibility response, from which one trivially obtains the permittivity. The position vector is $\mathbf{r}=\hat{{\boldsymbol{\rho}}}\rho +\hat{\mathbf{z}}z$.

Zoom In Zoom Out Reset image size

The δ region, to be discussed later, is called the 'dead layer' in natural excitonic materials [16], and is analogous to a transition layer or virtual interface for wire media [13, 34, 35]. Noting the translational invariance in the xy plane we write

$$\begin{equation} \bar{\boldsymbol{\chi}}( \mathbf{r,r}^{\prime}) =\bar{\boldsymbol{\chi}}( \vert {\boldsymbol{\rho}}-{\boldsymbol{\rho}}^{\prime}\vert ,z,z^{\prime}) =\bar{\boldsymbol{\chi}}(z,z^{\prime}) \delta( {\boldsymbol{\rho}}-{\boldsymbol{\rho}}^{\prime}),\end{equation} \tag{ 4 }$$

thus

$$\begin{equation} \mathbf{P}\left( {\boldsymbol{\rho}},z\right) =\varepsilon_{0}\int_{0}^{\infty }\bar{\boldsymbol{\chi}}( z,z^{\prime}) \cdot\mathbf{E}({\boldsymbol{\rho}},z^{\prime})\,\mathrm{d}z^{\prime}. \end{equation} \tag{ 5 }$$

In this section we determine the non-local response $\bar{\boldsymbol{\chi}}\left ( z,z^{\prime }\right )$ for uniaxial wire media that accounts for the interface. In section 3 we consider the connected 3D isotropic wire medium.

Consider a uniaxial wire medium consisting of perfect electrically conducting (PEC) wires immersed in a host medium characterized by relative permittivity ε_h, as depicted in figure 2.

Zoom In Zoom Out Reset image size

For the case of an infinite medium, in the spatial Fourier transform (FT) domain $z\leftrightarrow q_{z}$, assuming the usual homogenization conditions p/λ ≪ 1, the bulk material response is [12, 36]

$$\begin{equation} \bar{\boldsymbol{\varepsilon}}_{{\rm bulk}}\left( q_{z}\right) =\varepsilon_{\mathrm{h}}\varepsilon_{0}\left( \mathbf{1}+\hat{\mathbf{z}}\hat{\mathbf{z} }\frac{k_{\rm p}^{2}}{q_{z}^{2}-k_{\rm h}^{2}}\right), \end{equation} \tag{ 6 }$$

where $k_{\mathrm { h}}=\omega \sqrt {\mu _{0}\varepsilon _{0}\varepsilon _{\mathrm { h}}}=k_{0}\sqrt {\varepsilon _{\mathrm { h}}}$ is the wavenumber in the host medium and k_p = ω_p/c is the plasma wavenumber ($( k_{\mathrm { p}}p)^{2}\cong 2\pi /\ln(\frac {p^{2}}{4r\left ( a-r\right ) })\cong 2\pi /(\ln ( \frac {p}{2\pi r}) +0.5275)$ where p and r are the wire period and radius, respectively [14, (11)]). It is convenient to separate the local, bound-charge polarization response of the background (P^pol) from the non-local conductive polarization response (P^cond),

$$\begin{equation} \mathbf{P}^{{\rm pol}}\left( {\boldsymbol{\rho}},q_{z}\right) =\varepsilon _{0}\bar{\boldsymbol{\chi}}_{{\rm bulk}}^{{\rm pol}}\cdot\mathbf{E}\left( {\boldsymbol{\rho}},q_{z}\right) =\varepsilon_{0}\left( \varepsilon_{\rm h}-1\right) \mathbf{E}\left( {\boldsymbol{\rho}},q_{z}\right) \end{equation} \tag{ 7 }$$

and

$$\begin{equation} \mathbf{P}^{{\rm cond}}\left( {\boldsymbol{\rho}},q_{z}\right) =\mathbf{D}\left( {\boldsymbol{\rho}},q_{z}\right) -\varepsilon_{\rm h}\varepsilon_{0}\mathbf{E}\left( {\boldsymbol{\rho}},q_{z}\right) =\varepsilon_{0}\bar{\boldsymbol{\chi}}_{{\rm bulk}}^{{\rm cond}}\left( q_{z}\right) \cdot\mathbf{E}\left( {\boldsymbol{\rho}},q_{z}\right) , \end{equation} \tag{ 8 }$$

where

$$\begin{equation} \bar{\boldsymbol{\chi}}_{{\rm bulk}}^{{\rm cond}}\left( q_{z}\right) =\hat{\mathbf z}\hat{\mathbf z}\frac{\varepsilon_{\rm h}k_{\rm p}^{2}}{q_{z}^{2}-k_{\rm h}^{2}}. \end{equation} \tag{ 9 }$$

It is simple to invert (9) to the space domain, resulting in

$$\begin{eqnarray} \bar{\boldsymbol{\chi}}_{{\rm bulk}}^{{\rm cond}}\left( z-z^{\prime }\right) & =&\frac{1}{2\pi}\int_{-\infty}^{\infty}\bar{\boldsymbol{\chi}}_{{\rm bulk}}^{{\rm cond}}\left( q_{z}\right) \mathrm{e}^{\mathrm{j}q_{z}\left( z-z^{\prime}\right) }\mathrm{d}q_{z}\nonumber\\ & =&\hat{\mathbf{z}}\hat{\mathbf{z}}\varepsilon_{\rm h}k_{\rm p}^{2} \frac{\mathrm{e}^{-\mathrm{j}k_{\rm h}\left\vert z-z^{\prime}\right\vert }}{2\mathrm{j}k_{\rm h}} \end{eqnarray} \tag{ 10 }$$

using $\mathrm {e}^{-\mathrm {j}\gamma \vert z \vert }/2\mathrm {j}\gamma \leftrightarrow (q_{z}^{2}-\gamma ^{2}) ^{-1}$.

In the following we consider several equivalent models for determining the non-local conductive response for the half-space problem. Since the bound charge is assumed local, its response is trivial and we assume $\bar{\boldsymbol{\chi}}^{{\mathrm { pol}}}\left ( z,z^{\prime }\right )=\bar{\boldsymbol{\chi}}_{{\mathrm { bulk}}}^{{\mathrm { pol}}}\left ( z-z^{\prime }\right )$ throughout.

2.1. Model I: transport equation model

To determine $\bar{\boldsymbol{\chi}}\left ( z,z^{\prime }\right )$, we need to identify the differential equation that relates polarization and electric field. In particular, the drift-diffusion equation from semiconductor theory has recently been applied to model wire media [21–25] and provides the desired description. To adapt this formulation to wire media we start with the general anisotropic drift-diffusion model for a bulk medium

$$\begin{eqnarray} \mathbf{J}^{{\rm cond}}( \mathbf{r}) & =&\bar{\boldsymbol{\sigma}}_{0}\cdot\mathbf{E}( \mathbf{r}) -\bar{\mathbf{D}}_{0}\cdot\nabla\rho( \mathbf{r}) \nonumber\\ & =&\bar{\boldsymbol{\sigma}}_{0}\cdot\mathbf{E}( \mathbf{r}) +\frac{1}{\mathrm{j}\omega}\bar{\mathbf{D}}_{0}\cdot\nabla\nabla\cdot \mathbf{J}^{{\rm cond}}( \mathbf{r}), \end{eqnarray} \tag{ 11 }$$

where $\bar{\boldsymbol{\sigma}}_{0}=\bar{\boldsymbol{\sigma}}_{0}\left (\omega \right )$ and $\bar{\mathbf{D}}_{0}=\bar{\mathbf{D}}_{0}\left ( \omega \right )$ are the 'local'  conductivity and diffusion coefficient tensors that are assumed independent of position. If we assume conduction and diffusion only along the wire axis then $\bar{\bf D}_{0}=\hat{\mathbf{z}}\hat{\mathbf{z}}D_{z}$ and $\bar{\boldsymbol{\sigma}}_{0}=\hat{\mathbf{z}}\hat{\mathbf{z}}\sigma _{z}$, so that from (11) we have J_x = J_y = 0 and

$$\begin{equation} \left( 1-\frac{D_{z}}{\mathrm{j}\omega}\frac{\partial^{2}}{\partial z^{2}}\right) \mathrm{J}_{z}^{{\rm cond}}( \mathbf{r}) =\sigma_{z}E_{z}\left( \mathbf{r}\right). \end{equation} \tag{ 12 }$$

Fourier transformation $z\leftrightarrow q_{z}$ leads to

$$\begin{equation} \mathbf{J}^{{\rm cond}}\left( {\boldsymbol{\rho}},q_{z}\right) =\hat{\mathbf{z}}\hat{\mathbf{z}}\frac{\sigma_{z}}{1+\frac{D_{z}}{\mathrm{j}\omega} q_{z}^{2}}\cdot\mathbf{E}\left( {\boldsymbol{\rho}},q_{z}\right) =\bar{\boldsymbol{\sigma}}\left( q_{z}\right) \cdot\mathbf{E}\left( {\boldsymbol{\rho}},q_{z}\right), \end{equation} \tag{ 13 }$$

where $\bar{\boldsymbol{\sigma}}\left ( q_{z}\right )$ is now a non-local conductivity tensor that accounts for both conduction and diffusion [21, 22].

Since the bound-charge polarization response is local and governed by the permittivity tensor $\bar{\boldsymbol{\varepsilon}}_{\mathrm {b}}$, from Ampere's law

$$\begin{equation} \mathbf{\nabla}_{q_{z}}\times\mathbf{H}\left( {\boldsymbol{\rho}},q_{z}\right) =\mathrm{j}\omega\left( \bar{\boldsymbol{\varepsilon}}_{\mathrm{b}}-\mathrm{j}\frac{1}{\omega} \bar{\boldsymbol{\sigma}}\left( q_{z}\right) \right) \cdot\mathbf{E} \left( {\boldsymbol{\rho}},q_{z}\right) , \end{equation} \tag{ 14 }$$

where $\mathbf{\nabla }_{q_{z}}=\hat{\mathbf{x}}\partial /\partial x +\hat{\mathbf{y}}\partial /\partial y+\hat{\mathbf{z}}\left (\mathrm {j}q_{z}\right )$, we obtain the combined permittivity

$$\begin{eqnarray*} &&\bar{\boldsymbol{\varepsilon}}\left( q_{z},\omega\right) =\bar{\boldsymbol{\varepsilon}}_{\mathrm{b}} + \hat{\mathbf{z}}\hat{\mathbf{z} }\frac{\sigma_{z}}{\mathrm{j}\omega+D_{z}q_{z}^{2}}. \end{eqnarray*}$$

If we compare this expression to (7)–(10) we see that $\bar{\boldsymbol{\varepsilon}}_{\mathrm {b}}=\mathbf{1}\varepsilon _{\mathrm { h}}\varepsilon _{0}$ and

$$\begin{equation} \sigma_{z} =-\mathrm{j}\omega\varepsilon_{\rm h}\varepsilon_{0}\frac{k_{\rm p}^{2}}{k_{\rm h}^{2}}=\frac{\omega_{\rm p}^{2}\varepsilon_{0}}{\mathrm{j}\omega}=D_{z}\varepsilon_{\rm h}\varepsilon_{0}k_{\rm p}^{2}, \end{equation} \tag{ 15 }$$

$$\begin{equation} D_{z} =-\mathrm{j}\omega\frac{1}{k_{\rm h}^{2}}=\frac{v_{\rm h}^{2}}{\mathrm{j}\omega}, \end{equation} \tag{ 16 }$$

where $v_{\mathrm { h}}=1/\sqrt {\mu _{0}\varepsilon _{0}\varepsilon _{\mathrm { h}}}$ is the phase velocity in the host medium. Then, with J_z = jωP_z, (12) we have the desired differential equation for polarization

$$\begin{equation} \left( 1+\frac{1}{k_{\rm h}^{2}}\frac{\partial^{2}}{\partial z^{2}}\right) P_{z}^{{\rm cond}}( \mathbf{r}) =-\frac{k_{\rm p}^{2}}{k_{\rm h}^{2} }\varepsilon_{\rm h}\varepsilon_{0}E_{z}( \mathbf{r}). \end{equation} \tag{ 17 }$$

This is the same differential equation for the conductive part of the polarization as would be obtained starting from the bulk susceptibility (9). That is, $P_{z}^{{\mathrm { cond}}}\left ( {\boldsymbol{\rho}},q_{z}\right ) =\varepsilon _{0}\chi _{zz{\mathrm { , bulk}}}^{{\mathrm { cond}}}E_{z}\left ( {\boldsymbol{\rho}},q_{z}\right )$, and multiplying both sides by the factor q²_z − k²_h and inverting to the space domain we obtain (17).

We assume a generalized boundary condition (discussed in the following)

$$\begin{equation} \left. \left( P_{z}^{{\rm cond}}(z) +\alpha\frac {\mathrm{d}P_{z}^{{\rm cond}}(z) }{\mathrm{d}z}\right) \right\vert _{z=\delta}=0, \end{equation} \tag{ 18 }$$

where α = 0 is the correct ABC for a wire medium terminated by an insulator [13], α → ∞ is the correct ABC for a wire medium terminated by a perfect conductor [19] and $0{<}\left \vert \alpha \right \vert {<}\infty$ describes the case of a uniaxial wire medium terminated by a thin, imperfect conductor [3].

From (17) we can form a Green function problem

$$\begin{equation} \left( \!\frac{\partial^{2}}{\partial z^{2}}+k_{\rm h}^{2}\right) g(z,z^{\prime}) =-\delta( z-z^{\prime}) , \end{equation} \tag{ 19 }$$

$$\begin{equation} \left. \left( \!g( z,z^{\prime}) +\alpha\frac{\mathrm{d}g(z,z^{\prime}) }{\mathrm{d}z}\right) \right\vert _{z=\delta}=0, \end{equation} \tag{ 20 }$$

so that

$$\begin{equation} P_{z}^{{\rm cond}}(z) =k_{\rm p}^{2}\varepsilon_{\rm h}\varepsilon _{0}\int_{\delta}^{\infty}g( z,z^{\prime}) E_{z}(z^{\prime})\,\mathrm{d}z^{\prime}. \end{equation} \tag{ 21 }$$

Note that we enforce the same boundary condition on the Green function as on the polarization, which is based on microscopic conditions at the wire ends. Comparing with (5) adjusted to account for δ, we see that

$$\begin{equation} \chi^{{\rm cond}}( z,z^{\prime}) =\varepsilon_{\rm h}k_{\rm p} ^{2}~g( z,z^{\prime}) . \end{equation} \tag{ 22 }$$

Therefore, the usual Green function for local materials forms the boundary-dependent non-local susceptibility (and obviously the permittivity via $\varepsilon\left ( z,z^{\prime }\right ) =\varepsilon _{\mathrm { h}}k_{\mathrm { p}}^{2}g\left (z,z^{\prime }\right ) +\varepsilon _{\mathrm { h}}\delta \left ( z-z^{\prime }\right )$). This is the first main point of the paper.

We see that the susceptibility can be written as the sum of the principal part, which satisfies

$$\begin{equation} \left( \frac{\partial^{2}}{\partial z^{2}}+k_{\rm h}^{2}\right) \chi_{{\rm p} }^{{\rm cond}}( z-z^{\prime}) =-\frac{1}{\varepsilon_{\rm h} k_{\rm p}^{2}}\delta( z-z^{\prime}) \end{equation} \tag{ 23 }$$

and provides the z − z' dependence, and the scattered part which satisfies

$$\begin{equation} \left( \frac{\partial^{2}}{\partial z^{2}}+k_{\rm h}^{2}\right) \chi_{{\rm s} }^{{\rm cond}}( z,z^{\prime}) =0. \end{equation} \tag{ 24 }$$

Upon enforcing the same boundary conditions as for the polarization, the scattered part, not surprisingly, provides the dependence that is other than z − z'.

Note that the Green function is usually used to connect electric field and current via

$$\begin{equation} \mathbf{E( \mathbf{r}) }=\frac{1}{\varepsilon_{0}\varepsilon_{\rm h}}\left[ k_{\rm h}^{2}\mathbf{1}+\mathbf{\nabla\nabla}\right] \cdot\int \bar{\mathbf{g}}( \mathbf{r,r}^{\prime}) \cdot \mathbf{P}(\mathbf{r}^{\prime})\,\mathrm{d}\mathbf{r}^{\prime}+\mathbf{E}^{\mathrm{i}}(\mathbf{r}). \end{equation} \tag{ 25 }$$

The relationship between the electric field and current/polarization is non-local via the superposition integral involving $\bar{\mathbf{g}}$, albeit in a rather trivial (purely geometric) sense. However, as seen in (22), a similar Green function provides the non-local combined material–geometric response $\bar{\boldsymbol{\chi}}^{{\mathrm { cond}}}\left (z,z^{\prime }\right )$ that accounts for both the material boundary and the material spatial dispersion.

Next we will explicitly solve for the Green function assuming several different ABCs. We ignore the dead layer (restored below) and assume a material slab of thickness L, extending from z = 0 to L surrounded by vacuum regions. We therefore enforce

$$\begin{equation} g( 0,z^{\prime}) =g(L,z^{\prime}) =0. \end{equation} \tag{ 26 }$$

The solution is [37, p 302]

$$\begin{eqnarray} &&\fl g(z,z^{\prime}) =\frac{1}{2\mathrm{j}k_{\rm h}}(\mathrm{e}^{-\mathrm{j}k_{\rm h} \vert z-z^{\prime}\vert }-\mathrm{e}^{-\mathrm{j}k_{\rm h}z^{\prime}}\cos(k_{\rm h}z) + [ \mathrm{e}^{-\mathrm{j}k_{\rm h}z^{\prime}}\cot( k_{\rm h}L)-\mathrm{e}^{-\mathrm{j}k_{\rm h}( L-z^{\prime}) }\csc( k_{\rm h}L)]\sin(k_{\rm h}z)) .\nonumber\\ \end{eqnarray} \tag{ 27 }$$

Then, in the limit L → ∞ and allowing small loss

$$\begin{equation} g( z,z^{\prime}) =\frac{1}{2\mathrm{j}k_{\rm h}}( \mathrm{e}^{-\mathrm{j}k_{\rm h}\vert z-z^{\prime}\vert }-\mathrm{e}^{-\mathrm{j}k_{\rm h}( z+z^{\prime}) }) , \end{equation} \tag{ 28 }$$

such that, from (22),

$$\begin{equation} \chi^{{\rm cond}}( z,z^{\prime}) =\frac{\varepsilon_{\rm h}k_{\rm p} ^{2}}{2\mathrm{j}k_{\rm h}}\left( \mathrm{e}^{-\mathrm{j}k_{\rm h}\left\vert z-z^{\prime}\right\vert }-\mathrm{e}^{-\mathrm{j}k_{\rm h}( z+z^{\prime}) }\right). \end{equation} \tag{ 29 }$$

For the generalized ABC corresponding to (18),⁵

$$\begin{eqnarray} &&\begin{array}{ll} \displaystyle \left. \left( g(z,z^{\prime})+\alpha\frac{\mathrm{d}g( z,z^{\prime})}{\mathrm{d}z}\right) \right\vert _{z=0} =0,\\ \displaystyle \left. \left( g(z,z^{\prime})-\alpha\frac{\mathrm{d}g( z,z^{\prime})}{\mathrm{d}z}\right) \right\vert _{z=L} =0 \end{array} \end{eqnarray} \tag{ 31 }$$

as L → ∞ and using (22) we have

$$\begin{equation} \fl \chi^{{\rm cond}}( z,z^{\prime}) =\varepsilon_{\rm h}k_{\rm p}^{2}\left( \frac{\mathrm{e}^{-\mathrm{j}k_{\rm h}\left\vert z-z^{\prime}\right\vert }}{2\mathrm{j}k_{\rm h}}-\frac{1}{2\mathrm{j}k_{\rm h}}\frac{\left( 1+\alpha \mathrm{j}k_{\rm h}\right) }{\left( 1-\alpha \mathrm{j}k_{\rm h}\right) }\mathrm{e}^{-\mathrm{j}k_{\rm h}(z+z^{\prime}) }\right). \end{equation} \tag{ 32 }$$

Further, we can, for example, impose different generalized ABCs at different boundaries, e.g. α at z = 0 and β at z = L,

$$\begin{equation} g(0,z^{\prime})+\alpha\left. \frac{\mathrm{d}g( z,z^{\prime})}{\mathrm{d}z}\right\vert _{0}=g(L,z^{\prime})-\beta\left. \frac{\mathrm{d}g\left( z,z^{\prime }\right) }{\mathrm{d}z}\right\vert _{L}=0. \end{equation} \tag{ 33 }$$

Regarding the ABC, we note that the condition P^cond_z = 0 is actually just the usual boundary condition on current from Maxwell's equations, although in local problems it does not usually need to be explicitly applied. However, sometimes it does. For example, for a simple thin-wire antenna the condition J = 0 needs to be enforced at the wire ends (see e.g. [38, 39] for the Pocklington's integro-differential treatment). However, one does not think of this as an ABC as there are no additional waves.

2.2. Model II: charge carrier reflection model

In the preceding we have determined how to construct the non-local, boundary-dependent susceptibility $\bar{\boldsymbol{\chi}}^{{\mathrm { cond}}}\left ( z,z^{\prime }\right )$ from the differential equation for polarization. In this section we consider a completely different view of this susceptibility based on a physical model for charge carrier reflection [16] that leads to the same result, and which leads to insight into the assumption of translational invariance for convolution-based methods.

In a natural material, charge carriers (electrons, holes, excitons, etc) can interact with a boundary in various ways. If we assume that the most important process is reflection, then referring to figure 1 the total distance along the z coordinate that the particle travels upon leaving the position z', reflecting off of the boundary with reflection coefficient $\bar{\mathbf{U}}$, and arriving at position z, is z + z' − 2δ. For natural materials, the small region of width δ represents the dead layer, wherein the particle experiences strong repulsive forces associated with the image charge as the particle tries to leave the material [16, 17]. Impurity atoms at the surface and other surface states can also contribute to this effect. Thus, the typical procedure is to posit that the particle will not be found in the dead layer [16]. For a homogenized wire medium, the transport model [21, 22] indicates that we can consider effective charge carriers interacting with the boundary in a similar manner. Therefore, in the dead layer

$$\begin{equation} \bar{\boldsymbol{\chi}}^{{\rm cond}}( z,z^{\prime})=\bar{\mathbf{0}} \end{equation} \tag{ 34 }$$

for 0 < z,z' < δ, and in the material half-space outside of the dead layer

$$\begin{equation} \bar{\boldsymbol{\chi}}^{{\rm cond}}( z,z^{\prime})=\bar{\boldsymbol{\chi}}_{{\rm bulk}}^{{\rm cond}}( z-z^{\prime}) +\bar{\boldsymbol{\chi}}_{{\rm bulk}}^{{\rm cond}}(z+z^{\prime}-2\delta) \cdot\bar{\mathbf{U}} \end{equation} \tag{ 35 }$$

for z,z' > δ. That is, in (35) we assume the same form for the bulk and surface-related terms, but allow for different z dependences and the presence of a (charge-carrier) reflection tensor $\bar{\mathbf{U}}$; this method was developed in [16] for natural excitonic materials.

From (10)

$$\begin{equation} \bar{\boldsymbol{\chi}}^{{\rm cond}}( z,z^{\prime})=\frac{\varepsilon_{\rm h}k_{\rm p}^{2}}{2\mathrm{j}k_{\rm h}}\hat{\mathbf{z}}\hat{\mathbf{z}}\left( \mathrm{e}^{-\mathrm{j}k_{\rm h}\left\vert z-z^{\prime}\right\vert } +U_{zz}\mathrm{e}^{-\mathrm{j}k_{\rm h}\left( z+z^{\prime}-2\delta\right) }\right) \end{equation} \tag{ 36 }$$

for z,z' > δ, where we assumed that $\bar{\mathbf{U}}$ is diagonal. Therefore, with $\bar{\boldsymbol{\chi}}^{{\mathrm { cond}}}$ defined as (35) and (36) the non-local conductive polarization response is

$$\begin{equation} \mathbf{P}^{{\rm cond}}( \mathbf{r}) =\varepsilon_{0} \int_{\delta}^{\infty}\bar{\boldsymbol{\chi}}^{{\rm cond}}(z,z^{\prime}) \cdot\mathbf{E}({\boldsymbol{\rho}},z^{\prime})\mathrm{d}z^{\prime}. \end{equation} \tag{ 37 }$$

Note that $\bar{\mathbf{U}}=\pm \mathbf{1}$ corresponds to specular/antispecular particle scattering.

If we ignore the dead layer, this model with $\bar{\mathbf{U}}=\bar{\mathbf{0}}$ is known as the 'dielectric approximation' (DA), wherein the bulk response is assumed to apply right up to the interface, and where the interface does not affect the material response (other than terminating the material). That is, everywhere in the material half-space

$$\begin{equation} \bar{\boldsymbol{\chi}}( z,z^{\prime}) \equiv\bar{\boldsymbol{\chi}}_{{\rm bulk}}( z-z^{\prime}) . \end{equation} \tag{ 38 }$$

Note that in the local limit (setting $\chi _{zz}=\left ( \varepsilon _{\mathrm {h}}-1\right ) \delta \left ( z-z^{\prime }\right )$) we recover the usual local result $P_{z}^{{\mathrm { cond}}}\left ( \mathbf{r}\right ) =\varepsilon _{0}\left ( \varepsilon _{\mathrm { h}}-1\right ) E_{z}\left ( \mathbf{r}\right )$, which applies everywhere in the half-space. Although simple, the DA obviously cannot account for the particulars of the interface. Moreover, compared to the local material case, it is a much more questionable assumption for the conductive response of non-local materials since in that case the charge carrier dynamics at z depend on what happened at z', and as the particle travels from z' to z it may have encountered the material interface.

2.2.1. Boundary condition

An interesting aspect of the charge carrier reflection model is that it leads directly to the ABC—there is no ambiguity in specification of the correct (self-consistent) ABC to be prescribed at the point z = δ. Thus, for z = δ and z' > δ we have, from (37),

$$\begin{eqnarray} &&\begin{array}{ll} \displaystyle \mathrm{j}k_{\rm h}P_{z}^{{\rm cond}} =\varkappa\int_{\delta}^{\infty}(1+U_{zz}) \mathrm{e}^{-\mathrm{j}k_{\rm h}( z^{\prime}-\delta) }E_{z}(z^{\prime})\,\mathrm{d}z^{\prime},\\ \displaystyle \frac{\partial P_{z}^{{\rm cond}}}{\partial z} =\varkappa\int_{\delta}^{\infty}( 1-U_{zz}) \mathrm{e}^{-\mathrm{j}k_{\rm h}( z^{\prime}-\delta) }E_{z}( z^{\prime})\,\mathrm{d}z^{\prime}, \end{array} \end{eqnarray} \tag{ 39 }$$

where ϰ = ε₀ε_hk²_p/2. Upon adding these expressions we find

$$\begin{equation} \mathrm{j}k_{\rm h}P_{z}^{{\rm cond}}+\frac{\partial}{\partial z}P_{z}^{{\rm cond} }=2\varkappa \mathrm{e}^{\mathrm{j}k_{\rm h}\delta}\int_{\delta}^{\infty}\mathrm{e}^{-\mathrm{j}k_{\rm h}z^{\prime}}E_{z}( z^{\prime})\,\mathrm{d}z^{\prime} \end{equation} \tag{ 40 }$$

and subtracting the two expressions (39) and using (40) we obtain the generalized ABC [16, 17]

$$\begin{equation} \left. \left( P_{z}^{{\rm cond}}+\alpha\frac{\partial}{\partial z} P_{z}^{{\rm cond}}\right) \right\vert _{z=\delta}=0, \end{equation} \tag{ 41 }$$

where

$$\begin{equation} \alpha=-\frac{1}{\mathrm{j}k_{\rm h}}\frac{\left( 1+U_{zz}\right) }{\left( 1-U_{zz}\right) }. \end{equation} \tag{ 42 }$$

Obviously, (41), which applies to several different physical terminations of the wire medium, is the same as (18).

If U_zz = 0 (DA)

$$\begin{equation} P_{z}^{{\rm cond}}-\frac{1}{\mathrm{j}k_{\rm h}}\frac{\partial}{\partial z}P_{z} ^{{\rm cond}}=0 \end{equation} \tag{ 43 }$$

if U_zz = −1,

$$\begin{equation} P_{z}^{{\rm cond}}=0 \end{equation} \tag{ 44 }$$

and if U_zz = + 1,

$$\begin{equation} \frac{\partial}{\partial z}P_{z}^{{\rm cond}}=0. \end{equation} \tag{ 45 }$$

The case U_zz = −1 represents the ABC for wire media at the interface with an insulator [13]. In transmission line theory this can be seen to be the usual reflection coefficient for current at an open circuit (current I = 0). The case U_zz = 1 represents the ABC for wire media at the interface with a perfectly conducting surface [19], and corresponds to the usual transmission line reflection coefficient for current at a short-circuit (I is maximum). The DA case U_zz = 0 corresponds to the case of a matched termination in transmission line theory, where the current satisfies (43). A transmission line model is presented in appendix A. However, ignoring the dead layer, note that (43) is in conflict with the known physical boundary condition that the conductive part of the polarization must vanish at the interface with an insulator, P^cond_z = 0, which casts further doubt on the DA.

The charge carrier reflection method result (36) with U_zz = −1 is the same as the transport equation result (29) (with the dead layer restored), thus, if U_zz = −1 then solving the drift-diffusion equation and enforcing the ABC P^cond_z = 0 is equivalent to the charge carrier reflection model with U_zz = −1. This is the second main point of the paper—that one can assume a charge-carrier reflection model and, with the proper reflection coefficient, obtain an identical result to the transport model. The charge carrier reflection model begins with an assumption about particle reflection from the boundary (requiring specification of a particle reflection coefficient $\bar{\mathbf{U}}$) and results in determining $\chi ^{{\mathrm { cond}}}\left ( z,z^{\prime }\right )$ and the self-consistent ABC. The transport model involves solving the drift-diffusion equation, leading to $\chi ^{{\mathrm { cond}}}\left ( z,z^{\prime }\right ) =\varepsilon _{\mathrm { h}}k_{\mathrm { p}}^{2}~g\left ( z,z^{\prime }\right )$, and requires specifying an ABC prescribed from information about the boundary.

If α is known we have from (42)

$$\begin{equation} U_{zz}=\frac{\mathrm{j}k_{\rm h}\alpha+1}{\mathrm{j}k_{\rm h}\alpha-1}. \end{equation} \tag{ 46 }$$

In [3] we show that for the intersection of a wire medium and a thin metal (possibly homogenized) surface (or, e.g. a graphene sheet) characterized by sheet conductivity (S) σ_2d, then α = σ_2d/jωε₀ε_h, in which case

$$\begin{equation} U_{zz}=\frac{\sigma_{2\mathrm{d}}\eta_{\rm h}-1}{\sigma_{2\mathrm{d}}\eta_{\rm h}+1}, \end{equation} \tag{ 47 }$$

where $\eta _{\mathrm { h}}=\sqrt {\mu _{0}/\varepsilon _{0}\varepsilon _{\mathrm { h}}}$. In appendix B we consider the ABC and susceptibility functions for two uniaxial wire media connected by an interface.

2.3. Model III: the wave expansion method

2.4. Reflection from a uniaxial half-space

Consider a TM-polarized plane wave in vacuum incident on a non-local material interface, as depicted in figure 3. For simplicity, we assume ε_h = 1 so that we need to only consider the conductive response. We at first ignore the dead layer, which will be discussed later. Writing $\mathbf{k}^{\mathrm {i}}=k_{0}\left ( \hat{\mathbf{x}}\sin \theta _{i}+\hat{\mathbf{z}}\cos \theta _{i}\right )$ for TM polarization we have fields $(E_{x},E_{z},H_{y})$.

Zoom In Zoom Out Reset image size

Model II (charge carrier reflection model) involves solving (37). Using the lateral transform form of (25) (${\boldsymbol{\rho}}\mathbf{\leftrightarrow q }_{\rho }$) we have

$$\begin{eqnarray} &&\fl P_{z}^{{\rm cond}}(z) =\int_{0}^{\infty}\mathrm{d}z^{\prime}\frac{k_{\rm p}^{2}}{2\mathrm{j}k_{0}}\left( \mathrm{e}^{-\mathrm{j}k_{0}\left\vert z-z^{\prime}\right\vert}+U_{zz}\mathrm{e}^{-\mathrm{j}k_{0}( z+z^{\prime}) }\right)\nonumber\\ &&\times\ \left( \left[ k_{0}^{2}+\frac{\partial^{2}}{\partial z^{\prime2}}\right]\int_{0}^{\infty}\frac{\mathrm{e}^{-p\left\vert z^{\prime}-z^{\prime\prime}\right\vert}}{2p}P_{z}^{{\rm cond}}\left( z^{\prime\prime}\right)\,\mathrm{d}z^{\prime\prime}+\varepsilon_{0}E_{z}^{\mathrm{i}}( z^{\prime}) \right),\end{eqnarray} \tag{ 48 }$$

where $P_{z}^{{\mathrm { cond}}}(z ) =P_{z}^{{\mathrm { cond}}}(\mathbf{q}_{\rho },z)$ and similarly for Eⁱ_z, U_zz = −1, $p=\sqrt {q_{\rho }^{2}-k^{2}}$, q²_ρ = q²_x + q²_y and $k_{0}=\omega \sqrt {\mu _{0}\varepsilon _{0}}$. This form is the most time-consuming to compute since it involves a two-fold semi-infinite integral (for more general objects such as material spheres or cubes this would be a six-fold integration over the volume of the object). The DA would involve solving (48) with U_zz = 0 (i.e. in the absence of incorporating information about the boundary and simply using the bulk response (10)), however, the mathematically consistent ABC would be (43), which is at odds with the known physical ABC (44).

Model I (drift-diffusion model) involves solving (17). This can be done in two ways. One is by solving (17) directly as an integral–differential equation in the q_ρ transform domain

$$\begin{equation} \fl -\frac{k_{0}^{2}}{k_{\rm p}^{2}}\left( 1+\frac{1}{k_{0}^{2}}\frac{\partial^{2}}{\partial z^{2}}\right) P_{z}^{{\rm cond}}(z) =\left[ k_{0}^{2}+\frac{\partial^{2}}{\partial z^{2}}\right] \int_{0}^{\infty}\frac{\mathrm{e}^{-p\left\vert z-z^{\prime}\right\vert }}{2p} P_{z}^{{\rm cond}}( z^{\prime})\,\mathrm{d}z^{\prime}+\varepsilon_{0}E_{z}^{i}(z) . \end{equation} \tag{ 49 }$$

This form involves a single semi-infinite integral (for more general objects such as material spheres or cubes this would be a three-fold integration over the object's volume). The benefits of this method have been shown in [23, 24] for 3D objects.

The second method of solving (17) from the drift-diffusion model is via Green's functions using (21)

$$\begin{equation} P_{z}^{{\rm cond}}(z) =k_{\rm p}^{2}\varepsilon_{\rm h}\varepsilon_{0}\int_{0}^{\infty}g( z,z^{\prime}) E_{z}( z^{\prime})\,\mathrm{d}z^{\prime}. \end{equation} \tag{ 50 }$$

With (28) this results in the same equation as Model I.

Model III involves solving for the bulk plane waves that exist in each region and enforcing the usual boundary conditions along with the ABC. For q_y = 0 and assuming TM wave incidence, the fields for z < 0 are

$$\begin{eqnarray} H_{y} & =&( \mathrm{e}^{-\gamma_{0}z}-R\mathrm{e}^{\gamma_{0}z}) \mathrm{e}^{-\mathrm{j}q_{x}x},\nonumber\\ E_{x} & =&\frac{-1}{\mathrm{j}\omega\varepsilon_{0}}\frac{\partial H_{y}}{\partial z}=\frac{\gamma_{0}}{\mathrm{j}\omega\varepsilon_{0}}( \mathrm{e}^{-\gamma_{0}z}+R\mathrm{e}^{\gamma_{0}z}) \mathrm{e}^{-\mathrm{j}q_{x}x},\\ \ E_{z} & =&\frac{1}{\mathrm{j}\omega\varepsilon_{0}}\frac{\partial H_{y}}{\partial x}=\frac{-\mathrm{j}q_{x}}{\mathrm{j}\omega\varepsilon_{0}}( \mathrm{e}^{-\gamma_{0}z}-R\mathrm{e}^{\gamma_{0}z}) \mathrm{e}^{-\mathrm{j}q_{x}x},\nonumber \end{eqnarray} \tag{ 51 }$$

where R is the reflection coefficient and $\gamma _{0}=\sqrt {q_{x}^{2}-k_{0}^{2}}$. For z > 0,

$$\begin{eqnarray} H_{y} & =&( A_{{\rm TM}}\mathrm{e}^{-\gamma_{{\rm TM}}z}+B_{{\rm TEM} }\mathrm{e}^{-\gamma_{{\rm TEM}}z}) \mathrm{e}^{-\mathrm{j}q_{x}x},\nonumber\\ E_{x} & =&\frac{1}{\mathrm{j}\omega\varepsilon_{0}}( \gamma_{{\rm TM} }A_{{\rm TM}}\mathrm{e}^{-\gamma_{{\rm TM}}z}+\gamma_{{\rm TEM}}B_{{\rm TEM} }\mathrm{e}^{-\gamma_{{\rm TEM}}z}) \mathrm{e}^{-\mathrm{j}q_{x}x},\\ E_{z} & =&\frac{-\eta_{0}( k_{\rm p}^{2}+q_{x}^{2}) }{k_{0}q_{x} }A_{{\rm TM}}\mathrm{e}^{-\gamma_{{\rm TM}}z}\mathrm{e}^{-\mathrm{j}q_{x}x},\nonumber \end{eqnarray} \tag{ 52 }$$

where $\gamma _{{\mathrm { TM}}}=\sqrt {q_{x}^{2}+k_{\mathrm { p}}^{2}-k_{0}^{2}}$ and γ_TEM = jk₀. The ABC equivalent to P^cond_z = 0 is that E_z is continuous at z = 0 [13]; enforcing this condition and matching tangential fields results in q²_xB_TEM = k²_pA_TM

$$\begin{equation} R=\frac{\left( \gamma_{{\rm TM}}-\gamma_{0}\right) \left( \gamma_{{\rm TEM}}-\gamma_{0}\right) }{\left( \gamma_{0}+\gamma_{{\rm TM}}\right) \left( \gamma_{0}+\gamma_{{\rm TEM}}\right) } \end{equation} \tag{ 53 }$$

and

$$\begin{equation} A_{{\rm TM}}=\frac{2q_{x}^{2}\gamma_{0}}{( k_{\rm p}^{2}+q_{x}^{2}) \gamma_{0}+q_{x}^{2}\gamma_{{\rm TM}}+k_{\rm p}^{2}\gamma_{{\rm TEM}}}. \end{equation} \tag{ 54 }$$

It can be shown that these fields satisfy

$$\begin{eqnarray} &&\fl \nabla\times\mathbf{E} =-\mathrm{j}\omega\mu\mathbf{H},\nonumber\\ &&\fl \nabla\times\mathbf{H} =\mathrm{j}\omega\varepsilon_{0}\mathbf{E} +\hat{\mathbf{z}}\frac{k_{\rm p}^{2}}{2\eta_{0}}\int_{0}^{\infty}\left( \mathrm{e}^{-\mathrm{j}k_{0}\left\vert z-z^{\prime}\right\vert }-\mathrm{e}^{-\mathrm{j}k_{0}( z+z^{\prime}) }\right) E_{z}( z^{\prime})\,\mathrm{d}z^{\prime} \end{eqnarray} \tag{ 55 }$$

and therefore this solution is equivalent to the other methods. Numerical plots of internal fields are shown in [23].

2.4.1. Dead layer

In [13] it was shown that the model needs to incorporate a virtual air-layer (analogous to the dead layer), but that this layer is extremely thin (0 ⩽ δ ⩽ p/2π) and usually can be ignored. In the preceding example we ignored the dead layer, which we address here. For convenience with the previous results we assume the dead layer exists from −δ ⩽ z ⩽ 0 and the rest of the material occupies z > 0. Since ε_h = 1 there is no bound-charge polarization response and P^cond only exists for z > 0. Therefore, the dead layer is simply a small vacuum region existing for −δ ⩽ z ⩽ 0, and so this amounts to appending this thin vacuum region to be part of the material half-space. Thus, for Model I and Model II there is no change in (48) and (49); the only change is the interpretation of the vacuum dead layer as belonging to the material (e.g. such as defining the reflection coefficient occurring at z = −δ). In a similar manner, for Model III the fields for −δ ⩽ z ⩽ 0 and for z < −δ are the same as (51), and the rest of the solution is the same as above as well. In this case, the reflection coefficient including the dead layer is R_DL = R e^γ₀2δ. The three methods of solution are again equivalent, and, since γ₀ is imaginary-valued the dead layer only affects the reflection phase in this problem.

Finally, we can comment on the effect of the dead layer. Since 0 ⩽ δ ⩽ p/2π, then δγ₀ ≪ 1 and so the small shift in the reflection coefficient due to the dead layer is negligible. Regarding the fields, there are only transverse fields for z < −δ and for −δ ⩽ z ⩽ 0, and so by continuity of the transverse fields in the dead layer these will closely resemble the fields for z > 0. If we call the fields determined with the inclusion of the dead layer the 'exact' result, and the fields computed ignoring the dead layer as the approximate result, then the difference fields E^diff = E^exact − E^approx are, in the dead layer

$$\begin{equation} \left\vert E_{x}^{{\rm diff}}/E_{x}^{{\rm exact}}\right\vert \simeq \gamma_{0}\delta \end{equation} \tag{ 56 }$$

and for z > 0,

$$\begin{eqnarray*} & & \left\vert E_{x}^{{\rm diff, TM}}/E_{x}^{{\rm exact, TM}}\right\vert =\left\vert E_{z}^{{\rm diff, TM}}/E_{z}^{{\rm exact, TM}}\right\vert \simeq\gamma_{{\rm TM}}\delta,\ \\ & & \left\vert E_{x}^{{\rm diff, TEM}}/E_{x}^{{\rm exact, TEM}}\right\vert \simeq\gamma_{{\rm TEM}}\delta,\nonumber \end{eqnarray*}$$

where we used $\vert \gamma _{0,{\mathrm {TM,TEM}}} \vert \delta \ll 1$ such that $( 1-\mathrm {e}^{\pm \gamma _{0,{\mathrm { TM,TEM}}}\delta }) \simeq \mp \gamma _{0,{\mathrm { TM,TEM}}}\delta$. Thus, as expected, the difference fields are very small (note that in the dead layer $E_{z}^{{\mathrm { diff}}}= ( \eta _{0}(k_{\mathrm { p}}^{2}+q_{x}^{2}) /k_{0}q_{x}) A_{{\mathrm { TM}}}\mathrm {e}^{-\gamma _{{\mathrm { TM}}}z}\mathrm {e}^{-\gamma _{{\mathrm { TM}}}\delta }\mathrm {e}^{-\mathrm {j}q_{x}}$ since the exact result has E_z = 0 in the dead layer, and so in this case E^exact_z − E^approx_z = −E^approx_z).

At this point it is fruitful to discuss a correlation with the natural excitation case discussed in [33, 40]. In [40] the authors develop a wave expansion method for a non-local (excitonic semiconductor) half-space, similar in spirit to the wave expansion method discussed here. They ignore the dead layer and use the Boltzmann equation for the bulk response (i.e. the electron distribution function f does not depend on position z, and the boundary only enters via the usual conditions, including the ABC). The non-local response function obtained in [40] from Boltzmann's equation is analogous to the non-local wire medium permittivity used here, and so their wave expansion is analogous to the wave expansion method used here when one ignores the dead layer. In the second paper, [33], the authors use the Boltzmann equation and a distribution function $f(z )$ that accounts for the boundary, such that spatially dependent electron distributions can be obtained. Using this method, the dead layer emerges naturally, and material properties can vary smoothly over the dead layer into the bulk; the dead layer is implicitly included in the solution. Comparing these two methods, in [33] the conclusion is that the wave expansion method ignoring the dead layer (i.e. the solution in [40]) does not agree with the more accurate method in [33] (which includes the dead layer) over distances near the interface on the order of the dead layer. This is the same result as we find above for the wire medium problem. Since all three methods discussed here are equivalent, we can summarize by saying that ignoring the dead layer leads to one answer and including the dead layer leads to a slightly different answer, the differences being small and principally occurring within δ of the interface.

2.5. Longitudinal example

As another example of the above ideas, we consider a planar slab of material excited by a purely longitudinal (with respect to the slab normal) impressed field, like what would be found between the plates of a capacitor for a quasi-static excitation. The slab has width L, and is immersed in vacuum, as depicted in figure 4. For this excitation, the 3D wire mesh (connected or non-connected) provides the same response as the uniaxial wire medium. We assume ε_h = 1 for simplicity so there is no bound-charge polarization contribution.

Zoom In Zoom Out Reset image size

For Model I (drift-diffusion model), from (17) we have

$$\begin{equation} \left( k_{0}^{2}+\frac{\partial^{2}}{\partial z^{2}}\right) P_{z}^{{\rm cond}}(z) =-k_{\rm p}^{2}\varepsilon_{0}(E_{z}^{{\rm scat}}(z) +E_{z}^{{\rm inc}}(z)), \end{equation} \tag{ 57 }$$

where

$$\begin{equation} E_{z}^{{\rm scat}}(z) =\frac{1}{\varepsilon_{0}}\left(k_{0}^{2}+\frac{\mathrm{d}^{2}}{\mathrm{d}z^{2}}\right) \int_{0}^{L}\frac{\mathrm{e}^{-\mathrm{j}k_{0}\left\vert z-z^{\prime}\right\vert }}{2\mathrm{j}k_{0}}P_{z}^{\rm cond}( z^{\prime})\,\mathrm{d}z^{\prime}. \end{equation} \tag{ 58 }$$

Using Leibnitz's theorem [41], if $z\in \left ( 0,L\right )$ then

$$\begin{equation} \left( k_{0}^{2}\mathbf{+}\frac{\mathrm{d}^{2}}{\mathrm{d}z^{2}}\right) \int_{0}^{L}\frac{\mathrm{e}^{-\mathrm{j}k_{0}\left\vert z-z^{\prime}\right\vert }}{2\mathrm{j}k_{0}}P_{z}^{\rm cond}(z^{\prime})\,\mathrm{d}z^{\prime}=-P_{z}^{\rm cond}(z) \end{equation} \tag{ 59 }$$

such that $E_{z}^{{\mathrm { scat}}}(z ) =-P_{z}^{{\mathrm { cond}}}\left (z\right ) /\varepsilon _{0}$. Then, from (57),

$$\begin{equation} \left( \beta^{2}+\frac{\partial^{2}}{\partial z^{2}}\right) P_{z} ^{{\rm cond}}(z) =-k_{\rm p}^{2}\varepsilon_{0}E_{z}^{{\rm inc} }(z), \end{equation} \tag{ 60 }$$

where β² = k²₀ − k²_p.

Since $E_{z}^{{\mathrm { inc}}}(z )$ is constant we can solve (60) as

$$\begin{equation} P_{z}^{{\rm cond}}(z) =C\sin\left( \beta z\right) +D\cos\left( \beta z\right) -\frac{k_{\rm p}^{2}}{\beta^{2}}\varepsilon_{0} E_{z}^{{\rm inc}} \end{equation} \tag{ 61 }$$

and $P_{z}^{{\mathrm { cond}}}\left ( 0,L\right ) =0$ leads to

$$\begin{equation} P_{z}^{{\rm cond}}(z) =\frac{1}{\beta^{2}}k_{\rm p}^{2} \varepsilon_{0}E_{z}^{{\rm inc}}\left( \frac{\left( 1-\cos\beta L\right) }{\sin\beta L}\sin\left( \beta z\right) +\cos\left( \beta z\right) -1\right). \end{equation} \tag{ 62 }$$

Alternatively, we can define a Green function

$$\begin{equation} \left( \beta^{2}+\frac{\partial^{2}}{\partial z^{2}}\right) g(z,z^{\prime}) =-\delta( z-z^{\prime}) \end{equation} \tag{ 63 }$$

such that

$$\begin{equation} P_{z}^{{\rm cond}}(z) =k_{\rm p}^{2}\varepsilon_{0}\int_{0} ^{L}g( z,z^{\prime}) E_{z}^{{\rm inc}}( z^{\prime})\, \mathrm{d}z^{\prime}, \end{equation} \tag{ 64 }$$

where

$$\begin{eqnarray} &&\fl k_{\rm p}^{2}g( z,z^{\prime}) =\chi^{{\rm cond}}(z,z^{\prime}) =\frac{k_{\rm p}^{2}}{2\mathrm{j}\beta}\left( \mathrm{e}^{-\mathrm{j}\beta\left\vert z-z^{\prime}\right\vert }-\mathrm{e}^{-\mathrm{j}\beta z^{\prime}}\cos\left( \beta z\right) \right. \nonumber\\ &&+\left. \left[ \mathrm{e}^{-\mathrm{j}\beta z^{\prime}}\cot\left( \beta L\right) -\mathrm{e}^{-\mathrm{j}\beta( L-z^{\prime}) }\csc\left( \beta L\right) \right] \sin\left( \beta z\right) \right) . \end{eqnarray} \tag{ 65 }$$

In numerical examples, (62) and (64) give the same answer (and recall this is equivalent to method II with U_zz = −1). However, for this problem one cannot attempt to invoke the DA equivalent to U_zz = 0 (such that $g\left ( z,z^{\prime }\right ) =\mathrm {e}^{-\mathrm {j}\beta \left \vert z-z^{\prime }\right \vert }/2\mathrm {j}\beta$) since there is no way to enforce $P_{z}^{{\mathrm { cond}}}\left (0,L\right ) =0$.

Alternatively, we can start from Model II,

$$\begin{eqnarray} &&\fl P_{z}^{{\rm cond}} =\frac{\varepsilon_{0}k_{\rm p}^{2}}{2\mathrm{j}k_{0}}\int_{0} ^{L}\left( \mathrm{e}^{-\mathrm{j}k_{0}\left\vert z-z^{\prime}\right\vert }+U_{zz} \mathrm{e}^{-\mathrm{j}k_{0}( z+z^{\prime}) }+ U_{zz}\mathrm{e}^{-\mathrm{j}k_{0}\left( 2L-( z+z^{\prime}) \right) }+U_{zz}^{2}\mathrm{e}^{-\mathrm{j}k_{0}\left( 2L-\left\vert z-z^{\prime}\right\vert \right) }\right) E_{z}( z^{\prime})\,\mathrm{d}z^{\prime},\nonumber\\ \end{eqnarray} \tag{ 66 }$$

where the additional terms compared to (36) are due to the set of infinite multiple reflections from the two interfaces summed as a geometric series. Since $E_{z}^{{\mathrm { scat}}}(z ) =-P_{z}^{{\mathrm { cond}}}(z ) /\varepsilon _{0}$ we have (66) with $E_{z}\left (z\right ) =-P_{z}^{{\mathrm { cond}}}(z ) /\varepsilon _{0}+E_{z}^{{\mathrm { inc}}}$, which can be solved subject to a BC on P^cond_z.

We have solved (66) using a Galerkin solution involving complete set of expansion functions that automatically satisfy the physical boundary condition $P_{z}^{{\mathrm { cond}}}\left ( 0,L\right ) =0$

$$\begin{equation} P_{z}^{{\rm cond}}(z) =\sum_{n=1}^{N}a_{n}\sin\left( \frac{n\pi}{L}z\right) . \end{equation} \tag{ 67 }$$

Figure 5 shows the polarization distribution comparing Model I, (62), and the numerical solution of (66) from Model II. Wire period is 4 mm and slab thickness is L = 10p. It can be seen that when U_zz = −1 the numerical solution of (66) is in complete agreement with the analytical solution from Method I, (62). In figure 5 we also show the solution when U_zz = 0, a DA. In this case we have also enforced the ABC P^cond_z = 0 (rather than (43)) since this is the physically sensible condition. However, as described above this condition is not consistent with the ABC (43) associated with the U_zz = 0 case (which would result in an unphysical solution). The two solutions for U_zz = −1 and 0 differ considerably, but tend to agree away from the edges. In figure 6 we show the same result but for L = 2p, where, since the slab is thinner and the edges are more important, and the DA is considerably worse.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

In this section we discuss the case of isotropic wire media consisting of a 3D mesh of interconnecting wires (see, e.g.  [14, figure 1]; other wire media such as double wires [42, 43] could also be considered. The relative permittivity is [14]

$$\begin{equation} \bar{\boldsymbol{\varepsilon}}_{{\rm bulk}}\left( \mathbf{q}\right) =\mathbf{1}\varepsilon_{\rm h}-\kappa\left( \mathbf{1}-\frac{1}{q^{2}-\zeta^{2} }\mathbf{qq}\right) . \end{equation} \tag{ 68 }$$

Here, q is the 3D FT variable, $\mathbf{q}=\hat{{\boldsymbol{\rho}}}q_{\rho }+\hat{\mathbf{z}}q_{z}$, $\bar{\boldsymbol{\varepsilon}} (\mathbf{q}) =\bar{\boldsymbol{\varepsilon}}(\mathbf{q}_{\rho },q_{z})$, and

$$\begin{equation} \begin{array}{ll} \displaystyle \kappa =\left( \frac{k_{0}^{2}}{k_{\rm p}^{2}}-\frac{1}{\varepsilon_{\rm m}-\varepsilon_{\rm h}}\frac{1}{f_{\mathrm{v}}}\right) ^{-1},\\ \displaystyle\zeta^{2} =l_{0}\left( k_{\rm h}^{2}-\frac{\varepsilon_{\rm h}k_{\rm p}^{2}}{\varepsilon_{\rm m}-\varepsilon_{\rm h}}\frac{1}{f_{\mathrm{v}}}\right), \end{array}\end{equation} \tag{ 69 }$$

where f_v = πr²/p² is the volume fraction of the wires (r is the wire radius, p is the wire period), ε_m is the wire permittivity, $l_{0}=3/\left ( 1+2k_{\mathrm { p}}^{2}/\beta _{1}^{2}\right )$, and

$$\begin{equation} \frac{1}{\beta_{1}^{2}}=2\left( \frac{p}{2\pi}\right) ^{2}{\displaystyle\sum\limits_{n=1}^{\infty}} \frac{\left[ J_{0}\left( \frac{2\pi r}{p}n\right) \right] ^{2}}{n^{2}}, \end{equation} \tag{ 70 }$$

where J₀ is the zeroth-order Bessel function. As discussed in [14], this expression is very accurate below the effective plasma frequency. The isotropic wire medium permittivity (68) reduces to the simpler form [44]

$$\begin{equation} \bar{\boldsymbol{\varepsilon}}_{{\rm bulk}}\left( \mathbf{q}\right) =\mathbf{1}\varepsilon_{\rm h}-\frac{k_{\rm p}^{2}}{k_{0}^{2}}\left( \mathbf{1}-\frac{1}{q^{2}-l_{0}k_{\rm h}^{2}}\mathbf{qq}\right) \end{equation} \tag{ 71 }$$

when $\left \vert \varepsilon _{\mathrm { m}}\right \vert \rightarrow \infty$, i.e. as the wire conductivity becomes infinite.

The inverse transform of (68) is easily evaluated as

$$\begin{eqnarray} \bar{\boldsymbol{\varepsilon}}_{{\rm bulk}}( \mathbf{r}) &=&( \varepsilon_{\rm h}-\kappa) \delta( \mathbf{r}) \mathbf{1}-\kappa\nabla\nabla\frac{\mathrm{e}^{-\mathrm{j}\zeta r}}{4\pi r}\nonumber\\ &=&( \varepsilon_{\rm h}-\kappa) \delta( \mathbf{r}) \mathbf{1} -\kappa\left( \left( 3\hat{\mathbf{r}}\hat{\mathbf{r}} -\mathbf{1}\right) \left( \frac{1}{r^{2}}-\frac{\zeta}{\mathrm{j}r}\right) -\zeta^{2}\hat{\mathbf{r}}\hat{\mathbf{r}}\right) \frac{\mathrm{e}^{-\mathrm{j}\zeta r}}{4\pi r}. \end{eqnarray} \tag{ 72 }$$

From

$$\begin{equation} \bar{\boldsymbol{\chi}}_{{\rm bulk}}^{{\rm cond}}\left( \mathbf{q}\right) =-\kappa\left( \mathbf{1}-\frac{1}{q^{2}-\zeta^{2}}\mathbf{qq}\right) \end{equation} \tag{ 73 }$$

we have

$$\begin{eqnarray} \bar{\boldsymbol{\chi}}_{{\rm bulk}}^{{\rm cond}}\left( \mathbf{r} \right) & =&-\kappa\delta( \mathbf{r}) \mathbf{1}-\kappa \nabla\nabla\frac{\mathrm{e}^{-\mathrm{j}\zeta r}}{4\pi r}\nonumber\\ &=&-\kappa\delta( \mathbf{r}) \mathbf{1}-\kappa\left( \left( 3\hat{\mathbf{r}}\hat{\mathbf{r}}-\mathbf{1}\right) \left( \frac {1}{r^{2}}-\frac{\zeta}{\mathrm{j}r}\right) -\zeta^{2}\hat{\mathbf{r}} \hat{\mathbf{r}}\right) \frac{\mathrm{e}^{-\mathrm{j}\zeta r}}{4\pi r}. \end{eqnarray} \tag{ 74 }$$

For Model I (transport equation), to form the drift-diffusion equation we note that

$$\begin{eqnarray} \mathbf{P}\left( \mathbf{q}\right) & =& \varepsilon_{0}\left( \mathbf{1}\left( \varepsilon_{\rm h}-1\right) -\kappa\left( \mathbf{1}-\frac {1}{q^{2}-\zeta^{2}}\mathbf{qq}\right) \right) \cdot\mathbf{E}\left( \mathbf{q}\right) \nonumber\\ & =& \left[ \mathbf{P}^{{\rm pol}}\left( \mathbf{q}\right) +\mathbf{P} ^{{\rm cond}}\left( \mathbf{q}\right) \right] \cdot\mathbf{E}\left( \mathbf{q}\right) \end{eqnarray} \tag{ 75 }$$

such that

$$\begin{eqnarray} &&\fl \mathbf{P}^{{\rm cond}}\left( \mathbf{q}\right) =-\kappa\left( \mathbf{1}-\frac{1}{q^{2}-\zeta^{2}}\mathbf{qq}\right) \cdot\varepsilon _{0}\mathbf{E}\left( \mathbf{q}\right) \rightarrow\left( \mathbf{1}-\frac{1}{\zeta^{2}}\mathbf{qq}\right) \cdot\mathbf{P}^{{\rm cond}}\left( \mathbf{q}\right) =-\kappa \varepsilon_{0}\mathbf{E}\left( \mathbf{q}\right) \end{eqnarray} \tag{ 76 }$$

using

$$\begin{equation} \left( \mathbf{1}-\frac{1}{\zeta^{2}}\mathbf{qq}\right) ^{-1}=\left(\mathbf{1}-\frac{1}{q^{2}-\zeta^{2}}\mathbf{qq}\right).\end{equation} \tag{ 77 }$$

Therefore, the drift-diffusion equation is

$$\begin{equation} \left( \mathbf{1}+\frac{1}{\zeta^{2}}\mathbf{\nabla\nabla}\right)\cdot\mathbf{P}^{{\rm cond}}( \mathbf{r}) =-\kappa\varepsilon_{0}\mathbf{E}( \mathbf{r}) \end{equation} \tag{ 78 }$$

subject to $P_{z}\left ( 0\right ) =0$ (or one could use the more general form (18)). We therefore define a drift-diffusion Green function that satisfies

$$\begin{equation} \left( \mathbf{1}+\frac{1}{\zeta^{2}}\mathbf{\nabla\nabla}\right) \cdot\bar{\mathbf{g}}(\mathbf{r},\mathbf{r}^{\prime}) =-\mathbf{1}\delta\left( \mathbf{r}-\mathbf{r}^{\prime}\right) \end{equation} \tag{ 79 }$$

subject to $\hat{\mathbf{z}}\cdot \bar{\mathbf{g}}\left ( 0\right )=\mathbf{0}$.

For the principal Green function we have

$$\begin{eqnarray} &&\fl \left( \mathbf{1}-\frac{1}{\zeta^{2}}\mathbf{qq}\right) \cdot \bar{\mathbf{g}}_{\rm p}^{{\rm cond}}\left( \mathbf{q}\right) =-\mathbf{1,} \rightarrow\bar{\mathbf{g}}_{\rm p}^{{\rm cond}}\left( \mathbf{q} \right) =-\left( \mathbf{1}-\frac{1}{q^{2}-\zeta^{2}}\mathbf{qq}\right) \end{eqnarray} \tag{ 80 }$$

so that

$$\begin{equation} \bar{\mathbf{g}}_{\rm p}^{{\rm cond}}\left( \mathbf{r}-\mathbf{r}^{\prime }\right) =-\mathbf{1}\delta\left( \mathbf{r}-\mathbf{r}^{\prime}\right) -\mathbf{\nabla\nabla}\frac{\mathrm{e}^{-\mathrm{j}\alpha R}}{4\pi R}, \end{equation} \tag{ 81 }$$

where R = r − r' and $R=\sqrt {\left (x-x^{\prime }\right ) ^{2}+\left ( y-y^{\prime }\right ) ^{2}+\left (z-z^{\prime }\right ) ^{2}}$. In contrast, the usual free-space electric Green dyadic that relates current and field is [45]

$$\begin{eqnarray} \bar{\mathbf{g}}_{\rm p}^{{\rm fs}}( \mathbf{r},\mathbf{r}^{\prime},\omega) & =&\bar{\mathbf{g}}_{\rm p}^{{\rm fs}}(\mathbf{r}-\mathbf{r}^{\prime},\omega) \nonumber\\ & =&\frac{1}{\left( 2\pi\right) ^{3}}\int\frac{\mathbf{1}k^{2}-\mathbf{qq} }{k^{2}\left( q^{2}-k^{2}\right) }\mathrm{e}^{-\mathrm{j}\mathbf{q\cdot}\left( \mathbf{r} -\mathbf{r}^{\prime}\right) }d^{3}\mathbf{q}\\ & =&\left[ \mathbf{1}+\frac{\mathbf{\nabla\nabla}}{k^{2}}\right] \frac{\mathrm{e}^{-\mathrm{j}kR}}{4\pi R}.\nonumber \end{eqnarray} \tag{ 82 }$$

Because of the ABC P^cond_z = 0 (assuming an interface with vacuum), the scattered Green function should satisfy a perfect magnetic conductor (PMC) condition. Since

$$\begin{eqnarray} &&\fl \bar{\mathbf{g}}_{\rm p}^{{\rm cond}}( \mathbf{r}-\mathbf{r}^{\prime})=-( \hat{\mathbf{x}}\hat{\mathbf{x}} +\hat{\mathbf{y}}\hat{\mathbf{y}}+\hat{\mathbf{z}}\hat{\mathbf{z}}) \delta( \mathbf{r}-\mathbf{r}^{\prime}) -\mathbf{\nabla}\left( \hat{\mathbf{x}}\frac{\partial}{\partial x}+\hat{\mathbf{y}}\frac{\partial}{\partial y}+\hat{\mathbf{z}} \frac{\partial}{\partial z}\right) \frac{\mathrm{e}^{-\mathrm{j}\zeta R}}{4\pi R} \end{eqnarray} \tag{ 83 }$$

it is easy to see that the scattered Green function is

$$\begin{eqnarray} &&\fl \bar{\mathbf{g}}_{\rm s}^{{\rm cond}}( \mathbf{r}-\mathbf{r} _{1}^{\prime}) =-( \hat{\mathbf{x}}\hat{\mathbf{x}}+\hat{\mathbf{y}}\hat{\mathbf{y}}-\hat{\mathbf{z}}\hat{\mathbf{z}}) \delta(\mathbf{r}-\mathbf{r}_{1}^{\prime})-\mathbf{\nabla}\left( \hat{\mathbf{x}}\frac{\partial}{\partial x}+\hat{\mathbf{y}}\frac{\partial}{\partial y}-\hat{\mathbf{z}} \frac{\partial}{\partial z}\right) \frac{\mathrm{e}^{-\mathrm{j}\zeta R_{1}}}{4\pi R_{1}}, \end{eqnarray} \tag{ 84 }$$

where

$$\begin{eqnarray} &&\begin{array}{ll} \displaystyle \mathbf{r}_{1} =\hat{\mathbf{x}}x+\hat{\mathbf{y}}y-\hat{\mathbf{z}}z,\\ \displaystyle \mathbf{R}_{1} =\mathbf{r}-\mathbf{r}_{1}^{\prime}=\hat{\mathbf{x} }( x-x^{\prime}) +\hat{\mathbf{y}}( y-y^{\prime}) +\hat{\mathbf{z}}( z+z^{\prime}) \end{array} \end{eqnarray} \tag{ 85 }$$

which satisfies

$$\begin{equation} \left. \hat{\mathbf{z}}\cdot\left( \bar{\mathbf{g}}_{\rm p} ^{{\rm cond}}+\bar{\mathbf{g}}_{\rm s}^{{\rm cond}}\right) \right\vert _{z=0}=0. \end{equation} \tag{ 86 }$$

Thus, we have

$$\begin{eqnarray} \bar{\mathbf{g}}^{{\rm cond}}( \mathbf{r,r}^{\prime}) &=&\bar{\mathbf{g}}_{\rm p}^{{\rm cond}}(\mathbf{r}-\mathbf{r}^{\prime}) +\bar{\mathbf{g}}_{\rm s}^{{\rm cond}}(\mathbf{r}-\mathbf{r}_{1}^{\prime}) \nonumber\\ & =&\bar{\mathbf{g}}_{\rm p}^{{\rm cond}}( \mathbf{r}-\mathbf{r} ^{\prime}) +\bar{\mathbf{g}}_{\rm s}^{{\rm cond}}({\boldsymbol{\rho}}-{\boldsymbol{\rho}}^{\prime},z+z^{\prime}). \end{eqnarray} \tag{ 87 }$$

By superposition $\bar{\boldsymbol{\chi}}^{{\mathrm { cond}}}\left ( \mathbf{r},\mathbf{r}^{\prime }\right )$ and $\bar{\mathbf{g}}^{{\mathrm { cond}}}\left (\mathbf{r},\mathbf{r}^{\prime }\right )$ are simply related as in the scalar case,

$$\begin{equation} \bar{\boldsymbol{\chi}}^{{\rm cond}}( \mathbf{r,r}^{\prime}) =\kappa\bar{\mathbf{g}}^{{\rm cond}}( \mathbf{r,r}^{\prime}) . \end{equation} \tag{ 88 }$$

Comparing to Model II,

$$\begin{equation} \bar{\mathbf{g}}^{{\rm cond}}( \mathbf{r,r}^{\prime}) =\bar{\mathbf{g}}_{\rm p}^{{\rm cond}}( \mathbf{r}-\mathbf{r}^{\prime}) +\bar{\mathbf{g}}_{\rm p}^{{\rm cond}}( \mathbf{r}-\mathbf{r}_{1}^{\prime}) \cdot\bar{\mathbf{U}}, \end{equation} \tag{ 89 }$$

where $\bar{\mathbf{U}}=\hat{\mathbf{x}}\hat{\mathbf{x}}+\hat{\mathbf{y}}\hat{\mathbf{y}}-\hat{\mathbf{z}}\hat{\mathbf{z}}$. This is the isotropic case expression analogous to the uniaxial case (35) and (36) with U_zz = −1. Restoring the dead layer, for Model II (charge carrier reflection approximation)

$$\begin{equation} \bar{\boldsymbol{\chi}}^{{\rm cond}}(\mathbf{r},\mathbf{r}^{\prime}) =\bar{\mathbf{0}},\ \ \ \ 0 < z,z^{\prime} < \delta \end{equation} \tag{ 90 }$$

and for z,z' > δ,

$$\begin{eqnarray} \bar{\boldsymbol{\chi}}^{{\rm cond}}\left( \mathbf{r},\mathbf{r}^{\prime }\right) & =&\bar{\boldsymbol{\chi}}_{{\rm bulk}}^{{\rm cond}}(\mathbf{r}-\mathbf{r}^{\prime}) +\bar{\boldsymbol{\chi}}_{{\rm bulk} }^{{\rm cond}}(\mathbf{r}-\mathbf{r}_{1}^{\prime}) \cdot\bar{\mathbf{U}}\nonumber\\ & =&\bar{\boldsymbol{\chi}}_{{\rm bulk}}^{{\rm cond}}( \mathbf{r}-\mathbf{r}^{\prime}) +\bar{\boldsymbol{\chi}}_{{\rm s \ } }^{{\rm cond}}\left( {\boldsymbol{\rho}}-{\boldsymbol{\rho}}^{\prime},z+z^{\prime }-2\delta\right) . \end{eqnarray} \tag{ 91 }$$

Analogous to the procedure in section 2.2.1, assuming that $\bar{\bf U} =\hat{\mathbf{z}}\hat{\mathbf{z}}U_{zz}$ then the self-consistent ABC is

$$\begin{equation} P_{z}^{{\rm cond}}( \mathbf{q}_{\rho},z) -\frac{\left( 1+U_{zz}\right) }{\mathrm{j}k_{z}\left( 1-U_{zz}\right) }\frac{\partial}{\partial z}P_{z}^{{\rm cond}}( \mathbf{q}_{\rho},z) =0 \end{equation} \tag{ 92 }$$

which is (41) for the isotropic wire media case (k_h in (42) is replaced by $k_{z}=\sqrt {\zeta ^{2}-q_{\rho }^{2}}$ in (92)).

We have shown that when the polarization and electric field are related by a linear differential equation the non-local susceptibility $\bar{\boldsymbol{\chi}} (\mathbf{r},\mathbf{r}^{\prime })$ for a non-translationally invariant wire medium is given by a Green function related to the material geometry. Further, we have shown that two previous methods for solving wave interaction problems for bounded wire media are equivalent to each other, and to a third method involving particle reflection at the boundary.

MS was partially funded by Fundação para a Ciência e Tecnologia with the grants PEst-OE/EEI/LA0008/2013 and PTDC/EEI-TEL/2764/2012. AB was supported in part by NASA EPSCoR award NNX13AB31A.

Here we develop a transmission line analogy for both the isotropic wire medium [46] and the uniaxial wire medium. Starting with the homogeneous form of (78), in the transverse Fourier transform domain ${\boldsymbol{\rho}}\leftrightarrow \mathbf{q}_{\rho }$ we have

$$\begin{equation} \left( \mathbf{1}+\frac{1}{\zeta^{2}}\mathbf{\nabla}_{q}\mathbf{\nabla}_{q}\right) \cdot\mathbf{P}^{{\rm cond}}( \mathbf{q}_{\rho},z)=\mathbf{0}, \end{equation} \tag{ A.1 }$$

where $\nabla =-\mathrm {j}\mathbf{q}_{\rho }+\hat{\mathbf{z}}\,\mathrm {d}/\mathrm {d}z$. Upon defining

$$\begin{equation} V( \mathbf{q}_{\rho},z) \equiv\nabla_{q}\cdot\mathbf{P}(\mathbf{q}_{\rho},z) =-\mathrm{j}\mathbf{q}_{\rho}\cdot\mathbf{P}_{\rho} +\frac{\mathrm{d}P_{z}}{\mathrm{d}z} \end{equation} \tag{ A.2 }$$

we have, from (A.1),

$$\begin{equation} \nabla V=-\zeta^{2}( \mathbf{P}_{\rho}+\hat{\mathbf{z}}P_{z}). \end{equation} \tag{ A.3 }$$

Using $\nabla _{q}V=-\mathrm {j}\mathbf{q}_{\rho }V+\hat{\mathbf{z}}\,\mathrm {d}V/\mathrm {d}z$,

$$\begin{eqnarray} &&\begin{array}{ll} \displaystyle-\mathrm{j}\mathbf{q}_{\rho}V =-\zeta^{2}\mathbf{P}_{\rho},\\ \displaystyle \frac{\mathrm{d}V}{\mathrm{d}z} =-\zeta^{2}P_{z}. \end{array}\end{eqnarray} \tag{ A.4 }$$

From (A.2) and using (A.4),

$$\begin{equation} \frac{\mathrm{d}P_{z}}{\mathrm{d}z}=\frac{\zeta^{2}-q_{\rho}^{2}}{\zeta^{2}}V. \end{equation} \tag{ A.5 }$$

Defining $I( \mathbf{q}_{\rho },z) \equiv P_{z}(\mathbf{q}_{\rho },z)$, then the desired transmission line equations are, using (A.4),

$$\begin{eqnarray} &&\begin{array}{ll} \displaystyle\frac{\mathrm{d}V}{\mathrm{d}z} =-\zeta^{2}I=-Z_{\rm s}I,\\ \displaystyle\frac{\mathrm{d}I}{\mathrm{d}z} =-\frac{q_{\rho}^{2}-\zeta^{2}}{\zeta^{2}}V=-Y_{\rm p}V \end{array} \end{eqnarray} \tag{ A.6 }$$

and we have the propagation wavenumber and characteristic impedance

$$\begin{equation} k_{z} =\sqrt{-Z_{\rm s}Y_{\rm p}}=\sqrt{\zeta^{2}-q_{\rho}^{2}}, \end{equation} \tag{ A.7 }$$

$$\begin{equation} Z_{\rm c} =\sqrt{\frac{Z_{\rm s}}{Y_{\rm p}}}=\frac{\zeta^{2}}{\mathrm{j}k_{z}}. \end{equation} \tag{ A.8 }$$

If we consider a wire medium half-space (z < 0) and assuming a current reflection coefficient U at z = 0, we have an impedance

$$\begin{equation} Z( 0) =Z_{\rm c}\frac{1-U}{1+U} \end{equation} \tag{ A.9 }$$

and a boundary condition

$$\begin{equation} V( 0) =Z( 0) I( 0) \rightarrow(\nabla_{q}\cdot\mathbf{P}) _{z=0}=Z( 0) P_{z}(0).\end{equation} \tag{ A.10 }$$

This becomes

$$\begin{equation} \left( \frac{\mathrm{d}P_{z}}{\mathrm{d}z}\right) _{z=0}+\mathrm{j}k_{z}\frac{1-U}{1+U}P_{z}\left( 0\right) =0 \end{equation} \tag{ A.11 }$$

which is equivalent to (92) (the difference in sign being because here the material occupies the half-space z < 0, and for (92) the material occupies the half-space z > 0). For a uniaxial wire medium the same analysis holds with V =dP_z/dz.

Consider two identical uniaxial wire mediums connected by an interface as depicted in figure B.1. Writing

$$\begin{eqnarray} &&\begin{array}{ll} \mathbf{P}_{1}^{{\rm cond}}\left( {\boldsymbol{\rho}},z\right) =\varepsilon _{0}\int_{-\infty}^{0}\bar{\boldsymbol{\chi}}_{11}^{{\rm cond}}(z,z^{\prime}) \cdot\mathbf{E}_{1}({\boldsymbol{\rho}},z^{\prime})\,\mathrm{d}z^{\prime} +\varepsilon_{0}\int_{0}^{\infty}\bar{\boldsymbol{\chi}}_{12}^{{\rm cond}}( z,z^{\prime}) \cdot\mathbf{E}_{2}({\boldsymbol{\rho}},z^{\prime})\,\mathrm{d}z^{\prime},\\ \mathbf{P}_{2}^{{\rm cond}}\left( {\boldsymbol{\rho}},z\right) =\varepsilon _{0}\int_{-\infty}^{0}\bar{\boldsymbol{\chi}}_{21}^{{\rm cond}}(z,z^{\prime}) \cdot\mathbf{E}_{1}({\boldsymbol{\rho}},z^{\prime})\,\mathrm{d}z^{\prime} +\varepsilon_{0}\int_{0}^{\infty}\bar{\boldsymbol{\chi}}_{22}^{{\rm cond}}( z,z^{\prime}) \cdot\mathbf{E}_{2}({\boldsymbol{\rho}},z^{\prime})\,\mathrm{d}z^{\prime} \end{array} \end{eqnarray} \tag{ B.1 }$$

and using Model II (charge carrier reflection model) the susceptibilities are set to zero in the dead layer (analogous to (34)) and outside the dead layer we have, similar to (36),

$$\begin{eqnarray} &&\begin{array}{llll} \displaystyle \bar{\boldsymbol{\chi}}_{11}^{{\rm cond}}( z,z^{\prime}) =\hat{\mathbf{z}}\hat{\mathbf{z}}\frac{\varepsilon_{\rm h}k_{\rm p}^{2}}{2\mathrm{j}k_{\rm h}}\left( \mathrm{e}^{-\mathrm{j}k_{\rm h}\left\vert z-z^{\prime}\right\vert }+U_{11}\mathrm{e}^{\mathrm{j}k_{\rm h}\left( z+z^{\prime}+2\delta\right) }\right) ,\\ \displaystyle \bar{\boldsymbol{\chi}}_{12}^{{\rm cond}}( z,z^{\prime}) =\hat{\mathbf{z}}\hat{\mathbf{z}}\frac{\varepsilon_{\rm h}k_{\rm p}^{2}}{2\mathrm{j}k_{\rm h}}U_{12}\mathrm{e}^{\mathrm{j}k_{\rm h}\left( z-z^{\prime}+2\delta\right) },\\ \displaystyle \bar{\boldsymbol{\chi}}_{21}^{{\rm cond}}( z,z^{\prime}) =\hat{\mathbf{z}}\hat{\mathbf{z}}\frac{\varepsilon_{\rm h}k_{\rm p}^{2}}{2\mathrm{j}k_{\rm h}}U_{21}\mathrm{e}^{-\mathrm{j}k_{\rm h}\left( z-z^{\prime}-2\delta\right) },\\ \displaystyle \bar{\boldsymbol{\chi}}_{22}^{{\rm cond}}( z,z^{\prime}) =\hat{\mathbf{z}}\hat{\mathbf{z}}\frac{\varepsilon_{\rm h}k_{\rm p}^{2}}{2\mathrm{j}k_{\rm h}}\left(\mathrm{e}^{-\mathrm{j}k_{\rm h}\left\vert z-z^{\prime}\right\vert }+U_{22}\mathrm{e}^{-\mathrm{j}k_{\rm h}\left( z+z^{\prime}-2\delta\right) }\right). \end{array} \end{eqnarray} \tag{ B.2 }$$

Two ABCs are found as generalizations of (41),

$$\begin{eqnarray} &&\begin{array}{llll} \displaystyle \left. P_{z1}^{{\rm cond}}\right\vert _{-\delta}-\left. P_{z2}^{{\rm cond}}\right\vert _{\delta}+\alpha\left( \left. \frac{\partial P_{z1}^{{\rm cond}}}{\partial z}\right\vert _{-\delta}+\left. \frac{\partial P_{z2}^{{\rm cond}}}{\partial z}\right\vert _{\delta}\right) =0,\\ \displaystyle\left. P_{z1}^{{\rm cond}}\right\vert _{-\delta}+\left. P_{z2}^{{\rm cond}}\right\vert _{\delta}+\beta\left( \left. \frac{\partial P_{z1}^{{\rm cond}}}{\partial z}\right\vert _{-\delta}-\left. \frac{\partial P_{z2}^{{\rm cond}}}{\partial z}\right\vert _{\delta}\right) =0, \end{array} \end{eqnarray} \tag{ B.3 }$$

where

$$\begin{equation} \alpha=\frac{1+U_{R}-U_{T}}{\mathrm{j}k_{\rm h}\left( 1-U_{R}+U_{T}\right) },\ \ \beta=\frac{1+U_{R}+U_{T}}{\mathrm{j}k_{\rm h}\left( 1-U_{R}-U_{T}\right) } \end{equation} \tag{ B.4 }$$

and where U₂₁ = U₁₂ = U_T and U₁₁ = U₂₂ = U_R. For PEC (U_R = 1, U_T  = 0) and PMC (U_R = −1, U_T  = 0) terminations these reduce to the previous results, and for a thin conducting interface characterized by a two-dimensional surface conductivity σ_2d as considered in [47], then

$$\begin{eqnarray} &&\begin{array}{llll} \displaystyle U_{R} =\frac{\sigma_{2\mathrm{d}}\eta_{0}}{\sigma_{2\mathrm{d}}\eta_{0}+2\sqrt {\varepsilon_{\rm h}}},\\ \displaystyle U_{T} =\frac{2\sqrt{\varepsilon_{\rm h}}}{\sigma_{2\mathrm{d}}\eta_{0}+2\sqrt {\varepsilon_{\rm h}}}. \end{array} \end{eqnarray} \tag{ B.5 }$$

Zoom In Zoom Out Reset image size

For Method I (drift-diffusion model), we can form Green's functions from (17). For example, if the source is in region 1

$$\begin{eqnarray} &&\begin{array}{llll} \displaystyle \left( \frac{\partial^{2}}{\partial z^{2}}+k_{\rm h}^{2}\right) g_{11}(z,z^{\prime}) =-\delta( z-z^{\prime}), \\ \displaystyle \left( \frac{\partial^{2}}{\partial z^{2}}+k_{\rm h}^{2}\right) g_{21}(z,z^{\prime}) =0 \end{array} \end{eqnarray} \tag{ B.6 }$$

and if the source is in region 2

$$\begin{eqnarray} &&\begin{array}{llll} \displaystyle \left( \frac{\partial^{2}}{\partial z^{2}}+k_{\rm h}^{2}\right) g_{22}(z,z^{\prime}) =-\delta( z-z^{\prime}), \\ \displaystyle \left( \frac{\partial^{2}}{\partial z^{2}}+k_{\rm h}^{2}\right) g_{12}(z,z^{\prime}) =0. \end{array} \end{eqnarray} \tag{ B.7 }$$

Enforcing the conditions (B.3) on the Green functions, analogous to (22) this leads to

$$\begin{equation} \chi_{i\mathrm{j}}^{{\rm cond}}( z,z^{\prime}) =\varepsilon_{\rm h}k_{\rm p} ^{2}~g_{i\mathrm{j}}( z,z^{\prime}) \end{equation} \tag{ B.8 }$$

and the same susceptibilities are obtained as in (B.2).