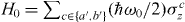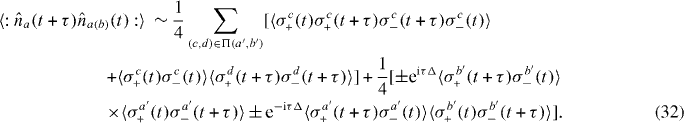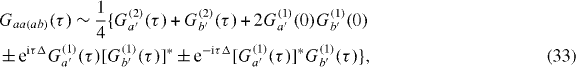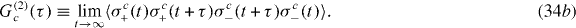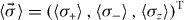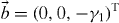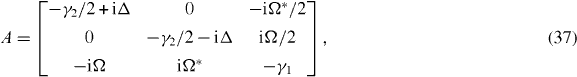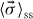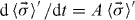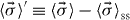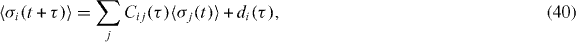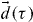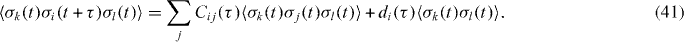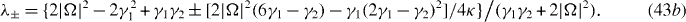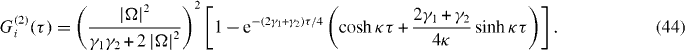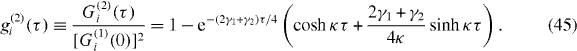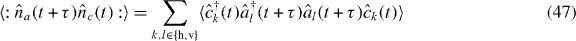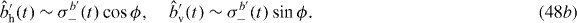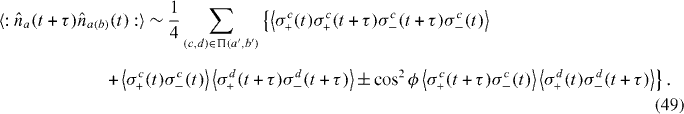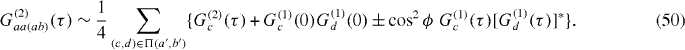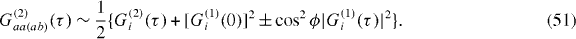Abstract
Two-photon quantum interference at a beam splitter, commonly known as Hong–Ou–Mandel interference, is a fundamental demonstration of the quantum mechanical nature of electromagnetic fields and a key component of various quantum information processing protocols. The phenomenon was recently demonstrated with microwave-frequency photons by Lang et al (2013 Nature Phys. 9 345–8). This experiment employed circuit QED systems as sources of microwave photons, and was based on the measurement of second-order cross-correlation and auto-correlation functions of the microwave fields at the outputs of the beam splitter using linear detectors. Here we present the calculation of these correlation functions for the cases of inputs corresponding to: (i) trains of pulsed Gaussian or Lorentzian single microwave photons and (ii) resonant fluorescent microwave fields from continuously driven circuit QED systems. In both cases, the signature of two-photon quantum interference is a suppression of the second-order cross-correlation function for small delays. The experiment described in Lang et al (2013) was performed with trains of Lorentzian single photons, and very good agreement with experimental data is obtained. The results are relevant not only to interference experiments using circuit QED systems, but any such setup with highly controllable sources and time-resolved detection.

Content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Hong–Ou–Mandel interference is a two-photon quantum interference effect whereby two indistinguishable photons, one in each of the two input ports of a balanced beam splitter, will always be detected to coalesce at one or the other output port of the beam splitter, but never with one photon at each output port. This interference effect diminishes as the distinguishability of the photons is increased. It was first demonstrated in 1987 using photons produced via parametric down-conversion [2]. The importance of this effect in optical implementations of quantum information processing schemes was realized later [3]. It is the basis of non-deterministic gates in linear optical quantum computation [4], it may be used for preparing maximally entangled Bell states [5], and it may be used to assess the quality of single-photon sources [6]. This has motivated further experiments, both with single sources [7, 8] and with two independent sources [9–11] of photons. In addition to these pulsed interference experiments, two-photon quantum interference using continuously driven sources of resonant fluorescent light has been demonstrated [12].
However, until the recent experiment of Lang et al [1], a demonstration of the same effect with microwave-frequency photons had been lacking. This experiment was performed using superconducting circuit QED systems [13, 14], configured as pulsed sources of single microwave photons [15–17]. This constitutes a fundamental demonstration of the quantum mechanical nature of microwave fields. Further, it is a first step in the extension of quantum information processing protocols designed for optics into the microwave domain, and offers the possibility of integration with existing quantum information processing devices based on superconducting circuits.
Following the original Hong–Ou–Mandel experiment, detailed calculations of the expected two-photon interference from atomic systems and parametric oscillators were provided [18]. A thorough treatment of time-resolved two-photon interference, accounting for experimental imperfections, was given by Legero et al [19], motivated by their group's experiments using trapped atom sources [8]. The theory of Hong–Ou–Mandel interference has also been generalized to multiport interference [20], multi-photon input states [6] and spatial multi-mode input states [21]. The effect may also be analysed using the theory of quantum measurement [22]. For the case of continuously driven sources, the expected two-photon interference where the distinguishability is introduced via a polarization degree of freedom has been determined [12].
For two-photon interference experiments at microwave frequencies there is no efficient photodetection available at present. Consequently, experiments must be performed using repeated measurements with linear detectors of long trains of single-photon pulses [16]. Also, the exquisite level of control of circuit QED sources opens up the possibility of performing such experiments using continuously driven sources with the distinguishability introduced using a frequency offset. Such sources, operating in the regime of resonant photon blockade, have already been demonstrated [23]. Here we present the calculation of the microwave field second-order auto-correlation and cross-correlation functions at the output of the beam splitter for input fields composed of trains of Gaussian photons, trains of Lorentzian photons and resonance fluorescence from detuned, continuously driven sources. These results are relevant not only to circuit QED systems and microwave fields, but to any interference experiment with highly controllable sources and time-resolved detection.
The second-order correlation functions at the output of the beam splitter are evaluated, in terms of correlation functions of input fields, in section 2. These are explicitly evaluated for both individual and trains of pulsed single-photons (Gaussian and Lorentzian) in section 3. The calculations proceed in a manner similar to those of Legero et al [19], though we generalize their calculations in a number of ways. Firstly, we consider Lorentzian (in addition to Gaussian) single photons. This is because in [1] the temporal properties of the emitted photons are mostly determined by the decay rate of the circuit QED source, rather than by additional broadening mechanisms. Secondly, we calculate the correlation functions for a train of single photons, leading to features in the calculated correlation functions at (and around) integer multiples of the pulse period. Finally, in order to make comparisons with experimental data, we subject the calculated correlation functions to filtering. The correlation functions for continuously driven sources, both without and with polarization degrees of freedom, are evaluated in section 4.
2. Output second-order correlation functions
2.1. Intensity correlation functions
Suppose that the two fields incident on the input ports of the beam splitter are described by dimensionless, time-dependent quantum fields denoted by and . Unitarity of the (balanced) beam splitter implies that the output fields, and , are then given by the Heisenberg picture evolution [24]
These fields are depicted in the Hong–Ou–Mandel interference experiment schematic of figure 1. Note that, in general, a variable phase may be included in the matrix of equation (1), though the results described here shall be independent of this phase. We are interested, primarily, in the statistics of the photons output from the beam splitter. These are described by correlation functions of the number operators of the output modes, the number operators being denoted by . Then, the quantities we seek are the normally ordered correlation functions of the output mode number operators:
with representing either (for the output intensity auto-correlation function) or (for the output intensity cross-correlation function). These correlation functions allow one to discriminate between quantum and classical fields [24]. Since the intensity of a field is proportional to the number of photons it contains, henceforth we shall refer to correlation functions of the form of equation (2) as intensity correlation functions. The term second-order correlation function shall be reserved here for functions of the difference in detection times (τ) alone, to be introduced below. The correlation functions give the same results due to the symmetry of equation (1).
Figure 1. Schematic view of Hong–Ou–Mandel interference experiment with microwave-frequency photons. Two separate circuit QED systems (denoted A and B) are employed as photon sources. The microwave fields leaking out of these systems are denoted and . They interfere at a beam splitter (BS), and the output modes from the beam splitter are denoted and . These output fields are amplified and subjected to (phase-sensitive) heterodyne detection via mixing with a local oscillator (LO). Figure reproduced from [1].
Download figure:
Standard image High-resolution imageClearly, we can obtain the intensity correlation functions of equation (2) in terms of the input fields by substituting the expressions in equation (1). The result includes 16 fourth-order moments of the time-dependent input fields. Now, if it is assumed that the sources produce separable (i.e. not entangled) fields (clearly a reasonable assumption for independent sources), the four-term cross-correlation functions of input fields may each be decomposed into products of two auto-correlation functions of the input fields. Therefore, the output intensity auto-correlation and cross-correlation functions are
where the + and − signs correspond to the auto-correlation and cross-correlation functions, respectively. Note that the summation is over the set of permutations of the input mode operators and ; that is, . The output intensity correlation functions depend on the input intensity correlation functions (first term in equation (3)), the products of the intensities of the two inputs (second term), the products of the first-order correlation functions of the two inputs (third term) and on a number of phase-dependent correlation functions of the inputs (terms four to eight).
2.2. Phase-dependent moments
For the purpose of demonstrating Hong–Ou–Mandel interference, the contributions of the fourth through to the eighth terms to the intensity correlation functions of equation (3) are neither necessary nor desirable. We will consider their contribution using the example of the fourth term, though the same arguments may be applied to the fifth through to the eighth terms.
Suppose that the fields corresponding to the input modes, and in equation (3), can be written as slowly varying fields modulating oscillations at carrier frequencies centred on ω0 and with a difference Δ, and with some relative phase offset θ: and . Accordingly, we can rewrite the fourth term in equation (3) as
There are a number of situations under which the contributions from such terms are negligible. If the inputs are single-photon pulses then the phase-dependent second moments in equation (3) will always evaluate to zero. For example, see equation (13), we can write
Even if the inputs are not single photons, the contribution of these terms may still be made to vanish by uniformly varying the relative phase θ of the two input fields over repeated runs of the experiment, and then averaging over these repeated runs. That is, for example,
where θj = 2πj/M with M being the number of measurements averaged over. Therefore, in all cases of interest to us, the phase-dependent moments will vanish and the expression in equation (3) reduces to
Here the bar over the correlation function indicates that it is to be evaluated over many runs of the experiment. Henceforth, this shall be assumed for the correlation functions quoted and we drop this notation. The output intensity correlation functions are completely determined by the input intensity correlation functions and products of the input first-order correlation functions. For the output intensity cross-correlation function, the two-photon interference is seen in the cancellation of the second and third terms at τ = 0 in equation (7). On the other hand, the second and third terms will add constructively for the output auto-correlation function at τ = 0, corresponding to photon coalescence. Whether or not this constitutes Hong–Ou–Mandel interference in the usual sense is determined by the input intensity correlation functions in the first term of equation (7). Although the preceding statements are true in general, the signature of the interference for non-zero τ will depend on the form of the input fields.
2.3. Second-order correlation functions
The output intensity correlation functions, as expressed in equations (3) and (7), are explicitly dependent on two detection times, t and t + τ. The second-order correlation functions, giving the likelihood of detecting a photon at some time τ assuming detection at time zero, may be obtained either by integrating or by taking a limit
respectively. Whether one integrates or takes a limit depends on whether the system's evolution is described in a (non-rotating) laboratory or a rotating frame. The quantities in equation (8) are conventionally referred to as second-order correlation functions [24]. Similarly, we introduce the first-order correlation functions
In the case where the second-order correlation functions are obtained by taking limits, the output second-order correlation functions follow immediately from equation (7) as
where we have introduced the short-hand notation G(2)c(τ) ≡ G(2)cc(τ). If both sources exhibit identical statistics, meaning G(1)a'(τ) = G(1)b'(τ) ≡ G(1)i(τ) and G(2)a'(τ) = G(2)b'(τ) ≡ G(2)i(τ), the output second-order correlation functions are simply
As for equation (7), the second and third terms of the second-order cross-correlation functions cancel at τ = 0, corresponding to photon interference at the beam splitter. We now consider the evaluation of these correlation functions for particular forms of the input fields.
3. Pulsed single-photon sources
3.1. Temporal modes and correlation functions
The case relevant to the experiment described in [1] is that in which each source produces a highly pure, microwave-frequency single-photon state. We shall evaluate the correlation functions of equation (7) by introducing temporal mode functions to describe these single photons. First, the time-dependent quantum fields introduced above, in general, may be represented in the frequency domain as . Then a single-photon pulse is conventionally represented using the spectral density Φ(ω), that is,
One can show, by considering the action of on the state , that the time-dependent quantum field may be represented as
is the temporal mode function of the single-photon pulse, and is the annihilation operator corresponding to this temporal mode. It is then clear that , giving the probability of the photon being detected at time t.
In the experiment of [1], there are two independent microwave-frequency sources producing highly pure single-photon states. The sources are characterized via measurements of their second-order correlation functions. We can write the beam splitter input fields (from each source) in terms of temporal mode functions as
Accordingly, the two-mode state input to the beam splitter may be written as . From equation (7), the output intensity correlation functions are
Here, as in equation (7), the potential for cancellation of the terms on the right-hand-side in the case of the intensity cross-correlation function is clear. Indeed, at τ = 0, we see that the intensity cross-correlation function vanishes irrespective of the precise form of the temporal mode functions. Since there are now no additional contributions to the output intensity cross-correlation functions, the intensity correlation function vanishes at τ = 0. This suppression is the signature of Hong–Ou–Mandel interference. On the other hand, the terms in equation (15) add constructively for the intensity auto-correlation function, indicative of photon coalescence. Of course, the form of the intensity correlation functions for non-zero τ depends on the form of the mode functions, and we evaluate this now for Gaussian and Lorentzian photons.
3.2. Single Gaussian photons
One form of mode function commonly produced by single-photon sources are Gaussian modes. For example, this is the case for trapped atom sources in which linewidth broadening mechanisms are dominant [8]. In the subsequent section we consider the case of Lorentzian mode functions, which arise naturally for circuit QED systems. Given the recently demonstrated ability to shape the waveforms of single photons [25–27], we could consider more general mode functions as well.
Two Gaussian modes, with a carrier frequency difference Δ (centred on ω0), a relative temporal offset δτ (centred on t = 0), and a common pulse width specified by σ, are described by the temporal mode functions:
Substituting equation (16) into equation (15) gives the explicit form of the output intensity correlation functions. Subsequently, integrating over the first detection time t leads to the second-order correlation functions
The total correlation probabilities, Paa and Pab, are then obtained by integrating over the detection time τ. The correlation probabilities Pcd simply give the probability of detecting one photon in mode c and one photon in mode d, for one pair of input photons, irrespective of the detection times. They are
Note that Pba = Pab and Pbb = Paa, such that , as required for a beam splitter that is assumed to be lossless. The total probability for photon coalescence at one output port is Paa + Pbb = 2Paa, while the total probability for one photon in either output port, the coincidence probability, is Pc ≡ Pab + Pba = 2Pab. The correlation probabilities may be regarded as probability distributions over the controlled parameters δτ and Δ. For indistinguishable photons (δτ = 0 and Δ = 0) the coincidence probability is Pc = 0, and for fully distinguishable photons (i.e. and/or ) we have Pc → 1/2. The coincidence probability, plotted as a function of either δτ or Δ, exhibits the classic Hong–Ou–Mandel dip [2].
3.3. Single Lorentzian photons
The same calculation may be performed for Lorentzian photons. In the experiment of [1] the temporal mode function of the released photon is determined by the decay rate of the coupled circuit QED system. Accordingly, these photons have the shape of a truncated exponential decay. Two such mode functions, with a relative temporal offset δt and a carrier frequency difference Δ, are given by
where γ is the field decay rate of the coupled system, ω0 is the frequency about which the two carrier frequencies are centred and u(...) denotes the unit step function. Note that the field decay rate is the characteristic decay rate of the electric field, in contrast to the commonly quoted (cavity) decay rate of the energy stored in the cavity. According to equation (19), the first photon (in mode a') is 'released' at t = −δt/2, while the second photon (in mode b') is released at t = + δt/2. In the frequency domain, the mode functions correspond to the spectral densities
This representation makes it clear why the exponentially decaying single-photon pulses described by equation (19) are referred to as Lorentzian photons. Of course, the mode function thus defined is unphysically sharp. The filtering effects of a finite measurement bandwidth shall be addressed below.
Substituting equation (19) into equation (15), assuming that δt > 0 and τ > 0, we find the output intensity correlation functions to be
where the upper (lower) result corresponds to the auto-correlation (cross-correlation) function. Equation (21) consists of two contributions, corresponding to different combinations of the unit step functions switching on. The first product of step functions in equation (21) switches on when both the first detection (t) is after the release of the first photon (− δt/2) and the second detection time (t + τ) is after the release of the second photon (+ δt/2). The second unit step function is switched on when the first, and therefore the second detection time (τ > 0) is after the release of the second photon. Integrating over the first detection time t leads to the output second-order correlation functions
Again, equation (22) is split into two terms, depending on whether the difference in measurement times (τ) is greater or less than the temporal delay (δt) between the release of photons from either source. Integrating over the difference in detection times τ (positive and negative) we obtain the correlation probabilities
As before, we have Pbb = Paa, Pba = Pab, , and the coincidence probability is Pc = Paa + Pbb = 2Paa. Again, these probabilities may be regarded as probability distributions over δt and Δ. If the photons are indistinguishable (δt = 0 and Δ = 0), Pc = 0, while for fully distinguishable photons (δt ≫ 1/γ and/or ), Pc → 1/2.
3.4. Trains of single photons
The experiment in [1] is performed with trains of pulsed single photons. In general, this can lead to features in the correlation functions at (and around) integer multiples of the pulse period. These are evaluated here. In order to determine the output intensity correlation functions in this case, we write the time-dependent quantum fields at the inputs as the sum of the fields corresponding to each temporal mode. For 2N + 1 photons in the pulse train we can write
with the temporal mode operator commutation relations being , where denotes an input mode lowering operator, or . The appropriate temporal mode functions for the kth photon of each input (assumed Lorentzian here) are
with tp denoting the pulse period. The Kronecker delta in the commutation relations is justified by the fact that the temporal mode functions are normalized and are approximately orthogonal in the limit that the pulse period is much greater than the pulse width. Substituting the field decompositions of equation (24) into the intensity correlation functions of equation (7) leads to
Using the assumption that the input state is separable with respect to the basis of temporal modes introduced, equation (26) reduces to
The output second-order correlation functions, G(2)aa(ab)(τ), are then obtained by integrating over the first detection time t, as in equation (8).
These correlation functions are plotted in figure 2. Note that we actually calculate circular correlation functions, meaning that we evaluate these sums for a finite pulse train, and then wrap the time index around the pulse train. This means that the peak heights at later pulse periods will be at the same height as those at earlier pulse periods, rather than showing an artificial decay in peak height that would otherwise be produced due to the finite nature of the pulse train. Furthermore, the correlation functions are normalized such that the peaks at ±ktp in G(2)ab(τ) are unity for indistinguishable photons input.
Figure 2. Output second-order (a) cross-correlation functions and (b) auto-correlation functions for trains of Lorentzian single photons input at each port of a beam splitter with pulse period tp, γ = 107 s−1 and Δ = 0. The delay of one source with respect to the other in each case is (from top to bottom in each column) δt = 0, 50 and 150 ns, with tp = 0.5 μs in each case. For indistinguishable photons, the signal in the first pulse period of the cross-correlation function is suppressed, indicating interference.
Download figure:
Standard image High-resolution imageAs expected, the signature of interference in figure 2 is the suppression of the output second-order cross-correlation function for small delays τ for indistinguishable photons (δt = 0). As the distinguishability of the photons is increased through increasing δt, one clearly sees corresponding peaks in the first repeat period. The peaks in the correlation functions at ±ktp (k an integer) exhibit side peaks at ±δt. This is easily understood: a given photon of each pair may be correlated with the first or second photon of the subsequent pair, as well as with the first or second photon of the preceding pair.
3.5. Filtered response
Integrating the intensity correlation function of equation (27) results in second-order correlation functions with the very sharp features seen in figure 2, due to the abrupt switching of the single-photon pulses described by the unit step and exponential function in equation (19). However, such features are not observed in experimental data due to filtering in the detection scheme. To facilitate comparison with experimental data, we incorporate this filtering into our calculations. The filtering is performed on the time-dependent signals obtained by the data acquisition scheme in [1], denoted by Sa(b)(t). The second-order correlation functions of the fields are obtained from the filtered version of these signals, Sfa(b)(t), given by the convolution integral
where f is a filter function in the time domain. Now the correlation functions of the output fields of interest may be obtained from the correlation functions of these measured signals, and so for the sake of calculations, we may implement the filtering directly on the temporal mode functions, that is,
The filtering in [1] was implemented as a finite-impulse-response filter [28]. For the purpose of calculations, equation (29) was implemented with a filter function representative of that done experimentally. The intensity correlation functions are then given by equation (27), evaluated using the filtered temporal mode functions of the form of equation (29). The second-order correlation functions are obtained by integrating over the first detection time t, as in equation (8). These are shown in figure 3, along with data from [1]. Very good agreement with the experimental data is obtained.
Figure 3. Output second-order (a)–(c) cross-correlation and (d) auto-correlation functions for inputs corresponding to trains of Lorentzian photons. The theory curves, including filtering as per equation (29), are shown as red lines. The experimental data obtained by Lang et al [1] are shown as blue dots. The numbers at the top right of each panel are offsets in the experimental data. The panels correspond to pulse delays (of one input with respect to the other) of (a) and (d) δt = 0 ns, (b) δt = 50 ns, and (c) δt = 150 ns. Figure adapted from [1].
Download figure:
Standard image High-resolution image4. Continuously driven sources
4.1. Introduction
Rather than assuming the circuit QED systems are configured as pulsed single-photon sources, we can assume that they are continuously driven and operated in the regime of resonant photon blockade [23]. The output microwave field from each source will exhibit sub-Poissonian and anti-bunched photon statistics [29, 30], leading to the possibility of observing Hong–Ou–Mandel interference at the beam splitter [12]. Treating only the lowest transition of the coupled circuit QED system [13], we consider the source simply as a driven quantum two-level system (TLS). The physics of each source is then essentially the physics of resonance fluorescence [31, 32], with additional dephasing included. Note that this TLS is in fact formed from the coupled system, and is therefore not the 'qubit' typically employed for superconducting quantum information processing.
We denote the TLS transition frequency by ωc (where c denotes the corresponding input mode, either a' or b'), and assume that it is subject to driving by a resonant monochromatic, large-amplitude microwave field. Each system is described, in a frame rotating with respect to H0 = (ℏωc/2)σz, by the Hamiltonian where Ω is the driving strength. The coupling of the TLS to its environment may be fully described, in the Markovian white noise approximation, by damping at a rate γ1 and dephasing at a rate γp. Accordingly, the evolution of the TLS density operator ρ may be given in the form of a Lindblad master equation [24] as
where is the so-called dissipative superoperator. Note that in this model each source is fully characterized by the parameters γ1,γp,Ω and ωc.
4.2. Output correlation functions
As in the case of pulsed sources, the quantities of interest are the second-order correlation functions of the microwave fields at the outputs of the beam splitter. The master equation (30) facilitates the evaluation of correlation functions of TLS operators, and from the theory of atomic spontaneous emission [32], we know that the output field will be proportional to the TLS lowering operator
where c denotes the input mode a' or b'. The output intensity correlation functions then follow from equation (3), to within a constant factor, by making the substitution in equation (31). Rather than explicitly evaluating the coefficient in equation (31), we shall ultimately calculate normalized (field) correlation functions for which the coefficients will cancel.
First we calculate the output correlation functions in terms of the input correlation functions. Suppose that the TLS transition frequencies are ω0 ± Δ/2 (for the sources corresponding to the input modes a' and b', respectively), and that we are working in an interaction picture with respect to . Then, from equations (7) and (31), the output intensity correlation functions (to within a constant factor) are
Note that the validity of this expression depends on averaging out explicitly phase-dependent contributions by randomizing the relative drive phases over repeated runs of the experiment, as discussed in section 2.2. Taking the limit t → ∞ of equation (32) we have the output second-order correlation functions
where the correlation functions on the right-hand-side are now TLS correlation functions:
Again, the second and third terms in the output cross-correlation function of equation (35) cancel at τ = 0. For non-zero τ, the interference is oscillatory, an effect sometimes referred to as a quantum beat [8].
4.3. Resonant photon blockaded inputs
Now we turn to the evaluation of the input TLS correlation functions. The system of equations for the expectations of TLS operators are readily calculated from equation (30). They are commonly referred to as the optical Bloch equations, and may be expressed as the inhomogeneous system [24]
where we have introduced the vector of expectations of TLS (Pauli) operators, . The inhomogeneity is given by , and the system matrix is given by
where we have also introduced the total dephasing rate, γ2 ≡ γ1 + 2γp. One can find the steady-state solution of equation (36), , and subsequently recast equation (36) as the homogeneous system, where . Now the time-dependent solution of the homogeneous system may be obtained by diagonalization, and subsequently the solution to equation (36) may be written in the form
where we have introduced the notation
The form of the solution in equation (38) is amenable to application of the quantum regression theorem [32]. In particular, for an element of the solution in equation (38), we can write
where i∈{ + ,−,z}, the summation index j runs over this set, and Cij(τ) and di(τ) denote elements of the matrix C(τ) and vector , respectively. The quantum regression theorem allows us to evaluate correlation functions as
The TLS correlation functions in equation (32) are obtained using equation (41) and the algebraic properties of Pauli operators.
According to equation (35), the output second-order correlation functions are fully determined by the input first-order and second-order correlation functions. We can write out G(1)i(τ) and G(2)i(τ), which are well-known results from the physics of resonance fluorescence [32]. For the first-order correlation functions we have
where we have introduced the notation
It is more common to quote the normalized result, which is
Of course, this is a normalized TLS correlation function. Here, we shall normalize the output field correlation functions by imposing the requirement that they asymptotically approach unity.
Now the output second-order correlation functions are given by equation (35), using the results in equations (42) and (44). They are shown in figure 4. As expected, the interference effect is observed in the suppression of the cross-correlation function for small delays τ, while introducing distinguishability through the frequency difference Δ leads to an oscillation in the observed interference for non-zero τ.
Figure 4. Output second-order (a) cross-correlation functions and (b) auto-correlation functions for each source continuously driven in the regime of resonant photon blockade. Again, interference is observed in the suppression of the cross-correlation function for small τ. Photon distinguishability may be introduced through a carrier frequency difference Δ, which leads to an oscillation in the observed interference.
Download figure:
Standard image High-resolution image4.4. Photon polarization
In the continuously driven case just considered, photon distinguishability can only be introduced through a difference in the carrier frequencies. An alternative approach, relevant in the trapped atom case [12] or in a three-dimensional circuit QED architecture [33], is to introduce distinguishability through a polarization degree of freedom. To treat this problem, we decompose the time-dependent fields into their (horizontal and vertical) polarization components
where the subscripts h and v denote the horizontally and vertically polarized components of the field, respectively. Generalizing the expression of equation (2) to include polarization indices, and then summing over these indices, we can write the output intensity correlation functions as
with c representing either output mode (a or b), as before.
Now we take the components of the input fields to be related to the TLS lowering operators by
The photon distinguishability, and therefore the presence or absence of two-photon quantum interference, is determined by the relative polarization angle ϕ. For ϕ = 0, the photons at either input are indistinguishable, and the second and third terms in equation (49) cancel for the cross-correlation function, corresponding to interference. For the auto-correlation function, the second and third terms will add constructively, indicative of photon coalescence. For ϕ = π/2, the photons at either input are fully distinguishable, and the last term in equation (49) makes no contribution. Now taking the limit t → ∞, as per equation (8), yields the second-order correlation functions
Under the additional assumption that the two sources (polarization aside) have identical properties, meaning G(2)a'(τ) = G(2)b'(τ) ≡ G(2)i(τ) and G(1)a'(τ) = G(1)b'(τ) ≡ G(1)i(τ), then we find
As for equation (49), the dependence of photon interference on the relative polarization angle ϕ is clear. These output correlation functions are shown in figure 5. Clearly, access to a polarization degree of freedom allows one to smoothly interpolate between the cases of distinguishable and indistinguishable photons in the continuously driven case.
Figure 5. Output second-order (a) cross-correlation and (b) auto-correlation functions for each source continuously driven in the regime of resonant photon blockade, for a range of polarizations of one input with respect to the other (ϕ = 0°,45°,90°). Here the carrier frequencies of both inputs are assumed to be the same. For indistinguishable photons (ϕ = 0°), the interference signature of a suppressed cross-correlation function for small τ is observed. As the indistinguishability (i.e. relative polarization) is increased, the interference effect is reduced.
Download figure:
Standard image High-resolution image5. Conclusions
Two-photon quantum interference at a beam splitter is observed in the suppression of the output second-order cross-correlation function for small detection delay times. In the case of pulsed single-photon sources, this quantity may be integrated over all detection delay times to reproduce the classic Hong–Ou–Mandel dip in the coincidence probability at the output. Accounting for a train of photons input leads to sidebands on the second-order correlation functions around integer multiples of the pulse period, while the inclusion of a finite detection bandwidth broadens the sharp features in the correlation functions that would otherwise be observed. The second-order correlation functions calculated show very good agreement with the experimental data in [1]. In the case of continuously driven sources, photon distinguishability may be introduced through a difference in carrier frequency or via a polarization degree of freedom. In the former case, an oscillation in the quantum interference is expected. These results can be expected to be useful in future interference experiments with well-controlled sources and time-resolved detection.
Acknowledgments
This work was supported by NSERC, CIFAR and the Alfred P Sloan Foundation. CL, CE and AW were supported by the European Research Council (ERC) through a Starting Grant and ETHZ. We thank Tom Stace, Andy Ferris and Clemens Müller for valuable discussions.




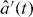
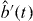
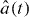
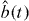

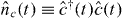
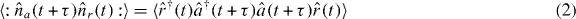
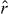
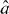
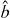


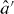
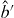
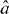

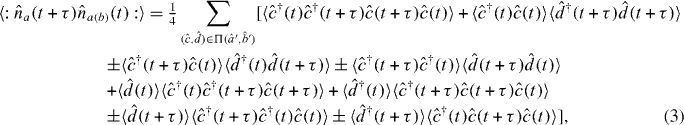
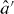
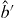
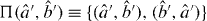
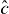
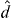

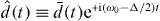
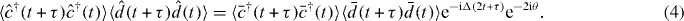
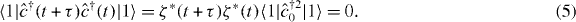

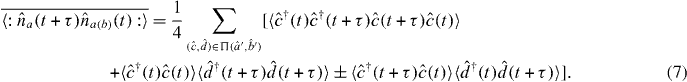
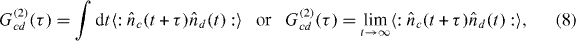

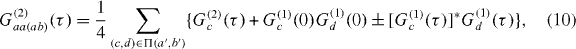
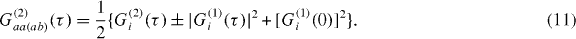

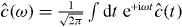

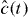


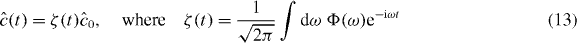



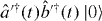
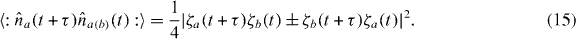
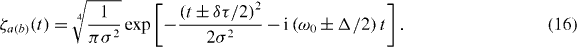

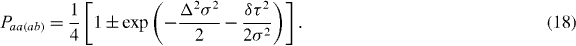
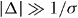

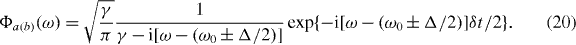

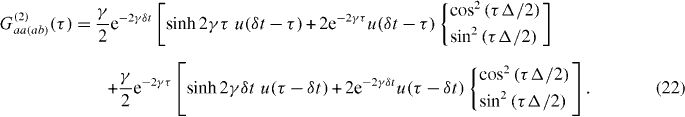

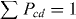
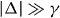

![$[ \hat {c}'_{0k}, \hat {c}'^\dagger _{0k'} ] = \delta _{kk'}$](https://content.cld.iop.org/journals/1367-2630/15/10/105025/revision1/nj478091ieqn34.gif)
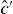
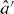
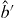
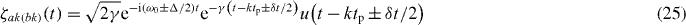

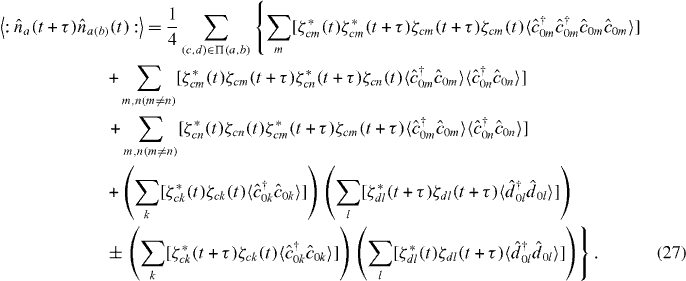




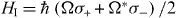
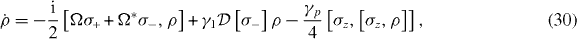
![$\mathcal {D}[ \skew3\hat{A} ] \equiv \skew3\hat{A}\rho \skew3\hat{A}^\dagger - \frac {1}{2} \skew3\hat{A}^\dagger \skew3\hat{A} \rho - \frac {1}{2} \rho \skew3\hat{A}^\dagger \skew3\hat{A}$](https://content.cld.iop.org/journals/1367-2630/15/10/105025/revision1/nj478091ieqn39.gif)