The power of noisy fermionic quantum computation

One interesting route towards universal quantum computation is through the realization of Majorana fermion qubits. Such Majorana fermion qubits, encoded in pairs of non-local fermionic zero-energy modes, are believed to be present in various quantum systems such as a ν = 5/2 fractional quantum Hall system, p_x + ip_y superconductors and recently proposed topological insulator/superconductor and semiconducting nanowires/superconductor structures (see [1] for a review). Braiding operations on such Majorana fermion qubits can implement certain topologically protected gates, namely single-qubit Clifford gates [2, 3]. A system of Majorana fermions initially prepared in a fermionic Gaussian state (see definition below) and undergoing braiding operations (which are a subset of non-interacting fermion operations⁴) can be classically efficiently simulated if it is not supplemented with additional resources. Universal quantum computation can be achieved if this supplement consists, for example, of either (i) gates which use quartic interaction between Majorana fermions [4] or (ii) a quartic parity measurement [5] or (iii) two ancillae in certain special states |a₄〉 and |a₈〉, involving respectively 4 and 8 Majorana fermions [2]. The advantage of the last realization is that even when these ancillae are noisy, one can purify them using braiding operations. This distillation of clean ancillae states, which are then used to implement the required gates for universality, is similar to the magic-state-distillation scheme by which Clifford group operations are used to distil almost noise-free single qubit π/8 ancillae from noisy ones [6]. For the model of computation based on braiding of Majorana fermions, distilled |a₄〉 states give the ability to perform single qubit π/8 gates, while distilled |a₈〉 states allow for the implementation of CNOT gates [2]. The noise threshold for such distillation schemes, which assume that the distilling gates and operations are noise-free, is of the order of tens of per cent, which makes them attractive. But one can also ask the converse question: how noisy are these ancillae allowed to be before one can efficiently classically simulate the entire quantum computation? This question has been addressed in the case of noisy single-qubit magic states and noisy single-qubit gates [7–9].

In this paper, we consider a similar question for computation using Majorana fermions. It is not hard to show (see section 5) that if the noisy ancillae are convex mixtures of Gaussian fermionic states and the computation involves only non-interacting fermionic operations, one can still classically efficiently simulate such a quantum computation. Hence we set out to develop a criterion that determines whether a state is a convex mixture of Gaussian fermionic states in section 3. We find such a criterion in the form of a hierarchy of semidefinite programs, similarly as for separable states [10]. Unfortunately, the computational effort for implementing this general criterion is too large to give decisive information for our problem of interest and we have recourse to an analytical approach for the noisy |a₈〉 ancilla in section 4. Even though our general criterion is not immediately useful for the problem at hand, its generality and similarity to separability criteria makes it interesting in itself.

Our work is different from previous work on criteria which determine whether a fermionic state with a fixed number of fermions has a single Slater determinant or whether a fermionic state can be written as a convex combination of states with a single Slater determinant [11, 12]. The important distinction is that we fix only the parity of the fermionic state and not the number of fermions. Our goal is to extend the class of Gaussian fermionic states in a natural way, by considering states which can be written as convex combinations of Gaussian states. We call such states convex-Gaussian or 'having a Gaussian decomposition'. Even though physical states have a fixed number of fermions, Gaussian fermionic states are important approximations to physically non-trivial states, such as the superconducting BCS state. Our criterion thus intends to separate Gaussian states, and convex combinations thereof, from fermionic states with a richer structure which cannot be simply viewed as states in which fermions are paired⁵. Note that the question of having a Gaussian decomposition is also different from the question of pairing that is analyzed in [14]: Gaussian fermionic states can be paired while single Slater determinant states cannot. We hope that our results of separating convex-Gaussian states from fermionic states with a richer structure may lead to tools for understanding ground states of interacting fermion systems beyond mean-field theory.

We consider a system of m fermionic modes, with the corresponding creation (a^†_k) and annihilation (a_k) operators (k = 1,...,m), respecting the Fermi–Dirac anti-commutation rules, {a_j,a_k} = 0 and {a_j,a^†_k} = δ_jkI. For systems in which fermionic parity is conserved, it is more convenient to use the 2m Majorana fermion operators defined as c_2k−1 = a_k + a^†_k and c_2k = −i(a^†_k − a_k). The operators {c_i}^2m_i=1 are Hermitian, traceless and form a Clifford algebra $\mathcal {C}_{2m}$ with {c_j,c_k} = 2δ_jkI.⁶

Any Hermitian operator $X\in {\mathcal {C}}_{2m}$ that can be written as the linear combination of products of an even number of Majorana operators is called an even operator, i.e.

$$\begin{equation} X=\alpha_0 I +\sum_{k=1}^{m} {\rm i}^k \sum_{1 \leqslant a_1 < a_2 < \cdots < a_{2k} \leqslant 2m} \alpha_{a_1,a_2,\ldots,a_{2k}} c_{a_1} c_{a_2} \ldots c_{a_{2k}}, \end{equation} \noindent \tag{ 1 }$$

where the coefficients α₀ and α_{a1,a2,...,a2k} are real, for (c_a1c_a2···c_a2k)^† = (−1)^kc_a1c_a2···c_a2k. The parity of the number of fermions is conserved by the action of an even operator X as X commutes with the fermionic number-parity operator $C_{\mathrm { all}}={\rm i}^{m} c_1 c_2 \ldots c_{2m} = \prod _{i=1}^m(I -2 a_i^\dagger a_i)$. Thus the projector onto a pure state |ψ〉 with fixed parity is an even fermionic operator, while |ψ〉 has eigenvalues C_all = ± 1 depending on whether the parity of the number of fermions in |ψ〉 is odd or even.

Given an even state $\varrho \in {\mathcal {C}}_{2m}$, the correlation matrix M is a 2m × 2m real, anti-symmetric matrix with elements

$$\begin{equation} M_{ab} := \frac{{\rm i}}{2} {\rm Tr} (\varrho[c_a, c_b]),\quad {\rm with}\; a,b=1,\ldots, 2m. \end{equation} \noindent \tag{ 2 }$$

Real, anti-symmetric matrices such as M can be brought to block-diagonal form by a real orthogonal transformation R∈SO(2m), i.e.

$$\begin{equation} M= R \;\bigoplus_{j=1}^m \left(\begin{array}{@{}cc@{}} 0 & \lambda_j \\ -\lambda_j & 0 \end{array} \right) R^{\mathrm{T}}. \end{equation} \noindent \tag{ 3 }$$

Let us now define fermionic Gaussian states. Fermionic Gaussian states ϱ are even states of the form $\varrho =K \exp (-{\mathrm { i}} \sum _{i \neq j} \beta _{ij} c_i c_j)$ with a real anti-symmetric matrix β_ij and normalization K. Hence Gaussian fermionic states are ground states and thermal states of non-interacting fermion systems. One can block-diagonalize β and re-express ϱ in standard form as

$$\begin{equation} \varrho=\frac{1}{2^m} \prod_{k=1}^m \chi_k, \quad {\rm where}\; \chi_k=I+{\rm i} \lambda_k \tilde{c}_{2k-1} \tilde{c}_{2k},\, \end{equation} \noindent \tag{ 4 }$$

where $\tilde {c}=R^{\mathrm {T}} c$ with R block-diagonalizing the matrix β_ij. The coefficients λ_j (which can be expressed in terms of the eigenvalues of β_ij) will lie in the interval [ − 1,1]. For Gaussian pure states, λ_j∈{ − 1,1} so that M^TM = I, while for Gaussian mixed states M^TM < I. In the theory of Gaussian fermionic states, a special role is played by those unitary transformations which map Gaussian states onto Gaussian states. These are the transformations generated by Hamiltonians of non-interacting fermionic systems, i.e. Hamiltonians which are quadratic in Majorana fermion operators. In this paper, we will refer to these unitary transformations as fermionic linear optics (FLO) transformations, as they, similarly as for bosonic linear optics transformations, have the property that

$$\begin{equation} U c_i U^{\dagger}=\sum_{j} R_{ij} c_j, \end{equation} \noindent \tag{ 5 }$$

where U is an FLO transformation and R∈SO(2m). Hence the transformations which block-diagonalize M (or β) are FLO transformations. Note that C_all is invariant under any unitary FLO transformation U, as UC_all = C_allU.

It is clear from the standard form, equation (4), that a fermionic state is fully determined by its correlation matrix M. The expectation of higher-order correlators for a Gaussian fermionic state are efficiently obtained by virtue of Wick's theorem

$$\begin{equation} {\rm Tr}(\varrho\, c_{a_1} c_{a_2}\ldots c_{a_{2k}}) = {\rm i}^{-k} {\rm Pf}(M|_{a_1,\ldots, a_{2k}}), \end{equation} \noindent \tag{ 6 }$$

where M|_a1,...,a2p is the sub-matrix of M which contains only the elements M_jk with j,k = a₁,...,a_2p and Pf(.) is the Pfaffian⁷.

Their efficient description (2) combined with the possibility to efficiently evaluate the expectation value of observables (6) makes fermionic Gaussian states a valuable tool for approximating ground states, thermal states or dynamically generated states using (generalized) Hartree–Fock methods of interacting fermion systems, see e.g. [13, 15–17]. Their concise representation together with equation (5) also allows for an efficient classical simulation of quantum computations that employ only FLO operations and are initialized with Gaussian states [18–21].

Given all the applications of Gaussian states, it is natural to try to enlarge this set of states to form a convex set, in analogy with extending product states to separable states. A first observation in this direction is that mixed Gaussian states are straightforward convex mixtures of pure Gaussian states. This is easily seen using the standard form (4), i.e. any Gaussian state can be written as $\varrho =\prod _{k=1}^m \chi _k/2^m$ with χ_k = I + i(2p_k − 1)c_2k−1c_2k = p_k(I + ic_2k−1c_2k) + (1 − p_k)(I − ic_2k−1c_2k), where 0 ⩽ p_k ⩽ 1 (by setting p_k = 1/2 we obtain the state I/2^m). However, the convex mixture of two Gaussian states is, in general, not a Gaussian state [22, 23]. This motivates the following definition:

Definition 1 An even density matrix $\varrho \in {\mathcal {C}}_{2m}$ is convex-Gaussian iff it can be written as a convex combination of pure Gaussian states in ${\mathcal {C}}_{2m}$, i.e. $\varrho =\sum _i p_i \sigma _i$ where σ_i are pure Gaussian states, p_i ⩾ 0 and $\sum _i p_i=1$.

Remark 1. Since every even state in ${\mathcal {C}}_{2m}$ is defined by 2^2m − 1 real coefficients, as is clear from equation (1) fixing the normalization α₀ = 1/2^m, Carathéodory's theorem guarantees that for any convex-Gaussian state there exists a Gaussian decomposition with at most 2^2m pure Gaussian states.

Remark 2. There is both similarity and difference between the set of separable states and the set of convex-Gaussian states. For example, for separable states local unitary transformations captured by O(m) parameters relate the extreme points of the set, whereas for convex-Gaussian states the extreme points are the pure Gaussian states which are related by FLO transformations, captured by O(m²) parameters. Note that the pure states σ_i in decomposition of a convex-Gaussian state will typically have a correlation matrix M(σ_i) which is block-diagonal in a different {c_i} basis. If we were to restrict ourselves to convex combinations of Gaussian states which are in standard form using one and the same set {c_i}, we would obtain a convex set isomorphic to the set of separable states diagonal in the classical bit-string basis.

We will now prove that for systems of 1,2 or 3 fermionic modes, all pure even states are Gaussian (a different proof of this result can be found in [24]). From this observation it is then immediate that any even state $\varrho \in {\mathcal {C}}_{2m}$, with m = 1,2,3, is convex-Gaussian. In order to prove this result we start with a useful known lemma, reproduced here for completeness, which shows that any fermionic even density matrix has a correlation matrix with eigenvalues in the complex [ − i,i] interval.

Lemma 1. The antisymmetric correlation matrix M of any even density matrix $\varrho \in {\mathcal {C}}_{2m}$ has eigenvalues ±iλ_k with λ_k∈[ − 1,1] and k∈{1,...,m}. We have M^TM ⩽ I with equality if and only if ϱ is a Gaussian pure state.

Proof. We present two proofs. The correlation matrix of an even density matrix is an antisymmetric matrix, and hence it can be block-diagonalized as in equation (3). Its eigenvalues are thus ±iλ_k and λ_k∈[ − 1,1], as from equation (2) λ_k is the expectation of the Hermitian operator ${\mathrm { i}} \tilde {c}_{2k-1} \tilde {c}_{2k}$ which has ±1 eigenvalues. We can also prove the lemma by using a dephasing approach introduced in [25]. We provide this alternative proof as it clearly shows that M^TM = I iff ϱ is a pure Gaussian state, and because we later use elements of this proof in proposition 1. Let $\varrho \in {\mathcal {C}}_{2m}$ be any density matrix and let {c_i}^2m_i=1 be the set of Majorana fermions in which M is block-diagonal (if the choice for {c_i} is not unique, pick one). Define the FLO transformation U_k, k = 1,...,m, as

$$\begin{eqnarray} &&\fl U_k c_{2k} U_k^{\dagger}=-c_{2k},\quad U_k c_{2k-1} U_k^{\dagger}=-c_{2k-1}, \quad U_k c_i U_k^{\dagger}=c_i,\quad \forall i\neq 2 k,\quad 2k-1.\qquad \end{eqnarray} \tag{ 7 }$$

Note that the FLO transformation U_k induces an orthogonal transformation R_k that leaves the correlation matrix M of ϱ invariant. Let $\varrho _k =\frac {1}{2}(\varrho _{k-1} +U_k \varrho _{k-1} U^\dagger _k)$, with ϱ₀ = ϱ. The iteration in k has the effect of dephasing ϱ in the eigenbasis of each ic_2k−1c_2k. Thus ϱ_m is a density matrix which contains only the mutually commuting operators ic_2k−1c_2k, and hence its eigendecomposition involves the eigenstates of these operators which are Gaussian pure states. Note that ϱ_m is not necessarily a Gaussian state, but its eigenstates are Gaussian pure states, each of which has correlation matrix block-diagonal in the same basis. This implies that the correlation matrix M is that of a Gaussian mixed state. Note that the dephasing procedure can only increase the entropy of ϱ. Therefore, if M^TM = I at the end of this procedure, then the state at the end of the procedure, ϱ_m, must be a pure Gaussian state. By the same token, ϱ at the beginning of the procedure (with the same M^TM = I) must be pure Gaussian. Thus M^TM = I iff ϱ is a pure Gaussian state.   □

Proposition 1. Any even pure state $| \psi \rangle \langle \psi |\in {\mathcal {C}}_{2m}$ for m = 1,2,3 is Gaussian.

Proof. The statement is trivial for m = 1. Consider m = 2 and observe that when we block-diagonalize its correlation matrix, any even pure state can written as some linear combination of I, quadratic terms ic_2k−1c_2k and C_all. The dephasing procedure in the proof of lemma 1 leaves any such even density matrix invariant—note that the operator C_all is invariant under FLO transformations. As the output is always convex-Gaussian, the input state was a pure Gaussian state. The proof for m = 3 follows the same structure as for m = 2, but employs the additional observation that C_all|ψ〉〈ψ| = ± |ψ〉〈ψ| for even pure states. Any pure state density matrix $| \psi \rangle \langle \psi |\in {\mathcal {C}}_6$, when written in the basis in which its correlation matrix is block-diagonal, can be expressed as $| \psi \rangle \langle \psi |=\alpha I+\beta C_{\mathrm { all}}+ {\rm i}\sum _k \gamma _k c_{2k-1} c_{2k} +\sum _{i < j < k < l} \eta _{ijkl} c_i c_j c_k c_l$. The condition that C_all|ψ〉〈ψ| = ± |ψ〉〈ψ| implies that the quartic terms only have paired correlators c_2k−1c_2k: this is because C_all interchanges the quartic and quadratic terms. Thus |ψ〉〈ψ| has quartic terms which only involve commuting operators c_2k−1c_2k. As argued in the proof of lemma 1, |ψ〉〈ψ| is then a convex mixture of pure Gaussian states, and the result follows.   □

As for separable states [26–28], the volume of convex-Gaussian states is non-zero for any m: any state $\varrho \in {\mathcal {C}}_{2m}$ is convex-Gaussian if it is 'close enough' to the maximally mixed state I/2^m, which is Gaussian. The following lemma proves this, using arguments similar to those in [27]:

Theorem 1. For every even state $\varrho \in {\mathcal {C}}_{2m}$ there exists a sufficiently small  > 0 such that ϱ = ϱ + (1 − )I/2^m is convex-Gaussian.

Proof. Consider the set $\{\sigma (\vec {\lambda },\pi )\}$ of pure Gaussian states, with each $\sigma (\vec {\lambda },\pi ) \in {\mathcal {C}}_{2m}$ defined as

$$\begin{equation} \sigma(\vec{\lambda}, \pi) = \frac{1}{2^m} \prod_{k=1}^m (I +{\rm i} \lambda_k c_{\pi(2k-1)}c_{\pi(2k)}), \end{equation} \tag{ 8 }$$

where $\vec {\lambda } \in \{-1,1\}^m$ and π∈S⁺_2m, with S⁺_2m the set of permutations with positive signature (these correspond to SO(2m) rotations of the correlation matrix, i.e. FLO operations). There are (2m)!/m! pure states in this set and we will show that they form an over-complete basis for ${\mathcal {C}}_{2m}$. We prove this by showing that any Hermitian ϱ can be written as

$$\begin{equation} \varrho=\sum_{(\vec{\lambda},pi)} w_{(\vec{\lambda},\pi)} \sigma(\vec{\lambda},\pi)-c \frac{I}{2^m}, \end{equation} \tag{ 9 }$$

where $w_{(\vec {\lambda },\pi )}\geqslant 0$ and c ⩾ 0. Furthermore, we can write

$$\begin{equation*} \frac{I}{2^m} = \frac{m!}{(2m)!} \sum_{\vec{\lambda},\pi} \sigma(\vec{\lambda}, \pi). \end{equation*}$$

If we find the decomposition in equation (9) with a certain c (which one could try to minimize in our construction of the decomposition), it then follows immediately that $\frac {1}{1+c}\varrho +\frac {c}{1+c} \frac {I}{2^m}$ is convex-Gaussian. Taking $\epsilon =\frac {1}{1+c}$ we obtain our result. One could in principle upper bound c as a function of m. Equation (9) can be proved by considering how to express a single correlator α_a1,...,a2kc_a1c_a2···c_a2k in terms of Gaussian states and I. Let us call the subset {a₁,...,a_2k} = S and the coefficient α_a1,...,a2k = α. Let C_S = c_a1c_a2...c_a2k. We will use Gaussian mixed states $\xi (\vec {\lambda }, \pi ) = \frac {1}{2^m} \prod _{k=1}^m (I +{\mathrm { i}} \lambda _k c_{\pi (2k-1)}c_{\pi (2k)})$ where λ_i∈[ − 1,1]; such states can in turn be expressed as convex mixtures of pure states $\sigma (\vec {\lambda },\pi )$ for λ_i∈{ − 1,1} as in equation (8). We have

$$\begin{equation} {\rm i}^k {\rm Tr} \,C_{S} \xi(\vec{\lambda}, \pi)=\Pi_{k:\pi(2k-1), \pi(2k) \in S}\lambda_k. \end{equation} \tag{ 10 }$$

By choosing λ_k∈{ − 1,1,0} we can make sure that (i) $|\alpha | \xi (\vec {\lambda }, \pi )=w_{\vec {\lambda },\pi } \xi (\vec {\lambda },\pi )$ has the correct expectation α for the correlator C_S (note that the sign of λ_k can be chosen to fit the sign of α) and (ii) $\xi (\vec {\lambda },\pi )$ has no higher-order correlators (by choosing some λ_k = 0). The state $\xi (\vec {\lambda },\pi )$ will then also have lower-order non-zero correlators C_S' for S'⊆S, including S' = ∅ corresponding to I. Thus we repeat the procedure with these various lower-order correlators, i.e. we represent them as a Gaussian mixed state $\xi (\vec {\lambda },\pi )$ plus additional correlators corresponding to subsets of S'. Proceeding in this way, we remove all correlators except I and end up expressing $\alpha C_S=\sum _{\vec {\lambda },\pi } w_{(\vec {\lambda },\pi )} \xi (\vec {\lambda },\pi )- \beta I$ for $\beta = 2^{-m}\sum _{\lambda ,\pi } w_{\lambda ,\pi }$. This procedure is probably far from optimal, i.e. gives rise to a large c. One can optimize this by applying the procedure to a density matrix ϱ from which we repeatedly take out Gaussian mixed states, i.e. ϱ → ϱ − wξ, which remove the current highest-order correlator and the Gaussian state ξ is chosen to be the one with minimum (but non-negative) weight Tr wξ.   □

Now that we have established the essential features of the set of convex-Gaussian states, the natural question that follows is how to determine whether a state has a decomposition in terms of Gaussian pure states. As for separability, there are two sides to this question. One is to find a Gaussian decomposition, a problem which is likely, as in the entanglement case, to be computationally hard in general. The reverse question is to find a criterion which establishes that a state is not convex-Gaussian. Note that the goal is to find a criterion which acts linearly on the pure Gaussian states, so that it can naturally be extended to convex mixtures thereof. The Hermitian operator $\Lambda =\sum _{i=1}^{2m} c_i \otimes c_i \in {\mathcal {C}}_{2m} \otimes {\mathcal {C}}_{2m}$, introduced in [19], will be useful in this context as it has been shown to lead to a necessary and sufficient criterion for a state to be Gaussian:

Lemma 2 An even state $\varrho \in {\mathcal {C}}_{2m}$ is Gaussian iff [Λ,ϱ⊗ϱ] = 0.

The operator Λ has the important property of being invariant under U⊗U where U is any FLO transformation. The action of Λ on ϱ⊗ϱ can be appreciated by considering the trace norm ∥.∥₁ of the positive operator Λ(ϱ⊗ϱ)Λ:

$$\begin{eqnarray} \Vert \Lambda (\varrho \otimes \varrho) \Lambda\Vert_1&=&\sum_{a,b=1}^{2m} {\rm Tr}[(c_a\otimes c_a)(\varrho\otimes \varrho)(c_b\otimes c_b)]\nonumber\\ &=& 2m-\sum_{a \neq b} \left( {\rm Tr} \, {\rm i} c_a c_b \varrho\right)^2\nonumber\\ &=&2m- \sum_{a, b} (M_{ab})^2=2m-{\rm Tr} \,M^{\mathrm{T}} M, \end{eqnarray} \tag{ 11 }$$

where M is the correlation matrix of the state ϱ. For a pure Gaussian state ϱ = σ, we have M^TM = I, implying that Λ(σ⊗σ) = 0. For a mixed Gaussian state or non-Gaussian state M^TM < I, see lemma 1, and hence ∥Λ(ϱ⊗ϱ)Λ∥₁ > 0. These observations are collected in the following corollary.

Corollary 1. For an even state $\varrho \in {\mathcal {C}}_{2m}$, Λ(ϱ⊗ϱ) = 0 iff ϱ is a pure Gaussian state.

Corollary 1 says that the state of two copies of pure Gaussian states is contained in the null space of the operator Λ. In lemma A.1, we will prove that the null space of the operator Λ is contained in the symmetric subspace $\bf{Sym}^2(\mathbbm{ C}^{2^m})$ spanned by vectors |ψ〉 which are invariant under the SWAP operator P, i.e. |ψ〉 = P|ψ〉. In particular, the null space of Λ is spanned by states |ψ,ψ〉 where ψ is Gaussian, while the symmetric subspace is spanned by |ϕ,ϕ〉 for any ϕ. We will call the null-space of Λ the Gaussian-symmetric subspace. As Λ is a sum of mutually commuting Hermitian operators c_i⊗c_i with μ_i = ± 1 eigenvalues, the projectors on the eigenstates are $P_{\vec {\mu }}=\frac {1}{2^{2m}}\prod_{i=1}^{2m} ( I + \mu _i c_i \otimes c_i)$ with eigenvalue $\sum _{i=1}^{2m} \mu _i$ of Λ. Hence the Gaussian-symmetric subspace is spanned by $2m \choose m$ orthogonal eigenvectors $P_{\vec {\mu }}$ with the property that $\sum _i \mu _i=0$. Clearly, the dimension of the Gaussian-symmetric subspace ${2m \choose m}$ is smaller than the dimension of the symmetric subspace $\bf{Sym}^2(\mathbbm{ C}^{2^m})$, which is ${2^m+1 \choose 2}$ for any m ⩾ 1.

In [10, 29], the authors established a series of tests for separability based on the existence of a symmetric extension of any separable state. The usefulness of these tests relies on the fact that they correspond to semi-definite programs, which for small numbers of extensions can be implemented numerically. Furthermore, these tests are complete, in the sense that an entangled state does not have a symmetric extension to an arbitrary number of parties in the extension. Here we formulate a similar series of extension tests which are all passed by convex-Gaussian states, but non-convex-Gaussian states fail in some of them. Our criterion is based on the following simple observation: let a density matrix $\varrho \in {\mathcal {C}}_{2m}$ be convex-Gaussian, i.e. we can write $\varrho =\sum _i p_i \sigma _i$ with σ_i pure Gaussian states, then there exists a symmetric extension $\varrho _{\mathrm { ext}} \in {\mathcal {C}}_{2m}^{\otimes n}$, namely $\varrho _{\mathrm { ext}}= \sum _i p_i \sigma _i^{\otimes n}$, which is annihilated by Λ acting on any pair of tensor-factors, and Tr_2,...,n−1ϱ_ext = ϱ. This immediately leads to the following feasibility semi-definite program:

Program 1. 

$$\begin{array}{ll} {\rm Input:}&\varrho \in {\mathcal {C}}_{2m} \ {\rm and \ an \ integer} \ n\geqslant 2\\ {\rm Body:}&{\rm Is \ there \ a} \ \varrho_{\rm ext} \in {\mathcal {C}}_{2m}^{\otimes n}\\ &\begin{array}{@{}ll} {\rm s.t.}&{\rm Tr}_{2,\ldots, n}\varrho_{ext}=\varrho\\ &{\rm Tr }\,\varrho_{\rm ext}=1\\ &\Lambda^{k,l} \varrho_{ext}=0, \forall k \neq l\\ &\varrho_{\rm ext}\geqslant 0 \end{array}\\ {\rm Output:}& \verb+yes+ \ ({\rm provide} \ \varrho_{\rm ext}) \ {\rm or} \ \verb+no+ \end{array} \noindent$$

As there exists an isomorphism between ${\mathcal {C}}_{2m}^{\otimes n}$ and ${\mathcal {C}}_{2m,n}$ (see the explicit map in [19] for ${\mathcal {C}}_{2m}\otimes {\mathcal {C}}_{2m}$ and ${\mathcal {C}}_{4m}$), one could alternatively express program 1 as an extension of ϱ to a physical system with 2m, n Majorana fermions.

Note that we do not need to enforce any permutation or Bose symmetry on the extension⁸ because of the following. By lemma A.1 in the appendix, the null space of Λ_k,l is spanned by vectors |ψ,ψ〉_k,l where |ψ〉 is any pure Gaussian state. Thus the intersection of null spaces of all Λ_k,l is spanned by vectors |ψ^⊗n〉 where ψ is a pure Gaussian state, which are vectors in the symmetric subspace of n parties. As ϱ_ext lies in this null space, it will thus be Bose symmetric [30], i.e. πϱ_ext = ϱ_ext, where π is any permutation in S_n.

It is easy to see that any state ϱ has a Bose-symmetric extension; hence the stronger constraint imposed by Λ is crucial. We say that a state ϱ has a Gaussian-symmetric extension if there exists an n for which program 1 returns yes. An explicit construction of the SDP for the case n = 2 is given in appendix B, and some numerical results are discussed in the following section. Here we will prove that only convex-Gaussian states have a Gaussian-symmetric extension to an arbitrary number of spaces, thus showing that these criteria form a complete hierarchy for deciding membership in the set of convex-Gaussian states.

Theorem 2. An even state $\varrho \in {\mathcal {C}}_{2m}$ has a Gaussian-symmetric extension to an arbitrary number of parties if and only if ϱ is convex-Gaussian.

Proof. One direction is immediate, and has already been alluded to in the formulation of the SDP. Assume that ϱ is convex-Gaussian, i.e. $\varrho =\sum _i p_i \sigma _i$ where σ_i are pure Gaussian states and {p_i} is a probability distribution. Then the extension $\varrho _{\mathrm { ext}}= \sum _i p_i \sigma _i^{\otimes n}$ has the property that Λ^k,lϱⁿ_ext = 0, where Λ^k,l acts on the tensor factors k and l by corollary 1.

To prove the other direction, we will invoke the quantum de Finetti theorem [30]. Let ϱⁿ_ext ⩾ 0 be the extension of ϱ to ${\mathcal {C}}_{2m}^{\otimes n}$ such that Λ^k,lϱⁿ_ext = 0 and Tr_2,...,nϱⁿ_ext = ϱ. Using lemma A.1 this shows that ϱⁿ_ext is Bose-symmetric. Let ϱⁿ_1,2 be the reduced density matrix for the first two tensor factors, i.e. ϱⁿ_1,2 = Tr_3,...,nϱⁿ_ext. Then theorem II.8 in [30] tells us that

$$\begin{equation} \left\Vert\varrho_{1,2}^n-\sum_a \gamma_a(n) \tau_a(n) \otimes \tau_a(n)\right\Vert_1 \leqslant \epsilon_m(n), \end{equation} \tag{ 12 }$$

with $\epsilon _m(n)=\frac {4 \times 2^m}{n}$. Here $\tau _a(n)\in {\mathcal {C}}_{2m}$ are density matrices and γ_a(n) are probabilities summing up to 1. We have

$$\begin{eqnarray} \left\Vert\, \Lambda \sum_a \gamma_a(n) \tau_a(n) \otimes \tau_a(n) \Lambda\,\right\Vert_1&=& \left\Vert\,\Lambda (\varrho_{1,2}^n-\sum_a \gamma_a(n) \tau_a(n) \otimes \tau_a(n)) \Lambda\,\right\Vert_1\nonumber\\\ms\ms &\leqslant&\left\Vert\Lambda\right\Vert_1^2 \epsilon_m(n) \equiv \tilde{\epsilon}_m(n) , \end{eqnarray}\noindent \tag{ 13 }$$

with $\Vert\Lambda\Vert_1^2=4(m+1)^2 {2m \choose m+1}^2$. For fixed m, in the limit n → ∞ the upper bounds $\epsilon _m(n), \tilde {\epsilon }_m(n) \rightarrow 0$, and by equation (12) $\varrho _{1,2}^n \rightarrow \sum _a \gamma _a(n) \tau _a(n) \otimes \tau _a(n)$. In this limit, equation (13) implies, using the observation in equation (11), that for each a either γ_a(n) → 0 or τ_a(n) converges to a Gaussian pure state. Hence for n → ∞ the state ϱⁿ_1,2 converges to a convex mixture of two copies of Gaussian pure states, and its reduced density matrix converges to a convex-Gaussian state.   □

Remark 3. More direct proofs (by establishing a Gaussian-fermionic de Finetti theorem directly using the existence of an extension in the Gaussian-fermionic subspace) and quantitative versions of this result should be possible.

Note that convex-Gaussian states always have a symmetric extension which is separable in relation to all tensor factors. This property can be used to provide an alternative formulation of the necessary and sufficient criterion for a state to be convex-Gaussian:

Proposition 2. A state $\varrho \in {\mathcal {C}}_{2m}$ is convex-Gaussian iff there exists an extension $\varrho _{\mathrm { ext}}\in {\mathcal {C}}_{2m}\otimes {\mathcal {C}}_{2m}$ that is a feasible solution to program 1 —input ϱ and n = 2—with the additional constraint that ϱ_ext is separable between the tensor factors.

Proof. As before one direction is immediate. For the other direction, assume that there exists a state $\varrho _{\mathrm { ext}}\in {\mathcal {C}}_{2m}\otimes {\mathcal {C}}_{2m}$ which is separable, i.e. it is of the form $\varrho _{\mathrm { ext}}= \sum _i p_i \tau _i \otimes \varsigma _i$, with {τ_i} and {ς_i} sets of density matrices in ${\mathcal {C}}_{2m}$ and {p_i} a probability distribution. From the constraint Λϱ_ext = 0, it follows that

$$\begin{eqnarray} 0&=&{\rm Tr} \Lambda \left( \sum_i p_i \tau_i \otimes \varsigma_i\right) \Lambda \nonumber \\\ms\ms &=&2m-\sum_i p_i \sum_{a \neq b}({\rm Tr}\; {\rm i} c_a c_b \tau_i)({\rm Tr} \; {\rm i} c_a c_b \varsigma_i)\nonumber\\\ms\ms &=&2m-\sum_i p_i {\rm Tr} M^{\mathrm{T}}(\tau_i) M(\varsigma_i), \end{eqnarray}\noindent \tag{ 14 }$$

where the notation M(ϱ) represents the correlation matrix of the state ϱ.

Using the triangle and Cauchy–Schwartz inequalities, we have

$$\begin{eqnarray} 2m &=& \left|\sum_i p_i {\rm Tr} M^{\mathrm{T}}(\tau_i) M(\varsigma_i)\right|\nonumber\\ &\leqslant& \sum_i p_i \sqrt{{\rm Tr} M^{\mathrm{T}}(\tau_i) M(\tau_i)}\sqrt{ {\rm Tr} M^{\mathrm{T}}(\varsigma_i) M(\varsigma_i)}. \end{eqnarray} \tag{ 15 }$$

From lemma 1, it follows that ${\mathrm { Tr}} M^{\mathrm {T}} M=2\sum _{i=1}^m |\lambda _i|^2 \leqslant 2m$ with equality iff M is the correlation matrix of a pure Gaussian state. In order for equality to hold in equation (15), each τ_i (and ς_i) must thus be a pure Gaussian state and therefore $\varrho =\sum _i p_i \tau _i$ is convex-Gaussian.   □

Including this extra separability constraint in program 1 breaks its SDP structure—checking separability can in itself be cast as an SDP [29], but this would give a nested SDP structure to the program deciding if a state is convex-Gaussian. A direct semi-definite relaxation of this criterion is obtained by employing the partial-transposition test for separability [31, 32], leading to the following SDP:

Program 2. 

$$\begin{array}{@{}ll@{}} {\rm Input:} & \varrho \in {\mathcal {C}}_{2m} \\ {\rm Body:} & {\rm Is \ there} \ \varrho _{\mathrm { ext}} \in {\mathcal {C}}_{2m}\otimes {\mathcal {C}}_{2m} \\ & {\rm s.t.}\quad{\rm Tr}_{2}\varrho _{{\rm ext}}=\varrho \\ & \hphantom{s.t.\quad}{\rm Tr}\varrho _{{\rm ext}}=1 \\ & \hphantom{s.t.\quad}\Lambda \varrho _{{\rm ext}}=0 \\ & \hphantom{s.t.\quad}\varrho _{{\rm ext}}\geqslant 0 \\ & \hphantom{s.t.\quad}\varrho ^{T_{1}}_{{\rm ext}}\geqslant 0 \\ {\rm Output:} & {\tt yes} \ ({\rm provide} \ \varrho _{{\rm ext}}) \ {\rm or} \ {\tt no} \\ \end{array} \noindent$$

Here T₁ is the transposition map on the first tensor factor. As for the previous program, a negative answer means that the state is not convex-Gaussian. For the converse, it is likely that the PPT criterion together with the constraint that the extension lives in the Gaussian-symmetric subspace is not sufficient to enforce separability (e.g. there exist symmetric bound-entangled states [33]); hence a positive answer is non-decisive, but we leave this as an open question.

As mentioned in the introduction, one way to turn ν = 5/2 topological quantum computation into a universal quantum computation scheme is to assume that one has access to the auxiliary states $| a_4 \rangle \in {\mathcal {C}}_4$ and $| a_8 \rangle \in {\mathcal {C}}_8$, as shown in [2]. In this section, we want to assess the amount of noise that can be added to these extra resources before they turn convex-Gaussian. From proposition 1, we know that any pure state in ${\mathcal {C}}_4$ is Gaussian, and therefore any noisy version of |a₄〉 is convex-Gaussian. We thus concentrate on the state |a₈〉 when undergoing depolarization. We consider the state

$$\begin{equation} \varrho_{a_8}(p) = (1-p)| a_8 \rangle \langle a_8 | + p I/16, \end{equation} \noindent \tag{ 16 }$$

with 0 ⩽ p ⩽ 1 and

$$\begin{equation} | a_8 \rangle \langle a_8 |=\textstyle\frac{1}{16}(I+S_1)(I+S_2)(I+S_3)(I+Q), \end{equation} \noindent \tag{ 17 }$$

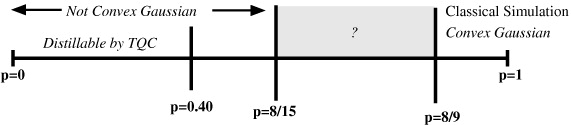
with S₁ = −c₁c₂c₅c₆, S₂ = −c₂c₃c₆c₇, S₃ = −c₁c₂c₃c₄ and Q = c₁c₂c₃c₄c₅c₆c₇c₈. Bravyi [2] has shown that ϱ_a8(p) can be distilled for p < 40% (corresponding to the parameter ₈ defined in [2] equal to 0.38). We would like to determine the noise threshold p_* such that ρ_a8(p ⩾ p_*) is convex-Gaussian. Note that ρ_a8 is Gaussian only for p = 1. The results in this section are summarized in figure 1.

Zoom In Zoom Out Reset image size

In order to give a lower bound on p_* we implemented the SDP program 1 for fixed n = 2 (see appendix B) with the aid of the cvxopt library for Sage [34]. The numerical results indicate that p_* ⩾ 0.25, as it is always possible to find a Gaussian-symmetric extension for ϱ_a8(p) with n = 2 for noise rates above this value. Our implementation of the feasibility SDP takes approximately one day for each value of p in a computer with 2.3 GHz processor, and takes about 30 GB of RAM memory. The implementation of the SDP with an additional PPT condition on the extension is likely to provide stronger results, but it is more computationally intensive. Given these limitations, we provide an alternative analysis of the properties of ϱ_a8(p) using the notion of witnesses: Hermitian operators which have expectation values in a restricted range (e.g. non-negative for all Gaussian states) whereas expectation values on non-Gaussian states can extend beyond this range (e.g. be negative). The existence of such witness operators is guaranteed by the fact that they represent hyperplanes separating the convex-Gaussian states from all even Hermitian operators in ${\cal C}_{2m}$ (in addition, similarly as in [29], witnesses could be constructed based on a negative output of feasibility SDP).

Clearly, such Hermitian witness operators, say W, should include terms which are quartic or higher-weight correlators, as the expectation value of quadratic Hamiltonians only depends on the correlation matrix of a state. For ϱ_a8(p) the obvious choice for such a witness operator is W = |a₈〉〈a₈|, for which ${\mathrm { Tr}} W \varrho _{a_8}(p)=1-\frac {15p }{16}$. Let us understand how we can bound $\min _{\psi _g} {\mathrm { Tr}} W | \psi _g \rangle \langle \psi _g |=|\langle \psi _g | a_8 \rangle |^2$ where ψ_g is any Gaussian pure state. We will use the fact that the correlation matrix of |a₈〉 is the null matrix, i.e. for all Majorana operators c_i,c_j, Tr c_ic_j|a₈〉〈a₈| = 0, which follows directly from equation (17). We will now prove that $|\langle \psi _g | a_8 \rangle |^2 \leqslant \frac {1}{2}$ which shows that for $p < \frac {8}{15} \approx 0.53$, the state ϱ_a8(p) is not convex-Gaussian. The following proposition proves our claimed bound and can be intuitively understood by interpreting the state |a₈〉 as a maximally entangled state while Gaussian states are product states:

Proposition 3. For all Gaussian pure states |ψ_g〉, we have $|\langle \psi _g | a_8 \rangle |^2 \leqslant \frac {1}{2}$.

Proof. Let c₁ and c₂, c₁c₂ = −c₂c₁, be two arbitrary Majorana fermion operators, from a complete set {c_2k−1,c_2k}⁴_k=1 (note the SO(8) freedom in choosing these). Let |x〉 denote an eigenvector of the mutually commuting operators ic₁c₂, ic_2k−1c_2k for k = 2,...,4 where the bits (0 or 1) of x label the eigenvalues (resp. +1 and −1) of these operators. The Gaussian states |x〉 form a basis for the four-fermion (or four-qubit) space; hence we can write $| a_8 \rangle =\sum _{x \in \{0,1\}^4} \alpha _x | x \rangle$ with $\sum _{x} |\alpha _x|^2=1$. Then

$$\begin{equation} {\rm Tr}\, {\rm i} c_1 c_2 | a_8 \rangle \langle a_8 |=\sum_{y\in \{0,1\}^3} |\alpha_{0y}|^2-\sum_{y \in \{0,1\}^3} |\alpha_{1y}|^2=0. \end{equation}\noindent \tag{ 18 }$$

This, together with normalization, implies that $\sum _y |\alpha _{0y}|^2=\sum _y |\alpha _{1y}|^2=\frac {1}{2}$, hence for all y, |α_0y|² and |α_1y|² are less than or equal to 1/2.   □

A tighter bound than the one in proposition 3 cannot be excluded if one uses further properties of the state |a₈〉—such a tighter bound would lead to a reduction of the gray area in figure 1.

To give an upper bound on p_* we construct explicit Gaussian decompositions of ϱ_a8(p) for large values of p. To do this we consider a subset of the convex-Gaussian states that share some key properties with ϱ_a8(p), namely: (i) zero correlation matrix, and (ii) only a small fraction of all possible correlators has non-zero coefficients.

To exploit these symmetries we define three types of states:

$$\begin{equation} \varrho_i({\lambda}) = \textstyle\frac{1}{2} \left(\varrho_{M_i({\lambda})} + \varrho_{M_i(- {\lambda})}\right), \end{equation} \tag{ 19 }$$

where ϱ_Mi(λ), for i = 1,2,3, is the Gaussian state generated by the correlation matrix M_i(λ), with λ∈[ − 1,1]⁴, and M_i(λ) assumes one of the following three forms:

$$\begin{eqnarray*} M_1({\lambda}) = \bigoplus_{i=1}^{4}\left( \begin{array}{@{}cc@{}} 0 & \lambda_i\\ -\lambda_i & 0 \end{array}\right),\\ M_2({\lambda}) = \bigoplus_{i=1}^{2}\left( \begin{array}{@{}cccc@{}} 0 & 0 & \lambda_i & 0\\ 0 & 0 & 0 & \lambda_{i+1}\\ -\lambda_i & 0 & 0 & 0\\ 0 & -\lambda_{i+1} & 0 & 0 \end{array}\right), \\ M_3({\lambda}) = \bigoplus_{i=1}^{2} \left(\begin{array}{@{}cccc@{}} 0 & 0 & 0 & \lambda_i \\ 0 & 0 & \lambda_{i+1} & 0\\ 0 & -\lambda_{i+1} & 0 & 0\\ -\lambda_{i} & 0 & 0 & 0 \end{array}\right). \end{eqnarray*}$$

By construction, these states are convex-Gaussian, have null correlation matrix, and any convex combination of them has an expansion in terms of Majorana operators with non-vanishing coefficients only on the same correlators as ϱ_a8(p). The aim is to find for which p's it is possible to decompose ϱ_a8(p) as a convex sum of these types of convex-Gaussian states.

In order to describe the convex hull of these states, first note that M₂ and M₃ are related to M₁ by permutations (different choices of pairings):

$$\begin{eqnarray*} &&M_2(\lambda)= \left(P_{12}\oplus P_{12}\right) M_1(\lambda) \left(P_{12}\oplus P_{12}\right)^{\mathrm{T}}, \\ &&M_3(\lambda)= \left(P_{13}\oplus P_{13}\right) M_1(\lambda) \left(P_{13}\oplus P_{13}\right)^{\mathrm{T}}, \end{eqnarray*}$$

where

$$\begin{equation} P_{12}=\left(\begin{array}{@{}cccc@{}} 1 & 0 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1 \end{array}\right),\quad P_{13}=\left(\begin{array}{@{}cccc@{}} 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 1\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0 \end{array}\right). \end{equation} \tag{ 20 }$$

Given that the transformation connecting the correlation matrices is formed by the direct sum of identical permutations, this transformation is in SO(8)—one always gets the signature of the permutation squared, and therefore the corresponding determinant is always 1. Rotations in SO of the correlation matrix induce unitary transformations on the level of the states [19]: P₁₂↦U₂, P₁₃↦U₃. Bearing in mind this connection among the three classes of states above, we now determine the extreme points of the set of type 1 states.

Lemma 3 Let $\overline {{\mathcal {S}}}_1 = {\mathrm { conv}}\{\varrho _1(\lambda ) | \lambda \in [-1,1]^4\}$. Then the extreme points of $\overline {{\mathcal {S}}}_1$ are given by

$$\begin{eqnarray*} &&\phi_1(x) \doteq \textstyle\frac{1}{2} \left( | x \rangle \langle x | + | \neg x \rangle \langle \neg x |\right),\end{eqnarray*}$$

with x∈{0,1}⁴ and ¬x is the bitwise negation of x.

Proof. It follows immediately from the expansion of the state ϱ₁(λ):

$$\begin{eqnarray} \varrho_1(\lambda) &=&\frac{1}{2^5}\sum_{x\in \{0,1\}^4} \left[ \prod_{k=1}^4 \left(1 - (-1)^{x_k}\lambda_k\right) + \prod_{k=1}^4 \left(1 - (-1)^{x_k}(-\lambda_k)\right) \right] | x \rangle \langle x |\nonumber\\ &=&\frac{1}{2^5} \sum_{x\in \{0,1\}^4} \prod_{k=1}^4 \left(1 - (-1)^{x_k}\lambda_k\right)\left( | x \rangle \langle x | +| \neg x \rangle \langle \neg x |\right)\nonumber\\ &=&\frac{1}{2^4} \sum_{x\in \{0,1\}^4} \prod_{k=1}^4 \left(1 - (-1)^{x_k}\lambda_k\right)\phi_1(x). \end{eqnarray} \noindent \tag{ 21 }$$

   □

Defining in a similar fashion $\overline {{\mathcal {S}}}_2$, $\overline {{\mathcal {S}}}_3$, ϕ₂(x) and ϕ₃(x), we can then define the convex hull of any convex combination of the three types of states as $\overline {{\mathcal {S}}} = {\mathrm { conv}}\{\overline {{\mathcal {S}}}_1,\overline {{\mathcal {S}}}_2,\overline {{\mathcal {S}}}_3\}$. More explicitly,

$$\begin{equation} \overline{{\mathcal{S}}}= \left\{\sum_{i=1}^3 \sum_{x=0}^7 \gamma_i(x) \phi_i(x) \Big | \; \gamma_i(x)\geqslant 0, \sum_{i=1}^3 \sum_{x=0}^7 \gamma_i(x)=1\right \}, \end{equation} \tag{ 22 }$$

where the summation in x is to be carried out over its binary expansion in three bits.

The problem now reduces to determining for which values of p∈[0,1] the linear system $\varrho _{a_8}(p) = \sum _{i=1}^3 \sum _{x=0}^7 \gamma _i(x) \phi _i(x)$, with {γ_i} a probability distribution, has a solution. Simple inspection shows that such a Gaussian decomposition is always possible whenever p ⩾ 8/9 ≈ 0.89, which is then an upper bound on p_*.

In contrast to bosonic linear optics, quantum computations based on FLO can be efficiently simulated by a classical computer even when augmented by measurements of fermionic number operators [18–20]. The simulation relies on the following facts

• (i)  
  Efficient encoding of Gaussian states—a Gaussian state of 2m Majorana fermions is fully described by its correlation matrix M, with O(m²) elements.
• (ii)  
  FLO transformations map Gaussian states onto Gaussian states, with an efficient update rule—every FLO transformation $V\in {\mathcal {C}}_{2m}$ induces a rotation R∈SO(2m) on the Majorana operators space, $V c_i V^\dagger = \sum _{j=1}^{2m} R_{ij} c_j$. This, in turn, induces the map M↦RMR^T on the 2m × 2m correlation matrix, and this update can be evaluated in O(m³) steps.
• (iii)  
  Efficient read-out of measurement probability distributions—via Wick's theorem (6) the probability of measuring the population in fermionic modes can be done efficiently, as the Pfaffian of a 2m × 2m matrix can be evaluated in O(m³). Furthermore, number operator measurements project Gaussian states onto Gaussian states.

With these three ingredients, the evolution of any initial Gaussian state can be efficiently followed by a classical computer at any time in the computation, and the output distribution can be exactly evaluated. In [19, 21], the allowed transformations in (ii) were extended to noisy Gaussian maps. These are completely positive channels, not necessarily FLO unitaries, that map Gaussian states onto Gaussian states, and as such still admit efficient classical simulation.

Our results imply that if p ⩾ 8/9, ϱ_a8(p) is convex-Gaussian and this allows for the classical simulation of the computation as follows. Given a noise strength p ⩾ 8/9, one finds the decomposition of ϱ_a8(p) in $\overline {{\mathcal {S}}}$, by solving the linear system $\varrho _{a_8}(p)=\sum _{i=1}^3\sum _{x=0}^7 \gamma _{i}(x) \phi _i(x)$—this has to be done only once for a fixed p. As each ϕ_i(x) is in itself a convex sum of two pure Gaussian states, this leads to a decomposition of ϱ_a8(p) in terms of at most 48 pure Gaussian states. Let p_i be the probability associated with the ith pure Gaussian state in such a decomposition. Then, whenever a state ϱ_a8(p) is requested in the computation, one samples from {p_i} and chooses the corresponding pure Gaussian state. From this point onwards, the simulation follows the scheme summarized in (i), (ii) and (iii) above.

The results in figure 1 leave some gaps in our understanding, in particular about the precise value of p_*. In order to improve the lower bounds on p_* one could consider distillation processes beyond the restricted set of braiding operations, but that still map Gaussian states onto Gaussian states, leaving thus the set of convex-Gaussian states unchanged. The distillation protocol of depolarized GHZ₄ states, which are isomorphic to ϱ_a8(p), proposed by Dür and Cirac at first sight suggests that our classical simulation threshold is tight, as it can distil a perfect GHZ₄ provided that p < 8/9. Nevertheless, their protocol uses non-FLO operations, as it assumes that one can locally create the GHZ₄ and uses distilled two-qubit maximally entangled pairs for distribution. The protocol devised by Murao et al in [35] directly distils GHZ₄ from depolarized copies of it for p < 0.7328. Despite the fact that this direct approach seems more related to our question, it employs gates that are not immediately translated into braiding operations or even to FLO transformations. Although the choice to distil via braiding operations is physically motivated—due to their topological protection—a different distillation threshold from FLO operations would suggest that either Bravyi's distillation protocol can be improved to higher depolarizing noise rates or that there exists a 'transition zone' in which the computation by braiding of Majorana fermions is neither quantumly universal nor can be efficiently simulated classically.

We acknowledge fruitful discussions with Akimasa Miyake, Ronald de Wolf, Sergey Bravyi and Volkher Scholz. We also thank Maarten Dijkema for IT support. Fd-M is supported by the Vidi grant 639.072.803 from the Netherlands Organization for Scientific Research (NWO).

Inspired by [36], we define a 'FLO twirl' as the map ${\cal S}(\varrho )=\frac {1}{{\mathrm { Vol}}(U)}\int _{\rm FLO} \mathrm {d}U U \otimes U \varrho U^{\dagger } \otimes U^{\dagger }$ where $\int _{\mathrm { FLO}} \mathrm {d}U$ is defined by taking the Haar measure over the real orthogonal matrices R induced by U. The map ${\cal S}(\varrho )$ is normalized such that it is trace-preserving.

Lemma A.1. The projector onto the null space of $\Lambda =\sum _i c_i \otimes c_i$ is $\Pi _{\Lambda =0}={2m \choose m} {\cal S}(| 0,0 \rangle \langle 0,0 |)$ where |0〉 is a (Gaussian) vacuum state with respect to some set of annihilation operators a_i. Thus the states |ψ,ψ〉 where ψ is a pure fermionic Gaussian state span the null space of Λ, which implies that the null space of Λ is a subspace of the symmetric subspace.

Proof. In order to prove that $\Pi _{\Lambda =0}={2m \choose m} {\cal S}(| 0,0 \rangle \langle 0,0 |)$, we note that both the lhs and the rhs are U⊗U-invariant where U is any FLO transformation. Thus instead of considering whether ${\mathrm { Tr}} X \Pi _{\Lambda =0}={\rm Tr}(X {2m \choose m} {\cal S}(| 0,0 \rangle \langle 0,0 |))$ for any X, we can just consider the trace with respect to invariant objects ${\cal S}(X)$. It can be shown that Λⁱ for i = 0,1,2,...,2m (and linear combinations thereof) are the only invariants under the group U⊗U where U is FLO transformation [37].⁹ Clearly, ${\mathrm { Tr}} \Lambda ^i {2m \choose m} {\cal S}(| 0,0 \rangle \langle 0,0 |)=0={\rm Tr} \Lambda ^i \Pi _{\Lambda =0}$ for all i ≠ 0 while ${\rm Tr} \Pi_{\Lambda=0}={2m \choose m}$ fixes the overall prefactor. Having established the form of the projector, it follows directly that the states |ψ,ψ〉 for any Gaussian ψ span the null space. (Assume that this is false and hence a state in the null space |χ〉 = |χ_in〉 + |χ_out〉 where |χ_in〉 is in the span of |ψ,ψ〉 while |χ_out〉 is w.l.o.g. orthogonal to any |ψ,ψ〉. We have Π_Λ=0|χ〉 = |χ〉 while ${2m \choose m} {\cal S}(| 0,0 \rangle \langle 0,0 |) | \chi \rangle =| \chi _{\mathrm { in}} \rangle$ arriving at a contradiction.) As |ψ,ψ〉 for Gaussian pure states ψ span the null space, and P|ψ,ψ〉 = |ψ,ψ〉 with P the SWAP operator, the null space is a subspace of the symmetric subspace.   □

Recall the series of tests constructed to detect if a state $\varrho \in {\mathcal {C}}_{2m}$ is not convex-Gaussian:

$$\begin{array}{@{}ll@{}} {\rm Input:} & \varrho \in {\mathcal {C}}_{2m} \ {\rm and \ an \ integer} \ n\geqslant 2 \\ {\rm Body:} & {\rm Is \ there} \ \varrho _{\mathrm { ext}} \in {\mathcal {C}}_{2m}^{\otimes n} \\ & {\rm s.t.}\quad\pi \varrho _{{\rm ext}}\pi ^{\dagger}=\varrho _{{\rm ext}}, \forall \pi \in S_{n} \\ & \hphantom{s.t.\quad}{\rm Tr}_{2,\ldots ,n}\varrho _{{\rm ext}}=\varrho \\ & \hphantom{s.t.\quad}{\rm Tr}\varrho _{{\rm ext}}=1 \\ & \hphantom{s.t.\quad}\Lambda ^{k,l}\varrho _{{\rm ext}}=0,\forall k\not= l \\ & \hphantom{s.t.\quad}\varrho _{{\rm ext}}\geqslant 0 \\ {\rm Output:} & {\tt yes} \ ({\rm provide} \ \varrho _{{\rm ext}}) \ {\rm or} \ {\tt no} \\ \end{array} \noindent$$

Note that we have explicitly kept the permutation-symmetry constraint in this program.

In this appendix, we convert this problem into a feasibility semi-definite programming problem. To do that we must show that the above problem can be cast as the standard form of SDPs, namely

$$\begin{array}{@{}ll@{}} {\rm minimize} & {\bf c}^{{\rm T}}{\bf x} \\ {\rm subject \ to} & F_0 + \sum _i x_i F_i \geqslant 0 \\ & A{\bf x}={\bf b} \\ \end{array} \noindent$$

where ${\mathbf {x}} \in \mathbbm{ R}^d$ is the unknown vector to be optimized over, c is a given vector in $\mathbbm{ R}^d$, and {F_i}_i=0,...,d are given symmetric matrices. For the equality constraint, $A \in \mathbbm{ R}^{p\times d}$ is a given matrix, with rank(A) = p, and ${\mathbf {b}} \in \mathbbm{ R}^p$. The restriction on the rank of A demands that the linear system has at least one solution, and all the rows are linearly independent.

The first step is to associate an Hermitian operator M_j with each term i^kc_a1c_a2···c_a2k in the expression (1). The set {M_j}_{0⩽j⩽2^2m−1−1} spans all the even Hermitian operators of ${\mathcal {C}}_{2m}$. Then any state $\varrho \in {\mathcal {C}}_{2m}$ can be written as

$$\begin{equation} \varrho = \sum_{k=0}^{2^{2m -1}-1} \alpha_k M_k, \end{equation} \tag{ B.1 }$$

and we choose M₀ = I.

For definiteness, in what follows we restrict ourselves to the case n = 2. Extensions to larger n follow the same structure and can be immediately constructed. That said, a general extension on ${\mathcal {C}}_{2m}\otimes {\mathcal {C}}_{2m}$ can be written as

$$\begin{equation} \varrho_{\rm ext} = \sum_{i,j=0}^{2^{2m -1}-1} \beta_{ij}M_i\otimes M_j, \end{equation} \tag{ B.2 }$$

with the coefficients $\beta _{ij}\in \mathbbm{ R}$ to be fixed by the constraints of our problem. The symmetry constraint can be taken directly into the parameterization of ϱ_ext by imposing that

$$\begin{equation} \varrho_{\rm ext} = \sum_{i=0}^{2^{2m -1}-1} \beta_{ii}M_i\otimes M_i + \sum_{0\leqslant i<j\leqslant 2^{2m -1}-1} \beta_{ij}(M_i\otimes M_j + M_j\otimes M_i). \end{equation} \tag{ B.3 }$$

At this point, the initially 2^4m−2 coefficients of ϱ_ext are reduced to 2^2m−2(1 + 2^2m−1).

The imposition that Tr₁(ϱ_ext) = ϱ further demands that

$$\begin{equation} 2^m \sum_{j=0}^{2^{2m-1}-1} \beta_{0,j} M_j = \sum_{j=0}^{2^{2m-1}-1} \alpha_j M_j. \end{equation} \tag{ B.4 }$$

Therefore, β_0,j = α_j/2^m. In this way, a further 2^2m−1 coefficients are determined, and thus there remain 2^2m−3(2^2m − 2) free parameters. Note that the normalization of ϱ_ext is already guaranteed as long as Tr(ϱ) = α₀ = 1.

The question of whether there exists an assignment of the remaining free coefficients respecting the last two constraints can be immediately posed as a feasibility SDP:

$$\begin{array}{@{}ll@{}} {\rm minimize} & 0 \\ {\rm subject \ to} & \varrho _{{\rm ext}}\geqslant 0 \\ & \Lambda \varrho _{{\rm ext}}=0. \\ \end{array} \noindent$$

Forgetting for the moment that the correlators are in general complex, a direct correspondence with the SDP standard form can be done as follows:

$$\begin{eqnarray} &&F_0 \rightarrow \beta_{0,0} M_0\otimes M_0 + \sum_{j=1}^{2^{2m-1}-1}\beta_{0,j}(M_0\otimes M_j + M_j\otimes M_0), \end{eqnarray} \tag{ B.5 }$$

$$\begin{eqnarray} &&F_i \rightarrow \left\{\begin{array}{@{}l@{}} M_j\otimes M_j, \;\; 1\leqslant j \leqslant 2^{2m-1}-1,\\ M_j\otimes M_k + M_k\otimes M_j, \;\; 1\leqslant j< k\leqslant 2^{2m-1}-1, \end{array}\right. \end{eqnarray} \noindent \tag{ B.6 }$$

with x = ({β_j,j}_{1⩽j⩽2^2m−1−1},{β_j,k}_{1⩽j<k⩽2^2m−1−1})^T.

The equality constraint then reads

$$\begin{equation} \sum_{i=1}^{2^{2m -3}(2^{2m}-2)} x_i \Lambda F_i = -\Lambda F_0. \end{equation} \noindent \tag{ B.7 }$$

This can be cast in the form Ax = b, by writing A = ([ΛF_i]_{1⩽i⩽2^2m−3(2^2m−2)}) and b = −[ΛF₀]. The notation [G] means a column matrix constructed by stacking each column of G below each other.

To finish the construction we must take into account that we are possibly dealing with complex values. To do that we employ the following well-known result.

Lemma B.1. Let $Z=Z^\dagger \in \mathbbm{ C}^{d\times d}$. Then Z ⩾ 0 iff ${\mathcal {T}}(Z) =\left (\begin {array}{@{}cc@{}} \mathrm {Re}(Z) & -\mathrm {Im}(Z)\\ \mathrm {Im}(Z) & \mathrm {Re}(Z) \end {array}\right )$.

Proof. (⇒) Let z = x + iy be an eigenvector of Z with eigenvalue λ. Then it is easy to see that (x,y)^T is an eigenvector of ${\mathcal {T}}(Z)$ with eigenvalue λ.

(⇐) By the same token, let (x,y) be an eigenvector of ${\mathcal {T}}(Z)$ with eigenvalue λ. Then z = x + iy is an eigenvector of Z with eigenvalue λ.   □

The final dimension of each F_i is then 2^2m+1 × 2^2m+1, and there are 2^2m−3(2^2m − 2) of such matrices. For the equality constraint we write

$$\begin{equation} \left(\begin{array}{@{}c@{}} \mathrm{Re}(A)\\ \mathrm{Im}(A) \end{array} \right) {\mathbf{x}} = \left(\begin{array}{@{}c@{}} \mathrm{Re}({\mathbf{b}})\\ \mathrm{Im}({\mathbf{b}}) \end{array}\right). \end{equation}\noindent \tag{ B.8 }$$

The final matrix (Re(A), Im(A))^T has dimension 2^4m+1 × 2^2m−3(2^2m − 2). Most likely, the rank of this matrix is not equal to the number of rows. Therefore, before plugging it into the SDP one must evaluate its reduced-row form (echelon form), and remove the all-zero lines.

If one wishes to include the PPT test, as in program 2, this can be done by rewriting the two positivity constraints, ϱext ⩾ 0 and ϱT1ext ⩾ 0, as a single one, ϱext⊕ϱT1ext ⩾ 0. One thus needs to map each complex Fi in the positivity constraint to F'i = Fi⊕FT1i. The final dimension of each real F'i is then 22m+2 × 22m+2. The equality constraint remains the same.