Abstract
We propose an experimental scheme to observe prethermalization and a dynamic phase transition in a one-dimensional XY spin chain with long-range interactions and inhomogeneous lattice spacing, which can be readily implemented with a recently developed trapped-ion quantum simulator. Local physical observables are found to relax to prethermal values at an intermediate timescale, followed by complete relaxation to thermal values at much longer time. The physical origin of prethermalization is shown to result from a non-trivial structure in the lower half of the energy spectrum. The dynamic behavior of the system is shown to cross different phases when the interaction range is continuously tuned, indicating the existence of a dynamic phase transition.
Export citation and abstract BibTeX RIS

Content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
The dynamic properties of isolated quantum many-body systems have garnered intense interest in recent years [1, 2]. On the theory side, research has been centered on whether and how an isolated quantum system approaches thermal equilibrium. While certain observables are found to relax to equilibrium in some large systems [3–7], it remains unclear under what conditions and on which timescale equilibration occurs in generic systems [8–11]. On the experimental side, recent progress with cold atoms [12–14] and trapped ions [15–20] has made it possible to simulate well controlled simple models, such as the one-dimensional (1D) Bose gas and transverse field Ising model. These quantum systems can be well isolated from the environment and have long coherence times, and their physical properties can be measured at the single-atom level, providing an unprecedented opportunity for studying non-equilibrium dynamics in closed interacting systems.
A particularly intriguing phenomenon in this context is prethermalization [21], which has been shown to emerge in various theoretical setups [22–24], and has been experimentally observed in ultracold atomic gas [14]. Prethermalization is characterized by the establishment of a quasi-stationary state at an intermediate timescale, followed by relaxation to a stationary state at a much longer timescale (thermalization). The physical origin of prethermalization, however, is still elusive, and is speculated to be related to the quasi-integrability of the model [14, 23].
In this paper, we propose a new experimental scheme for observing and studying prethermalization and a related dynamic phase transition in an XY spin model, which can be implemented with the current trapped-ion quantum simulator of [19]. Our model features long-range spin–spin interaction and an inhomogeneous lattice spacing, and unlike many other systems, the prethermalization can occur already for as few as a dozen spins, allowing for its observation in current experimental systems. The prethermalization found in this system results from a non-trivial structure in the energy spectrum, which in turn arises due to a combination of long-range interaction and inhomogeneous lattice spacing. In addition, by tuning the range of interactions with an experimental knob, we find that the dynamic behavior of this system exhibits three different phases: thermalization only, prethermalization followed by thermalization and prethermalization only. The transition between these different phases becomes sharper with an increasing number of spins, hinting at the existence of a dynamic phase transition [25] in the thermodynamic limit.
1. Model and its dynamics
Our spin model is based on the experimental system of a chain of ions confined in a linear Paul trap (figure 1). Through proper configuration of the Raman beams, the optical dipole force can generate an effective transverse field Ising model [16, 17, 26]

where σi is the spin-1/2 Pauli matrix for the ith ion qubit. The interaction coefficients Jij in equation (1) are given by
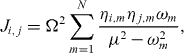
where μ is the Raman beatnote frequency, Ω is the effective Rabi frequency, which is assumed to be the same for all of the ions, {ωm} are the phonon mode frequencies of the ions in the x direction and ηi,m are the Lamb–Dicke parameters measuring the coupling between the ith ion and the mth phonon mode. We are interested in the region where  . In this limit, the σ+iσ+j and σ−iσ−j terms in equation (1) will be energetically forbidden, and we end up with the XY Hamiltonian
. In this limit, the σ+iσ+j and σ−iσ−j terms in equation (1) will be energetically forbidden, and we end up with the XY Hamiltonian

A unique feature of the Hamiltonians (1) and (2) realized with the ion system is that the interaction characterized by Jij is long ranged, and the interaction range is readily tuned by changing the beatnote frequency μ. In particular, in a range of μ, Jij can be roughly approximated by a power-law decay with Jij ∼ |i − j|−α, where α varies from 0 to 3 when we tune μ [19]. In the following analysis, for a given μ, we fit the coefficient Jij with Jij ∼ |i − j|−α and use the fitting parameter α as an indicator of the range of interaction.
Figure 1. Schematic view of the proposed experimental setup: a chain of N ions are trapped along the z direction in a 1D harmonic linear Paul trap. The global Raman beams generate a spin-dependent force along the x direction, resulting in effective Ising-type interaction. To induce the dynamics, a focused laser beam is applied on one end of the ion chain to selectively flip only the first spin.
Download figure:
Standard image High-resolution imageThe 1/rα Ising model (equation (1)) with no transverse field (essentially classical) can be analytically solved [27, 28]. Its dynamic properties have also been recently studied in [24, 29], where it is found that if α is smaller than the dimensionality of the system, the total interaction energy per site diverges, drastically changing the dynamics after a global quantum quench, with possible emergence of prethermalization. However, the long range XY model (equation (2)) contains non-commuting terms and is generally not exactly solvable, making its dynamic properties largely unknown. Here, we consider a particularly interesting setup that shows rich dynamic properties and is practical for experimental demonstration. We first initialize all of the spins through optical pumping to the spin down state with σzi = −1, which is an eigenstate of HXY and hence stationary. We then use a focused laser beam to flip the first spin (left end ion) to σzi = 1 (see figure 1). The starting state |ψ(0)〉 = |↑↓↓···↓〉 is no longer an eigenstate of HXY , and is subject to the dynamics with |ψ(t)〉 = eiHXY t/ℏ|ψ(0)〉. We consider the time evolution of the local observables 〈σzi(t)〉 and their correlations 〈σzi(t)σzj(t)〉, which can be directly measured in the experiments. For convenience of description of the dynamics, we introduce the operator

where the coefficients fi ≡ (2i − N − 1)/(N − 1) are equally distributed between [ − 1,1] from i = 1 to N. The expectation value of C varies between [ − 1,1], and physically measures the relative position of the spin excitation. It is easy to check that 〈ψ(0)|C|ψ(0)〉 = −1, meaning that the spin excitation is initially at the left edge of the chain. We also note that for any state with spatial inversion symmetry around the center of the chain, 〈C〉 = 0.
2. Prethermalization and dynamic phase transition
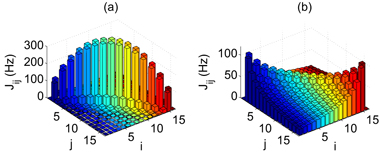
To explore the dynamic behavior, we first perform numerical calculations by using exact diagonalization of an N = 16 ion chain, which corresponds to the current size of the experimental trapped ion quantum simulator in [19]. As shown in figure 2, we choose two parameter settings with the corresponding fitting parameter α ≈ 2.6 and 0.52, which represent, respectively, the short-range and the long-range interactions. The distributions of the exact coupling coefficients Jij are shown in figure 2 for these two cases. Note that our calculation is based on the approximated XY Hamiltonian (equation (2)). However, we have numerically verified that the relative differences of the calculated 〈C〉 and 〈σiσj〉 obtained by solving the original transverse field Ising Hamiltonian (equation (1)) are negligible at all times (< 10−3) when B > 1000J0. It is worth mentioning that the error caused by the non-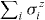 -conserving terms from the finite B field does not accumulate over time: the population of our state outside of the single excitation subspace can be estimated as
-conserving terms from the finite B field does not accumulate over time: the population of our state outside of the single excitation subspace can be estimated as  , which is independent of time and can be made arbitrarily small by choosing a sufficiently large B. In practice, as J0 ∼ Ω(ηx/N)(ηxΩ)/(μ − ωx), and a trapped ion quantum simulator requires ηx ≪ 1 and ηxΩ ≪ μ − ωx [26], Ω > 1000J0 is typical for N > 10 ions (see [19] and also example parameters in figure 2). Since the transverse magnetic field is generated by a resonant carrier transition [16, 17], by splitting the Raman laser power evenly between the two sidebands alongwith the carrier transition, B > 1000J0 can be readily achieved. Moreover,
, which is independent of time and can be made arbitrarily small by choosing a sufficiently large B. In practice, as J0 ∼ Ω(ηx/N)(ηxΩ)/(μ − ωx), and a trapped ion quantum simulator requires ηx ≪ 1 and ηxΩ ≪ μ − ωx [26], Ω > 1000J0 is typical for N > 10 ions (see [19] and also example parameters in figure 2). Since the transverse magnetic field is generated by a resonant carrier transition [16, 17], by splitting the Raman laser power evenly between the two sidebands alongwith the carrier transition, B > 1000J0 can be readily achieved. Moreover,  decreases with increasing N, as the Jij will scale down faster than 1/N for a given laser power [30].
decreases with increasing N, as the Jij will scale down faster than 1/N for a given laser power [30].
Figure 2. (a) Distribution of Jij for short-range interactions with the beatnote frequency set at μ = 5.2 MHz, a trap frequency in the z direction of ωz = 100 kHz, and ηxΩ = 40 kHz. The corresponding fitting parameter α ≈ 2.6 in this case. (b) Distribution of Jij for long-range interactions with μ = 5.02 MHz, ωz = 600 kHz, ηxΩ = 3.9 kHz, and the corresponding fitting parameter α ≈ 0.52. In both cases we choose a trap frequency in the x direction of ωx = 5 MHz and average interaction strength 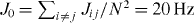 . Note that all of the frequencies here are angular frequencies.
. Note that all of the frequencies here are angular frequencies.
Download figure:
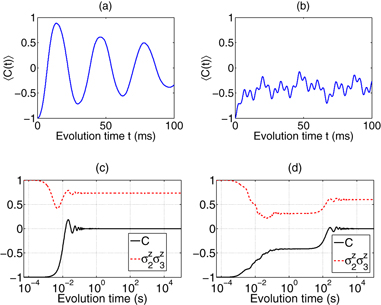
Standard image High-resolution imageFor these choices of parameters, the short-time dynamics with t∈[0,2/J0] for 〈C〉 is shown in figures 3(a) and (b). In the short-range interaction case, we observe that the spin excitation, initially located at the left edge of the chain, travels almost coherently to the other side and oscillates back and forth with relatively small dispersion. In contrast, in the long-range interaction case, the spin excitation diffuses and somehow gets locked before it reaches the middle of the chain (with 〈C〉 ≈ −0.4).
Figure 3. (a), (b) Short-time dynamics of σzi and C for short-range (a) and long-range (b) interactions. (c), (d) Long-time dynamics of time-averaged C and σziσzj for (c) short-range and (d) long-range interactions. The parameters for the short-range and the long-range interactions are the same as in figure 2.
Download figure:
Standard image High-resolution imageTo clarify the long-time dynamics, we use the finite-time-averaged quantity 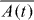 , defined as
, defined as 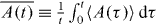 for the observable A [31, 32], thereby averaging out temporal fluctuations on short time scales (the following dynamic behaviors are qualitatively the same even without performing any time averaging). The long-time dynamics is shown in figures 3(c) and (d). In the short-range interaction case, the spin excitation position C, as well as the spin correlations σziσzj, relax to the stationary values at T0 ≈ 10/J0 = 500 ms. In the long-range interaction case, the observables first reach quasi-stationary (prethermal) values at a timescale T0, and further relax to the stationary (thermal) values at a much longer timescale (∼ 104T0). The emergence of prethermalization in the long-range interaction case is signaled by a nonzero value of
for the observable A [31, 32], thereby averaging out temporal fluctuations on short time scales (the following dynamic behaviors are qualitatively the same even without performing any time averaging). The long-time dynamics is shown in figures 3(c) and (d). In the short-range interaction case, the spin excitation position C, as well as the spin correlations σziσzj, relax to the stationary values at T0 ≈ 10/J0 = 500 ms. In the long-range interaction case, the observables first reach quasi-stationary (prethermal) values at a timescale T0, and further relax to the stationary (thermal) values at a much longer timescale (∼ 104T0). The emergence of prethermalization in the long-range interaction case is signaled by a nonzero value of  at the intermediate timescale T0. We can use
at the intermediate timescale T0. We can use  as an order parameter to characterize different dynamic behaviors. By continuously tuning the effective interaction range (indicated by the fitting parameter α) with the beatnote frequency μ, we find that (see figure 4) prethermalization only takes place when α is smaller than a critical value (αC ≈ 1.3 for N = 16). For larger system size, the prethermalization–thermalization transition still occurs, but αC becomes smaller and the transition becomes sharper. For the particular case α = 0, the system has uniform coupling and its dynamics can be solved exactly. The exact solution shows that the system stays in the prethermal state forever with
as an order parameter to characterize different dynamic behaviors. By continuously tuning the effective interaction range (indicated by the fitting parameter α) with the beatnote frequency μ, we find that (see figure 4) prethermalization only takes place when α is smaller than a critical value (αC ≈ 1.3 for N = 16). For larger system size, the prethermalization–thermalization transition still occurs, but αC becomes smaller and the transition becomes sharper. For the particular case α = 0, the system has uniform coupling and its dynamics can be solved exactly. The exact solution shows that the system stays in the prethermal state forever with  [33].
[33].
Figure 4. A dynamic 'phase diagram' with regard to the interaction range characterized by the fitting parameter α. The N = 16 case uses the parameters specified in figure 1, and the N = 64, N = 256 cases use the same parameters except that ωz is scaled down by 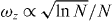 to maintain chain stability.
to maintain chain stability.
Download figure:
Standard image High-resolution image3. Mechanism of prethermalization and dynamic phase transition
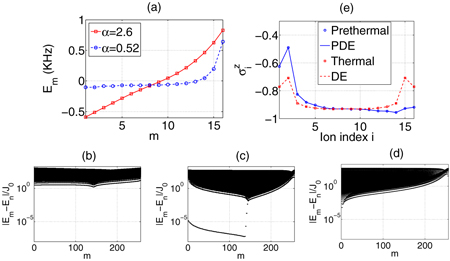
We now give a physical explanation of why prethermalization and the variety of observed dynamic behaviors occur in this model. The distinctive short-time dynamics of 〈σzi(t)〉 (figures 3(a) and (b)) can be explained by examining the energy spectrum of HXY in the single spin excitation subspace (shown in figure 5(a)). In the short-range interaction case, the energy spectrum is close to linear. This is because HXY can be roughly approximated with only neighboring interaction, and due to inhomogeneous lattice spacing, {Ji,i+1} are similar to those in the 'quantum mirror' model [34, 35], resulting in a near dispersion-free spin wave propagation until nonlinearity sets in. On the other hand, the energy spectrum for the long-range interaction case is highly nonlinear, so the dynamics of the spin excitation is strongly dispersive.
Figure 5. (a) Energy spectrum in the single spin excitation subspace for N = 16 spins with short and long-range interaction. (b)–(d) Scatter plot of the eigenenergy differences {Em − En} for N = 256 spins with (b) short-range interaction (α = 2.4), (c) long-range interaction (α = 0.74) and (d) long-range interaction (α = 0.74) but with ions confined in a ring geometry with equal spacing. (e) Comparison of prethermal values of 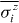 (blue circle, taken at t = T0 = 500 ms) with partial diagonal ensemble (PDE) prediction (blue solid line) and thermal values (red square, taken at t = 5 × 103s) with diagonal ensemble (DE) prediction (red dashed line) based on long-range interaction pattern Jij shown in figure 2(b).
(blue circle, taken at t = T0 = 500 ms) with partial diagonal ensemble (PDE) prediction (blue solid line) and thermal values (red square, taken at t = 5 × 103s) with diagonal ensemble (DE) prediction (red dashed line) based on long-range interaction pattern Jij shown in figure 2(b).
Download figure:
Standard image High-resolution imageThe reason for a prethermal stage in the long-time dynamics, however, is much more complicated. Naively, the spin flip–flop matrix Jij varies smoothly among sites for any α∈(0,3), so the spin excitation should continuously diffuse from one end of the chain to the whole chain, and is not expected to get trapped somewhere in the middle for a long time. The two stage dynamics indicates that there are two different timescales implicit in the Hamiltonian, which is not at all obvious by looking at the Jij. The time dynamics of any physical observable is simply given by

where ρmn(0) is the initial state's density matrix element in energy basis, the different timescales of the dynamics can be understood by computing the eigenenergy differences {Em − En}, as done in figure 5. In the short-range interaction case (figure 5(b)), all {Em − En} are continuously distributed from J0 to 100J0, so a single-stage relaxation is expected after T ∼ T0 = 10/J0. In the long-range interaction case (figure 5(c)), most {Em − En} still fall into the range of 1–100J0, but there is a striking separate (i.e. gapped) branch at the much lower rate (∼ 10−6J0). This branch results from the near-degenerate pairs ({E2k − E2k−1}) of the eigenenergies (figure 5(a)) that make up the first half energy spectrum, and the number of these pairs scale up with system size N. Note that if we put the ions into a ring trap so that the lattice is translationally invariant, we find that there is no separate branch of the {Em − En} (figure 5(d)), and hence there is no prethermalization even with long-range interactions. The appearance of near-degenerate pairs {E2k − E2k−1}) in the spectrum of our model seems to arise from the combined effect of long-range interactions and inhomogeneous lattice spacing. Intuitively, from figure 2(b), the inhomogeneity causes the middle part of the chain to have smaller flip–flop interactions Jij than the ends, potentially leading to a metastable state where the spin excitation is roughly localized in the left half of the chain. However, the existence of two distinct timescales is primarily due to the structure of the energy spectrum, which is not trivially related to inhomogeneity. We are still investigating if there is a wide class of inhomogeneous lattices that can give rise to similar dynamics.
Figure 5(e) shows that the thermal values can be well predicted by the DE, defined as
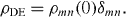
In the large N limit, under certain conditions implicit in the eigenstate thermalization hypothesis [3–5], the DE prediction will match the canonical ensemble prediction for thermalized states in classical statistical physics.
As prethermalization is due to an emergent small scale of energy differences in the Hamiltonian, to predict the prethermal values here, we can define the PDE:
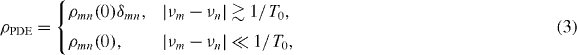
where {νm} are the eigenenergies. We find that the PDE can accurately predict the prethermal values of local observables  , as shown in figure 5(d). Roughly speaking, the prethermalization timescale is determined by the average level spacing (∼ 10/J0), and the thermalization timescale is determined by the minimum level spacing (∼ 104/J0 as in figure 5(d)).
, as shown in figure 5(d). Roughly speaking, the prethermalization timescale is determined by the average level spacing (∼ 10/J0), and the thermalization timescale is determined by the minimum level spacing (∼ 104/J0 as in figure 5(d)).
The dynamic phase transition can be associated with breaking of the lattice inversion (parity) symmetry, reminiscent of symmetry breaking in the equilibrium phase transitions. Our Hamiltonian HXY is symmetric under the space inversion around z = 0 (figure 1), but we start from an initial state that does not have this symmetry. The thermal state, with no memory of the initial state, is described by the diagonal ensemble ρDE and restores this symmetry as  . However, the prethermal state does not restore the Hamiltonian symmetry due to its non-zero
. However, the prethermal state does not restore the Hamiltonian symmetry due to its non-zero 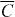 value, which indicates that some 'memory' of the initial state is preserved in the prethermal state. The intermediate timescale T0 for observation of the prethermal state gives a microscopic interpretation of why this state can break the parity symmetry: one cannot distinguish the near-degenerate pairs of eigenstates in the energy spectrum, so linear combinations within each pair are allowed. Since the two eigenstates of the pair have either even or odd parity, their linear combinations can break the parity symmetry. The dynamic phase diagram shown in figure 4 also has the hint of two non-analytical points: one is where
value, which indicates that some 'memory' of the initial state is preserved in the prethermal state. The intermediate timescale T0 for observation of the prethermal state gives a microscopic interpretation of why this state can break the parity symmetry: one cannot distinguish the near-degenerate pairs of eigenstates in the energy spectrum, so linear combinations within each pair are allowed. Since the two eigenstates of the pair have either even or odd parity, their linear combinations can break the parity symmetry. The dynamic phase diagram shown in figure 4 also has the hint of two non-analytical points: one is where  becomes non-zero, representing the appearance of prethermalization, and the other is where
becomes non-zero, representing the appearance of prethermalization, and the other is where  approaches
approaches 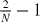 (α → 0), representing the disappearance of thermalization. Note that the thermodynamic limit of our system is not well defined, as to keep a linear ion chain stable, the length of the chain L cannot be kept proportional to N as N becomes large. Thus, it is not clear if a dynamical phase transition point can be obtained in some generalized thermodynamic limit (we are also limited by a finite number of lattice sites that can be studied using our numerical methods).
(α → 0), representing the disappearance of thermalization. Note that the thermodynamic limit of our system is not well defined, as to keep a linear ion chain stable, the length of the chain L cannot be kept proportional to N as N becomes large. Thus, it is not clear if a dynamical phase transition point can be obtained in some generalized thermodynamic limit (we are also limited by a finite number of lattice sites that can be studied using our numerical methods).
4. Discussion of experimental detection and summary
The transverse field Ising Hamiltonian equation (1) has already been experimentally simulated in [19] for the N = 16 ions, and highly efficient in situ measurement of spin polarization (σzi) and spin correlation (σziσzj) has been demonstrated. The XY Hamiltonian (equation (2)) can thus be readily obtained by turning up the effective transverse magnetic field. The non-equilibrium initial state preparation requires a focused laser beam, but is relatively easy due to the large ion spacing near the ends. The laser power and trap frequencies used for generating the interaction pattern Jij shown in figure 2 are within current experimental reach [17, 19]. The observation of prethermalization and the dynamic phase transition shown in figures 3 and 4 only requires the spin decoherence time to be longer than T0 = 10/J0 = 500 ms, and coherence times of up to 2.5 s have been experimentally achieved by using the hyperfine qubit of Yb+ ions [36]. However, the second stage of thermalization for the long-range interaction case requires much longer times, and is beyond current experimental reach, similar to the experiment on prethermalization using cold atoms in [14].
In summary, we have proposed a novel scheme to observe a peculiar prethermalization phenomenon and dynamic phase transitions in a trapped ion quantum simulator. The required conditions can be realized by using current experimental technology. We provide an explanation of the mechanism of prethermalization and the dynamic phase transition in our proposed model. We believe that the wealth of interesting dynamic properties for a system with continuously tunable range of interactions is far from exhausted.
Acknowledgments
We thank C Monroe, A Polkovnikov and A Gorshkov for helpful discussions, and Michael Foss--Feig for improving the writing of this paper. This work was supported by the NBRPC (973 Program) 2011CBA00302, the DARPA OLE program, the IARPA MUSIQC program and the ARO$/$AFOSR MURI program.
After completion of this work, we became aware of [37], in which similar local quench dynamics yields results consistent with the work presented here on the short-time behavior of small versus large α power law interaction, and [38], which studies entanglement growth following a global quench of the Hamiltonian given by equation (1) under different α.