Abstract
The impact of non-resonant background emitters in semiconductor quantum-dot microcavity lasers is addressed within theoretical investigations based on the solution of the von Neumann equation. Off-resonant coupling between emitter resonances and the cavity mode is enabled via phonons, which are included in the von Neumann dynamics by an effective Lindblad contribution. The results show enhanced coherent emission from non-resonantly coupled quantum dots, while the frequently used phenomenological cavity feeding mechanism only enhances the thermal component of the emission.
Export citation and abstract BibTeX RIS
Content from this work may be used under the terms of the Creative Commons Attribution-NonCommercial-ShareAlike 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Quantum-dot (QD) microcavity devices offer desirable properties for laser applications, such as low threshold currents and single-mode operation [1–3]. At the same time a miniaturization down to the very core of cavity-QED can be achieved, where a single emitter interacts with a single mode of the confined electromagnetic field [4, 5]. Besides being a profound testing ground for quantum optics, this regime offers application potential in the quantum-information technologies, where single photons are required on demand and at high repetition rates from integrated devices [4, 6].
The presence of a high-quality microcavity, associated with a narrow line width, strongly singles out particular transitions that are in resonance. Theoretical descriptions mostly focus on the resonant contributions while disregarding the background resulting from residual emitters, both spectrally and spatially detuned from the optimal overlap with the cavity mode. In early experiments on microcavity lasers using QDs as the active medium, this elusive background has been used to explain the lower threshold currents than were expected from an assessment of the resonant emitters alone. In many cases, lasing was achieved in experiments for which theoretical models without background contributions did not predict lasing for the estimated number of resonant emitters [7–9].
Residual emitters have played no lesser role in recent experiments on single-emitter lasing [10–12]. In fact, it has become customary in the literature to account for background emitters by describing them phenomenologically with a direct pumping of photons into the cavity mode [12, 13]. The drawback of this approach is twofold. Firstly, such a feeding mechanism, acting together with the cavity loss, gives rise to a thermal photonic state with a temperature defined by the pump-to-loss ratio. This overlooks the fact that the background photons are generated through exciting an active medium, and hence are expected to have a coherent component. Secondly, the procedure is limited to pump values lower than the cavity loss rate to prevent unphysical instabilities of the solution. Recent attempts to handle these problems have used indirect cavity feeding through additional emitters, interacting with the cavity mode either perturbatively [14] or intermittently [7, 15].
The origin of the efficient coupling of energetically detuned emitters to the cavity mode had been a mystery for quite a while, before a series of different mechanisms were discussed in the literature. Nowadays, it is widely accepted that phonons provide off-resonant cavity feeding if the detuning is small (∼2 meV) [16–19], whereas much larger energy gaps (∼10 meV) can be bridged via the coupling of multi-excitonic states and processes that include wetting-layer-assisted scattering processes [20–23]. The possible interplay of these mechanisms makes it difficult to rule out contributions from residual emitters even in state-of-the-art single-QD experiments.
Many recent publications address the spectral properties under the impact of off-resonant coupling, especially via phonons [16, 24–26]. In this work, we focus on the role of non-resonant coupling from background emitters for a single-QD microcavity system, i.e. the influence of additional detuned emitters on the production and statistical properties of the photons. To illustrate the significance of non-resonant coupling, we describe comparatively the following cases in which a QD–microcavity system is driven into stimulated emission. First, lasing is achieved with a few QDs in resonance with the cavity, but then it is lost when we detune all but one emitter. Finally, by switching on the non-resonant coupling, these 'background' emitters become efficient again and lasing is recovered. In all these cases the lasing is diagnosed by how close the photon statistics is to a Poissonian distribution. In other words, the lasing criterion we use is not limited to the lowest moments of the distribution, such as the mean photon number or the autocorrelation function g(2), but the whole statistics is explored.
Exemplary for the non-resonant coupling we consider phonon-assisted processes that prevail for small and moderate detunings. Rather than using a phenomenological approach, we start with the full Hilbert space for several QD emitters and the cavity mode. This way, the background is treated as gain material on an equal footing with the resonant emitter. Carrier dynamics and saturation effects are properly accounted for, which offers a more realistic description than the mere feeding of the cavity mode via Lindblad terms. This is particularly beneficial for small systems where the number of emitters is limited and operation takes place in or close to saturation of the electronic states.
We use a four-level QD model that can accommodate up to two electron–hole pairs. The resulting number of possible electronic configurations already describes features caused by the interplay of multi-exciton configurations [7, 21, 27], thus allowing for a description over a wide excitation range from weak to strong pumping. Scattering processes involving acoustic phonons are included via effective Lindblad contributions that we adopt from [16]. The resulting von Neumann–Lindblad equation comprises phonon-assisted recombination processes at temperature-dependent rates. In contrast to the Jaynes–Cummings (JC) mechanism of emitter–cavity energy transfer, these processes turn out to be less sensitive to detuning.
In the considered model the Hilbert space grows rapidly with the emitter number, which currently allows us to study up to four QDs in the presence of a cavity mode before the numerical effort becomes excessive. While a larger number is desirable, tendencies can already be extracted at this level. A numerical evaluation is possible for several more emitters if one considers two-level systems. Here we prefer to use four-level models to avoid artifacts, such as excitation-induced quenching [28], which has not been observed in QD-based systems [8, 9, 29].
2. Theoretical model
We start by giving an overview of the particular system under consideration. The multi-level configuration-based approach for the electronic degrees of freedom interacting with a cavity photonic mode is outlined in section 2.1, whereas the phonon-assisted light–matter coupling is presented in section 2.2. There the focus lies on the carrier interaction with acoustic phonons, which act not only as a thermal bath, but also produce polaronic effects and lead to the off-resonant coupling.
2.1. Quantum dot in interaction with a single photonic mode
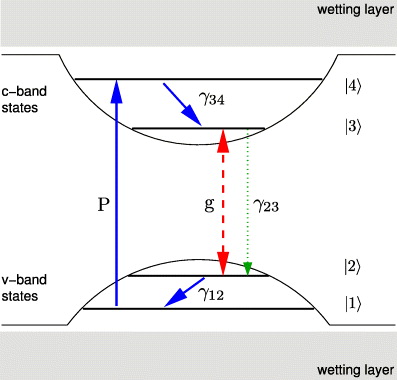
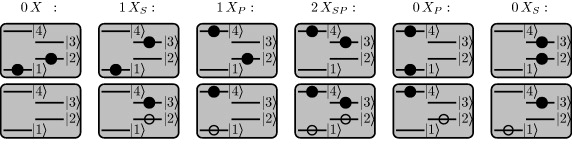
The Hilbert space of the multi-QD and cavity–photon system is spanned by the configurations that arise from populating the single-particle states with carriers, and the number of photons in the cavity mode. The first component grows rapidly with increasing number of QDs and QD states. As discussed in [7], a restriction to carriers of only one spin direction can be a sensible approximation, which we employ in the following. We assume two single-particle bound states in each band per QD, denoted as s- and p-states. The states are numbered in the order of increasing energy, as depicted in figure 1. Furthermore, only scattering processes that conserve the number of carriers in each QD are considered. Starting with full valence- and empty conduction-band states, we have six possible configurations per QD [15, 27], depicted in figure 2.
Figure 1. Schematic representation of the electronic level structure of each QD with the considered rates for electrons in the conduction and valance bands. Carrier generation is modeled by a transition process between the p-levels at the rate P. Light–matter coupling leads to recombination processes between the s-states with the light–matter coupling strength g. Carrier relaxation takes place at a rate γ34 (γ12) in the conduction (valence) band. Up-scattering processes are neglected due to their small effect at low temperatures. The possible configurations arising from this model are shown in figure 2.
Download figure:
Standard imageFigure 2. The possible configurations in a four-level QD, in which valence- and conduction-band carriers are excited and de-excited only in pairs. The representation is given in the c–v (upper row) and e–h pictures (lower row).
Download figure:
Standard imageWe begin by describing a single QD interacting with the cavity mode in terms of a density operator acting in the product of the photonic Hilbert space with the six-dimensional one spanned by the carrier configurations. Its time evolution is given by the von Neumann equation (ℏ = 1 throughout the paper)

where the system Hamiltonian 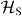 contains the QD carrier Hamiltonian, the cavity photon term and the JC carrier–photon interaction
contains the QD carrier Hamiltonian, the cavity photon term and the JC carrier–photon interaction

The QD Hamiltonian consists of a single-particle and a Coulomb interaction part

where ai, a†i are fermionic carrier operators with indices running over the set of QD single-particle states  . As shown in [30], the dominant Coulomb terms are Vijji, corresponding to the direct (Hartree) interaction and Vijij describing the exchange (Fock) contribution. Both are diagonal in the occupancy basis, i.e. commute with the number operators ni = a†ia
i. In the following, we employ the approximation to limit the influence of the Coulomb interaction to these dominant terms, in which case the configurations depicted in figure 2 form an eigenbasis also for
. As shown in [30], the dominant Coulomb terms are Vijji, corresponding to the direct (Hartree) interaction and Vijij describing the exchange (Fock) contribution. Both are diagonal in the occupancy basis, i.e. commute with the number operators ni = a†ia
i. In the following, we employ the approximation to limit the influence of the Coulomb interaction to these dominant terms, in which case the configurations depicted in figure 2 form an eigenbasis also for  . Further details of the QD model are discussed in [30].
. Further details of the QD model are discussed in [30].
The other two terms in equation (2) describe the photon mode and its interaction with the QD
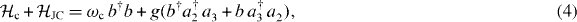
where b,b† are the photon operators, ωc is the mode frequency and g is the JC coupling constant. According to the above equation, the JC Hamiltonian gives rise to the coherent energy exchange between the cavity and the s-electron–hole pair. The p-pair, generated by a†4a 1, is energetically too far separated from the s-pair. Hence, emission from the p-shell into the cavity mode is neglected.
Also, the s-shell recombination can take place either in the presence or in the absence of the p-shell excitations. The transition energies in these two cases are detuned due to the Coulomb interaction with the 'spectator' p-carriers. In the numerical application below, we define the resonance between the QD and the cavity by the condition that ωc is equal to the energy of the sp-biexciton transition. This is because lasing is achieved in the high pumping regime, when the biexciton state has an overwhelmingly higher probability than the single exciton [7].4
The QD–cavity system is embedded in a surrounding semiconductor material and is therefore not isolated. The interaction with the environment enables scattering between QD states by exchange of energy with either the lattice vibrations or the carriers in the wetting layer or bulk continuum. With their large number of degrees of freedom, these continua play the role of thermal reservoirs and their influence on the system leads to irreversible processes of relaxation and dephasing.
The evolution of a system in contact with thermal reservoirs is commonly described by the von Neumann–Lindblad equation

The coherent dynamics is represented as before by the commutator with the system Hamiltonian  and the incoherent, dissipative evolution results from the system–bath interaction which, when treated in the Born–Markov limit [31], leads to the sum of Lindblad operators
and the incoherent, dissipative evolution results from the system–bath interaction which, when treated in the Born–Markov limit [31], leads to the sum of Lindblad operators
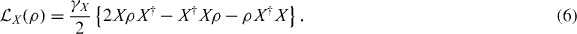
Here X is an operator that describes a reservoir-assisted transition taking place in the system. The relevant information about the bath and its interaction with the system is contained in the transition rate γX.
In the system we consider, X can be either a transition operator a†ia
j between two QD single-particle states or a photonic creation or annihilation operator, b† or b, respectively. The first case corresponds to a change of configurations in which a carrier moves from state  to state
to state  , while in the second case the photon subsystem undergoes a raising or lowering of the photon number.
, while in the second case the photon subsystem undergoes a raising or lowering of the photon number.
If X is an energy-lowering operator, i.e. X = b or a†ia
j with εi < εj, then it appears in the system–reservoir interaction Hamiltonian  in a product with an energy-raising bath operator Γ†. The term X Γ† leads, via the above-mentioned Born–Markov procedure, to the lowering Lindblad operator
in a product with an energy-raising bath operator Γ†. The term X Γ† leads, via the above-mentioned Born–Markov procedure, to the lowering Lindblad operator 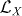 . The corresponding transition rate is given by the Fourier transform of a reservoir correlator
. The corresponding transition rate is given by the Fourier transform of a reservoir correlator 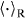 , taken at the frequency ω corresponding to the energy lost by the system
, taken at the frequency ω corresponding to the energy lost by the system

The inverse, energy-raising transition, generated by X† Γ, which is also present in 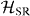 , appears in equation (5) as a raising Lindblad term
, appears in equation (5) as a raising Lindblad term 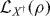 , with the transition rate given by
, with the transition rate given by

Strongly non-resonant contributions to  of the form X Γ or X† Γ† are usually discarded in the spirit of the rotating-wave approximation.
of the form X Γ or X† Γ† are usually discarded in the spirit of the rotating-wave approximation.
The Kubo–Martin–Schwinger (KMS) condition obeyed by the thermal equilibrium correlators implies that γX† = e−βωγX, with β the inverse reservoir temperature. In principle, both 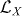 and
and 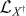 are contained in the generic sum over X in equation (5), but for transition energies much larger than the bath temperature one has e−βω ≪ 1, and the
are contained in the generic sum over X in equation (5), but for transition energies much larger than the bath temperature one has e−βω ≪ 1, and the 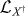 term is usually neglected.
term is usually neglected.
Under these circumstances we retain in the dissipative part of the von Neumann–Lindblad equation only the lowering terms

where the summation runs over the pairs (1, 2), (2, 3) and (3, 4). Pumping is also included in the summation as a (4, 1) raising Lindblad operator. All these incoherent processes are schematically depicted in figure 1. The last term in equation (9) describes the cavity losses at a rate γb which will be denoted below by κ.
2.2. Phonon-mediated cavity feeding
The acoustic phonons have been invoked [32–34] in connection with the line shape of the excitonic transition. The dominant contribution to the carrier–phonon coupling is contained in the diagonal matrix elements with respect to the carrier-state index, and this has allowed the application of the independent-boson-model techniques [35] in the line shape problem. More recently, the role of LA-phonons in the off-resonant cavity feeding was pointed out [36–39]. It was shown [16, 19, 40, 41] that the appropriate frame to describe the phonon-assisted energy transfer between the exciton and the cavity is provided by the polaronic picture.
The idea is illustrated by considering the QD–cavity system in contact with the phonons
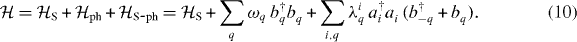
Here q runs over the continuum of phonon modes and λiq = λi*−q is the strength of the interaction between the state 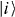 and the mode q. The operators bq and b†q with the subscript q annihilate/create a phonon in the mode q and must be distinguished from the photon operators b and b†, which we use without subscript.
and the mode q. The operators bq and b†q with the subscript q annihilate/create a phonon in the mode q and must be distinguished from the photon operators b and b†, which we use without subscript.
Considering the phonon subsystem as a thermal reservoir and treating  in the Born–Markov approximation would lead to pure-dephasing Lindblad terms
in the Born–Markov approximation would lead to pure-dephasing Lindblad terms 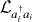 [42, 43], since no population redistribution would take place due to the corresponding system operator. With the other dissipation processes considered as in section 2.1, the only channel for energy exchange between the QD and the cavity is provided by the JC interaction, and is a coherent one. An alternative possibility of a phonon-assisted transfer process can be included in the kinetics by going to the polaron picture. To this end, one applies the unitary transform customary to the independent boson model [35]
[42, 43], since no population redistribution would take place due to the corresponding system operator. With the other dissipation processes considered as in section 2.1, the only channel for energy exchange between the QD and the cavity is provided by the JC interaction, and is a coherent one. An alternative possibility of a phonon-assisted transfer process can be included in the kinetics by going to the polaron picture. To this end, one applies the unitary transform customary to the independent boson model [35]

using
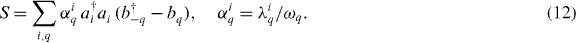
This changes the Hamiltonian into

where the QD Hamiltonian is modified as

The additional term, which is diagonal in the occupation numbers, renormalizes the configuration energies (polaron shift), very much like the Coulomb interaction. As a side remark, the polaron shift is neglected in the numerical calculations due to its small size in comparison to the Coulomb-induced renormalizations. The unitary operators Bi = eDi and B†i = e−Di are given by  , and are purely phononic.
, and are purely phononic.
The main results of the independent-boson-model transform are: (i) the disappearance of the system–phonon interaction Hamiltonian and (ii) the modification of the JC term, which now includes phonon operators, besides the usual carrier and photon ones. The first is due to the shift of the phonon operators  , and the second due to the change in the carrier ones
, and the second due to the change in the carrier ones  . Note that the products a†ia
i remain unchanged. Also unchanged are the photonic operators, which are not influenced by the unitary transform. This is important for the calculation of population averages such as 〈a†ia
i〉 which can be obtained directly using the transformed density operator
. Note that the products a†ia
i remain unchanged. Also unchanged are the photonic operators, which are not influenced by the unitary transform. This is important for the calculation of population averages such as 〈a†ia
i〉 which can be obtained directly using the transformed density operator  , and the same holds for the photon population
, and the same holds for the photon population 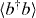 . Moreover, the Lindblad operators described in section 2.1 remain unchanged, too.
. Moreover, the Lindblad operators described in section 2.1 remain unchanged, too.
The JC term in equation (13) can be rewritten as

with B = B†3B 2. Using the fact that the operators Di commute, one has B = eD where
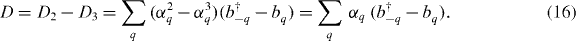
It is seen that the relevant coupling constant in the problem is the difference between those of the two s-levels, λq = αq ωq = λ2q − λ3q.
With the phonons in equation (13) acting as the thermal bath, the system–reservoir interaction is located now in the JC term. This is the main novel feature appearing in the polaronic frame, and accounts for the fact that changes in the electronic state are accompanied by lattice distortions. The JC Hamiltonian is separated as
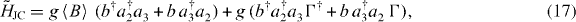
where  ,
,  and Nq is the thermal average phonon number in mode q. The first term has the JC structure with a renormalized coupling constant, while the second leads to two new Lindblad operators Lb†a†2a
3 and Lb a†3a
2. A prerequisite in deriving them is the fact that
and Nq is the thermal average phonon number in mode q. The first term has the JC structure with a renormalized coupling constant, while the second leads to two new Lindblad operators Lb†a†2a
3 and Lb a†3a
2. A prerequisite in deriving them is the fact that  , which is the reason for the separation in equation (17).
, which is the reason for the separation in equation (17).
Collecting the results, the time evolution of the unitary-transformed density operator obeys
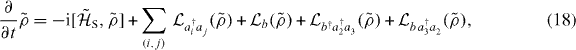
where the system Hamiltonian is given by
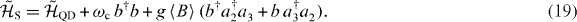
It is clear that the presence of phonons reduces the coherent JC energy transfer between the exciton and the cavity, since  , but at the same time opens new exchange channels via Lindblad terms: Lb†a†2a
3 describes the phonon-assisted transfer of excitation from the emitter to the cavity, and Lb a†3a
2 is responsible for the inverse process. The energies involved in phonon processes are too small to allow the use of the rotating wave approximation. Therefore both phonon emission and absorption terms are present in the reservoir operators Γ† and Γ, and their characterization as raising or lowering operators is ambiguous. For the associated system operators b†a†2a
3 and b a†3a
2, the classification depends on the system parameters. For instance, if the cavity is detuned below the s-pair recombination energy, then b†a†2a
3 is a lowering operator, because there is more energy released by the recombination than in the generated photon, and the difference Δ is absorbed by the phonon bath. Using equation (7) one obtains for the rate of the process [16]
, but at the same time opens new exchange channels via Lindblad terms: Lb†a†2a
3 describes the phonon-assisted transfer of excitation from the emitter to the cavity, and Lb a†3a
2 is responsible for the inverse process. The energies involved in phonon processes are too small to allow the use of the rotating wave approximation. Therefore both phonon emission and absorption terms are present in the reservoir operators Γ† and Γ, and their characterization as raising or lowering operators is ambiguous. For the associated system operators b†a†2a
3 and b a†3a
2, the classification depends on the system parameters. For instance, if the cavity is detuned below the s-pair recombination energy, then b†a†2a
3 is a lowering operator, because there is more energy released by the recombination than in the generated photon, and the difference Δ is absorbed by the phonon bath. Using equation (7) one obtains for the rate of the process [16]
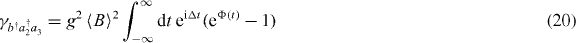
with Φ(t) given by
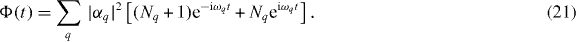
Expanding the Φ exponential in equation (20), all multi-phonon processes of emission and absorption that generate a total energy of Δ are seen to contribute. The rate of the inverse transition is related to the above one by the thermal factor e−β Δ, as prescribed by the KMS condition. Both processes have to be considered, because the detuning energy involved is small and the two rates have comparable values.
The summations over the continuum of phonon modes are actually integrals involving the coupling constants and the density of states. More precisely one defines J(ω), so that for any function f(ω) one has, with λq = αq ωq,
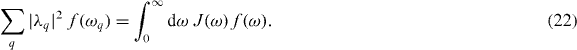
For acoustic phonons interacting with QD states, one finds that [16, 40, 41]

with the coupling constant A and the cutoff frequency ω0 depending on the material and the dot parameters. For our calculations, we use the following parameters typical of InAs/GaAs QDs [16]: A = 0.06 ps2, ω0 = 1.5 ps−1. For the polaron shift

we obtain a value of 174 μeV.
The numerical results discussed in this paper are obtained considering several copies of the QD described in this section, interacting with the same photon mode. Their parameters are chosen such that one of them (the main emitter) is resonant and the others (background emitters) are tuned out of resonance. The role of the phonon-assisted, off-resonant cavity feeding is probed in this way.
3. Lasing in the presence of an off-resonant emitter background
In the following, we consider a QD of which the recombination of the fully populated configuration (sp-biexciton) is in resonance with the cavity mode. We have previously demonstrated [7] that the highest multi-exciton configuration is the preferred QD configuration at high excitation and leads to the highest achievable photon output if in resonance with the cavity: on the one hand, the configuration 2Xsp is most likely generated due to the fast refilling. On the other hand, the biexction-to-exciton transition is not subject to excitation-induced dephasing, which would lead to quenching [7, 28] and drastically reduce the photon output.
The parameters are chosen as follows. In current experiments the vacuum-field Rabi splitting is of the order of 100 μ eV, corresponding to a light–matter coupling strength of g = 0.16 ps−1. The typical cavity decay rate of κ = 0.1 ps−1 corresponds to a cavity-Q of 20 000 in the red spectral range of the InGaAs QD emission. For the p-to-s intraband relaxation rates γ12 = γ34, we use 0.5 ps−1. Radiative losses into non-lasing modes are typically strongly suppressed in microcavity devices, and we consider γ23 = 0.01 ps−1. In particular, the parameters are chosen such that the single-QD emitter does not reach the regime of lasing even if its fully populated configuration transition is resonant with the cavity mode.
In figure 3, we show input/output curves for one, two and three identical QD emitters, all resonantly coupled to the cavity mode. As can be seen, in the last case the mean photon number is significantly increased by a factor of five over the single-emitter calculation, a superlinear enhancement due to onset of stimulated emission. The corresponding photon statistics (figure 4) reveals a Poissonian distribution, indicating coherent emission. The results shown in figure 3 purely rely on the JC coupling between the emitters and the cavity. In figure 5, we study the impact of detuning and off-resonant coupling. For this case, only one emitter is resonant with the cavity mode, while the fully populated configuration transition of the other two QDs is detuned to higher energies by 1.5 meV, which strongly reduces the coupling efficiency. For the dash-dotted line, the only coupling between the detuned resonances and the cavity mode is facilitated by the JC interaction due to the overlap of their Lorentzian tails.
Figure 3. The mean photon number as a function of the pump rate for 1, 2 and 3 identical QD emitters. For all QDs the highest multi-exciton s-transition is resonant with the cavity mode, which maximizes the photon production at high excitation. As can be seen, the single-QD emitter (dashed line) does not reach the regime of stimulated emission before saturation sets in. Two (dash-dotted line) and three (solid line) resonant emitters significantly increase the photon output. No coupling via phonons is assumed in this calculation.
Download figure:
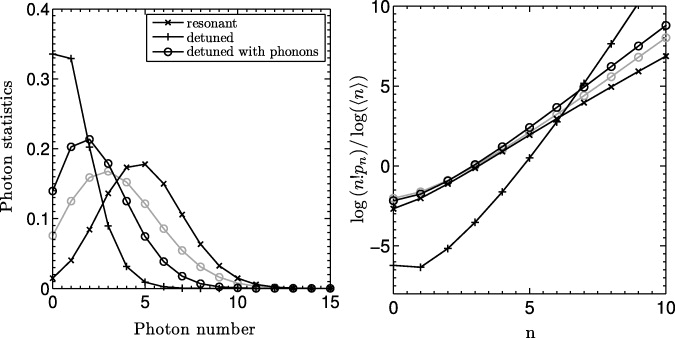
Standard imageFigure 4. Photon number distribution function pn associated with the cases shown in figure 3 at a pump rate of 10 ps−1.
Download figure:
Standard imageFigure 5. The mean photon number as a function of the pump rate for three QD emitters. The resonant case (solid line) corresponds to the solid line in figure 3, where the biexction transition of all three QD emitters is resonant with the cavity mode. Additional curves show the case in which two emitters are detuned to higher energies by 1.5 meV while one emitter is kept resonant with the cavity mode (dash-dotted line). As can be seen, taking the electron–phonon interaction into account at a temperature of 20 K significantly enhances the coupling of the detuned emitters to the cavity mode (dashed line) over the situation without phonon coupling.
Download figure:
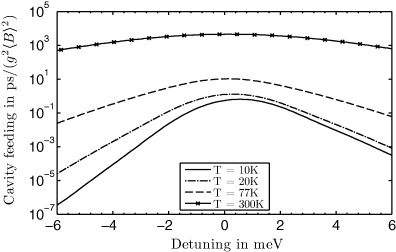
Standard imageThe dashed line represents the same situation but additionally the effect of electron–phonon coupling is considered. The feeding mechanism provided by the phonon-assisted recombination is asymmetric with regard to the detuning (see figure 7). Therefore, the off-resonant emitters are detuned to higher energies with respect to the cavity mode to allow for efficient cavity feeding by phonon emission. At a lattice temperature of 20 K the feeding rate can be estimated from figure 7 to be of the order of 10−2 ps−1. For the effective light–matter coupling g〈B〉, we have used the same value as without phonons (i.e. 〈B〉 = 1) to ensure comparability of the results. However, as measurements of the JC coupling constant are always made at finite temperature, the experimentally determined value must be identified with the renormalized one. Although the feeding rate is small, the additional coupling mechanism is sufficient to increase the mean photon number to about 2.5 and drive the system noticeably toward coherent emission. This can be inferred from the photon statistics shown in figure 6 for the same three cases as above: for all three emitters in resonance, the logarithmic representation of the photon statistics, given in the right panel, clearly shows a straight line with a slope close to unity. This is indicative of Poissonian statistics, which obeys

With only one QD in resonance and the other two detuned, the additional phonon coupling significantly changes the photon output and the statistics clearly evolves away from a Poissonian distribution in the absence of phonon coupling. When the latter is switched on, the peak of the distribution begins to move away from n = 0, and the logarithmic representations of the photon statistics come quite close to linear behavior.
Figure 6. Left panel: photon statistics pn associated with figure 5 for a pump rate of 10 ps−1. The right panel provides a logarithmic representation of n!pn, normalized by the logarithm of the mean photon number 〈n〉. In this representation, a perfect Poissonian distribution corresponds to a straight line with a slope of unity. Additionally, we have added in gray the result for four QDs, one resonant and three detuned in an analogous fashion to the three-emitter case.
Download figure:
Standard imageFigure 7. Effective cavity feeding rates due to QD–phonon coupling as a function of the detuning from the cavity resonance. Results are calculated from equation (20) and are shown for 10, 20, 77 and 300 K.
Download figure:
Standard imageIn many cases the actual number of background emitters is larger than the two off-resonant QDs considered. Nevertheless, our results are indicative of the discussed trends and demonstrate that coherent emission can be reached with the aid of detuned emitters. This we underline by showing the result for an equivalent calculation with one additional detuned emitter (four emitters in total) as gray lines in figure 6. As can be seen, the coherent proportion of the emission is increased in comparison to the calculation with three emitters.
4. Feeding of thermal cavity photons
In the literature an inverse cavity loss term (the last term in equation (9)) has been used to account for the effect of detuned emitters. In this section, we compare this 'effective' photon production to the full calculation with several emitters.
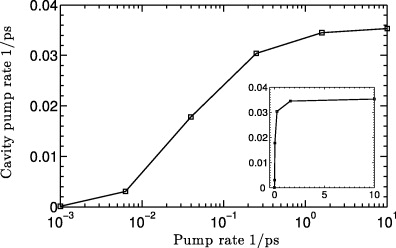
In order to single out the background contribution, we have performed a calculation for a single QD emitter with the same parameters as in the previous section, plus a cavity-feeding Lindblad term. The feeding rate has been chosen to reproduce the mean photon number that we have obtained from the full calculation with three emitters and phonon coupling (circles in figure 6). The resulting feeding rate is shown in figure 8 and clearly exhibits nonlinear behavior. In particular, at high excitation power all emitters are saturated by fast refilling processes, and the cavity-feeding mechanism saturates. This is the behavior expected for a gain material of a few emitters. In contrast, in the literature, often the cavity feeding rate is assumed to be proportional to the pump rate of the system, where the proportionality constant is a fit parameter to a particular experiment. On a linear scale, this would produce a straight line, which cannot be brought into agreement with the case studied here (cf the inset of figure 6). This approach is only justified if the gain material consists of many emitters like in a gas laser.
Figure 8. Cavity feeding rate versus pump rate for a single-emitter calculation. The feeding rate is determined so that the mean photon number of the three-emitter calculation with phonons (dashed line in figure 5) is reproduced. The inset shows the result on a linear scale.
Download figure:
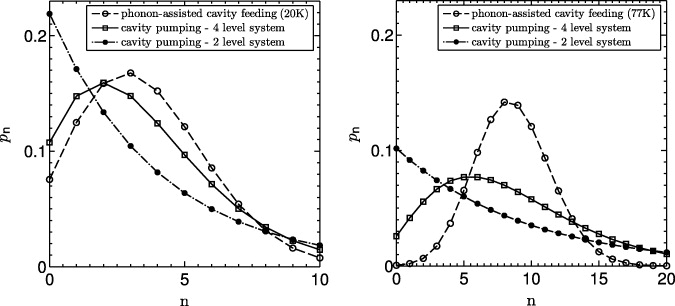
Standard imageThe photon statistics reflects the thermal component of the photons added via the cavity feeding term: in figure 9, the photon statistics is compared for the full calculation with four emitters and the single-emitter result. Again, for the latter, the photon production due to additional emitters is modeled via an inverse cavity-loss term. The comparison to the full calculation reveals a thermal component that is added by the 'effective' photons. In the calculation at elevated temperatures (right panel), the cavity feeding rate is enhanced by about one order of magnitude over the 20 K result. This leads to an accentuation of the difference between the coherent contribution provided by the phonon-mediated coupling of the detuned emitters, and the thermal component added by the 'effective' feeding term. Thus, with increasing number of photons produced by background emitters, the difference that is well perceivable but small for only two off-resonant emitters, will also become large for many background emitters. Then the cavity feeding term results in purely thermal photon statistics [7], whereas a calculation accounting for the gain material along the lines presented here is expected to result in a purely coherent photon population.
Figure 9. Photon statistics at a pump rate of 10 ps−1 at 20 K (left panel) and 77 K (right panel) for the same effective light–matter coupling of 0.16 ps−1. Compared are the results for a single-QD emitter plus cavity feeding, and the full calculation with four emitters and the phonon coupling mechanism described in section 2.2. The feeding rate (4.76 × 10−2 ps−1 at 20 K and 7.11 × 10−2 ps−1 at 77 K) is chosen to reproduce the same mean photon number of 3.6 (8.6 at 77 K) in the calculations. The result reveals a thermal component caused by the cavity feeding that is absent in the full calculation and that is distinctly more pronounced at 77 K, where the cavity feeding is stronger. Also shown is the result from a two-level system plus cavity feeding. At a pump rate of 10 ps−1, quenching has set in, and faster cavity feeding (6.8 × 10−2 ps−1 at 20 K, 7.98 × 10−2 ps−1 at 77 K) is required to produce the same mean photon number. The quenched two-level system in combination with the thermal photons added by the phenomenological cavity feeding leads to thermal photon statistics.
Download figure:
Standard imageUsing a two-level system under the same circumstances results in thermal photon statistics: pump-induced dephasing (inherent in the two-level model) quenches the photon output at the considered pump rate of 10 ps−1, so that a larger fraction of the photon production must come from the cavity feeding term to achieve the same mean photon number. The result in the right panel of figure 8 (dash-dotted line) demonstrates the thermal nature of the photons introduced by the phenomenological cavity feeding term. The latter plays a dominant role in the two-level model due to quenching of the QD emission, and a reduced role in the multi-configuration four-level model, where only some transitions are quenched while the total emission only saturates.
5. Discussion and summary
We have investigated the impact of additional QDs on the emission properties of a single resonant one. Our results indicate that a slight detuning in the meV range can be overcome by phonon-assisted recombination and lead to an emission enhancement that can show the difference between thermal and coherent emission. A comparison with a commonly used 'effective cavity feeding mechanism' reveals (i) that the feeding rate should reflect the properties of the gain material, rather than be chosen proportionally to the system pump rate, and (ii) that the fed photons possess a thermal signature in contrast to our full calculation, where the photon statistics evolves into a Poissonian distribution, reflecting coherent light emission.
A full solution of the von Neumann–Lindblad equation for a realistic QD model containing several configurations to properly reflect the interplay of multi-exciton states across the whole excitation range is computationally costly and here limited to four emitters. Nevertheless, the results are indicative of the situation in which many emitters couple off-resonantly and may guide the development of adequate effective models.
Acknowledgments
We gratefully acknowledge financial support from the Deutsche Forschungsgemeinschaft and the Bundesministerium für Bildung und Forschung.
Footnotes
- 4
We have limited our particular choice for the QD to contain only six configurations, among them the exciton and a biexciton. Beyond this limitation, when additional multi-exciton configurations can form, several recombination channels are available, one of which may turn out to be resonant with the cavity (see e.g. [20]). Here we focus on off-resonant feeding. Also, the realization of potential higher multi-exciton configurations depends on the excitation strength. Then the behavior over the whole excitation range from weak to strong pumping may well differ. Depending on the regime of interest and the system parameters, such as the Coulomb interaction and level spacing, additional configurations may play a role and should be considered.