A multi-state interferometer on an atom chip

The first demonstration of coherence of a Bose–Einstein condensate (BEC) [1] has led to dramatic advancements in atom interferometry. Long coherence times and the localization in phase space of cold-atom clouds, and in particular of BECs, enable high-precision interferometric measurements of the internal properties of atoms, many-body effects and gravity [2]. Some notable examples are the determination of spin squeezing [3, 4], recoil frequency [5], fine structure constant [6], density correlations [7], local gravitational acceleration [8, 9], Newtonian gravitational constant [10] and rotation rate [11]. The unprecedented measurement precision of these interferometers justifies the building of complex and bulky apparatuses such as atom fountains for the local gravity measurement [12]. At the same time, applications outside the laboratory depend on the compactness and robustness of interferometric setups to ensure their portability [13–15], which resulted in a number of interferometers built on atom chips (see, e.g. [4, 16, 17]).

In the classical limit the sensitivity of an interferometer, defined as the smallest signal that can be resolved, is determined by the slope of the interferometric signal and the measurement noise. The best achievable sensitivity of a conventional two-path interferometer is determined by the shot noise and hence scales as $1/\sqrt {N}$ with the number of atoms N. It is known as the standard quantum limit (SQL). An improvement in sensitivity beyond the SQL can be achieved by entangling the input and making a collective non-local measurement at the output. The best possible outcome in a lossless system is the sensitivity of 1/N, known as the Heisenberg limit [18]. An advancement in this direction has recently been demonstrated by employing nonlinear atom–atom interactions to produce entanglement and therefore reduce the phase-measurement error of a Ramsey interferometer below the SQL [3].

An alternative way of improving the interferometer sensitivity is to increase the fringe slope by increasing the number of paths M as in [19, 20]. However, this causes a decrease in the average number of atoms per path and hence a greater susceptibility to noise. If the scaling of slope with M exceeds $\sqrt {M}$ scaling of the shot noise, the sensitivity improves with the number of paths. The multi-path interferometry can also be seen as a fringe narrowing mechanism that increases measurement resolution [20, 21].

Several multi-path matter–wave interferometers have been proposed, the first being the atom–beam interferometer based on the optical pumping between Zeeman states [20]. Multi-path interferometry with cold atoms has been based on the property of optical lattices [5, 22–26], Raman laser pulses [27] and individual laser pulses [28] to cause a controlled atom recoil. While they offer advantages such as a large number of paths and compatibility with techniques for control of atom–atom interactions, these interferometers rely on the spatial separation of paths, and hence cannot be realized in a trap and crucially depend on alignment. They also require high-resolution imaging and sophisticated technology to make them compact and eventually portable.

Here, we present a novel multi-state cold-atom interferometer that is easy to use and fully merged with an atom chip. We do not rely on external variables, i.e. on spatially separated paths, but use internal atomic states. The multi-state functionality is achieved by coherent manipulation of BECs in different Zeeman states of the same hyperfine level by means of radio-frequency (RF) and static magnetic fields. The interferometric fringes are sharpened due to the higher-harmonic phase contributions of the multiple energetically equidistant Zeeman states. The complete coherence of the atom transfer between the condensates guarantees the full fringe visibility⁵. The increase in sensitivity is paid by a reduction in the interferometer sensing range [29] and an undesirable cross-sensitivity to magnetic fields. While the former is an intrinsic property of multi-path interferometers, here we suggest how the effects of the latter can be reduced by using a differential measurement configuration. In addition, our interferometer does not require either alignment or high-resolution imaging.

This paper is organized as follows. The working principle of the interferometer is explained in section 2. Sections 3 and 4 describe the experimental procedure and the theoretical treatment of the interferometer, respectively. In section 5, the main results are reported, which are then discussed in section 6. Finally, in section 7, conclusions are drawn and directions for future work are indicated.

The essential components of the proposed scheme are shown in figure 1. The initial state is a pure low-field-seeking |F = 2,m_F  = 2〉 state since during both the trap loading sequence and the RF evaporation procedure used for producing a condensate, all other magnetic sub-levels are lost. At the bottom of the trap the atoms experience a magnetic field of B₀ ≈ 1 G. Coherent transfer of the atoms to other Zeeman states of the same hyperfine state is realized by the application of a resonant RF pulse. The interferometer is closed by remixing these states by the second RF pulse after a controllable time delay T as in [30]. The second pulse maps the relative phases accumulated between different states during the delay into a population distribution at the output of the interferometer. The relative phases between the states are accumulated due to the presence of the magnetic field B at the bottom of the trap. In this field Zeeman states experience different potentials given by

$$\begin{equation} V=m_Fg_F\mu_0|{\bf B}|, \end{equation} \noindent \tag{ 1 }$$

where m_F and g_F are, respectively, the spin and Landé numbers and μ₀ is the Bohr magneton. Therefore, their relative phases evolve with frequencies equal to the multiples of the energy difference between the adjacent levels ω = g_F μ₀|B|/ℏ, yielding the interference signals rich in harmonics. The harmonics cause the fringe width to decrease with the number of states, which is the basic characteristic of a multi-state interferometer. In order to determine the population of each output state, these states are spatially separated by the application of the Stern–Gerlach method followed by the free-fall expansion and then imaged. The interferometer can be used to measure external fields whose interactions with atoms are state-sensitive. When an external signal is applied during the delay between the pulses, it contributes to the relative phases between the states, causing a shift in the output fringe positions.

Zoom In Zoom Out Reset image size

We note that experimental arrangements in which interferometric states do not separate in space were first used in longitudinal Stern–Gerlach atom–beam interferometers [32]. A variant of these interferometers also uses a detuned RF field to realize beam splitters [31].

Our interferometric setup was designed to be compact, fast and easy to use. It is based on an atom chip setup. Atom chips give the possibility to create a trapping field close to a current-carrying wire by compensating for the field generated by the wire $B=\frac {\mu _0}{2\pi }\frac {I}{r}$ with a constant magnetic field (bias) in a direction perpendicular to the wire. The presence of a bias field creates a zero of the magnetic field on the axis parallel to the wire direction at a height z₀. In close proximity to these axes, the field can be approximated with a quadrupole, thus creating a linear guide for spin aligned atoms. By bending the wire into a Z shape it is possible to create a three-dimensional harmonic trap of Ioffe–Pitchard type with a field minimum different from zero.

An atom chip carrying a z-shaped wire (cross section 2 × 125 μm²) was mounted on a holder (Shapal^® ceramics) with an embedded Z-wire and two U-wires (see figure 2). It was placed facing downwards into a high-vacuum glass cell. Golden chip coating was used to construct a reflection magneto-optical trap (MOT) for ⁸⁷Rb atoms. External coils were used to create all necessary magnetic fields for the MOT. The atoms were further cooled to 10 μK by an optical molasses phase and then pumped into the |F = 2,m_F  = 2〉 state before being loaded in two stages into the chip magnetic trap. First, an ancillary magnetic trap was generated 1.2 mm below the chip by the 25 A-guiding Z-wire in the chip holder. Compression and transfer to the magnetic trap, formed by a 1.7 A current through the z-wire defined on the chip surface, were then performed by simultaneous ramping of the trap and external bias currents. The chip trap had the frequencies (ν_⊥,ν_z) = (950,46 Hz). The atoms were evaporated to quantum degeneracy by ramping down the frequency of an RF field supplied by an RF generator (Agilent 33250A) connected to a U-wire in the chip holder. The BEC had 3 × 10⁴ atoms, a critical temperature of 0.5 μK and was at z₀ = 200 μm from the chip surface. The magnetic field at the bottom of the trap points in the y-direction (figure 2) and can be controlled by an external coil pair. The magnetic field stability was better than 1 mG.

Zoom In Zoom Out Reset image size

The RF pulses were generated by another Agilent 33250 A connected to the second U-wire (figure 2). The frequency was set to match the separation of the Zeeman sub-levels in the magnetic trap. The pulse duration τ was set to an integer number of cycles and chosen to be shorter than 100 μs to minimize the loss of atoms from the trapping region. The phase of each pulse was locked to its trigger and the time delay between the pulses was controlled in steps of 100 ns.

Distribution of atoms across the sub-levels was detected by a 7.5 × magnifying absorption imaging system and a CCD camera (SIS1-s285, Theta-System). The Zeeman states were separated for the imaging by switching off the external bias field and letting the atoms move in the field gradient of the chip z-wire. This rapid change of magnetic field direction did not cause more than 15% of the atoms to change their magnetic sub-level as will be confirmed later in the paper. The fields are shown in the graph of figure 2 and the absorption images in figure 4. The number of atoms in each state was divided by the total number of atoms, thus rendering insignificant the measurement-to-measurement fluctuations in the BEC atom number. The measurements were repeated three times at each point. For each measurement a new BEC was created. The statistical error of the population ratio measurement was 5%.

The proposed interferometer can be mathematically described by a transfer matrix J that acts on the atom-state wave-function vector $\Psi (t)=\left (\Psi _1(t), \Psi _2(t), \ldots , \Psi _M(t)\right )^{\mathrm { T}}$. It is a product of the matrices R that correspond to the coupling Rabi pulses and the operator P that describes the evolution of the states between the pulses, J = RPR. The matrix P is a diagonal matrix that adds a phase ϕ_n to the nth state during the delay T between the pulses, $P_{n,n}=\exp {(-\mathrm {i}E_n T/\hbar )}$, where E_n is the energy of the nth Zeeman level. The matrix R is derived by solving the time-dependent Schrödinger equation for M Zeeman states

$$\begin{equation} \mathrm{i}\hbar\frac{\mathrm{d}\Psi(t)}{\mathrm{d}t}=H\Psi(t), \end{equation} \tag{ 2 }$$

where H is the three-diagonal Hamiltonian that couples the neighbouring m_F states. The coupling strength can be obtained by applying the angular-momentum algebra and the rotating-wave approximation [33, 34] and is given by

$$\begin{equation} H_{F,m_F}=\sqrt{F(F+1)-m_F(m_F+1)}\hbar\Omega/2, \end{equation} \tag{ 3 }$$

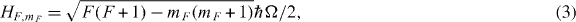
where Ω is the Rabi frequency. For calculation, it is convenient to relabel the |F,m_F 〉 states into |N = 2F + 1,n = F + 1 + m_F 〉. This transformation gives

$$\begin{equation} H_{n,n+1}=H_{n+1,n}=\sqrt{n(N-n)}\Omega/2, \end{equation} \tag{ 4 }$$

$$\begin{equation} H_{n,n}=\Delta_n \end{equation} \tag{ 5 }$$

for the non-zero terms of the final model Hamiltonian, where Δ_n is the detuning of the RF field from the Zeeman transition and δ is the Kronecker symbol [35, 36]. The spin system is a special periodic case of a generally quasi-periodic multi-level system [35, 37].

The Rabi pulse transfer matrix R can be found by diagonalization of $\hat {H}$ using the method described in [35] or its generalization given in [37]. The output of the interferometer is then easily calculated by the application of the transfer matrix J

$$\begin{equation} J_{j,k}= \sum_{l=1}^M R_{j,l}\,\mathrm{e}^{-\mathrm{i}(l-1)\Delta E~T/\hbar}R_{l,k} \end{equation} \tag{ 6 }$$

to the input state vector. The interferometer output has a form of a finite Fourier series whose terms correspond to the multiples of the energy difference ΔE between adjacent Zeeman states in a magnetic field. The pulse area Ωτ of the coupling pulse determines the number of populated states and, therefore, the number of harmonics. In general, an increase in the number of states M leads to an increase in the number of available harmonics, thus enabling further sharpening of the interferometric fringes. We note that the transfer function given by (6) is analogous to that of a Fabry–Pérot interferometer with a limited number of passes.

The simple model described above neglects atom–atom interactions and the relative motion of the condensates in different states. For the experimental setup used here, the collisionless model is valid due to a relatively small number of atoms in the condensate, while the stationary-condensate picture is justified for the short time delays during which movements of the condensates in their respective potentials do not degrade the fringe visibility. In the cases where these effects are present, the full Gross–Pitaevskii equation that includes many-body effects and the exact magnetic potentials should be used [38].

The efficient use of multiple Zeeman states critically depends on the availability of atoms in these states in the interval between the coupling pulses and, therefore, on the population transfer effected by the first Rabi pulse. The role of the Rabi pulses is analogous to the role of beam splitters in a Mach–Zehnder interferometer. The population transfer (splitting) can be controlled by varying the pulse parameters. The dependence of the interferometer signal on the Rabi pulse area can be understood from figures 3 and 4.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

Figure 3 shows the measured and the calculated population transfer between all five Zeeman states by a single resonant Rabi pulse. In the experiment, the pulse duration was kept constant, while a range of Rabi pulse frequencies was sampled by changing the amplitude of the RF pulse. Sampling was random in order to reduce the effect of drifts in the setup. The scaling factor s between the RF voltage V and the Rabi pulse area, Ωτ = sV , was obtained by fitting the measured to the calculated populations in all m_F states. This simple calibration was sufficient to get excellent agreement between the experiment and theory. Results confirm the periodicity of the coupled spin system and the characteristic features of Rabi coupling. The π Rabi pulse completes the population transfer between m_F  = 2 and −2 states, while the 2π pulse completes the whole cycle. The population of the pivot state m_F  = 0 oscillates twice faster than the populations of other states. We note that the same results can be obtained by changing the Rabi pulse duration and maintaining the duration–voltage product constant. Either method can be used to choose the state population at the output of the coupler.

State populations measured at the output of the interferometer oscillate as functions of the time delay between the coupling pulses, thus forming interferometric fringes in T space (figure 4). The fringe frequency corresponds to the energy difference between the adjacent m_F levels. The shape and sharpness of the fringes are controlled by changing the Ωτ of the coupling pulse. The sharp high-visibility interferometric fringes can be generated by pulses that populate all Zeeman states since in this case all harmonics allowed by the system contribute to the output signal (figures 4(b) and (c)). On the other hand, a Rabi pulse that populates only the highest or the lowest Zeeman states yields interferometric fringes with low visibility. The visibility approaches zero for Ωτ = Nπ, N = 1,2,3... in which case either the full population transfer (odd N) or the complete Rabi cycle (even N) is realized. The Ωτ = 2π case shown in figure 4(d) also confirms that the applied Zeeman technique does not alter the state populations by more than 15% and that very good reproducibility of the state readout was achieved.

The performance of the interferometer optimized in terms of the sensitivity and visibility of the m_F  = 2 fringes (figure 4(b)) was evaluated through a comparison with an ideal two-state interferometer. The best result was obtained by the Rabi pulses with the area of 1.55π (the line with circles in figure 5). The corresponding fringe slope was measured to be 0.63 ± 0.09 rad⁻¹ and is larger than the 0.5 rad⁻¹ slope of an ideal two-state interferometer. The estimated total error is due to the population measurement error (see figure 4 and its caption) and the uncertainty in the RF pulse triggering of 100 ns. Much smaller is the contribution of the residual magnetic field fluctuations, which were estimated to be 1 mG. The above values of sensitivity and error give rise to the minimum detectable phase shift of 80 mrad.

Zoom In Zoom Out Reset image size

A remarkable feature of our interferometer is that the enhancement of resolution, defined as (fringe period)/(fringe width), is achieved without reduction in visibility. Indeed, the complete transfer of atoms from m_F  = 2 to −2 and vice versa, see figures 4(a) and (b), confirms the coherence of the transfer and renders the fringe visibility of 1 within the 5% experimental error. The maximum visibility is maintained for delays between the pulses of up to 50 μs. For longer delays it decays exponentially with the half-maximum time decay constant of 100 μs. The decay pattern shown in figure 6 for the state m_F  = 2 is followed by all other states. The decay in visibility can be attributed to the dephasing induced by additional phases accumulated during the motion of the condensates in the inhomogeneous magnetic field [30] and by atom–atom interactions [23, 25]. The former is specific to the interferometer proposed here, while the latter pertains to all interferometers with dense cold-atom gases.

Zoom In Zoom Out Reset image size

The condensates move with respect to each other due to the difference in the potentials that different Zeeman states experience in the same magnetic field. The condensates created by the first Rabi pulse move towards the minima of their respective potentials with different accelerations. The thereby accumulated phase modulation across the condensate is state-dependent and affects the constructive interference with other condensates, for evolution times longer than 50 μs notably so. Moreover, the initial total overlap of the condensates decreases and the untrapped atoms in m_F  = 0 and high-field seeking states eventually leave the trapping region.

We assessed the impact of interactions on the observed decay in visibility by comparing the interferometer made with a BEC with an interferometer made with a coherent thermal cloud that had tens of times lower density. The thermal cloud was trapped in a less tight magnetic trap (ν_⊥ = 574 Hz), which additionally lowered the collision rate. The half-maximum decay time of the thermal interferometer was of the order of 60 μs that is significantly shorter than the decay time of the BEC interferometer, indicating that the interactions are not responsible for the observed decay in visibility. Instead, the larger aperture of the thermal-cloud trap causes larger relative displacements of the state-dependent potentials and hence faster dephasing. Therefore, we can conclude that the relative movement of the different m_F condensates in state-dependent potentials is the main cause of the reduction in visibility. This is in agreement with the result for the two-state interferometer reported in [30]. Such a dephasing can be ultimately avoided by making the measurements in a dipole trap and a constant bias magnetic field. Since the collisions do not significantly degrade performance of the interferometer, they can be used to effect the entanglement between atoms in different states and, hence, further increase the sensitivity towards and beyond the SQL.

The improvement of resolution achieved by the demonstrated interferometer is comparable with that obtainable in other five-state atom–beam interferometers. Here, the resolution is enhanced 1.75 times with respect to the ideal two-path interferometer (figure 5). In the five-path dark state Ramsey interferometer the corresponding improvement was 1.56 times [20], while in the interferometer with the atom–beam splitting realized by multiple light beams it was 1.96 times [28].

Applications of the interferometer proposed here are based on different responses of the Zeeman states to an external field. The interferometer can be used to measure the properties of light pulses, their relative phases and polarization, and the parameters of the light–atom interactions, e.g. the relative polarizability. We note that strong interaction can distort the fringes, making the readout of the signals difficult. However, this does not have severe consequences as it limits the application of the interferometer exactly to the regime in which it performs best—the small-signal regime in which a high sensitivity is required. Indeed, instead of taking the data points at different time delays, small population changes can be detected in the vicinity of the highest-sensitivity point, which significantly reduces the measurement time.

Another application of the interferometer is in measuring the magnetic field amplitude that is, by equations (1) and (6), directly mapped to the periodicity of the fringes. However, the essential role of the magnetic field in the Zeeman state separation also means the interferometer cross-sensitivity to this field, i.e. the dependence of the sensitivity to a measured signal on the magnetic field. This problem is solved by exploiting other signals available at the output of the interferometer to match the number of the measured signals with the number of outputs. This concept, known as multi-parameter sensing, is often exploited in optical fibre interferometers and fibre grating sensing schemes [39]. The corresponding applications of atomic interferometers are yet to be explored experimentally.

In the work described in this paper, the interferometer was optimized to have the highest-sensitivity fringes in the m_F  = 2 state, but it can also be optimized according to other criteria, which may require other input states. For example, a symmetric input state can be used to obtain the highest density of fringes in the m_F  = 0 state, in analogy with the multi-photon states in optics [21, 40]. However, a combination of various m_F states at the input requires an optical trap that traps all these states. The optical trap offers two additional advantages. Firstly, since all atoms are trapped in the coupling region, they can be probed during long delay times between the coupling pulses, which increases the sensitivity of the interferometer. Secondly, a constant magnetic field can be used to separate the states, which eliminates the mutual movement of the condensates and reduces dephasing. On the other hand, the dipole trap allows for collisions that maintain the total spin, which may lead to a redistribution of atoms into spin domains in the presence of the magnetic field [41]. The redistribution may have an adverse effect on the overlap of condensates in different m_F states and hence on coupling.

The integration of the interferometer with an atom chip offers several technical advantages. The small wires allow for fast switching of the magnetic fields, thereby shortening the experimental cycle several times with respect to the free-space setups. This is of particular importance for time-domain interferometers in which the signal is constructed from a series of measurements at different time delays. The proximity of the condensate to the chip wires enables large field gradients that facilitate imaging of the Zeeman states. The chip device is robust, easy to use and a good candidate for future portable cold-atom sensors. Another practical advantage of the described interferometer, which applies equally to the non-chip setups, is that it does not use light signals and therefore does not suffer from the instabilities related to the optical alignment.

We have demonstrated a compact time-domain multi-state interferometer on an atom chip whose sensitivity can be controlled by an RF pulse acting as a controllable coupler. The full population transfer achievable by the coupling pulse and the full fringe visibility of the interferometer guarantee the coherence of the measurement. Due to the interference of several states, the interferometer resolution surpasses that of the ideal two-state interferometer. The simultaneous measurement of all state signals at the output enables a range of advanced sensing applications in atomic physics and optics, while the integration of the interferometer with the chip puts it forward for consideration as a future portable cold-atom-based measurement apparatus. The presented multi-state interferometric scheme can be generalized to other atomic species and BEC setups. Finally, since the interferometer allows for quantum state preparation via many-body interactions, its sensitivity can be further enhanced towards and beyond the SQL.

We thank M Schramböck (Atominstitut, TU-Wien) at the ZMNS (TU-Wien) who realized the AtomChip we have used. We also thank M Inguscio for continuous support and many useful discussions. We acknowledge L Consolino and S Bartalini for help in the construction of the atom chip setup and C Fort, M Fattori and G Roati for useful discussions. We acknowledge financial support from the Future and Emerging Technologies (FET) programme within the Seventh Framework Programme for Research of the European Commission, under FET-Open grants MALICIA (265522) and CHIMONO (216774). JP acknowledges support from the Ministry of Science of Serbia (project no. III 45010) and the L'ORÉAL-UNESCO National Fellowship in Serbia, FS acknowledges the grant AQUTE and FSC acknowledges MIUR (project no. HYTEQ).