Abstract
Multi-channel spin–orbit quantum wires, when subjected to a magnetic field and proximity coupled to an s-wave superconductor, may support Majorana states. We study what happens to these systems in the presence of disorder. Inspired by the widely established theoretical methods of mesoscopic superconductivity, we develop á la Eilenberger a quasiclassical approach to topological nanowires valid in the limit of strong spin–orbit coupling. We find that the 'Majorana number' , distinguishing between the state with Majorana fermions (symmetry class B) and no Majorana fermions (class D), is given by the product of two Pfaffians of gapped quasiclassical Green's functions fixed by the right and left terminals connected to the wire. A numerical solution of the Eilenberger equations reveals that the class D disordered quantum wires are prone to the formation of the zero-energy anomaly (class D impurity spectral peak) in the local density of states that shares the key features of the Majorana peak. In this way, we confirm the robustness of our previous conclusions (Bagrets and Altland 2012 Phys. Rev. Lett. 109 227005) on a more restrictive system setup. Generally speaking, we find that the quasiclassical approach provides a highly efficient means to address disordered class D superconductors both in the presence and in the absence of topological structures.

Content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Semiconductor quantum wires proximity coupled to a conventional superconductor and subjected to a magnetic field may support Majorana fermion edge states [1, 2]. Building on relatively conventional device technology, this proposed realization of the otherwise evasive Majorana fermion has triggered a wave of theoretical and experimental activity, which culminated in the recent report of a successful observation by several experimental groups [3–5]. In these experiments, evidence for the presence of a Majorana is drawn from the observation of a zero-bias peak in the tunneling conductance into the wire. While the observed signal appears to be naturally explained in terms of a Majorana end state, two of us have pointed out that a midgap peak might be generated by an unrelated mechanism [6]: in the presence of even very moderate amounts of disorder, the semiconductor wire supports a zero-energy 'spectral peak' (an accumulation of spectral weight at zero energy) that resembles the Majorana peak in practically all relevant aspects. Specifically, it (i) is rigidly locked to zero energy, (ii) is of narrow width of , where δ is the single-particle level spacing, (iii) carries integrated spectral weight and (iv) relies on parametric conditions (with regard to spin–orbit interaction, proximity coupling, magnetic field and chemical potential) identical to those required by Majorana state formation. What makes the spectral peak distinct from the Majorana is that it relies on the presence of a moderate amount of disorder, viz. impurity scattering strong enough to couple neighboring single-particle Andreev levels. Besides, the spectral peak is vulnerable to temperature-induced dephasing. While this marks a difference to the robust Majorana state, the reported experimental data do show strong sensitivity to temperature, which may be due to either an intrinsic sensitivity of the peak or a temperature-induced diminishing of the measurement sensitivity or both. In either case, the situation looks inconclusive in this regard.
Generally speaking, the results of [6], as well as those of [7, 8], suggest that the observation of a midgap anomaly in the tunneling conductance might be due to either mechanism, disorder peak, Majorana peak or a superposition of the two, and this calls for further research.
Our previous study was based on an analytically tractable idealization of a semiconductor quantum wire subject to a magnetic field sweep. In this paper, we will explore the role of disorder scattering within a model much closer to the experimental setup. The price to be paid for this more realistic description is that a fully analytical treatment is out of the question. Instead, we will employ a semi-analytical approach based on the formalism of quasiclassical Green functions. Introduced in the late 1960s [9, 10], the latter has become an indispensable tool in mesoscopic superconductivity [11–14] and quantum transport in general [15]. We here argue that quasiclassical methods are, in fact, tailor made to the modeling of Majorana quantum wires (or, more generally, quasi-one-dimensional topological superconductors). Specifically, we will show that in the problem at hand, the quasiclassical 'approximation' is actually very mild. Further, the quasiclassical Green function affords a convenient description of the topological signatures of the system in terms of Pfaffians. Finally, the approach can be applied to systems for a given realization of the disorder, and at numerical cost much lower than that of exact diagonalization approaches. As a result, we will be in a position to accurately describe local spectral properties within a reasonably realistic model of a topological multi-channel superconductor. As we are going to discuss below, our findings support the principal statement made in [6].
The rest of the paper is organized as follows. In section 2, we discuss the principal role played by disorder in the system, the idea of the quasiclassical approach and its main results. In section 3, we specify our model system, the quasi-classical approach is introduced in section 4, and in section 5 we discuss the numerical solution of the quasiclassical equations. We conclude in section 6. A number of technical details are relegated to the appendices.
2. Qualitative discussion and results
A schematic view of the device currently under experimental investigation is shown in figure 1. A semiconductor quantum wire subjected to strong spin–orbit interaction is brought in contact with a superconductor (S), and via a tunnel barrier (T) to a normal metal lead (N). The application of a small excess voltage, V , to the latter induces a tunnel current into the central region. The differential conductance dI/dV probes the (tunneling) density of states (DoS) at an energy V (units e = ℏ = c = 1 throughout) relative to the systems chemical potential, μ. The physics we are interested in is contained in a band center (V =0) anomaly in that quantity.
Figure 1. A disordered spin–orbit nanowire, subjected to a collinear magnetic field, is proximity coupled to the s-wave superconductor (S) and terminated by the tunneling barrier (T) at one of its ends. The sketch below shows the profile of the induced superconducting gap Δ(x) and the gate-induced potential V (x) defining the tunnel barrier. Andreev bound states are depicted by dashed lines.
Download figure:
Standard image High-resolution imageIn a manner to be discussed in more detail below, one contribution to the band center DoS is provided by a Majorana bound state localized at the tunnel barrier. The second, spectral contribution is generated by a conspiracy between all the other low-lying quasiparticle states in the system. Technically, these are Andreev bound states forming at energies ±Ej in the region between the tunnel barrier and the superconductor. The number of these states increases with the extension of the wire—a few hundred nanometers in the experiment—and the number of transverse channels below the chemical potential. In the presence of disorder, the entity of these states defines an effective 'quantum dot'. The proximity of the superconductor, and the breaking of both spin rotation and time reversal symmetry imply that the system belongs to symmetry class D [16].
The symmetry of class D random systems implies a clustering of levels at zero energy. Loosely speaking, the conventional level repulsion of random spectra turns into a zero-energy level attraction. On a resolution limited to scales of the order of the mean level spacing, the zero-energy DoS is enhanced by a factor of two relative to the mean background, i.e. it shows a peak. This phenomenon manifests itself at relatively small sample-to-sample fluctuations, i.e. the peak is a sample-specific effect. In passing we note that the weak anti-localization phenomenon discussed in [8] rests on the same principal mechanism of midgap quantum interference.
Below, we will explore the phenomenon of spectral peak formation in a setting modeled to closely mimic 'experimental reality'. To be more specific, we consider a semiconductor wire supporting a number of N > 1 transverse channels below the chemical potential. We assume a value of the chemical potential such that the highest lying of these channels is 'topological' (chemical potential falling into the gap opened by the simultaneous presence of order parameter and magnetic field).
To quantitatively describe this phenomenon, we generalize the quasiclassical Green function approach to the present setting. Indeed, the phenomena we are interested in manifest themselves on length scales large in comparison with the Fermi wavelength, yet smaller than the relevant coherence length, and this makes them suitable for quasiclassical treatment. The quasiclassical theory of the present paper is formulated in terms of the Eilenberger function , which is a position- and energy-dependent matrix of size 8N × 8N. The factor of 8 = 2 × 2 × 2 accounts for spin, chiral (left/right modes) and particle–hole degrees of freedom. It turns out that the structure of the theory is most transparently exposed in the so-called Majorana basis, where the Eilenberger function becomes a real antisymmetric matrix. The Pfaffian of that matrix, , will be seen to assume two values (±1), which locally (in space) identify the invariant of the underlying one-dimensional class D superconductor, in dependence on system parameters: for values of the magnetic field smaller or larger than a critical field, , where μ and Δ are chemical potential and bulk order parameter, the invariant is trivial or non-trivial, respectively. In the latter case, the wire supports a Majorana state at the barrier; in the former it does not.
Figure 2 (left) shows a profile of the local DoS (LDoS) computed at the left end of the wire for typical system parameters as detailed below. The green dashed and red solid curves correspond to a situation without and with the Majorana state. Within our model, the states in the wire carry a narrow width, ∼gT δ, reflecting the possibility of decay through the tunnel barrier into the adjacent lead. (Here, δ is the mean level spacing of the wire, and gT ≲ 1 the barrier tunneling conductance.) This broadening accounts for the finite width of the Majorana peak in the topological regime. Loosely speaking, the negative shoulders observable next to the center peak are due to the repulsion of adjacent levels of the center Majorana level. A more substantial explanation is as follows. For an odd parity of the total number of levels—a signature of the topological regimes—the disordered quantum system falls into symmetry class B, rather than D. (Class B is the designation for a system with the same symmetries as a class D system, yet odd number of levels.) A universal signature of class B is a negative spectral peak at zero energy (the negative of the positive class D peak), superimposed on a single δ-peak (the Majorana). The joint signature of these two structures is seen in the solid curve in figure 2 (left).
Figure 2. Left panel: disorder averaged local DoS (LDoS) at the left end of the spin–orbit quantum wire sketched in figure 1 (in units ν = 1/2πv). The number of occupied bands N = 2 corresponds to four transport channels. Parameters are (i) red solid line (), B = 2.66Δ, μ = Δ—topological phase; and (ii) green dashed line (), B = 0.25Δ, μ = 0.5Δ—trivial phase. The wire length L = 4v/Δ, dimensionless strength of disorder γ2w/v = 0.16Δ, which translates into the mean free path l = 0.4L. Tunneling rate Γ = 5 × 10−2Δ. Velocities in two bands were taken to be equal, v1 = v2 = v. The inset shows profiles of the DoS resulting from random matrix theory. Right panel: the average LDoS (solid green line) and the square root of its second (reducible) moment 〈ν2L( )〉1/2 (dashed blue line) at the left end of the spin–orbit quantum wire in the trivial phase (). System parameters are the same as above. The inset shows profiles of the mean DoS and the square root of the two-level correlation function resulting from random matrix theory.
)〉1/2 (dashed blue line) at the left end of the spin–orbit quantum wire in the trivial phase (). System parameters are the same as above. The inset shows profiles of the mean DoS and the square root of the two-level correlation function resulting from random matrix theory.
Download figure:
Standard image High-resolution imageAt resolutions limited to values ∼δ, the superposition of the Majorana and the class B peak looks next to indistinguishable from the class D peak (dashed), and this similarity of unrelated structures might interfere with the unambiguous observation of the Majorana by tunneling spectroscopy. Indeed, the differential tunneling conductance monitored in the experiment,
is essentially determined by the LDoS2, i.e. the structures shown in figure 2 are expected to reflect directly in the measured signal. (Here, fF is the Fermi distribution, νL is the DoS at the left barrier, ν is the DoS in the single chiral channel per unit length and V is the applied voltage.)
The profiles of the curves shown in figure 2 were computed for a two-channel quantum wire at a mean free path l ≃ L of the order of the system size. We are addressing a system at the interface between the ballistic and the localized regime. In view of these system parameters, it is remarkable that the DoS profiles in figure 2 (left) show striking similarity to the average DoS of a class D and B random matrix model [16]. For comparison the average DoS of a class B and D random matrix Hamiltonian is shown as an inset in figure 2. The similarity of the results indicates that the system of subgap states in our system behaves as if it formed an effective chaotic quantum dot localized in the vicinity of the left system boundary (right to the tunnel barrier). Taking into account spin, chiral and channel quantum numbers, the mean level spacing in such a dot is given by δ ≃ πv/2NL. In the presence of a magnetic field, the quasiparticle gap in the superconducting region of the wire reads . The number of subgap Andreev levels forming the effective dot is thus given by Nlevels ≃ 2 −/δ.
−/δ.
The profiles shown in figure 2 (left) are ensemble averages, 〈νL〉, of the LDoS, νL, where the sampling was over ∼500 randomly chosen impurity configurations. To demonstrate the weakness of fluctuations, figure 2 (right) compares the average LDoS (solid line) to the 'typical' LDoS, i.e. the average . The relatively minor deviation between average and typical DoS demonstrates that the standard deviation
characterizing the strength of mesoscopic fluctuations is relatively small.
The weakness of fluctuations implies that the disorder peak is a realization-specific phenomenon. This is demonstrated explicitly in figure 3, where two unaveraged DoS profile individual disorder configurations are shown. The data are for a 'non-topological' system; no non-degenerate zero-energy level is present. Depending on whether the pair of lowest-lying Andreev states (+ min,−
min,− min) exceeds the level broadening Γ, the DoS enhancement will assume the form of a single peak (magenta solid) or a split peak (green dashed). In either case, an excess DoS of integrated spectral weight ∼1 is present.
min) exceeds the level broadening Γ, the DoS enhancement will assume the form of a single peak (magenta solid) or a split peak (green dashed). In either case, an excess DoS of integrated spectral weight ∼1 is present.
Figure 3. The sample-specific LDoS in the trivial phase without the Majorana state () for two different disorder realizations. Tunneling rate Γ = 0.05Δ; other system parameters are the same as in figure 2. Curves demonstrate two typical scenarios: (i) two conjugate Andreev bound states ± min lying close to the Fermi energy and having energy splitting ∼Γ (dotted green line); and (ii) particle and hole states merged into a single zero-energy peak of width Γ and not resolved by tunnel spectroscopy (solid magenta line). For the chosen set of parameters, the mean level spacing δ = 0.2Δ and the gap in the S region
min lying close to the Fermi energy and having energy splitting ∼Γ (dotted green line); and (ii) particle and hole states merged into a single zero-energy peak of width Γ and not resolved by tunnel spectroscopy (solid magenta line). For the chosen set of parameters, the mean level spacing δ = 0.2Δ and the gap in the S region  − = 0.87Δ. Thus one has approximately Nlevels ≃ 8 random Andreev levels.
− = 0.87Δ. Thus one has approximately Nlevels ≃ 8 random Andreev levels.
Download figure:
Standard image High-resolution imageWe finally note that both the Majorana peak and the D spectral peak crucially rely on the presence and the direction of a magnetic field. In the absence of a field time-reversal symmetry is restored, and the wire turns into a member of symmetry class DIII. Such systems display a DoS depletion at zero energy, rather than a peak. In other words, the spectral peak discussed here will disappear along with the Majorana resonance. The class D spectral peak will also disappear if the magnetic field is rotated perpendicular to the wire (along the -direction). As we discussed above, under the assumption of a thin wire, Lz ≪ ls.o., the spin–orbit term in the Hamiltonian (4) can be neglected. Then the Bogoliubov–de-Gennes (BdG) Hamiltonian is invariant under rotation about the z-axis, , and thus is split into two sectors, each of them belonging to symmetry class A. The wire will be in the gapped phase provided B < Δ. However, the class A one-dimensional insulator does not host boundary Majorana states, nor does the random matrix theory model of class A display any spectral anomaly at zero energy in the average DoS. Therefore, the disappearance of the conductance peak under the rotation of a magnetic field cannot be used as unambiguous evidence in favor of the Majorana particle.
In the rest of the paper, we discuss how the results summarized here were obtained by a combination of quasiclassical and numerical methods.
3. Model of the Majorana nanowire
We consider a multi-band quantum wire of width Lz, subject to Rashba spin–orbit coupling, proximity coupling to an s-wave superconductor, and to a magnetic field [18]. We choose coordinates such that the wire lies along the x-axis, parallel to the magnetic field, the y-axis is perpendicular to the surface of the superconductor, and the spin–orbit field is pointing along the z-axis.
In the rest of this section, we will specify the BdG Hamiltonian describing this system in the presence of disorder (section 3.1). We will then linearize the electron spectrum in the limit of strong spin–orbit coupling, thereby introducing a description in terms of right and left one-dimensional chiral fermions (section 3.2), and finally transform the Hamiltonian into the Majorana basis (section 3.3). Experts in the description of topological quantum wires may proceed directly to the end of the section.
3.1. Bogoliubov–de-Gennes Hamiltonian
Introducing a four-component spinor in the product of spin and particle–hole spaces, the BdG Hamiltonian describing the system in the xz-plane reads
with
Here, Δ = Δ(x) is the proximity amplitude induced by the superconductor, , where H is the external field, we have taken into account the transverse momentum (−i∂z) in the Rashba term, and is the random disorder Hamiltonian. The Pauli matrices operate in spin space.
We proceed by introducing a system of transverse wave functions, {Φσn(z)}, which leads to a linear decomposition of the Grassmann fields (σ = ↑,↓) as
Defining
the Hamiltonian then takes the form
where the one-dimensional Hamiltonian acts in the nth band as
In the case of an ideal waveguide the transverse wavefunctions are , so that μ(n)z = π2n2/(2mL2z) and the matrix elements of the spin–orbit interaction read
Let us now assume a thin wire, Lz ≲ lso = ℏ/(mα), where lso is the spin–orbit length3. In this case the matrix elements hs.o.nm ≪ μ(n)z can be treated as perturbations. To this end, we introduce a unitary transformation , which brings the high-energy part of the Hamiltonian, (μ(n)zδnm + hs.o.nm), to diagonal form. Due to the weakness of the perturbation, the transformation is close to unity, , with generators . To first-order perturbation theory their explicit form reads
The transformation and generates the approximate Hamiltonian
Here we have redefined our notation for the disorder potential , and introduced a small correction to the quasiparticle Hamiltonian, , and to the order parameter, . One can estimate the matrix elements of these operators as Vnm ∼  (Lz/lso) and (δΔ)nm ∼ Δ(Lz/lso), where
(Lz/lso) and (δΔ)nm ∼ Δ(Lz/lso), where  is the quasiparticle energy. Since we are primarily interested in the effects of disorder, we will limit our discussion to the situation when the low-energy physics is disorder dominated, i.e. the random potential masks the off-diagonal matrix elements of the deterministic Hamiltonian. Having this in mind we thus omit both and throughout the paper. However, this assumption does not affect our results in qualitative ways.
is the quasiparticle energy. Since we are primarily interested in the effects of disorder, we will limit our discussion to the situation when the low-energy physics is disorder dominated, i.e. the random potential masks the off-diagonal matrix elements of the deterministic Hamiltonian. Having this in mind we thus omit both and throughout the paper. However, this assumption does not affect our results in qualitative ways.
Assume that the chemical potential lies close to the bottom of the Nth band, μ ≃ μ(N)z. We refer to this band as the 'topological band', since in the absence of interband scattering it defines whether the quantum wire is in the topological phase or not. The condition of the topologically non-trivial phase reads B2 > B2c = Δ2 + (μ − μ(N)z)2. We also assume a hierarchy of energy scales μ(N)z − μ(N−1)z ≫ Eso ≫ Δ ∼ B, where Eso = mα2/2 is the spin–orbit energy. This condition implies that all other channels with the band index n < N are in the trivial phase, since for them B2 ≪ Δ2 + (μ − μ(n)z)2. In the current experiments Eso ≳ Δ, i.e. our theory is on the border of applicability.
3.2. One-dimensional chiral fermions
For strong spin–orbit coupling, Eso ≫ B, each band is characterized by two Fermi momenta,
as shown in figure 4. We aim to construct a low-energy Hamiltonian describing the system at energy scales ≲Eso. To this end we represent the fields ψ(n)σ as
in terms of a superposition of right (R) and left (L) chiral fermions, and then linearize the Hamiltonian (11) around the Fermi momenta. Modes with Fermi momenta of equal modulus define a conduction channel. We observe that each channel belongs to one of the two subsets, a or b. In the a-channel R-movers have spin up and L-movers have spin down, while for channels of type b spins are reversed. The a-channel of band index N plays a distinguished role in that it has zero Fermi momentum, kaN = 0. This particular mode defines what we call the 'topological channel'. For max{B,Δ} ≪ Eso it is the only channel strongly susceptible to the magnetic field, thus defining the topological phase of the whole wire. The effect of B (but not Δ) on other channels can be safely neglected.
Figure 4. Chiral one-dimensional fermions in the spin–orbit quantum wire: a and b channels are shown by open and filled dots, respectively. The magnetic field B affects the dispersion relation for the a-channel only if the chemical potential is close to μ(N)z.
Download figure:
Standard image High-resolution imageWe next collect all R and L fields into two spinors,
and where the band index (n) is left implicit. The spinor Ψ acts in an 8 × N-dimensional space, defined by the direct product of band (index n), channel (a/b), chiral (R/L) and particle–hole spaces. In this representation, the low-energy Hamiltonian is given by
where
Here, vn = [2m(μ(N)z − μ(n)z + Eso)]1/2/m is the Fermi velocity of the nth channel, the chemical potential μ is now defined relative to the energy μ(N)z, and is a random 8 × 8 matrix satisfying the Hermiticity condition . In deriving this Hamiltonian, we have neglected oscillatory terms with phases ix(±ka ± kb). This is justified because the typical lengths involved in the problem (ξ ∼ Δ/v and lB ∼ B/α) exceed by far the Fermi length λF ∼ max(1/ka,1/kb) determined by the large spin–orbit energy Eso. In the case of a topological channel with n = N, the Fermi momentum ka = 0; hence one has to keep the matrix element of magnetic field B between the R and L states. The quasiclassical approximation (i.e. the linearization of kinetic energy around the chemical potential μN) is, nevertheless, plausible here due to our assumption Eso ≫ max{B,Δ}. We have also used the fact that the order parameter Δ(x) can be chosen to be real.
3.3. Majorana representation
The 8N × 8N first-quantized matrix defining the Hamiltonian (16) satisfies the p–h symmetry
which is the defining condition for a class D Hamiltonian (here, the transposition acts on the kinetic term as ∂Tx = −∂x). However, all that follows will be more conveniently formulated in an alternative representation, in which the symmetry assumes a different form: for each band n, we define a set of eight Majorana fields
(and analogous relations for the L-movers, with spin reversed), which we combine into the 8N-spinor
The two spinors χ and Ψ are related by the unitary transformation
We combine the Majorana fields of the a and b channels as ξR = (ξRa,ξRb)T, and reorder the spinor components as
In this representation (which will be used throughout the rest of the paper), the Hamiltonian (16) takes the form
where the deterministic part reads
and the random matrices are constructed as
in terms of real (symmetric) and imaginary (antisymmetric) parts of the random matrices , etc. The remaining blocks of the -matrix are defined by
In the Majorana basis (21), the class D symmetry is expressed through the antisymmetry .
We finally specify the statistics of disorder. We choose to be a δ-correlated and Gaussian distributed random matrix of size 8N × 8N with a zero mean value and variance
Here, the composite indices (i,j, etc) label states in the direct product of band, channel and chiral spaces. The scattering matrices defined in this way break time reversal and spin rotation symmetry (e.g. random spin-flip scattering caused by random spin–orbit terms is included in (27)). The strength of disorder set by the coefficient γw translates into the 'golden rule' scattering rate
of the normal conducting (i.e. superconductor decoupled) quantum wire.
4. Quasiclassical approach
The kinetic term in the low-energy Hamiltonian (22) that was discussed in the previous section is linear in momentum, and this facilitates the formulation of quasiclassical equations of motion (aka Eilenberger equations) for the model at hand [9]. We here review the construction of these equations in a manner closely following the spirit of [19, 20]. After introducing the basics of the method (section 4.1), we construct the Eilenberger Q-function in the limit of a single clean 'topological channel' (section 4.2) and discuss the resulting DoS (section 4.3). In section 4.4, we define the topological invariant in terms of the Q-matrix. Section 4.5 outlines the general construction of the solution to the Eilenberger equation in the inhomogeneous disordered wire with boundary conditions.
4.1. Eilenberger method
We start by defining
where are the retarded and advanced Green functions of the system. Under transposition (which in our current representation represents the particle–hole symmetry), the function g behaves as
i.e. advanced and retarded Green functions get interchanged. It is not hard to derive the two mutually adjoint differential equations
describing the dynamical evolution of g. Here,
where matrix has elements
and the operator is related to the Hamiltonian matrix as
Due to the antisymmetry of , the operator obeys the particle–hole symmetry
We next define the Eilenberger function as
where the subtraction of the sgn-function regularizes a discontinuity arising in g at x = x' due to the combination of linear derivatives and δ-function inhomogeneity in equations (31). Subtracting the two equations in (31), we then obtain the Eilenberger equation of motion
The Eilenberger function Q obeys the particle–hole symmetry
and the normalization condition , where is the unit matrix (the latter condition can be checked by verifying that equation (37) preserves the normalization Q2 = const.). The unit value of the normalization constant is fixed by the jump height of the sgn-function in (36). We finally note that the operator can be straightforwardly constructed from equation (34); however, for our present purposes, we need not state its explicit form in generality.
4.2. Eilenberger function in the clean limit
As a warmup, we apply the quasiclassical approach to the limit () of an infinite clean quantum wire subjected to constant B,Δ. In this system all channels are decoupled, and we may concentrate on the 4 × 4 matrix Q (B,μ) describing the 'topological' channel a with n = N. (The Eilenberger function of the other channels may be obtained by setting B = 0, rescaling the velocity and transforming Δ → − Δ in the case of b-type channels.)
(B,μ) describing the 'topological' channel a with n = N. (The Eilenberger function of the other channels may be obtained by setting B = 0, rescaling the velocity and transforming Δ → − Δ in the case of b-type channels.)
We start by introducing the 4 × 4 operator
as the reduction of the general operator to a single channel. The solution Q is then determined by the relations [Q
is then determined by the relations [Q ,L
,L ] = 0 and . To solve these equations, we assume L
] = 0 and . To solve these equations, we assume L to be diagonalized as
to be diagonalized as
where the exact form of the (non-unitary) transformation matrix T will not be needed and
are the eigenvalues. The defining equations for Q are then solved by matrices of the form
where is a diagonal 4 × 4 matrix containing unit-modular entries in arbitrary configuration. The proper sign structure is determined by causality, i.e. the sign of the infinitesimal offset  →
→  ± i0 in the retarded/advanced Green function. That increment enters in the combination (
± i0 in the retarded/advanced Green function. That increment enters in the combination ( ± i0)σRLz, which means that the appropriate matrix structure of the retarded Green function (opposite for advanced) is given by
± i0)σRLz, which means that the appropriate matrix structure of the retarded Green function (opposite for advanced) is given by
A more explicit derivation of this structure is detailed in appendix A.
4.3. Clean density of states
The DoS in the bulk of the topological wire is given by ν( ) = (2πv)−1Re tr σRLzQ
) = (2πv)−1Re tr σRLzQ . The matrices T diagonalizing Q do not commute with σRLz, which means that a little extra work is required to evaluate the trace. We start from the representation
. The matrices T diagonalizing Q do not commute with σRLz, which means that a little extra work is required to evaluate the trace. We start from the representation
where P+ and P− are projectors on the space of L -eigenstates with eigenvalues ±λ+ and ±λ−, respectively:
-eigenstates with eigenvalues ±λ+ and ±λ−, respectively:
That this representation faithfully represents the matrix Q is checked by application of (44) in the eigenbasis where all matrices assume a diagonal form. It remains to obtain a representation of P± that does not make explicit reference to the diagonalizing matrices T. To this end, note that (eigenrepresentation understood) . This equation can be straightforwardly solved as
is checked by application of (44) in the eigenbasis where all matrices assume a diagonal form. It remains to obtain a representation of P± that does not make explicit reference to the diagonalizing matrices T. To this end, note that (eigenrepresentation understood) . This equation can be straightforwardly solved as
Substituting this expression into equation (44), we obtain a representation of Q that makes reference only to the operator (39), and its eigenvalues. Computing the trace, we obtain DoS profiles as shown in figure 5. Before discussing the structure of these results, a general remark may be in order: the DoS of a one-dimensional quantum system is determined by an interplay of the kinetic energy operator () and the 'potential' (). On the other hand, we computed the DoS from Q as determined by , and this matrix seems to be oblivious to the kinetic energy. A closer look, however, shows that information on the band dispersion sneaks in via the nonlinear constraint . Indeed, the conservation of the constraint, and the unit value of the normalization are consequences of the linearity of the derivative operator in (31), which in this way co-determines the structure of Q.
Figure 5. Sketch of the DoS and the corresponding dispersion relations in the clean nanowire. The gap is closed at the transition point μ = μc (a), and opened again (b), (c). For μ > μ* two minima develop (d).
Download figure:
Standard image High-resolution imageInspection of equation (44) shows that the DoS contains singularities at the zeros
λ±( ) = 0, which are located at
) = 0, which are located at
Let us assume that B > Δ. Figure 5(a) shows the ensuing DoS profile, along with the underlying dispersion relation for a value of the chemical potential μ < μc, where
defines a critical value where the lower of the DoS singularities,  −, touches zero and the band gap closes (figure 5(b)). At larger values μ > μc, the gap reopens, (c), the DoS looks qualitatively similar to that of the μ < μc regime, but the system is in a topologically distinct state (see the next section). Finally, at values μ > μ*, where
−, touches zero and the band gap closes (figure 5(b)). At larger values μ > μc, the gap reopens, (c), the DoS looks qualitatively similar to that of the μ < μc regime, but the system is in a topologically distinct state (see the next section). Finally, at values μ > μ*, where
the lower band  −(k) develops an extremum at finite values of k that manifests in a third van-Hove singularity at the energy
−(k) develops an extremum at finite values of k that manifests in a third van-Hove singularity at the energy
as shown in panel (d) of figure 5. This energy minimum corresponds to the Fermi momentum ka of the 'topological' channel that effectively becomes non-zero at high chemical potential μ (see equation (12)).
4.4. topological invariant
The symmetry equation (38) implies that at zero energy the product σRLzQ =0 is an antisymmetric 4 × 4 matrix, which implies the existence of a Pfaffian. Due to the signature of Λ, the determinant of Q is unity; the same is true for the determinant of the 4 × 4 matrix . Consequently, the Pfaffian of σRLzQ
=0 is an antisymmetric 4 × 4 matrix, which implies the existence of a Pfaffian. Due to the signature of Λ, the determinant of Q is unity; the same is true for the determinant of the 4 × 4 matrix . Consequently, the Pfaffian of σRLzQ =0—which squares to the determinant of that matrix—may take one of two values, ±1. This motivates the definition of the topological index
=0—which squares to the determinant of that matrix—may take one of two values, ±1. This motivates the definition of the topological index
distinguishing between the two phases. Computing Ntop from (44), we find the index structure stated in (51). (Right at the critical point μ = μc, the matrix Q =0 becomes singular and the index cannot be defined.)
=0 becomes singular and the index cannot be defined.)
4.5. Eilenberger equation with disorder
In this section, we discuss the formal solution of the Eilenberger equation in the presence of disorder. The solution is 'formal' in the sense that the Eilenberger Green function will be a functional of a given realization of the disorder. To obtain practically useful information, one will want to average over different realizations, and this step of the computation needs to be done numerically, as discussed in the next section.
To start with, consider the prototypical system geometry shown in figure 6. The terminals indicated at the left and right represent superconducting regions, assumed to be non-disordered for simplicity. (This is an inconsequential assumption provided the rate of disorder scattering τ−1 ∼ Nγ2w〈1/vn〉 does not exceed the energy gaps ( − or
− or  0) in the terminals.) In these regions, the Eilenberger equation can be solved analytically, as discussed in the previous section. Describing the disorder present in the center region in terms of a generalized variant of the quasiclassical evolution operator , we will show how the left and right asymptotic configurations of the Green function get connected by a transfer matrix, M, functionally depending on the disorder configuration. The ensuing generalized Green function will then be the starting point for our numerical analysis.
0) in the terminals.) In these regions, the Eilenberger equation can be solved analytically, as discussed in the previous section. Describing the disorder present in the center region in terms of a generalized variant of the quasiclassical evolution operator , we will show how the left and right asymptotic configurations of the Green function get connected by a transfer matrix, M, functionally depending on the disorder configuration. The ensuing generalized Green function will then be the starting point for our numerical analysis.
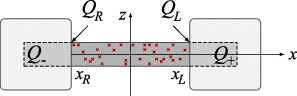
Figure 6. A disordered spin–orbit wire connected to two ideal superconducting terminals that are described by the Eilenberger functions Q+ and Q−. The Q-matrix at the boundaries between the scattering region and terminals is denoted by QR and QL. In the superconductors, the Q-matrix rapidly converges to either Q+ or Q− on a scale of coherence length.
Download figure:
Standard image High-resolution imageTo be more specific, we consider a quantum wire where the gap Δ(x) and/or chemical potential μ(x) vary in space in the region |x| < L/2 and saturate to some constants ΔL/R and μR/L at x ≪ − L/2 or x ≫ L/2, respectively (figure 6). These constants set asymptotic values of the Q-matrix,
where Q± are constructed using the results of section 4.2 for the homogeneous profile of Δ, B and μ. The boundary Green's function Q− and Q+ may describe different or equivalent topological phases of the wire.
We denote the Q-matrices obtained at the interface between the asymptotic superconducting regions, and the center disordered region, respectively, as
where xR = −xL = L/2. These two configurations are related by a transfer matrix,
For arbitrary positions x and x', the formal expression for the transfer matrix M(x,x') at a given energy  follows from the Eilenberger equation (37),
follows from the Eilenberger equation (37),
with denoting the path-ordering operator. A relation similar to equation (54) connects the boundary matrices QR/L with the Green function in the far right/left region of the wire,
assuming that x → ± ∞. The transfer matrix satisfies certain symmetries. Along with the unitarity condition (cf equation (34))
it also satisfies the p–h symmetry: with the use of equation (34) one obtains
and this yields
We now aim to represent the Q-matrix in the scattering region in terms of the transfer matrix M and the asymptotic Eilenberger functions Q±. We start by translating the transfer matrix relation (56) to a set of algebraic conditions relating the matrices QR/L to Q±. To this end, note that the action of the non-unitary (cf equation (57)) transfer matrix on a generic matrix QR will, in general, produce exponentially increasing and decreasing contributions. The former are inacceptable in that they lead to exponential divergencies in the quasiclassical Green function. As is detailed in appendix B, the requirement of a non-divergent Green function leads to the algebraic conditions
and the asymptotic Eilenberger functions Q±. We start by translating the transfer matrix relation (56) to a set of algebraic conditions relating the matrices QR/L to Q±. To this end, note that the action of the non-unitary (cf equation (57)) transfer matrix on a generic matrix QR will, in general, produce exponentially increasing and decreasing contributions. The former are inacceptable in that they lead to exponential divergencies in the quasiclassical Green function. As is detailed in appendix B, the requirement of a non-divergent Green function leads to the algebraic conditions
while the right matrix QR should obey the analogous relations
We finally combined these equations with the transfer matrix relation (56) to obtain closed expressions for QL/R in terms of the asymptotic configurations Q± and M. As a result of a straightforward calculation detailed in appendix B, we obtain
where M ≡ M(xR,xL).
These formulae define the starting point for an efficient numerical computation of the disordered Eilenberger function Q(x). To this end, one computes the transfer matrix M by numerical solution of the corresponding system of linear first-order differential equations. One next applies equations (62) and (63) to obtain QR/L. Finally, our main object of interest, Q(x), is obtained by application of M(x,xR/L) to either QR or QL.
So far we have considered a quantum wire connected to two superconducting terminals. However, the generalization of the method to the system shown in figure 1 is straightforward. The key observation is that in the limit of vanishing barrier conductance gT ≪ 1, the chiral fermion fields satisfy
where ϕ is the (energy-dependent) reflection phase shift. (Here, we assumed the absence of barrier spin-flip scattering, inter-channel scattering or related complications.) In the limit of asymptotically high potential barrier, ϕ = π. Relations (64) define boundary conditions for the Eilenberger function QL. As verified in appendix D, these conditions assume the form of equations (60), where, however, the role of Q− is taken by an 'effective' matrix Q− ≡ Q−(ϕ) describing the tunnel junction. The explicit form of this matrix reads
This matrix also satisfies , and the relations (62) and (63) stay intact.
We close this section with an important statement: the Eilenberger functions Q+ and Q− of the terminals define the 'Majorana number' [21] of the wire as
in terms of the product of two topological invariants given by equation (51). It is shown in appendix C that for the system supports a Majorana fermion localized in the scattering region between two terminals.
5. Numerics
We next turn to the discussion of our numerical results obtained for the setup shown in figure 1. We have solved the quasiclassical equations according to the algorithm of section 4.5 and from there computed the LDoS νL( ) = (2πv)−1Re tr(σRLzQL) at the left end of the wire close to the tunnel barrier. In the actual calculations, we shifted the energy into the complex plane,
) = (2πv)−1Re tr(σRLzQL) at the left end of the wire close to the tunnel barrier. In the actual calculations, we shifted the energy into the complex plane,  →
→  + iΓ. This shift accounts for the fact that in the 'real' system states may escape to a continuum of lead scattering states, which gives them the status of quantum resonances of finite lifetime ∼Γ−1. The corresponding decay rate [22] is given by the standard golden rule expression Γ ∼ gT
δ, where δ ∼ πv/2NL is the mean level spacing in the scattering region of size L. In principle, one might numerically compute the broadening by an extension of the numerical setup so as to include and extend the normal metallic scattering region to the left of the tunnel barrier. This, however, would slow down the performance of the numerics, which is why we prefer to introduce the broadening 'by hand'. At any rate, the Majorana peak, present for , will acquire a finite width ∼Γ. The DoS profiles obtained as a result of the procedure outlined above are presented and discussed in section 2 above.
+ iΓ. This shift accounts for the fact that in the 'real' system states may escape to a continuum of lead scattering states, which gives them the status of quantum resonances of finite lifetime ∼Γ−1. The corresponding decay rate [22] is given by the standard golden rule expression Γ ∼ gT
δ, where δ ∼ πv/2NL is the mean level spacing in the scattering region of size L. In principle, one might numerically compute the broadening by an extension of the numerical setup so as to include and extend the normal metallic scattering region to the left of the tunnel barrier. This, however, would slow down the performance of the numerics, which is why we prefer to introduce the broadening 'by hand'. At any rate, the Majorana peak, present for , will acquire a finite width ∼Γ. The DoS profiles obtained as a result of the procedure outlined above are presented and discussed in section 2 above.
6. Conclusions
In this paper, we have adapted the Eilenberger quasiclassical approach to the specific conditions of a class D topological quantum wire. The most striking feature of the quasiclassical approach is that the Green functions of the system are described by ordinary and hence easily solvable differential equations. A numerical solution of these equations for given realizations of the disorder produces accurate information on the spectral properties of reasonably realistic model systems hosting Majorana boundary states. Our results confirm the predictions made in [6] for a more idealized system, viz. that disorder generates spectral peaks that can be confused for genuine Majorana peaks. It thus seems that an unambiguous detection of the Majorana might call for a measurement scheme beyond direct tunneling spectroscopy.
Acknowledgments
We thank C W J Beenakker, F von Oppen and M Feigel'man for fruitful discussions. This work was supported by the collaborative research grant no. SFB/TR12 of the Deutsche Forschungsgemeinschaft.
Appendix A.: Derivation of equation (43)
The goal of this appendix is to derive the structure (43) by explicit calculation. Our starting point is the momentum representation of the equations of motion for the quasiclassical Green function g(x,x'; ) ≡ g(x − x';
) ≡ g(x − x'; ),
),
Assuming a diagonal representation as in (40), we obtain
The inspection of eigenvalues λ± shows that for the retarded Green function, i.e. at  →
→  + i0, one has Re (λ±) > 0. This gives
+ i0, one has Re (λ±) > 0. This gives
Sending x' → x and comparing to (36), we obtain the identifications (42) and (43).
Appendix B.: Boundary conditions
In this appendix, we derive the boundary conditions (60), (61) for the Q-matrix. The method we use is adapted from the circuit theory of [20, 23]. For simplicity, we consider the 4 × 4 matrices describing individual channels; generalization to many coupled channels is straightforward.
Consider the quasiclassical function g(x,x') ≡ g(x,x'; ) to the right of the right terminal, x,x' ⩾ xR. By assumption, the generator L
) to the right of the right terminal, x,x' ⩾ xR. By assumption, the generator L | x>xR is constant in space, and this means that equations (31) defining g admit the solutions
| x>xR is constant in space, and this means that equations (31) defining g admit the solutions
where we have again set v = 1 for notational simplicity. According to equation (A.3), we have
so that
Defining and , we next transform to the representation (40) to arrive at
The key observation now is that the matrix functions must remain finite as x → ∞. Due to the positivity of the matrix , this is equivalent to the condition . By the same token, we have . Finally, noting that TΛT−1 = Q+ represents the asymptotic form of the Q-matrix deep in the superconductor, we arrive at equations (61). Equations (60) are shown in an analogous way.
We are now in a position to derive equations (62) and (63). To this end, we take equations (60) and multiply it by the transfer matrix M from the left and by M−1 from the right. Bearing in mind equation (56), one obtains
Adding this relation to equations (61), we arrive at
which in one more step yields the result (62). Equation (63) is proven analogously.
Appendix C.: Majorana mode
In this appendix, we discuss the 'Majorana number' and show how the Majorana state emerges from the quasiclassical Eilenberger function.
We consider the spectrum {Ej} of Andreev bound states, which follows from the poles of the Q-function (62), (63). If we denote
then the energies Ej are solutions of the secular equation . The Majorana state, if it exists, corresponds to E0 = 0.
To proceed, we introduce matrices , and the secular matrix . Since in the subgap interval of energies there is no distinction between the retarded and advanced Green function, the unitarity relation (GR/A)† = GA/R, the basic definitions equations (29) and (36) imply . Further, particle–hole symmetry (38) yields . Taking into account the class D symmetry of the transfer matrix, equation (59), the secular matrix takes a form
It satisfies , and thereby guarantees that Andreev bound states appear in pairs ±Ej.
One may ask now whether a zero-energy solution of the secular equation exists or not. At  = 0, the particle-hole symmetry puts tighter restrictions on the matrices , M and (we omit the energy argument for brevity). One obtains
= 0, the particle-hole symmetry puts tighter restrictions on the matrices , M and (we omit the energy argument for brevity). One obtains
We thus observe that both and are real antisymmetric matrices of size 8N × 8N, which enables us to rewrite the secular equation in terms of a Pfaffian
Let us denote by ΩL0 the left null space of the matrix , i.e. any bra 〈ϕ|∈ΩL0 by definition satisfies . Since is antisymmetric, the dimension of its null space is even, . At this stage, we make use of a mathematical lemma proven in appendix A of [24]: the parity of the number can be expressed as
The particle–hole symmetry (C.4) implies that Det M = ± 1 at zero energy. Now, the transfer matrix M(x,x') is a continuous function of its arguments, with initial value . We thus conclude that Det M = + 1, so that the parity of is determined by the terminal configurations,
This parity is equal to the 'Majorana number' introduced in section 4.5.
Let us now focus on the most interesting case , corresponding, as we will see, to a single Majorana mode4. In this case, we have dim ΩL0 = 2, and the null space is spanned by two linearly independent vectors. Let 〈ϕ1|∈ΩL0 be the first basis vector. It is easy to check that 〈ϕ2| = 〈ϕ1|Q+∈ΩL0, and we may choose this state for the second basis vector in ΩL0. Indeed, for any 〈ϕ1|∈ΩL0 one has . Using the definition of , equation (C.1), we deduce that
This relation enables us to evaluate as
and hence we proved that 〈ϕ2|∈ΩL0. Since is a real antisymmetric matrix, its right null space is obtained as ΩR0 = (ΩL0)†. In other words, the two kets |ϕ1,2〉 = (〈ϕ1,2)|)† satisfy the relation .
Let us look at the Eilenberger function QR( ) around its pole at
) around its pole at  = 0. According to equation (62), it can be represented by two equivalent equations,
= 0. According to equation (62), it can be represented by two equivalent equations,
Multiplication by σRLz yields
At  → 0 the inverse operator from the secular matrix has the pole structure, , where the matrix is its residue at zero energy.
→ 0 the inverse operator from the secular matrix has the pole structure, , where the matrix is its residue at zero energy.
At this stage it is advantageous to introduce a new bra
and ket
basis in the null spaces ΩL0 and ΩR0, respectively The bra basis 〈χ±| is not orthogonal and we can denote by |η±〉 the ket basis, which is dual to it, 〈χσ|ησ'〉 = δσσ'. Using these definitions, we may formulate resolutions of unity,
where σ = ± is summed over.
Now let us look at the singular part of the matrix ,
We note that the matrix acts as the projector in the space ΩL0, since
Similar relations hold in the ket space ΩR0:
Equivalently, we may write
Using these properties, it follows that . Multiplying these relations by P− from the right, and using the projector property P2− = P−, we obtain the relation
or
where we defined . Taking into account our definition of the quasiclassical Green's function, equations (29) and (36), we finally obtain that the singular part of the propagator around zero energy at x = x' = xR takes the form
where is the diagonal velocity matrix.
This expression can be compared with the spectral decomposition of the Green function,
where |ψE(x)〉 are normalized eigenfunctions of the BdG Hamiltonian, Eg is the gap in the spectrum of the wire, the sum is going over the set of subgap Andreev levels (we have particle–hole symmetry E−j = −Ej) and the first term is present if the system contains a Majorana state. One thus concludes that
is the amplitude of the Majorana particle at the point xR. The amplitude of the Majorana state at any other point x can be obtained from |ψ0(xR)〉 by applying the transfer matrix M(x,xR).
To conclude, we have shown that if the Majorana number of our system is topologically non-trivial, i.e. , then the Green function has the pole at zero energy. Up to a prefactor, the residue at zero energy is then the projector on the one-dimensional linear subspace spanned by the Majorana particle.
Appendix D.: Matrix Q− of a tunnel junction
In this appendix, we show that the boundary conditions for the Eilenberger matrix Q of a spin–orbit wire terminated at the left end by a (infinitely high) tunnel barrier are equivalent to algebraic relations (60) with the effective matrix Q− given by equation (65).
Let us work in the original particle–hole basis where the spinor Ψ takes the form specified by equation (15). We start by rewriting the left boundary conditions (64) in a matrix form. If one defines the reflection matrix
in the particle space, then is the reflection matrix for holes. Consequently, the spinor Ψ(xL) satisfies the condition
The full reflection matrix is unitary obeying the particle–hole symmetry, σphxRTσphx = R. Hence the boundary condition for the bar spinor takes a similar form
According to the definition (29), the Green function ge(x,x') inherits the boundary condition right to the tunnel junction from those of the direct product of two spinors, . We thus conclude that
When deriving the second relation, we have taken into account that . The above conditions are valid for any x > xL. Sending now x → xL + 0 and using the relations (B.2) written for the matrix QL, one obtains
We see that these boundary conditions are equivalent to the algebraic conditions (60) if one identifies . The normalization guarantees that Q− belongs to the manifold of the quasiclassical Eilenberger functions. Transforming matrix Q− into the Majorana representation (21), we finally obtain the result (65). Note that Pf (Q− σRLz) = + 1; thus such a Q-matrix describes a topologically trivial insulator.
The scattering phase ϕ is the parameter of the matrix Q− that may depend on the band index n and characterizes the tunnel junction. In our numerical simulations we have used ϕ = π for all bands, which corresponds to the infinitely high barrier as compared to the energies of Andreev bound states.
Footnotes
- 2
- 3
Using the data of [3], one can estimate Lz ≃ 100 nm and lso ≈ 200 nm, justifying the considered limit of a thin wire.
- 4
In the case of odd as well as non-zero even , the -fold degeneracy of a zero level is accidental and not topologically protected. It can be reduced down to or 0 by continuous distortion of the transfer matrix M.

























![$[{\cal H}, \hat s_z] =0$](https://content.cld.iop.org/journals/1367-2630/15/5/055019/revision1/nj463982ieqn17.gif)






















![$\hat V = \alpha \, [\hat{X} , \hat s_z]\, \partial _x $](https://content.cld.iop.org/journals/1367-2630/15/5/055019/revision1/nj463982ieqn31.gif)
![$\delta \hat \Delta = - \Delta [ \hat X, \hat s_y ]$](https://content.cld.iop.org/journals/1367-2630/15/5/055019/revision1/nj463982ieqn32.gif)