Abstract
We introduce a new class of quantum many-particle entangled states, called the Dicke squeezed (or DS) states, which can be used to improve the precision in quantum metrology beyond the standard quantum limit. We show that the enhancement in measurement precision is characterized by a single experimentally detectable parameter, called the Dicke squeezing 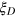 , which also bounds the entanglement depth for this class of states. The measurement precision approaches the ultimate Heisenberg limit as
, which also bounds the entanglement depth for this class of states. The measurement precision approaches the ultimate Heisenberg limit as 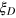 attains the minimum in an ideal Dicke state. Compared with other entangled states, we show that the DS states are more robust to decoherence and give better measurement precision under typical experimental noise.
attains the minimum in an ideal Dicke state. Compared with other entangled states, we show that the DS states are more robust to decoherence and give better measurement precision under typical experimental noise.
Export citation and abstract BibTeX RIS

Content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
Precision measurement plays an important role for scientific and technological applications. In many circumstances, precision measurement can be reduced to detection of a small phase shift by use of optical or atomic interferometry [1–4]. The precision of the phase measurement improves with increase of the number of particles (photons or atoms) in the interferometer. For N particles in non-entangled (classical) states, the phase sensitivity 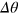 is constrained by the standard quantum limit
is constrained by the standard quantum limit 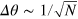 from the shot noise [1, 3, 4]. Schemes have been proposed to improve the measurement precision beyond the standard quantum limit by use of quantum entangled states [1–7]. Two classes of states are particularly important for this scenario: one is the GHZ state [6], also called the NOON state in the second quantization representation [7]; and the other is the spin squeezed state [1, 3, 4], which may include the squeezed state of light as a special limit. A number of intriguing experiments have been reported to prepare these states and use them for quantum metrology [8–14]. These states are typically sensitive to decohereand experimental noise [15, 16]. As a result, the number of particles that one can prepare into the GHZ state, or the maximal spin squeezing that one can achieve, are both severely limited by noise in experiment.
from the shot noise [1, 3, 4]. Schemes have been proposed to improve the measurement precision beyond the standard quantum limit by use of quantum entangled states [1–7]. Two classes of states are particularly important for this scenario: one is the GHZ state [6], also called the NOON state in the second quantization representation [7]; and the other is the spin squeezed state [1, 3, 4], which may include the squeezed state of light as a special limit. A number of intriguing experiments have been reported to prepare these states and use them for quantum metrology [8–14]. These states are typically sensitive to decohereand experimental noise [15, 16]. As a result, the number of particles that one can prepare into the GHZ state, or the maximal spin squeezing that one can achieve, are both severely limited by noise in experiment.
In this paper, we introduce a new class of many-particle entangled states for quantum metrology, which we name the Dicke squeezed (DS) states. The DS states have the following interesting features: (i) They represent a wide class of entangled states with possibly many different forms but can be characterized by a single parameter called the Dicke squeezing  , with
, with 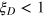 . The Dicke squeezing parameter
. The Dicke squeezing parameter 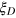 can be conveniently measured in experiments from detection of the collective spin operator of N particles. It provides the figure-of-merit for application of the DS states in quantum metrology in the following sense: for states with
can be conveniently measured in experiments from detection of the collective spin operator of N particles. It provides the figure-of-merit for application of the DS states in quantum metrology in the following sense: for states with  , the phase sensitivity
, the phase sensitivity  and the phase measurement precision
and the phase measurement precision  both improve from the standard quantum limit
both improve from the standard quantum limit 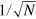 to the new scaling
to the new scaling 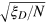 . The phase shift can be read out through the Bayesian inference for the DS states. Under a fixed particle number N, the parameter
. The phase shift can be read out through the Bayesian inference for the DS states. Under a fixed particle number N, the parameter  attains the minimum
attains the minimum 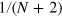 under the ideal Dicke state, and the phase sensitivity correspondingly approaches the Heisenberg limit
under the ideal Dicke state, and the phase sensitivity correspondingly approaches the Heisenberg limit 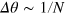 , in agreement with the previous result on the Dicke state [17, 18]. (ii) The entanglement of the DS states can be also characterized by the squeezing parameter
, in agreement with the previous result on the Dicke state [17, 18]. (ii) The entanglement of the DS states can be also characterized by the squeezing parameter  . For a many-body system with a large particle number N, we would like to know how many particles among them have been prepared into genuinely entangled states. This number of particles with genuine entanglement is called the entanglement depth for this system [19, 20]. A criterion proved in [20] indicates that
. For a many-body system with a large particle number N, we would like to know how many particles among them have been prepared into genuinely entangled states. This number of particles with genuine entanglement is called the entanglement depth for this system [19, 20]. A criterion proved in [20] indicates that 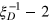 gives a lower bound of the entanglement depth for any DS states with the squeezing parameter
gives a lower bound of the entanglement depth for any DS states with the squeezing parameter 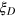 . (iii) Compared with the GHZ state or the spin squeezed states, we show that the DS states characterized by
. (iii) Compared with the GHZ state or the spin squeezed states, we show that the DS states characterized by 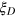 are much more robust to decoherence and experimental noise such as particle loss. Substantial Dicke squeezing
are much more robust to decoherence and experimental noise such as particle loss. Substantial Dicke squeezing 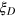 remains under a significant amount of noise under which spin squeezing would not be able to survive at all.
remains under a significant amount of noise under which spin squeezing would not be able to survive at all.
For a system of N particles, each of two internal states  (with effective spin-
(with effective spin-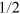 ), we can define a Pauli matrix
), we can define a Pauli matrix 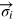 for each particle i and the collective spin operator
for each particle i and the collective spin operator  as the summation
as the summation  . Note that the components of
. Note that the components of  can be measured globally without the requirement of separate addressing of individual particles. If the particles are indistinguishable like photons or ultracold bosonic atoms, we can use the number of particles
can be measured globally without the requirement of separate addressing of individual particles. If the particles are indistinguishable like photons or ultracold bosonic atoms, we can use the number of particles 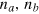 in each mode
in each mode 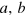 to denote the states. In this notation (second quantization representation), the GHZ state of N spins
to denote the states. In this notation (second quantization representation), the GHZ state of N spins 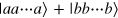 (unnormalized) is represented by
(unnormalized) is represented by 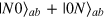 , the so called NOON state [7]. The collective spin operators can be expressed in term of the mode operators
, the so called NOON state [7]. The collective spin operators can be expressed in term of the mode operators 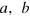 using the Schwinger representation
using the Schwinger representation  ,
,  ,
,  [2]. Asmall phase shift
[2]. Asmall phase shift 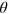 can be measured through the Mach–Zehnder(MZ) type of interferometer illustrated in figure 1 by inputting a state of two modes
can be measured through the Mach–Zehnder(MZ) type of interferometer illustrated in figure 1 by inputting a state of two modes 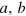 and measuring the number difference of the output modes (the output Jz operator). The two beam splitters in the interferometer exchange the Jz and Jy operators and the phase shifter is represented by a unitary operator
and measuring the number difference of the output modes (the output Jz operator). The two beam splitters in the interferometer exchange the Jz and Jy operators and the phase shifter is represented by a unitary operator 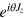 , which transforms Jy to
, which transforms Jy to  . Assume the input state has mean
. Assume the input state has mean 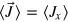 and minimum variance
and minimum variance  along the y -direction. By measuring
along the y -direction. By measuring  , the phase sensitivity
, the phase sensitivity  is characterized by
is characterized by 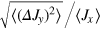 . This motivates definition of the spin squeezing parameter [3, 4]
. This motivates definition of the spin squeezing parameter [3, 4]

as the figure-of-merit for precision measurement. The phase sensitivity is estimated by 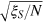 for this measurement scheme.
for this measurement scheme.
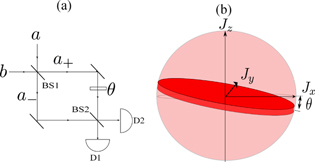
Figure 1. (a) The MZ interferometer setup to measure the relative phase shift 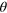 with input modes
with input modes  in DS states. The detectors D1 and D2 measure the Jz operator by recording the particle number difference in the two output modes. (b) In the Bloch sphere for the collective spin operator
in DS states. The detectors D1 and D2 measure the Jz operator by recording the particle number difference in the two output modes. (b) In the Bloch sphere for the collective spin operator 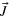 , a measurement of the phase shift by the MZ interferometer is represented by rotation of a thin disk (its size in
, a measurement of the phase shift by the MZ interferometer is represented by rotation of a thin disk (its size in 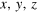 directions corresponds to the variance of
directions corresponds to the variance of 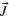 under the DS state) by an angle
under the DS state) by an angle 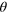 .
.
Download figure:
Standard image High-resolution imageNot all states useful for quantum metrology can be characterized by the spin squeezing  . An example is the Dicke state
. An example is the Dicke state  , which has been shown to give the Heisenberg limited phase sensitivity in [17]. However, for this state,
, which has been shown to give the Heisenberg limited phase sensitivity in [17]. However, for this state,  in all the directions, and the spin squeezing
in all the directions, and the spin squeezing  is not a good measure to characterize states of this kind with
is not a good measure to characterize states of this kind with  . To characterize a broad class of states that are useful for quantum metrology, we introduce the following Dicke squeezing parameter, defined as
. To characterize a broad class of states that are useful for quantum metrology, we introduce the following Dicke squeezing parameter, defined as

One can easily check that 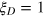 for the benchmark spin-coherent states. We call any states with
for the benchmark spin-coherent states. We call any states with 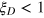 as the DS states and a major result of this paper is to show that such states are useful for quantum metrology, where the phase sensitivity is improved from
as the DS states and a major result of this paper is to show that such states are useful for quantum metrology, where the phase sensitivity is improved from  for the benchmark spin coherent state to about
for the benchmark spin coherent state to about  for the DS states. The parameter
for the DS states. The parameter 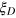 attains the minimum
attains the minimum 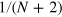 under the ideal Dicke state
under the ideal Dicke state 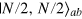 , and the phase sensitivity
, and the phase sensitivity  correspondingly approaches the Heisenberg limit
correspondingly approaches the Heisenberg limit 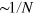 , in agreement with the results in [17, 18]. The definition of the parameter
, in agreement with the results in [17, 18]. The definition of the parameter  is motivated by a similar quantity first introduced in the work [20] for detection of many-particle entanglement. Another related parameter is
is motivated by a similar quantity first introduced in the work [20] for detection of many-particle entanglement. Another related parameter is ![${{\xi }_{os}}=(N-1)\langle {{(\Delta {{J}_{z}})}^{2}}\rangle /[\langle J_{x}^{2}+J_{y}^{2}\rangle -N/2]$](https://content.cld.iop.org/journals/1367-2630/16/10/103037/revision1/njp502275ieqn66.gif) , introduced in [21] for entanglement detection. Albeit similar in form, for metrological applications
, introduced in [21] for entanglement detection. Albeit similar in form, for metrological applications  makes more sense as it recovers the correct Heisenberg limit (
makes more sense as it recovers the correct Heisenberg limit (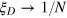 , in contrast with
, in contrast with 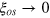 ) as one approaches the Dicke states.
) as one approaches the Dicke states.
The Dicke squeezing parameter  also characterizes the entanglement depth Ed for many-particle systems. For an N-qubit system, the entanglement depth Ed measures how many qubits have been prepared into genuinely entangled states [19, 20]. A theorem proven in Ref. shows that
also characterizes the entanglement depth Ed for many-particle systems. For an N-qubit system, the entanglement depth Ed measures how many qubits have been prepared into genuinely entangled states [19, 20]. A theorem proven in Ref. shows that 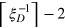 , where
, where 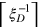 denotes the minimum integer no less than
denotes the minimum integer no less than 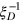 , gives a lower bound of the entanglement depth Ed. For the ideal Dicke state,
, gives a lower bound of the entanglement depth Ed. For the ideal Dicke state, 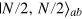 ,
,  and its entanglement depth is N [20]. Note that the entanglement depth characterizes the particle (qubit) entanglement when we express the state
and its entanglement depth is N [20]. Note that the entanglement depth characterizes the particle (qubit) entanglement when we express the state 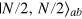 in the first quantization representation [19, 20], where one can easily see all the N qubits are genuinely entangled, so its entanglement depth is N. This should not be confused with the mode entanglement between the bosonic operators a and b , which is zero for the Dicke state
in the first quantization representation [19, 20], where one can easily see all the N qubits are genuinely entangled, so its entanglement depth is N. This should not be confused with the mode entanglement between the bosonic operators a and b , which is zero for the Dicke state 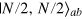 . So the defined Dicke squeezing parameter
. So the defined Dicke squeezing parameter  provides a figure-of-merit both for entanglement characterization and its application in quantum metrology, and this parameter can be conveniently measured in experiments through detection of the collective spin operator
provides a figure-of-merit both for entanglement characterization and its application in quantum metrology, and this parameter can be conveniently measured in experiments through detection of the collective spin operator 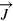 .
.
To show that 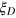 is the figure-of-merit for quantum metrology, we use two complementary methods to verify that the phase measurement precision is improved to
is the figure-of-merit for quantum metrology, we use two complementary methods to verify that the phase measurement precision is improved to 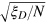 for a variety of states of different forms. First, in the MZ interferometer shown in figure 1(a), the phase sensitivity is estimated by the intrinsic uncertainty
for a variety of states of different forms. First, in the MZ interferometer shown in figure 1(a), the phase sensitivity is estimated by the intrinsic uncertainty  of the relative phase operator defined between the two arms (modes
of the relative phase operator defined between the two arms (modes  ). We calculate this phase uncertainty and find that it scales as
). We calculate this phase uncertainty and find that it scales as 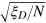 for various input states with widely different
for various input states with widely different 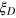 and N. Second, we directly estimate the phase shift θ by the Bayesian inference through detection of the spin operator Jz, and find that the measurement precision, quantified by the variance
and N. Second, we directly estimate the phase shift θ by the Bayesian inference through detection of the spin operator Jz, and find that the measurement precision, quantified by the variance  of the posterior phase distribution, is well estimated by
of the posterior phase distribution, is well estimated by 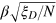 , where
, where  is a dimensionless prefactor. We perform numerical simulation of experiments with randomly chosen phase shift θ and find that the difference between the actual θ and the the measured value of θ obtained through the Bayesian inference is well bounded by the variance
is a dimensionless prefactor. We perform numerical simulation of experiments with randomly chosen phase shift θ and find that the difference between the actual θ and the the measured value of θ obtained through the Bayesian inference is well bounded by the variance  , so
, so 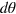 is indeed a good measure of the measurement precision.
is indeed a good measure of the measurement precision.
The Dicke state 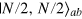 represents an ideal limit, and it is hard to obtain a perfect Dicke state in experiments in particular when the particle number N is large. Here, we consider two classes of more practical states as examples to show that
represents an ideal limit, and it is hard to obtain a perfect Dicke state in experiments in particular when the particle number N is large. Here, we consider two classes of more practical states as examples to show that  is the figure-of-merit for application in quantum metrology when the ideal Dicke state is distorted by unavoidable experimental imperfection. For the first class, we consider pure states of the form
is the figure-of-merit for application in quantum metrology when the ideal Dicke state is distorted by unavoidable experimental imperfection. For the first class, we consider pure states of the form  , where the total number of particles is fixed to be N but the number difference between the modes
, where the total number of particles is fixed to be N but the number difference between the modes  follows a Gaussian distribution
follows a Gaussian distribution 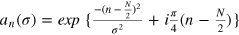 with different widths characterized by the parameter σ. The phase of
with different widths characterized by the parameter σ. The phase of  is chosen for convenience so that the variance of the state is symmetric along the
is chosen for convenience so that the variance of the state is symmetric along the 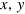 axes. For the second class, we consider mixed states
axes. For the second class, we consider mixed states 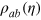 , which come from noise distortion of the Dicke state
, which come from noise distortion of the Dicke state  after a particle loss channel with varying loss rate η. To calculate
after a particle loss channel with varying loss rate η. To calculate 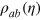 , we note that a loss channel with loss rate η can be conveniently modeled by the transformation
, we note that a loss channel with loss rate η can be conveniently modeled by the transformation  and
and  , where
, where 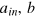 in denote the annihilation operators of the input modes that are in the ideal Dicke state
in denote the annihilation operators of the input modes that are in the ideal Dicke state 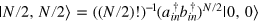 and
and 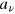 ,
, represent the corresponding vacuum modes. By substituting
represent the corresponding vacuum modes. By substituting 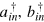 with
with 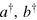 through the channel transformation and tracing over the vacuum modes
through the channel transformation and tracing over the vacuum modes  ,
,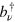 , we get the matrix form of ρab
, we get the matrix form of ρab in the Fock basis of the modes
in the Fock basis of the modes 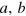 . The two classes of states
. The two classes of states 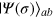 and
and 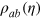 approach the ideal Dicke state when the parameters
approach the ideal Dicke state when the parameters  tend to zero.
tend to zero.
In the MZ interferometer shown in figure 1(a), the modes 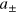 of the two arms are connected with the input modes
of the two arms are connected with the input modes 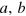 by the relation
by the relation 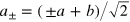 . The phase eigenstates
. The phase eigenstates  of the modes
of the modes 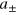 are superpositions of the corresponding Fock states
are superpositions of the corresponding Fock states  with
with 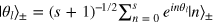 , where
, where  (
( ) and
) and 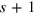 denotes the Hilbert space dimension that eventually takes the infinity limit [22]. For modes
denotes the Hilbert space dimension that eventually takes the infinity limit [22]. For modes 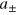 in a composite state denoted by its density matrix
in a composite state denoted by its density matrix 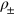 , the probability distribution
, the probability distribution 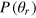 of the relative phase θr between the two interferometer arms can be expressed as
of the relative phase θr between the two interferometer arms can be expressed as

where  The phase distribution
The phase distribution 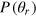 becomes independent of the Hilbert space dimension
becomes independent of the Hilbert space dimension  when s goes to infinity, and the half width
when s goes to infinity, and the half width 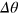 of
of 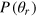 gives an indicator of the intrinsic interferometer sensitivity to measure the relative phase shift for the given input state [17, 18]. We use
gives an indicator of the intrinsic interferometer sensitivity to measure the relative phase shift for the given input state [17, 18]. We use 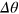 to quantify the phase sensitivity for our input states.
to quantify the phase sensitivity for our input states.
In figure 2, we show the calculated phase sensitivity 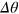 for the two classes of input states
for the two classes of input states 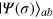 and
and  , by varying the parameters
, by varying the parameters 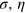 and the particle number N. With fixed parameters
and the particle number N. With fixed parameters 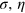 , when we vary the particle number N (typically from 20 to 200 in our calculation), the phase sensitivity
, when we vary the particle number N (typically from 20 to 200 in our calculation), the phase sensitivity 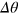 follows a linear dependence with the parameter
follows a linear dependence with the parameter 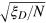 by
by 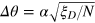 (note that the Dicke squeezing parameter
(note that the Dicke squeezing parameter  changes widely as we vary N and
changes widely as we vary N and 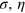 ). The slope α depends very weakly on the parameters
). The slope α depends very weakly on the parameters 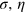 , as shown in figure 2(c) and (d), and roughly we have
, as shown in figure 2(c) and (d), and roughly we have  . This shows that, for different types of input states, the phase sensitivity
. This shows that, for different types of input states, the phase sensitivity 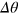 is always determined by the parameter
is always determined by the parameter 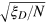 up to an almost constant prefactor α.
up to an almost constant prefactor α.
Figure 2. The phase sensitivity  versus the normalized Dicke squeezing
versus the normalized Dicke squeezing 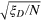 for two classes of input states: (a) States
for two classes of input states: (a) States  with Gaussian superposition coefficients. (b) Dissipative states
with Gaussian superposition coefficients. (b) Dissipative states  after a loss channel. The resulting points are on a straight line when we vary the particle number N from 20 to 200 (
after a loss channel. The resulting points are on a straight line when we vary the particle number N from 20 to 200 (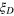 changes correspondingly) and the slope of the line changes slightly as we vary the parameter
changes correspondingly) and the slope of the line changes slightly as we vary the parameter 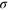 (from 0 to 6) or
(from 0 to 6) or 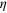 (from 0 to 0.4). (c) and (d) show the variation of the slope
(from 0 to 0.4). (c) and (d) show the variation of the slope 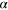 as a function of the parameter
as a function of the parameter  or
or 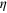 .
.
Download figure:
Standard image High-resolution imageA good phase sensitivity 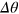 is an indicator of possibility of high-precision measurement of the relative phase shift θ, however, the sensitivity by itself does not give the information of θ. In particular, for the DS states, we typically have
is an indicator of possibility of high-precision measurement of the relative phase shift θ, however, the sensitivity by itself does not give the information of θ. In particular, for the DS states, we typically have 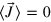 and therefore cannot read out the information of θ by measuring rotation of the mean value of
and therefore cannot read out the information of θ by measuring rotation of the mean value of 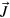 . A powerful way to read out the information of θ is through the Bayesian inference [17, 18]. Here, we show that with the Bayesian inference, we can faithfully extract the information of θ with a measurement precision
. A powerful way to read out the information of θ is through the Bayesian inference [17, 18]. Here, we show that with the Bayesian inference, we can faithfully extract the information of θ with a measurement precision  for the DS states, where the prefactor
for the DS states, where the prefactor  . We note that each instance of measurement by the MZ interferometer setup shown in figure 1 records one particular eigenvalue
. We note that each instance of measurement by the MZ interferometer setup shown in figure 1 records one particular eigenvalue 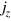 of the Jz operator, which occurs with a probability distribution
of the Jz operator, which occurs with a probability distribution 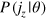 (called the likelihood) that depends on the relative phase shift θ. With a given input state ρab for the modes
(called the likelihood) that depends on the relative phase shift θ. With a given input state ρab for the modes 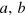 , the likelihood
, the likelihood 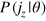 is given by
is given by
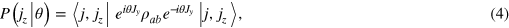
where  denotes the momentum eigenstate with
denotes the momentum eigenstate with  . The Bayesian inference is a way to use the Bayes' rule to infer the posterior distribution
. The Bayesian inference is a way to use the Bayes' rule to infer the posterior distribution 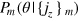 of the phase shift
of the phase shift 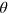 after m instances of measurements of the Jz operator with the measurement outcomes
after m instances of measurements of the Jz operator with the measurement outcomes 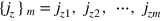 , respectively. After the mth measurement with outcome jzm, the phase distribution
, respectively. After the mth measurement with outcome jzm, the phase distribution  is updated by the Bayes' rule
is updated by the Bayes' rule

where  is the probability to get the outcome jzm conditional on the sequence
is the probability to get the outcome jzm conditional on the sequence 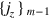 for the previous
for the previous 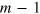 measurement outcomes. Before the first measurement, the prior distribution
measurement outcomes. Before the first measurement, the prior distribution  is assumed to be a uniform distribution between 0 and
is assumed to be a uniform distribution between 0 and  . When the instances of measurements
. When the instances of measurements  , the posterior distribution
, the posterior distribution  is typically sharply peaked around the actual phase shift, and we use the half width
is typically sharply peaked around the actual phase shift, and we use the half width 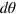 of
of 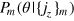 to quantify the measurement precision.
to quantify the measurement precision.
To show that the measurement precision  is indeed determined by
is indeed determined by 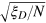 for the DS states, we numerically simulate the MZ experiment with a randomly chosen actual phase shift θr in the interferometer. We take input states of the forms of
for the DS states, we numerically simulate the MZ experiment with a randomly chosen actual phase shift θr in the interferometer. We take input states of the forms of  or
or  , as specified previously, with the corresponding likelihood
, as specified previously, with the corresponding likelihood 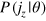 given by equation (4). With this likelihood, we get a sequence of measurement outcomes
given by equation (4). With this likelihood, we get a sequence of measurement outcomes  , which are sampled in our numerically simulated experiments using the corresponding probability distributions
, which are sampled in our numerically simulated experiments using the corresponding probability distributions 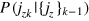 with
with 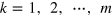 , respectively. For this sequence of outcomes, we obtain the corresponding sequence of posterior phase distributions
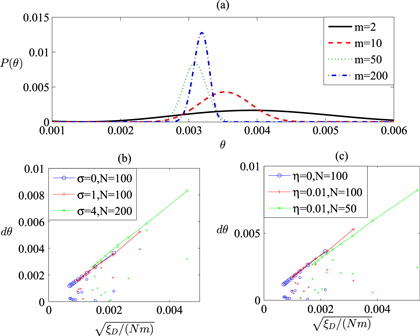
, respectively. For this sequence of outcomes, we obtain the corresponding sequence of posterior phase distributions 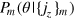 , with an example shown in figure 3(a). One can see that the distribution
, with an example shown in figure 3(a). One can see that the distribution 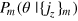 indeed gets increasingly sharper with m and its peak approaches the actual phase shift θr. We use the the central peak position θp of the distribution
indeed gets increasingly sharper with m and its peak approaches the actual phase shift θr. We use the the central peak position θp of the distribution  as an estimator of the measured phase shift, and the difference
as an estimator of the measured phase shift, and the difference 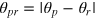 therefore quantifies the measurement error. This error
therefore quantifies the measurement error. This error 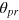 is typically bounded by
is typically bounded by 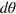 , indicating there is no systematic bias by this inference method.
, indicating there is no systematic bias by this inference method.
Figure 3. (a) The posterior phase distributions 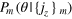 obtained from the Bayesian inference after the mth measurement with
obtained from the Bayesian inference after the mth measurement with 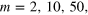 and 200 from our numerically simulated experiments. In the simulation, the actual phase shift
and 200 from our numerically simulated experiments. In the simulation, the actual phase shift  and the input state is
and the input state is 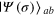 with N = 1000,
with N = 1000,  and
and  . (b) and (c): The measurement precision
. (b) and (c): The measurement precision 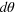 (the dots along a line fit by
(the dots along a line fit by 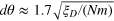 ) and the estimation error θpr (the scattered points below the line) as functions of the scaled parameter
) and the estimation error θpr (the scattered points below the line) as functions of the scaled parameter 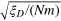 for the Gaussian input states
for the Gaussian input states 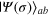 (b) and the dissipative input states
(b) and the dissipative input states 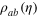 (c) with m varying from 20 to 200. The other parameters (
(c) with m varying from 20 to 200. The other parameters (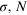 for
for  and
and 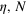 for
for  ) are specified by the inserts of the figure.
) are specified by the inserts of the figure.
Download figure:
Standard image High-resolution imageIn figure 3(b) and (c), we show the measurement precision  and the estimation error θpr as functions of the scaled parameter
and the estimation error θpr as functions of the scaled parameter 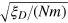 , as we vary the types of input states (the parameters
, as we vary the types of input states (the parameters 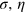 in states
in states 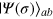 and
and 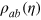 ), the particle number N, and the number of measurement instances m. All the points for the measurement precision
), the particle number N, and the number of measurement instances m. All the points for the measurement precision 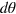 can be well fit with a linear function
can be well fit with a linear function  with
with 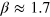 . The estimation error θpr from the simulated experiments (the scattered points) is typically below the corresponding
. The estimation error θpr from the simulated experiments (the scattered points) is typically below the corresponding 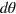 . This supports our central claim: the defined Dicke squeezing parameter
. This supports our central claim: the defined Dicke squeezing parameter  characterizes the improvement of measurement precision for the DS states compared with the standard quantum limit.
characterizes the improvement of measurement precision for the DS states compared with the standard quantum limit.
Compared with other entangled states used in quantum metrology, a remarkable advantage of the DS states characterized by the squeezing parameter 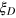 is its noise robustness. For instance, if the noise in experiments is dominated by the dephasing error that does not change the mode population, the numerator does not change in the definition equation (2) for the Dicke squeezing
is its noise robustness. For instance, if the noise in experiments is dominated by the dephasing error that does not change the mode population, the numerator does not change in the definition equation (2) for the Dicke squeezing 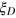 and only the denominator drops slowly. With a dephasing rate p (p is the probability for each qubit to become completely decoherent), the squeezing parameter reduces to
and only the denominator drops slowly. With a dephasing rate p (p is the probability for each qubit to become completely decoherent), the squeezing parameter reduces to ![${{\xi }_{D}}=1/[N(1-p)+2-{{p}^{2}}]$](https://content.cld.iop.org/journals/1367-2630/16/10/103037/revision1/njp502275ieqn224.gif) if we start with a Dicke state for N particles [20]. We still have substantial squeezing when
if we start with a Dicke state for N particles [20]. We still have substantial squeezing when  even if the dephasing error rate
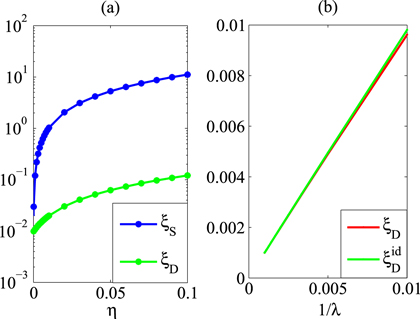
even if the dephasing error rate 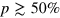 . More generic noise such as particle loss has a larger influence on the Dicke squeezing, however, the DS states are still more robust compared with other forms of entangled states such as the spin squeezed states. In figure 4(a), we show the influence of the particle loss to the Dicke squeezing
. More generic noise such as particle loss has a larger influence on the Dicke squeezing, however, the DS states are still more robust compared with other forms of entangled states such as the spin squeezed states. In figure 4(a), we show the influence of the particle loss to the Dicke squeezing 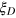 and the spin squeezing
and the spin squeezing  , starting with comparable values of
, starting with comparable values of 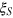 and
and 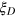 at the loss rate
at the loss rate 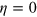 under the same particle number N. The spin squeezed state was determined by minimizing
under the same particle number N. The spin squeezed state was determined by minimizing 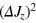 with
with 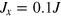 [19]. One can see that that the spin squeezing
[19]. One can see that that the spin squeezing 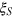 is quickly blown up by very small particle loss, but substantial Dicke squeezing
is quickly blown up by very small particle loss, but substantial Dicke squeezing  remains even under a significant loss rate. In the asymptotic limit with
remains even under a significant loss rate. In the asymptotic limit with 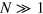 ,
, 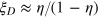 under a loss rate
under a loss rate  . Therefore, compared with the standard quantum limit, the measurement precision improves by a constant factor of
. Therefore, compared with the standard quantum limit, the measurement precision improves by a constant factor of 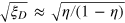 for the DS state under loss. This has saturated the bound derived in [23], which proves that under noise the measurement procession can be improved at most by a constant factor for any quantum entangled states (the factor is exactly
for the DS state under loss. This has saturated the bound derived in [23], which proves that under noise the measurement procession can be improved at most by a constant factor for any quantum entangled states (the factor is exactly 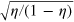 under a loss rate
under a loss rate  as proven in [23]). The saturation of the improvement bound shows that the DS states characterized by the parameter
as proven in [23]). The saturation of the improvement bound shows that the DS states characterized by the parameter 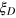 belong to the optimal class of states for improving the measurement precision under noise (note that the conventional spin squeezed states measured by the squeezing parameter
belong to the optimal class of states for improving the measurement precision under noise (note that the conventional spin squeezed states measured by the squeezing parameter 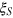 are not optimal for improving measurement precision under noise as
are not optimal for improving measurement precision under noise as 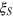 is quickly blown up to be larger than 1 (see figure 4 (a)), yielding no improvement compared with the standard quantum limit). Another source of noise important for experiments is the fluctuation in the total particle number N. The squeezing
is quickly blown up to be larger than 1 (see figure 4 (a)), yielding no improvement compared with the standard quantum limit). Another source of noise important for experiments is the fluctuation in the total particle number N. The squeezing  is robust to this fluctuation. To show this, we consider
is robust to this fluctuation. To show this, we consider 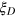 under an initial states, which is an ensemble of Dicke states with various particle numbers N mixed together according to the Poissonian distribution
under an initial states, which is an ensemble of Dicke states with various particle numbers N mixed together according to the Poissonian distribution 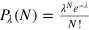 with
with  . In figure 4(b), we compare
. In figure 4(b), we compare 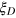 under this state and ξDid under a single Dicke state with a fixed particle number
under this state and ξDid under a single Dicke state with a fixed particle number 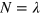 . One can see that the difference is small, indicating that the Dicke squeezing
. One can see that the difference is small, indicating that the Dicke squeezing 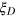 is insensitive to the total number fluctuation in the initial state.
is insensitive to the total number fluctuation in the initial state.
Figure 4. (a) Comparison of the spin squeezing 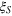 and the Dicke squeezing
and the Dicke squeezing 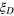 under influence of the particle loss with a loss rate
under influence of the particle loss with a loss rate 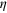 . We take the particle number N = 100 and the amounts of squeezing for
. We take the particle number N = 100 and the amounts of squeezing for  and
and  comparable initially at
comparable initially at 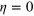 . (b) Comparison of the Dicke squeezing
. (b) Comparison of the Dicke squeezing  for a mixture of Dicke states Poissonian distributed in the total particle number according to
for a mixture of Dicke states Poissonian distributed in the total particle number according to 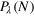 and ξidD for a single Dicke state with a fixed particle number
and ξidD for a single Dicke state with a fixed particle number 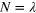 .
.
Download figure:
Standard image High-resolution imageIn summary, we have proposed a new class of many-particle entangled states characterized by the introduced Dicke squeezing parameter 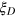 to improve the measurement precision in quantum metrology. We show that the phase information can be read out through the Bayesian inference and the measurement precision is improved by a factor of
to improve the measurement precision in quantum metrology. We show that the phase information can be read out through the Bayesian inference and the measurement precision is improved by a factor of 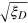 compared with the standard quantum limit. A distinctive advantage of the DS states is its noise robustness and we show that the Dicke squeezing
compared with the standard quantum limit. A distinctive advantage of the DS states is its noise robustness and we show that the Dicke squeezing 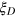 is much more robust compared with other forms of entangled states used in quantum metrology. Substantial Dicke squeezing can be generated in experiments, for instance, through the atomic collision interaction in spinor condensates [24, 25]. With the characterization and measurement method proposed in this paper, the Dicke squeezing may lead to a fruitful approach for precision quantum metrology using entangled quantum states.
is much more robust compared with other forms of entangled states used in quantum metrology. Substantial Dicke squeezing can be generated in experiments, for instance, through the atomic collision interaction in spinor condensates [24, 25]. With the characterization and measurement method proposed in this paper, the Dicke squeezing may lead to a fruitful approach for precision quantum metrology using entangled quantum states.
Acknowledgements
This work was supported by the NBRPC (973 Program) 2011CBA00300 (2011CBA00302), the IARPA MUSIQC program, the ARO and the AFOSR MURI programs.