Bosonic thermoelectric transport and breakdown of universality

Cold atom samples differ from electronic systems in significant ways that offer new opportunities to investigate transport phenomena [1–5]. Cold atom systems are highly versatile: many of them have tunable interactions, can be confined in a single potential well or in lattices, as well as in different dimensions. Furthermore, at nanoKelvin temperatures, the dynamics of atoms is very slow (milliseconds), in contrast to the fast dynamics (picoseconds) of electrons in materials. This allows a detailed scrutiny of atomic motion. One powerful tool in recent cold atom experiments is in situ imaging of atoms, which reveals high space-time resolution images of atomic distributions in snapshots [6–8]. In the condensed matter analogy, this technique is equivalent to following every electron with a femtosecond temporal resolution.

In further pursuit of understanding both these dynamics and the analogy between electrons and cold atoms, in this paper we apply the theory of dissipative transport (developed for electrons) to ultracold trapped atoms. In the last section of the paper we address recent experimental data [1].

Dissipative transport is to be contrasted with ballistic transport where there are no relevant scattering processes to limit the transport lifetime. Thus, ballistic transport is observable when the mean free path is long compared to the relevant dimensions of the system. We stress that the analogy between electrons and cold atoms requires careful consideration. Universal transport laws developed for electrons need to be revisited when applied to bosonic atoms. In addition, cold atom samples are trapped in a conservative potential and isolated in vacuum. The lack of thermal and particle reservoirs means total particle and total energy are usually conserved quantities. A statistical description based on a grand-canonical ensemble may apply only to local observables [9].

Furthermore, atoms are neutral and the analogue of electrical current will be the particle flow or mass flow driven, not by electric field, but by a chemical potential gradient $\nabla \mu$ or temperature gradient $\nabla T$. Interestingly, unlike neutral liquid Helium, cold gas superfluids allow the imposition of a non-zero $\nabla \mu$ and thus are rather uniquely amenable to the transport studies we present.

Finally, to employ dissipative, as distinguished from ballistic transport theory, the samples should be in the hydrodynamic regime with coherence length much shorter than the sample and relaxation time less than the measurement time resolution. When these criteria are satisfied the atoms can reach a local equilibrium associated with coarse graining the system over a proper length and time scale. Thermodynamic quantities such as temperature and chemical potential can therefore be defined locally, and their gradients constitute the thermodynamic forces. This approximation, which we will call the local equilibrium approximation (LEA), limits the resolution of both temporal and spatial measurements. It should not be confused with the local density approximation that describes inhomogeneously trapped atoms in equilibrium.

Since cold atoms are typically confined in conservative potentials, they are usually free from impurities and background ionic lattices, including their phononic excitations. The fact that atoms are in a clean environment, on the one hand, may simplify many-body calculations; this removes some complexity encountered in electron transport in materials. On the other hand, there must necessarily be a relaxation mechanism in order to achieve a steady state and apply the fundamentals of transport theory.

In this paper, we discuss the transport behavior of ultracold gases in the normal phase under the assumption of the LEA, the applicability of which is described in more detail below. We characterize transport in two limits where theory is relatively straightforward and well established. Thus we consider non-interacting particles as well as (generally interacting) particles but near superfluid condensation, emphasizing the similarities and differences between Fermi and Bose systems. When the interactions are essentially negligible, a normal degenerate Fermi gas in the dissipative transport regime has universal thermoelectric properties. By contrast universality is absent for the bosonic counterpart. As the system approaches the superfluid critical temperature, the transport tends to be dominated by condensate (superconducting and superfluid) fluctuations in which regime, the Fermi and Bose gases are more similar. It is in this latter regime where there are now (Bose gas) experiments [1]. Importantly these appear to be reasonably consistent with the theory presented here.

1.1. Transport equations

We define the transport coefficients in terms of the linear response of the particle current ${{{\bf J}}_{{\rm p}}}$ and the heat current ${{{\bf J}}_{Q}}$ to temperature gradient $\nabla T$ and chemical potential gradient $\nabla \mu$ as

$$\begin{eqnarray}&&{{{\bf J}}_{{\rm p}}}=-{{L}_{11}}\nabla \mu \;\;-{{L}_{12}}\nabla T,\end{eqnarray} \tag{ 1 }$$

$$\begin{eqnarray}&&{{{\bf J}}_{Q}}=-{{L}_{21}}\nabla \mu \;\;-{{L}_{22}}\nabla T,\end{eqnarray} \tag{ 2 }$$

where $\nabla \mu$ is analogous to the electric field for a charged system. It is convenient to introduce dimensionless ratios to write this equation in the form (We work with units such that $\hbar ={{k}_{B}}=1$.)

$$\begin{eqnarray}&&\left( \begin{array}{ccccccccccccccc} {{{\bf J}}_{{\rm p}}} \\ {{{\bf J}}_{Q}} \\ \end{array} \right)=-\sigma \left( \begin{array}{ccccccccccccccc} 1 & \mathcal{S} \\ \mathcal{P} & T\mathcal{L}+\mathcal{S}\mathcal{P} \\ \end{array} \right)\left( \begin{array}{ccccccccccccccc} \nabla \mu \\ \nabla T \\ \end{array} \right),\end{eqnarray} \tag{ 3 }$$

where the conductivity $\sigma \equiv {{L}_{11}}$, the Seebeck coefficient (or thermopower) $\mathcal{S}=\mathcal{P}/T\equiv {{L}_{12}}/{{L}_{11}}$ and the Lorenz number (which is given by ratio of thermal to mass conductivity, divided by temperature) $\mathcal{L}\equiv ({{L}_{22}}{{L}_{11}}-{{L}_{12}}{{L}_{21}})/TL_{11}^{2}$. Note that L₁₂ and L₂₁ satisfy the Onsager relation ${{L}_{12}}={{L}_{21}}/T$.

1.2. Kubo versus Boltzmann approaches

1.3. Role of dissipation

1.4. Local equilibrium approximation

The transport properties of weakly interacting, normal Bose and Fermi gases are strikingly different. In a degenerate Fermi gas, it is well known that the phase space contributions to transport are confined to a narrow energy range around the Fermi energy. By contrast, for Bose gases, there is no such constraint. As a consequence, the magnitude of transport coefficients L_ij for bosons tends to be much larger and much more sensitive to the detailed assumptions about the nature of the dissipation.

For a Hamiltonian with only one-body terms, we are able to compare the transport properties of bosons and fermions using an exact expression based on the Kubo formula first derived for fermions in [21] but readily generalized to bosons,

$$\begin{eqnarray}&&{{L}_{ij}}={{T}^{1-j}}\int _{0}^{\infty }{\rm d}\epsilon \;{{(\epsilon -\mu )}^{i+j-2}}\frac{2\epsilon }{md}\rho (\epsilon )\tau (\epsilon )b_{\pm }^{(1)},\end{eqnarray} \tag{ 4 }$$

where $i,j$ = 1 or 2, $b_{\pm }^{(1)}\equiv -{{\partial }_{\omega }}{{b}_{\pm }}(\omega )$, with ${{b}_{\pm }}(\omega )={{(z_{\pm }^{-1}{{{\rm e}}^{\omega /T}}\pm 1)}^{-1}}$ the Fermi/Bose distribution, and the fugacity ${{z}_{\pm }}$ is defined as ${{z}_{+}}={{{\rm e}}^{\mu /T}}$ for fermions, and ${{z}_{-}}={{{\rm e}}^{(\mu -{{\mu }_{c}})/T}}$ for bosons below critical chemical potential $\mu \lt {{\mu }_{c}}$. We introduce $\rho (\epsilon )={{(m/2\pi )}^{d/2}}{{\epsilon }^{d/2-1}}/\Gamma (d/2)$ the density of states for free particles of mass m in d dimensions. In order to describe a bosonic system at positive chemical potential, one has to include the (non-dissipative) inter-boson interactions, so that the chemical potential term is given by $\mu -{{\mu }_{c}}$. See for instance [22] for an estimate of ${{\mu }_{c}}$ in weak coupling.

The relaxation time introduced earlier appears as $\tau (\epsilon )$ in equation (4). This parameter plays the role of the relaxation time in Boltzmann theories of transport³ .

The transport coefficients for non-interacting fermions/bosons can be derived from equation (4) as

$$\begin{eqnarray}\begin{array}{rcl} \sigma & = & \frac{\Gamma (\zeta +1)\tau (T)}{\Gamma (d/2+1)m\lambda _{{\rm dB}}^{d}}|{\rm L}{{{\rm i}}_{\zeta }}(\mp {{z}_{\pm }})|, \\ \mathcal{S} & = & (\zeta +1)\frac{{\rm L}{{{\rm i}}_{\zeta +1}}(\mp {{z}_{\pm }})}{{\rm L}{{{\rm i}}_{\zeta }}(\mp {{z}_{\pm }})}-{\rm ln} {{z}_{\pm }}, \\ \mathcal{L} & = & (\zeta +1)(\zeta +2)\frac{{\rm L}{{{\rm i}}_{\zeta +2}}(\mp {{z}_{\pm }})}{{\rm L}{{{\rm i}}_{\zeta }}(\mp {{z}_{\pm }})}-{{\left( \mathcal{S}+{\rm ln} {{z}_{\pm }} \right)}^{2}}, \\ \end{array}\end{eqnarray} \tag{ 5 }$$

where $\zeta =(d+\eta )/2$, ${{\lambda }_{{\rm dB}}}=\sqrt{\frac{2\pi }{mT}}$ is the de Brogile length, and

$$\begin{eqnarray}&&{\rm L}{{{\rm i}}_{\alpha }}(\mp x)=\frac{\mp 1}{\Gamma (\alpha )}\int _{0}^{\infty }{\rm d}t\frac{{{t}^{\alpha -1}}}{{{x}^{-1}}{{{\rm e}}^{t}}\pm 1}\end{eqnarray} \tag{ 6 }$$

are the polylogarithm functions.

For degenerate fermions ${{z}_{+}}\gg 1$, the factor $b_{+}^{(1)}$ is strongly peaked at the Fermi energy. Thus the energy dependence of τ is not relevant and the Lorenz number in this regime is a universal number ${{\mathcal{L}}_{f}}={{\pi }^{2}}/3$ (independent of τ and η), known as the Wiedermann–Franz law. By contrast, for bosons all energies contribute to the integrals, so that $\mathcal{L}$ depends on the details of the dissipation and has a non-universal behavior.

Figure 1 presents a comparison of the behavior of fermionic and bosonic transport for one particular transport coefficient ratio (the Lorenz number) $\mathcal{L},$ for d = 2 as a function of the log of the fugacity. The figure illustrates how different values of the dissipation exponents ($\eta =-2$ and $\eta =0$) influence the transport. One sees that for very negative ${\rm ln} (z)$, the transport is independent of statistics and also sensitive to the details of the dissipation. Each component of $\mathcal{L}$ is larger for the bosonic case, but this effect is not apparent when plotted as a ratio. One sees that as the fermions cross over to the large positive fugacities, the Lorenz number approaches the universal Wiedermann–Franz law.

Zoom In Zoom Out Reset image size

While the universality in the fermionic case is evident, this is clearly not the case for bosons. For Bose systems, we observe that even in the quantum regime the behavior depends on the dissipation mechanism, implying a non-universality of the transport.

Although, experimentally it has not been tested in [1], here we argue that an scale invariance should be observed in transport in a 2D Bose gas⁴ . This scaling arises from physics similar to that found in the thermodynamics of 2D dilute Bose gases [16, 23]. This scale invariance reflects the $\mu =T=0$ quantum phase transition between the vacuum and superfluid phase [24]. This zero-temperature phase transition must not be confused with the finite-temperature phase transition between the normal and superfluid phase discussed in the rest of the paper. The presence of this quantum critical point (QCP) implies that a thermodynamic property such as the pressure is a universal function of the form

$$\begin{eqnarray}&&P(\mu ,T)=\frac{{{T}^{2}}}{m}\mathfrak{P}\left( \frac{\mu }{T},\tilde{g}(T) \right).\end{eqnarray} \tag{ 7 }$$

Here $\mathfrak{P}(x,y)$ is a universal function (independent of the microscopic details of the system) and $\tilde{g}(x)$ is a renormalized interaction depending logarithmically on x, which for weakly-interacting bosons can be taken as constant, which we assume in the following. (If $\tilde{g}(T)$ varies significantly, the scale invariance is then lost.) Under these circumstances there is scale invariance, so that all thermodynamic functions in the dilute 2D Bose gas depend only on $\mu /T$ once the interaction strength has been fixed. The scaling of the pressure is valid in the critical regime close to the QCP, that is $\mu m{{a}^{2}},Tm{{a}^{2}}\ll 1$ [25] (a is the s-wave scattering length). For dilute gases, this corresponds to the whole T–μ plane in the range of μ and T relevant for the experiments.

From these results at equilibrium, we can infer that due to this same QCP, the transport coefficients also obey scaling relations. Following [26], one shows that close to a critical point, the conductivity scale as

$$\begin{eqnarray}&&\sigma (\mu ,T,g)={{s}^{2-d}}\sigma \left( \mu {{s}^{1/\nu }},T{{s}^{z}},\tilde{g}(s) \right),\end{eqnarray} \tag{ 8 }$$

when lengths are rescaled by a factor $1/s$, where the correlation length exponent ν and the dynamical exponent z are given by $1/\nu =z=2$ at the QCP. (See [25] for a detailed discussion of the universal thermodynamics of Bose gases and its relation to the QCP.) Choosing $s={{T}^{-1/z}},$ one obtains

$$\begin{eqnarray}&&\sigma (\mu ,T)={{T}^{(d-2)/z}}{{\mathfrak{S}}_{d}}\left( \frac{\mu }{T},\tilde{g}(T) \right),\end{eqnarray} \tag{ 9 }$$

where ${{\mathfrak{S}}_{d}}(x,y)=\sigma (x,1,y)$ is a universal function. This reasoning is easily generalized to the other transport coefficients

$$\begin{eqnarray}\begin{array}{rcl} {{L}_{12}}(\mu ,T) & = & {{T}^{(d-2)/z}}{{\mathfrak{A}}_{d}}\left( \frac{\mu }{T},\tilde{g}(T) \right), \\ {{L}_{22}}(\mu ,T) & = & {{T}^{(d+z-2)/z}}{{\mathfrak{K}}_{d}}\left( \frac{\mu }{T},\tilde{g}(T) \right), \\ \end{array}\end{eqnarray} \tag{ 10 }$$

and explicitly in dimension two

$$\begin{eqnarray}&&{{L}_{ij}}(\mu ,T)={{T}^{i-1}}{{\mathcal{L}}_{ij}}\left( \frac{\mu }{T},\tilde{g} \right),\end{eqnarray} \tag{ 11 }$$

with $\mathfrak{A}$_d, $\mathfrak{K}$_d and $\mathcal{L}$_ij universal functions. Note that the scaling arguments are in principle valid only for the singular part of the transport coefficient, and one could expect the presence of a regular part, which would not scale accordingly. However, since all four transport coefficients vanish for all $\mu \leqslant 0$ at T = 0 (the system is empty), we can infer that the regular parts are identically zero in the vicinity of the QCP (i.e. for $\mu m{{a}^{2}},Tm{{a}^{2}}\ll 1$).

The normal-superfluid phase transition at finite T (as distinguished from the above vacuum-superfluid zero-temperature phase transition) is characterized by a singularity of the pressure, which translates into a singularity of $\mathfrak{P}(x,y)$ at a given x_c(y), where $\mathfrak{P}(x,y)$ is universal. One finds that the critical chemical potential (at a given temperature) is given by ${{\mu }_{c}}(T)=T\mathfrak{M}\left( \tilde{g} \right)$, where $\mathfrak{M}(x)$ is also universal. Building on the universality of ${{\mu }_{c}}(T)/T$, we arrive at

$$\begin{eqnarray}&&{{L}_{ij}}(\mu ,T)={{T}^{i-1}}{{\mathfrak{L}}_{ij}}\left( \frac{\mu -{{\mu }_{c}}}{T},\tilde{g},\eta \right).\end{eqnarray} \tag{ 12 }$$

Here, we have shown explicitly the dependence of the transport coefficients on the dissipation mechanism through the dissipative coefficient η introduced earlier. In particular, this scaling holds far from the normal-superfluid critical regime⁵ .

The dependence of the scaling functions on η, in turn, implies that even though for a given kind of dissipation (defined by η) the transport coefficients of a dilute Bose gas are universal (i.e. described by a function $\mathfrak{L}$_ij) in the whole μ–T plane, it will be different for different kinds of dissipation mechanisms (i.e. different power laws), thus defining different universality classes⁶ . It follows directly from equation (12) that the Seebeck coefficient (or thermopower) $\mathcal{S}$ and the Lorenz ratio $\mathcal{L}$ are also scale invariant.

4.1. Fluctuation theory

In section 2 we discussed transport in non-interacting normal gases. In this context we have seen that there is a dissipative constant parameterized by η which is generally unconstrained. Moreover η played a central role in determining the transport coefficients of Bose gases, leading to highly non-universal behavior. We turn now to Bose and Fermi systems which are normal but near condensation (Bose–Einstein condensation for bosons and the superconducting transition for fermions). This focus stems from recent Bose gas experiments [1]. For the Fermi case, interactions are essential and one cannot apply the theory of section 2. For the Bose case, the near-condensation regime provides constraints on the character of dissipation. In this regime we can appeal to theories of fluctuation dynamics (such as time dependent Landau Ginsburg theory (TDGL)) to constrain the time dependences and hence frequency dependences of the dissipation. This, in turn, serves to constrain η, as these dynamical theories contain linear time derivatives leading to lifetimes which vary linearly with frequency or energy. Relating to the discussion in section 2, interestingly one arrives at the same limiting behavior of the Bose transport coefficients using either the fluctuation scheme or equation (4) with the equivalent $\eta =-2$.

Our focus on normal state transport in the ultracold gases near their condensation temperatures stems both from recent Bose gas experiments [1] and also from the observation that Bose and Fermi superfluids have rather similar properties in this regime. Both are dominated by a bosonic condensate fluctuation contribution. In this context bosonic transport contributions in superconductors (in the narrow critical regime) have been of great interest to the condensed matter community over many decades [13, 14]. Here one attributes the transport coefficients to fermionic pairs ('composite' bosons) in low but non-zero momentum states. These pre-formed pairs yield a greatly enhanced transport in the normal state, as compared with the behavior deduced from weakly interacting fermion theories such as those in the previous section. More recently there has been a focus on the normal state of high temperature superconductors where it appears that condensate fluctuation transport may set in at much higher temperatures $T*$ well above the transition at T_c. This reflects the so-called 'pseudogap' physics [27] and this thought to be related to pre-formed pairs. We [27, 28] and others have argued that this pseudogap should be relevant to Fermi gases at unitarity, where pairing is strong, but the system is still fermionic. Thus, if indeed, there is a pseudogap at unitarity, the behavior of transport in the Fermi gases may serve to reveal it in future experiments.

Transport properties associated with condensate fluctuations are based on two assumptions. (i) The fluctuations (often called 'Gaussian fluctuations') represent relatively independent bosons. At most one introduces Hartree correlations, and (ii) The dynamics of the fluctuations incorporates linear time derivatives. Higher order derivatives are less important due to critical slowing down effects. This, importantly, has implications for the frequency dependence of the dissipation which ultimately affects the behavior of transport.

With these assumptions, the transport calculations are straightforward and one can evaluate [15, 29] the various transport coefficients following Gaussian fluctuation models [13, 30, 31]. Entering are two factors of the bosonic spectral function, called $A\equiv A({\bf k},\omega )$:

$$\begin{eqnarray}&&{{L}_{ij}}=\frac{{{T}^{1-j}}}{2{{m}^{2}}}\int \frac{{{{\rm d}}^{d}}k}{{{(2\pi )}^{d}}}\frac{{\rm d}\omega }{2\pi }{{\omega }^{i+j-2}}\frac{{{k}^{2}}}{d}{{\left[ A({\bf k},\omega ) \right]}^{2}}b_{-}^{(1)}(\omega ).\end{eqnarray} \tag{ 13 }$$

We characterize the spectral function in terms of the bosonic propagator

$$\begin{eqnarray}&&G({\bf k},\omega )\equiv {{\left( \omega -{{\Sigma }_{1}}({\bf k},\omega )-\frac{{{{\bf k}}^{2}}}{2m}+\mu -{{\mu }_{c}}+\frac{i}{2}{{\Sigma }_{2}}({\bf k},\omega ) \right)}^{-1}},\end{eqnarray} \tag{ 14 }$$

so that

$$\begin{eqnarray}&&A({\bf k},\omega )=\frac{{{\Sigma }_{2}}({\bf k},\omega )}{{{\left( \omega -\frac{{{{\bf k}}^{2}}}{2m}+\mu -{{\mu }_{c}}-{{\Sigma }_{1}}({\bf k},\omega ) \right)}^{2}}+\frac{1}{4}{{\left( {{\Sigma }_{2}}({\bf k},\omega ) \right)}^{2}}},\end{eqnarray} \tag{ 15 }$$

where the critical chemical potential ${{\mu }_{c}}$ is a phenomenological parameter, and we take ${{\Sigma }_{1}}(0,0)=0$. These constraints are convenient, rather than reflective of any deep physics. We view the effective Hamiltonian (including self energy and dissipation) as a Hartree-like theory [22] where by definition ${{\Sigma }_{1}}(0,0)=0$ and in this way the superfluid transition occurs at a finite (positive) chemical potential.

A crucial feature of bosons is that ${{\Sigma }_{2}}$ changes sign at $\omega =0$, so that the spectral function A has the sign of ω. This is satisfied in the usual TDGL dynamics, where at low ω one has

$$\begin{eqnarray}&&{{\Sigma }_{2}}\propto {{\omega }^{n}}\quad {\rm with}\quad n=1,\end{eqnarray} \tag{ 16 }$$

corresponding to Ohmic dissipation. It should be pointed out, the apparent absence of vertex correction terms in equation (13) has been validated in the TDGL literature (where the bosons only experience Hartree interactions) and more directly in [29] it can be seen to be consistent with the current conservation constraint which provides the framework for including vertex terms in a Kubo formalism.

For the purposes of completeness we briefly revisit the transport nomenclature found in superconducting fluctuation theories, [13, 14, 32], where the fluctuation propagator is found to be proportional to

$$\begin{eqnarray}&&{{D}^{{\rm fluc}}}({\bf q},{\rm i}\omega )\propto \frac{1}{[(-1+{\rm i}\lambda )({\rm i}\omega )+\mathcal{D}{{q}^{2}}+(8/\pi )(T-{{T}_{c}})]}.\end{eqnarray} \tag{ 17 }$$

Note that equation (17) can be seen to be equivalent to equation (14), when the dissipation is Ohmic. Here $\mathcal{D}$ is the so-called diffusion coefficient and $\lambda =[2\pi T/gN(0)][N^{\prime} (0)/N(0)]$ depends on the density of states at the Fermi energy $N(0)$ and its derivative. By way of further comparison, we note that in solid state physics one usually describes the approach of the transition by $T-{{T}_{c}}$, whereas $\mu -{{\mu }_{c}}$ is the variable associated with cold atom experiments, although these two parametrizations are equivalent.

4.2. Divergences in transport

As $\delta \tilde{\mu }\equiv (\mu -{{\mu }_{c}})/T$ goes to zero (but away from the strictly critical regime) we can deduce the transport coefficients for the 2D case from the integrals in equation (13) and their counterparts. The literature is based on the Ohmic case n = 1 which defines the nature of the divergences in the L_ij. These can be summarized [13, 14, 32] in terms of proportionality relations (with ${{\tilde{L}}_{ij}}$=T^1-i L_ij)

$$\begin{eqnarray}\begin{array}{rcl} {{\tilde{L}}_{11}} & \propto & \frac{1}{|\delta \tilde{\mu }|}, \\ {{\tilde{L}}_{12}} & \propto & -{\rm ln} |\delta \tilde{\mu }|, \\ {{\tilde{L}}_{22}} & \propto & {\rm const}.+|\delta \tilde{\mu }|{\rm ln} |\delta \tilde{\mu }|. \\ \end{array}\end{eqnarray} \tag{ 18 }$$

From equation (18) we deduce that the Seebeck coefficient (thermopower) and Lorenz number, which involve ratios of these coefficients, behave as

$$\begin{eqnarray}\begin{array}{rcl} \mathcal{S} & \propto & -|\delta \tilde{\mu }|{\rm ln} |\delta \tilde{\mu }|, \\ \mathcal{L} & \propto & |\delta \tilde{\mu }|. \\ \end{array}\end{eqnarray} \tag{ 19 }$$

Importantly, the thermopower changes sign at condensation and the Lorenz number tends to zero linearly. Recall that $\mathcal{L}$ must be greater or equal to zero for thermodynamic stability⁷ .

In figure 2 we plot the transport coefficients for d = 2 as obtained from the fluctuation theory (equation (13)) as a function of scaled chemical potential, for a typical $\Gamma =0.1$ [15]. We have checked that the value of Γ does not change qualitatively the transport coefficients or power laws for $|\delta \tilde{\mu }|\lesssim 1$. This figure shows that the thermal conductivity (related to L₂₂) and the mass conductivity (related to L₁₁) as well as the off-diagonal conductivity satisfying the Onsager relation (${{L}_{12}}={{L}_{21}}/T$) all diverge at the transition. It should be clear, however, that this divergence is strongest for the mass conductivity. Important here is that, because of the divergence of $\sigma ={{L}_{11}}$, as μ goes to ${{\mu }_{c}}$, $\mathcal{L}$ (and $\mathcal{S}$) vanish at T_c.

Zoom In Zoom Out Reset image size

We turn now to a comparison of theory and the experiments of [1]. In [1], a Bose gas was confined in an optical trap with peak density $n=5\times {{10}^{13}}\;{\rm c}{{{\rm m}}^{-3}}$, a large scattering length a = 22 nm, and the temperature T = 35 nK. The trap was highly oblate with very strong confinement in the z-direction and weak confinement in the two radial directions. The sample is thus in the quasi-2D regime. For these parameters we are able to address the validity of the LEA. In the normal gas regime, the scattering rate determines the thermalization time scale ${{\tau }_{c}}=\alpha /(4\pi n{{a}^{2}}v)=2$ ms, where $\alpha =2.7$ is a constant [33], and the coherence length scale is given by the mean-free path ${{l}_{c}}=3.5\;\mu {\rm m}$. An optical potential corrugation of up to 3 nK leads to a measured relaxation time of 20 ms of collective excitation. Both these length and time scales are small compared to the the sample size ${{l}_{{\rm s}}}=60\;\mu {\rm m}$ $\gg \;{{l}_{c}}$ and sample lifetime of ${{\tau }_{{\rm s}}}$ = 1 s $\gg \;{{\tau }_{c}}$, which suggests that the LEA is valid over a coarse grained spatial scale of $3.5\;\mu {\rm m}$ and time scale 20 ms.

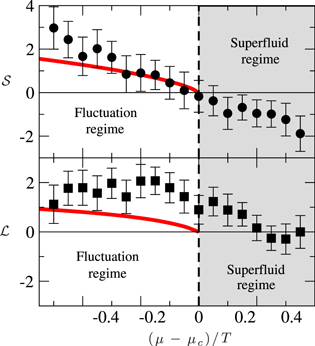
Our comparison between theory and experiment is plotted in figure 3. Here we show the thermopower (upper panel) and the Lorenz number (lower panel) for a 2D Bose gas, obtained from equation (13). In the simplest terms the data suggests that the thermopower changes sign at or near the transition. Experimentally, the Lorenz number approaches zero at or near T_c. The error bars are sufficiently large and one should not infer that $\mathcal{L}$ becomes negative on the other side of the transition, as this is unphysical. We stress that our theory is applicable only to the normal phase. Indeed, one does not have many reliable theoretical tools for treating bosons (in any capacity, not just transport) near, but below the transition.

Zoom In Zoom Out Reset image size

In the normal phase, the figure shows that the theory and experiment of [1] coincide rather well for the thermopower $\mathcal{S},$ particularly near the condensation regime. The Lorenz number is off by about a factor of 2. However, given the simplicity of the model, a disparity of order unity is not unreasonable. It should be stressed that the behavior of $\mathcal{S}$ and $\mathcal{L}$ are very strongly reflective of the divergence of the mass conductivity at the phase transition. The fact that both are found in the data to vanish at or near the transition in the experiments serves to help validate this experimental methodology [1].

Many communities from nuclear physics, astrophysics and condensed matter are interested in transport in the cold gases. The shear viscosity has been a rather recent focus [34–38] and, as in this paper, there is an emerging interest in thermoelectric properties [1, 3]. There will undoubtedly be many more such experimental transport studies with time. The theory in this paper is directed towards such experiments. We have emphasized that the mechanisms for momentum dissipation are very sensitive to the experimental cold atom set up. This has led us to adopt a Kubo formula approach which treats dissipation at a non-specific phenomenological level. An important consequence of our studies is the observation of quantum critical scaling and of the non-universality of (bosonic) transport, despite universality in thermodynamics. This is in contrast to Fermi liquid or gas systems where the processes contributing to transport are localized around the Fermi energy, and one finds, for example a Wiedermann–Franz law for the Lorenz ratio.

Another major finding of this work is the observation that bosonic transport in the normal state near condensation appears to be semi-quantitatively consistent with observations and theory in condensed matter studies of (bosonic) superconducting fluctuations [13, 14]. In this way our paper establishes a connection between transport properties in condensed matter and in normal-phase cold atom systems. This connection has other implications for future experiments. Because ultracold gases are clean and well controlled, they may help elucidate transport in (fermionic) high T_c systems [27] where bosonic degrees of freedom (through pre-formed pairs, or vortices or bipolarons, etc) are believed to dominate transport. In particular, high temperature superconductors in condensed matter appear to have an anomalously large critical regime where these fluctuation effects are observed which is associated with the famous 'pseudogap'. In the cold Fermi gases near unitarity there is some debate about whether such a pseudogap exists or not. This would suggest that future transport studies of fermionic superfluids may help elucidate this issue.

In contrast to the behavior of degenerate Fermi gases, we reiterate the strong sensitivity of Bose gases to the dissipation mechanism. For bosons, different dissipation mechanisms imply different scaling laws, possibly defining different universality classes. For the future, the universality found in the thermodynamics of dilute Bose gases, either loaded or not in a lattice, [16, 23, 25, 39], will also need to be addressed in the context of transport. This would allow a direct verification of our prediction of the breakdown of universality in transport.

This work is supported by NSF-MRSEC Grant 0820054; CC acknowledges support from NSF PHY-1206095 and ARO-MURI 63834-PH-MUR. We thank Chih-Chun Chien and Yan He for helpful conversations. CC thanks Grenier Charles and Antoine Georges for useful discussion.