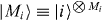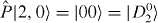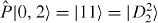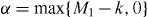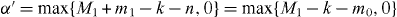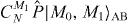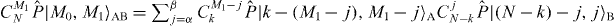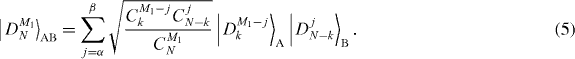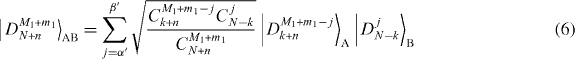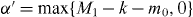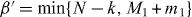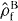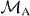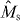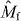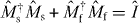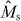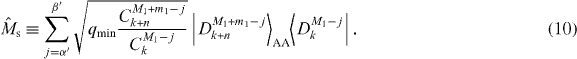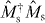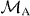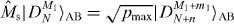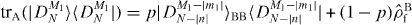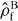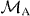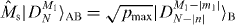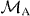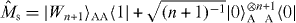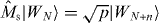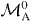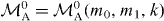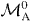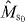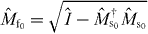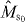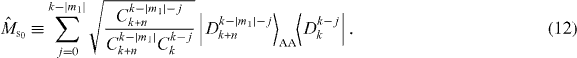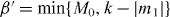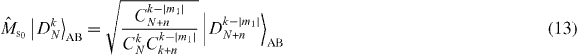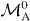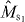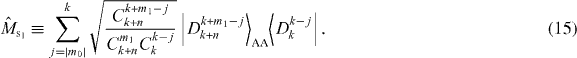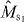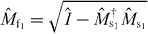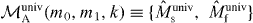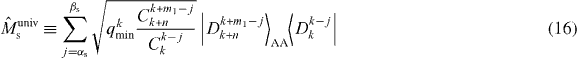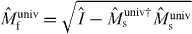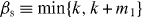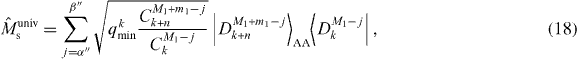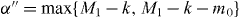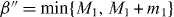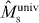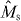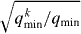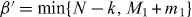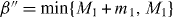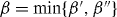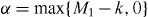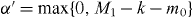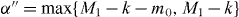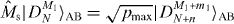Universal gates for transforming multipartite entangled Dicke states

Entanglement is a key resource facilitating a wide range of emerging quantum technologies, such as quantum computing [1], communication [2, 3] and sensing [4]. It has been well established theoretically [5] and experimentally demonstrated between various particles, including photons, atoms and ions [6]. Entanglement between two particles [7] has been routinely prepared and used in different physical systems for a variety of tasks [1–5]. However, in order to make full use of the power of entanglement for quantum technologies and to probe deeper into the foundations of quantum mechanics, there has been an increasing push toward making larger numbers of particles entangle with each other. As the number of particles increases beyond two, different types of entangled states that cannot be converted into each other using local operations and classical communication [8] emerge. Greenberger–Horne–Zeilinger (GHZ) [9], cluster [10], Dicke [11] and W states [12], are examples of such inequivalent classes. Dicke states in particular provide a rich variety of structurally complex states among many particles and hold great promise for a wide range of applications in quantum information. Recent experiments have demonstrated the generation of these states in physical systems such as ion traps [13, 14], all-optical setups [15–22] and cavity quantum electrodynamic (QED) settings [23]. Despite these impressive demonstrations, the complexity of Dicke states makes their preparation and manipulation difficult. Thus, understanding the limits for preparing and manipulating large multipartite entangled versions are of great interest and urgently needed.

In this paper, we derive the minimal number of qubits that it is necessary to have access to in order to expand and reduce any given Dicke state. We show that, unlike W [16], GHZ and cluster states [24], Dicke states in general cannot be transformed by local access to only a single qubit. We consider gates for transforming Dicke states by minimal access. In the case of the expansion of W states, by accessing only one qubit there is a universal optimal gate which can expand any size of W state with maximum success probability. Similarly to this case, we derive a universal optimal gate which adds either spin-up or spin-down qubits to Dicke states by minimal access. We then construct universal gates which can add or subtract given numbers of spin-up and spin-down qubits with a nonzero success probability, regardless of the size of an initial Dicke state. Our work has important implications for assessing the amount of control one needs in the preparation and manipulation of Dicke states in physical systems for a range of quantum information applications, such as quantum algorithms [25], quantum games [26], testing efficient tomographic techniques [22] and multi-agent quantum networking [18–21].

An N-qubit Dicke state with M₁ excitations is the equally weighted superposition of all permutations of N-qubit product states with M₁ spin-up (|1〉) and M₀ = N − M₁ spin-down (|0〉), and is written as

$$\begin{equation} \left| D_N^{M_1} \right\rangle =(C_N^{M_1})^{1/2}\hat{P}\left| M_0,M_1 \right\rangle, \end{equation} \tag{ 1 }$$

where |M0,M1〉 ≡ |M0〉|M1〉 with $| M_i \rangle \equiv | i \rangle ^{\bigotimes M_i}$ for i = {0,1}, CM1N ≡ N!/(M1!(N − M1)!) and $\hat {P}$ is a projector onto the symmetric subspace with respect to the permutation of any two particles. For example, $\hat {P}| 2,0 \rangle =| 00 \rangle =| D_2^0 \rangle$, $\hat {P}| 1,1 \rangle =(| 01 \rangle +| 10 \rangle )/2=| D_2^1 \rangle /\sqrt {2}$, and $\hat {P}| 0,2 \rangle =| 11 \rangle =| D_2^2 \rangle$. Equation (1) describes general symmetric Dicke states and the theory we develop covers this entire class.

We assume that |DM1N〉 is shared between two physical subsystems A and B, and denote this as |DM1N〉AB, with subsystem A holding a total of k qubits and subsystem B holding the remaining qubits, as shown in figure 1(a). Here we derive the minimum number k of qubits that it is necessary to have access to in order to transform the state |DM1N〉AB into a state |DM1+m1N+n〉AB, where |n| is the total number of qubits added for n > 0 and deleted for n < 0, and similarly |m1| is the added or deleted number of qubits in |1〉, while m0 ≡ n − m1 represents the added or deleted number of qubits in |0〉. For the trivial cases of M0 = 0 (M0 + m0 = 0) and M1 = 0 (M1 + m1 = 0), the states of system AB are product states |1...1〉 and |0...0〉, respectively. In the following, we will study only the nontrivial cases where M0 > 0, M1 > 0, M0 + m0 > 0 and M1 + m1 > 0. We consider a local transformation scenario in which access to subsystem B is forbidden, and the transformation task is carried out by collectively manipulating the k qubits of subsystem A only (see figure 1(b)). This limited-access scenario allows us to investigate the requirements for the number of qubits that one would need control over in a given physical system. In this scenario, the whole system after the transformation is composed of N − k qubits in subsystem B and k + n qubits in subsystem A. Thus, we have N + n ⩾ N − k, namely N ⩾ k ⩾ − n is necessary. In other words, the new total number of qubits must be at least as big as the number of qubits in subsystem B to which access is forbidden.

Zoom In Zoom Out Reset image size

We now derive a necessary condition for the transformation of Dicke states. When we consider the superposition of pure product states for the Dicke state in the computational basis, the minimum number of spin-up qubits in subsystem B is obtained by maximizing the number of spin-up qubits in subsystem A, and is given by $\alpha =\max \{M_1-k,0\}$ for the initial Dicke state |DM1N〉 and $\alpha '=\max \{M_1+m_1-k-n,0\}= \max \{M_1-k-m_0,0\}$ for the final Dicke state |DM1+m1N+n〉. Since subsystem B is left untouched in the transformation, the minimum number of spin-up qubits cannot decrease in subsystem B. However it may increase, for example if qubits are deleted from subsystem A. Thus, the relation α' ⩾ α should hold. This means that k ⩾ M1 is a necessary condition for the transformation with m0 > 0. Since a similar argument holds for the transformation with m1 > 0, we have

$$\begin{equation} k\geqslant\left\{ \begin{array}{@{}ll@{}} M_1 & {\rm for}~ m_0 > 0, \\ M_0 & {\rm for}~ m_1 > 0, \end{array} \right. \end{equation} \tag{ 2 }$$

as a necessary condition for transforming a Dicke state to another Dicke state. In other words, for spin-down (spin-up) qubits to be added, the necessary condition is that the number of qubits in subsystem A must be at least as big as the number of spin-up (spin-down) qubits in the total system. Note that for other cases, we have

$$\begin{equation} k\geqslant -n\ \ {\rm for}~ m_0 \leqslant 0 \ {\rm and}~ m_1\leqslant 0. \end{equation} \tag{ 3 }$$

This is a trivial condition that the number of qubits in subsystem A should be at least as big as the total number of qubits being deleted.

Here we show that conditions (2) and (3) are sufficient conditions for transformation of a Dicke state to another Dicke state for any given physical system, and we derive the maximum probability for the transformation. We first decompose the Dicke state in equation (1) by using the symmetric bases in subsystems A and B. When we expand $C_N^{M_1}\hat {P}| M_0,M_1 \rangle_{\rm{AB}}$ in the computational basis, it is given by the sum of CM1N terms with unit amplitude. From these terms, we select those that have j spin-up qubits in subsystem B. The sum of these selected terms is given by $C_{k}^{M_1-j}\hat {P}| k-(M_1-j), M_1-j \rangle_{\rm{A}}C_{N-k}^{j}\hat {P}| (N-k)-j,j \rangle_{\rm{B}}$. Thus we can write $C_N^{M_1}\hat {P}| M_0,M_1 \rangle_{\rm{AB}}=\sum_{j=\alpha }^\beta C_{k}^{M_1-j}\hat {P}| k-(M_1-j),M_1-j \rangle_{\rm{A}}C_{N-k}^{j}\hat {P}| (N-k)-j,j \rangle_{\rm{B}}$, where the range of the summation over j is given by

$$\begin{equation} \alpha=\max\{ M_1-k, 0\},\quad \beta=\min\{ N-k, M_1\} \end{equation} \tag{ 4 }$$

and β is calculated using similar methods to the derivation of α. Using this decomposition, we rewrite equation (1) as

$$\begin{equation} \left| D_N^{M_1} \right\rangle_{\rm{AB}} =\sum_{j=\alpha}^{\beta}\sqrt{\frac{C_{k}^{M_1-j}C_{N-k}^{j}}{C_N^{M_1}}} \left| D_k^{M_1-j} \right\rangle_{\rm{A}}\left| D_{N-k}^{j} \right\rangle_{\rm{B}}. \end{equation} \tag{ 5 }$$

In the following, we treat the case with k > −n and the case with k = −n separately. In each case, assuming the conditions (2) and (3), we show that the transformation is optimally achievable at a nonzero probability p_max.

For k > −n, decomposition of the desired state |DM1+m1N+n〉AB obtained from the transformation is

$$\begin{equation} \left| D_{N+n}^{M_1+m_1} \right\rangle_{\rm{AB}} =\sum_{j=\alpha'}^{\beta'} \sqrt{\frac{C_{k+n}^{M_1+m_1-j}C_{N-k}^{j}}{C_{N+n}^{M_1+m_1}}} \left| D_{k+n}^{M_1+m_1-j} \right\rangle_{\rm{A}}\left| D_{N-k}^{j} \right\rangle_{\rm{B}} \end{equation} \tag{ 6 }$$

with $\alpha '=\max \{ M_1-k-m_0, 0\}$ and $\beta '=\min \{ N-k, M_1+m_1\}$. Again, β' is calculated similarly to α'. Since access is allowed only to subsystem A, the marginal state in subsystem B does not change through the transformation process, which implies the relation ${{\rm tr}}_{\rm{A}}(| D_N^{M_1} \rangle \langle D_N^{M_1} |)=p {{\rm tr}}_{\rm{A}}(| D_{N+n}^{M_1+m_1} \rangle \langle D_{N+n}^{M_1+m_1} |)+(1-p)\hat {\rho }_{\rm{f}}^{\rm{B}}$ must hold. Here p is the success probability of the transformation and $\hat {\rho }_{\rm{f}}^{\rm{B}}$ is the state of subsystem B when the transformation fails. From equation (5), trA(|DM1N〉〈DM1N|) and tr A(|DM1+m1 N+n〉〈DM1+m1N+n|) are diagonalized by the basis {|DjN−k〉B}0⩽j⩽N−k. Thus, from the positivity of $\hat {\rho }_{\rm{f}}^{\rm{B}}$, we have p ⩽ pmax, where

$$\begin{equation} p_{\rm{max}} \equiv q_{\rm{min}} C_{N+n}^{M_1+m_1}/C_N^{M_1} \end{equation} \tag{ 7 }$$

with

$$\begin{equation} q_{\rm{min}}\equiv \min\limits_{\alpha' \leqslant j\leqslant \beta'} q_j \end{equation} \tag{ 8 }$$

and

$$\begin{equation} q_j \equiv C_k^{M_1-j}/C_{k+n}^{M_1+m_1-j}. \end{equation} \tag{ 9 }$$

Here it should be understood that C⁰₀ ≡ 1, and C^M₁−j_k = 0 for M₁ − j < 0 and M₁ − j > k. Since we are assuming conditions (2) and (3), we have α' ⩾ α and β' ⩽ β, resulting in p_max > 0. Under these conditions, we construct a gate $\mathcal {M}_{\rm{A}}$ which achieves the upper bound on the success probability in equation (7). The gate $\mathcal {M}_{\rm{A}}$ is composed of a success operator $\hat {M}_{\rm{s}}$ and a failure operator $\hat {M}_{\rm{f}}$ satisfying $\hat {M}_{\rm{s}}^\dagger \hat {M}_{\rm{s}}+ \hat {M}_{\rm{f}}^\dagger \hat {M}_{\rm{f}} = \hat {I}$. We define $\hat {M}_{\rm{s}}$ by

$$\begin{equation} \hat{M}_{\rm{s}}\equiv \sum_{j=\alpha'}^{\beta'}\sqrt{q_{\rm{min}}\frac{C_{k+n}^{M_1+m_1-j}} {C_k^{M_1-j}}} \left| D_{k+n}^{M_1+m_1-j} \right\rangle_{\rm{AA}}\hspace{-0.1cm}\left\langle D_k^{M_1-j} \right|. \end{equation} \tag{ 10 }$$

From equations (8) and (9), no coefficients of $\hat {M}_{\rm{s}}^\dagger \hat {M}_{\rm{s}}$ are larger than 1, and thus $\mathcal {M}_{\rm{A}}$ is a valid measurement process for any given physical system. From equations (5)–(7) and (10), we have $\hat {M}_{\rm{s}}| D_{N}^{M_1} \rangle_{\rm{AB}}=\sqrt {p_{\rm{max}}}| D_{N+n}^{M_1+m_1} \rangle_{\rm{AB}}$. As a result, for k > −n, the maximum probability of the transformation is given by p_max defined in equation (7), which is nonzero when conditions (2) and (3) hold.

For the case of k = −n, condition (2) implies m₀ ⩽ 0 and m₁ ⩽ 0 because k ⩾ M₁ ⩾ − m₁ > −m₀ − m₁ = −n for m₀ > 0 and k ⩾ M₀ ⩾ − m₀ > −m₀ − m₁ = −n for m₁ > 0. Thus the desired state after the transformation is |D^{M₁−|m₁|}_N−|n|〉_B. From the relation ${{\rm tr}}_{\rm{A}}(| D_N^{M_1} \rangle \langle D_N^{M_1} |)=p | D_{N-|n|}^{M_1-|m_1|} \rangle_{\rm{BB}}\langle D_{N-|n|}^{M_1-|m_1|} |+(1-p)\hat {\rho }_{\rm{f}}^{\rm{B}}$ and the positivity of $\hat {\rho }_{\rm{f}}^{\rm{B}}$, we have p ⩽ p_max, where p_max is given by equation (7) with α' = β' = M₁ − |m₁| and k = −n = |m₀| + |m₁|, and is strictly positive. In such a case, the success operator for the gate $\mathcal {M}_{\rm{A}}$ which achieves the upper bound on the success probability is defined by

$$\begin{equation} \hat{M}_{\rm{s}}\equiv _{\rm{A}}{\left\langle D_{|n|}^{|m_1|} \right|}, \end{equation} \tag{ 11 }$$

which is a linear functional but we denote it as a linear operator for convenience. From equations (5) and (11), we obtain $\hat {M}_{\rm{s}}| D_{N}^{M_1} \rangle_{\rm{AB}}=\sqrt {p_{\rm{max}}}| D_{N-|n|}^{M_1-|m_1|} \rangle_{\rm{B}}$. We thus conclude that conditions (2) and (3) are sufficient for the transformation, and the maximum success probability is given by p_max defined in equation (7).

A W state is a special case of Dicke states with only one excitation M₁ = 1, i.e. |W_N〉 = |D¹_N〉, recently generated in ion trap [13, 14], photonic [15–17] and cavity settings [23]. When we expand a W state, a universal optimal gate $\mathcal {M}_{\rm{A}}$ which achieves the expansion to |W_N+m0〉 = |D¹_N+m0〉 (m₀ > 0) by accessing only one qubit is constructed as $\hat {M}_{\rm{s}}=| W_{n+1} \rangle_{\rm{AA}}\langle 1 |+\sqrt {(n+1)^{-1}}| 0 \rangle ^{\otimes n+1}_{\rm{A} \ \ \rm{A}}\langle 0 |$. The expansion can be done regardless of the size of the W state as $\hat {M}_{\rm{s}}| W_{N} \rangle =\sqrt {p}| W_{N+n} \rangle$ with success probability p = (N + n)N⁻¹(n + 1)⁻¹, which coincides with p_max calculated from equations (7)–(9) for any N.

Here we show that such a universal optimality is partially generalized to Dicke states under the following conditions: (a) the gate increases at most one type of spin, and (b) the gate accesses the minimum number of qubits to achieve the transformation.

For a gate with m₀ ⩽ 0 and m₁ ⩽ 0, condition (b) means that k = −n = |m₀| + |m₁|. Then the gate shown in equation (11) achieving p_max only depends on m₁ and n. Thus it works as a universal optimal gate for any input with M₀ ⩾ |m₀| and M₁ ⩾ |m₁|, which is a trivial condition that the number of spin-up (spin-down) qubits in the input state is at least as big as the number of spin-up (spin-down) qubits to be deleted.

In the case of m₀ > 0, m₁ ⩽ 0, and k = M₁, i.e. adding only spin-down qubits by minimal access, we have α' = 0, and q_j defined in equation (9) satisfies q_j < q_j+1 for j = 0,1,..., β' − 1.⁶ As a result, we have p_max = q₀C^k−|m₁|_N+n/C^k_N = C^k−|m₁|_N+n/(C^k_NC^k−|m₁|_k+n) from definition (7). We give an explicit construction of a universal optimal gate $\mathcal {M}_{\rm{A}}^0$ which transforms a Dicke state |D^k_N〉 to |D^k−|m₁|_{N+m 0 − |m1|}〉. The gate is characterized by the three parameters m₀, m₁ and k, namely $\mathcal {M}_{\rm{A}}^0=\mathcal {M}_{\rm{A}}^0(m_0, m_1, k)$. The gate $\mathcal {M}_{\rm{A}}^0$ is a measurement represented by a success operator $\hat {M}_{\rm{s}_0}$ and a failure operator $\hat {M}_{\rm{f}_0} = \sqrt {\hat {I}-\hat {M}_{\rm{s}_0}^{\dagger }\hat {M}_{\rm{s}_0}}$, and we define $\hat {M}_{\rm{s}_0}$ by

$$\begin{equation} \hat{M}_{\rm{s}_0}\equiv \sum_{j=0}^{k-|m_1|} \sqrt{\frac{C_{k+n}^{k-|m_1|-j}}{C_{k+n}^{k-|m_1|}C_k^{k-j}}} \left| D_{k+n}^{k-|m_1|-j} \right\rangle_{\rm{AA}}\hspace{-0.1cm}\left\langle D_k^{k-j} \right|. \end{equation} \tag{ 12 }$$

Since $\beta =\min \{ M_0, k\}$ and $\beta '=\min \{ M_0, k-|m_1|\}$, either β ⩾ β' = k − |m₁| or β = β' = M₀ holds. Together with α = α' = 0, we see from equations (5) and (12) that

$$\begin{equation} \hat{M}_{\rm{s}_0}\left| D_N^k \right\rangle_{\rm{AB}}= \sqrt{\frac{C_{N+n}^{k-|m_1|}}{C_N^{k}C_{k+n}^{k-|m_1|}}} \left| D_{N+n}^{k-|m_1|} \right\rangle_{\rm{AB}} \end{equation} \tag{ 13 }$$

$$\begin{equation} =\sqrt{p_{\rm{max}}} \left| D_{N+n}^{k-|m_1|} \right\rangle_{\rm{AB}} \end{equation} \tag{ 14 }$$

for any Dicke state |D^k_N〉_AB. Thus the gate $\mathcal {M}_{\rm{A}}^0$ is the universal optimal gate for transforming Dicke states with minimal access of qubits for m₀ > 0 and m₁ ⩽ 0.

In the case of m₁ > 0, m₀ ⩽ 0 and k = M₀, i.e. adding only spin-up qubits by minimal access, we can also construct a universal optimal gate by using the symmetry between |0〉 and |1〉. Let us define a new operator $\hat {M}_{\rm{s}_1}$ by interchanging the definition of |0〉 and |1〉 in equation (12), namely, replacing m₁ by m₀ and |D^b_a〉_A by |D^a−b_a〉_A. After rewriting the parameter j by k − j, we arrive at

$$\begin{equation} \hat{M}_{\rm{s}_1}\equiv \sum_{j=|m_0|}^{k} \sqrt{\frac{C_{k+n}^{k+m_1-j}}{C_{k+n}^{m_1}C_k^{k-j}}} \left| D_{k+n}^{k+m_1-j} \right\rangle_{\rm{AA}}\hspace{-0.1cm}\left\langle D_k^{k-j} \right|. \end{equation} \tag{ 15 }$$

By symmetry, the gate $\mathcal {M}_{\rm{A}}^1$ defined by $\hat {M}_{\rm{s}_1}$ and $\hat {M}_{\rm{f}_1} = \sqrt {\hat {I}-\hat {M}_{\rm{s}_1}^\dagger \hat {M}_{{\mathrm { s}}_1}}$ achieves the optimal success probability p_max when it is applied to |D^N−k_N〉_AB.

Here we derive universal gates $\mathcal {M}^{\rm{univ}}_{\rm{A}}(m_0, m_1, k)\equiv \{ \hat {M}^{\rm{univ}}_{\rm{s}},\ \hat {M}^{\rm{univ}}_{\rm{f}}\}$ which transform all Dicke states |DM1N〉AB satisfying the conditions on M0 and M1 in equations (2) and (3) to |DM1+m1N+n〉AB with nonzero success probabilities. For k = −n = |m0| + |m1| with m0 ⩽ 0 and m1 ⩽ 0, it is easy to see that the gate defined in equation (11) is a universal gate for any Dicke state satisfying M0 ⩾ |m0| and M1 ⩾ |m1|. In the following, we therefore consider the case for k > −n.

We define the success operator of the gate by

$$\begin{equation} \hat{M}^{\rm{univ}}_{\rm{s}}\equiv \sum_{j=\alpha_{\rm{s}}}^{\beta_{\rm{s}}} \sqrt{q_{\rm{min}}^{k}\frac{C_{k+n}^{k+m_1-j}}{C_k^{k-j}}} \left| D_{k+n}^{k+m_1-j} \right\rangle_{\rm{AA}}\hspace{-0.1cm}\left\langle D_k^{k-j} \right| \end{equation} \tag{ 16 }$$

and define the failure operator by $\hat {M}^{\rm{univ}}_{\rm{f}}= \sqrt {\hat {I}-\hat {M}^{\rm{univ} \dagger }_{\rm{s}}\hat {M}^{\rm{univ}}_{\rm{s}}}$, where $\alpha_{\rm{s}}\equiv \max \{ 0, -m_0\}$, $\beta_{\rm{s}}\equiv \min \{ k, k+m_1\}$, and

$$\begin{equation} q_{\rm{min}}^{k}\equiv \min_{\alpha_{\rm{s}}\leqslant j\leqslant \beta_{\rm{s}}} \frac{C_k^{k-j}}{C_{k+n}^{k+m_1-j}} > 0. \end{equation} \tag{ 17 }$$

Here the positivity comes from α_s ⩽ j ⩽ β_s, implying that 0 ⩽ k − j ⩽ k and 0 ⩽ k + m₁ − j ⩽ k + n. In equation (16), by substituting j = k − M₁ + j', and relabeling j' as j, $\hat {M}^{\mathrm { univ}}_{\rm{s}}$ is rewritten as

$$\begin{equation} \hat{M}^{\rm{univ}}_{\rm{s}}= \sum_{j=\alpha''}^{\beta''} \sqrt{q^k_{\rm{min}}\frac{C_{k+n}^{M_1+m_1-j}} {C_k^{M_1-j}}} \left| D_{k+n}^{M_1+m_1-j} \right\rangle_{\rm{AA}}\hspace{-0.1cm} \left\langle D_k^{M_1-j} \right|, \end{equation} \tag{ 18 }$$

where $\alpha ''=\max \{ M_1-k, M_1-k-m_0\}$ and $\beta ''=\min \{ M_1, M_1+m_1\}$. From equations (10) and (18), $\hat {M}^{\rm{univ}}_{\rm{s}}$ only differs from $\hat {M}_{\rm{s}}$ by the overall factor $\sqrt {q_{\rm{min}}^k/q_{\rm{min}}}$ and the range of the summation over j. Because $\beta =\min \{ M_1, N-k\}$, $\beta '=\min \{ N-k, M_1+m_1\}$ and $\beta ''=\min \{ M_1+m_1, M_1\}$, either β' = β'' or $\beta =\min \{ \beta ', \beta ''\}$ is satisfied. Similarly, because $\alpha =\max \{ M_1-k, 0\}$, $\alpha '=\max \{ 0, M_1-k-m_0\}$ and $\alpha ''=\max \{ M_1-k-m_0, M_1-k\}$, either α' = α'' or $\alpha =\max \{ \alpha ', \alpha ''\}$ is satisfied. As a result we have

$$\begin{equation} \hat{M}^{\rm{univ}}_{\rm{s}}\left| D_{N}^{M_1} \right\rangle_{\rm{AB}} =\sqrt{\frac{q_{\rm{min}}^k}{q_{\rm{min}}}} \hat{M}_{\rm{s}}\left| D_{N}^{M_1} \right\rangle_{\rm{AB}}. \end{equation} \tag{ 19 }$$

From $\hat {M}_{\rm{s}}| D_{N}^{M_1} \rangle_{\rm{AB}}=\sqrt {p_{\rm{max}}}| D_{N+n}^{M_1+m_1} \rangle_{\rm{AB}}$, the success probability of the transformation is p' = p_maxq^k_min/q_min. From q^k_min > 0, we see that the transformation succeeds with a nonzero probability whenever p_max > 0.

For convenience, we classify the universal gates into four cases according to the signs of m₀ and m₁, and show the range of applicable input Dicke states (M₀,M₁) for each case in figure 2. The input states outside of the designated region are not transformable by any means (as p_max = 0), while those in the area are transformed with a nonzero success probability by the gate $\mathcal {M}_{\rm{A}}^{\rm{univ}}$. Thus, taken together the gates we have developed are universal gates for Dicke state transformation.

Zoom In Zoom Out Reset image size

Contrary to the expansion of GHZ, cluster and W states, Dicke states cannot be transformed by locally accessing only one qubit in general. We have derived the minimum number of qubits that should be accessed to transform a Dicke state to another Dicke state. Similarly to the expansion of W states, when we access the minimum number of qubits in a physical system for the transformation, one can construct universal optimal gates which add one type of spin to a given Dicke state. We have also constructed a universal optimal gate which deletes both types of spin from a Dicke state with the minimum access of qubits. Finally, we have shown the existence of universal gates which transform any Dicke state satisfying the derived condition for the transformation with nonzero probabilities. Our results are essential for understanding the amount of control needed in the preparation and manipulation of Dicke states in physical systems such as ion traps, all-optical setups and cavity-QED settings for future quantum information applications.

This work was supported by the Funding Program for World-Leading Innovative R & D on Science and Technology (FIRST), MEXT Grant-in-Aid for Scientific Research on Innovative Areas 21102008, MEXT Grant-in-Aid for Young scientists(A) 23684035, JSPS Grant-in-Aid for Scientific Research(A) 25247068 and (B) 25286077, UK EPSRC and the Leverhulme Trust. SKO thanks Dr Lan Yang for her support.