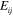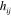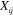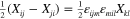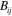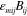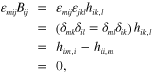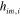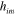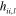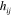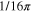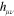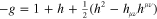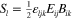Abstract
We present a theory in Maxwellian form for gravitational waves in a flat background. This requires us to identify the gravitational analogues of the electric and magnetic fields for light. An important novelty, however, is that our analogues are not vector fields but rather rank-two tensor fields; in place of a three-component vector at each point in space, as in electromagnetism, our fields are three by three symmetric matrices at each point. The resulting Maxwell-like equations lead directly to a Poynting theorem for the local energy density associated with a gravitational wave and to associated local properties including densities of momentum and angular momentum.
Export citation and abstract BibTeX RIS

Content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
The prediction of the existence of gravitational waves was one of the first applications made by Einstein of his general theory of relativity [1, 2]. In these papers, Einstein solved his field equations for weak fields to reveal the existence of plane waves travelling at the speed of light; a natural analogue of the familiar electromagnetic waves of Maxwell. He also showed that these waves should be generated by the non-uniform motion of masses, in much the same way that moving charges produce electromagnetic waves. Einstein's treatment and variants of it appear in numerous texts on general relativity [3–9], including some devoted primarily to gravitational waves [10–12].
Analogies between gravitation, as expressed in general relativity, and Maxwell's electromagnetism are often employed. This is entirely natural, of course, as both are relativistic theories. It is perhaps for gravitational waves that the links between the two are most readily apparent. In the absence of matter, both electromagnetic and gravitational waves are transverse and propagate at the speed of light. Both, moreover, display two orthogonal polarizations. The similarities between gravitational waves and their electromagnetic counterparts have been proposed as a route to a quantum theory of the gravitational field [13–16].
Our aim in this paper is to present the theory of gravitational waves in a manner that resembles as closely as possible the Maxwell theory of the free electromagnetic field. To this end we seek to treat only a very weak field in a flat, Minkowski, background. We introduce gravitational analogues of the electric and magnetic fields in this background and show that these are governed by a set of equations resembling Maxwell's equations. This is possible only because our dielectric and magnetic analogues are rank-two tensors, rather than the vectors encountered with electromagnetic waves. They should not be confused, moreover, with another analogy, gravito-electromagnetism, in which gravitational effects in the vicinity of of masses may be described in terms of gravitational vector analogues of the electric and magnetic fields [3, 8, 17]. The resemblance with Maxwell theory suggests forms for the mechanical properties of gravitational waves including an energy density and a density of helicity. We find that these obey local conservation laws with the local conservation of energy, in particular, having a form strongly reminiscent of Poynting's theorem [18, 19]. These conservation laws, together with expressions for the densities of linear and angular momentum, may be derived rigorously, moreover, as consequences of symmetries by Noether's theorem [20, 21].
We work with the natural system of units in which both the speed of light, c, and the universal gravitational constant, G, are set to unity, as are the electromagnetic constants 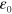 and
and 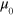 . There exist different conventions for the sign of the metric and of the curvature and these lead to different forms for the Einstein field equation. In this paper we follow the commonly used conventions advocated by Schutz [9] and others. Hence our Minkowski metric has the form
. There exist different conventions for the sign of the metric and of the curvature and these lead to different forms for the Einstein field equation. In this paper we follow the commonly used conventions advocated by Schutz [9] and others. Hence our Minkowski metric has the form 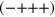 so that space-like distances are positive and our Riemann curvature is
so that space-like distances are positive and our Riemann curvature is
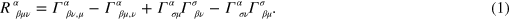
Here 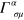 is the usual affine connection and a comma denotes partial differentiation. These choices determine our Einstein field equation to be
is the usual affine connection and a comma denotes partial differentiation. These choices determine our Einstein field equation to be

Adopting the opposite sign for the metric [6] or for the curvature [3] leads to a minus sign on the right-hand side of the field equation.
2. Qualitative comparison of gravitational and electromagnetic waves
Let us begin with a qualitative description of gravitational and electromagnetic waves. This will serve both to highlight similarities and differences between them and also to describe some of the properties we aim to quantify.
We consider both gravitational and electromagnetic waves in free space far removed from any matter. With this idealization, both types of wave propagate at the speed of light, both are transverse and they each have two orthogonal polarizations. By this we mean that both exist as (quasi-)plane waves and that the associated fields lie in the plane perpendicular to the wave-vector. The two types of wave differ, however, in a way that is usually discussed using quantum language; an elementary excitation of the electromagnetic field (a photon) has spin, or helicity, 1 [22, 23] but an excitation of the gravitational field (a graviton) has spin 2 [11, 15, 16]. The origin of this difference has been traced to the fact that in electromagnetism like charges repel, but in gravity particles with the same sign of mass attract (there is only one sign of mass, of course) [15].
It is reasonable to ask whether the spin-1 and spin-2 nature of the electromagnetic and gravitational waves might be identifiable by classical, rather than quantum reasoning. To this end consider that transverse waves might be produced by the motion of a system of charges or masses for electromagnetic or gravitational waves respectively. Consider, in particular, the situation depicted in figure 1 in which either a pair of bound charges or a pair of bound masses are in orbit about their centre of mass. A transverse electromagnetic wave has a natural direction identified which, by convention, we take to point from the positive to the negative charge. If we consider rotating the field about its direction of propagation then it is clear that a rotation of  is required in order to return to the original orientation. It is in this sense that we can identify light as having spin 1. For the gravitational source, however, the line joining the masses is clearly identified, but there is no preferred sense of direction along this line as the two masses have the same sign. In this sense 'up' is much the same as 'down' and we can represent the polarization by a double-headed arrow. A rotation of this field about the direction of propagation through π
, then, first brings us to the initial situation and it is in this sense that we can associate a spin of 2 with the gravitational wave.
is required in order to return to the original orientation. It is in this sense that we can identify light as having spin 1. For the gravitational source, however, the line joining the masses is clearly identified, but there is no preferred sense of direction along this line as the two masses have the same sign. In this sense 'up' is much the same as 'down' and we can represent the polarization by a double-headed arrow. A rotation of this field about the direction of propagation through π
, then, first brings us to the initial situation and it is in this sense that we can associate a spin of 2 with the gravitational wave.
Figure 1. Polarization of (a) an electromagnetic wave radiated by a pair of oppositely charged particles and (b) a gravitational wave radiated by a pair of masses.
Download figure:
Standard image High-resolution imageBefore presenting the quantitative details, it is worth pausing to understand what it is that we hope to achieve. The principal aim is to obtain a quantitative theory of gravitational waves in Maxwellian form and then to exploit this to obtain expressions for the densities of mechanical properties including energy, momentum, angular momentum and helicity. There are pit-falls to be avoided, however. In particular, we note the warning given by Misner, Thorne and Wheeler that the energy of the gravitational field cannot be localized [4]. Einstein, moreover, deduced only a pseudo energy–momentum tensor, which does not transform like a true tensor; indeed he wrote of this description that 'I am still convinced that a more useful determination of the energy components of the gravitational field—other than the one I have chosen—is not possible' [24]. The quantities we seek are intended very much in this spirit. Hence we seek expressions for the mechanical properties of gravitational waves in a flat background, very much as we describe the properties of electromagnetic waves.
3. Gravitational and electromagnetic waves
The theory of gravitational waves is presented in detail in the texts listed in the introduction with detailed presentations, in particular, given in [9–12]. Here we give only a brief outline of the basic ideas and compare this with the analogous derivation for electromagnetic waves from Maxwell's equations [19].
We recall that gravitational waves in free space are weak-field solutions of the Einstein field equation in the absence of matter:

Here the indices represent the four dimensions of space–time, with 0, 1, 2 and 3 denoting the 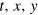 and z coordinates respectively. To obtain a weak-field solution in a flat background we write the metric in the form
and z coordinates respectively. To obtain a weak-field solution in a flat background we write the metric in the form

where 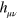 is small, by which we mean that the magnitudes of the elements of
is small, by which we mean that the magnitudes of the elements of 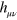 are all very much less than unity.
are all very much less than unity.
We shall develop a natural analogy between the quantities 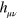 and the more familiar potential
and the more familiar potential 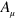 from electromagnetism. In particular, we note that we are free to change
from electromagnetism. In particular, we note that we are free to change 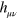 , which we shall refer to as the gravitational potential, in the following way without changing the Riemann curvature:
, which we shall refer to as the gravitational potential, in the following way without changing the Riemann curvature:

Here 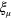 is any differentiable four-vector and the comma represents differentiation so that
is any differentiable four-vector and the comma represents differentiation so that 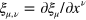 . Transformation (5) is analogous to the gauge transformation of the electromagnetic potential
. Transformation (5) is analogous to the gauge transformation of the electromagnetic potential

which leaves the electric and magnetic fields unchanged. For this reason we refer to the transformation (5) as a gauge transformation [25]. It is convenient to exploit this gauge freedom to impose the transverse-traceless gauge, by which we mean the following conditions:

Here we employ the usual summation convention in which a summation is implied over repeated indices
1
. With this choice of gauge, our gravitational potential is reduced to five independent components as 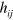 is symmetric under interchange of the indices; we can think of it as a rank-three symmetric matrix.
is symmetric under interchange of the indices; we can think of it as a rank-three symmetric matrix.
With our choice of the transverse symmetric gauge, our field equation (3) becomes a wave-equation for 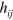 :
:

The natural solutions of this equation are plane waves propagating at the speed of light. This, together with our transverse-traceless gauge conditions (7), leads to two orthogonal polarizations for 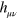 in the plane perpendicular to the wave vector
in the plane perpendicular to the wave vector 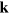 . For a plane wave propagating in the z-direction, for example, these two polarizations correspond to the non-vanishing elements
. For a plane wave propagating in the z-direction, for example, these two polarizations correspond to the non-vanishing elements

We note that each of these two polarizations do not correspond to a simple direction but rather to an oscillation between two orthogonal directions. The two polarizations are orthogonal to each other in the sense that 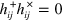 .
.
Let us compare what we have presented for gravitational waves with the more familiar electromagnetic waves. In the absence of matter, light, and its associated electric and magnetic fields, 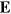 and
and  , obey the free-field Maxwell equations:
, obey the free-field Maxwell equations:

To make contact with the analysis of gravitational waves we recall that we can write  and
and 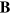 in terms of the vector potential
in terms of the vector potential  and the scalar potential φ
:
and the scalar potential φ
:

Our first Maxwell equation fixes the longitudinal and transverse parts of 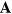 ,
, 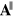 and
and  , in the sense that
, in the sense that
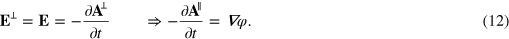
If we adopt the Coulomb gauge, so that  and
and 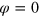 , then we have the simple condition
, then we have the simple condition

By choosing the Coulomb gauge, we can reduce the free-field Maxwell equations to a wave-equation for A:

which is the analogue of (8). As with gravitational waves, the natural solutions are plane waves propagating with the speed of light. This, together with our Coulomb-gauge condition, 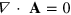 , leads to two orthogonal polarizations for
, leads to two orthogonal polarizations for 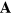 in the plane perpendicular to the wave vector
in the plane perpendicular to the wave vector 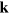 . For a plane wave propagating in the z-direction, for example, these two polarizations correspond to non-vanishing values for
. For a plane wave propagating in the z-direction, for example, these two polarizations correspond to non-vanishing values for 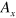 and
and 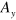 .
.
4. Duplex symmetry
The duplex symmetry for the free electromagnetic field [19, 26] (also referred to as duality, the Heaviside–Larmor symmetry and electric–magnetic democracy [26–35]) is a statement that the free-field Maxwell equations (10) are unchanged by the transformation:

for any θ
. This expresses the fact that we cannot tell if light from a distant source was generated by a source formed from charges or monopoles [36] or, less provocatively, emitted by an electric or a magnetic dipole [33]. The symmetry is useful, in particular, because it tells us that the mechanical properties of the electromagnetic field must be invariant under transformation (15) [33]. Important examples include the energy density, 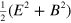 , and Poynting's vector,
, and Poynting's vector, 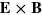 . We find that an analogous duplex symmetry holds also for gravitational waves and, moreover, that it is also reflected in the form of the mechanical properties of the waves.
. We find that an analogous duplex symmetry holds also for gravitational waves and, moreover, that it is also reflected in the form of the mechanical properties of the waves.
We can extend the duplex symmetry to the level of the potentials by introducing a second potential [28, 29], 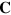 , which we take to be transverse (
, which we take to be transverse (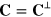 ), such that
), such that

With this identification, we find that 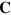 , like the vector potential
, like the vector potential 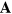 , satisfies the wave equation
, satisfies the wave equation

As we have shown previously, the two potentials also satisfy Maxwell-like equations:

The duplex symmetry is associated with a conserved quantity, of course, which is the helicity [37–42]:

Although the potentials appear in the helicity it is, in fact, a gauge-independent quantity.
It is instructive to reflect on the physical content of the Maxwell equations (18) or, indeed, (10). There are three points only: (i) both the potentials, 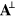 and
and 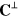 , satisfy the wave equation and so there are plane waves travelling at the speed of light, (ii) for each plane wave
, satisfy the wave equation and so there are plane waves travelling at the speed of light, (ii) for each plane wave 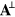 and
and 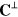 are perpendicular to the wave vector
are perpendicular to the wave vector  and (iii) for each plane wave,
and (iii) for each plane wave, 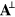 and
and 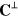 are mutually orthogonal and
are mutually orthogonal and  points in the direction of
points in the direction of  .
.
Turning to gravitational waves we recall that, in the transverse-traceless gauge, we have plane waves with two polarizations in the plane perpendicular to the wave vector 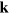 . It necessarily follows that we can write Maxwell-like equations for gravitational waves. To see this we introduce, in analogy with
. It necessarily follows that we can write Maxwell-like equations for gravitational waves. To see this we introduce, in analogy with 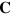 , a second gravitational potential,
, a second gravitational potential,  , which also respects the transverse-traceless conditions (7). The two gravitational potentials then satisfy the equations
, which also respects the transverse-traceless conditions (7). The two gravitational potentials then satisfy the equations

where 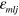 is the familiar permuting symbol [43]. The form of these equations suggests that we seek analogies with electromagnetism based on the associations
is the familiar permuting symbol [43]. The form of these equations suggests that we seek analogies with electromagnetism based on the associations

We find this association to be most fruitful.
4.1. Gauge dependence?
Before proceeding too far, we should address the point that the electromagnetic potentials, 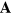 and
and 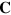 , and the gravitational potentials,
, and the gravitational potentials,  and
and 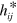 , are gauge-dependent. The simplicity of their properties, and in particular the fact that they satisfy Maxwell-like equations, is based on the gauge choices that have been made (Coulomb and transverse traceless). It is important to realize, however, that these gauges have a special, indeed privileged, status for the free fields.
, are gauge-dependent. The simplicity of their properties, and in particular the fact that they satisfy Maxwell-like equations, is based on the gauge choices that have been made (Coulomb and transverse traceless). It is important to realize, however, that these gauges have a special, indeed privileged, status for the free fields.
For the electromagnetic fields we have

because both  and
and  are themselves transverse. It necessarily follows that we can write (for example, by means of a Fourier transform) the quantities
are themselves transverse. It necessarily follows that we can write (for example, by means of a Fourier transform) the quantities 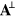 and
and 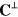 uniquely in terms of the gauge-invariant fields
uniquely in terms of the gauge-invariant fields  and
and 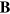 . Hence
. Hence  and
and 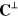 are themselves gauge-invariant; they are the gauge-invariant parts of
are themselves gauge-invariant; they are the gauge-invariant parts of 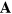 and
and 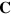 .
.
For gravitational waves we can relate, in the transverse-traceless gauge, 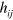 and
and 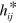 , to the curvature. For example [12]
, to the curvature. For example [12]

The curvature, 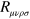 , is gauge-invariant [9] and it necessarily follows that
, is gauge-invariant [9] and it necessarily follows that  is the gauge-invariant part of the gravitational potential
is the gauge-invariant part of the gravitational potential 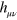 . Similarly
. Similarly 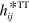 is the gauge-invariant part of
is the gauge-invariant part of  .
.
We can only conclude that quantities based on 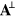 and
and 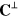 , for electromagnetism, or on
, for electromagnetism, or on 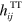 and
and 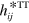 , for gravity, have a gauge-invariant meaning; we can express physical properties of light or of gravitational waves in terms of them. Henceforth we specify that all quantities are written in the Coulomb or transverse-traceless gauge and drop the superscripts.
, for gravity, have a gauge-invariant meaning; we can express physical properties of light or of gravitational waves in terms of them. Henceforth we specify that all quantities are written in the Coulomb or transverse-traceless gauge and drop the superscripts.
4.2. Duplex symmetry for the potentials
The electromagnetic potentials, 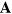 and
and 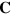 , satisfy the Maxwell equations (18) and this leads us to require that all physical properties of light are unchanged if we make the duplex transformation [35]
, satisfy the Maxwell equations (18) and this leads us to require that all physical properties of light are unchanged if we make the duplex transformation [35]

The gravitational potentials, 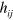 and
and 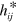 , also satisfy Maxwell equations (20) and we therefore require all physical properties of gravitational waves to be unchanged if we make the duplex transformation
, also satisfy Maxwell equations (20) and we therefore require all physical properties of gravitational waves to be unchanged if we make the duplex transformation

This symmetry will be our guiding principle in studying the mechanical properties of gravitational waves.
5. Maxwellian equations for gravitational waves
Associating our electromagnetic and gravitational potentials, as in (21), suggests that we introduce gravitational analogues of the electric and magnetic fields. These we define by the relationships:

Both these fields are symmetric under interchange of the indices 2 . It follows, by virtue of our Maxwell-like equations (20), that we can also write these quantities in terms of our second gravitational potential:

These definitions, (26) and (27), are the direct analogues of the electromagnetic expressions

Our Maxwellian equations for gravitational waves are then the natural analogues of those for electromagnetism:

These equations are the main result of our paper and the mechanical properties we derive arise directly from them. We should note, for the avoidance of any possible confusion, that other quite distinct quantities associated with the gravitational field have also been written as 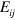 and its magnetic analogue. Two important examples are the 'electric' and 'magnetic' parts of the Weyl tensor (which are antisymmetric) [44, 45] and parts of the Riemann tensor [14, 39, 46]. The quantities we have introduced are quite distinct from these, although there is a differential relationship between our quantities and those in [14, 39, 46].
and its magnetic analogue. Two important examples are the 'electric' and 'magnetic' parts of the Weyl tensor (which are antisymmetric) [44, 45] and parts of the Riemann tensor [14, 39, 46]. The quantities we have introduced are quite distinct from these, although there is a differential relationship between our quantities and those in [14, 39, 46].
6. Conserved quantities
If we can construct a Lagrangian for our electromagnetic or gravitational waves, then we can employ Noether's theorem to extract conserved quantities [20, 21, 47, 48]. The Lagrangian density is not unique, of course, and this task may be considerably simpler with some forms of Lagrangian than with others. We proceed by constructing manifestly duplex-symmetric forms.
6.1. Electromagnetic waves
As a prelude to discussing conserved quantities for gravitational waves, we first review the theory of conserved quantities for the free electromagnetic field. A fuller account may be found in [47]. Our presentation differs somewhat from that in [47] in that we work throughout with the Coulomb-gauge potentials 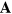 and
and 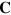 .
.
The conventional Lagrangian density for the free electromagnetic field is
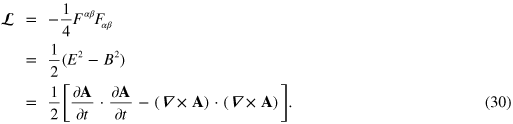
In this form the Lagrangian density is clearly not duplex-symmetric. We can impose the duplex symmetry, however, by replacing it with the new Lagrangian density
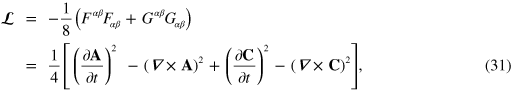
where 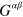 is the dual of the field tensor
is the dual of the field tensor  . It should be noted that applying the relationships between
. It should be noted that applying the relationships between 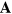 and
and  , implicit in the Maxwell equations (18), gives
, implicit in the Maxwell equations (18), gives 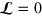 . It is necessary, however, to be able to vary
. It is necessary, however, to be able to vary 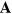 and
and 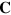 independently and only to apply the relationship between
independently and only to apply the relationship between 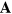 and
and 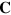 after performing the variation.
after performing the variation.
Noether's theorem tells us how to extract conserved quantities associated with symmetries of the Lagrangian. For brevity we present here only two of these, those associated with time-translation invariance and with the duplex symmetry. Time-translation invariance of the Lagrangian density leads to the conserved quantity

where the dots denote a time derivative. The quantity 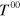 is, of course, the familiar energy density [19]
3
. Our second example is the duplex symmetry which, in infinitesimal form, is
is, of course, the familiar energy density [19]
3
. Our second example is the duplex symmetry which, in infinitesimal form, is

This is, by construction, an explicit symmetry of the Lagrangian density (31). The density of the associated conserved quantity, obtained by applying Noether's theorem, is [47]

which is the natural (albeit non-unique) density associated with the total helicity (19).
6.2. Gravitational waves
We can apply the methods of the preceding section to gravitational waves if we can identify a suitable Lagrangian density. Our starting point is the familiar action integral for the gravitational field [6, 11, 16],

where g is the determinant of the metric and R is the Ricci scalar
4
. For gravitational waves we work to the lowest order in 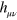 which, for the action, is second order. In the transverse-traceless gauge
which, for the action, is second order. In the transverse-traceless gauge 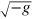 is second order in
is second order in 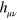 but R is zero to zeroth order and hence we can replace
but R is zero to zeroth order and hence we can replace 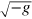 by unity to obtain
5
by unity to obtain
5

The Ricci scalar
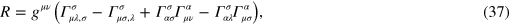
where 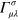 is the usual affine connection, gives terms containing first derivatives of
is the usual affine connection, gives terms containing first derivatives of 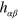 and also second derivatives. We can get rid of the problematic second derivatives using integration by parts [6], which gives the action integral
and also second derivatives. We can get rid of the problematic second derivatives using integration by parts [6], which gives the action integral
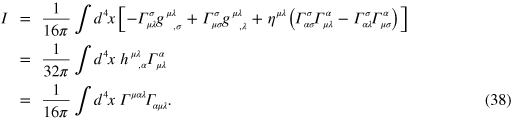
Comparison of this with our electromagnetic Lagrangian density (30) suggests, or perhaps reinforces, the idea that 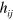 is the analogue of
is the analogue of 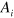 and
and 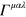 is the analogue of
is the analogue of 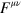 .
6
.
6
The most natural step is to write our Lagrangian density in a form that expresses, manifestly, our duplex symmetry. In order to achieve this, however, we first need to exploit the lack of uniqueness of the Lagrangian density to modify the obvious candidate for Lagrangian density. Let us start by writing this Lagrangian density in terms of 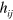 :
:

The action integral is unchanged if we add to 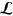 any four-divergence and the Lagrangian is unchanged if we add to
any four-divergence and the Lagrangian is unchanged if we add to 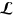 any three-divergence. Hence we can obtain from
any three-divergence. Hence we can obtain from 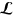 the physically equivalent form
the physically equivalent form
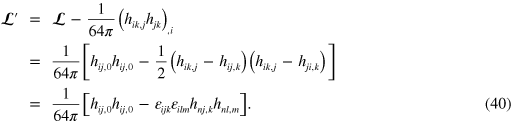
If write this Lagrangian density in terms of our gravitational analogues of the electric and magnetic field (26) then we arrive at the suggestive form

which is clearly analogous to the familiar Lagrangian density for the electromagnetic field, 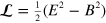 .
.
Our next step is to impose our duplex symmetry directly [47] by writing a new duplex-symmetric Lagrangian density
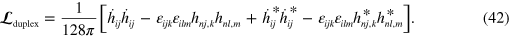
As with the duplex-symmetric electromagnetic Lagrangian density, this gravitational-wave Lagrangian density will be zero if we impose on it equations (20), exactly as is found for the corresponding electromagnetic field [47]. It is necessary, however, to allow for independent variation of 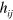 and
and 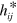 and to impose the relationship between them only after this has been done.
and to impose the relationship between them only after this has been done.
We can apply Noether's theorem to determine, from our duplex-symmetric Lagrangian density, the conserved quantities associated with the symmetries of the action. There exists an infinity of conservation laws for the gravitational field [49], much as is the case for the electromagnetic field [47]. We restrict our analysis only to the two quantities derived for electromagnetic waves in the preceding section, namely those associated with time-translation invariance and the duplex symmetry itself. Time-translation invariance of the Lagrangian density leads directly to the energy density
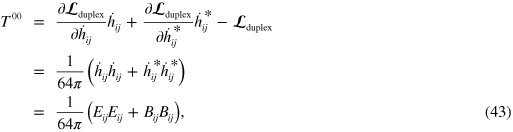
which is the natural analogue of the electromagnetic energy density, 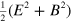 .
7
We note that an essentially equivalent expression was given previously by Afanasiev and Stepanovsky, although these authors consider the quantities we denote as
.
7
We note that an essentially equivalent expression was given previously by Afanasiev and Stepanovsky, although these authors consider the quantities we denote as  and
and 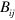 to be potentials, rather than the analogues of the electric and magnetic fields [39]. To obtain the conserved quantity associated with the duplex symmetry we consider this symmetry for
to be potentials, rather than the analogues of the electric and magnetic fields [39]. To obtain the conserved quantity associated with the duplex symmetry we consider this symmetry for 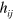 and
and 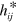 in infinitesimal form:
in infinitesimal form:

The density of the associated conserved quantity is given by Noether's theorem:
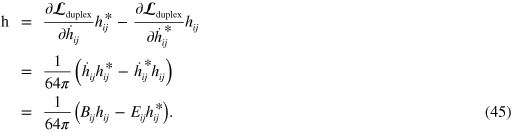
Hence the gravitational-wave analogue of the electromagnetic helicity is simply

which is analogous to the electromagnetic helicity 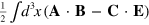 . There is an important subtlety associated with this gravitational helicity. An effective rotation generated by it, through the angle
. There is an important subtlety associated with this gravitational helicity. An effective rotation generated by it, through the angle 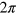 , transforms the fields into themselves, but for gravitational waves this first occurs on physically rotating each plane-wave component about its direction of propagation through a physical angle of π
radians. It is usual to define the helicity in terms of the spin in the direction of propagation so that a
, transforms the fields into themselves, but for gravitational waves this first occurs on physically rotating each plane-wave component about its direction of propagation through a physical angle of π
radians. It is usual to define the helicity in terms of the spin in the direction of propagation so that a 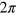 effective rotation corresponds to a physical
effective rotation corresponds to a physical 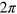 rotation. In order to conform with this conventional use of the term 'helicity' we prefer as our gravitational-wave helicity the form
rotation. In order to conform with this conventional use of the term 'helicity' we prefer as our gravitational-wave helicity the form

which is also a conserved quantity, of course.
6.3. Example: a plane wave
As an illustration of our results, let us consider the simple case of a plane gravitational wave propagating in the z-direction. Let us suppose that this plane wave resides in a cubic box of side L and impose periodic boundary conditions such that 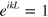 . For such a plane wave we can write
. For such a plane wave we can write

where the overbar denotes complex conjugation. The complex amplitudes  and
and 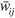 lie in the x–y plane, of course, by virtue of our choice of the transverse-traceless gauge. It is straightforward to calculate from
lie in the x–y plane, of course, by virtue of our choice of the transverse-traceless gauge. It is straightforward to calculate from 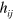 the other quantities we need, for example:
the other quantities we need, for example:

For the total energy we find

where we have made use of the 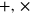 notation from (9). The total helicity (47) is
notation from (9). The total helicity (47) is
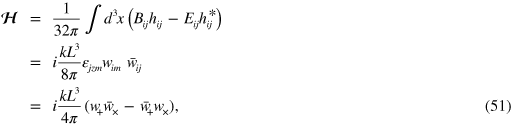
so that the ratio of the helicity to the energy density is

This takes its extremum values of 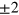 if
if 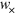 has the same magnitude as
has the same magnitude as 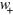 but is
but is 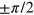 out of phase, so that
out of phase, so that 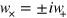 . For such circularly polarized plane waves we find that
. For such circularly polarized plane waves we find that

which may be compared with the corresponding extremum values for an electromagnetic plane wave,

The factor of 2 difference is a manifestation in the quantum theory, of course, of the spins respectively of the graviton and the photon.
6.4. Energy scale
Our analysis has not yet set a scale to the energy, helicity and other conserved quantities. As for the free electromagnetic field, there is no reason to prefer one energy scale over another; if the integral of  is a conserved quantity, then so too is
is a conserved quantity, then so too is 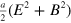 , for any constant a. In electromagnetism it is the coupling to charged matter that sets the energy scale; the electron-volt, for example, is defined in this way. For gravitational waves, it is the coupling to matter that sets the energy scale. Our Maxwellian theory does not, as yet, include coupling to material sources of gravitational radiation. A brief account of this is presented in the appendix, but it is more straightforward to appeal to the existing literature. Doing so has the benefit, moreover, of providing an independent check on the validity of our expressions.
, for any constant a. In electromagnetism it is the coupling to charged matter that sets the energy scale; the electron-volt, for example, is defined in this way. For gravitational waves, it is the coupling to matter that sets the energy scale. Our Maxwellian theory does not, as yet, include coupling to material sources of gravitational radiation. A brief account of this is presented in the appendix, but it is more straightforward to appeal to the existing literature. Doing so has the benefit, moreover, of providing an independent check on the validity of our expressions.
There are two simple expressions with which we can make a comparison, the form of the energy–momentum tensor advocated by Brill, Hartle and Isaacson [11, 50, 51] and the energy–momentum pseudo-tensor introduced by Einstein [1]. The Brill–Hartle–Isaacson energy–momentum tensor has the form

where the angle brackets denote a (local) spatial average. If we use our preferred transverse-traceless gauge then we find the energy density [12]

To compare this expression and our energy density (43), let us write

To connect this with the Brill–Hartle–Isaacson energy density we need only note that the local averages (or cycle averages) of 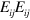 and of
and of 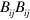 are equal and it follows that
are equal and it follows that

Evidently, performing a local average of our energy density gives the Brill–Hartle–Isaacson expression. In our notation, Einstein's pseudo energy–momentum tensor is

so that the energy density is

In order to arrive at a form that is directly comparable with our energy density, we subtract from this a total divergence (which does not change the total volume-integrated energy, of course):

where we have used the transverse property of  . This is the same expression as arrived at starting from the Brill–Hartle–Isaacson energy density.
. This is the same expression as arrived at starting from the Brill–Hartle–Isaacson energy density.
In summary, the quantities

may be adopted, respectively, as the energy density, helicity density and momentum density for our gravitational waves, in direct analogy with the corresponding electromagnetic quantities.
7. Poynting theorem for gravitational waves
The similarity between our Maxwellian equations for gravitational waves and the more familiar electromagnetic Maxwell equations leads directly to a Poynting theorem for the local conservation of energy [18, 19]. We derive this from our Lagrangian by use of Noether's theorem or, more appealingly, directly from our gravitational Maxwell equations (29). This leads to the local conservation law
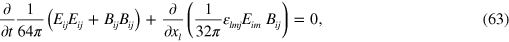
from which we obtain the Poynting vector for gravitational waves:

Our gravitational Poynting theorem is the clear and natural analogue of that for the free electromagnetic field,

We can incorporate, into these conservation laws, sources of gravitational or electromagnetic waves by coupling to matter or charges. A brief indication of how this may be achieved is given in the
8. Momentum and angular momentum for gravitational waves
It remains to determine the linear and angular momentum of gravitational waves and to address the separation of the total angular momentum into its component spin and orbital parts. As in our derivations of the energy and the helicity, our guide will be Noether's theorem as applied to our dual symmetric Lagrangian density (42). Translation invariance leads directly to the (canonical) momentum density
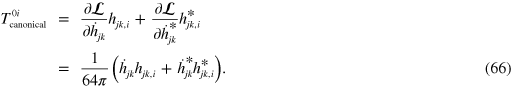
As in the corresponding electromagnetic analysis, we can exploit the non-uniqueness of densities obtained from Noether's theorem by adding to this the divergence of a quantity to give
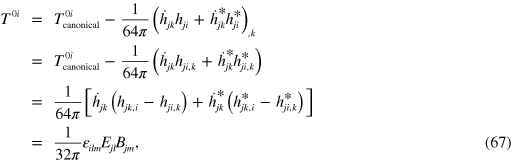
which is the natural analogue of Poynting's vector:

which therefore plays the dual role of both momentum density and also energy flux, just as in electromagnetism.
In order to obtain the angular momentum, we need to consider a rotation of both the magnitude of 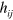 and also of the indices. It is straightforward to see that a rotation through the infinitesimal angle θ
(that is, a rotation through θ
about an axis in the direction of θ
) gives the change
and also of the indices. It is straightforward to see that a rotation through the infinitesimal angle θ
(that is, a rotation through θ
about an axis in the direction of θ
) gives the change
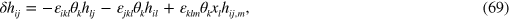
where 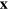 is a vector joining the local point to the axis of rotation. It is straightforward to confirm that this rotation preserves the transverse-traceless character of
is a vector joining the local point to the axis of rotation. It is straightforward to confirm that this rotation preserves the transverse-traceless character of 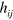 :
:

Applying this symmetry transformation to our Lagrangian density gives the canonical density of the conserved total angular momentum:
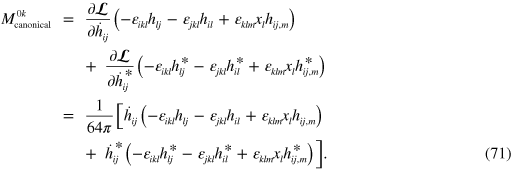
We can replace this by a more familiar form by, once again, subtracting a total divergence:
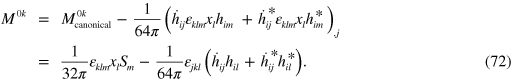
Here, at last, we have a difference with electromagnetism in that this is not simply the cross-product of the local position, 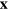 , and our Poynting vector. The additional pieces reflect the spin-2 nature of the polarization and have their origin in the fact that there are two indices to rotate on the
, and our Poynting vector. The additional pieces reflect the spin-2 nature of the polarization and have their origin in the fact that there are two indices to rotate on the 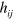 .
.
Returning to our original canonical angular momentum density (71), it is natural to separate this angular momentum density into spin and orbital parts:
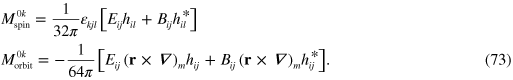
The volume-integrals of these are then the total spin and orbital parts of the angular momentum. As is the case in optics, neither of these integral quantities, alone, is a true angular momentum [35, 52, 53]. The principal reason for this is that the transformation generated by each of them alone is not a true rotation but rather that part of a rotation that preserves the transverse (and for gravitational waves traceless) character of the fields. We note that the total spin and orbital angular momenta have also been obtained previously, but not in a form that is manifestly duplex-symmetric [11].
9. Conclusion
Our aim in this work was to express the theory of gravitational waves in a form that is as close as possible to the more familiar Maxwell theory of electromagnetic waves. The benefits to be gained, one would hope, are to draw on new insights drawn from electromagnetism, such as the role of the duplex symmetry, and also an easier access to the phenomenon of gravitational waves for those without a strong background in general relativity. To reach such a description we have had to forego some of the 'generality' of general relativity, most particularly in that our description is very much of a gravitational field in a flat background space–time. Perhaps this is not too surprising, however, as it is precisely in this context that the Maxwell theory of the electromagnetic field is presented. It is for the reader to judge, of course, whether this is a price worth paying.
The astute reader will have noticed that our gravitational analogues of the electric and magnetic fields, 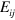 and
and 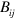 , are not gauge-invariant. By this we mean that they do not keep their form under transformation (5). It is perhaps principally for this reason that components of the (fully gauge-invariant) curvature have been compared with the electric and magnetic fields, rather than those adopted here [14]. The gravitational gauge transformation is intimately connected, however, with a change of coordinate system [25] and hence, in a description such as ours in which this is fixed, the lack of gauge invariance may be understood; indeed it would be remarkable were our expressions to be fully gauge-invariant. There is, nevertheless, a natural explanation for the simplicity of the expressions we have derived which is that, relative to our chosen background space–time, we have expressed our mechanical properties in terms of the gauge-invariant parts of our two potentials
, are not gauge-invariant. By this we mean that they do not keep their form under transformation (5). It is perhaps principally for this reason that components of the (fully gauge-invariant) curvature have been compared with the electric and magnetic fields, rather than those adopted here [14]. The gravitational gauge transformation is intimately connected, however, with a change of coordinate system [25] and hence, in a description such as ours in which this is fixed, the lack of gauge invariance may be understood; indeed it would be remarkable were our expressions to be fully gauge-invariant. There is, nevertheless, a natural explanation for the simplicity of the expressions we have derived which is that, relative to our chosen background space–time, we have expressed our mechanical properties in terms of the gauge-invariant parts of our two potentials 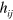 and
and 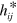
With the above caveats in mind, we have presented a theory of gravitational waves in Maxwellian form by writing a set of Maxwell-like equations for the fields associated with a gravitational wave. The reasons for the success of such a programme derive, fundamentally, from the similarities between electromagnetic and gravitational plane waves: they are both transverse, have two orthogonal polarizations and propagate, in the absence of matter, at the speed of light.
Acknowledgments
This work was supported by the Leverhulme Trust and by the UK EPSRC. I am most grateful to them and also to Robert Cameron, Sarah Croke, Martin Hendry, James Hough, John Jeffers, Fiona Speirits, Henry Ward and Alison Yao for their encouragement and advice. I thank also members of the School of Physics and Astronomy and especially those of the Institute for Gravitational Research for their hospitality whilst pursuing this research project.
Appendix.: Coupling of gravitational waves to matter
We have seen that freely propagating gravitational waves in a flat background have many properties in common with electromagnetic waves in free space. It remains to determine how gravitational waves are generated by matter sources in our Maxellian theory.
As a starting point we take the linearized Einstein field equation which, with a suitable choice of gauge, may be written as

where 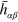 is the trace-reversed
is the trace-reversed 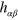 . The transverse-traceless part of
. The transverse-traceless part of 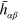 (or equivalently of
(or equivalently of 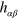 ) couples to the transverse-traceless part of the matter energy–momentum tensor. Hence we can write
) couples to the transverse-traceless part of the matter energy–momentum tensor. Hence we can write

Henceforth we shall drop the TT superscript and understand that all quantities are the transverse-traceless parts.
Equation (A.2) is reminiscent of the corresponding electromagnetic equation

This suggests that we might associate the transverse-traceless part of the matter energy–momentum tensor for gravitational waves with the transverse part of the electric current for electromagnetic waves. As further evidence that this is indeed a suitable association, we note that including the transverse-traceless part of the matter energy–momentum tensor leads to the modified Maxwellian

which is analogous to the electromagnetic Maxwell equations for the transverse parts of the fields:

From these equations we can readily derive two 'Poynting' theorems:
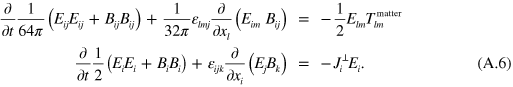
Footnotes
- 1
We use Greek indices to denote the four space–time dimensions and a summation involving these four naturally requires a raised and a lowered index. We use Roman indices to denote the three spatial dimensions and there is no need to raise these, so any repeated Roman indices denotes summation over the three spatial dimensions.
- 2
The symmetry of
 follows directly from the symmetry of
follows directly from the symmetry of  . To show that
. To show that  is also symmetric, we note that we can write the antisymmetric part of a quantity
is also symmetric, we note that we can write the antisymmetric part of a quantity  as
as  . Hence we can show that
. Hence we can show that  is symmetric by showing that
is symmetric by showing that  is zero:
is zero:
where
 is zero because
is zero because  is transverse and
is transverse and  is zero because
is zero because  is traceless.
is traceless. - 3
It is important to realize that the local conserved quantities generated by this procedure can always be supplemented by the time-component of a four-divergenceless quantity. This is sometimes useful as, for example, in obtaining the momentum density.
- 4
The pre-factor
 is not strictly necessary at this stage [6] but we include it in anticipation of coupling to matter which will set the energy scale.
is not strictly necessary at this stage [6] but we include it in anticipation of coupling to matter which will set the energy scale. - 5
Writing
 and evaluating the determinant as a power series in
and evaluating the determinant as a power series in  gives
gives  . In the transverse-traceless gauge h = 0 and hence the determinant is quadratic in h.
. In the transverse-traceless gauge h = 0 and hence the determinant is quadratic in h. - 6
It should be emphasized that the derivation of (38) made explicit use of the transverse-traceless gauge and so is not expressed in gauge-invariant form.
- 7
A bit more work gives also the momentum density associated with spatial homogeneity:
 , which is satisfyingly reminiscent of Poynting's vector for the electromagnetic field. This is demonstrated in section 8.
, which is satisfyingly reminiscent of Poynting's vector for the electromagnetic field. This is demonstrated in section 8.