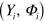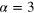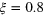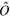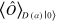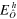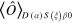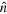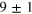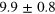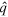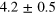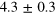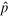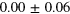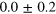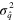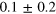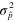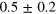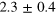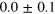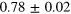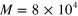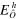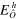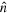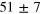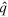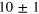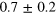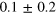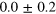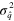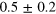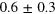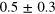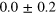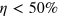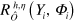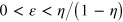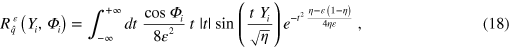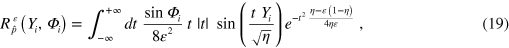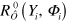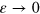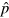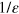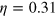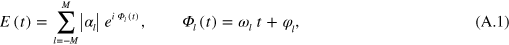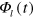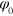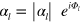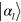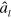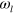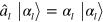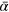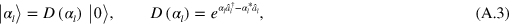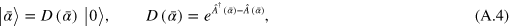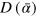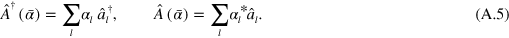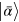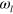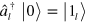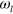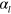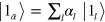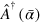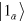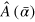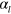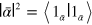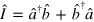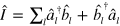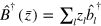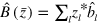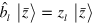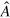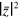Abstract
Pulsed homodyne quantum tomography usually requires a high detection efficiency, limiting its applicability in quantum optics. Here, it is shown that the presence of low detection efficiency () does not prevent the tomographic reconstruction of quantum states of light, specifically, of Gaussian states. This result is obtained by applying the so-called 'minimax' adaptive reconstruction of the Wigner function to pulsed homodyne detection. In particular, we prove, by both numerical and real experiments, that an effective discrimination of different Gaussian quantum states can be achieved. Our finding paves the way to a more extensive use of quantum tomographic methods, even in physical situations in which high detection efficiency is unattainable.

Content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Standard homodyne detection is an experimental method that is used for the reconstruction of quantum states of monochromatic light. In this framework, the quantum state is characterized by feeding to appropriate tomographic techniques the repeated measurement of a discrete set of field quadratures [1–3]. Quantum state reconstruction methods turn out to be of paramount importance for quantum information, for they can reveal the presence of quantum coherence and entanglement that might be used to perform tasks not possible in a classical setting [4].
For these experiments, a very high detection efficiency is typically required, along with ad-hoc designed apparatus [5]. However, new methods capable of discriminating between different quantum states of light, which demand lower detection capabilities typical of commercially available components, would facilitate the experimental realization of such apparatuses. Moreover, it would make it possible to apply quantum homodyne detection to study different physical systems where high noise conditions are unavoidable, such as out of equilibrium light matter dynamics [6]. For this purpose, non standard tomographic methods for reconstructing the state of light need to be adopted, specifically the so-called 'minimax' adaptive estimation of a quantum state [7, 8], allowing the full reconstruction of the associated Wigner function. These powerful statistical techniques are able to overcome the difficulties that arise when the more standard pattern function-based quantum tomography is used [9–16], allowing state reconstruction for arbitrary low detection efficiency, provided a sufficiently large number of data are collected.
In this article, we report on the commissioning and characterization of a time-domain homodyne detection apparatus working with coherent ultra-short light pulses, built using commercial detectors and operating in a regime of large electronic noise. By treating the shot-to-electronic-noise ratio (about 2 dB) as a detector inefficiency [17, 18], we obtain an overall detection efficiency of about 30%. By extending single-mode tomographic techniques to the pulsed regime, we show that even in these low efficiency conditions, it is still possible to discriminate between coherent and squeezed photon states with high accuracy.
The validity of the adopted minimax state reconstruction method has been tested by numerical experiments, using both coherent and squeezed states, and in real experiments for the tomographic reconstruction of coherent states with different mean photon number. These results provide concrete support for the effectiveness of the minimax adaptive state estimation even in low efficiency detection conditions, thus opening the way to wider applications of homodyne tomographic techniques to situations in quantum optics and non equilibrium spectroscopy, where the use of dedicated, highly efficient detectors is precluded.
2. Homodyne detection
In standard single-mode homodyne detection, the photon state under investigation, the signal, is mixed with a strong coherent reference state, the local oscillator (LO), by a beam splitter. The outputs are collected by two photodiodes and the difference photocurrent (homodyne photocurrent) is measured. It can be proven that when the LO is significantly more intense than the signal, the homodyne photocurrent is proportional to the signal quadrature [19]. Denoting by and the single-mode annihilation and creation operators associated with the signal, the quadrature operator is defined as
where is the relative phase between the signal and the LO. The continuum set of quadratures with provides a complete characterization of the signal state.
The standard techniques developed for the reconstruction of single-mode photon states need to be generalized when pulsed light is used [20–26]. In this case, the optical pulses are equally prepared multi mode coherent quantum states. For each single pulse a quadrature measurement is performed. In such regime, the single-mode description can still be used if the single-mode field operators are replaced by multi mode annihilation and creation operators. For this reason we make use in the following of the single-mode notation. A thorough theoretical treatment for pulsed homodyne detection is presented in the
2.1. Experimental setup
The scheme of the experimental set-up is shown in figure 1. The laser source is a mode-locked Ti:Sapphire oscillator with 80 MHz repetition rate. A beam splitter divides the incoming beam in two parts, which then interfere in a second beam splitter (NPBS in figure 1). The outputs are detected and subtracted by a commercial differential photodetector. The latter is made up of two Si/PIN photodiodes with nominal quantum efficiency at 800 nm wavelength and linear response up to 0.6 mW LO power. The detector subtraction efficiency is quantified by the common mode rejection ratio (CMRR), defined as the ratio between the detector output power when both photodiodes are illuminated and the power when one of the two is screened [25]. For the present experiment CMRR dB.
Figure 1. Scheme of the opto-mechanical setup.
Download figure:
Standard image High-resolution imageThe homodyne photocurrent is recorded by a digital oscilloscope with a bandwidth of 500 MHz and a sampling rate of 5 GSamples . The digitized output is numerically integrated over time intervals corresponding to the duration of the pulse. Each integral is associated with a single quadrature measurement.
In the shot noise regime with the signal beam blocked, i.e., with the signal in the vacuum state, the homodyne detector noise variance is expected to change linearly with the LO power on the top of a constant offset representing the electronic noise [27]. Figure 2 shows the detector noise variance of pulses, for different values of the LO power. The noise variance grows linearly up to 0.6 mW LO power, instead, at higher powers, the photodiodes non linear effects are significant. To have the maximum shot-to-electronic noise ratio ( dB) achievable in the linear regime, the experiments have been performed at 0.6 mW LO power.
Figure 2. Detector noise variance versus LO power in absence of signal (vacuum state); shot noise contribution (dashed curve); electronic noise background (dashed-dotted curve).
Download figure:
Standard image High-resolution imageConversely, when the signal beam is not blocked, it can be attenuated with respect to the LO by neutral density filter ( in figure 1). The phase difference between the two arms of the interferometer can be modulated in the range using a piezoelectric translator in the LO arm (PZT in figure 1). The homodyne photocurrent is acquired by the digital oscilloscope, and each difference pulse is integrated.
2.2. Homodyne traces
In the absence of electronic noise, the voltage V corresponding to the homodyne photocurrent, namely the experimentally accessible quantity, is proportional to the quadrature operator , , with an appropriate constant γ. The electronic noise can be generically described by a classical stochastic process δ that can be assumed to be Gaussian distributed, with zero average and variance . The value of δ must be experimentally measured. Under these conditions the electronic noise is independent from the quadrature, and it contributes to the homodyne voltage as
A homodyne trace is obtained by collecting a set of homodyne voltage values , corresponding to different phase values , associated with a large number M of piezo positions.
In the case of the vacuum state (absence of signal), these considerations are outlined in figure 2. The total vacuum homodyne variance for the chosen LO power is indeed composed of two independent contributions. An intrinsic contribution () is actually the shot noise, while an extrinsic contribution () is due to the electronic noise. Following [18], the electronic noise can be treated as an optical loss channel with an equivalent transmission efficiency given by
where . Here we estimate . Thus the total apparatus efficiency is .
Considering that the variances of independent stochastic variables are additive, can be determined by using the vacuum state as reference and by assuming the variance of the quadrature operator in the vacuum to be ,
where is the experimental voltage variance for the vacuum state.
To consistently apply the quantum state reconstruction to the collected experimental homodyne data, it is convenient to rescale the raw data by the constant ,
so that the new, calibrated quantities have variance . Figure 3 shows the case of two optical coherent states with different mean photon numbers, each homodyne trace consisting of experimental data. The data were collected using two different optical density for the signal attenuator (see in figure 1). Clearly even with a very low mean photon number signal (see figure 3(b)), the phase modulation of the homodyne trace is detectable.
Figure 3. Calibrated homodyne traces of two optical coherent states. Each trace is acquired using a different optical density OD of the filter . (a) OD = 4.5; (b) OD = 7. In the inset of (a) we show the interference figure obtained by measuring the mean value of four integrated pulses versus the piezo position. The homodyne traces are measured in the piezo range corresponding to the central optical cycle of the interference figure.
Download figure:
Standard image High-resolution image3. Quantum state reconstruction
In the following, we prove that a minimax estimation of the Wigner function [7] can discriminate between quantum coherent and squeezed states even under the low efficiency condition of our experiment.
3.1. Minimax estimation of the Wigner function
Using the annihilation and creation operators one constructs position, respectively momentum-like operators, , respectively . Given a density matrix representing a generic photon state, the associated Wigner function in the variables (q, p) is defined by
Then, the mean value of any observable , expressible as a function of and , reads
where the function is connected to the operator as the Wigner function is to as in (6). The Wigner function is therefore sufficient to evaluate the average value of any observable with respect to any state .
The minimax reconstruction algorithm precisely gives an estimator for the Wigner function, allowing its reconstruction from the collected homodyne data , provided a proper calibration is used (equation (5)). The estimator is given by
and it depends on the overall detector efficiency η, the number of collected data M and an adaptive parameter h [7]. The kernel function is explicitly given by
The truncation of the integration due to the parameter h is necessary because of the diverging inverse Gaussian present in the integral. In [7] it is shown that the optimal adaptive estimator, i.e., the one that minimizes uncertainties, is obtained when , with
Notice that the optimally adapted cutoff depends both on the detector efficiency η and the number M of collected data. When the efficiency becomes small, in order to have a good estimator of the Wigner function, a larger number M of data is needed. However, we stress that no inferior bound on η exists that prevents the convergence of the algorithm 5 .
Once the Wigner function is reconstructed, the expectation value of any observable of the system can be estimated as follows,
where the corresponding kernel function is given by
3.2. Numerical experiments
For testing the effectiveness of this approach under our experimental conditions, we first analyze sets of numerically generated data that simulate the quadratures of a known pure quantum state . By knowing in advance the quantum state, it is possible to verify whether the minimax technique allows a proper reconstruction.
The generation of the fictitious data starts by using the quadrature probability distribution with associated with a quantum state, and afterwards in adding to each numerically generated state quadrature a Gaussian noise that exactly simulates the electronic noise associated with the efficiency, i.e., , of our set up. The analysis of the simulated data proceeds, as for experimental data, through a calibration using the vacuum noise as reference. In particular, we perform two numerical experiments. The first with a coherent state and another one with a displaced-squeezed state , where
are the displacement and squeezing operators, respectively. Each data set consists of quadrature measurements with the relative phase ranging in the interval .
Following the algorithm sketched before, we reconstruct the Wigner function of the two quantum states. They are shown in figures 4 (a) and (b) for the coherent and the squeezed state, respectively. To remove the artifacts resulting by the numerical integration, the reported Wigner functions have been filtered by an image processing algorithm (low-pass Gaussian convolution filtering). The blue and red curves are bidimensional cuts of the Wigner functions in correspondence of the expectation value of the position and momentum operator, respectively.
Figure 4. Reconstructed Wigner function using the adaptive minimax estimation from quadratures of (a) a coherent state () and (b) a displaced-squeezed state (, ). The used detector efficiency is in both cases . The inserts show representative two-dimensional cuts of the reconstructed Wigner function.
Download figure:
Standard image High-resolution imageIn order to assess the similarity between the reconstructed state , corresponding to the reconstructed Wigner function , and the expected state, , with Wigner function , we use as figure of merit, the fidelity . This quantity essentially measures the overlap between the two quantum states; indeed, , reaching the value 1 only when the two states coincide [4]. In our case, this measure is given by
We obtained a fidelity of 0.97 and 0.92 for the coherent and the squeezed state, respectively, despite the large noise affecting the reconstruction 6 . These results, together with the actual values of the quadrature variances, prove that the squeezed and coherent states can be discriminated under high noise conditions. Indeed, the features of the reconstructed Wigner functions clearly reflect the different nature of the two quantum states.
From the reconstructed Wigner function, it is possible to compute the expectation values of relevant observables with respect to the coherent and the displaced-squeezed state, in particular, the number operator and the position and momentum operators. For and it also possible to derive the variances, and , and to estimate the squeezing parameter,
The results are summarized in table 1. For the errors evaluation we have used the standard expression for the mean average error relative to a data set (recall equations (11) and (12)),
The averages computed using the Wigner function estimated from the data set fully agree with those analytically calculated from the known quantum states. In particular, even the estimated value of the squeezing parameter agrees with the expected one. This explicitly shows that the minimax adaptive estimation algorithm results are highly effective in reconstructing quantum states of light, and more specifically, in discriminating different Gaussian quantum states even under low-efficiency conditions.
Table 1. Estimate of different expectation values for simulated quadratures associated to the coherent state () and the displaced-squeezed state (, )
| 9 | 9.89 | |||
| 4.24 | 4.24 | |||
| 0 | 0 | |||
| 0.5 | 0.1 | |||
| 0.5 | 2.48 | |||
| ξ | 0 | 0.8 |
3.3. Real experiments
The real data in figure 3 can now be treated in the same way. In this case, the collected homodyne traces are two coherent states with very different mean photon number.
The first step in the reconstruction procedure and determination of relevant observables is to use the estimator (8) to obtain the Wigner functions associated with the two states. The results are shown in figure 5; as in the previous numerical experiments, in order to minimize artifacts related to the numerical integration in (9), a low-pass Gaussian filter has been applied to the raw images.
Figure 5. Reconstructed Wigner function using the adaptive minimax estimation from quadratures of attenuated laser states with (a) OD = 4.5 and (b) OD = 7. The inserts show representative two-dimensional cuts of the reconstructed Wigner function.
Download figure:
Standard image High-resolution imageWith these results, one can then estimate the mean values of relevant observables, as number, position, and momentum operators together with the squeezing parameter, obtained from the computation of the variances of position and momentum. The results are summarized in table 2. The obtained expectation values for the number operator explicitly exhibit the three order of magnitude difference between the two states. Furthermore, these results show that the analyzed experimental states are indeed minimum uncertainty states, with vanishing squeezing parameter.
Table 2. Estimate of different expectation values for the experimental coherent states with optical density OD = 4.5 and OD = 7, respectively.
| (OD = 4.5) | (OD = 7) | |
|---|---|---|
| ξ |
4. Discussion
The previous results demonstrate the effectiveness of the minimax statistical techniques in the reconstruction of quantum states of light in presence of large electronic noise. These methods allow us to circumvent convergence problems that arise when using standard pattern function methods in estimating observable averages with low-detection efficiency, namely [9–15]. Nevertheless, it is interesting to investigate the possible relations between these two approaches by replacing the cutoff truncation in the integration with respect to t in (9) with a suitable Gaussian regularization. In particular, we consider the following alternate kernel functions instead of ,
where ε is a positive regularization parameter. In principle, this allows for a more direct estimate of the expectation values of any observable, provided . For instance, in the case of position, momentum, and number operators, one finds:
Notice that these quantities converge to functions in the limit :
These expressions coincide with the so-called kernel functions of the standard pattern function-based tomographic techniques [15]. Unfortunately, the limit cannot be taken in the case of more general observables with higher powers of and since the integrals diverge as powers of . This fact may be related to the mentioned convergence problems of the standard pattern function method.
It is important to note that the estimation of the mean values of , , and through the use of the limit kernel functions (21)–(23) is not sufficient to completely characterize quantum states, not even Gaussian ones, like coherent and squeezed states. Instead, the minimax techniques allow the full reconstruction of the state through its Wigner function and in principle for arbitrarily low detector efficiency η. However, as already mentioned in section 3.1, as η becomes small, a larger set of experimental data points is needed in order to have a reliable estimation of the Wigner function. This condition may de facto limit the applicability of the minimax adaptive state reconstruction techniques in special experimental instances, where a very high repetition rate state preparation is unattainable.
5. Conclusions
Here we report the characterization of a time domain balanced homodyne detection apparatus operating in the presence of large electronic noise corresponding to an overall detection efficiency . We used the detector combined with tomographic reconstruction techniques for discriminating between different quantum states of light. A minimax adaptive reconstruction of the Wigner function has been adopted. This approach allows us to circumvent possible convergence problems arising from low detector efficiency in the standard pattern function-based quantum tomography.
The effectiveness of such a method has been verified in two ways. At first, we calculated the Wigner function for simulated data of coherent and squeezed states and then for real experimental homodyne data of coherent states with different mean photon numbers. In all cases it is proved that it is possible to efficiently reconstruct the associated Wigner function, asserting the Gaussian character of the quantum states, and evaluating their relevant parameters.
The present study demonstrates that even low efficient () homodyne detectors can be usefully employed to study the nature of quantum states of light, provided that non-standard statistical tools as the minimax methods are used to reconstruct their Wigner functions. These results may be important whenever quantum optics techniques are employed to investigate the dynamics of out-of-equilibrium states and the presence of quantum coherence in condensed matter.
Acknowledgments
Useful discussions with Simone Cialdi and Marco Barbieri are acknowledged. This work has been supported by MIUR (FIRB 'LiCHIS'-RBFR10YQ3H), University of Trieste ('FRA 2009' and 'FRA 2011') and European Union, Seventh Framework Programme, under the project GO FAST, grant agreement no. 280555.
Appendix.: Homodyne detection in the pulsed regime: multimode treatment
Homodyne detection in a pulsed regime requires a formal generalization of its theoretical description with respect to the one-mode regime; indeed, the LO and the signal at the beam splitter are not monochromatic. Classically, the electric field of a pulsed laser beam can be represented as a mode-locked superposition of amplitudes:
where the phases are mode-locked by the condition , with a reference phase. Each frequency contributes to the field with the amplitude and the number of contributing frequencies depends on the shape of the pulse. Quantized pulsed laser light is described by associating to each monochromatic component a coherent state , that is an eigenstate of the annihilation operator of photons in the mode of frequency , , and to the entire pulse the tensor product
where is the vector whose components are the amplitudes . By means of the creation and annihilation operators and each monochromatic coherent state reads
where is the vacuum state and is the so-called displacement operator.
Since the creation and annihilation operators pertaining to different modes commute, the pulsed coherent state (A.2) can be conveniently recast as
by means of a displacement operator expressed in terms of multi mode operators
The reason for labeling the pulsed coherent state by can now be easily understood. The state of one photon of frequency is given by , while a generic non-monochromatic superposition of frequencies with amplitudes corresponds to the state that results from applying the multimode operator to the vacuum state:
Therefore, is the creator operator of a single photon in the (not normalized) superposition state , while destroys a photon in the same state; thus, the quantum state of the pulsed laser is a coherent state associated not with a single amplitude , but with the vector of all the amplitudes contributing to the pulse: in other words, we have a Poissonian distribution not with respect to the number of photons in a monochromatic wave, but to the number of photons in the superposition .
The normalized operators
where , satisfy the canonical commutation relations
By means of them we can now extend the state-tomography techniques to the case in which the signal and the LO are pulsed. In the monochromatic case, when the signal mode a interferes with the LO mode b on the beam splitter, the photo-current operator is [19].
If more frequencies are present in both the LO and in the signal, each one of the corresponding mode operators will be subjected to the beam splitting transformation and the detectors will ideally register photons of all involved frequencies. Then, the photo-current operator becomes .
If the LO is in a pulsed coherent state , with generalized creation and annihilation operators and , the phase difference between the LO and the signal is changed by the action of the piezoelectric translator placed in the LO arm on all the LO modes:
The photo-current operator, which is measured by the pulsed homodyne setup, is thus given by
Let denote the quantum state (density matrix) of the signal field and by the projector onto the (coherent) state of the incoming pulse. Then, using that and the expressions in (A.5), the expectation value of the photo-current is calculated as follows:
Using (A.7) and comparing these results in the standard treatment of homodyne detection for the single-mode case, realize that in the pulsed regime one measures a quantity ,
proportional to a quadrature, which generalizes that in (1):
For this reason, in the main text of the letter we have limited the discussion to the simpler case of a single-mode homodyne detection, with the proviso that whenever a quadrature is used, it actually refers to its expression (A.13) in the pulsed regime. In particular, the measured data can be used to reconstruct the expectation values of all signal observables that can be expressed as functions of the operators and . For instance, the mean value of the photo-current operator second moment with respect to the LO pulsed coherent state is
and differs from the pulsed quadrature second moment by the number of photons in the pulsed signal, which is to be taken much smaller than the intensity of the pulsed LO. A similar suppression by occurs for the correction terms appearing in higher moments so that the distribution of the outcomes of the homodyne photocurrent is equal to that of the corresponding field quadratures. As a final remark, notice that, in the case of only one frequency mode, the above setting reduces to the standard homodyne tomographic one.
Footnotes
- 5
The interplay between η and M is crucial in rigorously proving the convergence of the reconstruction algorithm. As a result, the minimax adaptive technique completely differs from the standard tomographic methods, e.g., as presented in [9], where the number of collected data plays essentially no role. In this respect, see also the discussion in [10, 11].
- 6
The obtained estimates for the fidelity differ from the ideal value 1 due to the experimental uncertainties in the state reconstruction process: the fidelity is in fact a very sensitive measure of the overlap between two states. In this respect, the quoted values should be taken as just a further indicator of the good performance of the minimax reconstruction algorithm [28].




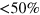
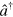

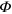
![$\Phi \in \left[ 0,2\pi \right]$](https://content.cld.iop.org/journals/1367-2630/16/4/043004/revision1/njp488044ieqn6.gif)

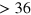



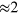

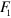
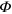
![$\left[ 0,2\pi \right]$](https://content.cld.iop.org/journals/1367-2630/16/4/043004/revision1/njp488044ieqn14.gif)

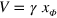
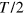

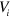
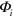
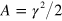
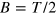

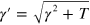
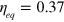





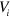
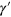

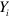
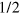
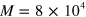
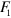

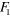
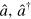
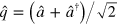
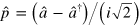
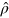
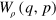
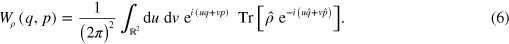
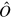
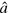
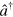
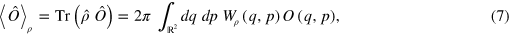
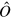
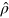
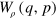

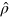
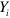

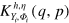
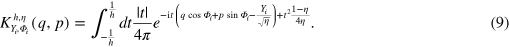
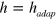

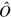
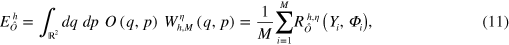
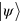
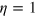
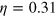
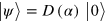

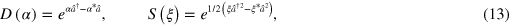
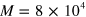
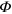
![$\left[ 0,2\pi \right]$](https://content.cld.iop.org/journals/1367-2630/16/4/043004/revision1/njp488044ieqn60.gif)

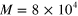
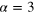
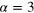
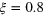

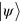
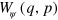
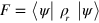

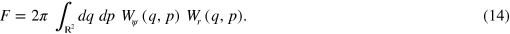
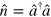
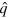
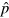
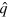
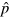
![${{\sigma }^{2}}\left[ \hat{q}\, \right]$](https://content.cld.iop.org/journals/1367-2630/16/4/043004/revision1/njp488044ieqn77.gif)
![${{\sigma }^{2}}\left[ \hat{p}\, \right]$](https://content.cld.iop.org/journals/1367-2630/16/4/043004/revision1/njp488044ieqn78.gif)