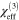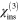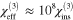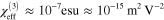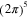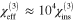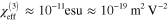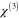Abstract
We perform a perturbative calculation of the third order optical conductivities of doped graphene, using approximations valid around the Dirac points and neglecting effects due to scattering and electron–electron interactions. In this limit analytic formulas can be constructed for the conductivities. We discuss in detail the results for third harmonic generation, the Kerr effect and two-photon carrier injection, parametric frequency conversion, and two-color coherent current injection. We find a complicated dependence on the chemical potential and photon energies. The linear dispersion causes resonances over a wide range of photon energies, and it is possible to obtain large optical nonlinearities by tuning the chemical potential.
Export citation and abstract BibTeX RIS

Content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Due to the gapless linear dispersion of its low energy electronic excitations, graphene exhibits unique and remarkable optical properties: the linear optical response is characterized by a universal conductivity [1] 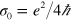 at wavelengths from the mid-infrared to the visible, with a monolayer absorbance about
at wavelengths from the mid-infrared to the visible, with a monolayer absorbance about 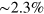 [2]. Thus while a single layer of graphene is highly transparent, considered as a monolayer it is a highly absorbing material, and saturated absorption is easy to achieve [3]. With its strong optical coupling, broadband absorption, and other novel material and electronic properties [4], graphene is a natural candidate for use in optically controlled devices in photonics and optoelectronics [5, 6]. In moving towards any application, an important step is understanding the optical nonlinearities of graphene. The graphene structure has center-of-inversion symmetry, and while second-order nonlinear response can arise from interface effects [7], nonuniformity of optical field [8], or the presence of dc currents [9], the first nonvanishing nonlinear susceptibility arising in pristine graphene is the third order susceptibility [10], and that is the focus of this paper.
[2]. Thus while a single layer of graphene is highly transparent, considered as a monolayer it is a highly absorbing material, and saturated absorption is easy to achieve [3]. With its strong optical coupling, broadband absorption, and other novel material and electronic properties [4], graphene is a natural candidate for use in optically controlled devices in photonics and optoelectronics [5, 6]. In moving towards any application, an important step is understanding the optical nonlinearities of graphene. The graphene structure has center-of-inversion symmetry, and while second-order nonlinear response can arise from interface effects [7], nonuniformity of optical field [8], or the presence of dc currents [9], the first nonvanishing nonlinear susceptibility arising in pristine graphene is the third order susceptibility [10], and that is the focus of this paper.
Third order nonlinearities in graphene have been experimentally investigated; however, the extracted effective bulk susceptibilities 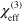 values show discrepancies and strongly depend on measurement method, light frequency, and perhaps sample preparation. In their pioneering work on the nonlinear response of graphene, Hendry et al [11] presented an expression for
values show discrepancies and strongly depend on measurement method, light frequency, and perhaps sample preparation. In their pioneering work on the nonlinear response of graphene, Hendry et al [11] presented an expression for  for four-wave mixing experiments, and then approximated their expression to find a value of about
for four-wave mixing experiments, and then approximated their expression to find a value of about 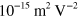 in the near-infrared, weakly dependent on frequency; they found agreement between experiment and their approximated expression by comparing their signal from graphene with that from a gold film. Using a sample with about 100 layers of graphene, Wu et al [12] found agreement with this approximated expression as well. However, in fact a direct calculation from the expression of Hendry et al gives a value only about
in the near-infrared, weakly dependent on frequency; they found agreement between experiment and their approximated expression by comparing their signal from graphene with that from a gold film. Using a sample with about 100 layers of graphene, Wu et al [12] found agreement with this approximated expression as well. However, in fact a direct calculation from the expression of Hendry et al gives a value only about  3
. Yang et al [13] observed no detectable two-photon absorption in monolayer graphene by the Z-scan method at a wavelength of 780 nm, which limits
3
. Yang et al [13] observed no detectable two-photon absorption in monolayer graphene by the Z-scan method at a wavelength of 780 nm, which limits ![$\text{Im}\left[ \chi _{\text{eff}}^{(3)} \right]$](https://content.cld.iop.org/journals/1367-2630/16/5/053014/revision1/njp494077ieqn15.gif) to less than
to less than 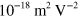 . The same experimental technique was used by Zhang et al [14] to measure the nonlinear refractive index at 1.55 μm, and they found
. The same experimental technique was used by Zhang et al [14] to measure the nonlinear refractive index at 1.55 μm, and they found 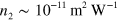 , six orders of magnitude larger than the value of
, six orders of magnitude larger than the value of 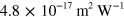 obtained at a similar wavelength by Gu et al [6], which matches a theoretical prediction using Hendry's original expression. Kumar et al [15] found a value of about
obtained at a similar wavelength by Gu et al [6], which matches a theoretical prediction using Hendry's original expression. Kumar et al [15] found a value of about 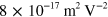 by measuring third harmonic generation at a fundamental wavelength of 1720 nm, while Hong et al [16] found a value about two orders of magnitude smaller for third harmonic photon transitions at the M points in graphene. Sun et al [17] showed that two-color coherent injected currents can induce an observable terahertz radiation signal. Theoretically, besides the expression provided by Hendry et al, Rioux et al [18] investigated two-photon absorption and two-color coherent by using Fermi's Golden Rule for pristine graphene, and Jafari [19] calculated the nonlinear optical response in gapped graphene by adding a mass term. Zhang et al [20] used the density matrix method to study four wave mixing at the saturation regime in undoped graphene, and found an effective
by measuring third harmonic generation at a fundamental wavelength of 1720 nm, while Hong et al [16] found a value about two orders of magnitude smaller for third harmonic photon transitions at the M points in graphene. Sun et al [17] showed that two-color coherent injected currents can induce an observable terahertz radiation signal. Theoretically, besides the expression provided by Hendry et al, Rioux et al [18] investigated two-photon absorption and two-color coherent by using Fermi's Golden Rule for pristine graphene, and Jafari [19] calculated the nonlinear optical response in gapped graphene by adding a mass term. Zhang et al [20] used the density matrix method to study four wave mixing at the saturation regime in undoped graphene, and found an effective  about
about 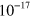 m
m
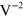 which decreased with increasing light intensity. A giant optical nonlinearity [21–23] in the presence of a strong magnetic field has also been calculated from a density matrix formalism. Third and higher harmonic generations from intraband contributions have been investigated in detail in the THz regime [10, 24, 25]. Yet a general calculation of even third order nonlinearities at higher frequencies, including the optical regime where interband contributions can play a central role, is still lacking.
which decreased with increasing light intensity. A giant optical nonlinearity [21–23] in the presence of a strong magnetic field has also been calculated from a density matrix formalism. Third and higher harmonic generations from intraband contributions have been investigated in detail in the THz regime [10, 24, 25]. Yet a general calculation of even third order nonlinearities at higher frequencies, including the optical regime where interband contributions can play a central role, is still lacking.
A full calculation of the nonlinear response, even in the perturbative limit, would require the inclusion of electron–electron and electron–phonon scattering in the construction of a self-energy. Thermal effects caused by a high repetition rate of laser pulses, as used in Z-scan experiments, also cannot be ignored [26, 27]. In this paper, we neglect these complications, restrict ourselves to frequencies such that we can use approximations relevant around the Dirac cone, and perform a simple, zero-temperature perturbative calculation at the independent particle level, but fully taking into account both the interband and intraband motion of the electrons as perturbed by an incident field. The advantage of such a simplified approach is that we can obtain analytic results for the third order conductivity 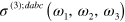 in doped graphene; one can then determine an effective bulk susceptibility [11] by
in doped graphene; one can then determine an effective bulk susceptibility [11] by
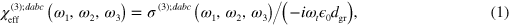
with
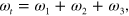
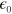 being the vacuum permittivity, and
being the vacuum permittivity, and 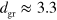 Å an effective thickness of graphene. These elementary but analytic results allow us to explore predictions for a number of third order nonlinear optical effects; they provide both an indication of what ranges of parameter space would be interesting to explore experimentally, and a benchmark for more sophisticated calculations.
Å an effective thickness of graphene. These elementary but analytic results allow us to explore predictions for a number of third order nonlinear optical effects; they provide both an indication of what ranges of parameter space would be interesting to explore experimentally, and a benchmark for more sophisticated calculations.
For undoped graphene, we find that this model leads to a simple expression for the fully symmetrized conductivity
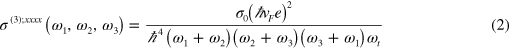
where 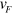 is the Fermi velocity. For doped graphene with a chemical potential
is the Fermi velocity. For doped graphene with a chemical potential 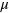 , however, our formulas show divergences related to the resonances between any involved photon energy and the chemical potential gap
, however, our formulas show divergences related to the resonances between any involved photon energy and the chemical potential gap 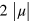 , with results quite different for different frequency combinations. Combined with the tunability of
, with results quite different for different frequency combinations. Combined with the tunability of 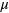 by an external gate voltage [28] or chemical doping [29] this should lead to novel approaches for controlling the nonlinear optical properties of graphene, and indeed to the possibility of graphene-based 'nonlinear optics on demand'.
by an external gate voltage [28] or chemical doping [29] this should lead to novel approaches for controlling the nonlinear optical properties of graphene, and indeed to the possibility of graphene-based 'nonlinear optics on demand'.
2. Model
We describe the electronic states in the 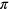 and
and 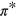 bands of graphene by a tight binding model employing carbon
bands of graphene by a tight binding model employing carbon 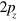 orbitals; we denote by
orbitals; we denote by 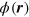 centered at the origin. The Bloch states can be written as
centered at the origin. The Bloch states can be written as

Here 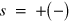 are band indexes for
are band indexes for 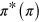 bands, and
bands, and 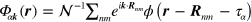 are tight binding basis functions for carbon atoms at sites
are tight binding basis functions for carbon atoms at sites 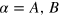 in unit cell
in unit cell 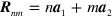 , where n and m are integers;
, where n and m are integers; 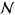 is the number of unit cells in the normalization area. We take the primitive lattice vectors to be
is the number of unit cells in the normalization area. We take the primitive lattice vectors to be 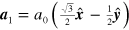 and
and 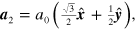 with the lattice constant
with the lattice constant 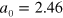 Å. In our tight binding model, we set the energy reference by taking the onsite energy to be zero; we take the nearest neighbor coupling to be
Å. In our tight binding model, we set the energy reference by taking the onsite energy to be zero; we take the nearest neighbor coupling to be 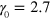 eV [4], and denote the nearest neighbor overlap of the
eV [4], and denote the nearest neighbor overlap of the 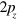 orbitals as
orbitals as 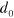 . Neglecting overlaps of neighboring
. Neglecting overlaps of neighboring  beyond the first nearest neighbor, the Schrödinger equation for the
beyond the first nearest neighbor, the Schrödinger equation for the  is
is
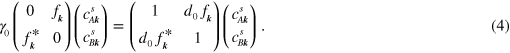
Here  is the structure factor. The amplitudes of the eigenfunctions identified by equation (4) are then found to be
is the structure factor. The amplitudes of the eigenfunctions identified by equation (4) are then found to be
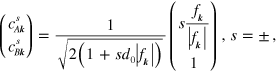
and eigenvalues are

Moving to a continuous range of crystal wavevectors  , we write the Bloch functions as
, we write the Bloch functions as 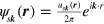 , where
, where  for any
for any  . From the normalization of the Bloch functions
. From the normalization of the Bloch functions 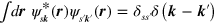 where the integral is over all space and we take
where the integral is over all space and we take 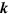 and
and 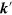 to be in the first Brillouin zone, the
to be in the first Brillouin zone, the 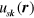 are normalized according to
are normalized according to
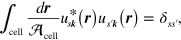
where the indicated integral is over a unit cell with area 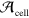 in the xy plane and over all z. The Berry connections [30–32],
in the xy plane and over all z. The Berry connections [30–32],

are then found to be
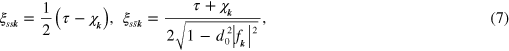
with ![${{\chi }_{\boldsymbol{k}}}=\text{Im}\left[ {{\nabla }_{\boldsymbol{k}}}{{f}_{\boldsymbol{k}}}/{{f}_{\boldsymbol{k}}} \right],$](https://content.cld.iop.org/journals/1367-2630/16/5/053014/revision1/njp494077ieqn59.gif)
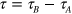 , and
, and 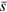 the index of the band that is not the s band. At the Dirac points,
the index of the band that is not the s band. At the Dirac points, 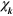 is singular.
is singular.
Under the approximation that the optical field is treated as uniform, the light-matter interaction can in principle be described either through the use of a scalar potential or a vector potential associated with the electric field 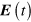 . Both treatments have disadvantages. The first involves introducing the position operator
. Both treatments have disadvantages. The first involves introducing the position operator 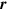 , which does not have well-behaved matrix elements between the periodic Bloch functions
, which does not have well-behaved matrix elements between the periodic Bloch functions 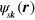 . Starting with the work of Blount [30], a number of strategies and techniques have been developed for working with the effective matrix elements of the position operator that arise; these matrix elements are linked to the Berry connections [32]. Such problems do not arise if the vector potential is used to represent the electric field, but the inevitable band truncation in numerical calculations can result in false divergences [32, 33]. This problem does not plague calculations based on the position operator. And while these divergences can be eliminated using proper sum rules that involve all the bands, since only two bands are included in our tight binding model we use the approach based on introducing the position operator, and take the interaction Hamiltonian to be
. Starting with the work of Blount [30], a number of strategies and techniques have been developed for working with the effective matrix elements of the position operator that arise; these matrix elements are linked to the Berry connections [32]. Such problems do not arise if the vector potential is used to represent the electric field, but the inevitable band truncation in numerical calculations can result in false divergences [32, 33]. This problem does not plague calculations based on the position operator. And while these divergences can be eliminated using proper sum rules that involve all the bands, since only two bands are included in our tight binding model we use the approach based on introducing the position operator, and take the interaction Hamiltonian to be 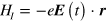 , where we take the electronic charge to be
, where we take the electronic charge to be 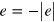 . In the independent particle approximation we adopt in this paper, the proper treatment of the position operator then leads to the description of the system by the semiconductor Bloch equations [32]
. In the independent particle approximation we adopt in this paper, the proper treatment of the position operator then leads to the description of the system by the semiconductor Bloch equations [32]
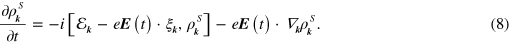
Here 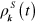 is
is 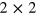 density matrix, with elements
density matrix, with elements 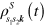 , in which diagonal term
, in which diagonal term 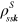 describes the population of band s at
describes the population of band s at 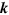 and off-diagonal terms
and off-diagonal terms 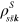 describe the optical polarization; similarly
describe the optical polarization; similarly 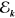 denotes the matrix with elements
denotes the matrix with elements 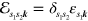 and
and  denotes the matrix with elements
denotes the matrix with elements 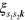 . The areal current density is then calculated by
. The areal current density is then calculated by
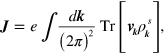
where the integral is over the Brillouin zone and the 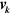 are the matrix elements of the velocity operator
are the matrix elements of the velocity operator ![$\boldsymbol{v}=-i{{\hbar }^{-1}}\left[ \boldsymbol{r},{{H}_{0}}+{{H}_{I}} \right],$](https://content.cld.iop.org/journals/1367-2630/16/5/053014/revision1/njp494077ieqn79.gif) given by
given by

The direct perturbative solution of equation (8) has been discussed in detail before [32], in fact for a 3D crystal, using an approach in which interband and intraband contributions are separated as the perturbation expansion is developed. Here we introduce a simpler strategy by shifting to a moving frame that essentially follows the intraband motion of the carriers; we put 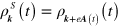 , where
, where 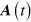 is the vector potential used to describe the electric field,
is the vector potential used to describe the electric field, 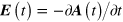 . In a rough sense we are using the vector potential to treat the intraband motion, and the scalar potential to treat the interband motion. Equation (8) then reduces to
. In a rough sense we are using the vector potential to treat the intraband motion, and the scalar potential to treat the interband motion. Equation (8) then reduces to
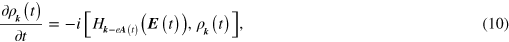
with  . The
. The 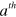 Cartesian component of the areal current density is then written as
Cartesian component of the areal current density is then written as ![${{J}^{a}}\left( t \right)=e\mathop{\int }^{}\frac{d\boldsymbol{k}}{{{\left( 2\pi \right)}^{2}}}\text{Tr}\left[ v_{\boldsymbol{k}-e\boldsymbol{a}\left( t \right)}^{a}\;{{\rho }_{\boldsymbol{k}}}\left( t \right) \right]$](https://content.cld.iop.org/journals/1367-2630/16/5/053014/revision1/njp494077ieqn85.gif) .
.
We wish to generate a perturbative expansion of the solution of (10), which will then allow us to write an expansion of 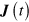 in terms of powers of the electric field,
in terms of powers of the electric field,
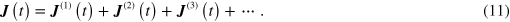
Because graphene has center-of-inversion symmetry the second order term 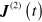 will be identically zero in the dipole approximation.
will be identically zero in the dipole approximation.
We begin by writing

and expand 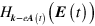 in
in 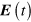 and
and 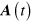 to find
to find
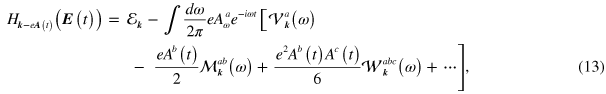
where superscripts indicate Cartesian components, to be summed over if repeated, and with 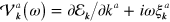 ,
, ![$\mathcal{M}_{\boldsymbol{k}}^{ab}\left( \omega \right)=\partial \left[ \partial {{\mathcal{E}}_{\boldsymbol{k}}}/\partial {{k}^{a}}+2i\omega \xi _{\boldsymbol{k}}^{a} \right]/\partial {{k}^{b}}$](https://content.cld.iop.org/journals/1367-2630/16/5/053014/revision1/njp494077ieqn92.gif) , and
, and ![$\mathcal{W}_{\boldsymbol{k}}^{abc}\left( \omega \right)={{\partial }^{2}}\left[ \partial {{\mathcal{E}}_{\boldsymbol{k}}}/\partial {{k}^{a}}+3i\omega \xi _{\boldsymbol{k}}^{a} \right]/\partial {{k}^{b}}\partial {{k}^{c}}$](https://content.cld.iop.org/journals/1367-2630/16/5/053014/revision1/njp494077ieqn93.gif) . In doped graphene, the singularities of
. In doped graphene, the singularities of 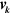 and
and 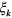 at Dirac points can be ignored. For weak external electric fields
at Dirac points can be ignored. For weak external electric fields 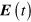 , equation (10) can then be solved iteratively. By expanding
, equation (10) can then be solved iteratively. By expanding 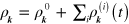 with
with 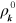 being the density matrix at equilibrium states and
being the density matrix at equilibrium states and
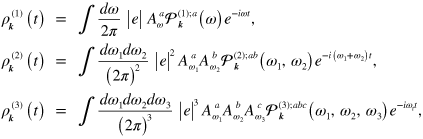
the iterative solutions are given as
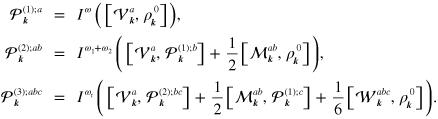
Hereafter we keep the dependence of the terms on frequencies implicit, always linking the frequencies 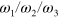 to the Cartesian components
to the Cartesian components 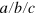 . The matrix function
. The matrix function 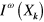 , where
, where 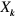 is any
is any  matrix associated with wavevector
matrix associated with wavevector  , is defined as
, is defined as 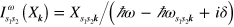 with
with 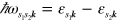 . Expanding
. Expanding
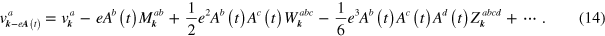
where 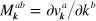 ,
,  , and
, and 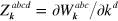 , we find that in an expansion of the
, we find that in an expansion of the 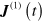 of (11) according to (12) we have
of (11) according to (12) we have
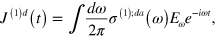
where the linear conductivity 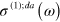 is given by
is given by

We also find
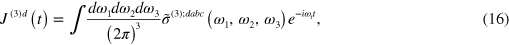
where as in equation (1) we have 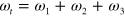 , and the (nonsymmetrized) third order conductivity
, and the (nonsymmetrized) third order conductivity 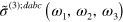 is
is
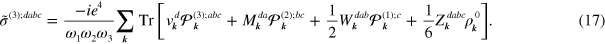
In graphene, the hexagonal lattice has 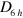 symmetry, which results in zero second order conductivity. The linear conductivity has only one independent nonzero component
symmetry, which results in zero second order conductivity. The linear conductivity has only one independent nonzero component 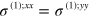 . For the third order conductivity there are in all eight nonzero components, among which three are independent; we have
. For the third order conductivity there are in all eight nonzero components, among which three are independent; we have
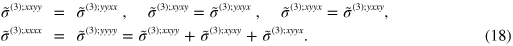
In nonlinear optics it is standard to symmetrize the terms 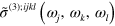 by permuting the indices
by permuting the indices  and the corresponding frequency variables
and the corresponding frequency variables 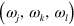 ; [34] it is easy to confirm that such symmetrized coefficients, which we denote by
; [34] it is easy to confirm that such symmetrized coefficients, which we denote by  can without impunity be used in place of
can without impunity be used in place of  in the expression for
in the expression for 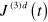 , and they satisfy the symmetry relations given above.
, and they satisfy the symmetry relations given above.
3. Approximations around dirac points
The expressions given above are exact for the two-band model. However, for studying optical transitions around the Dirac points 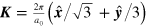 or
or 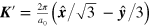 , it is usual to approximate the electronic dispersion relation as linear, i.e.
, it is usual to approximate the electronic dispersion relation as linear, i.e. 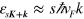 with Fermi velocity
with Fermi velocity 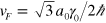 , the velocity matrix elements as
, the velocity matrix elements as 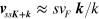 and
and 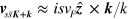 , and the interband Berry connection as
, and the interband Berry connection as 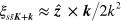 . These approximations follow immediately from equations (5), (6), and (9), and when they are made an analytic result is found for the linear optical conductivity,
. These approximations follow immediately from equations (5), (6), and (9), and when they are made an analytic result is found for the linear optical conductivity,

where
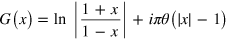
is a dimensionless complex function of a real variable x. Here  is the Heaviside step function, equal to 0 for
is the Heaviside step function, equal to 0 for 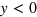 and 1 for
and 1 for 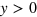 . Compared to a full band structure calculation based on our tight-binding model, this analytic result gives an error less than 15% for
. Compared to a full band structure calculation based on our tight-binding model, this analytic result gives an error less than 15% for 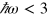 eV. We also find an analytic result for the third order optical conductivity,
eV. We also find an analytic result for the third order optical conductivity,
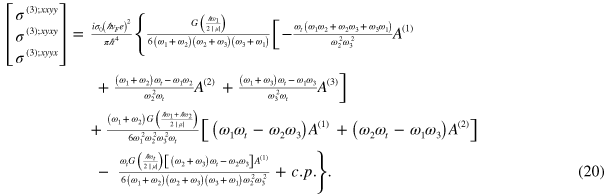
Here  stands for the simultaneous cycle permutation of indexes in
stands for the simultaneous cycle permutation of indexes in 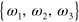 and
and 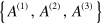 with
with
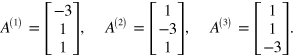
The linear conductivity is the same as found by, e.g. Gu et al [6], and reduces to the universal conductivity 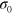 when taking the Fermi energy
when taking the Fermi energy 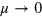 . We plot
. We plot 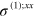 in figure 1(a). Due to the gapless linear dispersion, the third order conductivities contain many possible divergences as the photon energies involved—including all the
in figure 1(a). Due to the gapless linear dispersion, the third order conductivities contain many possible divergences as the photon energies involved—including all the 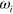 and their combinations—go to zero or to the doping induced gap (
and their combinations—go to zero or to the doping induced gap (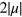 ).
).
Figure 1. (a) Linear conductivity 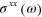 , (b) third harmonic generation coefficient
, (b) third harmonic generation coefficient 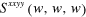 , (c) two-photon absorption and Kerr effect coefficient
, (c) two-photon absorption and Kerr effect coefficient 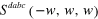 for
for 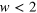 , (d) parametric frequency conversion coefficient
, (d) parametric frequency conversion coefficient 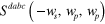 . Beside w = 0, divergences also exist at (a) w = 2, (b)
. Beside w = 0, divergences also exist at (a) w = 2, (b) 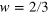 , 1, and
, 1, and  , (c) w = 1 and w = 2, (d)
, (c) w = 1 and w = 2, (d)  , 2, and 3.
, 2, and 3.
Download figure:
Standard image High-resolution imageIn limit of zero doping, 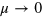 and
and 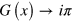 ; then
; then 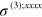 simplifies to equation (2), and
simplifies to equation (2), and 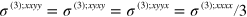 . These terms all exhibit power-law divergences as photon energies vanish. For doped graphene, the chemical potential is only involved in the function
. These terms all exhibit power-law divergences as photon energies vanish. For doped graphene, the chemical potential is only involved in the function 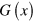 , and a logarithmic divergence appears for suitable chemical potentials. This could be utilized as a flexible method of controlling the third order nonlinearities, by tuning the doping through adjusting a gate voltage or applying chemical doping. To present a summary of the results we scale all photon energies by the chemical potential and rewrite the third order conductivity as
, and a logarithmic divergence appears for suitable chemical potentials. This could be utilized as a flexible method of controlling the third order nonlinearities, by tuning the doping through adjusting a gate voltage or applying chemical doping. To present a summary of the results we scale all photon energies by the chemical potential and rewrite the third order conductivity as
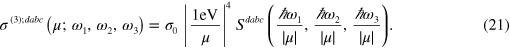
We show the coefficient 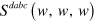 describing third harmonic generation in figure 1 (b), the coefficient
describing third harmonic generation in figure 1 (b), the coefficient 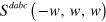 describing two-photon absorption and Kerr effects for
describing two-photon absorption and Kerr effects for 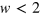 in figure 1(c), and typical components
in figure 1(c), and typical components  for parametric frequency conversion in figure 1(d). For the validity of the perturbation theory, the electric field should be less than a value
for parametric frequency conversion in figure 1(d). For the validity of the perturbation theory, the electric field should be less than a value 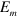 at which the contributions to the optical current from the third order term are comparable to those from the linear term. Away from the divergent regime in figure 1,
at which the contributions to the optical current from the third order term are comparable to those from the linear term. Away from the divergent regime in figure 1, 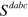 is usually of the order of
is usually of the order of 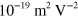 , which gives an estimated
, which gives an estimated  for a chemical potential
for a chemical potential 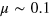 eV, which then leads to
eV, which then leads to 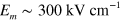 . This value is at the high end of the range of electric field amplitudes used in experiments.
. This value is at the high end of the range of electric field amplitudes used in experiments.
3.1. Third harmonic generation
For third harmonic generation we set 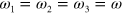 and show the transitions at the left hand side of figure 2(a). From equation (20) the third order conductivity for this effect is given by
and show the transitions at the left hand side of figure 2(a). From equation (20) the third order conductivity for this effect is given by

with 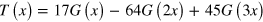 ; the other components are
; the other components are 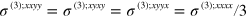 . If we take
. If we take 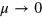 , using (1) we find the effective bulk susceptibility is
, using (1) we find the effective bulk susceptibility is 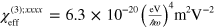 . For nonzero
. For nonzero  ,
, 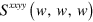 is plotted in figure 1(b). The divergence at w = 2 is very weak compared to those at
is plotted in figure 1(b). The divergence at w = 2 is very weak compared to those at 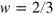 and w = 1, due to cancellations in T(x). Setting
and w = 1, due to cancellations in T(x). Setting  eV, as in the experiment by Kumar et al [15], our results are
eV, as in the experiment by Kumar et al [15], our results are 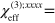
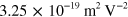 for
for 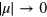 , and
, and 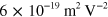 for
for  eV (
eV (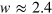 ); these are both two orders of magnitude smaller than the experimental value. While our calculations do not include scattering and the effects of electron–electron interactions, there are a number of other possible reasons for this discrepancy, which include: (i) for third harmonic generation, the imaginary part of
); these are both two orders of magnitude smaller than the experimental value. While our calculations do not include scattering and the effects of electron–electron interactions, there are a number of other possible reasons for this discrepancy, which include: (i) for third harmonic generation, the imaginary part of 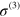 has the same importance as the real part, and the contribution from
has the same importance as the real part, and the contribution from 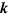 points far away from Dirac points may be not ignorable. (ii) Even around the Dirac points, the widely used linear dispersion approximation, which we have adopted here, may not be adequate for an accurate calculation of optical nonlinearities. Likely more important are the following reasons: (iii) for a very low doping level, the strong light intensity used in THG measurements may cause saturated absorption, especially if excited by high-repetition-rate laser pulses, this would lead to a nonlinearity of a totally different type, beyond the perturbation approach we apply here. (iv) Thermal effects may lead to a higher effective nonlinearity than the intrinsic one calculated here; their study is beyond the scope of the present work.
points far away from Dirac points may be not ignorable. (ii) Even around the Dirac points, the widely used linear dispersion approximation, which we have adopted here, may not be adequate for an accurate calculation of optical nonlinearities. Likely more important are the following reasons: (iii) for a very low doping level, the strong light intensity used in THG measurements may cause saturated absorption, especially if excited by high-repetition-rate laser pulses, this would lead to a nonlinearity of a totally different type, beyond the perturbation approach we apply here. (iv) Thermal effects may lead to a higher effective nonlinearity than the intrinsic one calculated here; their study is beyond the scope of the present work.
Figure 2. Illustration of the nonlinear optical transition processes for THG (left hand side of (a)), parametric frequency conversion (right hand side of (a)), two-photon absorption (b), and two-color coherent current injection. (c) Diagram (a) illustrates the nonresonant transitions, but the contribution will be maximized when any resonant condition is satisfied. The peaks of the coefficients in figure 1 correspond to resonant transitions occurring at the Fermi surface. Diagrams (b) and (c) illustrate only resonant transitions.
Download figure:
Standard image High-resolution image3.2. Kerr effects and two-photon absorption
We now look at the frequency components  . A direct calculation of
. A direct calculation of 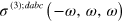 leads to a divergent result which can be understood by rewriting equation (21) as
leads to a divergent result which can be understood by rewriting equation (21) as
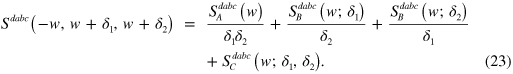
The divergent terms are related to the optical transition shown at the left hand side in figure 2 (b) and determined by
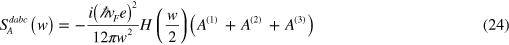
and
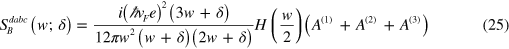
with 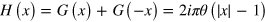 . The term
. The term 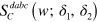 has no singularity as
has no singularity as 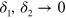 . Its components satisfy
. Its components satisfy 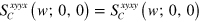 and
and
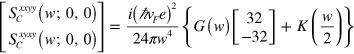
with
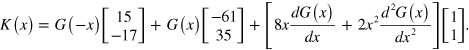
We point out that the divergences as 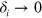 associated with
associated with 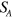 and
and 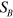 only appear for frequencies satisfying
only appear for frequencies satisfying 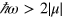 , where one-photon absorption is nonzero. So we focus on the frequencies satisfying
, where one-photon absorption is nonzero. So we focus on the frequencies satisfying 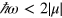 , which is the regime where only two-photon absorption occurs, analogous to the situation in a gapped semiconductor with a gap corresponding to
, which is the regime where only two-photon absorption occurs, analogous to the situation in a gapped semiconductor with a gap corresponding to 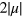 . In this regime, we find
. In this regime, we find ![$\operatorname{Re}\left[ S_{C}^{xyxy} \right]=-\operatorname{Re}\left[ S_{C}^{xxyy} \right]$](https://content.cld.iop.org/journals/1367-2630/16/5/053014/revision1/njp494077ieqn193.gif) , and plot the w-dependence of
, and plot the w-dependence of 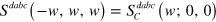 in figure 1(c).
in figure 1(c).
The two-photon absorption rate is written as

where n(t) is the areal density (for monolayer structures such as graphene) of electron-hole pairs injected. The coefficient 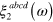 can be linked with the real part of
can be linked with the real part of 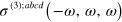 by matching the energy loss of the light field
by matching the energy loss of the light field 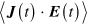 , written in terms of
, written in terms of 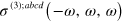 , with the total energies of excited electron-hole pairs
, with the total energies of excited electron-hole pairs 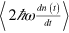 , written in terms of
, written in terms of 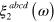 ; we find
; we find ![$\xi _{2}^{abcd}\left( \omega \right)=3{{\left( \hbar \omega \right)}^{-1}}\operatorname{Re}\left[ {{\sigma }^{(3);abcd}}\left( -\omega ,\omega ,\omega \right) \right]$](https://content.cld.iop.org/journals/1367-2630/16/5/053014/revision1/njp494077ieqn201.gif) yielding
yielding
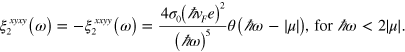
This result agrees with calculations based on Fermi's Golden Rule [18] where only transitions at the right hand side of figure 2 (b) are considered and give 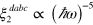 for
for 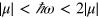 .
.
In bulk materials the Kerr effect can be described by a nonlinear index of refraction 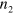 , leading to an index of refraction given by
, leading to an index of refraction given by  where I is the light intensity and
where I is the light intensity and 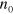 is the index at very low intensities. With the very naïve model of graphene behaving as a thin layer of macroscopic material with effective response coefficients, we would have
is the index at very low intensities. With the very naïve model of graphene behaving as a thin layer of macroscopic material with effective response coefficients, we would have ![${{n}_{2}}=3\chi _{\text{eff}}^{(3)}/\left[ 4{{\epsilon }_{0}}c\left( 1+\chi _{\text{eff}}^{(1)} \right) \right]$](https://content.cld.iop.org/journals/1367-2630/16/5/053014/revision1/njp494077ieqn207.gif) [34]; in these formulas we assume that the light is linearly polarized,
[34]; in these formulas we assume that the light is linearly polarized, 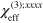 is related to
is related to  by equation (1), and
by equation (1), and 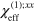 to
to 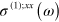 by the corresponding relation,
by the corresponding relation,
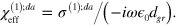
Hence starting from our calculated quantities we can extract an effective 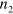 . In the experiment by Zhang et al [14], the photon energy was
. In the experiment by Zhang et al [14], the photon energy was 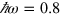 eV. Assuming
eV. Assuming ![$\mu \in \left[ 0.4,0.7 \right]$](https://content.cld.iop.org/journals/1367-2630/16/5/053014/revision1/njp494077ieqn214.gif) eV, we calculate
eV, we calculate 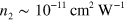 , much less than their measured value. However, if the doping level were much lower the experiment could have fallen in the divergent regime identified above, where we would not expect the perturbation approach adopted here would be sufficient.
, much less than their measured value. However, if the doping level were much lower the experiment could have fallen in the divergent regime identified above, where we would not expect the perturbation approach adopted here would be sufficient.
3.3. Parametric frequency conversion
With a strong pump at frequency 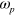 , a signal photon at frequency
, a signal photon at frequency 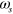 can be converted to an idler photon at
can be converted to an idler photon at 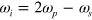 ; this process is described by
; this process is described by 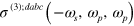 and the corresponding optical transitions are illustrated at the right hand side of figure 2 (a). At
and the corresponding optical transitions are illustrated at the right hand side of figure 2 (a). At 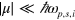 we find the conductivity given by equation (2) is
we find the conductivity given by equation (2) is

This differs from the formula of Hendry et al [11] for the same process, although both this formula and that of Hendry et al exhibit an overall frequency dependence of 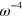 . In the experiments of Hendry et al [11] the photon energies were
. In the experiments of Hendry et al [11] the photon energies were 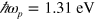 and
and 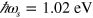 (corresponding to wavelengths of 950 nm and 1210 nm, and direct calculations from both formulas give similar values of
(corresponding to wavelengths of 950 nm and 1210 nm, and direct calculations from both formulas give similar values of  (or
(or  ), smaller by two orders of magnitude than the experimental values they extracted by comparing the nonlinear response with that of gold.
), smaller by two orders of magnitude than the experimental values they extracted by comparing the nonlinear response with that of gold.
For large  , in figure 1(d) we plot the dependence of
, in figure 1(d) we plot the dependence of 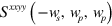 and
and 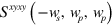 on
on  for a given
for a given 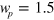 . For both components, divergences appear in the imaginary parts as
. For both components, divergences appear in the imaginary parts as 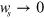 and in the real parts as
and in the real parts as 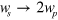 , and scale as
, and scale as  and
and 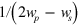 respectively. These divergences correspond to two interesting physical processes: as
respectively. These divergences correspond to two interesting physical processes: as 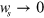 , the idler frequency is close to twice
, the idler frequency is close to twice 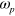 , which indicates that graphene could manifest very high second order nonlinearities in the presence of an external DC field [12]. For
, which indicates that graphene could manifest very high second order nonlinearities in the presence of an external DC field [12]. For 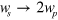 , the idler frequency vanishes, and the divergence
, the idler frequency vanishes, and the divergence 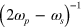 shows the existence of two-color coherent current injection, to which we turn in the next section. For
shows the existence of two-color coherent current injection, to which we turn in the next section. For 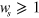 , two photon absorption (or one photon absorption (
, two photon absorption (or one photon absorption (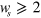 )) will occur and reduce the signal light intensity. However, the imaginary parts of
)) will occur and reduce the signal light intensity. However, the imaginary parts of 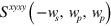 show logarithmic divergences at
show logarithmic divergences at  and
and 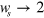 , which could enhance the idler intensity.
, which could enhance the idler intensity.
3.4. Two-color coherent current injection
To link up with earlier treatments we now consider 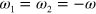 and
and 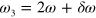 , as
, as 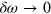 . The divergence, as
. The divergence, as 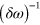 , indicates the injection of current through the interference of one- and two-photon absorption processes [35],
, indicates the injection of current through the interference of one- and two-photon absorption processes [35],
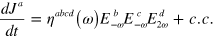
The tensor  can be calculated directly from Fermi's Golden Rule [18], but it also can be extracted from the expression for
can be calculated directly from Fermi's Golden Rule [18], but it also can be extracted from the expression for 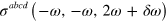 ,
,
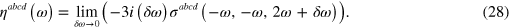
We find 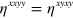 and
and
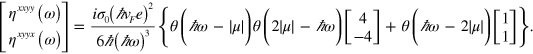
Again, we can identify different regimes here: (i) 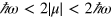 . Here only the first term contributes to the injection rates. This corresponds to the interference of one-photon absorption at
. Here only the first term contributes to the injection rates. This corresponds to the interference of one-photon absorption at 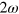 with two photon absorption at
with two photon absorption at 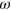 (see the transitions at the right hand side of figure 2 (c)), and corresponds to the usual current injection observed in semiconductors where
(see the transitions at the right hand side of figure 2 (c)), and corresponds to the usual current injection observed in semiconductors where 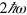 is greater than the band gap but
is greater than the band gap but 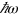 is not. (ii)
is not. (ii) 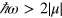 . In this regime one-photon absorption occurs at the fundamental frequency, and the second order contribution to current injection at the same position in the Brillouin zone leads to a divergent result. However, a new contribution to the coherent current injection appears and is finite; it arises from a new process of interfering pathways involve
. In this regime one-photon absorption occurs at the fundamental frequency, and the second order contribution to current injection at the same position in the Brillouin zone leads to a divergent result. However, a new contribution to the coherent current injection appears and is finite; it arises from a new process of interfering pathways involve 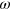 and
and  transitions [36] (at the left hand side of figure 2 (c)). For experiments in semiconductors, where the fundamental energy
transitions [36] (at the left hand side of figure 2 (c)). For experiments in semiconductors, where the fundamental energy 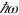 is typically less than the band gap, this regime is usually not explored. But note that in graphene the onset of this new channel leads to obvious amplitude changes in η, which could be easily detected in experiments by measuring the sudden change of the injection currents amplitude with scanning the fundamental frequencies across
is typically less than the band gap, this regime is usually not explored. But note that in graphene the onset of this new channel leads to obvious amplitude changes in η, which could be easily detected in experiments by measuring the sudden change of the injection currents amplitude with scanning the fundamental frequencies across  .
.
4. Conclusion
We investigated the linear and third order nonlinear optical conductivity of doped graphene, at zero temperature in the tight binding model, using the semiconductor Bloch equations. Analytic results were obtained around the Dirac points by using the widely accepted linear dispersion approximation. The third order optical conductivities exhibit a complicated dependence on the photon frequencies and chemical potential. We discussed in detail third harmonic generation, Kerr effects and two-photon absorption, parametric frequency conversion, and two-color coherent current injection. A nonvanishing chemical potential mimics many of the features that result from the presence of a band gap in normal semiconductors, and divergences can result when the energy of the effective gap is matched to any of the photon energies involved. The different third order processes considered exhibit a wide range of behavior, with each process having its own signature features. The important role played by the chemical potential allows for the generation of desired nonlinearities by electrically tuning or chemical doping; for low doping levels, the easily saturated absorption may lead to a nonlinear response totally different than those calculated here in the perturbative regime. Both systematic experiments and full band structure calculations, including finite temperature effects, thermal effects, scattering processes, and saturation, are clearly required to identify the true nature of the nonlinear response. But the perturbative calculations presented here identify a host of frequency regimes where very interesting behavior can be expected, even if more sophisticated calculations are required to elucidate it.
Acknowledgments
This work has been supported by the EU-FET grant GRAPHENICS (618086), by FWO-Vlaanderen which provides funding through the FWO project G.A002.13N and the Postdoctoraal Onderzoeker grant for N Vermeulen, by the Natural Sciences and Engineering Research Council of Canada, by VUB-Methusalem, VUB-OZR, and IAP-BELSPO under grant IAP P7-35.
Footnotes
- 3
Some confusion has entered the literature here. Hendry et al [11] made some approximations in their expression and wrote it in a form where they could compare
 for graphene with the third order nonlinear optical response of a typical insulator,
for graphene with the third order nonlinear optical response of a typical insulator,  . Evaluating the coefficient they found to relate the two, they quoted
. Evaluating the coefficient they found to relate the two, they quoted  . This led them to estimate
. This led them to estimate  . However, a factor of
. However, a factor of  was missed in their evaluation of their coefficient; if their coefficient is evaluated correctly the result is
was missed in their evaluation of their coefficient; if their coefficient is evaluated correctly the result is  , or
, or  . We mention that the experimental comparison they made with the nonlinear response of gold could be questioned, since while their experiments on gold and graphene were done at 820 nm with 6 ps pulses, the reference value they used for the
. We mention that the experimental comparison they made with the nonlinear response of gold could be questioned, since while their experiments on gold and graphene were done at 820 nm with 6 ps pulses, the reference value they used for the  of gold came from experiments done at 532 nm with 35 ps pulses; the effective nonlinear optical response of metals is well-known to be strongly dependent on wavelength [37] and pulse duration.
of gold came from experiments done at 532 nm with 35 ps pulses; the effective nonlinear optical response of metals is well-known to be strongly dependent on wavelength [37] and pulse duration.