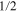Abstract
We extend the concept of superadiabatic dynamics, or transitionless quantum driving, to quantum open systems whose evolution is governed by a master equation in the Lindblad form. We provide the general framework needed to determine the control strategy required to achieve superadiabaticity. We apply our formalism to two examples consisting of a two-level system coupled to environments with time-dependent bath operators.
Export citation and abstract BibTeX RIS

Content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
The adiabatic theorem in quantum mechanics states that a physical system remains in the instantaneous eigenstate of the Hamiltonian that rules its dynamics, if a given perturbation is acting on it slowly enough [1, 2]. The slower the time-dependence of the Hamiltonian the better the system is able to adapt to the corresponding changes. The implications of the adiabatic theorem have found key roles in the context of quantum computation [3], in the physics of quantum phase transitions (see [4] for a review), quantum ratchets, and pumping.
Adiabatic dynamics is a way to control the evolution of the state of a quantum system through the time-dependence of some Hamiltonian parameters, typically performed varying appropriately chosen external potentials. As perfect adiabaticity would require infinitely slow changes, the desired evolution can only be achieved approximately. In general, non-adiabatic corrections, although possibly very small, should thus be accounted for.
At the opposite side of the spectrum lies optimal quantum control [5], which relies on the ability to engineer time-dependent Hamiltonians that allow to reach, in principle with unit fidelity, a given target state. Optimal quantum control [6–8] has recently found very important applications in quantum information processing, where it has been shown to be crucial for the design of fast and high-fidelity quantum gates [9–13], the efficient manipulation of simple quantum systems [14–16], and the state preparation of quantum many-body systems [17, 18].
A very interesting connection between adiabatic dynamics and optimal control stems from a problem posed and solved in [19–22], and that can stated as follows: given a time-dependent Hamiltonian 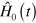 with instantaneous eigenstates
with instantaneous eigenstates 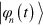 , is it possible to identify an additional term
, is it possible to identify an additional term 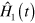 such that the time-dependent Schrödinger equation driven by
such that the time-dependent Schrödinger equation driven by 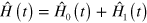 admits
admits 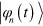 as an exact solution? With the provision of an explicit construction of
as an exact solution? With the provision of an explicit construction of 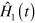 and the discussion of simple examples, [19–22] have basically initiated a new field of investigations currently known as transitionless quantum driving, shortcut to adiabaticity or superadiabatic dynamics. Protocols based on superadiabatic dynamics have been applied to a variety of different situations in atomic and molecular physics, cold atomic systems, and many-body state engineering. The field has been recently reviewed in [23], while the experimental realizations have been reported for artificial two-level quantum system realized with Bose–Einstein condensates in optical lattices [24] and for nitrogen vacancies in diamonds [25].
and the discussion of simple examples, [19–22] have basically initiated a new field of investigations currently known as transitionless quantum driving, shortcut to adiabaticity or superadiabatic dynamics. Protocols based on superadiabatic dynamics have been applied to a variety of different situations in atomic and molecular physics, cold atomic systems, and many-body state engineering. The field has been recently reviewed in [23], while the experimental realizations have been reported for artificial two-level quantum system realized with Bose–Einstein condensates in optical lattices [24] and for nitrogen vacancies in diamonds [25].
To the best of our knowledge, the superadiabatic approach has only been considered for closed quantum systems (see however [26–28]). Very recently, it was shown that when applied to quantum many-body systems, transitionless quantum driving may be achieved at the cost of highly non-local operations [29, 30]. Quite clearly, though, a rigorous extension of the concept of superadiabaticity to open-system dynamics would be much needed in order to enlarge the range of physical situations that can be addressed.
The provision of a framework for such generalization is exactly the subject of this work. We reformulate the superadiabatic framework so as to adapt it to the case of an open-system dynamics written in a general Lindblad form. Our approach will be built on the definition of open adiabatic dynamics as given in [31] and will lead us to the statements given in equations (12), (13) and (15), which represent the main results of our work. We will then illustrate the effectiveness of our framework using two examples involving the open dynamics of a single spin in a time-dependent environment.
1. Unitary evolution
In order to set the ground for the discussion on superadiabatic dynamics for open quantum system it is useful to rephrase the results in [22] using a different approach, which will be perfectly suited for a generalization to the case of non-unitary evolutions.
Let us consider a system spanning a Hilbert space of dimension N and ruled by a time-dependent Hamiltonian 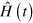 with a discrete, non-degenerate spectrum. By choosing the time-independent basis
with a discrete, non-degenerate spectrum. By choosing the time-independent basis 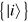
 , we can represent the Hamiltonian as
, we can represent the Hamiltonian as 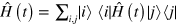 , and diagonalize it using the (time-dependent) similarity transformation
, and diagonalize it using the (time-dependent) similarity transformation

where 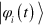 is the
is the 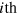 instantaneous eigenvector of
instantaneous eigenvector of 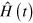 , associated to the eigenvalue
, associated to the eigenvalue 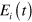 . It is straightforward to check that
. It is straightforward to check that 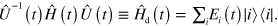
Following [31], let us now consider the time-dependent Schrödinger equation 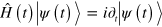 and transform it to the picture defined by
and transform it to the picture defined by 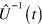 , which gives us
, which gives us
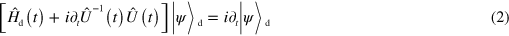
with 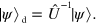 By splitting
By splitting 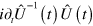 into the sum of a diagonal term
into the sum of a diagonal term 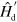 and an off-diagonal one
and an off-diagonal one 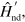 equation (2) is recast in the form
equation (2) is recast in the form
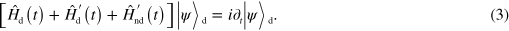
The explicit form of 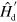 and
and 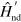 can be given as
can be given as
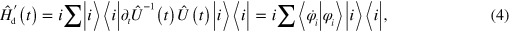
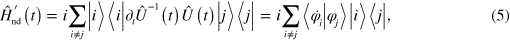
where we have dropped the explicit time dependence of the instantaneous eigenstates 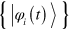 . While
. While 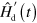 encompasses the contribution that leads to the geometric phases [33], adiabaticity is enforced when
encompasses the contribution that leads to the geometric phases [33], adiabaticity is enforced when 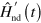 is neglected. This can be easily seen by noticing that both
is neglected. This can be easily seen by noticing that both 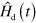 and
and  are diagonal in the basis
are diagonal in the basis 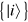 and, by neglecting
and, by neglecting 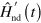 , different eigenvectors will not be mixed across the evolution. In transitionless quantum driving, the goal is to find an additional term
, different eigenvectors will not be mixed across the evolution. In transitionless quantum driving, the goal is to find an additional term 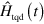 such that the Schrödinger equation for the Hamiltonian
such that the Schrödinger equation for the Hamiltonian 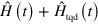 admits the adiabatic evolution of an eigenvector of
admits the adiabatic evolution of an eigenvector of 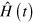 as an exact solution. From the discussion above, it is straightforward to see that such additional term is given by
as an exact solution. From the discussion above, it is straightforward to see that such additional term is given by

Indeed, by applying 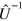 to both side of the Schrödinger equation for the Hamiltonian
to both side of the Schrödinger equation for the Hamiltonian 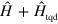 , it is straightforward to get
, it is straightforward to get ![$\left[ {{\hat{H}\,}_{\text{d}}}\left( t \right)+\hat{H}\,_{\text{d}}^{\prime }\left( t \right) \right]|\psi {{\rangle }_{\text{d}}}=i{{\partial }_{t}}|\psi {{\rangle }_{\text{d}}}$](https://content.cld.iop.org/journals/1367-2630/16/5/053017/revision1/njp493973ieqn36.gif) . That is, the non-adiabatic term responsible for the coupling between different eigenspaces of
. That is, the non-adiabatic term responsible for the coupling between different eigenspaces of 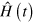 , which is usually neglected in the adiabatic approximation, can be cancelled exactly by adding the term
, which is usually neglected in the adiabatic approximation, can be cancelled exactly by adding the term 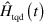 to the original Hamiltonian. Needless to say, the explicit calculation of
to the original Hamiltonian. Needless to say, the explicit calculation of 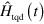 leads to the same expression given in [22].
leads to the same expression given in [22].
2. Superadiabatic dynamics: Lindblad dynamics
We are now in a position to generalize the framework discussed above to the case of non-unitary evolutions. We will consider a general master equation in the Lindblad form ![$\mathcal{L}\left[ \varrho \right]=\dot{\varrho }$](https://content.cld.iop.org/journals/1367-2630/16/5/053017/revision1/njp493973ieqn40.gif) for the density matrix ϱ of the system. Here,
for the density matrix ϱ of the system. Here, 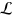 is the time-dependent superoperator describing the non-unitary dynamics of the system and given by the general form
is the time-dependent superoperator describing the non-unitary dynamics of the system and given by the general form
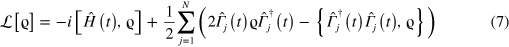
with 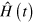 the Hamiltonian of the system and
the Hamiltonian of the system and 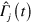 the operators describing the system-environment interaction. Here
the operators describing the system-environment interaction. Here 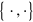 stands for the anticommutator.
stands for the anticommutator.
The adiabatic dynamics in open system needs to be defined with care. In fact, due to the coupling of the system with the environment, the energy-difference between neighbouring eigenvalues of the Hamiltonian no longer provides the natural time-scale with respect to which a time-dependent Hamiltonian could be considered to be slow-varying. Here we follow the approach developed in [31], according to which adiabaticity of open systems is reached when the evolution of the state of a system occurs without mixing the various Jordan blocks into which 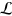 can be decomposed. The use of Jordan block decomposition is necessary due to the fact that the Lindblad operator
can be decomposed. The use of Jordan block decomposition is necessary due to the fact that the Lindblad operator 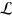 might not be diagonalizable in general. Although many important problems deal with diagonalizable Lindblad superoperators, a general treatment of transitionless quantum driving in open systems requires the Jordan formalism. Explicit ad hoc examples of non-diagonalizable Lindblad superoperators can be constructed even for simple systems such a single qubit, as shown in [31]. Although for the sake of our analysis it is the general formalism to be relevant, we stress that the search for less contrived instances is the topic of current studies.
might not be diagonalizable in general. Although many important problems deal with diagonalizable Lindblad superoperators, a general treatment of transitionless quantum driving in open systems requires the Jordan formalism. Explicit ad hoc examples of non-diagonalizable Lindblad superoperators can be constructed even for simple systems such a single qubit, as shown in [31]. Although for the sake of our analysis it is the general formalism to be relevant, we stress that the search for less contrived instances is the topic of current studies.
Equipped with this definition we are now ready to describe superadiabatic dynamics of open systems. In order to use the formalism introduced above for the case of pure states undergoing a unitary evolution, we need to write all superoperators as matrices and all density matrices as vectors. Following [31, 32], we start by defining a time-independent basis in the 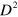 -dimensional space (where D is the dimension of the Hilbert space) of the density matrices as
-dimensional space (where D is the dimension of the Hilbert space) of the density matrices as 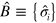 . This could consist, for example, the three Pauli matrices and the identity matrix in the case of a single spin-
. This could consist, for example, the three Pauli matrices and the identity matrix in the case of a single spin-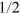 . Once we have defined the basis
. Once we have defined the basis 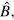 the density matrix can be transform into a 'coherence vector' living in a
the density matrix can be transform into a 'coherence vector' living in a 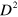 -dimensional space as
-dimensional space as 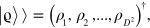 where
where ![${{\rho }_{j}}=\text{Tr}\left[ \hat{\sigma }\,_{j}^{\dagger }\varrho \right].$](https://content.cld.iop.org/journals/1367-2630/16/5/053017/revision1/njp493973ieqn53.gif) On the other hand, the Lindblad superoperator
On the other hand, the Lindblad superoperator 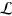 becomes a
becomes a 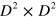 time-dependent matrix L(t) (which we will call a 'supermatrix') whose elements are given by
time-dependent matrix L(t) (which we will call a 'supermatrix') whose elements are given by ![${{L}_{jk}}\left( t \right)=\text{Tr}\left[ \hat{\sigma }\,_{j}^{\dagger }\left( {{\mathcal{L}}_{t}}\left[ {{\hat{\sigma }\,}_{k}} \right] \right) \right].$](https://content.cld.iop.org/journals/1367-2630/16/5/053017/revision1/njp493973ieqn56.gif) With this notation, the master equation now reads
With this notation, the master equation now reads

Although the supermatrix L(t) might be non-Hermitian, in which case it cannot be diagonalized in general, it is always possible to find a similarity transformation C(t) such that L(t) is written in the canonical Jordan form
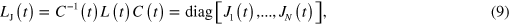
where 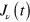 represents the Jordan block (of dimension
represents the Jordan block (of dimension 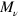 ) corresponding to the the eigenvalue
) corresponding to the the eigenvalue 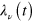 of
of 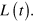 The number N of Jordan blocks is equal to the number of linear independent eigenvectors of L(t) and the similarity transformation is given by
The number N of Jordan blocks is equal to the number of linear independent eigenvectors of L(t) and the similarity transformation is given by

where  is a basis of right instantaneous quasi-eigenvectors of L(t) associated with the eigenvalues
is a basis of right instantaneous quasi-eigenvectors of L(t) associated with the eigenvalues 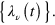 The set of right quasi-eigenstates
The set of right quasi-eigenstates 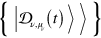 is defined through the equation
is defined through the equation
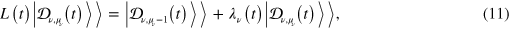
where  represents the eigenvector of L(t) corresponding to the eigenvalue
represents the eigenvector of L(t) corresponding to the eigenvalue 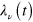 and
and 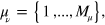 with
with 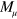 the dimension of block
the dimension of block 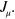 On the other hand,
On the other hand, 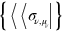 are the vector of the basis B introduced above with the index i now defined as
are the vector of the basis B introduced above with the index i now defined as 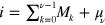 (
(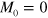 ). The inverse transformation
). The inverse transformation 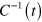 (such that
(such that 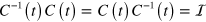 ) can be defined in a conceptually analogous way by considering the set of left instantaneous quasi-eigenvectors of L(t). As the set
) can be defined in a conceptually analogous way by considering the set of left instantaneous quasi-eigenvectors of L(t). As the set 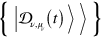 embodies the basis where L(t) is in Jordan form, we immediately get that
embodies the basis where L(t) is in Jordan form, we immediately get that 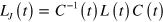 . Needless to say, when L(t) is diagonalizable the same arguments and definitions above apply with
. Needless to say, when L(t) is diagonalizable the same arguments and definitions above apply with 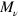 becoming the multiplicity of the eigenvalue
becoming the multiplicity of the eigenvalue 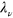 and right (left) quasi-eigenvectors being promoted to the role of exact right (left) eigenvectors of
and right (left) quasi-eigenvectors being promoted to the role of exact right (left) eigenvectors of 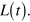
Exploiting the formal equivalence between equation (8) and the (imaginary-time) Schrödinger equation for non-Hermitian Hamiltonians, the same arguments illustrated above in the context of unitary evolutions can be used here. We thus apply the transformation 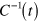 to both side of equation (8). After some straightforward manipulation, the latter is rewritten in the form
to both side of equation (8). After some straightforward manipulation, the latter is rewritten in the form
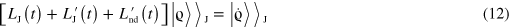
which is analogous to equation (3) and where we have introduced

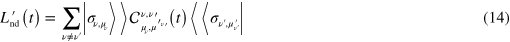
with 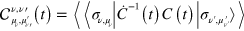 . In both equations (12) and (13), the pedex
. In both equations (12) and (13), the pedex 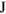 indicates that the matrix L(t) is in the Jordan form and the coherence vectors are transformed as
indicates that the matrix L(t) is in the Jordan form and the coherence vectors are transformed as 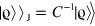 .
.
For open systems, the problem of transitionless quantum driving consists of finding an additional term 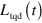 such that different Jordan blocks of L alone evolve independently under the action of
such that different Jordan blocks of L alone evolve independently under the action of 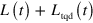 . Since the two terms
. Since the two terms 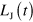 and
and 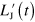 preserve the Jordan blocks structure, any admixture between different Jordan blocks is bound to arise from
preserve the Jordan blocks structure, any admixture between different Jordan blocks is bound to arise from 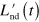 . Therefore, by using the same approach sketched in the unitary case, we can infer the form of the additional term
. Therefore, by using the same approach sketched in the unitary case, we can infer the form of the additional term 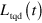 as
as

equation (15) extends and generalizes the result valid for the unitary case (cf equation (24)) to quantum open-system dynamics and is the main result of this work. Just like in the unitary case, 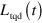 encompasses the control that should be implemented so that the state of the system remains, across the evolution, in an instantaneous eigenstate. The required control term could be either on the unitary part of the dynamics (i.e. an additional Hamiltonian term), or in the non-unitary one, which would require the engineering of a proper quantum channel. While we identify a physically relevant condition that ensures that the correction term is of Hermitian nature in the following paragraph, in the latter case there is no guarantee that the correction adds up to the dynamics of the system so as to give a completely positive map
9
. When this is the case, though, it is sufficient to add an effective damping term diagonal in the correction term, large enough to re-instate complete positivity.
encompasses the control that should be implemented so that the state of the system remains, across the evolution, in an instantaneous eigenstate. The required control term could be either on the unitary part of the dynamics (i.e. an additional Hamiltonian term), or in the non-unitary one, which would require the engineering of a proper quantum channel. While we identify a physically relevant condition that ensures that the correction term is of Hermitian nature in the following paragraph, in the latter case there is no guarantee that the correction adds up to the dynamics of the system so as to give a completely positive map
9
. When this is the case, though, it is sufficient to add an effective damping term diagonal in the correction term, large enough to re-instate complete positivity.
It is worth noting that, analogously to the case of adiabatic unitary dynamics, the term 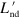 cancels exactly the terms in the evolution that would be neglected when the adiabatic approximation is enforced. By differentiating equation (11) it is possible to explicitly link the correction term
cancels exactly the terms in the evolution that would be neglected when the adiabatic approximation is enforced. By differentiating equation (11) it is possible to explicitly link the correction term 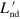 to the neglected terms under the adiabatic approximation. For example, for unidimensional Jordan blocks (i.e. for a fully diagonalizable Lindblad operator with non-degenerate spectrum) we can write the off-diagonal matrix elements of the correction term as [31]
to the neglected terms under the adiabatic approximation. For example, for unidimensional Jordan blocks (i.e. for a fully diagonalizable Lindblad operator with non-degenerate spectrum) we can write the off-diagonal matrix elements of the correction term as [31]
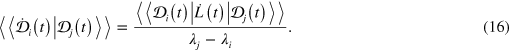
The general case of non-trivial Jordan block can be treated analogously, although the correction term would assume a more complicated (although conceptually equivalent) expression (cf [31] for more details about the adiabatic approximation in open systems).
We now address the question of whether is possible to provide a necessary condition for the Hermitian nature of the correction term in equation (15) is always Hermitian. Let us now consider a Lindblad superoperator on the form
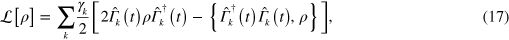
where we assumed 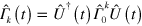 for a given global unitary operator
for a given global unitary operator 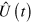 and time-independent jump operators
and time-independent jump operators 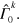 By moving to a rotating frame defined by
By moving to a rotating frame defined by 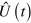 and calling
and calling 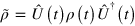 the density matrix in such a frame, we get the Lindblad equation
the density matrix in such a frame, we get the Lindblad equation
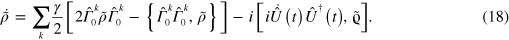
That is, in the rotating frame generated by 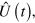 the time dependence of the Lindblad operator is cancelled, and different eigenvectors will evolve independently. This simple argument shows that, whenever the non-unitary part of the evolution of a system is governed by jump operators such as
the time dependence of the Lindblad operator is cancelled, and different eigenvectors will evolve independently. This simple argument shows that, whenever the non-unitary part of the evolution of a system is governed by jump operators such as 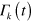 , the superadiabatic correction is provided by the Hamiltonian term
, the superadiabatic correction is provided by the Hamiltonian term 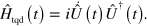 A more formal proof is given in the appendix.
A more formal proof is given in the appendix.
3. Examples
In order to illustrate the general formalism described above, let us now discuss some simple examples involving a single-spin system. The first addresses the case of a single spin affected by a dissipative mechanism described by the super operator

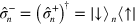 the lowering ladder operator along the direction
the lowering ladder operator along the direction 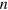 , and
, and 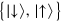 the two spin states of the system. The dissipation occurs along a direction in the single-spin Bloch sphere identified by the unit vector
the two spin states of the system. The dissipation occurs along a direction in the single-spin Bloch sphere identified by the unit vector 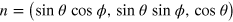 with θ and ϕ the azimuthal and equatorial angle, respectively. In order to write explicitly both the Liouvillian supermatrix
with θ and ϕ the azimuthal and equatorial angle, respectively. In order to write explicitly both the Liouvillian supermatrix 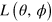 and the corresponding coherence vector, we choose the ordered basis
and the corresponding coherence vector, we choose the ordered basis 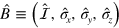 . Let us now consider the case in which the direction of the dissipation
. Let us now consider the case in which the direction of the dissipation  precesses around the z-axis of the Bloch sphere at a constant angular velocity ω, maintaining a fixed azimuthal angle
precesses around the z-axis of the Bloch sphere at a constant angular velocity ω, maintaining a fixed azimuthal angle  , and a constant damping rate γ. By setting
, and a constant damping rate γ. By setting 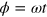 and employing the result in equation (15), we can find the explicit form of the 4 × 4 supermatrix
and employing the result in equation (15), we can find the explicit form of the 4 × 4 supermatrix 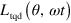 required to achieve superadiabaticity in this example. An explicit calculation shows that a purely Hamiltonian contribution of the form
required to achieve superadiabaticity in this example. An explicit calculation shows that a purely Hamiltonian contribution of the form ![${{\mathcal{L}}_{\text{tqd}}}\left[ \varrho \right]=-i\left[ {{\hat{H}\,}_{\text{tqd}}}\left( t \right),\varrho \right]$](https://content.cld.iop.org/journals/1367-2630/16/5/053017/revision1/njp493973ieqn111.gif) with
with 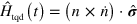 , is sufficient to achieve superadiabaticity. Indeed, the correction term is a magnetic field which at any instant induces a rotation that cancels the time-dependence of the original Lindblad superoperator. Being equation (19) a particular case of the more general expression in equation (17), the correction term corresponds to
, is sufficient to achieve superadiabaticity. Indeed, the correction term is a magnetic field which at any instant induces a rotation that cancels the time-dependence of the original Lindblad superoperator. Being equation (19) a particular case of the more general expression in equation (17), the correction term corresponds to 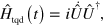 as expected.
as expected.
Let us now consider a simple example involving two qubits. We start by designing a Lindblad operator which generate a time evolution map whose fix point is a Bell state 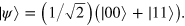 Such state can be obtain by applying a unitary operation
Such state can be obtain by applying a unitary operation 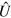 to the state
to the state 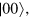 where
where 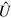 represent an Hadamard transformation on one of the qubit followed by a C-NOT gate. The operation
represent an Hadamard transformation on one of the qubit followed by a C-NOT gate. The operation  can be represented by the 4 × 4 matrix
can be represented by the 4 × 4 matrix

The Lindblad map having the state  as a fix point has the form given in equation (17) with jump operators
as a fix point has the form given in equation (17) with jump operators
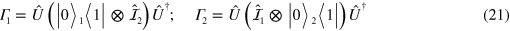
Let us now consider a unitary operation
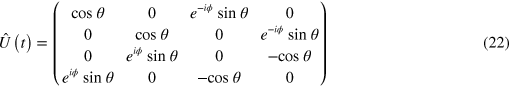
This unitary operation represents a generalization of the one given in equation (20) in which the Hadamar transformation is substituted by a general rotation specified by the angles ϕ and  The case we are interested in is the one in which such angles are time-dependent. For simplicity, we assume
The case we are interested in is the one in which such angles are time-dependent. For simplicity, we assume 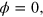 so the only time-dependent parameter is
so the only time-dependent parameter is 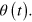 This means that the Jump operators
This means that the Jump operators 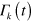 are now time dependent, with the time dependence included in the parameter
are now time dependent, with the time dependence included in the parameter 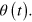
The scenario we consider is the following: we consider a Lindblad whose fix point is a particular state, for example 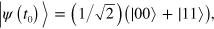 which correspond to
which correspond to 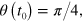 with
with 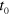 the time at which the system has reached such state. At this point, we can change the parameter
the time at which the system has reached such state. At this point, we can change the parameter 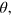 and consequently the jump operators
and consequently the jump operators 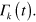 In such a way, the stationary state of the system can be dragged from the initial state
In such a way, the stationary state of the system can be dragged from the initial state 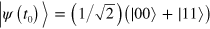 to the state
to the state 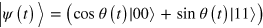 at time
at time 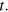 If the changes in the parameter
If the changes in the parameter 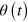 are slow, the system will remain in the instantaneous fix point at all times t with good approximation. On the other hand, by implementing the super-adiabatic protocol for open systems, we can change the prepared state exactly and without the constrain of slowly changing jump operators.
are slow, the system will remain in the instantaneous fix point at all times t with good approximation. On the other hand, by implementing the super-adiabatic protocol for open systems, we can change the prepared state exactly and without the constrain of slowly changing jump operators.
In this particular example, the super-adiabatic correction needed to obtain an exact driving can be easily calculated as 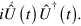 Using equation (22) with
Using equation (22) with 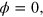 the correction is given by
the correction is given by
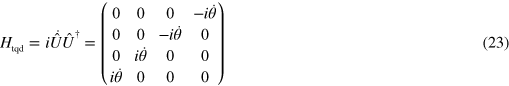
which can be written as
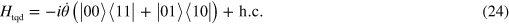
4. Conclusions
We have proposed the extension of superadiabatic dynamics to systems undergoing an explicitly open evolution. Although we have considered, for the sake of simplicity, examples involving only a small number of spins, the method that we have proposed is entirely general and can indeed be applied to instances of more complex systems. For example, we foresee that superadiabatic techniques for open system will play a key role in the context of dissipative quantum state engineering [34–39] and in the emerging field of thermodynamics of quantum systems. A promising result in this sense is provided by [40], where the design of superadiabatic quantum engines has been reported. Moreover, in general, the class of problems for which the time-dependent Lindblad superoperator admits one non-degenerate Jordan block with eigenvalue 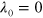 for any t is of particular interest in the context of transitionless quantum driving. Indeed, in this cases the system admit a unique stationary state for any time. The correction term, in such case, can be seen as the one needed to keep the system in its exact stationary state throughout the whole evolution.
for any t is of particular interest in the context of transitionless quantum driving. Indeed, in this cases the system admit a unique stationary state for any time. The correction term, in such case, can be seen as the one needed to keep the system in its exact stationary state throughout the whole evolution.
Acknowledgments
We would like to thank V Giovannetti, J Goold, and A Monras for useful discussions. We acknowledge the Ministry of Education of Singapore, the EU (IP-SIQS, TherMiQ), the MIUR–PRIN 2010/11, the UK EPSRC (EP/G004579/1), DFG via SFB/TRR21, and the John Templeton Foundation (grant ID 43467) for financial support. VV is a fellow of Wolfson College Oxford and is supported by the John Templeton Foundation and the Leverhulme Trust (UK).
Appendix
For simplicity, we assume that the Lindblad operator is diagonalizable. This is the case considered by Kraus et al in the context of quantum state preparation of a chain of qubits [34]. However, the proof can be generalize to the case in which the Lindblad admits only a Jordan block decomposition.
Let us consider a Lindblad operator in the general form given in equation (17) with the jump operators given by 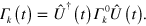 Following [34], we notice that the problem of finding the instantaneous eigenstates of equation (17) can be reduced to the problem of finding the eigenstates for the time-independent Lindblad operator at time
Following [34], we notice that the problem of finding the instantaneous eigenstates of equation (17) can be reduced to the problem of finding the eigenstates for the time-independent Lindblad operator at time 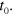 Let us denote by
Let us denote by 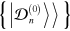 the eigenstates of the time-independent Lindblad operator
the eigenstates of the time-independent Lindblad operator 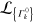 and by
and by 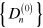 the corresponding eigen-matrices, i.e.
the corresponding eigen-matrices, i.e.

The set of matrices 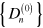 forms a basis in
forms a basis in 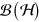 (this is also true for the set of quasi-eigenstates of
(this is also true for the set of quasi-eigenstates of 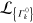 when the Lindblad operator is not diagonalizable). Moreover, the eigenstates of the time-dependent Lindblad operator
when the Lindblad operator is not diagonalizable). Moreover, the eigenstates of the time-dependent Lindblad operator 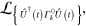 which we will denote by
which we will denote by 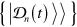 and
and 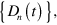 can be found as [34]
can be found as [34]

As above, this relation also hold in the case of non-diagonalizable Lindblad operators for the quasi-eigenstates. Equation (A.2) gives the important link between the eigenvectors of 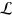 at the initial time
at the initial time  (indeed, we choose the initial time such that
(indeed, we choose the initial time such that 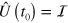 ) and the eigenstates at a generic time
) and the eigenstates at a generic time 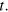
Let us now prove that the general correction term 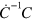 corresponds to an Hamiltonian term
corresponds to an Hamiltonian term 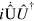 if the jump operators can be written in the form
if the jump operators can be written in the form 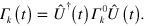 Since we are allowed to choose any time-independent basis for describing the system in Banach space, we pick the basis of quasi-eigenvectors of
Since we are allowed to choose any time-independent basis for describing the system in Banach space, we pick the basis of quasi-eigenvectors of 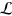 at time
at time 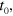 i.e. the set of matrices
i.e. the set of matrices 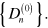 We then have that
We then have that
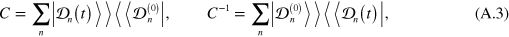
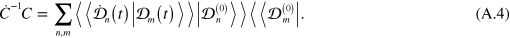
By definition, the matrix 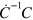 corresponds to a superoperator
corresponds to a superoperator 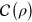 through the relation
through the relation

From equation (A.3), we also have

This can be written in terms of density matrices as

Using equation (A.2), this can be written as
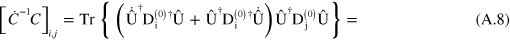
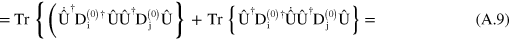
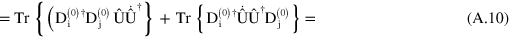
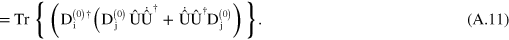
As 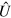 is unitary, we have that
is unitary, we have that
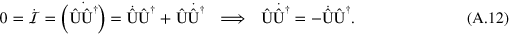
Substituting in equation (A.8), we obtain
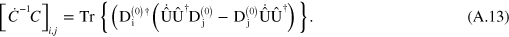
Using the definition given in equation (A.5), the superoperator  corresponding to
corresponding to  is then given by
is then given by

Footnotes
- 9
This is the case, for instance, for a spin-
 particle subjected to a magnetic filed along the z-axis and a dephasing mechanism rotating at frequency ω in the z = 0 plane. In such instance, it is straightforward to see that the superadiabatic correction is not Hermitian and that the Kossakowski matrix of the overall master equation is, in general, not positive definite.
particle subjected to a magnetic filed along the z-axis and a dephasing mechanism rotating at frequency ω in the z = 0 plane. In such instance, it is straightforward to see that the superadiabatic correction is not Hermitian and that the Kossakowski matrix of the overall master equation is, in general, not positive definite.