Abstract
We propose a model for the electric current in graphene in which electric carriers are supplied by virtual particles allowed by the uncertainty relations. The process to make a virtual particle real is described by a weak value of a group velocity: the velocity is requisite for the electric field to give the virtual particle the appropriate changes of both energy and momentum. With the weak value, we approximately estimate the electric current, considering the ballistic transport of the electric carriers. The current shows the quasi-Ohmic with the minimal conductivity of the order of per channel. Crossing a certain ballistic time scale, it is brought to obey the Schwinger mechanism.

Content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Graphene is fascinating material due to its applicability for electronic devices, and its physical properties are also attractive in fundamental physics [1]. In a single-layer graphene, the low-energy excitation of a quasi particle can be well described by the 2 + 1 dimensional massless Dirac equation. With Pauli matrices , the Hamiltonian can be represented by
where is the Fermi velocity, which corresponds to the velocity of light c. The absolute velocity of a particle always takes like a photon. Consequently, graphene can be a tool for demonstrating relativistic phenomena like Kleinʼs paradox [2] and the Schwinger mechanism [3, 4], which must be confirmed in the electrodynamics.
On the electric current in graphene, when the chemical potential and the temperature were zero, the minimal conductivity was experimentally found, of which the order was per channel (per valley and per spin) [5]: the electric current j shows a linear response on the electric field ε as , which is called quasi-Ohmic. Theoretical works have succeeded in obtaining a minimal conductivity using linear response theory [6–11], the Landauer formula [12] and the dynamical approach [13, 14]. Although their results show subtly different values, like , there is a consensus on the minimal conductivity of the order of per channel. Furthermore, it was also predicted that, as the electric field is stronger, so the electric current is beyond the linear response to the electric field as , which is owing to the Schwinger mechanism [3, 4, 13, 14]. The Schwinger mechanism originally represented a particle–antiparticle creation from a vacuum in a uniform electric field [15], while a hole substitutes for the antiparticle in graphene. The electric current can be considered as the ballistic transport of charges, since the ballistic time is long in graphene: the physical behavior can be assigned by the ballistic time. In fact, with the ballistic time , the electric current given by the Schwinger mechanism is approximately , where represents the density of the electric carriers (charges). can be derived from the 2 + 1 dimensional massless (m = 0) pair creation rate of the Schwinger mechanism [3, 16],
Whether the electric current shows the quasi-Ohmic or the Schwinger mechanism, at first glance it is surprising that graphene is capable of leading a current. There is no electric carrier when the chemical potential and the temperature are zero: the density of states is proportional to the absolute value of the energy, [1]. Consequently, there must be two processes for the electric current: creation and acceleration (or reorientation 1 ). If the ballistic time is long enough, an electric carrier can be accelerated to the direction of the electric field after creation. When the electric current is mostly composed of the creation processes, it behaves as the quasi-Ohmic. On the other hand, as the contribution of the acceleration processes surpasses the previous one, it shows the Schwinger mechanism, in which all the electric carriers are effectively in the direction of the electric field with the velocity of , i.e. . The time scale of the ballistic time for their crossover is given by
As the electric field is stronger, this crossover time becomes smaller and the Schwinger mechanism will appear. In earlier studies [4, 13, 14], it was found that, while the quasi-Ohmic current could be obtained with a perturbation of the electric field, the electric current showed the Schwinger mechanism at last, in which the perturbative treatment failed beyond the time scale (4).
In [17], we showed the case when a group velocity of a quantum particle was given by a weak value in the 1 + 1 dimensional Dirac equation, which was applied to a transmission through a supercritical step potential. In this paper, we show that this weak-value formalism is also valid for describing the creation process of an electric carrier in graphene. In fact, it has been pointed out that a weak value is useful for a description of a localized event like a pair creation [18].
To begin with, a weak value is introduced as a result of weak measurements: using weak measurements, we can extract a physical value from an observable without disturbing the quantum system to be measured [19, 20]. Actually, direct observations of quantum systems have been performed [21–23]. In optical physics, the signal amplification effect of weak measurements has also been studied for high sensitivity measurements like observations of the Hall effect [24], a beam deflection [25], a phase shift [26, 27] and the Kerr nonlinearities [28], including theoretical research [29–32]. In solid systems, such an effect has been used for charge sensing [33] and atomic spontaneous emission [34]. In addition to the applications mentioned above, weak measurements have offered interesting approaches for the foundation of quantum mechanics such as quantum paradoxes [35–39] and the violation of the Leggett–Garg inequality [40–43]. Apart from weak measurements, a weak value has been useful for explaining quantum phenomena [17, 18, 44–47]. Then, the significance of a weak value itself has also been discussed in the context of a measurement [48–51] and the validity for a description of quantum mechanics [43, 52–56].
Our result shows one of the interesting cases in which a weak value emerges as a real value of a physical quantity like [17]. In addition, aside from the issue of a weak value, it also gives a new insight into graphene in the sense that the creation process is related to virtual particles allowed by the uncertainty relations. We focus on just the creation process and do not consider the acceleration one. Nevertheless, it is enough for approximating the electric current for each mechanism, the quasi-Ohmic and the Schwinger mechanism.
We show that a weak value may also appear as a group velocity, even in the 2 + 1 dimensional massless Dirac equation here [17]. According to equation (1), a plane wave with a (positive or negative) energy and a momentum can be described as follows,
where shows the direction of the momentum. They satisfy the energy–momentum relation, . is independent of x and y, which is called the chirality. The dependent part is called the space part. Consider the case that a chirality prepared in the initial state is finally found in , which is referred to as the preselection in and the postselection in . When t is small enough, the time evolution of the space part is given as follows,
where is a weak value,
and the weak value of is given in a similar way. and correspond to the (group) velocities in the x and y directions, respectively. In fact, without the postselection, they give and . If represents the chirality of the eigenstate of the energy and the momentum , the weak values are given as follows,
where . Although a weak value is generally a complex number, as shown in equation (9), it is always real number as far as considering energy eigenstates in our case. That is why we treat a weak value as a real number hereafter.
In the next section, considering a transition between energy eigenstates, we try to describe a creation process in graphene by the pre-postselection of a chirality. We show that the weak value of a group velocity (9) is requisite for the electric field to yield the changes of both the energy and the momentum appropriately for such a transition. In section 3, we assume that the creation process for an electric carrier is triggered by a virtual particle, which is allowed by the uncertainty relations. The weak-value formalism for describing a time evolution like (8) is justified for such virtual particles, although t is not always . In section 4, we approximately estimate the electric current in graphene, using a weak value of a group velocity. It is shown that, crossing the time scale (4), the current flows in different manners, namely, the quasi-Ohmic and the Schwinger mechanism. Section 5 is devoted to our conclusion.
2. A transition for creating an electric carrier in graphene
First of all, there must be a creation process of an electric carrier in graphene so as to be capable of leading an electric current. An electric carrier will be supplied by creating a particle–hole pair, which is represented by the transition of a particle in the Dirac sea (valence band) to the vacuum (conduction band). For this purpose, we consider a transition as shown in figure 1, supposing that the electric field ε is in the x direction. Initially, a particle in the Dirac sea has a negative (kinetic) energy and a momentum , where . Because of the electric field, the particle might change to one with a positive (kinetic) energy and a momentum , where . The momentum in the y direction does not change, because the electric field is zero in this direction. The signs of and provide the velocities, which are in the direction of the electric field, because they give the group velocities and , respectively. As an energy eigenstate can be specified by a chirality as shown in equation (5), this transition process can be described by the pre-postselection on the chirality, and . Like equation (8), when the time t is very small, the time evolution of the space part can be approximately expressed as follows
This is different from equation (8) in the respect that there is a momentum shift for due to the electric field [17]. At this stage, however, it is not clear whether this weak-value formalism is valid, as we have not yet verified that the time is small enough for this approximation. The validity of the approximation will be discussed in the next section. At any rate, the weak values of the group velocities in the x and y directions can be respectively defined by equations (10) and (11), with and . These group velocities represent the velocities driven by the transitions. Because the electric field is zero in the y direction, the group velocity in this direction should be zero, namely:
equivalently,
If not, particles seem to accomplish transitions with zero electric field and the velocity, which causes the current, emerges in the y direction. Equation (16) shows that a transition is selective [57]: a particle with a negative energy and a momentum may turn out one with E and . In this case, is given by
which is a strange value; that is, the corresponding group velocity is more than [47, 58, 59]. The appearance of such a strange weak value agrees with the result of [17] due to a transition from a negative energy state to a positive one.
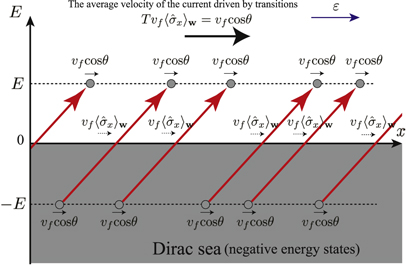
Figure 1. A transition from a negative energy to a positive one. During the transition, a particle moves into , which takes the time . The vacancy of a particle in the Dirac sea corresponds to a hole; that is, a transition represents the creation of a particle–hole pair.
Download figure:
Standard image High-resolution imageTo clarify the meaning of this strange velocity, we consider the inside details of the transition process. During the transition, the changes of the energy and the momentum are and , respectively. The force by the electric field acts on a particle in the x direction. Define as the moving distance for the duration of the transition. As the energy change is equivalent to the work done by the electric field, it satisfies,
With the time needed for the transition , we also obtain
because of the equivalence between the momentum change and the impulse. Then, we can define the average (group) velocity during the transition process as follows,
From equations (17) and (21), we can find,
which shows that, in fact, the weak value of the group velocity (17) is requisite to satisfy the energy change (18) and the momentum change (19) simultaneously.
Using a weak value, we can also estimate a probability of a transition occurring. In a specific postselection, a weak value may take a strange value that lies outside of the spectra of eigenvalues. However, the average value should be within the conventional range of values in considering all of the possible postselection. In our case, when it succeeds in postselecting a chirality by a positive energy eigenstate , is more than , as shown in equation (17). Such a weak value yields a group velocity of a current due to the transition process, because a transition corresponds to a creation of a particle–hole pair, namely, a carrier. Note that the current does not contain the effect of the process after the creation, i.e. the acceleration. Without a transition, it brings about zero group velocity and does not contribute to generating a current, because a particle remains in the Dirac sea as before. Including such non-transition particles, the average velocity should be conventionally less than , by which the net velocity of the current is given. After all, the current does not flow beyond like the superluminal velocity: it never occurs as a strange physical phenomenon with a strange value of a physical quantity as the whole. For this reason, all of the particles do not transmit to a positive energy, and such a transition happens with some probability T. In [17], we could actually estimate the transmission probability for a step potential by making a weak value of a group velocity at the step consistent with an average velocity of the flux outside the step. In a similar way, we can obtain a transition probability T as shown in figure 2. The number of transition particles in a positive energy eigenstate is equivalent to the one in a negative energy eigenstate , which corresponds to the holes. In addition, the group velocities of particles just before and just after a transition, namely, the group velocities in and , are the same as . Consequently, the average velocity of the current driven by the transition should also be . On the other hand, as we have mentioned, the transition itself generates the group velocity more than . If the transition probability is given by T, the average velocity has to satisfy
From this equation, we can find the transition probability as follows:
This transition probability is the same as the transmission probability for the step potential shown in [57], in which an n-p junction in graphene is considered. This agreement is plausible, as we have derived the 'transition' probability in the same manner as the 'transmission' probability for the step potential in [17]. They have the common point that the electric field brings about the process (transition or transmission) that generates and determines the velocity of the current.
Figure 2. The current due to transitions from a negative energy level to the positive one E, except for accelerations after the transitions. A particle in (E) has the group velocity just before (after) a transition. The current driven by the creations is composed of such particles with a homogeneous density. Note that the current in the negative energy states corresponds to the flux of holes in the opposite direction. The entire flux shows the current of the charges in the direction. As a particle has the group velocity during a transition, a transition should occur with a probability T to agree with the average velocity of the flux as shown in equation (23).
Download figure:
Standard image High-resolution imageWe have discussed a transition between energy eigenstates by an electric field. A creation of an electric carrier in graphene should be described by this picture. In the next section, we consider how much energy states can participate in such transitions for creating electric carriers.
3. An electric carrier and the uncertainty relations
We assume that a transition for creating an electric carrier is triggered by fluctuations allowed by the uncertainty relations. According to the uncertainty relation between energy and time,
an energy fluctuation can occur during a time , which means that a virtual particle with the energy can exist during the lifetime . In a similar way, a virtual particle with a momentum can be considered within a space in the x direction, and they satisfy the uncertainty relation
In our case, the virtual particle can correspond to a virtual transition, like the one shown in figure 1, and has the energy and the momentum . Note that we are concerned about the case in which the momentum change in the y direction is zero due to zero electric field and do not have to consider the fluctuation of the momentum in this direction. Such a virtual transition with the energy and the momentum , however, is not always consistent with a real particle, because it does not always satisfy the appropriate energy–momentum relation, : a virtual particle satisfies the uncertainty relations (25) and (26) independently. In fact, to make a virtual particle contribute to the electric current as a real one would, the electric field must satisfy (18) and (19) simultaneously, which is, as we mentioned before, accomplished by the weak value of the group velocity (17). In other words, a virtual particle gives the electric field a chance to do the work and the impulse, by which we mean the electric current is able to pass in graphene. Within the lifetime , the electric field must achieve the impulse , which takes the time (see equation (19)), namely
from which we can obtain
(28) assigns the energy states that may contribute to the electric carriers via virtual particles. The same result can be derived from the relation between the work and the space instead of the impulse and the time: according to equation (18), the work needs the space , which should be smaller than the fluctuation , as follows:
Satisfying (18) and (19) simultaneously, the weak value makes the uncertainty relations (25) and (26) equivalent in the sense that it selects a real particle from virtual particles in the independent uncertainty relations (25) and (26). As a result, it is plausible that (27) and (29) derive the same result (28), because the weak value satisfies the appropriate changes of both the energy and the momentum.
So far, we have proceeded to a discussion as if the approximation of the weak-value formalism, equation (14), is valid and the velocity of a particle during a transition is given by a weak value. As follows, we verify that this approximation is adequate as far as the above-mentioned transition stemming from a virtual particle. Expanding on t, we can describe equation (12) as follows:
This equation coincides with equation (13) by the first order of t, which is given by
Consequently, equation (12) can be approximated to equation (13), when the terms of can be neglected, which should be properly satisfied in . If it satisfies not but that the higher terms of are smaller than the first one, however, this approximation will also stand for rough estimations. In our case, we can obtain all that we need to valuate the higher terms: , , , , , and . For example, one of the second terms in equation (31) can be estimated as follows:
Because of , this term is smaller than the first one. In a similar way, we can verify that the other higher terms are also smaller. As a result, it is reasonable to describe the weak-value formalism for the transition starting from a virtual particle in the uncertainty relations as follows: as far as the rough estimation of the electric current, we can regard the velocity of a particle as the weak value during the transition process.
4. The ballistic transport in graphene with a weak value
In graphene, the ballistic time is long, within which we can pay no attention to the interactions with phonons, electrons and so on. The effect of the disorder can also be ignored. In the spirit of the Drude model, the electric current in graphene can be explained with such ballistic transport [13, 14]: the ballistic time , which is mostly given by with the size of the graphene sample L, corresponds to the mean free time. Moving the Dirac point, the net velocity appears along the electric field and brings about the current [1], the behavior of which is assigned by . In our case, should similarly participate in the electric current. The transition time for creating an electric carrier must be smaller than , namely, , from which we can obtain
The distance to achieve the transition is also smaller than L, i.e. . Then, we can find:
which includes (33): the energy states satisfying (34) can actually participate in the electric current, given . As a result, the actual electric current should consist of the energy states in both (28) and (34). Note that (28) represents candidates for electric carriers via virtual particles.
We have not been concerned about the amount of itself. However, if is small enough, the energy fluctuation may be effective on the current where is given by the uncertainty relation of . With the energy fluctuation (), it gives
within which the energy states are involved in the energy fluctuation . Figure 3 represents (28), (34), and (35) for the various amounts of . Clearly, they show the different features, crossing the time scale given by (4). In , all states to be considered are included in the energy fluctuation by the ballistic time (35), as denoted by O, while they are divided into two regions, namely, the inside and the outside of the fluctuation (O and S) in . After all, when , the most states are out of the energy fluctuation and belong to S. It follows that each case of shows a different mechanism of the electric current.
Figure 3. The figures of (28), (34), and (35) in the various cases of : (a), (b), and . Their values of are chosen appropriately. and are also normalized suitably. The regions surrounded by the blue curves represent (28), which provide candidates for electric carriers via virtual particles. The regions assigned by the ballistic times, i.e. (34), are within the red solid circles. The energy fluctuations due to the ballistic times, which are given by (35), are indicated by the dashed circles. The regions satisfying both (28) and (34), which are within both the blue curves and the red solid circles, are colored. Depending whether they are on the inside or the outside of the dashed circle, they are color-coded by dark green or pale gray and are referred to as O and S, respectively. Note that are considered, because the initial momentum should be negative. These colored regions provide the energy states contributing to the electric current: they assign the regions of the integrations, (36) and (40), for counting the energy states. In (a), the colored region is utterly within the dashed circle, as shown by O. With a larger , the size of the red circle overtakes the dashed one in (b). In (c), the colored regions are divided into O and S by the dashed circle, namely, the energy fluctuation by the ballistic time.
Download figure:
Standard image High-resolution imageThe time scale of corresponds to the quasi-Ohmic. In this case, the electric current is significantly composed of the creation processes, because is not long enough for an acceleration after a creation [13, 14]. For this reason, although our model describes just the creation process, we can actually try to attain the result of the quasi-Ohmic. As shown in figure 3(a), all of the energy states contributing to the creation process are within the energy fluctuation by the ballistic time, (35). Then, for each state of an energy E, we can consider the number of virtual particles as : one state may supply more than one virtual particle. This means that, in addition to approximating the number of contributing energy states by the uncertainty relations (25) and (26), we are also trying to approximate the contribution per state, using the uncertainly relation on the ballistic time scale. Each virtual particle provides an opportunity for the electric field to work of , which is accomplished with the time needed, . Then, the work per unit time for each state is given by . With the transition probability , the whole work per unit time done by the electric field can be estimated as follows:
When the electric current is proportional to the electric field as with the conductivity σ, the work per unit time is given by . Comparing equation (37) to , we can find the electric current,
and the conductivity,
We have obtained the linearity of the electric current, namely, the quasi-Ohmic. The estimated conductivity (39) almost accords with the minimal conductivity per channel, especially a theoretical value like . In this case, -fold virtual particles play the roles of the electric carriers per state. Of course, the electric field actually performs the corresponding work and impulse, which is the cause of the conductivity or the resistivity unlike Joule heat in the Ohmic. It resembles a pi-meson taking on a nuclear force between nuclear particles, as we can approximate the mass of the pi-meson with the energy–time uncertainty relation, . corresponds to the lifetime of the pi-meson. Such a pi-meson is effective within , namely, the Compton wave length, . Estimating this length as the size of the atomic nuclei, , we can find , which agrees with . It is a fact that the atomic nuclei is stable due to the nuclear force with the mediation of a virtual particle of a pi-meson, which does not emerge from the nuclei. In this sense, the virtual particle is real as far as no violation of the energy conservation, which is the same as an electric carrier for the quasi-Ohmic in graphene.
When , the energy fluctuation due to the ballistic time is very small for most states, which belong to the region S as shown in figure 3(c). For such states, the effect of the fluctuation can be neglected unlike the quasi-Ohmic case: one state supplies one particle. While the region O provides the quasi-Ohmic current as mentioned before, the contribution of the region S to the electric current can also be valuated. The ballistic time is enough to accelerate a created carrier to effectively in the x direction. Then, all that we need is the density of electric carriers , with which we can estimate the electric current as approximately [13, 14]. can be derived from the creation rate of the electric carriers , which should correspond to the pair creation rate by the Schwinger mechanism, equation (2). As we mentioned before, in a state of an energy E and a momentum , it takes the time to accomplish the transition of the creation. With the transition probability , the number of created particles per unit time is given by for the state. Consequently, the rate is given as follows:
where represents the beta function 2 . In the above approximation, the higher-order terms above have been neglected because of . As is about 0.6, this result roughly corresponds to the rate of the Schwinger mechanism, equation (2) 3 . Note that, compared to this current by the Schwinger mechanism, the quasi-Ohmic current can be ignored in this case.
5. Conclusion
We have shown that the creation process of an electric carrier in graphene can be described by a weak-value formalism. Although our weak-value model did not cover the entire physics, namely, the acceleration process, it was enough to show the feature of the electric currents for the cases of the quasi-Ohmic () and the Schwinger mechanism (). Our goal was not to make a strict estimation: not to settle in the value of the minimal conductivity. However, our estimation of the currents approximately agrees with the earlier studies. At the cost of a rigorous discussion, we have clarified the process to supply electric carriers in graphene related to virtual particles by the uncertainty relations. In this sense, our approach is different from the earlier studies. In the dynamical approach [13, 14], the crossing time scale (4) was derived, beyond which the perturbative treatment failed. There, the Schwinger mechanism can be understood as a transmission picture with the WKB approximation or be comprehensible in the context of the Landau–Zener transition [16, 60, 61]: considering the infinite past and future, the entire physics can be determined. In contrast, our model describes the physics of the turning point of transition from a negative energy state to a positive one, i.e. the creation process itself, by which we have tried to valuate the entire current in graphene. Note that the transition probability T of equation (24) is irrelevant to the Landau–Zener transition probability.
A weak value was originally introduced by Aharonov, Albert and Vaidman as a result of weak measurements [19]. According to a weak value, a pointer of a measurement apparatus is surely moved, although the weak value may take a strange value lying outside the eigenvalue spectrum. While such a physical effect to the pointer is one of the actual phenomena of a weak value, our model shows the case that a weak value emerges as an actual value of a physical quantity, following [17]. In addition, we have found a new insight in that a weak value of a group velocity makes a virtual particle in the uncertainty relations real. Irrespective of a strange value, a weak value has often allowed us to treat a quantum particle as a classical one. Interestingly, the figure depicted by (quantum) weak values, however, does not always accord with the one of classical physics as shown in [62]. A weak value seems to be simple, but not to be superficial. Then, as we have seen, it needs to clarified how a weak value becomes effective in physics for understanding the meaning of the value.
Acknowledgments
This work was supported by the Funding Program for World-Leading Innovative R & D on Science and Technology (FIRST), and JSPS Grant-in-Aid for Scientific Research(A) 25247068.
Footnotes
- 1
Note that the absolute velocity of a particle must be . Then, 'reorientation' will be more precise.
- 2
- 3
In a similar way, the rates of the Schwinger mechanism in the 1 + 1 and 3 + 1 dimensional cases can be also obtained, despite of some difference in the estimation for each dimensional case (in preparation).