Abstract
We report on stress induced changes in the dispersion relations of acoustic phonons propagating in 27 nm thick single crystalline Si membranes. The static tensile stress (up to 0.3 GPa) acting on the Si membranes was achieved using an additional strain compensating silicon nitride frame. Dispersion relations of thermally activated hypersonic phonons were measured by means of Brillouin light scattering spectroscopy. The theory of Lamb wave propagation is developed for anisotropic materials subjected to an external static stress field. The dispersion relations were calculated using the elastic continuum approximation and taking into account the acousto-elastic effect. We find an excellent agreement between the theoretical and the experimental dispersion relations.
Export citation and abstract BibTeX RIS

Content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
In the last two decades the interest devoted to phonon engineering has grown. In particular it has been shown that dispersion relations can be significantly modified e.g. by means of phononic crystals [1–7], spatial confinement [8–13] or external stress field [14–20]. Recently, single-crystalline inorganic membranes with thicknesses ranging from few hundred nanometers to the ultimate down-scaling limit represented by graphene, a truly 2D system, have received considerable attention [21]. Here, the dynamic features at reduced dimensions offer opportunities in basic and applied research, as well as in technology.
One such area concerns the thermal conductivity in nonmetals, which results from the cumulative contribution of the transport of phonons with a broad range of wavevectors and mainly from long-wavevector phonons. Thus, heat transport at room temperature can be influenced by the reduction of the membrane thickness as the dispersion relation of the short-wave-phonons starts to be affected by emerging new vibrational modes arising from the boundary conditions at the membrane surface [22]. At low temperatures, however, the wavelength of the dominant thermal phonons is large enough so that their dispersion relation is strongly affected by characteristic sizes of the order of the micrometer [23]. The introduction of a controlled stress on the membrane presents an additional degree of freedom to modify the phonon dispersion relation, which could lead to the tuning of the thermal conductivity [16]. Understanding the effect of stress on the characteristic mechanical modes of ultra-thin membranes offers an excellent avenue toward experimental and theoretical research on the thermal properties in low dimensional structures. The vibrational acoustic properties of nanomembranes have been studied by inelastic light scattering. Recently, synchrotron x-ray thermal diffuse scattering was used to probe phonons with wave vectors spanning the entire Brillouin zone of nanoscale silicon membranes [24]. In this paper we show experimental evidence on the stress induced changes in the dispersion relations of hypersonic acoustic phonons propagating in ultra-thin Si membranes. Experimental results obtained by means of Brillouin light scattering (BLS) are compared with theoretical calculations based on the elastic continuum approach and acousto-elastic theory.
2. Materials and experimental methods
Typically stress-dependent optical or electrical measurements are carried out following many diverse approaches. For example, compressive hydrostatic stress measurements are usually conducted using a diamond anvil cell, typically using He or alcohol mixtures as pressure transmitting media [25]. Experiments under uniaxial compressive stress are done using a lever arm or gas chamber to increase the uniaxial force acting on the sample [26]. The case of biaxial stress is usually approached using the ball-on-ring technique as described in [27–29]. A fundamental difference between these techniques is that whereas hydrostatic or uniaxial measurements are usually done applying compressive stress, biaxial experiments are based on tensile stress. An alternative approach to apply stress is given by heteroepitaxy, i.e. making use of the lattice mismatch between two materials to apply biaxial stress [30, 31]. Herein, we use a method based on a similar concept by taking advantage of the controllable tensile stress of chemical vapour deposited (LPCVD) Si3N4 films. The biaxial static tensile stress acting on membranes was achieved by the strain tuning method of [32], where a Si3N4 frame generates well defined biaxial stress (see figures 1(a) and (b)). The tensile stress can be adjusted by changing the strain compensation ratio 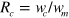 , where
, where 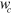 stands for the width of the area of the released membrane covered with the
stands for the width of the area of the released membrane covered with the 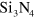 and
and 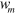 is the width of the uncovered Si part of the membrane. Measurements were performed on three suspended single crystalline Si membranes with the same membrane thickness of
is the width of the uncovered Si part of the membrane. Measurements were performed on three suspended single crystalline Si membranes with the same membrane thickness of 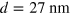 and three different values of the tensile stress
and three different values of the tensile stress 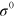 (
(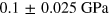 ,
, 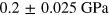 and
and 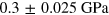 ) obtained by Raman spectroscopy. Details on the sample fabrication and Raman stress measurements can be found from [32].
) obtained by Raman spectroscopy. Details on the sample fabrication and Raman stress measurements can be found from [32].
Figure 1. Schematic illustration of (a) the membrane structure, (b) top view—relative orientation of sample and biaxial stress, (c) lateral view—Brillouin light scattering geometry. Symbol d stands for the membrane thickness, 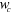 is the width of the area of the released membrane covered with the
is the width of the area of the released membrane covered with the 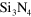 and
and 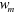 is the width of the uncovered Si part of the membrane,
is the width of the uncovered Si part of the membrane, 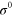 is the component of the stress tensor
is the component of the stress tensor 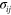 .
. 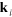 ,
, 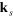 and
and 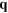 denote incident light, scattered light and scattering wavevectors respectively, θ is the scattering angle.
denote incident light, scattered light and scattering wavevectors respectively, θ is the scattering angle.
Download figure:
Standard image High-resolution imageBLS spectroscopy allows the investigation of thermally activated acoustic phonons (waves) in the GHz range of frequencies. BLS is a well established technique commonly used in nondestructive testing of elastic properties in bulk materials and thin films [33–37]. BLS has been also found as an excellent tool to characterize phonons propagation in the nm-scale systems, such as ultra-thin free standing membranes [13] and phononic crystals [3, 5, 38]. BLS experiments provide information on the relative change in the frequency (Stokes and anti-Stokes components) of laser light undergoing inelastic coherent scattering by acoustic phonons. Brillouin spectroscopy measurements were performed on a six-pass tandem type Fabry–Perot interferometer (JRS Scientific Instruments) in the 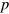 –
–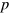 (incident and scattered light polarization parallel to the plane of incidence) backscattering geometry, which ensured the best intensity of the inelastically scattered light [39]. The light source was a solid-state laser generating light at
(incident and scattered light polarization parallel to the plane of incidence) backscattering geometry, which ensured the best intensity of the inelastically scattered light [39]. The light source was a solid-state laser generating light at  . The light was focused and collected by using an Olympus
. The light was focused and collected by using an Olympus  microscope objective with a numerical aperture of 0.5. The laser spot diameter was approximately of 12.5
microscope objective with a numerical aperture of 0.5. The laser spot diameter was approximately of 12.5 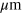 and the incident power was kept below 2 mW. For the backscattering geometry (see figure 1(c)), the angle of the laser beam incidence onto a given surface studied is equal to the scattering angle and denoted by θ. For opaque or semi-transparent materials, the main contribution to the scattered light comes from the surface ripple mechanism. Therefore, the momentum conservation holds only for the in-plane components and the magnitude of the scattering wavevector
and the incident power was kept below 2 mW. For the backscattering geometry (see figure 1(c)), the angle of the laser beam incidence onto a given surface studied is equal to the scattering angle and denoted by θ. For opaque or semi-transparent materials, the main contribution to the scattered light comes from the surface ripple mechanism. Therefore, the momentum conservation holds only for the in-plane components and the magnitude of the scattering wavevector 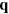 is given by [33, 34, 40]:
is given by [33, 34, 40]:

BLS measurements were performed at room temperature for scattering angle θ varied in the range 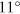 –
–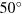 , which according to (1), corresponds approximately to the range of wavenumbers
, which according to (1), corresponds approximately to the range of wavenumbers 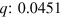 –
–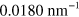 .
.
3. Lamb waves in pre-stressed anisotropic membranes
In the case of plates and membranes, normal acoustic modes are classified in terms of the spatial symmetry of the deformation with respect to the plate mid-plane into asymmetric (flexural), symmetric (dilatational) and SH (shear-horizontal) families of Lamb waves (LW). Although they were described for the first time by Lamb in 1917 [41], they are still of particular interest, resulting in a large number of both theoretical and experimental papers, monographs and technological applications [8–10, 13, 42, 43]. The undeformed, original state of a membrane in the absence of any strain and stress is called the 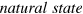 . According to the linear theory of elasticity, the velocity of any possible acoustic wave depends only on elastic parameters defined at the natural state. Therefore, constant values of these parameters during a deformation cannot lead to any change of the acoustic wave velocity. The
. According to the linear theory of elasticity, the velocity of any possible acoustic wave depends only on elastic parameters defined at the natural state. Therefore, constant values of these parameters during a deformation cannot lead to any change of the acoustic wave velocity. The 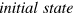 (further denoted by the superscript 0) describes the pre-deformed state of the membrane under the action of an applied static stress. A motion of an acoustic wave in the membrane in the initial state leads to the
(further denoted by the superscript 0) describes the pre-deformed state of the membrane under the action of an applied static stress. A motion of an acoustic wave in the membrane in the initial state leads to the 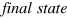 with an additional dynamic deformation, which is assumed to be small in comparison to the static one. The problem of acoustic wave propagation requires applying the nonlinear theory of elasticity due to the large deformation from the natural to the initial state [14, 44]. The schematic representation of the considered issue in the adopted coordinate system (
with an additional dynamic deformation, which is assumed to be small in comparison to the static one. The problem of acoustic wave propagation requires applying the nonlinear theory of elasticity due to the large deformation from the natural to the initial state [14, 44]. The schematic representation of the considered issue in the adopted coordinate system (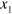 ,
, 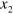 ,
, 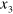 ) is shown in figure 1(b), where
) is shown in figure 1(b), where 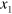 and
and 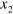 are the directions parallel to diagonals of the square defined by the membranes. The initial biaxial stress acting on the membrane, given by the Cauchy stress tensor
are the directions parallel to diagonals of the square defined by the membranes. The initial biaxial stress acting on the membrane, given by the Cauchy stress tensor  , after the rotation to the coordinate system associated with the membrane takes the form:
, after the rotation to the coordinate system associated with the membrane takes the form:

where 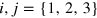 . The initial pre-deformation of the membrane is static, thus
. The initial pre-deformation of the membrane is static, thus 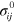 satisfies the equation of equilibrium, which using the convention of summation over repeated subscripts takes the form:
satisfies the equation of equilibrium, which using the convention of summation over repeated subscripts takes the form: 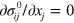 . Additionally, we assume that
. Additionally, we assume that 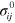 can be related to the initial strain tensor
can be related to the initial strain tensor 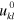 by means of Hookeʼs law
by means of Hookeʼs law 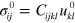 . Here
. Here 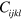 is the fourth order elastic tensor, which can be expressed as 6 × 6 matrix of second order elastic constants (SOE) in the Voigt notation (
is the fourth order elastic tensor, which can be expressed as 6 × 6 matrix of second order elastic constants (SOE) in the Voigt notation (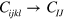 and
and 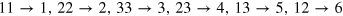 ). The nonzero and independent SOE constants
). The nonzero and independent SOE constants 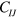 for the natural state of silicon (cubic symmetry) are given by
for the natural state of silicon (cubic symmetry) are given by 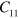 ,
, 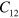 ,
, 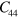 [45]. Considering the above, the equation of motion for the pre-stressed and hyperelastic body is [44]:
[45]. Considering the above, the equation of motion for the pre-stressed and hyperelastic body is [44]:

where 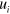 denotes the components of a displacement from the initial to the final state. The mass density
denotes the components of a displacement from the initial to the final state. The mass density 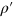 of the initial and final state can be approximated using the definition of the cubic dilatation as
of the initial and final state can be approximated using the definition of the cubic dilatation as 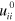 and ρ of the natural state
and ρ of the natural state 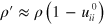 . The stress tensor
. The stress tensor 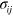 (related to wave propagation) satisfies Hookeʼs law, which for this case is given by
(related to wave propagation) satisfies Hookeʼs law, which for this case is given by 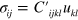 .
. 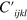 stands for the elastic tensor modified by the static pre-deformation, which can be expressed as:
stands for the elastic tensor modified by the static pre-deformation, which can be expressed as:
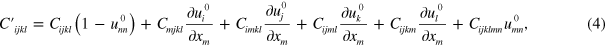
where 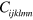 are third order elastic (TOE) constants. For the natural state of silicon TOE, which are invariant due to the symmetry operations of the
are third order elastic (TOE) constants. For the natural state of silicon TOE, which are invariant due to the symmetry operations of the 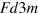 space group, are given in the Voigt notation (
space group, are given in the Voigt notation (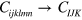 ) by:
) by: 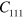 ,
, 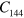 ,
, 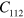 ,
, 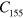 ,
, 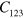 ,
, 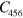 [44, 46]. For a homogeneous elastic medium one can assume a solution of the equation of motion (3) in the form of the linear combination of the plane waves with the amplitudes
[44, 46]. For a homogeneous elastic medium one can assume a solution of the equation of motion (3) in the form of the linear combination of the plane waves with the amplitudes 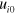 :
:

where ν denotes the phase velocity along the 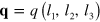 vector, which lies on the
vector, which lies on the 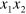 plane and the direction cosines of which are given by
plane and the direction cosines of which are given by 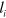 . Substituting the plane wave equation (5) into the equation of motion (3) gives nontrivial solutions for
. Substituting the plane wave equation (5) into the equation of motion (3) gives nontrivial solutions for 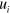 only if
only if

where 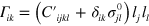 is called the acoustic tensor and
is called the acoustic tensor and 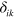 is the Kronecker delta. Boundary conditions for the membrane, which is infinite in the
is the Kronecker delta. Boundary conditions for the membrane, which is infinite in the 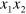 plane and limited in the
plane and limited in the 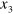 direction so that
direction so that 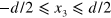 , are given by:
, are given by:

In the general case, calculations of dispersion relations for LW propagating in an anisotropic free standing membrane require applying a numerical procedure based on the partial waves approach [47].
The main goal of this method (see appendix) is to find phase velocities of LW satisfying simultaneously the elastodynamic equation of motion (3) and the stress-free boundary conditions given by (7). Due to the symmetry of the problem one can separate the numerical solutions in terms of the displacement about the midplane of the membrane (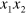 plane at
plane at 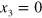 ) , into so-called symmetric (S), asymmetric (A) and shear horizontal (SH) families of waves. In the general case, A and S modes in anisotropic materials can have a small component of the displacement perpendicular to the sagittal plane, here, the plane containing the phonon wavevector and perpendicular to the
) , into so-called symmetric (S), asymmetric (A) and shear horizontal (SH) families of waves. In the general case, A and S modes in anisotropic materials can have a small component of the displacement perpendicular to the sagittal plane, here, the plane containing the phonon wavevector and perpendicular to the 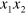 plane). Pure A and S waves are typical for isotropic media or high symmetry directions in anisotropic materials.
plane). Pure A and S waves are typical for isotropic media or high symmetry directions in anisotropic materials.
4. Results and discussion
Measurements of angle-resolved BLS were performed for the 27 nm thick membranes with the orientation as shown in figures 1(b), (c). Figure 2 presents several representative spectra differing in the scattering angle and obtained for the membrane with tensile stress magnitude 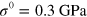 . Peaks identified as coming from the inelastic light scattering by A0 (fundamental flexural) acoustic waves were fitted using a Lorentzian function. Here, the position of the particular peak indicates the value of the phonon frequency or the Brillouin shift
. Peaks identified as coming from the inelastic light scattering by A0 (fundamental flexural) acoustic waves were fitted using a Lorentzian function. Here, the position of the particular peak indicates the value of the phonon frequency or the Brillouin shift 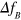 (in GHz). Thus, using (1) the phase velocity is given by:
(in GHz). Thus, using (1) the phase velocity is given by:

Figure 2. Brillouin spectra (anti-Stokes components) of the A0 mode of the 27 nm thick Si membrane obtained for different scattering angles θ and the applied load 
Download figure:
Standard image High-resolution imageApart from the value of the Brillouin shift, figure 2 also contains information related to the intensity and the spectral full width at half maximum (FWHM) of the scattered light. The intensity depends on the mean-squared amplitude of the out-of-plane surface displacement, while the FWHM can be expressed as a function of the phonon lifetime [34, 40]. However, both also depend strongly on the optical setup characteristics and its alignment, therefore, any quantitative conclusions concerning absolute out-of-plane displacement and phonon lifetime need further measurements, e.g., reference samples and calculations. In the range of observed reduced wavenumbers (qd) the total displacement of the S0 (fundamental dilatational) waves is dominated by the in-plane longitudinal component [48], therefore they are not visible in the BLS spectra.
Figure 3 shows the experimental dispersion curves in the form 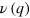 compared to the theoretical calculations for three exemplary values of
compared to the theoretical calculations for three exemplary values of 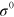 . As expected, the measured changes in ν progressively depend on the stress magnitude. The theoretical curves in figure 3 are calculated using the formalism presented in section 2 and appendix A without any free parameter. The elastic properties used can be found in table 1 and are taken from [46], while the stress magnitude
. As expected, the measured changes in ν progressively depend on the stress magnitude. The theoretical curves in figure 3 are calculated using the formalism presented in section 2 and appendix A without any free parameter. The elastic properties used can be found in table 1 and are taken from [46], while the stress magnitude 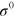 is estimated independently by Raman spectroscopy in the same samples [32]. Flexural waves are not detectable for small θ due to the presence of an elastic scattering peak (see figure 2), thus the smallest measurable values of
is estimated independently by Raman spectroscopy in the same samples [32]. Flexural waves are not detectable for small θ due to the presence of an elastic scattering peak (see figure 2), thus the smallest measurable values of 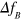 were about
were about 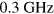 . The agreement between experimental data and theory also confirms the values of the stress tensor adopted in calculations and measured by Raman spectroscopy. Dispersion relations can also be presented in the
. The agreement between experimental data and theory also confirms the values of the stress tensor adopted in calculations and measured by Raman spectroscopy. Dispersion relations can also be presented in the  form (see insets in figure 3), which is more convenient as a starting point to study phonon group velocities, density of states, heat capacity and thermal conductivity [19, 49].
form (see insets in figure 3), which is more convenient as a starting point to study phonon group velocities, density of states, heat capacity and thermal conductivity [19, 49].
Figure 3. Comparison between experiment and theory of the A0 mode dispersion relations in the form of 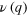 and
and 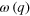 (inset) of the 27 nm thick Si membrane under the applied load (a)
(inset) of the 27 nm thick Si membrane under the applied load (a) 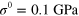 , (b)
, (b) 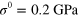 and (c)
and (c) 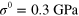 .
.
Download figure:
Standard image High-resolution imageTable 1.
Mass density ρ 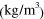 , second (SOE) and third (TOE) order elastic constants of Si at 298 K in units of
, second (SOE) and third (TOE) order elastic constants of Si at 298 K in units of 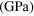 [46].
[46].
| ρ |
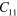
|
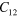
|
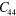
|
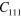
|

|
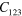
|
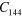
|
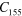
|
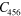
|
|---|---|---|---|---|---|---|---|---|---|
| 2329 | 165.64 | 63.94 | 79.51 |
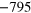
|
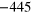
|
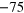
|
15 |
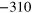
|
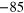
|
Based on the formalism presented in section 2 and appendix A we can investigate theoretically the changes of A0 modes propagation in terms of tensile or compressive stresses. In the appendix we show also dispersion relations for the families of A, S and SH waves propagating in the Si membrane subjected to the static positive or negative biaxial stress. Figure 4 presents dispersion curves in the form (a) 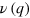 and (b)
and (b) 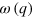 , which were calculated for a 27 nm thick membrane for the wavenumbers which coincide with the range reachable by angle-resolved BLS following (1). Here we can find remarkable changes of the A0 mode both for compressive and tensile stresses. For small values of q and
, which were calculated for a 27 nm thick membrane for the wavenumbers which coincide with the range reachable by angle-resolved BLS following (1). Here we can find remarkable changes of the A0 mode both for compressive and tensile stresses. For small values of q and 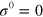 (black line in figure 4(a)) the phase velocity of the A0 mode is proportional to the wavenumber with
(black line in figure 4(a)) the phase velocity of the A0 mode is proportional to the wavenumber with 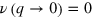 . From figure 4(a) we can find that both tensile and compressive stresses lead to the nonlinear behaviour of
. From figure 4(a) we can find that both tensile and compressive stresses lead to the nonlinear behaviour of 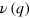 , which was also predicted recently for graphene [19, 20]. Considering the stress influence on dispersion curves in the form
, which was also predicted recently for graphene [19, 20]. Considering the stress influence on dispersion curves in the form 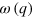 (see figure 4(b)) we can find that for small q values,
(see figure 4(b)) we can find that for small q values, 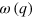 cannot be approximated by a quadratic function as for
cannot be approximated by a quadratic function as for  case. We can validate further the theory by calculating the limiting cases and recovering well-known physical effects as corollaries. In the tensile stress case we see that as q tends to 0, ν attains values different than 0. Solving (A.5) with
case. We can validate further the theory by calculating the limiting cases and recovering well-known physical effects as corollaries. In the tensile stress case we see that as q tends to 0, ν attains values different than 0. Solving (A.5) with 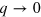 we find that for the A0 mode:
we find that for the A0 mode:

Figure 4. Calculated dispersion curves (a) 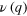 and (b)
and (b)  of the A0 mode propagating in a 27 nm thick membrane under exemplary values of stress
of the A0 mode propagating in a 27 nm thick membrane under exemplary values of stress 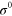 .
.
Download figure:
Standard image High-resolution imageThat is, ν depends only on the stress component parallel to 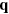 and on a single material parameter
and on a single material parameter 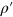 . It is interesting to note that (9) is also the solution of the well-known problem of a wave velocity in a stretched (guitar) string. Moreover, for the compressive loads we find ranges of forbidden wavenumbers q. For the range of wavenumbers between 0 and
. It is interesting to note that (9) is also the solution of the well-known problem of a wave velocity in a stretched (guitar) string. Moreover, for the compressive loads we find ranges of forbidden wavenumbers q. For the range of wavenumbers between 0 and 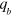 , velocities ν and frequencies ω of A0 modes were found to be imaginary values. This behaviour can be explained taking into account the stability of the membrane subjected to compressive forces. Therefore, for small negative values of
, velocities ν and frequencies ω of A0 modes were found to be imaginary values. This behaviour can be explained taking into account the stability of the membrane subjected to compressive forces. Therefore, for small negative values of  and
and 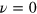 we find from (A.5) that:
we find from (A.5) that:

which is the Euler load equation [43, 50] describing the critical compressive load necessary to produce buckling of a plate, beam or membrane. On the other hand, for a given membrane with thickness d, (10) determines the width of the membrane (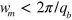 ) that does not undergo the buckling instability due to the compressive stress (see figure 1). At this point it is worth noticing, that BLS allows directional measurements of stress, since the value of (9) depends only on the stress component parallel to the wavevector. It offers the possibility of further measurements in the presence of a non-uniform biaxial stress, to obtain, e.g., stress mapping of the sample.
) that does not undergo the buckling instability due to the compressive stress (see figure 1). At this point it is worth noticing, that BLS allows directional measurements of stress, since the value of (9) depends only on the stress component parallel to the wavevector. It offers the possibility of further measurements in the presence of a non-uniform biaxial stress, to obtain, e.g., stress mapping of the sample.
5. Concluding remarks
Using BLS we measured the fundamental flexural mode of 27 nm thick membranes subjected to different homogeneous tensile biaxial stresses. We showed that dispersion relations of LW in ultra-thin silicon membranes can be tuned in a controlled manner by means of applied stress. The experimental results show a good agreement with theoretical calculations based on the elastic continuum approach without any free parameter. The experimentally proved stress tuning of flexural phonons dispersion relations opens the door to thermal management and energy conversion in low dimensional structures. It is expected that this effect of tuning the dispersion relation translates into changes in the thermal properties when the wavelength of the phonons involved in the heat transport is commensurate to the thickness of the membrane [15, 16, 49] or at low temperatures [23]. In addition, we showed how Brillouin spectroscopy provides a contactless and nondestructive tool for the stress measurements in the nm-scale systems. Our findings are essential for micro- and nano-electromechanical (MEMS and NEMS) systems development and have deep implications in engineering of the thermal conductivity.
Acknowledgments
The authors acknowledge financial support from the FP7 project MERGING (grant no. 309150); the Spanish MICINN projects nanoTHERM (grant no. CSD2010-0044) and TAPHOR (MAT2012-31392). JGB gratefully acknowledges support from the Spanish government through a Juan de la Cierva fellowship. MP and AS acknowledge funding from the Academy of Finland (grant no. 252598).
: Appendix
A detailed derivation of (3) and (6) can be found in [44]. The general solution procedure assumes that (6) is solved for 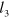 with ν as a parameter. All of n = 6 possible solutions
with ν as a parameter. All of n = 6 possible solutions 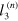 satisfy the wave equation (5), therefore, in the general case the displacement
satisfy the wave equation (5), therefore, in the general case the displacement 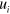 is given by the superposition:
is given by the superposition:
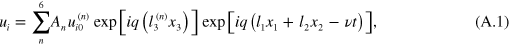
where 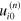 are normalized components of an amplitude which are eigenvectors corresponding to
are normalized components of an amplitude which are eigenvectors corresponding to  and the eigenvalue
and the eigenvalue 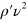 . Six weighting factors
. Six weighting factors 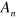 should satisfy the boundary conditions given by (7), which can be rewritten as a set of six homogeneous equations:
should satisfy the boundary conditions given by (7), which can be rewritten as a set of six homogeneous equations:
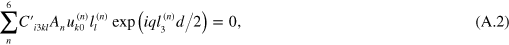
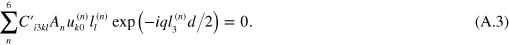
This homogeneous set of six linear equations can be rewritten in matrix form as a multiplication of the 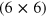
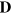 matrix of the coefficients by the
matrix of the coefficients by the 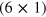 column vector
column vector 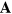 of the weighting factors:
of the weighting factors:

where 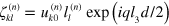 and
and 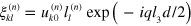 . The nontrivial solutions for
. The nontrivial solutions for  exist if the determinant of the
exist if the determinant of the 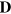 matrix equals zero:
matrix equals zero:

In the general case the adopted iterative search procedure sweeps ν and qd as the parameters looking for the phase velocities of LW for the given qd, corresponding to the minima of the boundary condition determinant. Moreover, these solutions can be classified in terms of the polarization or symmetry by means of the evaluated weighting factors 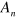 and (A.1). All calculations were performed for Si membranes oriented as shown schematically in figure 1 (b). Figure A1
presents the dispersion curves with exemplary values of both tensile and compressive biaxial load for A, S and SH modes, respectively, with
and (A.1). All calculations were performed for Si membranes oriented as shown schematically in figure 1 (b). Figure A1
presents the dispersion curves with exemplary values of both tensile and compressive biaxial load for A, S and SH modes, respectively, with ![${\bf q}\parallel \left[ {\bf 110} \right]$](https://content.cld.iop.org/journals/1367-2630/16/7/073024/revision1/njp496945ieqn147.gif) . From figure A1 we can find that the magnitude or even the sign of the applied load does not lead to simple and unambiguous changes in the dispersion relations. In general, the change of phase velocity depends on the direction of propagation with respect to applied load, qd, type of wave/polarization and order of a given mode.
. From figure A1 we can find that the magnitude or even the sign of the applied load does not lead to simple and unambiguous changes in the dispersion relations. In general, the change of phase velocity depends on the direction of propagation with respect to applied load, qd, type of wave/polarization and order of a given mode.
Figure A1. Dispersion curves 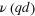 of the flexural (A), dilatational (S) and shear horizontal (SH) modes calculated for three values of
of the flexural (A), dilatational (S) and shear horizontal (SH) modes calculated for three values of 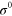 .
.
Download figure:
Standard image High-resolution image






